|
|
|
| A denoising method for microseismic signal based on the ensemble empirical mode decomposition of sample entropy threshold |
| Ya-Juan WANG1,2, Huai-Liang LI1,2,4, Xian-Guo TUO1,2,3,4, Tong SHEN1,2,3,4 |
1. National Institute of Defense Technology,Southwest University of Science and Technology,Mianyang 621010,China
2. Fundamental Science on Nuclear Wastes and Environmental Safety Laboratory,Southwest University of Science and Technology,Mianyang 621010,China
3. Sichuan University of Science & Engineering,Zigong 643002,China;
4. State Key Laboratory of Geohazard Prevention and Geoenvironment Protection,Chengdu University of Technology,Chengdu 610059,China |
|
|
|
|
Abstract It is inevitable to mix up non-stationary random noise in the process of microseismic signal acquisition.However,the practice shows that the traditional linear filtering and spectrum analysis methods are not idealistic for this mixed signal.In view of such a situation,this paper presents a new method to suppress nonstationary random noise.Firstly,the Ensemble Empirical Mode Decomposition (EEMD) is carried out for noise-containing microseismic signals,and a series of Intrinsic Mode Functions (IMF) with different frequencies components are obtained.In order to accurately identify the signal and noise in these IMF components,the authors calculated the sample entropy of each IMF in this paper.The threshold value of sample entropy was used to extract the IMF components conformable to the characteristics of microseismic signal,and these IMF components are reconstructed in order to suppress random noise.The proposed method has been applied to simulated data and measured microseismic data,and it is indicated that the method has ideal effect for noise reduction.
|
|
Received: 08 April 2019
Published: 25 October 2019
|
|
|
|
Corresponding Authors:
Huai-Liang LI
|
|
|
|

|
The EEMD decomposition result of microseismic signals containing high-noise (The signal to noise ratio is -5 db, the frequency of microseismic signal is 120 Hz, and the sampling interval is 6 KHz)
|
|
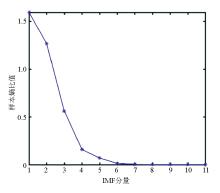
The sample entropy of IMF
|
|
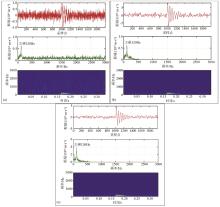
Comparision of time-frequency analysis beween the above synthesized microseismic data and reconstructed data
a—the synthesized microseismic data;b—the reconstructed signal;c—the result of ban-dpass filter
|

低信噪比信号
(信噪/dB) | 信噪比/dB | 均方根误差 | | 带通滤波 | 小波多尺度分析 | 文中方法 | 带通滤波 | 小波多尺度分析 | 文中方法 | | -6 | -0.6685 | 3.4813 | 4.2578 | 1.2541×10-6 | 8.4185×10-7 | 7.4916×10-7 | | -7 | -0.7374 | 2.4833 | 3.2462 | 1.3264×10-6 | 9.4437×10-7 | 8.4995×10-7 | | -8 | -0.8780 | 1.4848 | 2.2462 | 1.3323×10-6 | 1.0594×10-6 | 9.4804×10-7 | | -9 | -0.8968 | 0.4861 | 1.2818 | 1.3358×10-6 | 1.8850×10-6 | 1.0692×10-6 | | -10 | -1.2649 | -0.5130 | 0.3064 | 1.3999×10-6 | 1.3334×10-6 | 1.1989×10-6 |
|
Signal to noise ratio and root-mean-square error after micro seismic signal synthesized under different signal to noise ratio
|
|
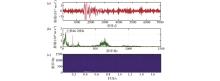
The spectrum analysis and time-frequency analysis of actual microseismic datasets
a—the synthesized microseismic data;b—the reconstructed signal;c—the result of ban-dpass filter
|

|
Comparison of denoising effect of actual microseismic data
a—the result of the method in this paper;b—the result of wavelet multi scale analysis;c—the result of ban-dpass filter;d—the result of low-dpass filter
|
| [1] |
芮拥军 . 地面微地震水力压裂监测可行性分析[J]. 物探与化探, 2015,39(2):341-345.
|
| [1] |
Rui Y J . Feasibility analysis of surface micro-seismic hydraulic fracturing monitoring[J]. Geophysical and Geochemical Exploration, 2015,39(2):341-345.
|
| [2] |
张永华, 陈祥, 杨道庆 , 等. 微地震监测技术在水平井压裂中的应用[J]. 物探与化探, 2013,37(6):1080-1084.
|
| [2] |
Zhang Y H, Chen X, Yang D Q , et al. The application of micro-seismic monitoring technology to the study of horizontal well fracturing[J]. Geophysical and Geochemical Exploration, 2013,37(6):1080-1084.
|
| [3] |
何柯, 周丽萍, 于宝利 , 等. 基于补偿阈值的曲波变换地面微地震弱信号检测方法[J]. 物探与化探, 2016,40(1):55-60.
|
| [3] |
He K, Zhou L P, Yu B L , et al. The ground microseismic weak signal detection method based on compensation threshold of curvelet transform[J]. Geophysical and Geochemical Exploration, 2016,40(1):55-60.
|
| [4] |
Beenamol M, Prabavathy S, Mohanalin J. Wavelet based seismic signal de-noising using Shannon and Tsallis entropy[M].Pergamon Press Inc.., 2012: 3580-3593.
|
| [5] |
Said G . The use of wavelet-based denoising techniques to enhance the first-arrival picking on seismic traces[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014,52(8):4558-4563.
|
| [6] |
李月, 彭蛟龙, 马海涛 , 等. 过渡内蕴模态函数对经验模态分解去噪结果的影响研究及改进算法[J]. 地球物理学报, 2013,56(2):626-634.
|
| [6] |
Li Y, Peng J L, Ma H T , et al. Study of the influence of transition IMF on EMD de-noising and the improved algorithm[J]. Chinese. J. Geophys., 2013,56(2):626-634.
|
| [7] |
陈凯 . 基于经验模式分解的去噪方法[J]. 石油地球物理勘探, 2009,44(5):603-608.
|
| [7] |
Chen K . A new denoising method based on Empirical Mode Decomposition (EMD)[J]. OGP, 2009,44(5):603-608.
|
| [8] |
Huang N E, Shen Z, Long S R , et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings A, 1998,454(1971):903-995.
|
| [9] |
Li Y, Xu M, Wei Y , et al. An improvement EMD method based on the optimized rational Hermite interpolation approach and its application to gear fault diagnosis[J]. Measurement, 2015,63:330-345.
|
| [10] |
Linderhed A . Image empirical mode decomposition:a new tool for image processing[J]. Advances in Adaptive Data Analysis, 2014,1(2):265-294.
|
| [11] |
Wang T, Zhang M C., Yu Q.H .,et al.Comparing the applications of EMD and EEMD on time-frequency analysis of seismic signal[J]. Journal of Applied Geophysics, 2012,83:29-34.
|
| [12] |
Wu Z, Huang N E . A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of the Royal Society A: Mathematical,Physical and Engineering Sciences, 2004,460(2046):1597-1611.
|
| [13] |
Wu Z . Ensemble empirical mode decomposition: a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009,1(1):1-41.
|
| [14] |
Flandrin P, Rilling G, Goncalves P . Empirical Mode Decomposition as a Filter Bank[J]. IEEE Signal Processing Letters, 2004,11(2):112-114.
|
| [15] |
Richman J S, Randall M J . Physiological time-series analysis, using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000,278(6):H2039-H2049.
|
| [16] |
李余兴, 李亚安, 陈晓 , 等. 一种基于样本熵与EEMD的舰船辐射噪声特征提取方法[J]. 水下无人技术学报, 2018,26(1):28-34.
|
| [16] |
Li Y X, Li Y A, Chen X , et al. A feature extraction method of ship-radiated noise based on sample entropy and ensemble empirical mode decomposition[J]. Journal of Unmanned Undersea Systems, 2018,26(1):28-34.
|
| [17] |
宋晓霞, 向北平, 倪磊 , 等. 基于样本熵的改进空域相关去噪算法[J]. 机械设计与研究, 2018,34(4):31-36.
|
| [17] |
Song X X, Xiang B P, Ni L , et al. Research of improved spatial correlation denoising algorithm based on sample entropy[J]. Machine Design and Research, 2018,34(4):31-36.
|
| [18] |
尚传福 . 基于多尺度样本熵的时间序列复杂度研究[J]. 现代电子技术, 2017,40(17):40-43.
|
| [18] |
Shang C F . Time series complexity research based on multiscale sample entropy[J]. Modern Electronics Technique, 2017,40(17):40-43.
|
| [1] |
CHEN Liang, FU Li-Heng, CAI Dong, LI Fan, LI Zhen-Yu, LU Kai. Suppression method of multi-source harmonic noise in magnetic resonance sounding based on simulated annealing method[J]. Geophysical and Geochemical Exploration, 2022, 46(1): 141-149. |
| [2] |
YANG Dan, LI Wei, WEI Yong-Liang, SONG Bin. Application of dual-tree complex wavelet transform in advanced geological prediction of the tunnel section in Lalin of Sichuan-Tibet Railway[J]. Geophysical and Geochemical Exploration, 2021, 45(6): 1504-1511. |
|
|
|
|
