大深度激电法中电磁耦合效应分析与去除方法

doi:10.11720/wtyht.2025.1499

大深度激电法中电磁耦合效应分析与去除方法

冀振兴^,¹, 秦浩杰²^,³, 陈儒军^,²^,³^,⁴^,⁵, 王权功¹

1.江苏省地质局, 江苏南京 210018

2.中南大学地球科学与信息物理学院, 湖南长沙 410083

3.中南大学 AIoT(人工智能物联网)与地质地球物理创新创业教育中心, 湖南长沙 410083

4.有色资源与地质灾害探查湖南省重点实验室, 湖南长沙 410083

5.中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 湖南长沙 410083

Analysis and removal of electromagnetic coupling effects in the large-depth induced polarization method

JI Zhen-Xing^,¹, QIN Hao-Jie²^,³, CHEN Ru-Jun^,²^,³^,⁴^,⁵, WANG Quan-Gong¹

1. Jiangsu Geological Bureau, Nanjing 210018, China

2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China

3. AIoT Innovation and Entrepreneurship Education Center for Geology and Geophysics, Central South University, Changsha 410083, China

4. Hunan Key Laboratory of Non-ferrous Resources and Geological Hazard Exploration, Changsha 410083, China

5. Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Ministry of Education, Central South University, Changsha 410083, China

通讯作者: 陈儒军(1973-),副教授,博士,主要从事地球物理电法勘探仪器与信号处理工作。Email:chrujun12358@gmail.com

第一作者: 冀振兴(1983-),高级工程师,硕士研究生,主要从事物化遥和测绘相关技术工作。Email:187277894@qq.com

收稿日期: 2024-12-26 修回日期: 2025-03-25

基金资助:

国家自然科学基金基础科学中心项目(72088101)

Received: 2024-12-26 Revised: 2025-03-25

摘要

随着浅层矿产资源的逐渐枯竭,深部矿产勘探成为矿业发展的必然趋势,增大勘探深度最直接、最有效的方法是增加激电装置的供电极距。然而,长供电极距会引发强烈的电磁耦合效应,从而对激电信号造成严重干扰。针对这一问题,本文基于解析方法计算了不同测量装置在均匀半空间和层状介质中的电磁耦合效应,通过对比,分析了测量装置类型、布线方式、供电极距、大地电阻率及频率等因素对电磁耦合强度的影响。最后,根据激电效应和电磁耦合效应在频率域内相位的差异,推导了相对相位谱的计算公式,并针对不同的应用场景对其去耦效果进行理论分析。研究结果表明,供电极距的增大、大地电阻率的降低以及工作频率的升高均会显著增强电磁耦合的干扰强度。在相同条件及探测深度下,四极装置受到的电磁耦合干扰通常高于三极装置。相较于传统的激电相位谱,相对相位谱的引入使三极装置和四极装置的最大工作频率分别提高了4倍和10.6倍,表明相对相位法在大深度激电法勘探中具有一定的去耦效果。本研究对大深度激电勘探的现场施工具有重要的指导意义。

关键词： 大深度激电法; 去耦; 相对相位法; 电极

Abstract

With the gradual depletion of shallow mineral resources, deep mineral exploration has emerged as an essential development trend in the mining industry. Increasing the distance between receiver electrodes of induced polarization (IP) devices is the most direct and effective approach to enhance the exploration depth. However, a long distance can cause strong electromagnetic (EM) coupling effects, severely interfering with IP signals. Addressing this challenge, this study calculated the EM coupling effects of various measuring devices in homogeneous half-space and layered media using analytical methods. Furthermore, this study comparatively analyzed the impacts of various factors, including measuring device type, wiring layout, distance between receiver electrodes, earth resistivity, and frequency, on the EM coupling intensity. Based on the phase differences between IP and EM coupling effects in the frequency domain, this study derived the calculation equation of the relative phase spectrum, followed by a theoretical analysis of the decoupling effects in application scenarios. The results indicate that increasing distance between receiver electrodes, decreasing earth resistivity, and raising working frequency all significantly intensified the EM coupling interference. Under consistent conditions and detection depths, the Schlumberger array suffered from higher EM coupling interference compared to the pole-dipole array. Compared to the traditional IP phase spectrum, the relative phase spectrum enhanced the maximal working frequency of the pole-dipole and Schlumberger arrays by four and 10.6 times, respectively, suggesting the decoupling capability of the relative phase method in large-depth IP exploration. Overall, this study provides significant guidance for the field implementation of large-depth IP exploration.

Keywords： large-depth induced polarization (IP) method; decoupling; relative phase method; electrode

PDF (5982KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

冀振兴, 秦浩杰, 陈儒军, 王权功. 大深度激电法中电磁耦合效应分析与去除方法[J]. 物探与化探, 2025, 49(6): 1393-1401 doi:10.11720/wtyht.2025.1499

JI Zhen-Xing, QIN Hao-Jie, CHEN Ru-Jun, WANG Quan-Gong. Analysis and removal of electromagnetic coupling effects in the large-depth induced polarization method[J]. Geophysical and Geochemical Exploration, 2025, 49(6): 1393-1401 doi:10.11720/wtyht.2025.1499

0 引言

丰富的矿产资源是现代工业和经济快速发展的重要前提,随着浅层矿产资源的逐渐减少,对深部金属矿勘探提出了更高的要求^[1-3]。激电法作为一种多功能的地球物理勘探方法,在了解地质结构、寻找地下水和金属矿勘探中有着非常广泛的应用^[4-7]。然而,该方法在进行频散率和相位测量时容易受到电磁耦合的影响,特别是在大深度或低阻勘探过程中,电磁耦合效应更加强烈,从而对激电信号造成严重干扰^[8-9]。

上述问题可以从硬件采集端和数据处理两个方面来解决。前者可通过增大发射电流提高数据采集信噪比,再经选频接收、相干检测等手段增强接收机抗干扰能力^[10-13]。后者主要是利用去耦方法对测量信号进行后处理,从而消除电磁耦合效应的影响,前人已经在这方面做了大量的工作,可总结分为3大类:

第一类是假设频率域激电效应的振幅随频率对数近似线性增加,而电磁耦合的振幅则随频率呈指数增加,从而可以通过两频校正方法去除电磁耦合效应^[14-16]。例如,郭鹏等^[17-18]研究了中梯装置中电磁耦合效应的影响因素和频率特征,并利用两频校正方法消除了电磁耦合的影响。第二类是假设低频段激电效应的相位随频率变化不大,而电磁耦合引起的相位则随频率线性增大,从而可利用相对相位法进行线性校正。例如,陈儒军等^[19]基于这一特性推导了相对相位谱的计算公式,并通过实验证明相对相位谱测量不仅能有效抑制电磁耦合感应,还能消除由于发送机与接收机之间同步误差造成的影响。李栋等^[20]研究了偶极装置中的电磁耦合响应,并将相对相位法应用于实测激电资料的处理中,进一步验证了该去耦方法的有效性。第三类是根据电磁耦合效应和激电效应在时间域的差异进行斩波去耦。例如,向毕文等^[21]利用指数函数在时间域内对激电效应进行拟合,从而在保留激电信号的同时去除了电磁耦合效应,取得了良好的效果。

上述研究成果对激电信号的高质量提取有着重要的意义,但他们的研究对象均为浅层矿体,没有考虑在深部勘探中电磁耦合对激电信号的影响。在大深度勘探中,由于供电极距的增加导致电磁耦合强度增大,测量信号也会变得更加复杂,上述方法假设的有效性需要进一步的验证。为此,本文基于Thomas等^[22]发布的CR1Dmod开源程序对大深度激电中的电磁耦合效应进行研究,分析装置类型、布线方式、大地电阻率阻值和频率等因素对电磁耦合强度的影响。同时从相对相位谱的计算原理出发,分析其在处理大深度激电数据的适用性,并定量考察其在三极装置和四极装置中的去耦效果,得到的结论对大深度激电找矿的现场施工有一定的指导意义。

大深度激电法中的电磁耦合是利用激电法进行矿产勘探时,供电线路与测量线路之间的电性感应,主要包括电容耦合和电磁耦合。电容耦合是指供电线路与测量导线以及大地之间因存在分布电容而导致的假激电异常,Madden等^[23]通过研究证明,只要供电导线和测量导线之间的距离足够大,电容耦合的影响就可以忽略不计。因此,本文仅考虑外在因素对电磁耦合强度的影响。

1 电磁耦合计算原理

电磁耦合指的是发射导线和接收导线间随频率变化的互感应阻抗。Sunde^[24]在1968年指出地表任意两条接地导线之间的电磁耦合响应可以通过对ds和dS这两个偶极子的互阻抗沿各自的导线分别进行积分得到,并给出了其理论解,如式(1)所示:

(1)$Z={\int }_{A}^{B}{\int }_{M}^{N}\left[P\left(r\right)cos\theta +\frac{{\partial }^{2}Q\left(r\right)}{\partial s\partial S}\right]dsdS,$

式中:ds和dS分别是测量导线MN和供电导线AB上面的线元;r为两个线元之间的距离;θ是两个线元之间的夹角。为了简单起见,本文仅考虑供电线路和测量线路之间共线或平行的情况,即θ=0。

式(1)中的P(r)只与供电导线、测量导线和大地相互间的电磁耦合效应有关,因此称为感应函数,Q(r)只与供电电极和测量电极的相互位置有关,因此称为接地函数。Dey等^[25]在1973年进一步给出了P(r)和Q(r)的表达式:

(2)$\begin{array}{l}P\left(r\right)=\frac{j\omega {\mu }_{0}}{4\pi }{\int }_{0}^{\infty }\frac{\lambda }{{u}_{0}}\left[1\right.+{R}_{TE}\left(\lambda \right)\left]{J}_{0}\right(\lambda r)d\lambda,\\ Q\left(r\right)=-\frac{j\omega {\mu }_{0}}{4\pi {k}_{0}^{2}}{\int }_{0}^{\infty }\left\{\frac{\lambda }{{u}_{0}}\left[1\right.+{R}_{TE}\left(\lambda \right)]-\frac{\lambda }{{u}_{0}}\right.·\\ \left.\frac{　}{　}\left[{R}_{TM}\right(\lambda)+{R}_{TE}(\lambda \left)\right]\right\}{J}_{0}\left(\lambda r\right)d\lambda \end{array}$

式中:u₀=$\sqrt{{\lambda }^{2}-{k}_{0}^{2}}$,k₀是空气中的传播常数,其表达式为k₀=$\sqrt{{\mu }_{0}\epsilon {\omega }^{2}-j\omega {\mu }_{0}/{\rho }_{0}}$;μ₀、ε和ρ₀分别是空气中的磁导率、介电常数和电阻率;R_TE(λ)和R_TM(λ)分别是空气—大地分界面处的横向的电反射系数和磁反射系数。

在均匀半空间中,P(r)和Q(r)的表达式可以通过推导进一步简化为式(3)的形式^[26]:

(3)$\begin{array}{l}P\left(r\right)=\frac{{\rho }_{0}}{2\pi }\frac{1-(1+j{k}_{0}r){e}^{-j{k}_{0}r}}{{r}^{3}},\\ Q\left(r\right)=\frac{{\rho }_{0}}{2\pi r}\end{array}$

接地相Q(r)只与电极位置有关,其表达式可以表示为:

(4)$\begin{array}{l}{\int }_{A}^{B}{\int }_{M}^{N}\frac{{\partial }^{2}Q\left(r\right)}{\partial s\partial S}dsdS=Q\left(\right|AM\left|\right)-Q\left(\right|AN\left|\right)-\\ Q\left(\right|BM\left|\right)+Q\left(\right|BN\left|\right)\end{array}$。

因此在均匀半空间地层中,供电线路和测量线路之间总阻抗的表达式为:

(5)$\begin{array}{l}Z=K·({Z}_{EM}+{Z}_{IP}),\\ {Z}_{EM}={\int }_{A}^{B}{\int }_{M}^{N}\frac{{\rho }_{0}}{2\pi }\frac{1-(1+j{k}_{0}r){e}^{-j{k}_{0}r}}{{r}^{3}}dsdS,\\ {Z}_{IP}=\frac{{\rho }_{0}}{2\pi }\left(\frac{1}{\left|AM\right|}-\frac{1}{\left|AN\right|}-\frac{1}{\left|BM\right|}+\frac{1}{\left|BN\right|}\right)\end{array}$

式中:K为装置系数,只与电极位置有关。对于层状介质中的电磁耦合,本文利用发布的CR1Dmod开源程序进行计算,其正确性已经在多篇文献中得到了验证^[27-29]。

常规的激电法勘探中常用测量阻抗的相位来表示测量信号,其计算方法如式(6)所示:

(6)$\varphi =arctan\left[\frac{Im\left(Z\right)}{Re\left(Z\right)}\right]={\varphi }_{IP}+{\varphi }_{EM}$

式中:Re和Im分别代表取阻抗的实部和虚部;ϕ为相位,主要有激电信号ϕ_IP和电磁耦合信号ϕ_EM两部分组成。

2 影响电磁耦合强度的因素分析

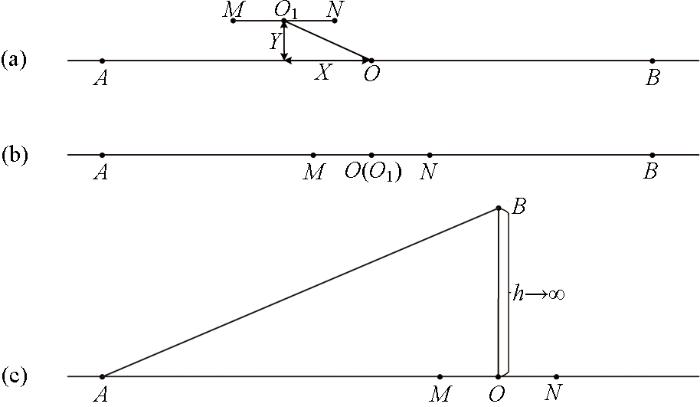
激电法勘探中常用的3种装置类型如图1所示,其中图1为旁侧中梯装置,O和O₁分别为供电导线AB和测量导线MN的中点,X和Y分别为水平方向和垂直方向上的旁侧距离;图1b为斯伦贝谢装置,它是旁侧中梯装置中X和Y同时为0的一种特殊情况。由于图1、b中均为4个电极同时供电,因此前两者被称为四极装置。而在图1c中,供电电极B被放置在测量电极MN中垂线上无穷远的位置,对测量信号有影响的只有A、M和N 3个电极,被称为三极装置。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 常用电极装置结构

Fig.1 Schematic of the electrode arrays in common use

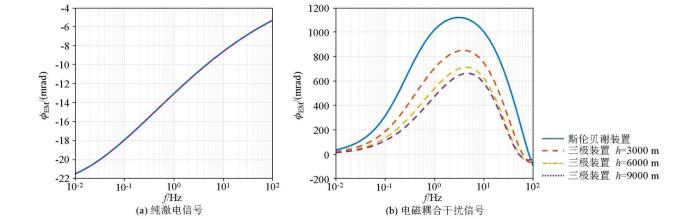
为对比不同装置在大深度激电法中的探测性能,分别计算了斯伦贝谢装置(AB=6 000 m)和三极装置(AO=3 000 m)在两层介质模型中的激电信号和电磁耦合信号。该两层介质模型中的第一层电阻率为100 Ω·m,厚度为1 000 m,第二层电阻率为10 Ω·m,厚度为无限厚。考虑到实际测量时,三极装置的供电电极B无法真正放到无穷远的位置,其距测量点的长度h(图1c)可能会对测量结果造成影响,因此还对比了三极装置在不同h下的测量信号,具体如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 不同电极装置中激电相位和电磁耦合相位

Fig.2 The phase of IP and EM coupling in different electrode arrays

图2展示的是不同装置参数下的纯激电相位谱,可以看到当频率极低或极高时相位较小,在中间的某个频段取得极大值,这是由不同频率下的探测深度差异引起的。当频率极低时,探测深度较大,测量信号只受第二层电阻率的影响(近似为均匀半空间),因此相位几乎为0。同样,当频率极高时,测量信号只受第一层电阻率的影响,相位值也相对较低。此外,图2中4条激电信号曲线完全重合,说明四极装置和三极装置的探测深度都只与AO的长度有关,从而验证了它们理论探测深度的统一性(即三极装置的探测深度d₁≈AO/3,对称四级的装置的探测深度d₂≈AB/6=AO/3)。从图2b中可以看出不同装置参数下的电磁耦合大小是不同的,四极装置受电磁耦合干扰程度明显大于三极装置,且三极装置中h越大,电磁耦合效应越小。因此在实际测量时,三极装置中的B电极应放置在尽可能远的位置。

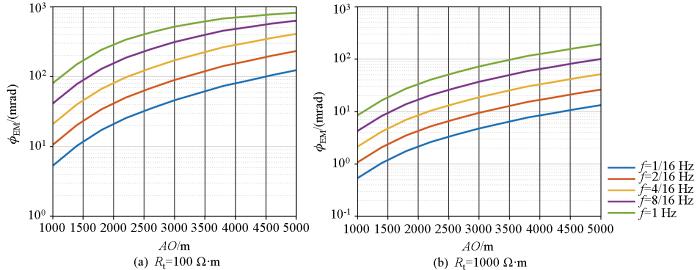
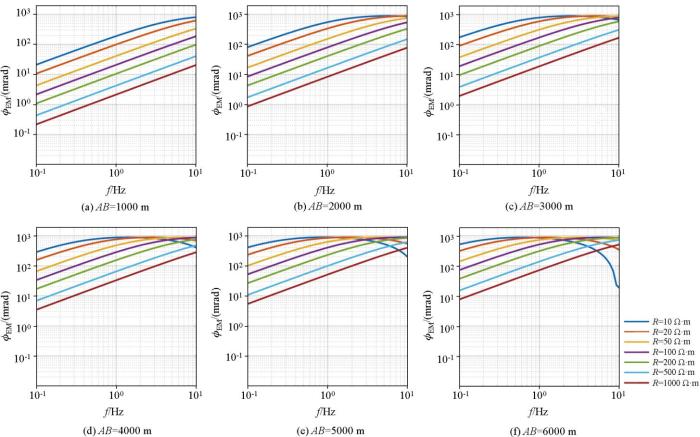
为进一步测试电磁耦合效应随供电极距和频率的变化规律,计算了不同供电极距下的三极装置在均匀半空间中电磁耦合效应。由于在三极装置中,BO>5AO时即可认为电极B在无穷远的位置^[29],因此在下述实验中,BO长度均被设置为15 000 m。激电法在大深度测量时,工作频率通常小于1 Hz,因此共设置了1/16 Hz、2/16 Hz、4/16 Hz、8/16 Hz和1 Hz 5个频点,具体计算结果如图3所示。其中图3是电阻率为100 Ω·m时的计算结果,图3b是电阻率为1 000 Ω·m时的计算结果。通过图3和3b对比发现,无论在低阻地层中还是在高阻地层中,电磁耦合效应随供电极距和频率的变化规律是完全一致的,即电磁耦合效应总是随着供电极距的增加而增大,随着频率的增高而变强。此外能发现在同样的供电极距和频率下,高阻层中的电磁耦合强度总是比低阻层更弱,说明电磁耦合效应随大地电阻率的升高而降低。同时也在斯伦贝谢装置中进行了同样的实验,得到的结论与三极装置中完全一致,此处不再赘述。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 三极装置中电磁耦合效应随供电极距的变化规律

Fig.3 The variation of the EM coupling with the spacing of the current-electrodes in the pole-dipole array

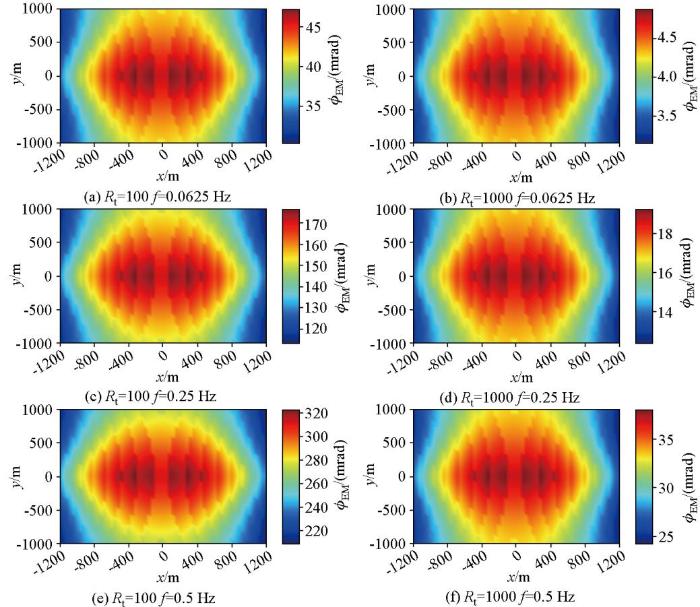
在图1所示的旁侧中梯装置中,常通过改变旁侧距离来调整测量点位置和探测深度,因此有必要研究旁侧距离大小对电磁耦合效应的影响。图4展示了在不同大地电阻率和频率下,电磁耦合强度随旁侧距离的变化规律。其中,x和y的负值分别代表测量导线MN中点O₁在供电导线中点O的左侧和下方,反之则代表O₁在O的右侧和上方。从图中可以看出,在不同电阻率和频率下,电磁耦合强度的数值差别很大,但每一幅子图中电磁耦合强度随旁侧距离的变化规律完全一致,即旁侧距离越大,电磁耦合效应越小。此外,每幅子图均呈现中心对称性,这说明电磁耦合强度只与旁侧距离的大小有关,而与O及O₁之间的相对位置无关。不同子图中电磁耦合强度的差异再次验证了上述实验结论,即频率越高,大地电阻率越小,电磁耦合强度越大。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 中梯装置中旁侧距离对电磁耦合强度的影响

Fig.4 Impact of side distance on EM coupling in intermediate gradient array

3 　相对相位谱在不同测量装置中的去耦效果分析

常规的激电相位谱作为激电法的测量信号,在大深度勘探时极易受到电磁耦合效应的影响。前人已经验证了相对相位谱在常规深度勘探中的良好去耦效果,本章将进一步从计算原理出发,分析其适用场景,并定量考察其在大深度激电勘探中的应用效果。

3.1 相对相位谱计算原理

相对相位谱的计算如式(7)所示:

(7)${\varphi }_{r}\left(f\right)=\frac{k·\varphi \left(f\right)-\varphi (k·f)}{k-1}$

式中:ϕ_r(f)和ϕ(f)分别是频率为f时的相位和相对相位;k为相对相位法中的频比,一般来说,k越大,激电相位谱和相对相位谱的差异越小^[19]。

相位谱由激电信号和电磁耦合效应两部分组成,二者的频率特性有很大差异,在一定频率范围内近似满足式(8):

(8)$\begin{array}{l}\varphi ={\varphi }_{EM}+{\varphi }_{IP},\\ {\varphi }_{EM}(k·f)\approx k·{\varphi }_{EM}\left(f\right),\\ {\varphi }_{IP}(k·f)\approx {\varphi }_{IP}\left(f\right)\end{array}$。

将式(8)代入式(7)可将相对相位谱的计算公式进一步推导为式(9),可以发现最终得到的相对相位ϕ_r与激电相位ϕ_IP近似相等,从而消除了电磁耦合效应ϕ_EM的影响。

(9)$\begin{array}{l}{\varphi }_{r}\left(f\right)=\\ \frac{k·{\varphi }_{EM}\left(f\right)+k·{\varphi }_{IP}\left(f\right)-{\varphi }_{EM}(k·f)-{\varphi }_{IP}(k·f)}{k-1}\approx \\ \frac{(k-1){\varphi }_{IP}\left(f\right)}{k-1}={\varphi }_{IP}\left(f\right)\end{array}$。

从上述公式的推导可以发现,相对相位法的去耦效果主要取决于式(8)中“≈”两侧数值之间的差异。当两侧数值完全相等时,电磁耦合的影响能够完全消除;反之,二者之间的差异越大,相对相位谱计算过程中引入的误差也越大,从而影响去耦效果。为了定性的分析相对相位法的应用场景,计算了斯伦贝谢装置在不同电阻率下的频率特性,结果如图5所示。可以看到图5中由于供电极距较小,几乎所有曲线都呈现良好的线性关系,说明相对相位谱在常规勘探深度中具有良好的去耦效果。然而,随着供电极距(勘探深度)的增大,低阻和高频段的曲线形态不再满足式(8)所述的线性关系,且供电极距越大,电磁耦合效应与频率之间的线性关系越差,表明相对相位谱在长极距、高频和低阻条件下的去耦效果较差。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 斯伦贝谢装置中电磁耦合响应频率特性

Fig.5 The frequency response characteristics of EM coupling in Schlumberger array

3.2 相对相位法在不同装置类型中的去耦效果

在长极距、低阻和高频情况下,相对相位法难以完全去除电磁耦合效应,此时式(8)中的ϕ_r≈ϕ_IP不再成立,而是也包含了一部分电磁耦合干扰,即ϕ_r=ϕ_IP+ϕ_EM。因此,可以通过计算不同装置类型、频率和大地电阻率下的ϕ_EM分量,从而定量分析相对相位法在大深度(主要针对1 000 m的勘探深度)激电法中的应用效果。

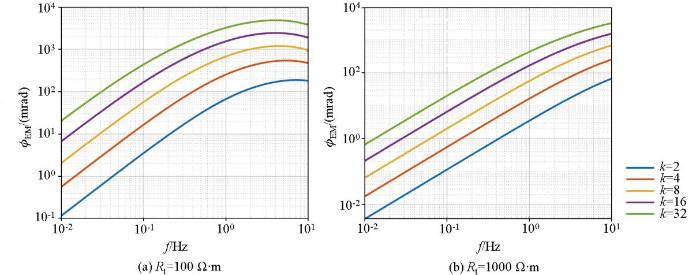
首先基于斯伦贝谢装置(AB=6 000 m)考察了相对相位法中频比对去耦效果的影响。大地电阻率和频比不同时,电磁耦合ϕ_EM大小随频率的变化规律如图6所示,其中图6是电阻率为100 Ω·m时的计算结果,图6b是电阻率为1 000 Ω·m时的计算结果。可以发现,在相同频率条件下,无论是在低阻层还是高阻层中,电磁耦合效应均随着频比的增大而增强,当频比设置为2时有着最佳去耦效果。然而,即使如此,随着频率的升高或电阻率的降低,由于电磁干扰强度的增加,相对相位中的电磁耦合分量也迅速增大。这说明,利用相对相位法只能去除一部分电磁耦合干扰。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 相对相位法中频比对去耦效果的影响

Fig.6 The impact of frequency ratio on decoupling effect in the relative phase method

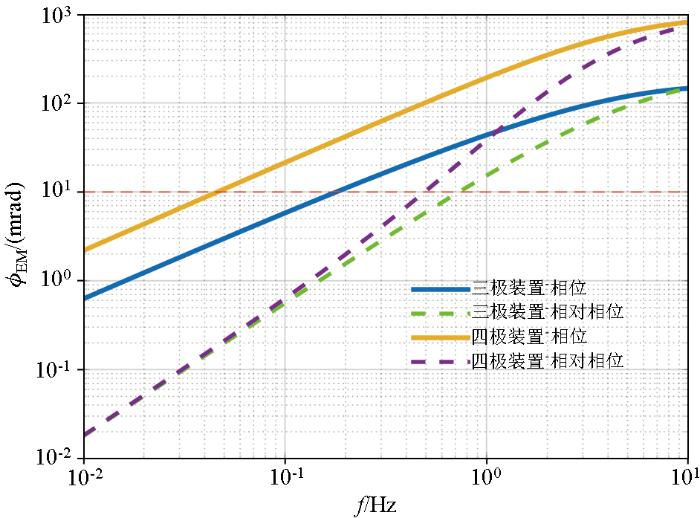
为分析相对相位法在不同测量装置中的去耦效果,首先基于均匀半空间(R_t=350 Ω·m)地层计算了三极装置(AO=3 000 m)和四极装置(AB=6 000 m)常规激电相位谱中的电磁耦合分量,如图7中的两条实线所示。然后将频比设置为2,计算相对相位谱中的电磁耦合分量,如图7中的两条虚线所示。对同一测量装置而言,在低频段激电相位谱中的电磁耦合效应总是强于相对相位谱,说明相对相位法能够去除一部分耦合干扰。然而,随着频率的增高,激电相位谱和相对相位谱之间的差异逐渐减小,说明相对相位法的去耦效果随着频率的升高而变差,尤其是当频率增加到10 Hz时,相位和相对相位几乎相等,说明此时由于式(8)中“≈”两侧数值之间的差异过大,导致相对相位法不再具有去耦能力。此外,在同一频率下,三极装置测量的激电相位或相对相位中的电磁耦合分量均小于四极装置,再次验证了在相同的勘探深度下,三极装置受电磁耦合干扰程度更小。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同测量装置的激电相位谱和相对相位谱对比

Fig.7 Comparison of IP phase and relative phase in different electrode arrays

从图7中能够看出,激电相位谱和相对相位谱中的电磁耦合分量随着频率的升高而增大,当其大于10 mrad(图7中红色虚线所示)时,则认为激电信号被严重干扰。因此可以基于这个指标确定三极装置和四极装置采用激电相位以及相对相位作为探测信号时的最大工作频率,从而定量分析相对相位法在不同测量装置中的去耦效果。

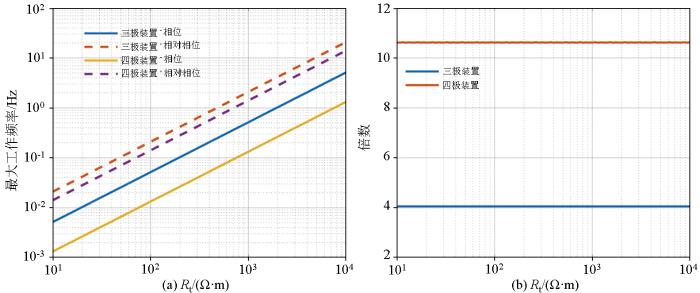
针对1 000 m的探测深度,将三极装置的供电极距AO设置为3 000 m,斯伦贝谢装置的供电极距AB设置为6 000 m,分别计算它们在不同电阻率下的最大工作频率,结果如图8所示。可以看到,随着大地电阻率的增加,由于电磁耦合干扰强度的降低,常规的激电相位谱法和相对相位谱法的最大工作频率都在线性变大。利用激电相位谱测量时,三极装置的最大工作频率明显大于四极装置,而采用相对相位谱进行测量时,虽然三极装置的最大工作频率依然大于四极装置,但二者之间的差距变得更小,说明相对相位法在不同测量装置中的去耦效果是不同的。图8b进一步展示了相对相位谱的去耦效果,可以看到三极装置在采用相对相位谱后,最大工作频率提升了4倍,而四极装置则提升了近11倍,且最大工作频率提升的倍数均为常数,不随大地电阻率的变化而变化。通过将激电相位谱和相对相位谱的最大工作频率作对比,证明相对相位法在大深度激电法中也有一定的去耦效果。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 激电相位谱和相对相位谱的最大工作频率对比

Fig.8 Comparison of the maximum working frequency of IP phase and relative phase

3.3 相对相位法去耦案例

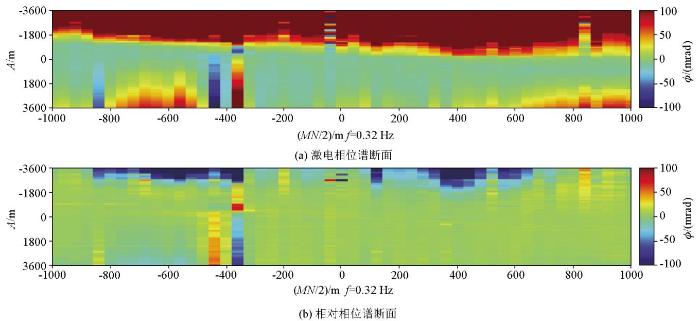
为了验证相对相位法去除电磁耦合干扰的有效性,本文对阿拉善呼和沙拉某矿区的扩频激电测量数据进行了分析。数据采集时使用三极装置,供电电极(A)数量为66个,分布在-3 600~3 600 m的测线上,测量电极共有51对,均匀分布在-1 000~1 000 m的位置上。通过对所有测量数据进行处理,形成如图9所示的两个断面,分别为激电相位谱断面(图9)和相对相位谱断面(图9b)。从图9中可以看出常规的激电相位谱受到了严重的电磁耦合干扰,导致相位谱图中出现了严重的噪声和伪影,无法区分出激电异常信号,导致无法识别出潜在的异常区域。采用相对相位法后,图9b中的电磁耦合干扰显著减少,激电异常信号的识别变得更加清晰,在测线-700~-500 m、300~500 m的区域内出现了明显的激电异常。通过对比两幅图像可以发现,相对相位法能够有效去除电磁耦合的影响,显著提高了激电异常识别的准确性。因此,基于相对相位法的去耦技术在扩频激电测量中的应用具有重要的实际意义。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 相对相位法去耦效果(以呼和沙拉某矿区为例)

Fig.9 The decoupling effect of the relative phase method (a case study of the Huhe-shala mining area)

4 结论

1)三极装置和对称四级装置的理论探测深度只与AO的长度有关,在AO长度相同时,两种测量装置测得的纯激电信号是完全一样的,而主要区别在于在相同的探测条件下,四极装置受电磁耦合干扰程度总是强于三极装置。

2)三极装置和四极装置中的电磁耦合强度主要受到工作频率、供电极距和大地电阻率的影响,其中大地电阻率越小、电极距越长、工作频率越高,电磁耦合强度越大。此外,旁侧中梯装置的电磁耦合强度还受到旁侧距离的影响,旁侧距离越小,电磁耦合强度越大,当垂直旁侧距离和水平旁侧距离均为0时,电磁耦合强度最大。三极装置中的电磁耦合强度还受到OB距离的影响,即B点放置的越远,电磁耦合效应越小,因此在实际施工时,电极B应放置的尽可能远。

3)由于相对相位法中假设的条件,即k·ϕ_EM(f)≈ϕ_EM(k·f)并不总是满足,特别是在长极距、高频、低阻情况下,因此其去耦效果及应用场景是有限的。针对1 000 m的探测深度,相对相位谱的引入可将对称四极装置和三极装置的最大工作频率分别提高10.6倍和4倍。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

滕吉文, 杨立强, 姚敬全, 等.

金属矿产资源的深部找矿、勘探与成矿的深层动力过程

[J]. 地球物理学进展, 2007, 22(2):317-334.