0 引言
在对油气藏的研究中,沉积盆地的超压现象越来越受到重视。超压体通常具备良好的油气成藏条件,提供油气运移的动力和封存力,异常高压的流体活动可以有效地改善储层物性,控制圈闭的形成与分布,因此,针对超压流体活动对油气运聚成藏分布的研究越来越多[1 5] 。目前全球大约有180个超压地层体系的沉积盆地,占世界盆地数量的2/3,其中我国典型的超压盆地有渤海湾盆地、松辽盆地等[6 8] ,超压沉积盆地的现象在海域中普遍存在且分布广泛,因此加强对海域超压分布的研究,对于油气资源的评价以及勘探部署而言,有着极为关键的导向作用。
三维压力预测[9 -10 ] 是研究超压分布的主要手段,但无论是哪种压力预测方法,地层的速度数据都是其中的关键参数。而速度的获取主要来源于地震数据和测井数据,其中地震数据可以提供三维地震速度体,测井仅提供井点速度[11 ] 。因此,在进行三维压力预测时主要使用的速度为地震速度,测井速度则作为约束和质控。
由于地下超压分布一般在速度上呈现低速特征[12 ] ,因此地震速度体上的异常低速现象对超压分布范围具有一定的指示作用。随着压力预测精度要求的提高,地震速度的精度、分辨率及与测井速度的匹配度成为超压分析的关键制约因素。对于海洋勘探而言钻井成本相对较高,井网较陆地钻井更为稀疏,而地震速度的可靠性一般需要高质量的地震数据支撑和钻井约束,因此,在做压力预测时对于一般地震速度的可靠性需要进行多方面的评价分析。同时经常规速度分析或建模方法获取的地震速度的分辨率不足以准确反映目标地层速度的精细变化,难以判断是否存在异常压力地层等。
综上所述,在进行压力预测前需要对现有的地震速度进行综合评价分析,对于可靠性和分辨率不足的地震速度需进行优化处理,以此提高速度的精度和准确率,以此更好地满足预测地层异常压力大小和指示地层异常压力分布的需求。传统地震速度建模通常基于各向同性介质假设,这一简化模型难以体现地层的非均质特征(如岩性突变、裂缝网络)及各向异性(VTI/HTI)对地震波传播路径的影响,导致实际走时残差未被有效校正[13 ] 。因此,本文考虑以Siliqi等[14 16] 提出的非相关参数的高阶动校正为理论基础的高密度双谱速度拾取方法来获取更高分辨率的地震速度体,并通过与测井速度对比验证其可靠性。
1 理论与方法
地层的各向异性广泛存在,由于垂向非均质性(射线弯曲或分层效应)和地下的各向异性介质所形成的反射动校时差曲线为非双曲线型,采用常规的动校正和速度分析方法不能将地震道集完全拉平,因此,在复杂介质中的动校正和速度分析必须考虑各向异性的问题[17 ] 。
许多学者针对各向异性的速度分析问题进行了多方面的研究,早在1989年Byun等[18 ] 提出了应用于鉴别岩性的各向异性速度分析方法;然后Alkhalifah[19 ] 在常规双曲线时差方程(式(1))速度分析的基础上引入各向异性参数η ,得到相应的非双曲时差方程(式(2)),并将该方程应用于VTI介质的速度分析中。
(1) $t({V}_{NMO}{)}^{2}={t}_{{p}_{0}}^{2}+\frac{{x}^{2}}{{V}_{NMO}^{2}\left(0\right)}$
(2) $\begin{array}{l}t({V}_{NMO}{,\eta)}^{2}={t}_{{p}_{0}}^{2}+\frac{{x}^{2}}{{V}_{NMO}^{2}\left(0\right)}-\\ \frac{2\eta ·{x}^{4}}{{V}_{NMO}^{2}\left(0\right)\left[{t}_{{p}_{0}}^{2}{V}_{NMO}^{2}\right(0)+(1+2\eta \left){x}^{2}\right]}\end{array}$
式中:t (V NMO )和t (V NMO ,η )均表示总旅行时;η 表示椭圆率参数(即时差非双曲程度的各向异性参数);V NMO 为动校正速度;tp0 表示纵波零偏移距的旅行时;x 表示偏移距。从式(1)~(2)中可以推出,只需要椭圆率参数η 和V NMO 两个参数就可以处理一切时间域成像处理(如 NMO 校正、DMO 校正、叠前和叠后时间偏移等)。
基于波传播的相速度公式,Thomsen[20 ] 提出了表征TI介质弹性性质的5个参数,分别为vp0 、vs0 、ε 、γ 和δ ,对于VTI介质而言:
(3) ${V}_{NMO}\left(0\right)={v}_{{p}_{0}}\sqrt{1+2\delta }$
(4) $\eta =\frac{(\epsilon -\delta)}{(1+2\delta)}$
式中:vp0 为准纵波速度(即沿TI介质垂直对称轴方向传播的相速度);参数ε 表示垂直纵波速度和水平纵波速度差值与垂直纵波速度的比值,是度量纵波各向异性强度的参数;δ 为纵波变异系数,表示垂向纵波各向异性变化的快慢程度。
在此基础上,Siliqi 等[14 ] 针对各向异性主要集中出现在道集远偏移距范围的性质,对非双曲线时差方程(式(2))进一步修正得到:
(5) $\begin{array}{l}t({V}_{NMO},\eta)={t}_{{p}_{0}}\frac{8\eta }{1+8\eta }+\\ \sqrt{{\left(\frac{{t}_{{p}_{0}}}{1+8\eta }\right)}^{2}+\frac{{x}^{2}}{(1+8\eta){V}_{NMO}^{2}\left(0\right)}}\end{array}$
式中:V NMO 和η 是两个非相关的关键参数,并且它们随偏移距对时差的影响是不规则分布的。其中V NMO 参数对道集的全偏移距范围都有影响,而η 只在远偏移距范围处有较大影响,当η =0时,式(5)又变为常规双曲线时差方程(式1),因此,必须将两个参数结合起来充分考虑才能更好地解决由于各向异性所导致的地震速度精度问题,即非相关参数的高阶动校正。
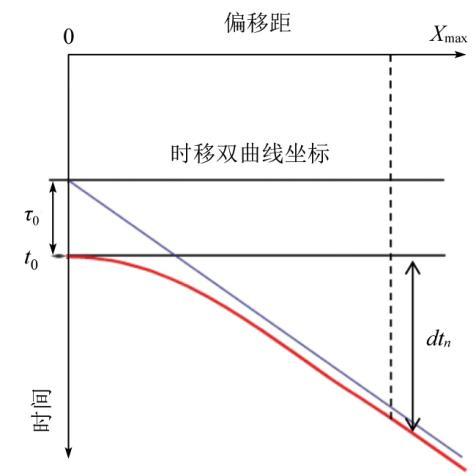
基于以上理论,采用由Siliqi等[15 -16 ] 提出的高密度双谱速度拾取方法,通过参数化非双曲线的时差,将常规的二维速度谱转换为三维的速度谱(t 0 ,dtn ,τ 0 )进行拾取,获得密度和精度更高的速度体。其具体实现是将式(5)中常规时移校正的参数椭圆率η 和V NMO 转换为描述各向异性的时移参数的零偏移距走时τ 0 和最大偏移距下的剩余时差dtn ,参数关系如图1 所示,可知当τ 0 =t 0 / (1+8η )时,dtn =tx =X max -tx =0 ,相应的式(5)可转换为:
(6) $t={t}_{0}-{\tau }_{0}+\sqrt{{\tau }_{0}^{2}+\frac{d{t}_{n}(d{t}_{n}+2{\tau }_{0})}{{X}_{max}^{2}}{X}^{2}}$。
图1
图1
时差参数dtn 和τ 0 之间的关系
Fig.1
Relation between time-difference parameters dtn and τ 0
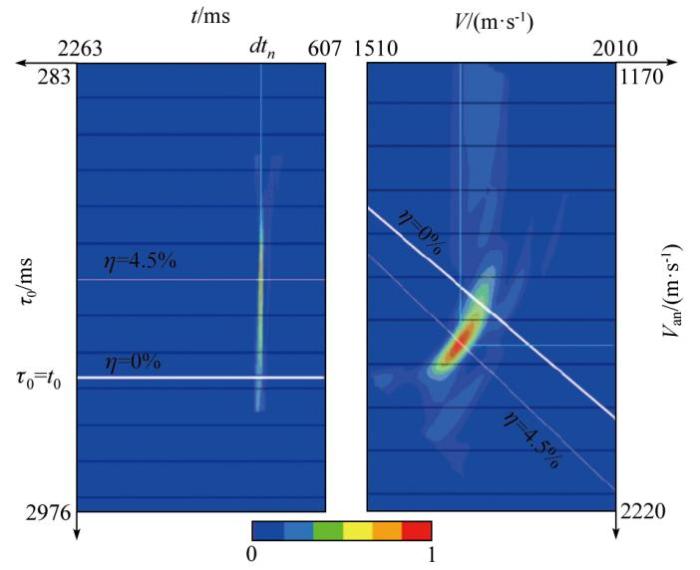
图2 是高密度双谱速度分析,是基于V 和η 参数与τ 0 和dtn 参数的非双曲线动校式(5)和式(6)形成的双谱面板左(dtn ,τ 0 )和右(V ,V an ),其中dtn 为剩余时差、τ 0 为零偏移距走时、V 为NMO速度、V an 为各向异性速度,面板上的颜色表示Semblance值(无量纲,范围 0~1),颜色越亮(红)表示相似性越高,参数组合更可靠。在拾取(dtn , τ 0 )面板中相应的dtn ,τ 0 参数后再转换到(V ,V an )面板中获取相应的V 和η 参数。从图2 中可以看出左图中(dtn ,τ 0 )面板高semblance区域(亮色)集中在一个狭窄范围内,比(V ,V an )面板具有更好的约束性,表明dtn 和τ 0 的解更稳定,τ 0 的变化被限制在表面最大值附近的一个小区域内(即颜色最亮区域对应的纵轴范围)。
图2
图2
双谱面板左图(dtn ,τ 0 )和右图(V ,V an )之间的差异
Fig.2
Difference between parameters (dtn ,τ 0 ) and (V ,V an ) in bispectral panels
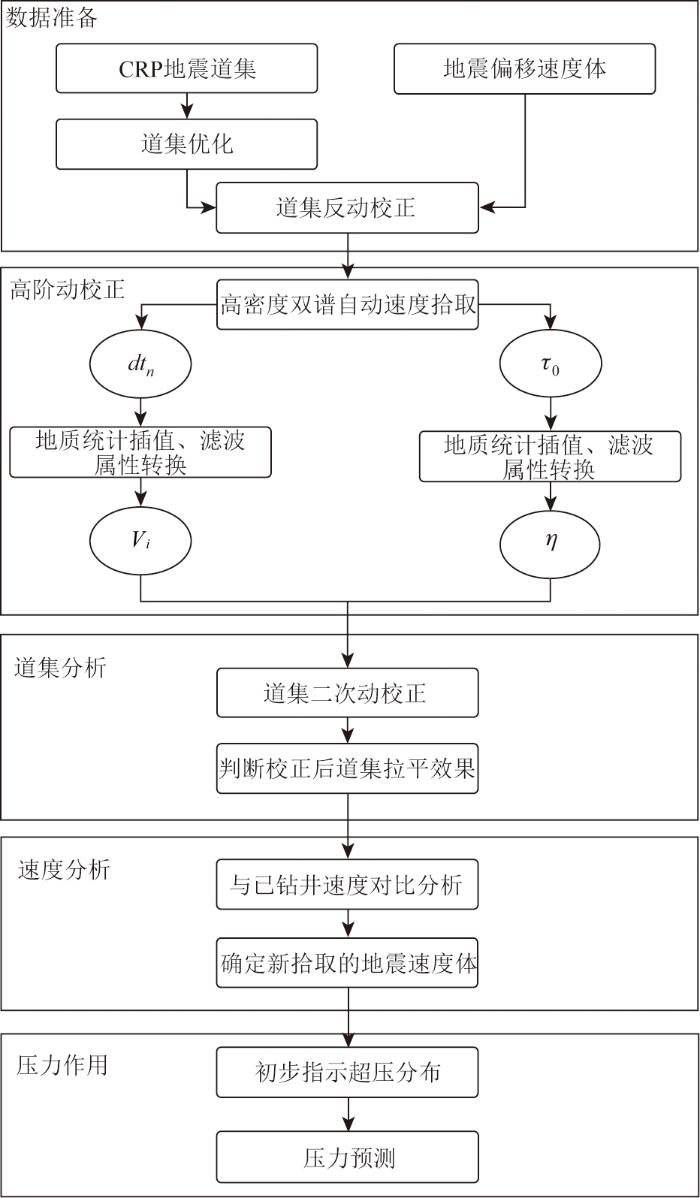
为提升地震速度的分辨率来指示海域超压分布,采用基于非相关参数的高阶动校正理论的双谱速度拾取方法获取新的地震速度体,具体步骤如图3 所示。
图3
图3
高阶动校正指示超压分布处理流程
Fig.3
Processing flowchart for non-hypobolic moveout correction in overpressure distribution indicatioon
1)数据准备:收集研究区的CRP地震道集和地震偏移速度体,首先对CRP地震道集进行优化处理,然后对道集进行反动校正处理;
2)高阶动校正:对反动校正后的道集采用高密度双谱自动速度拾取dtn 和τ 0 参数,对拾取后的参数进行地质统计插值和滤波处理,然后属性转换为相应的V 和η 参数;
3)道集分析:将获取到的V 和η 数据应用到初始反动校正后的CRP地震道集,进行道集的二次动校正,通过道集的拉平效果判断新速度体的适用性;
4)分析结果质控:将高阶动校正后获得的新的地震速度体与已钻井速度进行对比分析,判断新速度体的可靠性;
5)压力应用:采用确定后的新速度体对超压分布有初步的指示作用,后续可以用于压力预测相关工作。
使用高阶动校正后获取的新的速度体相比于原始地震速度更能反映出地层内局部细小的速度差异,相应的更能反映地下的实际情况,对超压在地下的分布范围具有一定的指示作用,同时也为后续的压力预测工作提供了更高精度的地震速度体。
2 应用效果
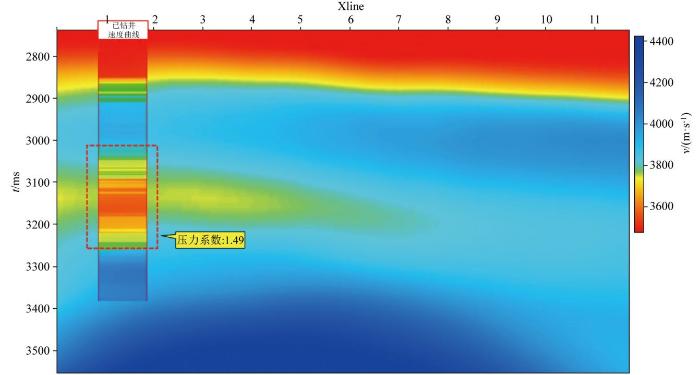
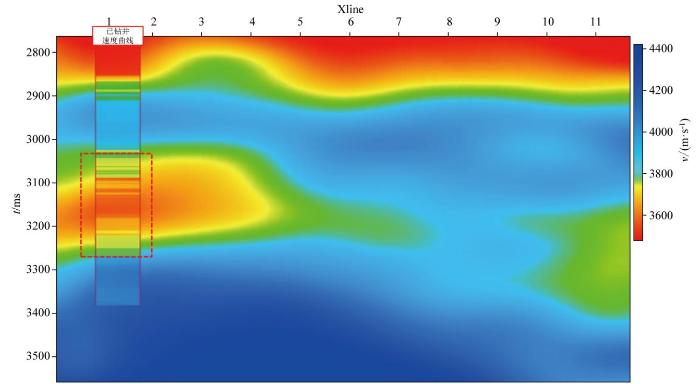
为了验证采用上述流程获得的新速度体对超压分布的指示作用,本文选取了东海某工区的相关数据进行应用。该区域的前期钻探已获得较好的油气突破,目前通过钻井已确认井中存在异常高压区域(图4 ),压力系数达到1.49(压力系数>1为超压),由于地层压力与声波时差(可转换为声波速度)呈现负相关关系,因此,在出现异常高压区域范围应出现异常低速现象[12 ] 。将声波测井速度曲线以井柱的形式投影到地震速度体上可以看出(图4 ),井速度曲线的速度变化与地震偏移速度基本一致,但在异常高压位置(虚线红框)井速度呈现明显的低速特征(色彩柱红黄色区域为低速区域),而速度体在异常高压位置(虚线红框)虽存在低速特征,但其大小和范围并不明显。
图4
图4
原始偏移速度体与井速度和高压分布的关系
Fig.4
Diagram of relationship between the initial migration velocity data and high pressure distribution through well
因此,本文针对以上问题在原始CRP地震道集和地震偏移速度的基础上,通过高密度双谱速度拾取方法对地震偏移速度进行高阶动校正处理,以获取新的地震速度体数据,如图5 所示。与地震偏移速度体相比,经过高阶动校正所获取的新的速度体在异常高压位置(虚线红框)出现相应明显的异常低速现象(图5 红框中的黄红色低速现象),且低速范围与井速度曲线对应的低速范围基本一致。
图5
图5
高阶动校正后速度体与井速度和高压分布的关系
Fig.5
Diagram of relationship between the velocity data after non-hypobolic moveout correction and high pressure distribution through well
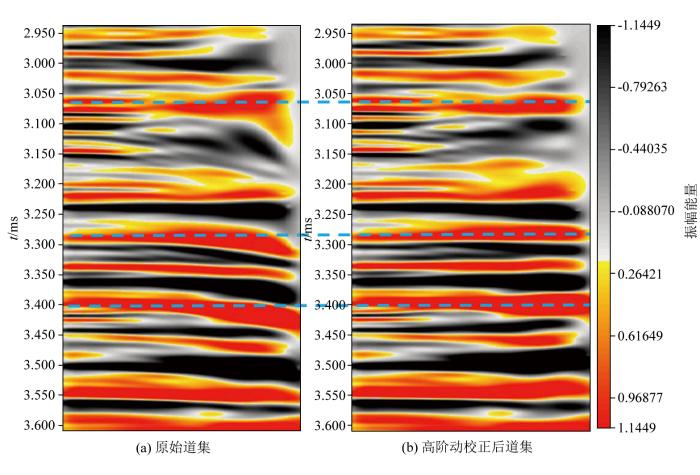
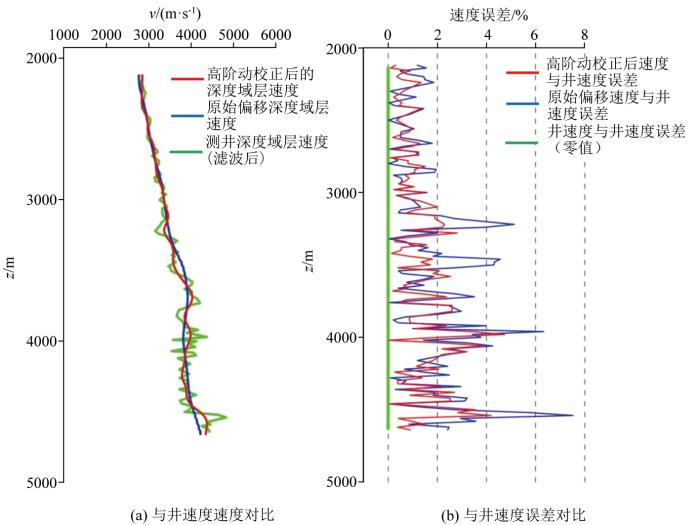
为了验证高阶动校正得到的地震速度体的准确性,采用新的地震速度对原始反动校正后的CRP地震道集进行动校正拉平。图6 是经过高阶动校正处理前后的道集对比,可以看出双参数高阶算法处理后的道集在大偏移距可以得到进一步的拉平,提高CRP地震道集质量,初步证明了高阶动校正得到的地震速度体的准确性。之后将声波测井速度、原始地震偏移速度以及高阶动校正后的新速度进行对比分析,如图7 与井速度对比。可以看出高阶动校正后的新速度与声波测井速度更加匹配;从图7b 所示的与井速度误差对比可以看出,高阶动校正后的新速度与测井声波速度的误差整体上低于原始地震偏移速度与测井声波速度的误差,因此,可以证明高阶动校正后的新速度是准确的,并且相比原始地震偏移速度具有更高的精度。
图6
图6
道集高阶动校正前后对比
Fig.6
Comparison of seismic gather before and after applying non-hypobolic moveout correction
图7
图7
高阶动校正后速度与原始地震偏移速度和测井速度对比
Fig.7
Comparison between original seismic migration velocity,corrected seismic velocity and acoustic logging velocity after non-hypobolic moveout correction
3 结论
基于Siliqi等[14 16] 提出的非相关参数高阶动校正方法,优化后的地震速度体相比传统偏移速度体具有更高的准确度,能够更精确地刻画地下超压带的分布特征。通过与声波测井速度的吻合度分析,验证了该方法在速度场可靠性上的提升。东海工区的实例表明,经高阶动校正处理的地震速度体在超压异常检测中表现显著,速度异常区与已知超压层位空间分布一致性高,准确度提升有助于识别薄层超压单元。
但值得注意的是该方法对原始地震数据质量具有依赖性,原始CRP道集的信噪比直接影响参数拾取精度,未消除的噪声可能导致各向异性假象或异常速度值,因此该方法在应用前需确保道集经过充分的噪声压制和振幅补偿处理,并进行参数敏感性分析(如V ±5%、η ±5%的扰动测试)评估参数稳定性。最终成果应综合测井曲线分析等进行多维度验证,以规避单一方法的不确定性风险。
参考文献
View Option
[1]
Hunt J M Generation and migration of petroleum from abnormally pressured fluid compartments
[J]. AAPG Bulletin , 1990 , 74 (1 ):1 -12 .
[本文引用: 1]
[2]
马启富 , 陈斯忠 , 张启明 , 等 . 超压盆地与油气分布 [M]. 北京 : 地质出版社 , 2000 .
Ma Q F Chen S Z Zhang Q M et al. Overpressure basin and oil and gas distribution [M]. Beijing : Geological Publishing House , 2000 .
[3]
郝芳 . 超压盆地生烃作用动力学与油气成藏机理 [M]. 北京 : 科学出版社 , 2005 .
Hao F Kinetics of hydrocarbon generation and hydrocarbon accumulation mechanism in overpressure basin [M]. Beijing : Science Press , 2005 .
[4]
蒋有录 , 王鑫 , 于倩倩 , 等 . 渤海湾盆地含油气凹陷压力场特征及与油气富集关系
[J]. 石油学报 , 2016 , 37 (11 ):1361 -1369 .
Jiang Y L Wang X Yu Q Q et al. Pressure field characteristics of petroliferous depressions and its relationship with hydrocarbon enrichment in Bohai Bay Basin
[J]. Acta Petrolei Sinica , 2016 , 37 (11 ):1361 -1369 .
[5]
Liu H Jiang Y L Song G Q et al. Overpressure characteristics and effects on hydrocarbon distribution in the Bonan Sag,Bohai Bay Basin,China
[J]. Journal of Petroleum Science and Engineering , 2017 , 149 :811 -821 .
[本文引用: 1]
[6]
杜栩 , 郑洪印 , 焦秀琼 . 异常压力与油气分布
[J]. 地学前缘 , 1995 , 2 (4 ):137 -148 .
[本文引用: 1]
Du X Zheng H Y Jiao X Q Abnormal pressure and hydrocarbon accumulation
[J]. Earth Science Frontiers , 1995 , 2 (4 ):137 -148 .
[本文引用: 1]
[7]
Osborne M J Swarbrick R E Mechanisms for generating overpressure in sedimentary basins:A reevaluation:Reply
[J]. AAPG Bulletin , 1997 , 90 (81 ):1023 -1041 .
[8]
张启明 , 董伟良 . 中国含油气盆地中的超压体系
[J]. 石油学报 , 2000 , 21 (6 ):1 -11 ,127.
[本文引用: 1]
Zhang Q M Dong W L Overpressure system of hydrocarbon-bearing basins in China
[J]. Acta Petrolei Sinica , 2000 , 21 (6 ):1 -11 ,127.
[本文引用: 1]
[9]
Baouche R Sen S Sadaoui M et al. Characterization of pore pressure,fracture pressure,shear failure and its implications for drilling,wellbore stability and completion design:A case study from the Takouazet field,Illizi Basin,Algeria
[J]. Marine and Petroleum Geology , 2020 , 120 :104510 .
[本文引用: 1]
[10]
Azadpour M Shad Manaman N Kadkhodaie-Ilkhchi A et al. Pore pressure prediction and modeling using well-logging data in one of the gas fields in south of Iran
[J]. Journal of Petroleum Science and Engineering , 2015 , 128 :15 -23 .
[本文引用: 1]
[11]
张勇刚 , 王红平 , 王朝锋 , 等 . 地震资料在海域勘探初期地层压力预测中的应用
[J]. 石油地质与工程 , 2020 , 34 (6 ):8 -12 ,19.
[本文引用: 1]
Zhang Y G Wang H P Wang C F et al. Application of seismic data in formation pressure prediction at the initial stage of offshore exploration
[J]. Petroleum Geology and Engineering , 2020 , 34 (6 ):8 -12 ,19.
[本文引用: 1]
[12]
张勇刚 . 准噶尔盆地中央坳陷异常压力研究
[J]. 新疆石油学院学报 , 2003 (4 ):26 -29 .
[本文引用: 2]
Zhang Y G The abnormal.pressure researches in central depression of Junggar basin
[J]. Journal of Xinjiang Petroleum Institute , 2003 (4 ):26 -29 .
[本文引用: 2]
[13]
刘本晶 , 梁兴 , 侯艳 , 等 . 叠前道集优化技术在页岩储层预测中的应用
[J]. 石油地球物理勘探 , 2018 , 53 (S2 ):189 -196 ,14-15.
[本文引用: 1]
Liu B J Liang X Hou Y et al. Prestack gather conditioning in shale reservoir prediction
[J]. Oil Geophysical Prospecting , 2018 , 53 (S2 ):189 -196 ,14-15.
[本文引用: 1]
[14]
Siliqi R Bousquié N Anelliptic time processing based on a shifted hyperbola approach
[C]// SEG Technical Program Expanded Abstracts 2000.Society of Exploration Geophysicists , 2000 :2245 -2248 .
[本文引用: 3]
[15]
Siliqi R Le Meur D Gamar F et al. High-density moveout parameter fields V and η .Part one:Simultaneous automatic picking
[C]// SEG Technical Program Expanded Abstracts 2003.Society of Exploration Geophysicists , 2003 :2088 -2091 .
[本文引用: 1]
[16]
Le Meur D Siliqi R Gamar F et al. High density moveout parameter fields V and η .Part two:Simultaneous geostatistical filtering
[C]// SEG Technical Program Expanded Abstracts 2003.Society of Exploration Geophysicists , 2003 :2092 -2095 .
[本文引用: 3]
[17]
徐翠娥 , 郝晓红 , 王影 . 高密度双谱分析法在各向异性介质速度分析中的初步应用
[J]. 海洋石油 , 2008 , 28 (1 ):1 -5 .
[本文引用: 1]
Xu C E Hao X H Wang Y Application of high density bispectral analyzing method to velocity analysis in anisotropy media
[J]. Offshore Oil , 2008 , 28 (1 ):1 -5 .
[本文引用: 1]
[18]
Byun B S Corrigan D Gaiser J E Anisotropic velocity analysis for lithology discrimination
[J]. Geophysics , 1989 , 54 (12 ):1564 -1574 .
[本文引用: 1]
[19]
Alkhalifah T Velocity analysis using nonhyperbolic moveout in transversely isotropic media
[J]. Geophysics , 1997 , 62 (6 ):1839 -1854 .
[本文引用: 1]
[20]
Thomsen L Weak elastic anisotropy
[J]. Geophysics , 1986 , 51 (10 ):1954 -1966 .
[本文引用: 1]
Generation and migration of petroleum from abnormally pressured fluid compartments
1
1990
... 在对油气藏的研究中,沉积盆地的超压现象越来越受到重视.超压体通常具备良好的油气成藏条件,提供油气运移的动力和封存力,异常高压的流体活动可以有效地改善储层物性,控制圈闭的形成与分布,因此,针对超压流体活动对油气运聚成藏分布的研究越来越多[1 5 ] .目前全球大约有180个超压地层体系的沉积盆地,占世界盆地数量的2/3,其中我国典型的超压盆地有渤海湾盆地、松辽盆地等[6 8 ] ,超压沉积盆地的现象在海域中普遍存在且分布广泛,因此加强对海域超压分布的研究,对于油气资源的评价以及勘探部署而言,有着极为关键的导向作用. ...
渤海湾盆地含油气凹陷压力场特征及与油气富集关系
0
2016
渤海湾盆地含油气凹陷压力场特征及与油气富集关系
0
2016
Overpressure characteristics and effects on hydrocarbon distribution in the Bonan Sag,Bohai Bay Basin,China
1
2017
... 在对油气藏的研究中,沉积盆地的超压现象越来越受到重视.超压体通常具备良好的油气成藏条件,提供油气运移的动力和封存力,异常高压的流体活动可以有效地改善储层物性,控制圈闭的形成与分布,因此,针对超压流体活动对油气运聚成藏分布的研究越来越多[1 5 ] .目前全球大约有180个超压地层体系的沉积盆地,占世界盆地数量的2/3,其中我国典型的超压盆地有渤海湾盆地、松辽盆地等[6 8 ] ,超压沉积盆地的现象在海域中普遍存在且分布广泛,因此加强对海域超压分布的研究,对于油气资源的评价以及勘探部署而言,有着极为关键的导向作用. ...
异常压力与油气分布
1
1995
... 在对油气藏的研究中,沉积盆地的超压现象越来越受到重视.超压体通常具备良好的油气成藏条件,提供油气运移的动力和封存力,异常高压的流体活动可以有效地改善储层物性,控制圈闭的形成与分布,因此,针对超压流体活动对油气运聚成藏分布的研究越来越多[1 5 ] .目前全球大约有180个超压地层体系的沉积盆地,占世界盆地数量的2/3,其中我国典型的超压盆地有渤海湾盆地、松辽盆地等[6 8 ] ,超压沉积盆地的现象在海域中普遍存在且分布广泛,因此加强对海域超压分布的研究,对于油气资源的评价以及勘探部署而言,有着极为关键的导向作用. ...
异常压力与油气分布
1
1995
... 在对油气藏的研究中,沉积盆地的超压现象越来越受到重视.超压体通常具备良好的油气成藏条件,提供油气运移的动力和封存力,异常高压的流体活动可以有效地改善储层物性,控制圈闭的形成与分布,因此,针对超压流体活动对油气运聚成藏分布的研究越来越多[1 5 ] .目前全球大约有180个超压地层体系的沉积盆地,占世界盆地数量的2/3,其中我国典型的超压盆地有渤海湾盆地、松辽盆地等[6 8 ] ,超压沉积盆地的现象在海域中普遍存在且分布广泛,因此加强对海域超压分布的研究,对于油气资源的评价以及勘探部署而言,有着极为关键的导向作用. ...
Mechanisms for generating overpressure in sedimentary basins:A reevaluation:Reply
0
1997
中国含油气盆地中的超压体系
1
2000
... 在对油气藏的研究中,沉积盆地的超压现象越来越受到重视.超压体通常具备良好的油气成藏条件,提供油气运移的动力和封存力,异常高压的流体活动可以有效地改善储层物性,控制圈闭的形成与分布,因此,针对超压流体活动对油气运聚成藏分布的研究越来越多[1 5 ] .目前全球大约有180个超压地层体系的沉积盆地,占世界盆地数量的2/3,其中我国典型的超压盆地有渤海湾盆地、松辽盆地等[6 8 ] ,超压沉积盆地的现象在海域中普遍存在且分布广泛,因此加强对海域超压分布的研究,对于油气资源的评价以及勘探部署而言,有着极为关键的导向作用. ...
中国含油气盆地中的超压体系
1
2000
... 在对油气藏的研究中,沉积盆地的超压现象越来越受到重视.超压体通常具备良好的油气成藏条件,提供油气运移的动力和封存力,异常高压的流体活动可以有效地改善储层物性,控制圈闭的形成与分布,因此,针对超压流体活动对油气运聚成藏分布的研究越来越多[1 5 ] .目前全球大约有180个超压地层体系的沉积盆地,占世界盆地数量的2/3,其中我国典型的超压盆地有渤海湾盆地、松辽盆地等[6 8 ] ,超压沉积盆地的现象在海域中普遍存在且分布广泛,因此加强对海域超压分布的研究,对于油气资源的评价以及勘探部署而言,有着极为关键的导向作用. ...
Characterization of pore pressure,fracture pressure,shear failure and its implications for drilling,wellbore stability and completion design:A case study from the Takouazet field,Illizi Basin,Algeria
1
2020
... 三维压力预测[9 -10 ] 是研究超压分布的主要手段,但无论是哪种压力预测方法,地层的速度数据都是其中的关键参数.而速度的获取主要来源于地震数据和测井数据,其中地震数据可以提供三维地震速度体,测井仅提供井点速度[11 ] .因此,在进行三维压力预测时主要使用的速度为地震速度,测井速度则作为约束和质控. ...
Pore pressure prediction and modeling using well-logging data in one of the gas fields in south of Iran
1
2015
... 三维压力预测[9 -10 ] 是研究超压分布的主要手段,但无论是哪种压力预测方法,地层的速度数据都是其中的关键参数.而速度的获取主要来源于地震数据和测井数据,其中地震数据可以提供三维地震速度体,测井仅提供井点速度[11 ] .因此,在进行三维压力预测时主要使用的速度为地震速度,测井速度则作为约束和质控. ...
地震资料在海域勘探初期地层压力预测中的应用
1
2020
... 三维压力预测[9 -10 ] 是研究超压分布的主要手段,但无论是哪种压力预测方法,地层的速度数据都是其中的关键参数.而速度的获取主要来源于地震数据和测井数据,其中地震数据可以提供三维地震速度体,测井仅提供井点速度[11 ] .因此,在进行三维压力预测时主要使用的速度为地震速度,测井速度则作为约束和质控. ...
地震资料在海域勘探初期地层压力预测中的应用
1
2020
... 三维压力预测[9 -10 ] 是研究超压分布的主要手段,但无论是哪种压力预测方法,地层的速度数据都是其中的关键参数.而速度的获取主要来源于地震数据和测井数据,其中地震数据可以提供三维地震速度体,测井仅提供井点速度[11 ] .因此,在进行三维压力预测时主要使用的速度为地震速度,测井速度则作为约束和质控. ...
准噶尔盆地中央坳陷异常压力研究
2
2003
... 由于地下超压分布一般在速度上呈现低速特征[12 ] ,因此地震速度体上的异常低速现象对超压分布范围具有一定的指示作用.随着压力预测精度要求的提高,地震速度的精度、分辨率及与测井速度的匹配度成为超压分析的关键制约因素.对于海洋勘探而言钻井成本相对较高,井网较陆地钻井更为稀疏,而地震速度的可靠性一般需要高质量的地震数据支撑和钻井约束,因此,在做压力预测时对于一般地震速度的可靠性需要进行多方面的评价分析.同时经常规速度分析或建模方法获取的地震速度的分辨率不足以准确反映目标地层速度的精细变化,难以判断是否存在异常压力地层等. ...
... 为了验证采用上述流程获得的新速度体对超压分布的指示作用,本文选取了东海某工区的相关数据进行应用.该区域的前期钻探已获得较好的油气突破,目前通过钻井已确认井中存在异常高压区域(图4 ),压力系数达到1.49(压力系数>1为超压),由于地层压力与声波时差(可转换为声波速度)呈现负相关关系,因此,在出现异常高压区域范围应出现异常低速现象[12 ] .将声波测井速度曲线以井柱的形式投影到地震速度体上可以看出(图4 ),井速度曲线的速度变化与地震偏移速度基本一致,但在异常高压位置(虚线红框)井速度呈现明显的低速特征(色彩柱红黄色区域为低速区域),而速度体在异常高压位置(虚线红框)虽存在低速特征,但其大小和范围并不明显. ...
准噶尔盆地中央坳陷异常压力研究
2
2003
... 由于地下超压分布一般在速度上呈现低速特征[12 ] ,因此地震速度体上的异常低速现象对超压分布范围具有一定的指示作用.随着压力预测精度要求的提高,地震速度的精度、分辨率及与测井速度的匹配度成为超压分析的关键制约因素.对于海洋勘探而言钻井成本相对较高,井网较陆地钻井更为稀疏,而地震速度的可靠性一般需要高质量的地震数据支撑和钻井约束,因此,在做压力预测时对于一般地震速度的可靠性需要进行多方面的评价分析.同时经常规速度分析或建模方法获取的地震速度的分辨率不足以准确反映目标地层速度的精细变化,难以判断是否存在异常压力地层等. ...
... 为了验证采用上述流程获得的新速度体对超压分布的指示作用,本文选取了东海某工区的相关数据进行应用.该区域的前期钻探已获得较好的油气突破,目前通过钻井已确认井中存在异常高压区域(图4 ),压力系数达到1.49(压力系数>1为超压),由于地层压力与声波时差(可转换为声波速度)呈现负相关关系,因此,在出现异常高压区域范围应出现异常低速现象[12 ] .将声波测井速度曲线以井柱的形式投影到地震速度体上可以看出(图4 ),井速度曲线的速度变化与地震偏移速度基本一致,但在异常高压位置(虚线红框)井速度呈现明显的低速特征(色彩柱红黄色区域为低速区域),而速度体在异常高压位置(虚线红框)虽存在低速特征,但其大小和范围并不明显. ...
叠前道集优化技术在页岩储层预测中的应用
1
2018
... 综上所述,在进行压力预测前需要对现有的地震速度进行综合评价分析,对于可靠性和分辨率不足的地震速度需进行优化处理,以此提高速度的精度和准确率,以此更好地满足预测地层异常压力大小和指示地层异常压力分布的需求.传统地震速度建模通常基于各向同性介质假设,这一简化模型难以体现地层的非均质特征(如岩性突变、裂缝网络)及各向异性(VTI/HTI)对地震波传播路径的影响,导致实际走时残差未被有效校正[13 ] .因此,本文考虑以Siliqi等[14 16 ] 提出的非相关参数的高阶动校正为理论基础的高密度双谱速度拾取方法来获取更高分辨率的地震速度体,并通过与测井速度对比验证其可靠性. ...
叠前道集优化技术在页岩储层预测中的应用
1
2018
... 综上所述,在进行压力预测前需要对现有的地震速度进行综合评价分析,对于可靠性和分辨率不足的地震速度需进行优化处理,以此提高速度的精度和准确率,以此更好地满足预测地层异常压力大小和指示地层异常压力分布的需求.传统地震速度建模通常基于各向同性介质假设,这一简化模型难以体现地层的非均质特征(如岩性突变、裂缝网络)及各向异性(VTI/HTI)对地震波传播路径的影响,导致实际走时残差未被有效校正[13 ] .因此,本文考虑以Siliqi等[14 16 ] 提出的非相关参数的高阶动校正为理论基础的高密度双谱速度拾取方法来获取更高分辨率的地震速度体,并通过与测井速度对比验证其可靠性. ...
Anelliptic time processing based on a shifted hyperbola approach
3
2000
... 综上所述,在进行压力预测前需要对现有的地震速度进行综合评价分析,对于可靠性和分辨率不足的地震速度需进行优化处理,以此提高速度的精度和准确率,以此更好地满足预测地层异常压力大小和指示地层异常压力分布的需求.传统地震速度建模通常基于各向同性介质假设,这一简化模型难以体现地层的非均质特征(如岩性突变、裂缝网络)及各向异性(VTI/HTI)对地震波传播路径的影响,导致实际走时残差未被有效校正[13 ] .因此,本文考虑以Siliqi等[14 16 ] 提出的非相关参数的高阶动校正为理论基础的高密度双谱速度拾取方法来获取更高分辨率的地震速度体,并通过与测井速度对比验证其可靠性. ...
... 在此基础上,Siliqi 等[14 ] 针对各向异性主要集中出现在道集远偏移距范围的性质,对非双曲线时差方程(式(2))进一步修正得到: ...
... 基于Siliqi等[14 16 ] 提出的非相关参数高阶动校正方法,优化后的地震速度体相比传统偏移速度体具有更高的准确度,能够更精确地刻画地下超压带的分布特征.通过与声波测井速度的吻合度分析,验证了该方法在速度场可靠性上的提升.东海工区的实例表明,经高阶动校正处理的地震速度体在超压异常检测中表现显著,速度异常区与已知超压层位空间分布一致性高,准确度提升有助于识别薄层超压单元. ...
High-density moveout parameter fields V and η .Part one:Simultaneous automatic picking
1
2003
... 基于以上理论,采用由Siliqi等[15 -16 ] 提出的高密度双谱速度拾取方法,通过参数化非双曲线的时差,将常规的二维速度谱转换为三维的速度谱(t 0 ,dtn ,τ 0 )进行拾取,获得密度和精度更高的速度体.其具体实现是将式(5)中常规时移校正的参数椭圆率η 和V NMO 转换为描述各向异性的时移参数的零偏移距走时τ 0 和最大偏移距下的剩余时差dtn ,参数关系如图1 所示,可知当τ 0 =t 0 / (1+8η )时,dtn =tx =X max -tx =0 ,相应的式(5)可转换为: ...
High density moveout parameter fields V and η .Part two:Simultaneous geostatistical filtering
3
2003
... 综上所述,在进行压力预测前需要对现有的地震速度进行综合评价分析,对于可靠性和分辨率不足的地震速度需进行优化处理,以此提高速度的精度和准确率,以此更好地满足预测地层异常压力大小和指示地层异常压力分布的需求.传统地震速度建模通常基于各向同性介质假设,这一简化模型难以体现地层的非均质特征(如岩性突变、裂缝网络)及各向异性(VTI/HTI)对地震波传播路径的影响,导致实际走时残差未被有效校正[13 ] .因此,本文考虑以Siliqi等[14 16 ] 提出的非相关参数的高阶动校正为理论基础的高密度双谱速度拾取方法来获取更高分辨率的地震速度体,并通过与测井速度对比验证其可靠性. ...
... 基于以上理论,采用由Siliqi等[15 -16 ] 提出的高密度双谱速度拾取方法,通过参数化非双曲线的时差,将常规的二维速度谱转换为三维的速度谱(t 0 ,dtn ,τ 0 )进行拾取,获得密度和精度更高的速度体.其具体实现是将式(5)中常规时移校正的参数椭圆率η 和V NMO 转换为描述各向异性的时移参数的零偏移距走时τ 0 和最大偏移距下的剩余时差dtn ,参数关系如图1 所示,可知当τ 0 =t 0 / (1+8η )时,dtn =tx =X max -tx =0 ,相应的式(5)可转换为: ...
... 基于Siliqi等[14 16 ] 提出的非相关参数高阶动校正方法,优化后的地震速度体相比传统偏移速度体具有更高的准确度,能够更精确地刻画地下超压带的分布特征.通过与声波测井速度的吻合度分析,验证了该方法在速度场可靠性上的提升.东海工区的实例表明,经高阶动校正处理的地震速度体在超压异常检测中表现显著,速度异常区与已知超压层位空间分布一致性高,准确度提升有助于识别薄层超压单元. ...
高密度双谱分析法在各向异性介质速度分析中的初步应用
1
2008
... 地层的各向异性广泛存在,由于垂向非均质性(射线弯曲或分层效应)和地下的各向异性介质所形成的反射动校时差曲线为非双曲线型,采用常规的动校正和速度分析方法不能将地震道集完全拉平,因此,在复杂介质中的动校正和速度分析必须考虑各向异性的问题[17 ] . ...
高密度双谱分析法在各向异性介质速度分析中的初步应用
1
2008
... 地层的各向异性广泛存在,由于垂向非均质性(射线弯曲或分层效应)和地下的各向异性介质所形成的反射动校时差曲线为非双曲线型,采用常规的动校正和速度分析方法不能将地震道集完全拉平,因此,在复杂介质中的动校正和速度分析必须考虑各向异性的问题[17 ] . ...
Anisotropic velocity analysis for lithology discrimination
1
1989
... 许多学者针对各向异性的速度分析问题进行了多方面的研究,早在1989年Byun等[18 ] 提出了应用于鉴别岩性的各向异性速度分析方法;然后Alkhalifah[19 ] 在常规双曲线时差方程(式(1))速度分析的基础上引入各向异性参数η ,得到相应的非双曲时差方程(式(2)),并将该方程应用于VTI介质的速度分析中. ...
Velocity analysis using nonhyperbolic moveout in transversely isotropic media
1
1997
... 许多学者针对各向异性的速度分析问题进行了多方面的研究,早在1989年Byun等[18 ] 提出了应用于鉴别岩性的各向异性速度分析方法;然后Alkhalifah[19 ] 在常规双曲线时差方程(式(1))速度分析的基础上引入各向异性参数η ,得到相应的非双曲时差方程(式(2)),并将该方程应用于VTI介质的速度分析中. ...
Weak elastic anisotropy
1
1986
... 基于波传播的相速度公式,Thomsen[20 ] 提出了表征TI介质弹性性质的5个参数,分别为vp0 、vs0 、ε 、γ 和δ ,对于VTI介质而言: ...