面向高陡构造的棱柱波地震干涉成像方法

doi:10.11720/wtyht.2025.0138

面向高陡构造的棱柱波地震干涉成像方法

罗宇晨^,¹, 罗章清¹, 刘胜¹, 欧成华², 王泽宇², 刘畅³

1.中石化石油工程地球物理有限公司南方分公司, 四川成都 610213

2.西南石油大学石油与天然气工程学院, 四川成都 610500

3.中国石化胜利油田物探研究院, 山东东营 257000

An imaging method integrating prismatic waves and seismic interferometry for high-steep structures

LUO Yu-Chen^,¹, LUO Zhang-Qing¹, LIU Sheng¹, OU Cheng-Hua², WANG Ze-Yu², LIU Chang³

1. South Branch, Sinopec Geophysical Corporation, Chengdu 610213, China

2. Petroleum Engineering School, Southwest Petroleum University, Chengdu 610500, China

3. Geophysical Research Institute, Shengli Oilfield Company,SINOPEC, Dongying 257000, China

第一作者: 罗宇晨(1998-),男,硕士,2023年毕业于西南石油大学资源与环境专业,主要从事地震资料采集处理解释工作。Email:465501669@qq.com

收稿日期: 2025-04-24 修回日期: 2025-08-14

基金资助:

四川科教联合基金重点项目“页岩储层天然裂缝跨视域表征与二氧化碳协同压驱控制机理研究”(2024NSFSC1960)

Received: 2025-04-24 Revised: 2025-08-14

摘要

常规偏移成像由于只考虑一次反射波,因此难以对地下高陡地质体进行有效成像。棱柱波相较于一次反射波多传播一段路径,因此可以对高陡构造进行成像,但由于地震波多传播一段路径,因此计算量会增加。地震干涉可以将地表观测系统下移到地下人为选取的校准面,因此后期的计算只需要对地下校准面以下的模型进行计算,可以提高计算效率。本文融合棱柱波与地震干涉技术,提出新型成像方法;以棱柱波方程替代声波方程,通过地表与地下基准面数据互相关生成虚拟记录,结合逆时偏移成像。采用水平层状、L型和盐丘模型验证;水平模型成像与全局基准面下一致;L模型陡倾构造还原优于常规方法;盐丘模型盐下分辨率提升。由于下沉了观测系统,因此在后期的成像过程中,计算的模型纵向深度减少,炮记录时间也减少了,因此采用本文偏移成像方法的计算成本是常规全模型RTM的26.6%。本文提出的方法通过观测系统下移和多次波利用,兼顾精度与效率,突破传统干涉限制,为高陡构造勘探提供新方案;模型简化与实际非均质性存在差异,计算成本需进一步优化。

关键词： 地震干涉; 棱柱波; 互相关; 逆时偏移; 高陡构造

Abstract

Conventional migration imaging,which only considers primary reflected waves,fails to effectively image subsurface high-steep geobodies.Compared to primary reflected waves,prismatic waves travel an additional path, enabling the imaging of high-steep structures.However,the additional travel path increases the computational load.Seismic interferometry can shift the surface observation system downward to an artificially selected subsurface calibration plane.Consequently,subsequent calculations only need to be performed on the model below the subsurface calibration plane,there by improving computational efficiency.Hence,this study proposed a novel imaging method integrating prismatic waves and seismic interferometry.In the proposed method,the acoustic wave equation was replaced by the prismatic wave equation.Virtual records were generated through cross-correlations between data from the surface and subsurface reference planes.These records were combined with reverse time migration(RTM) for imaging.The proposed method was verified using the horizontal layered, L-shaped, and salt dome models.Specifically,the horizontal layered model exhibited consistent imaging results with those below the global reference plane;the L-shaped model outperformed conventional methods in imaging steep structures;the salt dome model displayed enhanced pre-salt imaging resolution.Due to the downward shift of the surface observation system,the following imaging process entailed a reduced vertical depth and a shorter shot record time.The proposed method reduced the computational cost to 26.6% of that using the conventional RTM imaging.Overall,through the downward shift of the observation system and the utilization of multiples,the proposed method achieved both satisfactory accuracy and efficiency,overcoming the limitations of traditional interferometry and providing a novel solution for exploring high-steep structures.Notably,there still exist discrepancies between the simplified models and the actual heterogeneity,requiring further optimization of the computational cost.

Keywords： seismic interferometry; prism waves; cross-correlation; reverse time migration(RTM); high-steep structures

PDF (3991KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

罗宇晨, 罗章清, 刘胜, 欧成华, 王泽宇, 刘畅. 面向高陡构造的棱柱波地震干涉成像方法[J]. 物探与化探, 2025, 49(6): 1372-1379 doi:10.11720/wtyht.2025.0138

LUO Yu-Chen, LUO Zhang-Qing, LIU Sheng, OU Cheng-Hua, WANG Ze-Yu, LIU Chang. An imaging method integrating prismatic waves and seismic interferometry for high-steep structures[J]. Geophysical and Geochemical Exploration, 2025, 49(6): 1372-1379 doi:10.11720/wtyht.2025.0138

0 引言

在复杂介质中,双程波偏移具有更高的成像精度^[1],但该方法的前提条件是使用精确的偏移速度。逆时偏移(reverse time migration,RTM)就是一个例子。RTM由Baysal等^[2]、Loewenthal等^[3]、McMechan^[4]和Whitmore^[5]提出。基于双程波方程的高精度模拟地震波传播路径,RTM没有倾角限制,可模拟地震波在任何角度的传播^[6]。与基于射线的方法^[7-9]和基于单程波方程的方法^[10]相比,RTM在复杂地下结构成像方面具有很大优势^[11-12]。

地震数据的重校准是地震处理中的一项经典技术。其目的是在基准面上模拟出虚拟的地震数据^[13-14]。一般位于离目标更近的特定地下区域。重校准技术的主要应用在垂直地震剖面(vertical seismic profile,VSP)数据,以适应不规则地表采集或覆盖层中复杂地质结构的影响,如低速层或强烈的横向变化。其目的是改进单井剖面数据,使其更易于处理并更好地显示目标^[15]。

近年来,人们对利用干涉技术改进地震数据处理越来越感兴趣。地震干涉是一门基于光学物理的学科。它利用地震数据中包含的信息,而这些信息在传统处理过程中并未考虑到^[16]。Claerbout^[17]是第一个使用干涉技术的人。干涉可以将震源重新定位到接收器所在的位置,也可以将接收器重新定位到震源所在的位置,因此可以将地震采集数据从地表传输到地下基准面。Xiao等^[18]在共中点域数据中实施了地震干涉,以恢复盐体下的地质结构成像。Schuster等^[19]总结了基于相关性的干涉处理方法,并与基于模型的技术进行了比较。Dong等^[20]采用了Luo等^[21]的基于时域相关性的干涉技术。它将得到的虚拟地震数据作为RTM的输入,完成盐下的高清成像,以改善基准面下方区域的成像结果。Lu等^[22]介绍了一种利用基于相关性干涉的盐丘侧翼成像新策略。Vander等^[23]提出了通过多维解卷积进行弹性波干涉处理的方法,提高了弹性波干涉成像的质量。Curtis等^[24]提出了一种结合了相关型和卷积型的统一表达式。Poliannikov^[25]在Curtis和Halliday的初步工作基础上,提出了一种干涉方法,以补偿因地震波照明不足而导致的虚拟地震数据中反射波缺失问题。Ruigrok等^[26]探索了一种称为全局相位地震干涉法的新方法,该方法采用全局相位,提高了干涉的实用性。Tao等^[27]提出了一种新方法,可从平面波域中获取的地震响应的交叉相关中恢复虚拟地震数据。牟新刚等^[28]提出一种改进的地震干涉法,该方法拓展了高频段,提高了浅层分辨率,有效地解决浅部勘探盲区问题。王一臣^[29]提出了地震干涉法与S变换相结合的研究思路,与传统的时间域干涉相比,具有较高信噪比。

传统的地震干涉技术是针对垂直井间系统设计的,而在实际操作中这种采集系统占比很少,因此有必要提出适用于地表观测系统的地震干涉技术。现有的适用于地表观测系统的地震干涉技术具有众多约束,例如靶区面积远小于实际工具面积、上覆介质水平均匀,无法针对基准面下的高陡构造成像等,因此有必要克服上述束缚,研发出适用于高陡构造的地震干涉成像技术。

1 原理

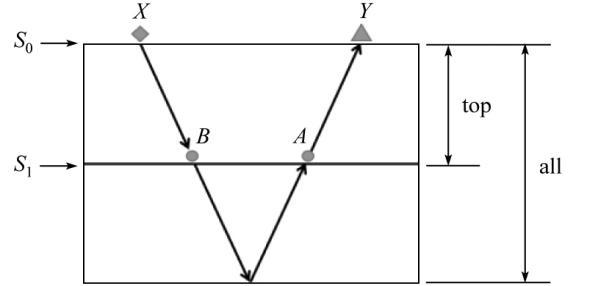
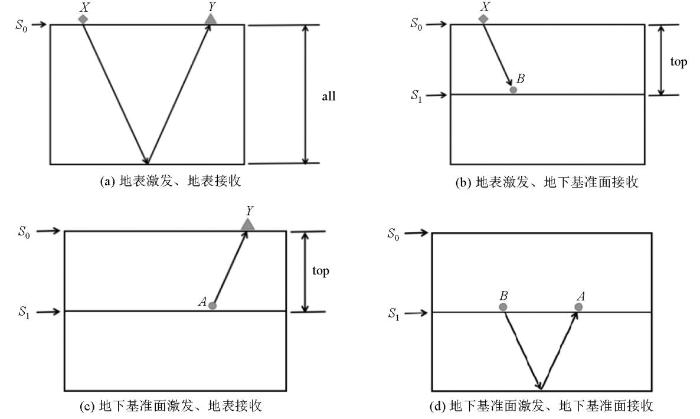
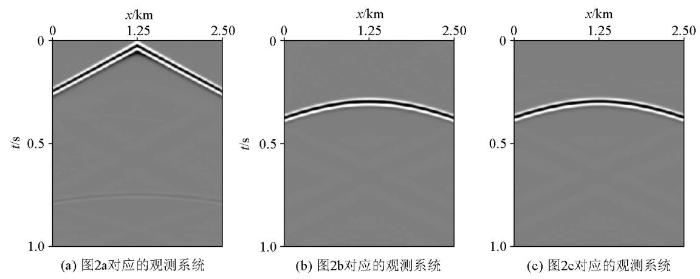
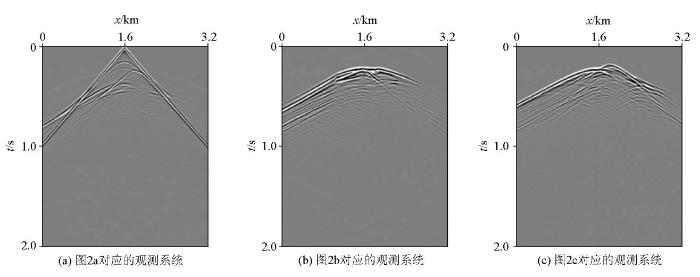
在实际应用中,地震干涉法可以用于处理各种复杂的地质构造,如高陡构造、断层、裂缝等。例如,针对近地表散射波分离问题,地震干涉法提供了一种有效的技术手段。通过将地震干涉理论与散射理论结合起来,可以导出近地表散射波地震干涉表达式,这些表达式由实际波场和背景波场干涉构成,有助于提高地震数据的信噪比和成像质量。本文提出一种面向高陡构造的地震干涉成像方法,通过将棱柱波方程代替传统的声波波动方程实现。通过图1说明本文提出方法的作用是将观测系统从地表S₀下移到地下基准面S₁,最终形成500 m×500 m网格数据成图(图1)。这需要输入3个观测系统下得到的炮记录,具体流程如图2~d所示。最终得到的是图2d所示的观测系统产生的炮记录。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 基于互相关原理的双重格林函数干涉方法示意

Fig.1 Schematic of the double Green’s function interferometry method based on the cross-correlation principle

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 基准面下移中间步骤

Fig.2 Intermediate steps of datum downward shift

在正演模拟计算时,记录下震源点到地下校准面的格林函数(图2b所示),采用互易定理,即可得到地下校准面到地表检波点的格林函数(图2c所示),无须二次计算。

传统地震干涉采用的是声波波动方程,得到的是一次反射波。不同观测系统下地震波的一次波炮记录,如式(1)~(3)所示:

(1)$\frac{\partial^{2} p_{0\left(\text { all }, S_{0}\right)}}{\partial t^{2}}=v^{2} \nabla^{2} p_{0\left(\text { all }, S_{0}\right)}+s_{\left(\text {all }, S_{0}\right)} \text {, }$

(2)$\frac{\partial^{2} p_{0\left(\text { top }, S_{0}\right)}}{\partial t^{2}}=v^{2} \nabla^{2} p_{0\left(\text { top }, S_{0}\right)}+s_{\left(\text {top }, S_{0}\right)},$

(3)$\frac{\partial^{2} p_{0\left(\text { top }, S_{1}\right)}}{\partial t^{2}}=v^{2} \nabla^{2} p_{0\left(\text { top }, S_{1}\right)}+s_{\left(\text {top }, S_{1}\right)},$

式中:p₀表示一次波;v表示速度;s表示震源;$\nabla^{2}$表示梯度算子。

式(1)表达了图2所示的观测系统,该系统是在整个速度模型中计算,震源和检波点都放置在地表,得到的是整个模型的一次波炮记录;式(2)表达了图2b所示的观测系统,该系统是在基准面以上的速度模型中计算,震源放置在地表,检波点放置在地下基准面,得到的是基准面以上的模型的一次波炮记录;式(3)表达了图2c所示的观测系统,与式(2)相同的是,该系统也是在基准面以上的速度模型中计算,得到的是基准面以上的模型的另一种传播路径下的一次波炮记录,与式(2)不同的是,该系统震源放置在地下基准面,检波点放置在地表。

本文提出的地震干涉采用的是棱柱波波动方程,得到的是包含高陡构造信息的多次反射波。不同观测系统下地震波的棱柱波炮记录,如式(4)~(6)所示:

(4)$\left(\nabla^{2}+\omega^{2} s_{\left(\text {all }, S_{0}\right)}^{2}\right) p_{0\left(\text { all }, S_{0}\right)}=\omega^{2} m_{\text {all }} p_{1\left(\text { all }, S_{0}\right)},$

(5)$\left(\nabla^{2}+\omega^{2} s_{\left(\mathrm{top}, S_{0}\right)}^{2}\right) p_{0\left(\mathrm{top}, S_{0}\right)}=\omega^{2} m_{\mathrm{top}} p_{1\left(\mathrm{top}, S_{0}\right)},$

(6)$\left(\nabla^{2}+\omega^{2} s_{\left(\mathrm{top}, S_{1}\right)}^{2}\right) p_{0\left(\mathrm{top}, S_{1}\right)}=\omega^{2} m_{\mathrm{top}} p_{1\left(\mathrm{top}, S_{1}\right)}$

式中:p₀表示一次波;p₁表示棱柱波;s表示震源;$\nabla^{2}$表示梯度算子;ω表示角频率;m_all表示全模型偏移结果;m_top表示基准面上覆介质偏移结果。式(4)~(6)是式(1)~(3)的棱柱波表达形式。

为了简化表达,不同观测系统下地震波的棱柱波炮记录用格林函数G表达,如式(7)~(9)所示:

(7)G_(Y,X)=p_{(all,S₀;Y,X)},

(8)G_(B,X)=p_{(top,S₀;B,X)},

(9)G_(Y,A)=p_{(top,S₁;Y,A)},

式中:G表示格林函数;X,Y,A,B表示坐标位置;top表示计算范围是基准面上侧的模型区域;all表示计算范围是全模型区域;S₀表示地表处激发震源;S₁表示地下基准面处激发震源。图2所示的X激发、Y接收的棱柱波炮记录与图2b所示的X激发、B接收的棱柱波炮记录进行互相关处理,前者传播路径为X-B-Y,后者传播路径为X-B,两者互相关处理消去X-B,得到B激发、Y接收的棱柱波炮记录,如式(10)所示:

(10)${G}_{(Y,B)}=-2i\omega {\sum }_{m}^{}{\sum }_{n}^{}{G}_{(B,X)}^{\ast }{G}_{(Y,X)}$

式(10)所示的B激发、Y接收的棱柱波炮记录与图2c所示的A激发、Y接收的棱柱波进行互相关处理;*表示取共轭。前者传播路径为B-A-Y,后者传播路径为A-Y,两者互相关处理消去A-Y,得到B激发、A接收的棱柱波炮记录,如式(11)所示:

(11)${G}_{(A,B)}=-2i\omega {\sum }_{m}^{}{\sum }_{n}^{}{G}_{(Y,A)}^{\ast }{G}_{(Y,B)}$

式中:G表示格林函数;X,Y,A,B表示坐标位置;m表示地表处检波点个数;n表示地下基准面处检波点个数;i表示虚部单位;ω表示角频率。

输出校准后的格林函数并作逆傅里叶变换,将棱柱波炮记录从频率域中变换到时间域中,如式(12)所示:

(12)${G}_{(A,B)}{|}_{output}=ifft\left({G}_{(A,B)}\right){|}_{({t}_{0},{t}_{max})}$

式中:G表示格林函数;A,B表示坐标位置;t₀表示激发时间;t_max表示人为选择的有效信号时长;ifft表示逆傅里叶变换;output表示输出。

用输出的炮记录做逆时偏移,采用互相关成像条件,如式(13)所示:

(13)$I(x,z)={\int }_{0}^{T}S(x,z,t)R(x,z,t)dt$

式中:I表示成像结果;S表示正传波场;R表示反传波场;x,z表示坐标位置;t表示时间;T表示总接收时间。

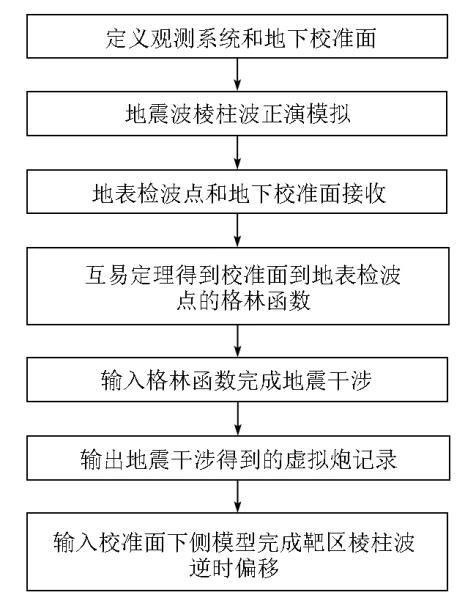
本文主要采用了两种技术,棱柱波逆时偏移和地震干涉。地震干涉的输入是炮记录,输出也是炮记录,需要将炮记录从时间域转换到频率域完成计算。计算参数是炮记录的采样点数。如果优化干涉效果,那么可以考虑对输入炮记录做汉宁窗处理,此时输入参数会额外包含汉宁窗的大小和位置。地震干涉完成后的逆时偏移处理的参数包含了网格大小,子波主频,采样间隔,采样点数。虽然输入的炮记录是做完地震干涉得到的虚拟炮记录,但是网格大小无需改变,常规逆时偏移网格大小精度即可满足本文方法。本文方法整体的技术实施方案流程如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 算法流程

Fig.3 Algorithm flow

2 模型试算

2.1 水平层状模型

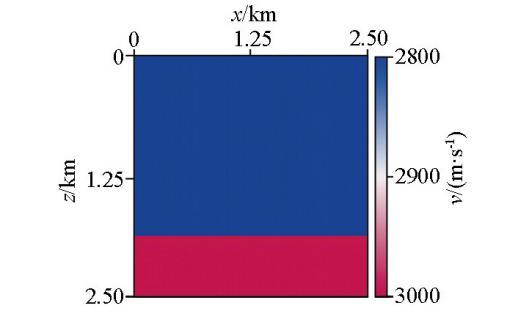
先对简单模型进行测试,如图4所示的两层水平模型,模型横向网格点数为251,纵向网格点数为251,基准面选在纵向深度1 500 m处。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 两层水平模型

Fig.4 Two-layer horizontal model

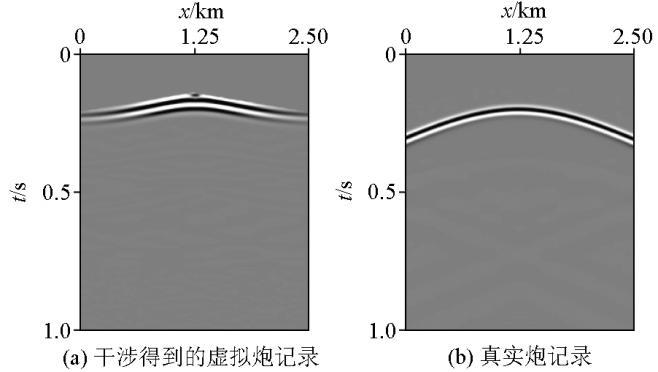
图5是图4在地表激发地表接收得到的炮记录。由于校准面上侧是均匀介质,因此图5b和图5c表现一致。图6为两层水平模型的干涉效果炮记录对比,其中,图6为重校准得到炮记录,图6b为真实情况下炮记录,通过对比可以看出本文方法得到炮记录具有真实炮记录的特征。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 模型下的输入炮记录

Fig.5 Input shot records under the model in figure 4

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 两层水平模型的干涉效果炮记录对比

Fig.6 Comparison of interference effect shot records of the two-layer horizontal model

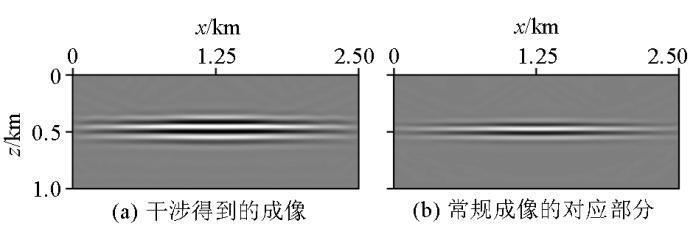
图7为两层水平模型的干涉效果逆时偏移对比,其中,图7为图6的干涉效果逆时偏移结果,图7b为图5的成像结果只取基准面下的部分,通过对比可以看出本文方法得到炮记录的逆时偏移结果与全局速度模型逆时偏移结果的基准面下的部分一样。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 两层水平模型的干涉效果逆时偏移对比

Fig.7 Comparison of reverse time migration of interference effect for the two-layer horizontal model

2.2 L模型

为了突显本文算法对棱柱波的作用,设计一个L模型,见图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 L模型

Fig.8 L model

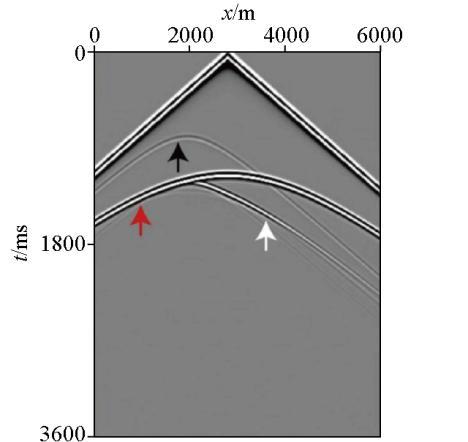
该模型横向600个网格点,纵向200个网格点,网格间距10 m。该模型的单炮记录见图9,由于模型较为简单,因此地震波类型较少,红色箭头和白色箭头所指的是水平地层处产生的反射波。黑色箭头所指的是棱柱波,相较于其他复杂模型,该模型的棱柱波清晰可见,因此是验证本文算法的代表性模型。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 L模型的单炮记录

Fig.9 Single shot record of the L model

针对该模型,设计校准面为地下500 m处,震源点和检波点均位于地表,均匀分布,间隔3个网格点。常规干涉后的成像剖面见图10,棱柱波干涉后的成像剖面见图10b,对比两图的红色箭头处,可以发现本文算法可有效对高陡构造进行还原,证明了本文算法对棱柱波进行了下移处理。常规干涉和棱柱波干涉方法的处理流程并没有什么差异,只是输入和输出有差异。常规干涉需要输入一次反射波的格林函数,棱柱波干涉需要输入棱柱波格林函数。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 L模型的成像效果对比

Fig.10 Comparison of imaging effects of the L model

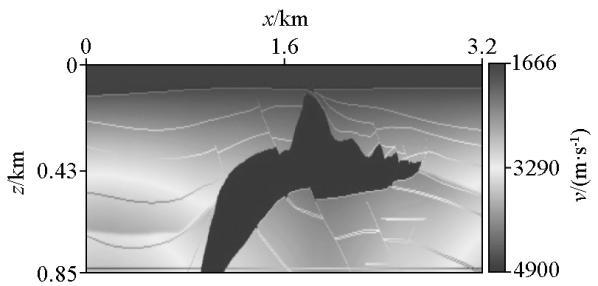
2.3 盐丘模型

再对复杂模型进行测试,如图11所示的盐丘模型。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 盐丘模型

Fig.11 Salt dome model

该模型横向网格点数为641,纵向网格点数为170,基准面选在纵向深度550 m处,震源点数均匀分布在地表,个数为214,检波点和震源点完全重合,炮记录接收时间长度为2 s,选用雷克子波,主频25 Hz,采样间隔0.5 ms。图12为图11模型下的输入炮记录。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 盐丘模型的输入炮记录

Fig.12 Input shot records of the salt dome model

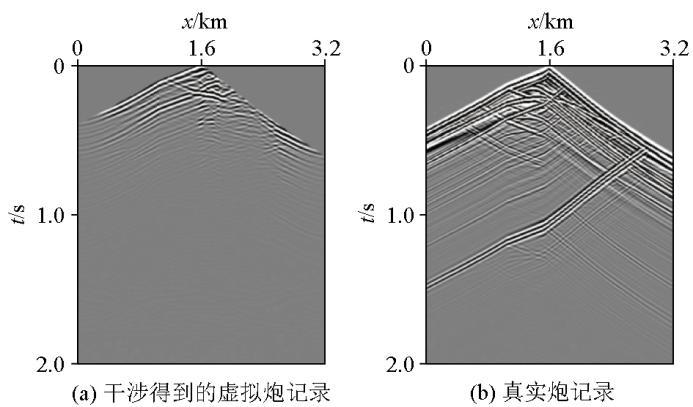
图13为盐丘模型的干涉效果炮记录对比,其中,图13为重校准得到炮记录,图13b为真实情况下炮记录,通过对比可以看出本方法得到炮记录具有真实炮记录的特征。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 盐丘模型的干涉效果炮记录对比

Fig.13 Comparison of interference effect shot records of the salt dome model

图14为盐丘模型的干涉效果逆时偏移对比,其中,图14为图13的干涉效果逆时偏移结果,图14b为图12的成像结果只取基准面下的部分,通过对比可以看出本方法得到炮记录的逆时偏移结果与全局速度模型逆时偏移结果的基准面下的部分一样,且盐丘下侧(箭头指示)成像结果更好。图15展示了未考虑棱柱波的常规干涉成像效果,可以发现倾斜构造的还原程度不如图14。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 盐丘模型的干涉效果逆时偏移对比

Fig.14 Comparison of reverse time migration of interference effect for the salt dome model

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 常规干涉成像效果

Fig.15 Conventional interferometric imaging effect

地震干涉的用处主要是用来降低计算成本。表1将3种计算方法进行了对比。通过表1可以看出,常规RTM的计算成本是常规干涉的5.7倍左右,证明了干涉确实减少了计算成本。棱柱波干涉的计算成本是常规干涉的1.5倍左右,但是提高了计算精度并且计算量还是小于常规RTM。在地震干涉的两次互相关运算中,地震子波发生改变,旁瓣变宽,此时如果直接将地震干涉得到的虚拟炮记录作为逆时偏移的输入炮记录进行处理,得到的剖面分辨率会降低。如果不做其他处理,那么得到的偏移结果分辨率确实无法满足超深层的生产需求。但通过地表一致性反褶积对地震子波进行压缩,压缩后的优化虚拟炮记录作为逆时偏移的输入炮记录进行处理,那么会提高地震剖面的分辨率,解决超深层的生产问题。

表1 计算成本对比

Table 1 Comparison of computational costs

计算时间	棱柱波干涉	常规干涉	常规RTM
s	997	662	3752

新窗口打开| 下载CSV

2.4 实际资料测试

为了验证本文方法的实用性。在我国某东部工区实际资料进行了测试。图16展示了常规逆时偏移成像,可以看到同相轴不连续,可追踪性较差。图16b展示了本文方法成像结果,可以看到地下高陡构造的成像精度得到提升。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 我国某东部工区实际资料

Fig.16 Actual data from an eastern work area in China

3 讨论

本文方法主要适用于地层倾角大于45°的高陡构造区域,如盐丘侧翼、逆冲断层带等。其有效性依赖于棱柱波的激发与传播,因此模型中存在明显的速度梯度,以确保棱柱波能够有效产生并携带陡倾角构造信息。通过数值模拟发现,速度误差超过5%时,棱柱波成像的分辨率显著下降。

本文方法考虑了计算效率和高陡构造成像问题,但整体还是基于逆时偏移技术开展的。目前还不能有效的解决起伏地表问题,粘介质问题,各向异性介质问题。其中,地震干涉只需要输入格林函数进行互相关运算,无关乎地表问题,介质问题,但棱柱波逆时偏移方程需要考虑上述问题。地震干涉相较于最近提出的Marchenko技术和最小二乘地震干涉,计算精度低,但是计算效率高,且Marchenko技术对原始输入地震资料的要求较高。因此,为了实用化,以后的研究方向考虑将地震干涉技术与人工智能相结合,将旁瓣拓宽的地震子波进行有效压缩,提高分辨率。

4 结论

观测系统下移分为两部分,第一部分是消去震源点到校准面的地震波传播路径下的反射波,第二部分是消去检波点到校准面的地震波传播路径下的反射波,这两部分都是在频率域内完成互相关计算,占比不到逆时偏移成像的百分之一,因此可忽略不计。棱柱波是一种多次波,传统成像方法中,多次波通常被视为噪声并被去除。然而,棱柱波在高陡构造的成像中具有独特优势,能够有效成像。尽管如此,棱柱波的计算量通常大于常规一次波,这在实际生产中会增加勘探成本并延长成像周期。为了在提高计算效率的同时加强高陡构造的成像精度,本文提出了一种结合地震干涉数据处理技术与棱柱波逆时偏移技术的方法。通过引入互易定理,避免了地表观测系统和地下校准面之间格林函数的二次计算,从而显著提高了计算效率。在地震干涉处理中,观测系统的下移分为两部分:消去震源点到校准面的地震波传播路径下的反射波。消去检波点到校准面的地震波传播路径下的反射波。这两部分均在频率域内完成互相关计算,其计算量仅占逆时偏移成像的不到百分之一,因此可以忽略不计。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Biondi

B L

, Clapp

R G

, Prucha

, et al.

3D prestack wave-equation imaging-a rapidly evolving technology

[C]//Florence: 64^th EAGE Conference & Exhibition, European Association of Geoscientists & Engineers, 2002:cp-5-00159.