基于深度学习的零井源距VSP上、下行波分离方法

doi:10.11720/wtyht.2025.0115

基于深度学习的零井源距VSP上、下行波分离方法

王腾宇^,¹^,²^,³, 邓丁丁^,⁴, 郑多明¹^,²^,³, 刘洋⁴, 张振¹, 罗文君⁵

1.中国石油天然气股份有限公司塔里木油田分公司勘探开发研究院, 新疆库尔勒 841000

2.中国石油天然气集团有限公司超深层复杂油气藏勘探开发技术研发中心, 新疆库尔勒 841000

3.新疆维吾尔自治区超深层复杂油气藏勘探开发工程研究中心, 新疆库尔勒 841000

4.中国石油大学(北京) 油气资源与工程全国重点实验室, 北京 102249

5.北京博豪罗根石油技术有限公司, 北京 100085

A deep learning-based method for separating up- and down-going waves in zero-offset vertical seismic profiles

WANG Teng-Yu^,¹^,²^,³, DENG Ding-Ding^,⁴, ZHENG Duo-Ming¹^,²^,³, LIU Yang⁴, ZHANG Zhen¹, LUO Wen-Jun⁵

1. Research Institute of Exploration and Development, Tarim Oilfield Company, PetroChina, Korla 841000, China

2. R&D Center for Ultra-Deep Complex Reservoir Exploration and Development, CNPC, Korla 841000, China

3. Engineering Research Center for Ultra-deep Complex Oil and Gas Reservoir Exploration and Development, Xinjiang Uygur Autonomous Region, Korla 841000, China

4. State Key Laboratory of Petroleum Resources and Engineering, China University of Petroleum (Beijing), Beijing 102249, China

5. Beijing Borehole Logging Petroleum Technology Co., Ltd., Beijing 100085, China

通讯作者: 邓丁丁(1999-),男,博士在读,主要研究方向为人工智能地震资料处理方法。Email:dantecup@163.com

第一作者: 王腾宇(1992-),男,物探高级工程师,主要从事井中地震、重磁电方向技术研究相关工作。Email: wtyu-tlm@petrochina.com.cn

收稿日期: 2025-04-1 修回日期: 2025-08-8

基金资助:

中石油塔里木项目“超深层井中地震与重磁电研究”(YF202401.01.05)

Received: 2025-04-1 Revised: 2025-08-8

摘要

波场分离是垂直地震剖面(VSP)数据处理的关键步骤,其精度直接影响地震成像、弹性参数反演、岩性识别和含油气性解释的精度。中值滤波分离波场时需要人工操作,往往会造成误差,影响波场分离的精度;FK滤波方法分离精度高,但效率低;深度学习技术的自动化程度更高,可以实现高精度、高效率的波场分离。本文提出了一种基于深度学习进行VSP数据上、下行波分离的方法。首先,利用FK变换对零井源距VSP数据进行上、下波分离以制作数据集;然后,构建了一种用于分离VSP上、下行波的深度学习模型——Unet++;最后,为了减轻上、下行波振幅差异对网络更新的影响,在损失函数中加入了相对下行波场(通过从全波场中减去预测的上行波场得到),同时引入结构性相似指数作为正则化约束来辅助网络学习波场的结构特征。实际数据测试结果表明,训练后的网络可以有效地学习到上、下行波的特征,可实现高精度、高效率的波场分离。

关键词： 深度学习; 波场分离; 垂直地震剖面(VSP); Unet++

Abstract

Wavefield separation serves as a key step in processing the data of vertical seismic profiles (VSPs). Its accuracy directly influences seismic imaging, inversion of elastic parameters, lithology identification, and interpretation of hydrocarbon-bearing properties. Traditional methods face challenges in wavefield separation. For example, the median filtering requires manual intervention, often introducing errors and thus compromising separation accuracy; the FK filtering yields high accuracy but low efficiency. In contrast, deep learning techniques offer high automation, enabling both high accuracy and efficiency in wavefield separation. Hence, this study proposed a deep learning-based method for separating up- and down-going waves in zero-offset VSPs. First, the up- and down-going waves were separated through FK transform, generating a dataset. Second, a deep learning-based model, Unet++, was constructed for separating these waves in VSPs. Third, the relative down-going wavefield (obtained by subtracting the predicted up-going wavefield from the full wavefield) was incorporated into the loss function to mitigate the impacts of amplitude differences between up- and down-going waves on network updates. Moreover, the structural similarity index measure (SSIM) was employed as a regularization constraint to assist the network in learning the structural characteristics of the wavefield. The test results of actual VSP data demonstrate that the trained network can effectively learn the characteristics of the up- and down-going waves, achieving high accuracy and efficiency in wavefield separation.

Keywords： deep learning; wavefield separation; vertical seismic profile (VSP); Unet++

PDF (10274KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王腾宇, 邓丁丁, 郑多明, 刘洋, 张振, 罗文君. 基于深度学习的零井源距VSP上、下行波分离方法[J]. 物探与化探, 2025, 49(6): 1319-1332 doi:10.11720/wtyht.2025.0115

WANG Teng-Yu, DENG Ding-Ding, ZHENG Duo-Ming, LIU Yang, ZHANG Zhen, LUO Wen-Jun. A deep learning-based method for separating up- and down-going waves in zero-offset vertical seismic profiles[J]. Geophysical and Geochemical Exploration, 2025, 49(6): 1319-1332 doi:10.11720/wtyht.2025.0115

0 引言

与地面地震资料相比,垂直地震剖面(vertical seismic profiling,VSP)资料具有初至波清晰、波场信息丰富、信噪比高等特点。其中零井源距VSP资料,因为偏移距较小,其下行初至波可认为是垂直传播,通常可利用其上行波场和下行波场提取地层纵横波速度比、泊松比等物性参数^[1]。上行波场可用于开展反射波成像,而下行波场用于计算速度、品质因子等^[2]。然而,井内检波器接收的VSP数据包含混叠的上行和下行波场,因此,获得高精度的上行和下行波场至关重要^[3]。此外,这一过程的准确性直接影响到随后的偏移成像、衰减分析^[4]、地震解释^[5]和反演^[6]。有多种方法可以实现VSP波场分离,包括中值滤波^[7]、FK滤波^[8]和Radon变换^[9]等。然而,这些方法存在一定的局限性:中值滤波由于其平均效应,会模糊波场中的一些细节;FK滤波和Radon变换由于其算法机制,会引入截断伪影,影响VSP波场分离的精度;此外,变换域滤波方法需要在变换域中手动设置窗口,人工操作会影响波场分离精度。

目前,人工智能在油气地震数据的处理和解释领域发展迅速^[10-11],深度学习方法以其多层网络结构和非线性激活函数为特征,在解决复杂非线性问题方面得到了广泛关注^[12-14]。深度学习方法已成功应用于初至波拾取^[15-16]、速度自动拾取^[17]、分离地震数据^[18-19]、去噪^[20-22]、地震反演^[23-24]和地震相识别^[25]。深度学习技术可以克服传统VSP波场分离方法的局限性,实现高精度波场分离。Tao等^[26]提出了利用深度学习进行VSP上、下行波分离并将其应用于实际数据,取得了良好的效果,但是使用Unet进行VSP波场分离会导致分离结果中一些有效信号的丢失。Cao等^[27]利用生成对抗网络(GAN)进行VSP上、下行波分离,取得了很好的效果,但是GAN网络训练困难,限制了其实际应用。

本文采用Unet++模型,将来自编码器网络的特征图与不同解码器网络的相应波场分离的特征图融合,以更有效地分离VSP数据中的上、下行波。

1 数据集准备

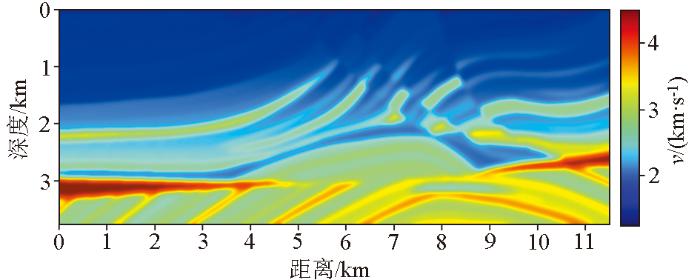
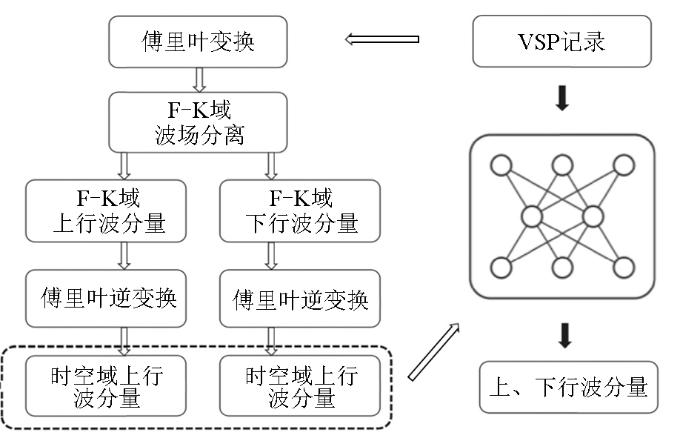
本文利用A区实测的零井源距VSP数据进行深度学习模型的训练和验证。首先,利用图1所示Marmousi模型进行有限差分正演模拟VSP数据,并通过FK滤波方法得到上、下行波标签。起始井x=1 km,井间距为1 km,共得10口井(M1~M10)的零井源距VSP数据。对实际零井源距VSP数据进行去噪处理;然后,通过FK变换滤波得到上、下行波并利用滤波器去除截断伪影;接着,需要对准备好的VSP数据进行归一化处理;最后,利用滑动分块技术构建训练样本。图2为基于FK滤波的VSP上、下行波分离流程。图3为A区w1井的零井源距VSP数据的分块部分结果展示。表1为合成数据和野外零井源距VSP数据分块前、后的维度一览。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 Marmousi模型

Fig.1 Marmousi model

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 基于数据驱动深度学习的VSP上、下行波分离流程

Fig.2 Data driven deep learning based up-/ downgoing wave separation process for VSP

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 A区部分VSP数据的分块(同一颜色表示相同的振幅值)

Fig.3 Block of VSP data for part of survey A (the same color indicates the same amplitude value)

表1 合成数据集和A区零井源距VSP数据分块前、后的维度

Table 1 Dimensional overview before and after block division of synthetic dataset and zero-offset VSP data in area A

井号	分块前	分块后
M1~M10	10×(3381, 316)	10×(335, 128, 128)
w1	(5001, 388)	(693, 128, 128)
w2	(6001, 407)	(833, 128, 128)
w3	(6001, 337)	(714, 128, 128)
w4	(5001, 677)	(1188, 128, 128)

新窗口打开| 下载CSV

利用预先准备的数据集进行Unet++模型的训练和参数调整。使用Huber范数和结构性相似指数(SSIM)作为损失函数更新网络。在波场分离任务中,Unet++输出上行波场和下行波场,由于下行波能量强于上行波,如果按相同权重计算损失函数,则损失函数受下行波场的影响大,这会使得网络参数主要基于下行波的梯度反向传播进行更新,导致网络优先学习下行波场特征而对上行波特征的学习不充分,因此会影响上行波场的分离精度。在损失函数中加入相对下行波场(通过从整个波场中减去预测的上行波场得到)可以缓解这一问题。Huber范数巧妙地融合均方误差(MSE)和平均绝对误差(MAE)的优势,对异常值提供了更强的鲁棒性^[29],同时,引入结构性相似指数SSIM^[30]来辅助网络学习上、下行波的方向特征,因此,采用Huber损失和SSIM的组合作为神经网络的损失函数。Huber范数表达式为:

在使用深度学习进行波场分离时,训练数据的生成和网络结构的设计至关重要。为了解决训练样本缺乏的问题,对合成数据和实际数据进行了滑动切块,形成了一个信息丰富的数据集。考虑到上、下行波的传播方向不同,引入了SSIM来提高网络的识别能力。为了减轻上、下行波之间能量差对网络更新的影响,使用相对下行波场来表示损失函数的正则化项,进一步减小分离误差。

选取M2~M10井、w1井、w2井和w4井的VSP分块后数据作为神经网络模型的训练集和验证集,比例为8∶2,将w3井的VSP数据作为测试集。

2 方法原理

2.1 网络结构

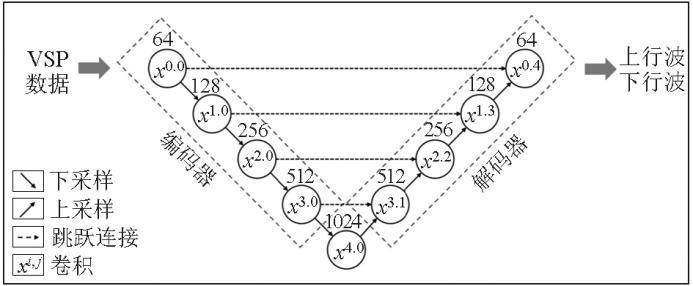
Unet是地震资料信号处理领域中最常用的深度学习模型,其网络结构如图4所示。Unet模型由编码器(下采样)和解码器(上采样)两部分构成。编码器是传统的CNN结构,通过增加特征图数量并减少空间分辨率,提取从深层次到浅层次的特征。解码器负责在编码过程中逐步恢复输入数据的特征,同时提高分辨率。跳跃连接将低分辨率的全局特征和高分辨率的局部特征有效融合,从而提升输出的有效性。用于波场分离任务的Unet,其工作原理是:首先,利用编码器将时空域的VSP地震信号进行编码,通过下采样的方式在高维特征空间中提取信号的特征,并分离VSP信号中耦合的上、下行波分量;接着,将分离后的上、下行波信号进行解码,通过上采样的方式将数据恢复为时空域的上、下行波。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 Unet网络结构示意

Fig.4 Schematic diagram of Unet network structure

Unet的每个编码器层由两个无偏差的级联卷积层构成,以提升波场分离精度。每个卷积层值的计算公式为:

(1)${Z}_{i,j,k}^{n}={w}_{k}^{nT}{X}_{i,j}^{n}+{b}_{k}^{n}$

式中:${Z}_{i,j,k}^{n}$是第n个隐藏层第k维特征图(i,j)处的值;${w}_{k}^{n}$是第n个隐藏层第k维卷积层的权重矩阵;${b}_{k}^{n}$是第n个隐藏层第k维卷积层的偏置项;${X}_{i,j}^{n}$是以第n个隐藏层的输入。

Unet模型存在两个局限性:一是最优深度未知,需要进行大量架构搜索或低效集成不同深度的模型;二是跳跃连接施加了不必要的限制性融合方案,即跳跃连接仅在相同比例特征映射的编码器和解码器网络上^[28]。为了解决这两个局限性并且满足VSP高精度波场分离的需求,引入了一种新的基于嵌套和密集跳跃连接的深度学习架构Unet++,构建了一种基于Unet++的VSP上、下行波分离的方法。该方法的主要优势在于:①通过集成不同深度的Unet模块来解决网络深度不明确的问题,多个Unet部分共享编码器,并采用深度监督共同学习;②对跳跃连接进行了重新设计,融合了来自不同尺度解码器子网络的特征,形成了灵活的特征整合方案;③提出了一种剪枝策略,模型训练完毕后可以通过裁剪冗余的分支结构来提升Unet++的推理效率。该方法的工作原理是:首先,利用编码器将VSP地震信号进行编码,通过下采样的方式在高维特征空间中提取信号的特征,并分离VSP信号中耦合的上、下行波分量;然后,聚合并解码不同尺度子网络中的特征,通过上采样的方式获得上、下行波。

Unet++采用来自编码器网络的高分辨率特征图与来自不同解码器网络的相应波场分离的特征图融合,以更有效地捕获VSP数据中上、下行波的特征。与Unet中常用的普通跳过连接形成对比,Unet++独特的跳跃连接方式直接将高分辨率特征图从编码器快速推进到解码器网络,从而导致不同的特征图融合。这一操作,让Unet++具备了更好的网络连通性。设Xⁱ^,^j表示节点i,j的输出,即特征映射堆栈,其中i表示沿编码器的下采样层,j表示沿跳过连接的密集块的卷积层。其计算公式为:

(2)${X}^{i,j}=\left\{\begin{array}{ll}H\left(D\right({X}^{i-1,j}\left)\right),& j=0;\\ H\left(\right[({X}^{i,k}{)}_{k=0}^{j-1},U({X}^{i+1,j-1}\left)\right]),& j0。\end{array}\right.$

式中:函数H(·)代表卷积操作,随后利用一个激活函数进行非线性变换;U(·)和D(·)分别表示上采样和下采样;[]表示连接层。

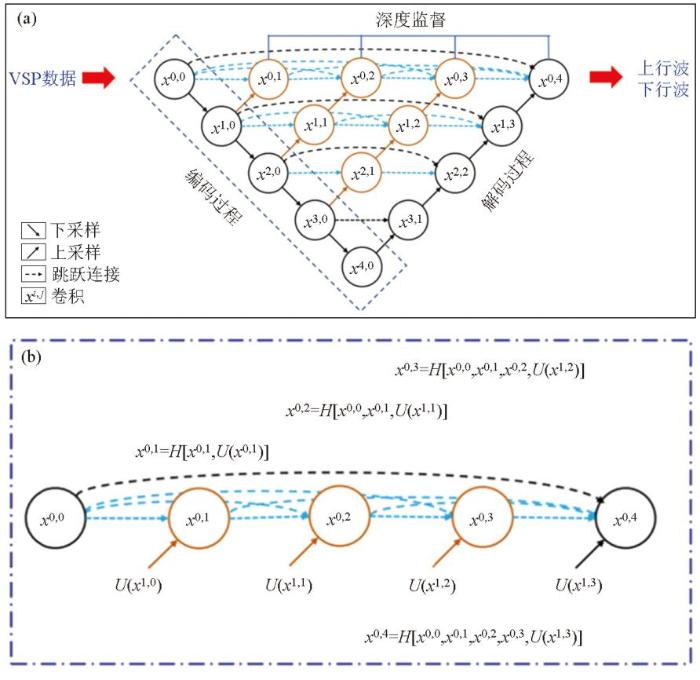
如图5所示, 层级j=0的节点仅接收上一层的单一输入;层级j=1的节点接收来自两个连续层级的编码器子网络的输入;层级j>1的节点接收j+1个输入,其中j个输入是同一跳跃连接中前j个节点的输出,层级j+1输入来源于下层跳跃连接的上采样结果。所有先前的特征映射累积并到达当前节点,在每个跳跃连接上使用了密集的卷积块。Unet++通过引入深度监督提高了模型适应性。为此,通过向节点X^0,1、X^0,2、X^0,3和X^0,4的输出附加一个1×1卷积和一个ReLU激活函数进行特征融合。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 Unet++网络结构示意(a)及其第一次跳跃路径的详细分析(b)

Fig.5 Schematic of Unet++ network architecture(a)and detailed analysis of the first skip connection pathway(b)

2.2 模型训练和验证

(3)$\begin{array}{l}{L}_{huber}(y,G(x\left)\right)=\\ \left\{\begin{array}{l}\sum _{i=1}^{N}\frac{1}{2\beta }\left(G\right({x}_{i})-{y}_{i}{)}^{2},\left|G\right.({x}_{i})-{y}_{i}|\beta ;\\ \sum _{i=1}^{N}\left|G\right.({x}_{i})-{y}_{i}|-\frac{1}{2}\beta,\left|G\right.\left({x}_{i}\right)-{y}_{i}|\ge \beta 。\end{array}\right.\end{array}$

式中:x、y分别为输入和输出数据;β为超参数;N为样本数;G表示神经网络的映射关系。

(4)$\begin{array}{l}SSIM[y,G(x\left)\right]=\\ \frac{\left(2\right.{\mu }_{G\left(x\right)}{\mu }_{y}+{C}_{1}\left)\right(2{\sigma }_{G\left(x\right)}{\sigma }_{y}+{C}_{2})}{({\mu }_{G\left(x\right)}^{2}+{\mu }_{y}^{2}+{C}_{1})({\sigma }_{G\left(x\right)}^{2}+{\sigma }_{y}^{2}+{C}_{2})}\end{array}$

式中:μ为均值;σ为方差;C₁、C₂为常数,本文分别取0.01和0.03。

本文深度学习模型的损失函数表达式为:

(5)$\begin{array}{l}Loss={L}_{huber}[{y}_{down},G({x}_{down}\left)\right]+{L}_{huber}[{y}_{down},x-\\ G\left({x}_{up}\right)]+{L}_{ssim}[{y}_{down},G\left({x}_{down}\right)]+{L}_{ssim}[{y}_{up},\\ G\left({x}_{up}\right)]\end{array}$。

为了更有效地优化Unet++网络参数,选择自适应矩估计(Adam)算法作为优化器。

2.3 网络模型实现

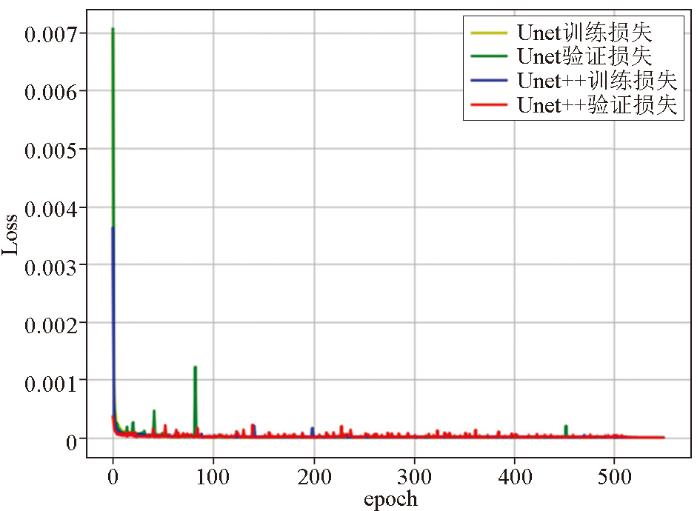
在PyTorch框架下搭建Unet和Unet++网络,分别实现了VSP数据上、下行波分离。网络模型在16 GB内存的NVIDIA Tesla V100 GPU 高性能计算显卡上进行了训练、验证和测试。使用Adam优化器对模型参数进行优化,批次大小为16,分块大小为128×128。图6为模型学习曲线。初始学习率设置为1e^-4,学习率在500个周期后开始衰减,每个周期遍历完所有训练集,并用验证集调整模型参数,最终在第550个周期后停止训练。由图6可知,在模型训练初期,Unet++网络的训练和验证损失(loss)小于Unet,并且随着迭代次数的增加,Unet++的学习曲线更加平稳。两种模型的训练、验证损失都趋于0,说明模型充分收敛。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 模型学习曲线

Fig.6 Model learning curve

3 合成数据示例

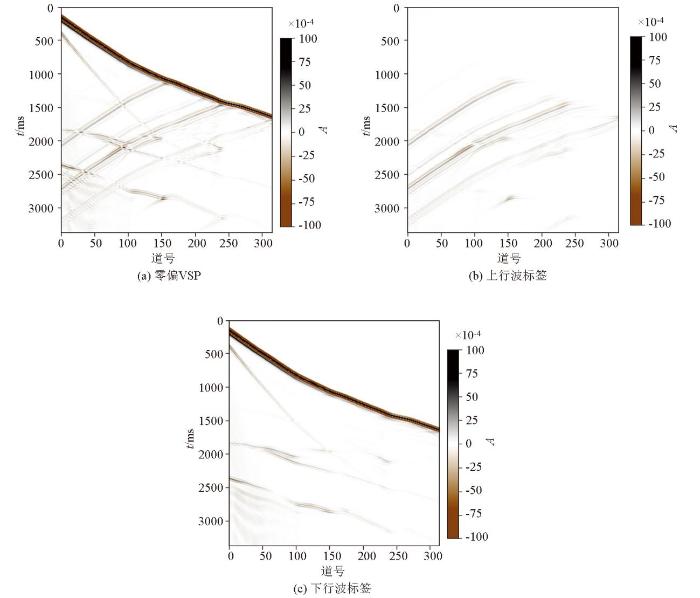
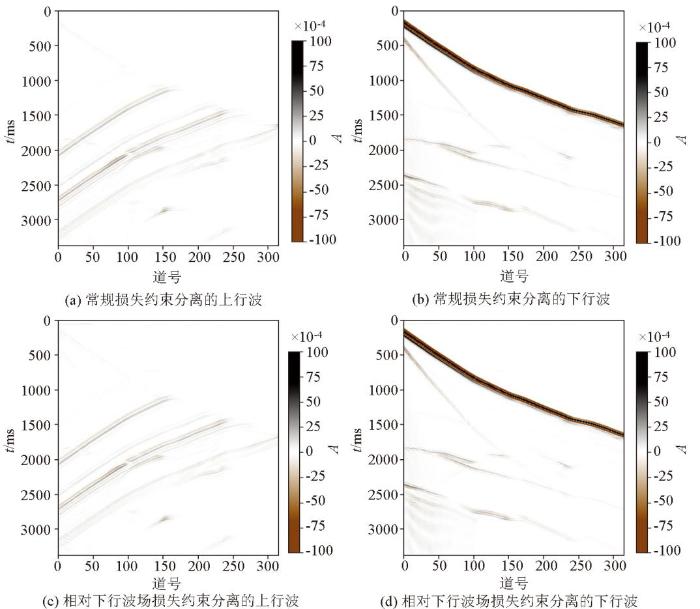
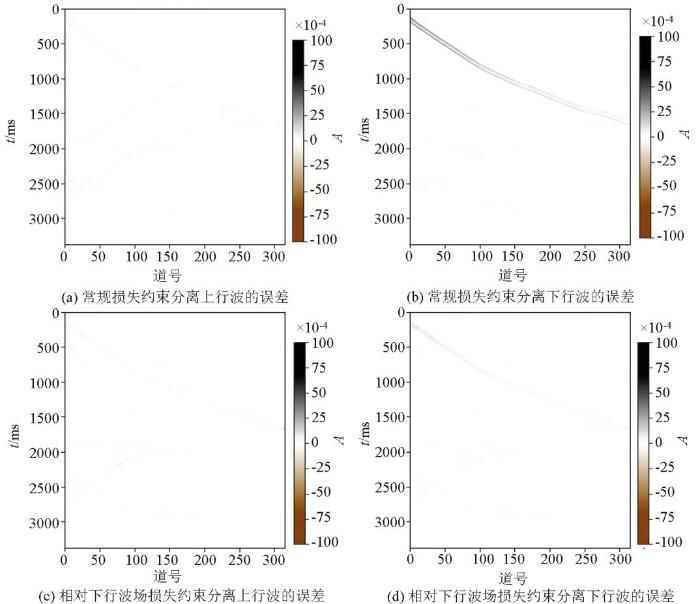
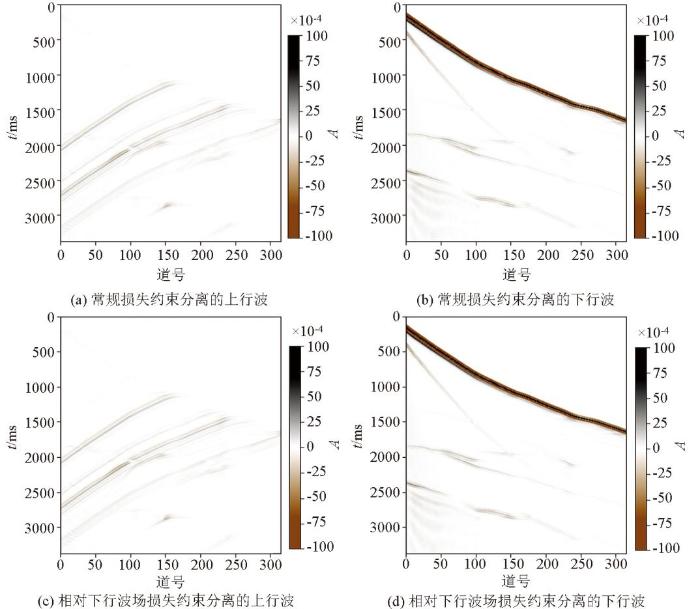
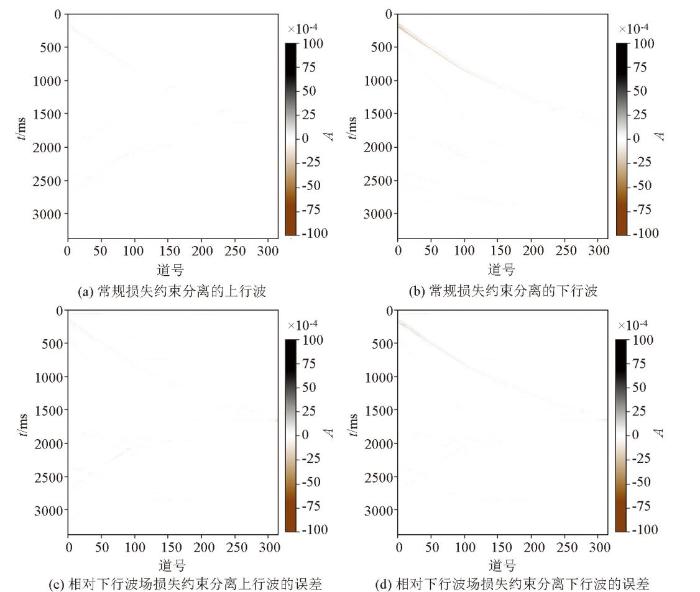
为了减轻上、下行波振幅差异对模型参数的影响,在损失函数中加入相对下行波波场(通过从全波场中减去预测的上行波场得到),使用合成VSP数据评估不同损失函数对Unet和Unet++模型的影响。图7b、c分别为图7数据经FK分离后的上、下行波标签,图8为M1零井源距合成VSP数据在常规损失和加入相对下行波场损失条件下的Unet波场分离结果对比,图9为常规损失和加入相对下行波场损失Unet波场分离结果与标签的残差对比;结果表明,当引入了相对下行波场之后,Unet分离得到了更准确的上、下行波。图10为M1零井源距合成VSP数据在常规损失和加入相对下行波场损失条件下的Unet++波场分离结果对比,图11为常规损失和加入相对下行波场损失的Unet++波场分离结果与标签的残差对比,可见相对下行波场的引入,改进了Unet++波场分离的准确性。图9b和图11b的误差对比结果表明,在同等约束条件下,Unet++相比较Unet的波场分离精度更高。实验结果表明,常规损失没有考虑到上、下行波的能量差异,在初至波处存在较大误差;相对下行波场损失可以缓解上、下行波能量差异的问题,从而提高波场分离的精度。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 M1零井源距合成VSP数据及上、下行波标签

Fig.7 M1 zero-offset synthetic VSP data and up- /down going wave labels

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 M1零井源距合成VSP数据在常规损失和加入相对下行波场损失条件下的Unet波场分离结果对比

Fig.8 Comparison of Unet wavefield separation results for M1 zero-offset synthetic VSP data with conventional loss and adding relative downgoing wavefield loss

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 常规损失和加入相对下行波场损失Unet波场分离结果与标签的残差对比

Fig.9 Comparison of residuals between Unet wavefield separation results and labels with conventional loss and adding relative downgoing wavefield loss

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 M1零井源距合成VSP数据在常规损失和加入相对下行波场损失条件下的Unet++波场分离结果对比

Fig.10 Comparison of Unet++ wavefield separation results for M1 zero-offset synthetic VSP data with conventional loss and adding relative downgoing wavefield loss

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 常规损失和加入相对下行波场损失Unet++波场分离结果与标签的残差对比

Fig.11 Comparison of residuals between Unet++ wavefield separation results and labels with conventional loss and adding relative downgoing wavefield loss

4 实际数据测试

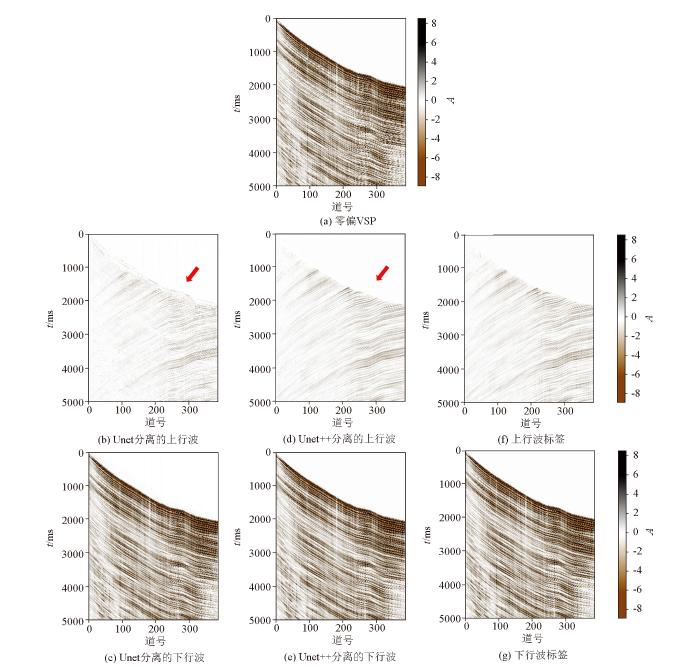
为了评估深度学习模型的性能,使用A区w1零井源距VSP数据进行了波场分离测试。图12展示了A区w1零井源距数据,由于复杂的地质条件,VSP记录呈现出明显的复杂性,包含上行波和下行波。图12b、c分别为图12数据经Unet模型分离后的上、下行波,结果表明,分离过程中有效信号出现了显著损失,与其他方法分离的上行波场能量相比,在图12b中能够明显观察到信号损失的差异。图12d、e展示了使用Unet++模型进行分离的上、下行波,波场连续性好,有效信号损失较少。图12f、g为对应的上、下行波标签。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 A区w1零井源距VSP数据在不同深度学习模型的波场分离结果对比

Fig.12 Comparison of wavefield separation results for zero-offset VSP data in A-w1 using different deep learning models

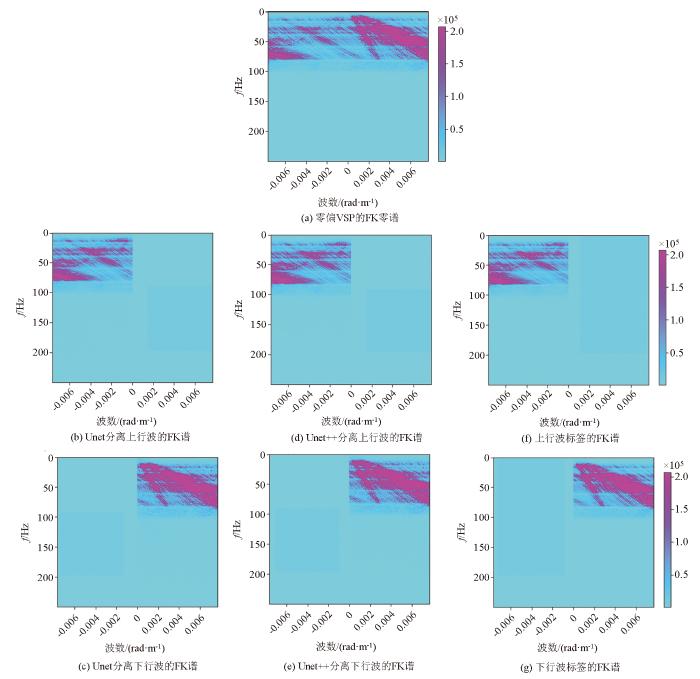
图13为图12对应的FK谱。图中表明:Unet模型分离的上、下行波产生了少量空间假频(图13b、c中红箭头所指);相对Unet而言,Unet++模型分离的上、下行波的频率特征与标签更吻合。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 不同深度学习模型波场分离结果的FK谱

Fig.13 FK spectra of wave field separation results of different deep learning models

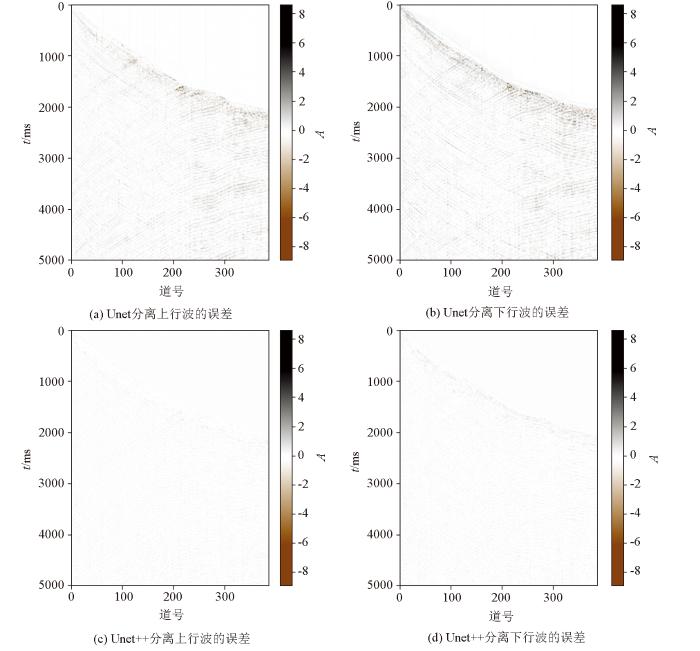
图14展示了A区w1零井源距VSP数据在不同深度学习模型下波场分离结果与标签的残差对比,表明Unet模型分离后的有效信号的损失较为显著,而Unet++模型分离后有效信号的损失较少。与Unet方法相比,Unet++通过不同深度的Unet的有效集成来增强模型表达能力,这些Unet部分共享编码器并使用深度监督同时共同学习,聚合解码不同尺度子网络中的特征,形成高度灵活的特征融合方案,可以更有效地捕获原始VSP数据中上、下行波的特征。这与Unet中常用的普通跳过连接形成对比,后者直接将高分辨率特征图从编码器快速推进到解码器网络,从而导致不同的特征图融合。结果表明,Unet方法波场分离精度较低,而Unet++方法可以更有效地分离VSP数据中上、下行波。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 不同深度学习模型波场分离结果与标签的残差对比

Fig.14 Residual comparison between wavefield separation results and labels across different deep learning models

表2列出了A区不同方法的波场分离计算成本。由表可知,Unet++模型训练所需的计算成本比Unet模型更高,但推理时间相差无几。深度学习模型训练完毕后,可以实现VSP上、下行波智能分离。相比较FK滤波方法,深度学习模型可以实现自动化、高效率的波场分离。

表2 A区不同方法的波场分离计算成本

Table 2 Computational cost of wave-field separation for different methods in area A

	FK滤波	Unet	Unet++
占用显存/MiB	-	5874	15114
耗时/s	258.8	81.2	110.4

新窗口打开| 下载CSV

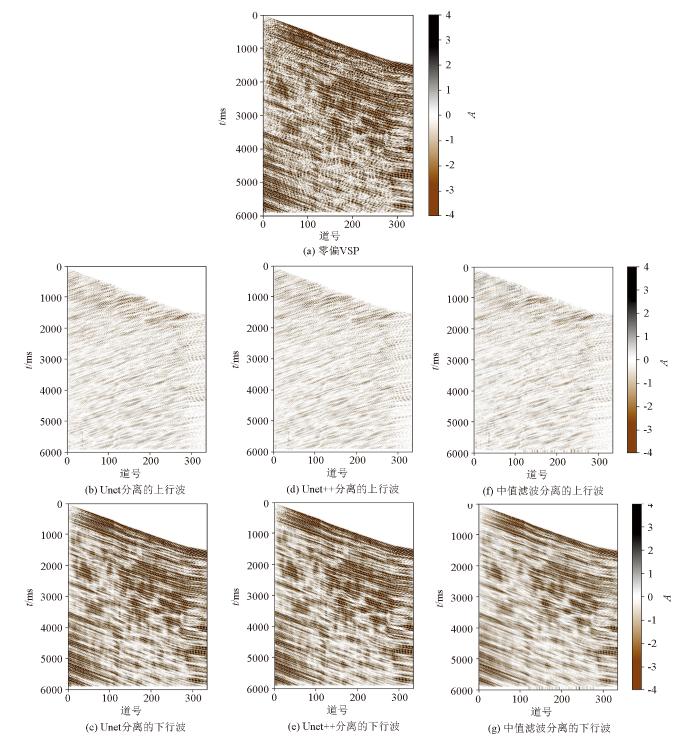
为了进一步验证所提出方法的有效性,使用A区w3零井源距VSP数据进行了测试,旨在评估该方法的适用性及泛化能力。图15展示了A区w3零井源距VSP数据及不同方法的波场分离结果。Unet模型在分离过程中有效信号出现了显著损失,图15b中能够明显观察到信号损失的差异。而使用Unet++模型进行分离的上、下行波,波场连续性好有效信号损失较少。中值滤波分离的上、下行波的波场连续性差,有效信号损失较多。相比之下,Unet++方法波场分离的上、下行波连续性更好,波场分布更稳定(图12d中红箭头所指),对野外数据具有一定的鲁棒性。与Unet方法相比,Unet++通过聚合解码不同尺度的子网络中的特征(图5)形成高度灵活的特征融合方案,可以更有效地分离VSP数据中上、下行波(见图13)。Unet方法波场分离过程中,有效信号的损失较多(见图14)。相比之下,Unet++方法波场分离产生的上、下行波波场连续性更好,分布更稳定。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 A区w4零井源距VSP数据在不同方法的波场分离结果对比

Fig.15 Comparison of wavefield separation results for zero-offset VSP data in A-w4 using different deep learning models

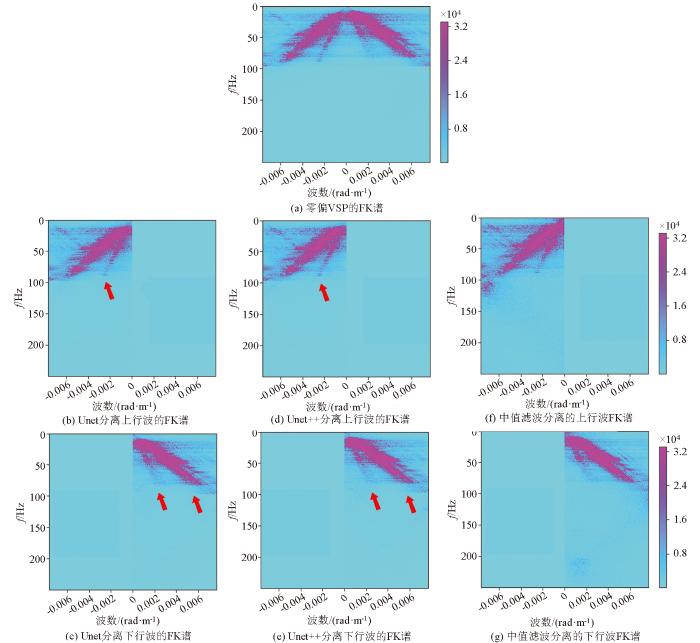
图16为图15对应的FK谱。图中显示,Unet模型分离的上、下行波产生了一定的空间假频(图16中红色箭头所指)。相较于深度学习方法,中值滤波方法会产生大量空间假频。中值滤波方法产生的假高频在时空域表现为信号波形呈锯齿状。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 不同方法波场分离结果的FK谱

Fig.16 FK spectra of wave field separation results of different deep learning models

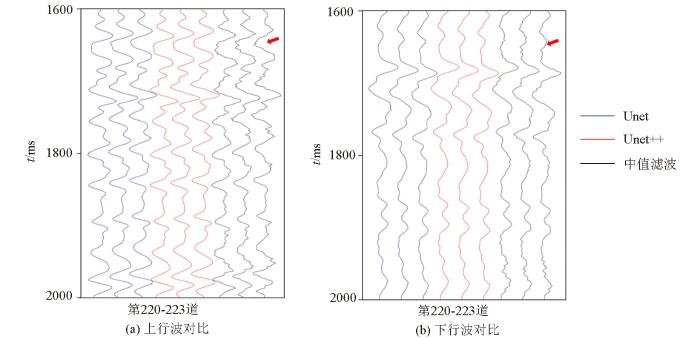
图17为A区w4零井源距VSP数据分别在Unet、Unet++和中值滤波方法处理结果的多道波形对比,分别对应图10中时窗为1 600~2 000 μs和第220~223道位置的波形。结果表明,中值滤波方法分离的上、下行波的波形存在一定程度的失真,而Unet和Unet++方法波形更可靠。中值滤波由于其算法机制会损失大量有效性信号,Unet方法精度较低,而Unet++方法可以更有效地分离VSP数据中上、下行波。因此,Unet++方法分离的上、下行波在波场连续性和精度方面优于中值滤波方法和Unet方法,具有更好的综合性能。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 A区w4零井源距VSP数据在不同方法的多道波形对比

Fig.17 Multi-trace waveform comparison of zero-offset VSP data from well A-w4 using different processing methods

5 结论

针对目前传统方法VSP波场分离精度低、效率低的现状,结合深度学习技术,本文提出一种基于深度学习的VSP数据上、下行波自动化分离方法。该方法在波场分离过程中避免了人工操作,主要时间成本在于网络训练,而一旦训练完成,Unet++可以快速有效地分离上、下行波。

对合成数据和实际VSP数据的测试表明,Unet++方法在VSP波场分离任务中具有较高的分离精度和较强的细节处理能力。利用A区的零井源距VSP数据进行训练、测试,得到以下认识:①相较于传统方法,深度学习模型一旦训练完毕后,VSP上、下行波分离自动化程度高、计算效率快;②相较于Unet方法,Unet++通过融合来自不同解码器网络的特征,可以更好地进行VSP波场分离;③相较于中值滤波方法,Unet++方法的波场分离精度更高。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

胡东海, 杨少辉, 闫有平, 等.

VSP资料地震属性的提取和应用

[J]. 石油物探, 2004, 43(S1):83-85.