0 引言
地球上空存在着非常丰富的天然源平面电磁波,当它们从空气中入射到大地时将在地空分界面产生反射与折射,由于大地导电性差异将引起电磁波反射系数和折射系数的差异,从而引起地表观测的电磁场差异。通过在地表观测相互正交的电场和磁场并计算地面波阻抗,即可评估大地的电阻率分布信息。天然源平面电磁波频谱丰富,高频可以达到几百kHz,低频可以低至几千秒。由于不同频率平面电磁波的趋肤深度不同,因此观测由不同频率的电磁场计算的波阻抗可以评估地下不同深度的电阻率信息。利用天然源平面电磁波来进行电阻率测深的方法包括了传统的大地电磁法(MT)、音频大地电磁法(AMT)和射频大地电磁法(RMT)。MT观测频率一般低于1 Hz,主要用于探测几十千米至几百千米深的地壳、地幔信息;AMT观测频率范围一般是1 Hz~10 kHz,用于探测几十米至几千米深的地下水和金属矿产等;RMT观测频率范围10~1 000 kHz,探测几米至几十米的浅层地质情况[1 4] 。在层状地电模型中,频率与探测深度的对应关系良好,即高频反映浅部地电信息,低频反映深部地电信息。然而浅层局部不均匀地电体却不仅影响高频电磁场,同时也影响低频电磁场。在MT或AMT中,由于浅层局部不均匀地电体的存在,将使得相对低频段的视电阻率曲线出现整体向上或向下偏移,即静态偏移,从而对深部观测产生不利影响。过往的研究大多是把浅层不均匀地电体视为地质干扰体,主要研究其带来的静态偏移干扰,研究的目标是消除浅部不均匀体对深部探测的影响[5 9] 。在实际中,浅部不均匀地电体也可能是待探测的目标,比如地质灾害调查或工程地质勘察中常探测的岩溶、采空区、破碎断裂、塌陷体等不良地质体,此时所谓的静态效应就不再是干扰效应,而成为目标异常响应[10 ] 。因此有必要对其浅层不均匀体的平面波电磁响应特征做更全面的研究。本文通过正演计算不同参数条件下浅层局部良导体的平面电磁波响应特征,为利用平面电磁波法探测浅层地电异常体提供思路。
1 方法理论
平面电磁波从空气中入射至非磁性水平均匀半空间大地,设地表的入射电场沿x 方向且幅度为E 0 ,则大地表面的透射电场、磁场分别为[11 ] :
(1) $E_{x}=2 E_{0} Z_{1} /\left(Z_{0}+Z_{1}\right),$
(2) $H_{y}=2 E_{0} /\left(Z_{0}+Z_{1}\right),$
式中:Z 0 =$\sqrt{{\mu }_{0}/{\epsilon }_{0}}$ Z 1 |=$\sqrt{\omega {\mu }_{0}\rho }$ ω 为平面电磁波角频率,μ 0 为大地和空气的磁导率,ε 0 为大地和空气的介电常数,ρ 为大地电阻率。
(3) $Z_{1}=E_{x} / H_{y},$
(4) $\rho =\frac{|{Z}_{1}{|}^{2}}{\omega {\mu }_{0}}=\frac{1}{\omega {\mu }_{0}}{\left|\frac{{E}_{x}}{{H}_{y}}\right|}^{2}$ 。
大地电阻率变化引起波阻抗变化,从而引起地表观测电磁场的变化。通过在地表观测相互正交的电场和磁场计算地面波阻抗,即可评估大地的电阻率。若大地是水平层状的,根据地表不同频率电磁场计算得到的是不同趋肤深度范围内的视波阻抗和视电阻率,再通过层状递推公式[12 ] 反演即可求得各层电阻率和厚度信息,从而实现平面波电磁测深。
在实际应用中,特别是工程地质勘察中,探测目标往往是局部的不均匀地电体。不均匀地电体在一次电场的作用下,在电性分界面上形成积累电荷,并产生二次电场[13 ]
(5) ${E}_{s}=-\frac{1}{4\pi }{\int }_{S}\frac{(\nabla \sigma )}{\sigma }·\frac{{E}_{p}}{\left|r\right.{|}^{2}}{e}_{r}ds$
式中:Ep 为一次电场;σ 为大地电导率;Ñσ 为一次电场方向的电导率梯度;ds 为面积微元;r 表示面元ds 与观测点间的向量;er 表示沿r 方向的单位向量。
通过二次电场公式可以直观看出,不均匀体与背景围岩电导率差异越大、距离观测点越近,二次场越强。该二次场叠加于一次场之上,呈现为异常场,根据该异常场可以发现局部不均匀地电体。
2 模型计算
2.1 模型及算法
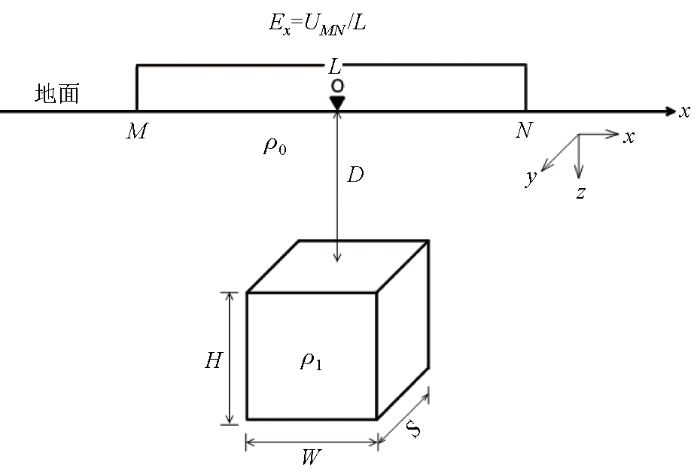
为了简便直观地分析局部良导体产生的异常响应,本文采用相对简单的三维模型进行正演分析。如图1 所示,设宏观背景为层状大地,电阻率为ρ 0 (电导率σ 0 =1/ρ 0 );局部良导体为长方体,其走向长S ,宽W ,高为H ,其电阻率为ρ 1 (电导率σ 1 =1/ρ 1 )。背景围岩和良导体磁导率都为μ 0 ,在良导体正上方地表进行观测,以良导体在地面投影中心点为原点建立笛卡尔坐标系,长方体走向沿y 轴,测线沿x 轴,垂直长方体走向,电场观测极距L 。
图1
图1
简化模型
Fig.1
Simplified model
本文采用三维数值模拟方法是积分方程法[14 ] ,其方法理论较成熟,应用也较广泛。该方法仅需对异常体进行精细剖分,未知数较少,对于单个小异常体计算比较经济,计算精度也相对较高,具体算法可参考相关文献[15 17]。本文简述其算法如下。
如图1 所示,当半空间地下存在局部良导体时,总电场为一次电场Ep 与二次电场Es 之和,即E =Ep +Es 。一次电场为良导体不存在情况下的正常场,二次场为局部良导体引起的异常场,可以用矢量位A 和标量位ϕ 表示,认为是由良导体内的散射电流Js 引起,即
(6) ${E}_{s}=-i\omega {\mu }_{0}A-\nabla \varphi,$
(7) $A\left(r\right)={\int }_{v}{J}_{s}\left(r\text{'}\right)G(r,r\text{'})dv\text{'},$
(8) $\varphi \left(r\right)=-{\rho }_{1}{\int }_{v}\nabla ·{J}_{s}\left(r\text{'}\right)G(r,r\text{'})dv\text{'},$
(9) $G(r,r\text{'})=\frac{{e}^{-ik|r-r\text{'}|}}{4\pi \left|r\right.-r\text{'}|},$
其中:r =(x ,y ,z ),为测点位置;r '=(x' ,y' ,z' ),为散射电流元位置;k =(-iωμ 0 σ 0 )1 / 2 ,为背景电磁场波数。
(10) $\begin{array}{l}E\left(r\right)={E}_{p}\left(r\right)+({\sigma }_{1}-{\sigma }_{0}){\int }_{v}G(r,r\text{'})·\\ E\left(r\text{'}\right)dv\text{'}\end{array}$ 。
为了进行数值求解,将良导体离散剖分成N 个线性尺寸相同的立方体单元,并假设各立方体内的电导率和电场为常数,于是电场可以表示为:
(11) $\begin{array}{l}E\left(r\right)={E}_{p}\left(r\right)+\sum _{n=1}^{N}({\sigma }_{1}-{\sigma }_{0}\left){\int }_{v}G\right(r,r\text{'})dv\text{'}·{E}_{n}\\ ={E}_{p}\left(r\right)+\sum _{n=1}^{N}\frac{{\sigma }_{1}-{\sigma }_{0}}{{\sigma }_{0}}\Gamma (r,r\text{'})·{E}_{n}\end{array}$
式中:G 为相对无限小电流元的并矢格林函数;Γ 为并矢格林函数的体积分, 计算Γ 时须考虑其在r =r '存在奇异性。
(12) ${E}_{m}={E}_{m}^{p}+\frac{{\sigma }_{1}-{\sigma }_{0}}{{\sigma }_{0}}\sum _{n=1}^{N}{\Gamma }_{mn}·{E}_{n}$
(13) $\sum _{n=1}^{N}\left(\frac{{\sigma }_{1}-{\sigma }_{0}}{{\sigma }_{0}}{\Gamma }_{mn}-{\delta }_{mn}\right){E}_{n}=-{E}_{m}^{p}$
(14) ${\delta }_{mn}=\left\{\begin{array}{l}I(m=n)\\ O(m\ne n)\end{array}\right.$
通过式(13)可以解出异常体内的电场值,再根据式(11)可以求出异常体外任意点的电场值,再根据法拉第电磁感应定律即可求出任意点的磁场。
本文采用加拿大EiKon Technologies Ltd.的EMIGMA软件进行正演。EMIGMA软件是一款比较先进的综合地球物理解释平台,其配套MT/AMT模块可以实现快速3D正演,可模拟电偶极及磁偶极接收机数据,能通过积分沿接收端方向的电场来模拟实际测量长度的电偶极接收机数据,可模拟不限制数目的长方体、薄板及多面体目标,可模拟地形影响,有处理层结构和异常体之间的全部差异的能力[14 ] 。
在本文模拟计算中,入射平面电磁波电场极化方向沿y 轴,计算频率范围1~106 Hz,每个数量级对数等间距分布5个频点,共31个频点。分别计算了不同观测极距、不同埋深、不同厚度、不同走向长度、不同宽度等条件下的结果,以分析各个参数对异常响应影响规律。
三维目标体的大地电磁响应的TE模式(Ey -Hx )和TM模式(Ex -Hy )都会产生异常响应。在实际应用中,特别是工程地质勘察中,为了提高探测效率,通常采用标量观测,测线方向横跨异常体走向,观测沿测线方向的电场和垂直测线方向的磁场。本文主要研究TM模式下相对于背景的视电阻率ρxy 和视相位φxy 频率响应特征,并分析它们的相对异常${\delta }_{{\rho }_{xy}}$ ${\delta }_{{\phi }_{xy}}$
(15) $\begin{array}{l}{\delta }_{{\rho }_{xy}}=|{\rho }_{xy}-{\rho }_{0}|/{\rho }_{0}\times 100\%,\\ {\delta }_{{\phi }_{xy}}=|{\phi }_{xy}-{\phi }_{0}|/{\phi }_{0}\times 100\%\end{array}$ 。
2.2 不同参数计算结果
2.2.1 不同观测极距
大地电磁法在地面观测水平电场的方式是先测量两个测量电极M 、N 之间的电位差ΔUMN 及二者水平间距L ,再通过公式计算求得M 、N 电极之间的平均电场
(16) ${E}_{MN}=-\frac{\Delta {U}_{MN}}{L}=\frac{{\int }_{M}^{N}E·dl}{L}$
式中:EMN 是测量电极M 、N 之间的平均电场;ΔUMN 是测量电极M 、N 之间的电位差;L 是测量电极M 、N 之间的水平距离;E 是电极M 、N 之间的点电场;dl 是沿着M 、N 连线的矢量积分因子。
如果大地为水平层状结构,M 、N 之间各点电场均匀,测得电场将与M 、N 的位置无关。如果测点下方出现不均匀地电体,M 、N 电极位置差异对电场观测结果将产生影响。因为在电性分界面上的积累电荷产生的二次电场,对不同位置的影响程度不同,距离不均匀体越远,影响越小。
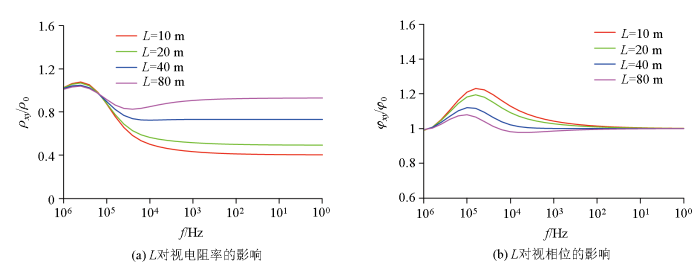
如表1 所示,计算不同观测极距时,不均匀体正上方中心测点的响应曲线,计算结果见图2 。可见,视电阻率和相位异常最大值都随着极距的增加而减小:当L =10 m时,观测电极置于异常体正上方,视电阻率异常最大,达60%,相位异常达23%;当L =20 m时,观测电极置于异常体边界上方,视电阻率异常幅度略减小,达50%,相位异常达19%;当L =40、80 m时,随着观测电极远离异常体,异常幅值快速减小,视电阻率最大异常分别减小至28%和17%,相位最大异常分别减小至12%和8%。所以如果探测目的是发现浅部不均匀体,则设计观测极距宜不大于不均匀体的横向尺寸。
图2
图2
L 变化时目标体正上方中心测点归一化响应
Fig.2
Normalized responses of the center point right above the target when electrode distance varies
2.2.2 不同电阻率
基于方法原理,不均匀体产生的异常场主要由不均匀体边界上的积累电荷产生,而异常场的大小与电性分界面上积累电荷的量成正比,积累电荷的量与电性分界面的电阻率相对梯度变化成正比。
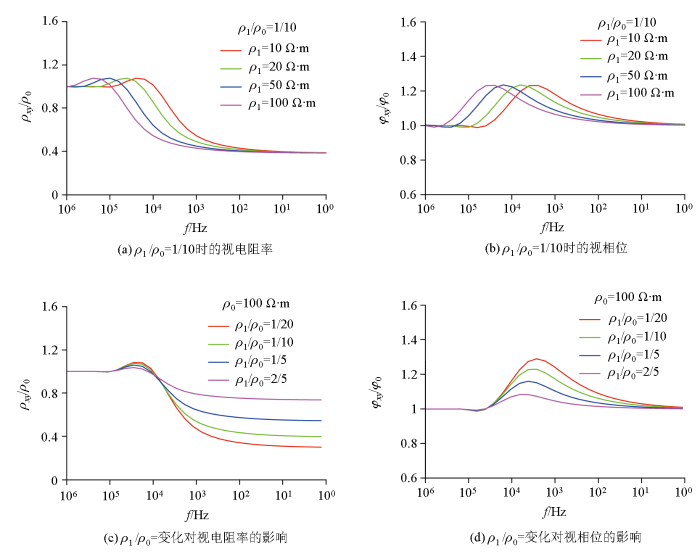
如表2 所示,计算不同电阻率时不均匀体正上方中心测点的响应曲线,计算结果见图3 。图3a 、3b 中保持ρ 0 /ρ 1 =1∶10不变,同时ρ 0 、ρ 1 同步按比例变大,发现4种不同电阻率情况下,视电阻率和相位的异常最大值都相同,表明当目标体电阻率与围岩电阻率比值相同时,相对异常最大值也相同。图3c 、d 中ρ 0 =100 Ω·m,研究ρ 1 取不同值对异常的影响:当目标体电阻率与围岩电阻率差异变大时,异常最大值也增大。另外还发现,相位异常极大值出现的频点随着围岩电阻率减小而减小。因为趋肤深度与围岩电阻率的开方成正比,与频率开方成反比,所以围岩电阻率越小,到达相同的埋深所需要的频率越低。
图3
图3
电阻率变化时目标体正上方中心测点归一化响应
Fig.3
Normalized responses of the center point right above the target when resistivity varies
2.2.3 不同尺寸
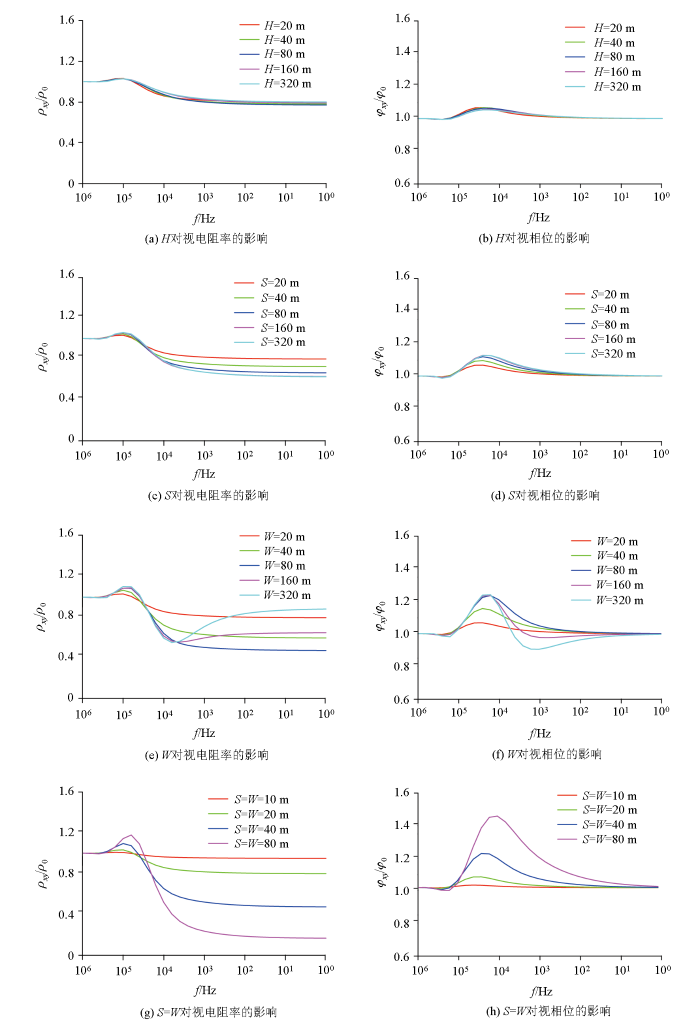
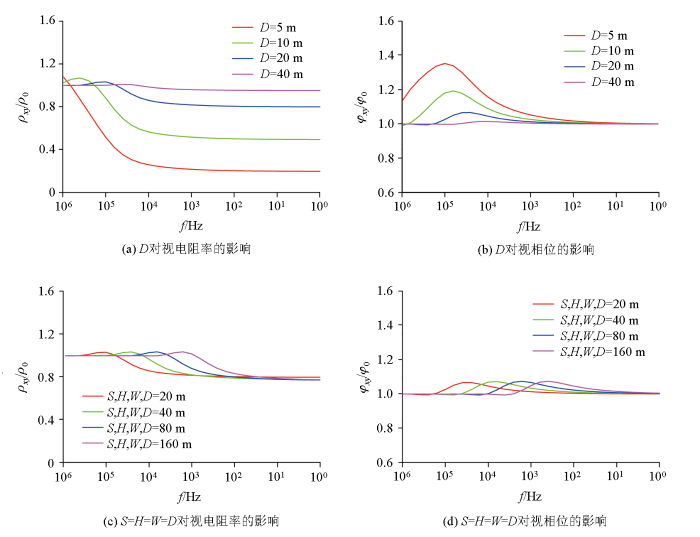
如表3 所示,计算不同方向尺寸变化(纵向厚度,走向长度、横向宽度)时不均匀体正上方中心测点的响应曲线,计算结果见图4 。图4a 、b 显示纵向厚度变化对异常的影响:最大异常值先是随着厚度增加略微增加,当厚度达到横向宽度的2倍后,纵向厚度增加异常不变。图4c 、d 显示目标体走向长度变化对异常的影响:最大异常先是随着走向长度增加而增加,但是当走向长度达到横向宽度8倍以后,再增加走向长度将不再增加异常幅度。图4e 、f 横向宽度变化对异常的影响:当W =20、40、80 m时,视电阻曲线形态类似于由高变低的二层D型测深曲线,在低频段(低于25 kHz),视电阻率值随着频率降低而减小后渐趋于平稳值,相位曲线则是随着频率降低而增大至极大值后再随着频率降低而减小且渐趋于平稳值。当W =160、320 m时,视电阻率曲线呈现类似于高—低—高变化的三层H型测深曲线:视电阻率先是随着频率降低而减小至极小值,然后随着频率降低而增大且逐渐趋于平稳值;相位曲线则是随着频率降低先逐渐增大至极大值,然后随着频率降低减小至极小值,再转折逐渐增加且渐趋于平稳值。图4g 、h 显示走向长度、横向宽度两个维度同时变化对异常的影响:由于走向长度和横向宽度相同,而纵向厚度影响不大,所以响应曲线形态是类似于由高变低的二层D型测深曲线,异常强度随平面边长增大而显著增大。
图4
图4
目标体尺寸变化时其正上方中心测点归一化响应
Fig.4
Normalized responses of the center point right above the target when its size varies
2.2.4 不同埋深
图5 显示了立方体目标埋深变化时不均匀体正上方中心测点的响应曲线。计算模型参数及异常最大值见表4 。图5a 、b 显示当埋深变化对异常的影响,可见随着埋深增加,异常最大值减小。相位异常极大值出现的频率随着埋深增加而减小,因为趋肤深度与频率的开方成反比。图5c 、d 显示立方体目标埋深与边长相当时,视电阻率异常最大值都约为20%,相位异常最大值都为7%。可见,根据视电阻率异常判断,若可探测相对异常阈值设为20%,则当立方体电阻率与围岩背景电阻率比值为1∶10时,其可探测最大埋深约为立方体边长。
图5
图5
目标体埋深变化时其正上方中心测点归一化响应
Fig.5
Normalized responses of the center point right above the target when its depth varies
2.2.5 剖面分析
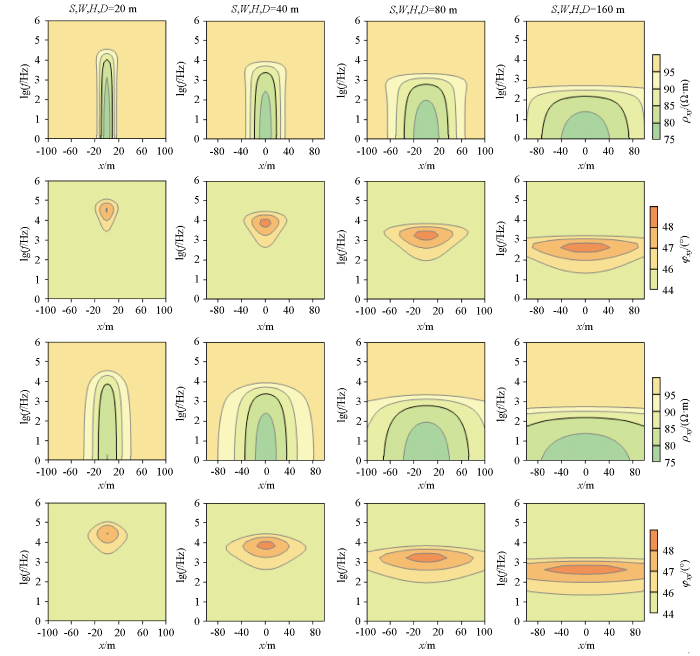
以上分析的是异常体正上方中心测点响应及相对异常曲线,分析不同模型参数对相对异常的影响。在实际勘察工作中,横向异常通常是通过与相邻测点的差异来发现,即通过不同测点响应数据组成的剖面数据来发现异常。以图5c 、d 中4个模型的响应为例,观测剖面跨度x =-100~100 m,点距5 m,视电阻和相位的频率剖面见图6 ,横轴为测点号,纵轴为频率对数值。很显然,TE模式和TM模式的视电阻率剖面和相位剖面都能体现异常,而且视电阻率剖面和相位剖面的横向异常范围与目标体横向尺寸对应良好,相位异常在纵向上也有对应,而视电阻率异常纵向上遵循静态效应规律,在高频出现异常后将一直延伸至低频,因此无法判断目标体纵向延伸的厚度。虽然如此,这并不妨碍利用它来发现异常。前面分析中发现,相位相对异常比电阻率相对异常小很多,所以就发现异常而言,优先选用视电阻率数据。而且可以充分利用视电阻率异常的静态效应特点,利用相对低频的数据来发现浅部目标体。如图6 所示,若认为相对异常大于15%可分辨,则对于边长和埋深都为20 m的立方体目标,频率低于10 kHz的数据都可以发现异常;对于边长和埋深都为40 m的立方体目标,频率低于2.5 kHz的数据都可以发现异常;对于边长和埋深都为80 m的立方体目标,频率低于630 Hz的数据都可以发现异常;对于边长和埋深都为160 m的立方体目标,频率低于160 Hz的数据都可以发现异常。当然要确定目标体的顶部埋深,则需要获得出现异常的起始最高频率。在实际应用中,如果条件受限,如尚未配备RMT仪器,或者有配备仪器但是有些测区30 kHz以上的天然大地电磁信号微弱难以实现,此时可以采用频率更低的AMT快速扫面发现异常,然后在异常区补充其他测深方法以确定埋深。
图6
图6
立方体状目标体异常剖面
Fig.6
Profile response of cuboidal target
3 结论
本文针对简单的均匀半空间背景下的三维低阻体模型进行正演计算,在三维低阻体正上方中心测点的大地电磁响应具有以下特征:
1)相同条件下,三维地电体电阻率与围岩电阻率相对差异越大,响应相对异常越大;
2)观测电极极距会影响异常响应,极距越小,响应相对异常越大;
3)三维地电体尺寸的影响具有方向性:当水平方向两个尺寸相差不大时,视电阻率响应曲线形态呈现类似于二层D型测深曲线,响应相对异常随水平尺寸变大而变大; 当水平方向两个尺寸相差较大时(大尺寸达到小尺寸的8倍以上),沿着大尺寸方向观测与沿着小尺寸方向观测得到曲线形态不同,沿着大尺寸方向观测时视电阻率响应曲线形态呈现类似于高—低—高变化的三层H型测深曲线;纵向厚度变化对异常影响较小。
4)视电阻和相位都有异常响应,视电阻率相对异常一般为相位相对异常的2倍以上,因此就发现异常而言,视电阻率异常更具优势。
5)另外从频率响应剖面分析。视电阻率剖面和相位剖面的横向异常范围与目标体横向尺寸对应良好,相位异常在纵向上也有对应,而视电阻率异常纵向上遵循静态效应规律,在高频出现异常后将一直延伸至低频,因此可以充分利用视电阻率异常的静态效应特点,利用相对低频的数据来发现浅部目标体。
参考文献
View Option
[1]
陈乐寿 , 王光锷 . 大地电磁测深法 [M]. 北京 : 地质出版社 ,1990.
[本文引用: 1]
Chen L S Wang G E Magnetotelluric sounding method [M]. Beijing : Geological Publishing House ,1990.
[本文引用: 1]
[2]
李金铭 . 地电场与电法勘探 [M]. 北京 : 地质出版社 , 2005 .
Li J M Geoelectric field and electrical exploration [M]. Beijing : Geological Publishing House , 2005 .
[3]
Kaufman A A Keller G V The magnetotelluric sounding method,method in geochemistry and geophysics [M]. Berlin : Springer , 2020 . Amsterdam : Elsevisr Scientific ,1981.
[4]
汤井田 , 任政勇 , 周聪 , 等 . 浅部频率域电磁勘探方法综述
[J]. 地球物理学报 , 2015 , 58 (8 ):2681 -2705 .
DOI:10.6038/cjg20150807
[本文引用: 1]
适用于近地表(2000m以内)勘探的频率域电磁法主要有音频大地电磁法(audio-frequency magnetotellurics, AMT), 无线电大地电磁法(radio-magnetotellurics, RMT), 可控源音频大地电磁法(controlled source audio-frequency magnetotellurics, CSAMT), 广域电磁法(Wide Field Electromagnetic Method, WFEM).本文拟从最新的数据采集技术、数据处理技术、正反演算法、实例等四个方面, 论述适用于浅部勘探的AMT, RMT, CSAMT和WFEM方法的国内外最新进展, 总结目前AMT, RMT, CSAMT和WFEM方法遇到的困难, 对潜在的发展方向提出建议.综述表明:(1)张量测量、多站阵列、多站叠加可提高AMT、RMT和CSAMT数据的质量.利用近区数据WFEM法可获得良好的效果.国产与国外仪器在质量方面的差距正在逐步缩小.(2)数学形态滤波技术、Hilbert-Huang变换等可有效分离出有用的数据, 局部畸变仍然是亟待解决的难题, 需要更为深入的研究.(3)矢量有限元与非结构网格的出现大幅度提高了有限元处理复杂电磁问题模拟的精度与应用范围, 成为目前电磁正演的首选工具.完全非线性反演算法仍然局限于1D、2D问题, 共轭梯度法和高斯牛顿算法等为解决3D问题的发展趋势.地质约束的引入和多数据联合反演可以减小反演的非唯一性.各向异性的反演为目前反演研究的热点之一.(4)野外数据解释的正确性严重依赖于对地下结构先期的维性判别, 在2D特性不明显、3D特性明显时, 需要采用3D进行反演解释.
Tang J T Ren Z Y Zhou C et al . Frequency-domain electromagnetic methods for exploration of the shallow subsurface:A review
[J]. Chinese Journal of Geophysics , 2015 , 58 (8 ):2681 -2705 .
[本文引用: 1]
[5]
Lei D Fayemi B Yang L Y et al . The non-static effect of near-surface inhomogeneity on CSAMT data
[J]. Journal of Applied Geophysics , 2017 ,139:306 -315 .
[本文引用: 1]
[6]
Li J Zhang X Tang J T Noise suppression for magnetotelluric using variational mode decomposition and detrended fluctuation analysis
[J]. Journal of Applied Geophysics , 2020 ,180:104127.
[7]
伍亮 , 李桐林 , 朱成 , 等 . 大地电磁测深法中静态效应及其反演
[J]. 地球物理学进展 , 2015 , 30 (2 ):840 -846 .
Wu L Li T L Zhu C et al . Research and inversion static effect in magnetotelluric
[J]. Progress in Geophysics , 2015 , 30 (2 ):840 -846 .
[8]
李国瑞 , 席振铢 , 龙霞 . 基于实测积累电荷静电场消除静态效应的方法
[J]. 物探与化探 , 2017 , 41 (4 ):730 -735 .
Li G R Xi Z Z Long X Static displacement correction for frequency domain electromagnetic method based on second electrostatic field
[J]. Geophysical and Geochemical Exploration , 2017 , 41 (4 ):730 -735 .
[9]
刘桂梅 , 马为 , 刘俊昌 , 等 . 大地电磁测深静态效应空间域拓扑处理技术研究
[J]. 物探与化探 , 2018 , 42 (1 ):118 -126 .
[本文引用: 1]
Liu G M Ma W Liu J C et al . Spatial domain topological processing technique for studying static effect in magnetotelluric sounding
[J]. Geophysical and Geochemical Exploration , 2018 , 42 (1 ):118 -126 .
[本文引用: 1]
[10]
杨天春 , 胡峰铭 , 于熙 , 等 . 天然电场选频法的响应特性分析与应用
[J]. 物探与化探 , 2023 , 47 (4 ):1010 -1017 .
[本文引用: 1]
Yang T C Hu F M Yu X et al . Analysis and application of the responses of the frequency selection method of telluric electricity field
[J]. Geophysical and Geochemical Exploration , 2023 , 47 (4 ):1010 -1017 .
[本文引用: 1]
[11]
Roy K K Natural electromagnetic fields in pure and applied geophysics [M]. Cham : Springer Cham .
[本文引用: 1]
[12]
Vozoff K Electromagnetic methods in applied geophysics
[J]. Geophysical Surveys , 1980 , 4 (1 ):9 -29 .
[本文引用: 1]
[13]
Jiracek G R Near-surface and topographic distortions in electromagnetic induction
[J]. Surveys in Geophysics , 1990 , 11 (2 ):163 -203 .
[本文引用: 1]
[14]
Eikon Technologies Ltd. EMIGMA_full_manual.version 11.11.0,2024 [K].https://www.petroseikon.com/EMIGMA/77ps/mt.php.
URL
[本文引用: 2]
[15]
Wannamaker P E Hohmann G W SanFilipo W A Electromagnetic modeling of three-dimensional bodies in layered earths using integral equations
[J]. Geophysics , 1984 , 49 (1 ):60 -74 .
[本文引用: 1]
[16]
Ting S C Hohmann G W Integral equation modeling of three-dimensional magnetotelluric response
[J]. Geophysics , 1981 , 46 (2 ):182 -197 .
[17]
任政勇 , 陈超健 , 汤井田 , 等 . 一种新的三维大地电磁积分方程正演方法
[J]. 地球物理学报 , 2017 , 60 (11 ):4506 -4515 .
DOI:10.6038/cjg20171134
[本文引用: 1]
采用规则六面体单元和并矢Green函数奇异积分等效积分技术,已有的大地电磁积分正演方法具有不能有效模拟地下复杂地质体和计算精度偏低的缺点.本文提出了一种新的三维大地电磁积分方程正演技术,即采用四面体单元、解析的并矢Green函数奇异积分表达式,达到既能模拟地下复杂异常体,又能有效提高已有积分方程法计算精度的目的.首先,采用四面体网格技术离散地下复杂异常体,获得四面体单元上的大地电磁积分方程.然后,利用针对四面体单元开发的新的奇异值积分的解析表达式,准确计算线性方程中的并矢Green函数的奇异积分,从而获得精确的线性方程.借助于PARDISO高性能并行直接求解器,实现了三维大地电磁问题的高精度求解.最后,基于国际标准3D-1模型和六棱柱模型,通过与其他方法结果的对比分析,验证了本文方法的正确性、处理高电导率对比度的能力(1000:1)和处理复杂模型的能力.
Ren Z Y Chen C J Tang J T et al . A new integral equation approach for 3D magnetotelluric modeling
[J]. Chinese Journal of Geophysics , 2017 , 60 (11 ):4506 -4515 .
[本文引用: 1]
1
... 地球上空存在着非常丰富的天然源平面电磁波,当它们从空气中入射到大地时将在地空分界面产生反射与折射,由于大地导电性差异将引起电磁波反射系数和折射系数的差异,从而引起地表观测的电磁场差异.通过在地表观测相互正交的电场和磁场并计算地面波阻抗,即可评估大地的电阻率分布信息.天然源平面电磁波频谱丰富,高频可以达到几百kHz,低频可以低至几千秒.由于不同频率平面电磁波的趋肤深度不同,因此观测由不同频率的电磁场计算的波阻抗可以评估地下不同深度的电阻率信息.利用天然源平面电磁波来进行电阻率测深的方法包括了传统的大地电磁法(MT)、音频大地电磁法(AMT)和射频大地电磁法(RMT).MT观测频率一般低于1 Hz,主要用于探测几十千米至几百千米深的地壳、地幔信息;AMT观测频率范围一般是1 Hz~10 kHz,用于探测几十米至几千米深的地下水和金属矿产等;RMT观测频率范围10~1 000 kHz,探测几米至几十米的浅层地质情况[1 4 ] .在层状地电模型中,频率与探测深度的对应关系良好,即高频反映浅部地电信息,低频反映深部地电信息.然而浅层局部不均匀地电体却不仅影响高频电磁场,同时也影响低频电磁场.在MT或AMT中,由于浅层局部不均匀地电体的存在,将使得相对低频段的视电阻率曲线出现整体向上或向下偏移,即静态偏移,从而对深部观测产生不利影响.过往的研究大多是把浅层不均匀地电体视为地质干扰体,主要研究其带来的静态偏移干扰,研究的目标是消除浅部不均匀体对深部探测的影响[5 9 ] .在实际中,浅部不均匀地电体也可能是待探测的目标,比如地质灾害调查或工程地质勘察中常探测的岩溶、采空区、破碎断裂、塌陷体等不良地质体,此时所谓的静态效应就不再是干扰效应,而成为目标异常响应[10 ] .因此有必要对其浅层不均匀体的平面波电磁响应特征做更全面的研究.本文通过正演计算不同参数条件下浅层局部良导体的平面电磁波响应特征,为利用平面电磁波法探测浅层地电异常体提供思路. ...
1
... 地球上空存在着非常丰富的天然源平面电磁波,当它们从空气中入射到大地时将在地空分界面产生反射与折射,由于大地导电性差异将引起电磁波反射系数和折射系数的差异,从而引起地表观测的电磁场差异.通过在地表观测相互正交的电场和磁场并计算地面波阻抗,即可评估大地的电阻率分布信息.天然源平面电磁波频谱丰富,高频可以达到几百kHz,低频可以低至几千秒.由于不同频率平面电磁波的趋肤深度不同,因此观测由不同频率的电磁场计算的波阻抗可以评估地下不同深度的电阻率信息.利用天然源平面电磁波来进行电阻率测深的方法包括了传统的大地电磁法(MT)、音频大地电磁法(AMT)和射频大地电磁法(RMT).MT观测频率一般低于1 Hz,主要用于探测几十千米至几百千米深的地壳、地幔信息;AMT观测频率范围一般是1 Hz~10 kHz,用于探测几十米至几千米深的地下水和金属矿产等;RMT观测频率范围10~1 000 kHz,探测几米至几十米的浅层地质情况[1 4 ] .在层状地电模型中,频率与探测深度的对应关系良好,即高频反映浅部地电信息,低频反映深部地电信息.然而浅层局部不均匀地电体却不仅影响高频电磁场,同时也影响低频电磁场.在MT或AMT中,由于浅层局部不均匀地电体的存在,将使得相对低频段的视电阻率曲线出现整体向上或向下偏移,即静态偏移,从而对深部观测产生不利影响.过往的研究大多是把浅层不均匀地电体视为地质干扰体,主要研究其带来的静态偏移干扰,研究的目标是消除浅部不均匀体对深部探测的影响[5 9 ] .在实际中,浅部不均匀地电体也可能是待探测的目标,比如地质灾害调查或工程地质勘察中常探测的岩溶、采空区、破碎断裂、塌陷体等不良地质体,此时所谓的静态效应就不再是干扰效应,而成为目标异常响应[10 ] .因此有必要对其浅层不均匀体的平面波电磁响应特征做更全面的研究.本文通过正演计算不同参数条件下浅层局部良导体的平面电磁波响应特征,为利用平面电磁波法探测浅层地电异常体提供思路. ...
浅部频率域电磁勘探方法综述
1
2015
... 地球上空存在着非常丰富的天然源平面电磁波,当它们从空气中入射到大地时将在地空分界面产生反射与折射,由于大地导电性差异将引起电磁波反射系数和折射系数的差异,从而引起地表观测的电磁场差异.通过在地表观测相互正交的电场和磁场并计算地面波阻抗,即可评估大地的电阻率分布信息.天然源平面电磁波频谱丰富,高频可以达到几百kHz,低频可以低至几千秒.由于不同频率平面电磁波的趋肤深度不同,因此观测由不同频率的电磁场计算的波阻抗可以评估地下不同深度的电阻率信息.利用天然源平面电磁波来进行电阻率测深的方法包括了传统的大地电磁法(MT)、音频大地电磁法(AMT)和射频大地电磁法(RMT).MT观测频率一般低于1 Hz,主要用于探测几十千米至几百千米深的地壳、地幔信息;AMT观测频率范围一般是1 Hz~10 kHz,用于探测几十米至几千米深的地下水和金属矿产等;RMT观测频率范围10~1 000 kHz,探测几米至几十米的浅层地质情况[1 4 ] .在层状地电模型中,频率与探测深度的对应关系良好,即高频反映浅部地电信息,低频反映深部地电信息.然而浅层局部不均匀地电体却不仅影响高频电磁场,同时也影响低频电磁场.在MT或AMT中,由于浅层局部不均匀地电体的存在,将使得相对低频段的视电阻率曲线出现整体向上或向下偏移,即静态偏移,从而对深部观测产生不利影响.过往的研究大多是把浅层不均匀地电体视为地质干扰体,主要研究其带来的静态偏移干扰,研究的目标是消除浅部不均匀体对深部探测的影响[5 9 ] .在实际中,浅部不均匀地电体也可能是待探测的目标,比如地质灾害调查或工程地质勘察中常探测的岩溶、采空区、破碎断裂、塌陷体等不良地质体,此时所谓的静态效应就不再是干扰效应,而成为目标异常响应[10 ] .因此有必要对其浅层不均匀体的平面波电磁响应特征做更全面的研究.本文通过正演计算不同参数条件下浅层局部良导体的平面电磁波响应特征,为利用平面电磁波法探测浅层地电异常体提供思路. ...
浅部频率域电磁勘探方法综述
1
2015
... 地球上空存在着非常丰富的天然源平面电磁波,当它们从空气中入射到大地时将在地空分界面产生反射与折射,由于大地导电性差异将引起电磁波反射系数和折射系数的差异,从而引起地表观测的电磁场差异.通过在地表观测相互正交的电场和磁场并计算地面波阻抗,即可评估大地的电阻率分布信息.天然源平面电磁波频谱丰富,高频可以达到几百kHz,低频可以低至几千秒.由于不同频率平面电磁波的趋肤深度不同,因此观测由不同频率的电磁场计算的波阻抗可以评估地下不同深度的电阻率信息.利用天然源平面电磁波来进行电阻率测深的方法包括了传统的大地电磁法(MT)、音频大地电磁法(AMT)和射频大地电磁法(RMT).MT观测频率一般低于1 Hz,主要用于探测几十千米至几百千米深的地壳、地幔信息;AMT观测频率范围一般是1 Hz~10 kHz,用于探测几十米至几千米深的地下水和金属矿产等;RMT观测频率范围10~1 000 kHz,探测几米至几十米的浅层地质情况[1 4 ] .在层状地电模型中,频率与探测深度的对应关系良好,即高频反映浅部地电信息,低频反映深部地电信息.然而浅层局部不均匀地电体却不仅影响高频电磁场,同时也影响低频电磁场.在MT或AMT中,由于浅层局部不均匀地电体的存在,将使得相对低频段的视电阻率曲线出现整体向上或向下偏移,即静态偏移,从而对深部观测产生不利影响.过往的研究大多是把浅层不均匀地电体视为地质干扰体,主要研究其带来的静态偏移干扰,研究的目标是消除浅部不均匀体对深部探测的影响[5 9 ] .在实际中,浅部不均匀地电体也可能是待探测的目标,比如地质灾害调查或工程地质勘察中常探测的岩溶、采空区、破碎断裂、塌陷体等不良地质体,此时所谓的静态效应就不再是干扰效应,而成为目标异常响应[10 ] .因此有必要对其浅层不均匀体的平面波电磁响应特征做更全面的研究.本文通过正演计算不同参数条件下浅层局部良导体的平面电磁波响应特征,为利用平面电磁波法探测浅层地电异常体提供思路. ...
The non-static effect of near-surface inhomogeneity on CSAMT data
1
2017
... 地球上空存在着非常丰富的天然源平面电磁波,当它们从空气中入射到大地时将在地空分界面产生反射与折射,由于大地导电性差异将引起电磁波反射系数和折射系数的差异,从而引起地表观测的电磁场差异.通过在地表观测相互正交的电场和磁场并计算地面波阻抗,即可评估大地的电阻率分布信息.天然源平面电磁波频谱丰富,高频可以达到几百kHz,低频可以低至几千秒.由于不同频率平面电磁波的趋肤深度不同,因此观测由不同频率的电磁场计算的波阻抗可以评估地下不同深度的电阻率信息.利用天然源平面电磁波来进行电阻率测深的方法包括了传统的大地电磁法(MT)、音频大地电磁法(AMT)和射频大地电磁法(RMT).MT观测频率一般低于1 Hz,主要用于探测几十千米至几百千米深的地壳、地幔信息;AMT观测频率范围一般是1 Hz~10 kHz,用于探测几十米至几千米深的地下水和金属矿产等;RMT观测频率范围10~1 000 kHz,探测几米至几十米的浅层地质情况[1 4 ] .在层状地电模型中,频率与探测深度的对应关系良好,即高频反映浅部地电信息,低频反映深部地电信息.然而浅层局部不均匀地电体却不仅影响高频电磁场,同时也影响低频电磁场.在MT或AMT中,由于浅层局部不均匀地电体的存在,将使得相对低频段的视电阻率曲线出现整体向上或向下偏移,即静态偏移,从而对深部观测产生不利影响.过往的研究大多是把浅层不均匀地电体视为地质干扰体,主要研究其带来的静态偏移干扰,研究的目标是消除浅部不均匀体对深部探测的影响[5 9 ] .在实际中,浅部不均匀地电体也可能是待探测的目标,比如地质灾害调查或工程地质勘察中常探测的岩溶、采空区、破碎断裂、塌陷体等不良地质体,此时所谓的静态效应就不再是干扰效应,而成为目标异常响应[10 ] .因此有必要对其浅层不均匀体的平面波电磁响应特征做更全面的研究.本文通过正演计算不同参数条件下浅层局部良导体的平面电磁波响应特征,为利用平面电磁波法探测浅层地电异常体提供思路. ...
Noise suppression for magnetotelluric using variational mode decomposition and detrended fluctuation analysis
0
2020
基于实测积累电荷静电场消除静态效应的方法
0
2017
基于实测积累电荷静电场消除静态效应的方法
0
2017
大地电磁测深静态效应空间域拓扑处理技术研究
1
2018
... 地球上空存在着非常丰富的天然源平面电磁波,当它们从空气中入射到大地时将在地空分界面产生反射与折射,由于大地导电性差异将引起电磁波反射系数和折射系数的差异,从而引起地表观测的电磁场差异.通过在地表观测相互正交的电场和磁场并计算地面波阻抗,即可评估大地的电阻率分布信息.天然源平面电磁波频谱丰富,高频可以达到几百kHz,低频可以低至几千秒.由于不同频率平面电磁波的趋肤深度不同,因此观测由不同频率的电磁场计算的波阻抗可以评估地下不同深度的电阻率信息.利用天然源平面电磁波来进行电阻率测深的方法包括了传统的大地电磁法(MT)、音频大地电磁法(AMT)和射频大地电磁法(RMT).MT观测频率一般低于1 Hz,主要用于探测几十千米至几百千米深的地壳、地幔信息;AMT观测频率范围一般是1 Hz~10 kHz,用于探测几十米至几千米深的地下水和金属矿产等;RMT观测频率范围10~1 000 kHz,探测几米至几十米的浅层地质情况[1 4 ] .在层状地电模型中,频率与探测深度的对应关系良好,即高频反映浅部地电信息,低频反映深部地电信息.然而浅层局部不均匀地电体却不仅影响高频电磁场,同时也影响低频电磁场.在MT或AMT中,由于浅层局部不均匀地电体的存在,将使得相对低频段的视电阻率曲线出现整体向上或向下偏移,即静态偏移,从而对深部观测产生不利影响.过往的研究大多是把浅层不均匀地电体视为地质干扰体,主要研究其带来的静态偏移干扰,研究的目标是消除浅部不均匀体对深部探测的影响[5 9 ] .在实际中,浅部不均匀地电体也可能是待探测的目标,比如地质灾害调查或工程地质勘察中常探测的岩溶、采空区、破碎断裂、塌陷体等不良地质体,此时所谓的静态效应就不再是干扰效应,而成为目标异常响应[10 ] .因此有必要对其浅层不均匀体的平面波电磁响应特征做更全面的研究.本文通过正演计算不同参数条件下浅层局部良导体的平面电磁波响应特征,为利用平面电磁波法探测浅层地电异常体提供思路. ...
大地电磁测深静态效应空间域拓扑处理技术研究
1
2018
... 地球上空存在着非常丰富的天然源平面电磁波,当它们从空气中入射到大地时将在地空分界面产生反射与折射,由于大地导电性差异将引起电磁波反射系数和折射系数的差异,从而引起地表观测的电磁场差异.通过在地表观测相互正交的电场和磁场并计算地面波阻抗,即可评估大地的电阻率分布信息.天然源平面电磁波频谱丰富,高频可以达到几百kHz,低频可以低至几千秒.由于不同频率平面电磁波的趋肤深度不同,因此观测由不同频率的电磁场计算的波阻抗可以评估地下不同深度的电阻率信息.利用天然源平面电磁波来进行电阻率测深的方法包括了传统的大地电磁法(MT)、音频大地电磁法(AMT)和射频大地电磁法(RMT).MT观测频率一般低于1 Hz,主要用于探测几十千米至几百千米深的地壳、地幔信息;AMT观测频率范围一般是1 Hz~10 kHz,用于探测几十米至几千米深的地下水和金属矿产等;RMT观测频率范围10~1 000 kHz,探测几米至几十米的浅层地质情况[1 4 ] .在层状地电模型中,频率与探测深度的对应关系良好,即高频反映浅部地电信息,低频反映深部地电信息.然而浅层局部不均匀地电体却不仅影响高频电磁场,同时也影响低频电磁场.在MT或AMT中,由于浅层局部不均匀地电体的存在,将使得相对低频段的视电阻率曲线出现整体向上或向下偏移,即静态偏移,从而对深部观测产生不利影响.过往的研究大多是把浅层不均匀地电体视为地质干扰体,主要研究其带来的静态偏移干扰,研究的目标是消除浅部不均匀体对深部探测的影响[5 9 ] .在实际中,浅部不均匀地电体也可能是待探测的目标,比如地质灾害调查或工程地质勘察中常探测的岩溶、采空区、破碎断裂、塌陷体等不良地质体,此时所谓的静态效应就不再是干扰效应,而成为目标异常响应[10 ] .因此有必要对其浅层不均匀体的平面波电磁响应特征做更全面的研究.本文通过正演计算不同参数条件下浅层局部良导体的平面电磁波响应特征,为利用平面电磁波法探测浅层地电异常体提供思路. ...
天然电场选频法的响应特性分析与应用
1
2023
... 地球上空存在着非常丰富的天然源平面电磁波,当它们从空气中入射到大地时将在地空分界面产生反射与折射,由于大地导电性差异将引起电磁波反射系数和折射系数的差异,从而引起地表观测的电磁场差异.通过在地表观测相互正交的电场和磁场并计算地面波阻抗,即可评估大地的电阻率分布信息.天然源平面电磁波频谱丰富,高频可以达到几百kHz,低频可以低至几千秒.由于不同频率平面电磁波的趋肤深度不同,因此观测由不同频率的电磁场计算的波阻抗可以评估地下不同深度的电阻率信息.利用天然源平面电磁波来进行电阻率测深的方法包括了传统的大地电磁法(MT)、音频大地电磁法(AMT)和射频大地电磁法(RMT).MT观测频率一般低于1 Hz,主要用于探测几十千米至几百千米深的地壳、地幔信息;AMT观测频率范围一般是1 Hz~10 kHz,用于探测几十米至几千米深的地下水和金属矿产等;RMT观测频率范围10~1 000 kHz,探测几米至几十米的浅层地质情况[1 4 ] .在层状地电模型中,频率与探测深度的对应关系良好,即高频反映浅部地电信息,低频反映深部地电信息.然而浅层局部不均匀地电体却不仅影响高频电磁场,同时也影响低频电磁场.在MT或AMT中,由于浅层局部不均匀地电体的存在,将使得相对低频段的视电阻率曲线出现整体向上或向下偏移,即静态偏移,从而对深部观测产生不利影响.过往的研究大多是把浅层不均匀地电体视为地质干扰体,主要研究其带来的静态偏移干扰,研究的目标是消除浅部不均匀体对深部探测的影响[5 9 ] .在实际中,浅部不均匀地电体也可能是待探测的目标,比如地质灾害调查或工程地质勘察中常探测的岩溶、采空区、破碎断裂、塌陷体等不良地质体,此时所谓的静态效应就不再是干扰效应,而成为目标异常响应[10 ] .因此有必要对其浅层不均匀体的平面波电磁响应特征做更全面的研究.本文通过正演计算不同参数条件下浅层局部良导体的平面电磁波响应特征,为利用平面电磁波法探测浅层地电异常体提供思路. ...
天然电场选频法的响应特性分析与应用
1
2023
... 地球上空存在着非常丰富的天然源平面电磁波,当它们从空气中入射到大地时将在地空分界面产生反射与折射,由于大地导电性差异将引起电磁波反射系数和折射系数的差异,从而引起地表观测的电磁场差异.通过在地表观测相互正交的电场和磁场并计算地面波阻抗,即可评估大地的电阻率分布信息.天然源平面电磁波频谱丰富,高频可以达到几百kHz,低频可以低至几千秒.由于不同频率平面电磁波的趋肤深度不同,因此观测由不同频率的电磁场计算的波阻抗可以评估地下不同深度的电阻率信息.利用天然源平面电磁波来进行电阻率测深的方法包括了传统的大地电磁法(MT)、音频大地电磁法(AMT)和射频大地电磁法(RMT).MT观测频率一般低于1 Hz,主要用于探测几十千米至几百千米深的地壳、地幔信息;AMT观测频率范围一般是1 Hz~10 kHz,用于探测几十米至几千米深的地下水和金属矿产等;RMT观测频率范围10~1 000 kHz,探测几米至几十米的浅层地质情况[1 4 ] .在层状地电模型中,频率与探测深度的对应关系良好,即高频反映浅部地电信息,低频反映深部地电信息.然而浅层局部不均匀地电体却不仅影响高频电磁场,同时也影响低频电磁场.在MT或AMT中,由于浅层局部不均匀地电体的存在,将使得相对低频段的视电阻率曲线出现整体向上或向下偏移,即静态偏移,从而对深部观测产生不利影响.过往的研究大多是把浅层不均匀地电体视为地质干扰体,主要研究其带来的静态偏移干扰,研究的目标是消除浅部不均匀体对深部探测的影响[5 9 ] .在实际中,浅部不均匀地电体也可能是待探测的目标,比如地质灾害调查或工程地质勘察中常探测的岩溶、采空区、破碎断裂、塌陷体等不良地质体,此时所谓的静态效应就不再是干扰效应,而成为目标异常响应[10 ] .因此有必要对其浅层不均匀体的平面波电磁响应特征做更全面的研究.本文通过正演计算不同参数条件下浅层局部良导体的平面电磁波响应特征,为利用平面电磁波法探测浅层地电异常体提供思路. ...
1
... 平面电磁波从空气中入射至非磁性水平均匀半空间大地,设地表的入射电场沿x 方向且幅度为E 0 ,则大地表面的透射电场、磁场分别为[11 ] : ...
Electromagnetic methods in applied geophysics
1
1980
... 大地电阻率变化引起波阻抗变化,从而引起地表观测电磁场的变化.通过在地表观测相互正交的电场和磁场计算地面波阻抗,即可评估大地的电阻率.若大地是水平层状的,根据地表不同频率电磁场计算得到的是不同趋肤深度范围内的视波阻抗和视电阻率,再通过层状递推公式[12 ] 反演即可求得各层电阻率和厚度信息,从而实现平面波电磁测深. ...
Near-surface and topographic distortions in electromagnetic induction
1
1990
... 在实际应用中,特别是工程地质勘察中,探测目标往往是局部的不均匀地电体.不均匀地电体在一次电场的作用下,在电性分界面上形成积累电荷,并产生二次电场[13 ] ...
2
... 本文采用三维数值模拟方法是积分方程法[14 ] ,其方法理论较成熟,应用也较广泛.该方法仅需对异常体进行精细剖分,未知数较少,对于单个小异常体计算比较经济,计算精度也相对较高,具体算法可参考相关文献[15 17 ].本文简述其算法如下. ...
... 本文采用加拿大EiKon Technologies Ltd.的EMIGMA软件进行正演.EMIGMA软件是一款比较先进的综合地球物理解释平台,其配套MT/AMT模块可以实现快速3D正演,可模拟电偶极及磁偶极接收机数据,能通过积分沿接收端方向的电场来模拟实际测量长度的电偶极接收机数据,可模拟不限制数目的长方体、薄板及多面体目标,可模拟地形影响,有处理层结构和异常体之间的全部差异的能力[14 ] . ...
Electromagnetic modeling of three-dimensional bodies in layered earths using integral equations
1
1984
... 本文采用三维数值模拟方法是积分方程法[14 ] ,其方法理论较成熟,应用也较广泛.该方法仅需对异常体进行精细剖分,未知数较少,对于单个小异常体计算比较经济,计算精度也相对较高,具体算法可参考相关文献[15 17 ].本文简述其算法如下. ...
Integral equation modeling of three-dimensional magnetotelluric response
0
1981
一种新的三维大地电磁积分方程正演方法
1
2017
... 本文采用三维数值模拟方法是积分方程法[14 ] ,其方法理论较成熟,应用也较广泛.该方法仅需对异常体进行精细剖分,未知数较少,对于单个小异常体计算比较经济,计算精度也相对较高,具体算法可参考相关文献[15 17 ].本文简述其算法如下. ...
一种新的三维大地电磁积分方程正演方法
1
2017
... 本文采用三维数值模拟方法是积分方程法[14 ] ,其方法理论较成熟,应用也较广泛.该方法仅需对异常体进行精细剖分,未知数较少,对于单个小异常体计算比较经济,计算精度也相对较高,具体算法可参考相关文献[15 17 ].本文简述其算法如下. ...