基于地震干涉的复杂构造局部成像

doi:10.11720/wtyht.2025.1272

基于地震干涉的复杂构造局部成像

刁瑞^,¹, 葛大明¹, 孔庆丰¹, 燕新跃², 韩睿², 谷丙洛²

1.中国石油化工股份有限公司胜利油田分公司物探研究院, 山东东营 257022

2.中国石油大学(华东) 地球科学与技术学院, 山东青岛 266580

Local imaging of complex structures based on seismic interferometry

DIAO Rui^,¹, GE Da-Ming¹, KONG Qing-Feng¹, YAN Xin-Yue², HAN Rui², GU Bing-Luo²

1. Geophysical Research Institute, Shengli Oilfield Branch Company,SINOPEC, Dongying 257022, China

2. School of Geosciences, China University of Petroleum(East China), Qingdao 266580, China

第一作者: 刁瑞(1985-),男,博士,研究员,主要从事油气地球物理方法和油藏地球物理监测技术研究工作。Email:diaorui1985@163.com

责任编辑: 叶佩

收稿日期: 2024-07-10 修回日期: 2025-06-10

基金资助:

国家自然科学基金面上项目(42374151)

山东省泰山产业领军人才项目“新一代井地立体地震技术研究及产业化应用”

Received: 2024-07-10 Revised: 2025-06-10

摘要

随着我国油气勘探的不断深入,如今地震勘探成像的重点从大尺度整体成像逐渐转向小尺度复杂构造体成像。受地震波传播机理的限制,小尺度、高陡等复杂构造存在界面反射信息拾取困难、反射能量弱等问题,常规地面地震勘探成像方式难以实现精确成像。通过地震干涉法能够使虚拟观测系统更靠近目标区域,提高对复杂界面的成像分辨率,实现面向目标构造的高精度成像。笔者对地震干涉原理进行理论推导,对小尺度模型进行正演模拟,将生成的干涉道集与实际参考道集进行对比,验证了干涉方法的正确性。将该方法应用到BP气云模型和高陡构造—薄互层模型进行数值试算,并将成像结果与常规RTM成像结果进行对比,证明了地震干涉法可以实现对深层复杂构造的高精度成像。

关键词： 复杂构造; 波场重构; 地震干涉成像

Abstract

With the continuous advancement of oil and gas exploration in China,the focus of seismic imaging has gradually shifted from large-scale overall imaging to small-scale complex structure imaging.Due to the inherent limitations of seismic wave propagation,small-scale and highly steep complex structures pose challenges such as difficulty in capturing interface reflection information and weak reflection energy.Consequently,conventional surface seismic imaging methods struggle to achieve accurate imaging of these targets.The seismic interferometry method can render the virtual observation system closer to the target area,improving the imaging resolution of complex interfaces, and achieving high-precision target-oriented imaging.This study conducted a theoretical derivation of the seismic interferometry mechanism and forward modeling of small-scale models.By comparing the generated interferometric gathers with actual reference gathers,this study verified the accuracy of the seismic interferometry method.Subsequently,this study applied the method to the backpropagation(BP) gas cloud model and a highly-steep structure- thin interbed model for numerical tests.The imaging results were finally compared with conventional reverse time migration(RTM) results,demonstrating that the seismic interferometry method enables high-precision imaging of deep complex structures.

Keywords： complex structure; wavefield reconstruction; imaging based on seismic interferometry

PDF (7041KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刁瑞, 葛大明, 孔庆丰, 燕新跃, 韩睿, 谷丙洛. 基于地震干涉的复杂构造局部成像[J]. 物探与化探, 2025, 49(4): 869-877 doi:10.11720/wtyht.2025.1272

DIAO Rui, GE Da-Ming, KONG Qing-Feng, YAN Xin-Yue, HAN Rui, GU Bing-Luo. Local imaging of complex structures based on seismic interferometry[J]. Geophysical and Geochemical Exploration, 2025, 49(4): 869-877 doi:10.11720/wtyht.2025.1272

0 引言

随着石油工业的发展和油气勘探程度的提高,油气燃料作为能源主体成分的需求增加,对地震资料处理精度和准确度的要求也不断提高,精细化勘探技术成为油气勘探新的发展趋势^[1]。精细勘探、寻找增储目标的需要使油气开发的重点由浅层转向中深层以及超深层,勘探对象从大储量油藏、构造油气藏转移到剩余油、隐蔽油气藏,勘探区域地表、地下条件从简单区向复杂区转移,油气勘探面临的“低、深、隐、难”的问题愈来愈突出^[2]。在我国西部地区,地表起伏较大,近地表构造复杂,这对深层复杂构造高精度成像提出了新的挑战^[3]。

受地震波传播机理的限制,复杂构造存在反射信息拾取困难、反射能量弱等问题,常规的地面地震勘探难以对其进行精确成像^[4]。地震干涉法是一种数据驱动的基准面延拓方法,它克服了模型驱动类基准面延拓法对模型精度、地表一致性假设以及特定反射层的依赖,能够使观测系统更加靠近目标地层,提高目标界面的成像分辨率,实现面向复杂构造的高精度成像^[5]。

地震干涉法基于源检互易定理,对不同检波点处地震记录进行褶积/相关处理,重构虚拟震源数据,得到以某一检波点为虚拟震源,另一检波点处接收到的虚拟地震记录^[6]。干涉概念最早由Claerbout提出,给出了地下震源透射响应与地表反射响应间的关系:水平层状介质中,对检波器接收的透射波进行自相关运算可以获得以该检波器为震源的自激自收记录。Schuster等^[7]将该方法引入勘探地震学,提出“干涉成像”概念。

地震干涉法通过对格林函数进行一系列的数学运算来延长或消除波场路径,实现数据重构,使观测系统更加靠近目标地质体。根据地震干涉法中格林函数恢复算法的不同,可将其分为相关型干涉和褶积型干涉^[8]。相关型干涉算法简单、稳定性好,但得到的虚拟地震记录存在虚假同相轴;褶积型算法生成虚拟地震记录较为准确,但存在计算量大、稳定性差等问题^[9]。

本文先介绍了地震干涉的原理,然后应用小尺度模型进行了正演模拟,并对正演结果进行干涉运算,将得到的干涉道集与真实记录的参考道集进行对比,验证了该方法的正确性。将该方法应用到BP气云模型和高陡构造—薄互层模型上,并将干涉成像结果与常规RTM成像结果进行对比,得到对目标地质体的高精度成像,验证了该方法的有效性。

1 地震干涉基础理论

地震干涉法本质是构建虚拟地震记录,即对两个检波点处获得的地震记录进行相关/褶积处理,来消除/延长地震波在介质中的传播路径,得到某一个检波点作为虚拟震源、其他检波点作为虚拟检波点的虚拟地震记录^[10]。

1.1 格林函数表征

地震干涉法的数学实现方式主要体现在格林函数的提取上,地震干涉通常也被称为格林函数检索。对于任意常密度声学介质,时间域波动方程可表示为波场关于时间和空间的双曲型偏微分方程:

(1)

$\frac{1}{c} \frac{\partial^{2} p}{\partial t^{2}}-\nabla^{2} p=0$

式中:p(x,y,z,t)为数值模拟的声波波场;c表示声波传播速度;${\nabla }^{2}$是拉普拉斯微分算子;t表示声波传播时间。

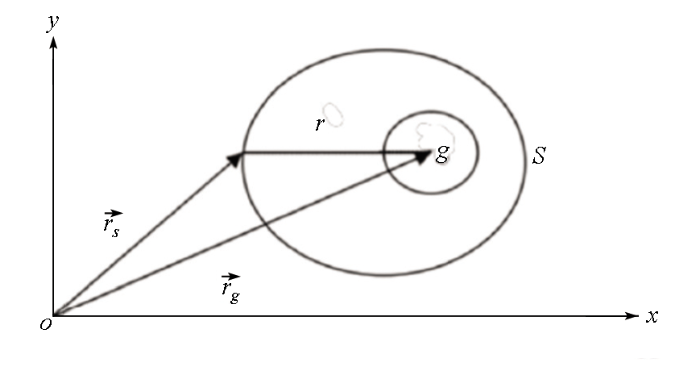
如图1所示,封闭曲面S内含有均匀速度介质,根据Helmholtz-Kirchhoff公式,检波点g处的波场值可以根据曲面S的波场值P_S和震源振动速度$\frac{\partial {P}_{S}}{\partial n}$来计算:

(2)

${P}_{g}=\frac{1}{4\pi }\underset{S}{\int \int }\left\{\frac{{e}^{ikr}}{r}\frac{\partial {P}_{S}}{\partial n}-{P}_{S}\frac{\partial }{\partial n}\left(\frac{{e}^{ikr}}{r}\right)\right\}dS$

式中:n代表封闭界面S的外法线方向;$\frac{{e}^{ikr}}{r}$为辅助函数,使方程在r≠0时满足在曲面S与外界具有连续性、有界性和无穷性的假设。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 Helmholtz-Kirchhoff积分原理示意

Fig.1 Schematic of Helmholtz-Kirchhoff integral principle

可以对该点源接收到的波场进行叠加来计算任意源的场。假设格林函数是脉冲点源的声波介质响应,对于任意常密度声学介质,它满足频率域Helmholtz方程:

(3)$\left(\nabla^{2}+k^{2}\right) G(g \mid s)=-\delta(s-g),$

式中:波数k=ω/v(g),ω表示震源频率,v为速度;δ(s-g)=δ(x_s-x_g)δ(y_s-y_g),表示震源函数;x_s、y_s代表炮点的空间坐标,x_g、y_g代表检波点的空间坐标,G(g|s)代表s为源、g处接收波场的格林函数。δ(s-g)的二阶偏微分方程有两个独立的解,分别是向外传播的因果格林函数G(g|s)和向回传播的非因果格林函数G(g|s)^*。

在任意速度v的均匀介质中,因果格林函数G(g|s)可表示为^[11]:

(4)

$G\left(g\right|s)=\frac{1}{4\pi }\frac{{e}^{ikr}}{r}$

式中:波数k=ω/v;炮检距r=|g-s|;1/r为几何扩散因子;eⁱ^kr为反傅里叶变换的傅里叶核。对于三维声波介质,格林函数G(g|s)代表震源s处激发、检波点g处接收到的地震响应。

2001年,Bleistein通过几何扩散函数和时间因子给出了速度分布平滑时的高频渐进格林函数形式表达:

(5)

$G\left(g\right|s)=A(g,s){e}^{i\omega {\tau }_{gs}}$

式中:A(g,s)为几何扩散衰减影响因子;${e}^{i\omega {\tau }_{gs}}$为时间因子;τ_gs表示地震波从震源到检波器位置传播的旅行时,通过求解程函方程获得。实际应用中,可以通过不同类型的射线追踪方法来计算其格林函数。

1.2 互易方程推导

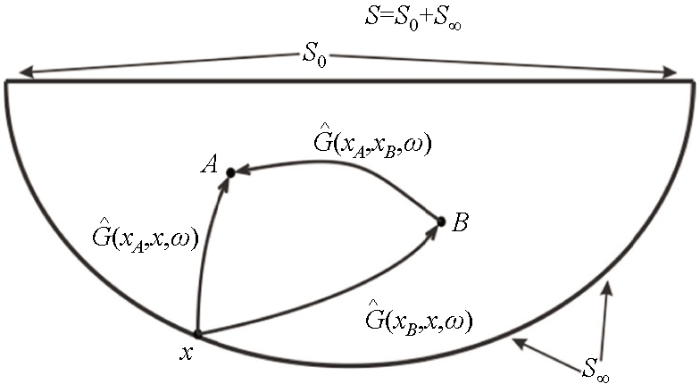
互易方程是地震干涉测量的基本控制方程,是地震干涉技术的基础。通过改变互易方程中积分区域的范围,能够应用地震干涉法实现不同类型的数据转换^[12]。如图2所示,假设在自由表面S₀和任何形状边界S_∞组成的封闭空间S内介质是无损的,空间S外部的介质是均匀的。任意位置x处布设点脉冲震源,且x_A和x_B都在区域S内,外部应力为零,那么A状态下的波场可以表示为:

(6)$\hat{p}_{A}(x, \omega) \stackrel{\Delta}{=} \hat{G}\left(x, x_{A}, \omega\right) \text {, }$

(7)

$\hat{v}_{i, A}(x, \omega)=-[\mathrm{j} \omega p(x)]^{-1} \partial_{1} \hat{G}\left(x, x_{A}, \omega\right),$

式中:$\hat{G}$(x,x_A,ω)为频率域因果格林函数。由方程(6)可知,频率域格林函数等价于x处接收到的压力场。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 地震干涉原理示意

Fig.2 Schematic of seismic interference principle

同理,将状态B的波场表达式与状态A的波场表达式合并,可得频率域格林函数:

(8)

$\begin{array}{c}\hat{G}\left(x_{B}, x_{A}, \omega\right)-\hat{G}\left(x_{A}, x_{B}, \omega\right)=\oint_{\partial D} \frac{-1}{\mathrm{j} \bar{\omega} p(\omega)} \cdot \\{\left[\hat{G}\left(x, x_{A}, \omega\right) \partial_{i} \hat{G}\left(x, x_{B}, \omega\right)-\partial_{i} \hat{G}\left(x, x_{A}, \omega\right) \cdot\right.} \\\left.\hat{G}\left(x, x_{B}, \omega\right)\right] \boldsymbol{n}_{i} \mathrm{~d}^{2} x,\end{array}$

式中:$\hat{G}$(x_A,x_B,ω)和$\hat{G}$(x_B,x_A,ω)为频率域因果格林函数。由于∂D为半径无限大的球面,根据散射条件,格林函数在∂D上的积分为零,可知方程(8)右侧的结果与∂D的选择无关。因此,对于任意的∂D可得:

(9)$\hat{G}({x}_{B},{x}_{A},\omega )=\hat{G}({x}_{A},{x}_{B},\omega )$。

故方程(9)为声波格林函数的源—检互易方程。将B状态的频率域震源和波场表达式代入方程(9)中可得:

(10)$\begin{array}{c}2 \Re\left(\hat{G}\left(x_{A}, x_{B}, \omega\right)\right)=\oint_{\partial D} \frac{-1}{\mathrm{j} \omega p(\omega)}\left(\hat{G}\left(x_{A}, x, \omega\right)\right. \\\left.\partial_{i} \hat{G}\left(x_{B}, x, \omega\right)-\left(\partial_{i} \hat{G}\left(x_{A}, x, \omega\right)\right) \hat{G}\left(x_{B}, x, \omega\right)\right) \\n_{j} \mathrm{~d}^{2} x\end{array}$。

方程(10)为声学介质干涉基本方程^[13]。式中:R表示取实部;$\hat{G}$和∂_i$\hat{G}$n_i表示单极震源和偶极震源激发波场在x处的响应,该响应可看作震源位于x时,对x_A和x_B处接收到的地震响应进行互相关,之后再进行傅立叶变换并积分。由于方程(10)积分中包含了两个需要单独计算的互相关项,并且要求对于在∂D上任意x处由单极源和偶极源激发产生的响应都应被接收到,在高频情况下,可通过格林函数的方向导数对各个成分(直达波、散射波等)乘以±j$\frac{\omega }{c\left(x\right)}$|cos(α(x))|来近似,其中:c(x)为地震波在∂D上的传播速度;α(x)为射线和法线的夹角。当∂D为不规则表面,即震源随机分布时,在高频近似条件下,频率域格林函数重建关系式可表示为 :

(11)$\begin{array}{c}2 \Re\left[\hat{G}\left(x_{B}, x_{A}, \omega\right)\right] \approx \\\frac{2}{\rho c} \oint_{S} \hat{G}\left(x_{B}, x, \omega\right) \hat{G}^{*}\left(x_{A}, x, \omega\right) \mathrm{d}^{2} x。\end{array}$

式中:R表示实部;$\hat{G}$(x_B,x_A,ω)表示在以x_A为震源、x_B为检波器的频率域重建格林函数;ρ和c分别表示界面S及其外部介质的密度和波速,它与频率、震源处弹性性质及震源边界几何形态有关;$\hat{G}$(x_A,x,ω)和$\hat{G}$(x_B,x,ω)分别表示在边界S_∞上的震源x在x_A和x_B处的格林函数;*表示复共轭。

方程(11)说明,当震源数量足够多,且围绕检波点均匀分布在封闭边界上时,对两个检波点的记录互相关并求和,能够得到以其中一个检波点为虚拟震源、另一个检波点为虚拟检波点的地震记录。

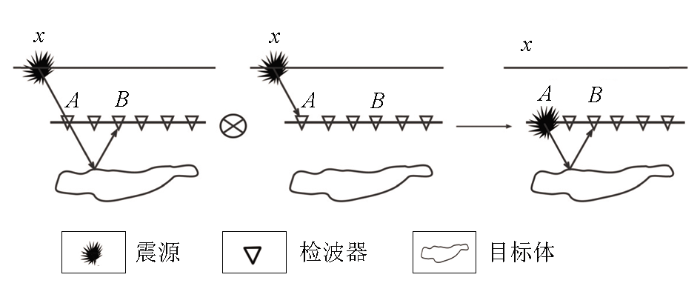
由于实际勘探中震源不可能完全沿某一封闭曲线均匀分布,故地震干涉法在实际应用中也有多种实现方式,本文应用图3所示的波场路径来进行地震干涉。如图3所示,通过地震干涉原理,可以将以x位置为震源、B位置为检波器得到的地震记录与以x位置为震源、A位置为检波器得到的地震记录进行相关运算,消除x位置处发出波场的共同路径,得到以A位置处为虚拟震源、B位置为虚拟检波器的地震干涉记录。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 地震干涉实现方法示意

Fig.3 The schematic of seismic interference realization method

地震干涉法的具体实现流程如下:依据勘探目标及勘探工区地质地球物理条件,构建目标工区的速度模型;基于局部构造成像需求,对实际地震共炮点道集每一炮实施特定的波场分离运算;依据实际地震观测系统和井中地震观测系统分布特征,设计面向局部目标的虚拟采集系统;对地震资料进行道集重排并作为输入数据,进行干涉处理,得到虚拟共炮点道集;提取地震子波并采用反褶积方法对虚拟共炮点道集进行处理;应用干涉成像条件进行成像。

2 数值试算

2.1 小尺度模型

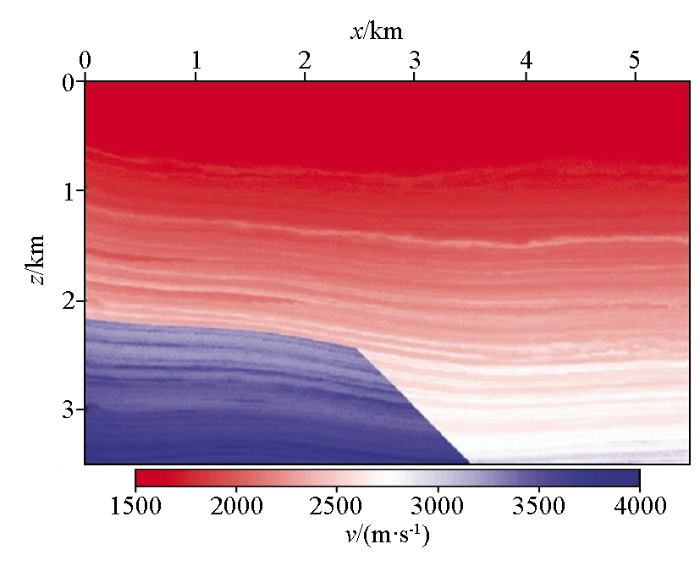
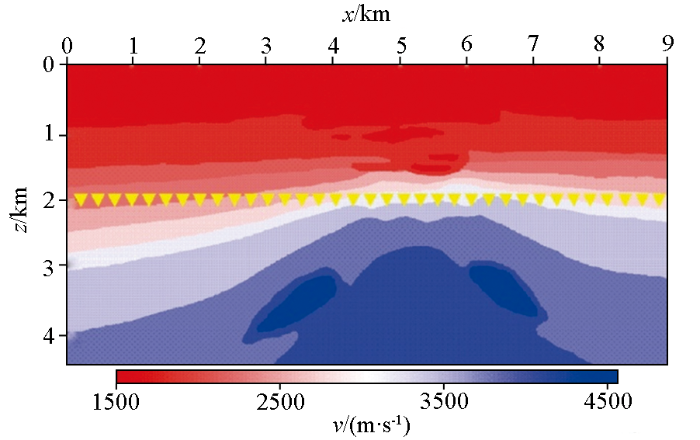
按照上述地震干涉方法对小尺度模型进行数值试算,并将得到的干涉道集与实际道集进行对比分析,验证方法的正确性。采用如图4所示的小尺度模型进行干涉试算,该模型网格点数为551×351,横向和纵向采样间隔均为10 m。在深度1 500 m处布置水平井,井中布设551个检波器,道间距为10 m。共111个震源在地表水平布设,震源间隔为50 m。采用主频为20 Hz的Ricker子波作为震源时间函数,记录时长为3.5 s,采样间隔0.5 ms。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 小尺度模型

Fig.4 Small-scale model

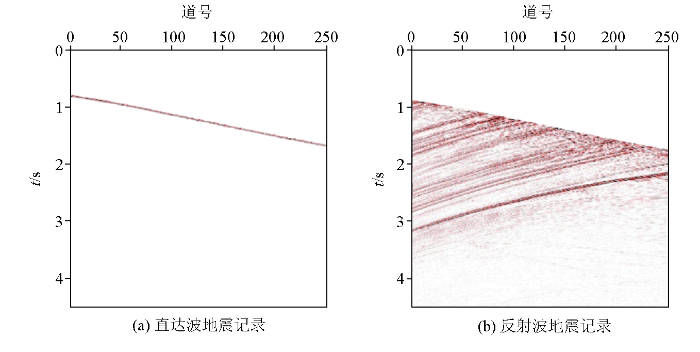
按照上述观测系统对图4所示模型进行正演模拟,得到直达波与反射波的地震记录如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 地震正演记录

Fig.5 Seismic forward modeling record

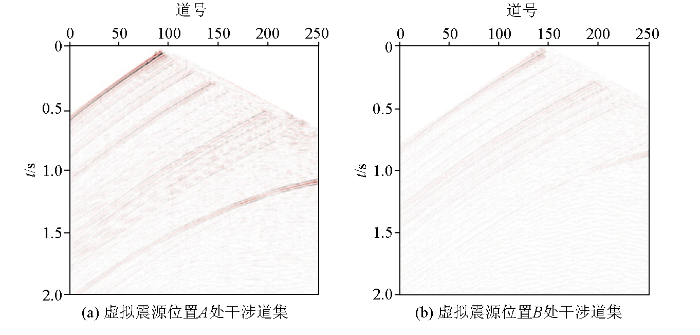
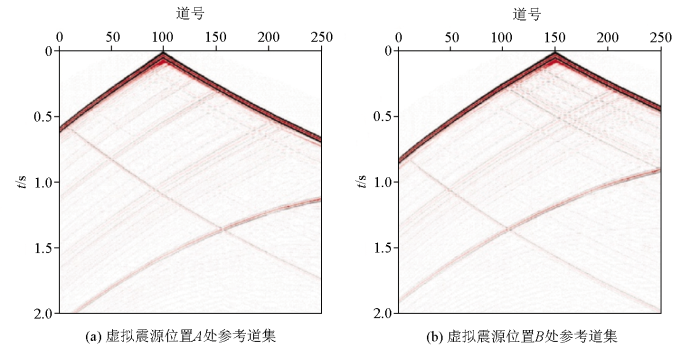
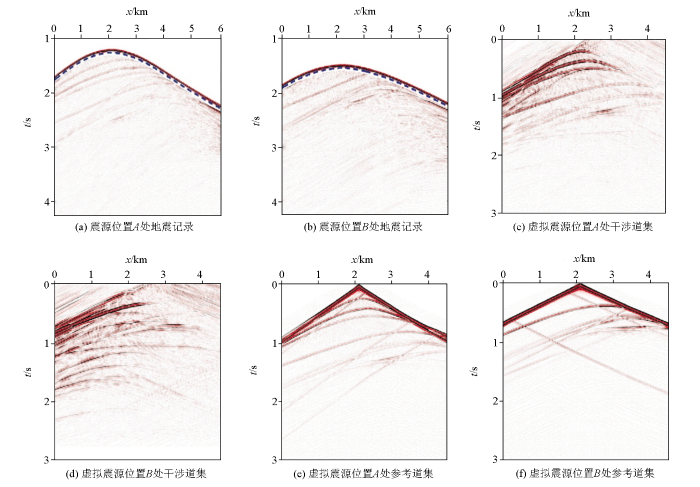
利用地震干涉法对该数据进行处理,能够得到深度1 500 m处不同水平位置作为虚拟震源的干涉道集,如图6所示。将实际震源沿1 500 m深度水平布设,对其正演模拟可以得到真实的地震记录,如图7所示。通过将真实地震记录作为参考道集与干涉道集进行比较,验证了本文方法的正确性。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 干涉道集

Fig.6 Interference gathers

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 参考道集

Fig.7 Reference gathers

将通过地震干涉得到的干涉道集(图6)与实际正演模拟得到的参考道集(图7)进行对比分析,可以看出,干涉道集与参考道集的主要波场信息都保持一致。基于地震干涉法,能够对正演地震记录的直达波和反射波通过数学运算来得到深度基准面的虚拟反射地震记录。

2.2 BP气云模型

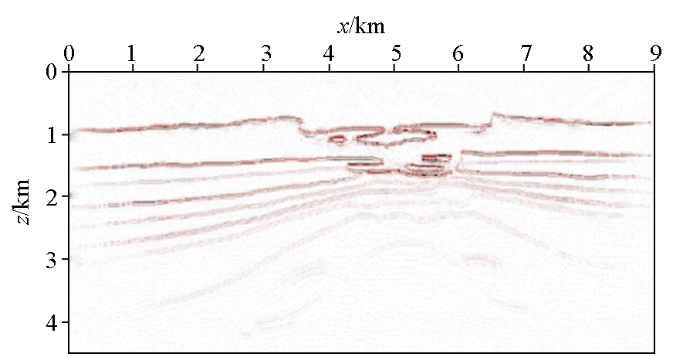
应用地震干涉法对BP气云模型进行成像试算,图8为数值模拟所用BP气云模型,模型网格点数为901×451,横向和纵向采样间隔均为10 m。共181个震源沿地表水平布设,震源间隔为50 m。地面观测系统的检波点位于地表,井中观测系统的检波点在深度2 000 m的水平井中分布,共901个检波器,道间距为10 m。采用子波主频为20 Hz的Ricker子波作为震源时间函数,记录时长为4.25 s,时间采样步长为0.5 ms。应用常规RTM对地面观测系统正演模拟数据进行全局成像,得到的成像结果如图9所示,RTM成像剖面中潜山深部不规则高速体的成像精度低,无法满足深层精细勘探需要。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 BP模型

Fig.8 BP model

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 RTM成像结果

Fig.9 RTM imaging results

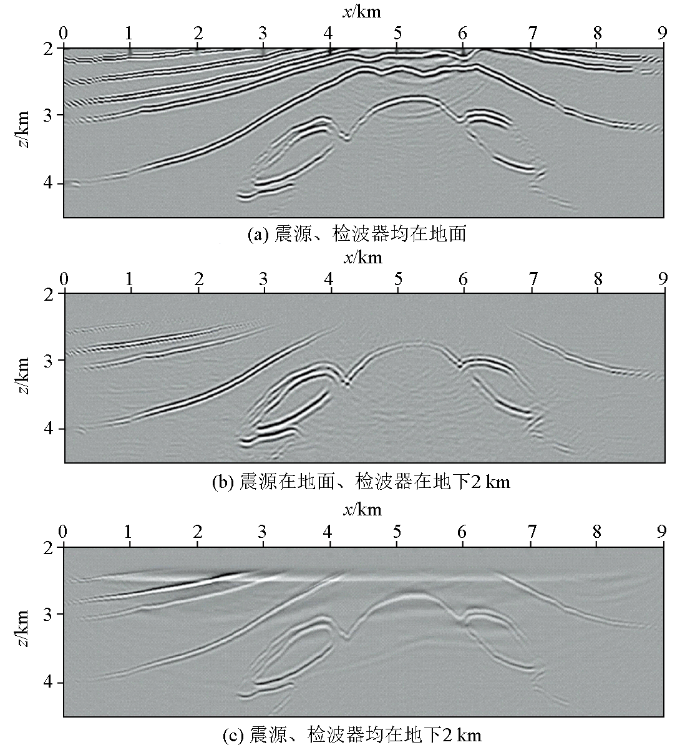
按照观测系统对BP气云模型进行正演模拟,可以得到震源位于地表和深度2 km的地震记录,如图10所示。基于BP气云模型的深层地质构造特征,应用地震干涉法,分别将震源、检波点重构到地下2 km,得到不同虚拟采集系统的成像剖面如图11所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 不同观测系统地震记录对比

Fig.10 Comparison of seismic records of different observation systems

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 不同虚拟采集系统成像剖面

Fig.11 Imaging profiles of different virtual acquisition systems

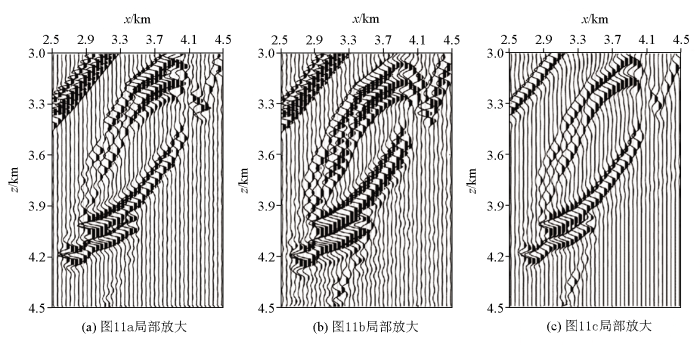
将图11中不同虚拟采集系统的目标构造进行放大,得到目标构造的成像剖面局部放大图,如图12所示。通过对比目标成像剖面(图12b)和参考剖面(图12c)可知,本文提出的基于维纳滤波的地震干涉成像方法能够实现震源、检波器的重构,生成靠近目标地质体的虚拟采集系统,得到目标成像剖面。将目标成像剖面(图12b)与地面地震剖面(图12a)对比可知,针对BP气云模型的高陡构造,地震干涉成像剖面的成像精度和分辨率均高于常规的地面地震剖面,证明了本文提出方法的有效性。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 不同虚拟采集系统目标构造成像剖面局部放大

Fig.12 Zoomed views of imaging profiles of different virtual acquisition systems

2.3 高陡构造—薄互层模型

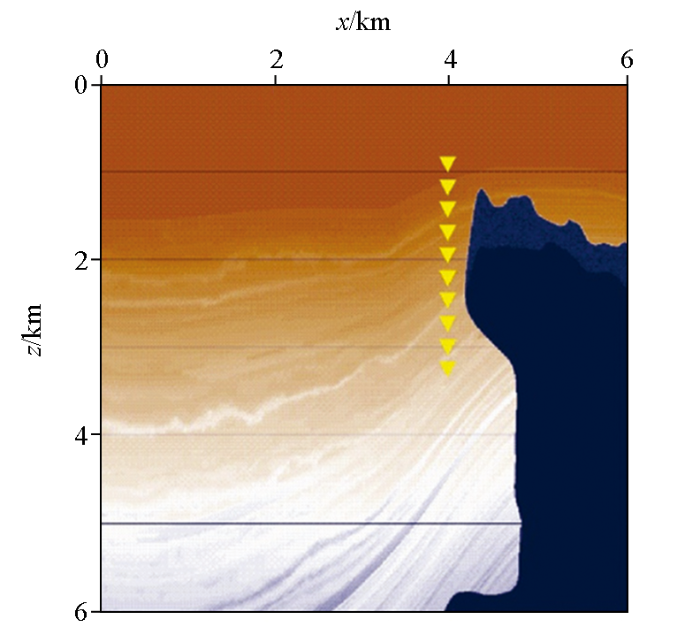
进一步验证所提出的地震干涉成像方法对复杂模型的适用性,对高陡构造—薄互层模型进行了成像试算。图13为高陡构造—薄互层模型,模型网格点数为601×601,横向和纵向采样间隔均为10 m,黄色倒三角代表检波器布设。在水平方向4 000 m处布置垂直井,井中布设451个检波器,道间距为10 m,井深度为800~3 300 m。共301个震源在地表水平布设,震源间隔为20 m。采用主频为20 Hz的Ricker子波作为震源时间函数,记录时长为6 s,采样间隔1 ms。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 高陡构造—薄互层模型

Fig.13 High-steep structure-thin interbed model

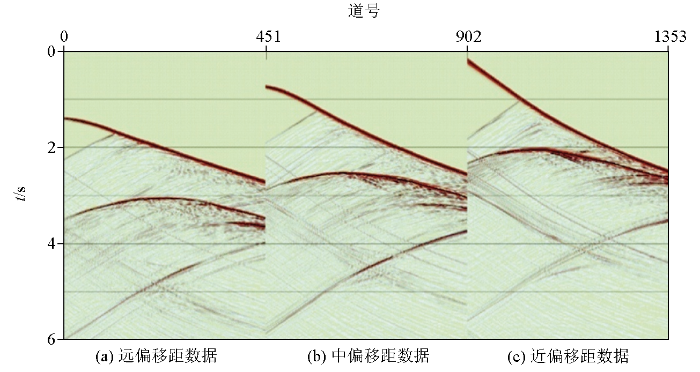
按照上述观测系统对图13所示模型进行正演模拟,得到不同偏移距的VSP地震记录如图14所示。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 不同偏移距正演结果

Fig.14 Forward results of different offsets

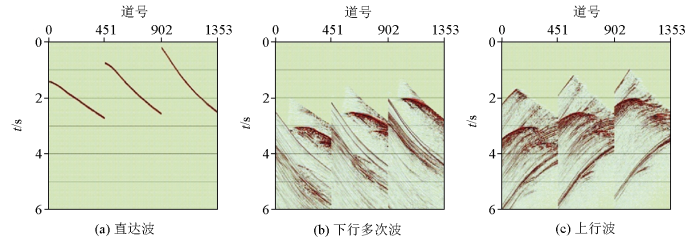
基于高陡构造—薄互层模型的地质特征,选用合适的地震干涉方法设计虚拟观测系统,并对图14所示共炮点道集进行波场分离,生成不同波形的VSP地震记录,如图15所示。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 VSP地震记录不同波型

Fig.15 VSP seismic records of different wave types

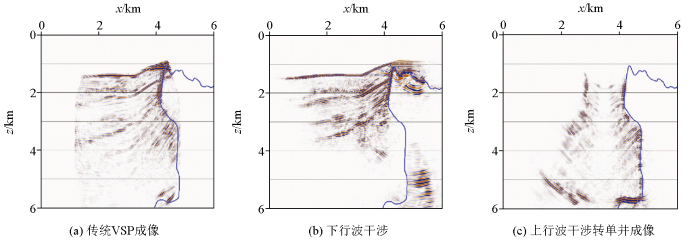
分别采用传统VSP成像法、下行波干涉成像法、上行波干涉转单井成像法对该模型进行成像,成像结果如图16所示。通过对比可得,传统VSP成像仅能够对井周构造进行成像,无法对检波器上方区域进行成像。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 不同方法成像结果对比

Fig.16 Comparison of imaging results of different methods

地震干涉法通过对不同类型地震资料进行处理,使重构的观测系统更靠近目标构造,能够得到更好的局部目标成像效果。对于井周陡倾角构造,可以通过地震干涉法提升其有效反射角来实现该构造的高精度成像。与常规RTM成像方法相比,地震干涉法可将基准面延拓到目的层,使得观测系统更靠近目标地质体,减少地层反射信息的散射,深层地震波能量得到加强,地震剖面的成像精度明显提高。高精度成像数据能够提升储层精细解释和油气识别的精度,为复杂隐蔽油气藏和页岩油气的勘探开发提供了数据基础^[14-16]。

3 结论

笔者针对常规地震勘探效果不好的复杂构造,基于地震干涉理论将得到的干涉道集与实际正演得到的参考道集进行对比分析,验证了本文干涉方法的正确性。然后将该方法应用到BP气云模型和高陡构造—薄互层模型中,实现了对BP气云模型和高陡构造—薄互层模型复杂构造的高精度成像。由此得出以下结论:

1)基于地震干涉法,能够利用地震资料的直达波和上行反射波来获得深度基准面的虚拟反射地震记录。该虚拟采集方式能够有效突出深层小尺度地质体引起的弱反射,获得更大反射角的信息,为深部小尺度构造成像奠定数据基础,实现对目标构造的高精度成像。

2)与常规RTM成像相比,基于干涉的局部成像对于小尺度目标更有优势。虚拟检波点位置距离目标构造更近时,局部目标成像质量更佳。应用地震干涉法能够实现BP气云模型和高陡构造—薄互层模型深层复杂构造的高精度成像。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

贾承造, 王祖纲, 姜林,

等.

中国页岩油勘探开发研究进展与科学技术问题

[J]. 世界石油工业, 2024, 31(4):1-11.