频率域地空电磁法磁场三分量全域视电阻率的定义

doi:10.11720/wtyht.2025.1204

频率域地空电磁法磁场三分量全域视电阻率的定义

罗姣^,¹, 郭文波¹, 刘长生^,², 张继锋³, 王伟¹^,³, 徐毅¹^,³, 张鑫鑫¹, 陈靖¹

1.西安西北有色物化探总队有限公司,陕西西安 710068

2.长沙航空职业技术学院,湖南长沙 410124

3.长安大学地质工程与测绘学院,陕西西安 710054

Definition of global apparent resistivity based on three components of the magnetic field for the interpretation of the ground-airborne frequency-domain electromagnetic data

LUO Jiao^,¹, GUO Wen-Bo¹, LIU Chang-Sheng^,², ZHANG Ji-Feng³, WANG Wei¹^,³, XU Yi¹^,³, ZHANG Xin-Xin¹, CHEN Jing¹

1. Xi'an Northwest Colored Geophysical and Geochemical Exploration Company Limited, Xi'an 710068, China

2. Changsha Aeronautical Vocational and Technical College, Changsha 410124, China

3. College of Geological Engineering and Geomatics, Chang'an University, xi'an 710054, China

通讯作者: 刘长生(1966-),男,教授,主要从事电磁法理论正反演、计算机应用技术研究工作。Email:30623297@qq.com

第一作者: 罗姣(1988-),女,硕士,高级工程师,主要从事电磁法勘探研究工作。Email:342579518@qq.com

责任编辑: 王萌

收稿日期: 2024-05-8 修回日期: 2024-07-24

基金资助:

国家自然科学基金(42174168)
长安大学中央高校基本科研业务费专项资金(300102262201)
陕西有色金属控股集团战略新兴产业重点科技攻关项目(第二批)
陕西省自然科学基础研究计划专项资金(2025JC-YBQN-379)

西安西北有色物化探总队有限公司科技项目

Received: 2024-05-8 Revised: 2024-07-24

摘要

频率域地空电磁法(ground-airborne frequency-domain electromagnetic,GAFDEM)相比传统地面电磁法具有工作效率高、成本低、可适用于复杂地形地貌环境的特点,是一种很有发展潜力的方法。已经成功研制与该方法相关的仪器和设备,并得到了初步应用,但其解释方法还有待于发展。本文研究了均匀半空间下磁场三分量随电阻率的变化规律,提出了用基于泰勒级数展开的方式,采用迭代法计算全域视电阻率的方法。通过对典型地层模型的计算,分析了不同分量、不同频域、不同飞行高度、不同偏移距下全域视电阻率的特征。结果表明,该全域视电阻率定义方法基本不受收发距、飞行高度等参数的影响,能够正确地反映地层电阻率的变化,为后续频率域地空电磁法数据的处理和解释提供了理论指导。

关键词： 频率域; 地空电磁系统; 全域视电阻率; 磁场三分量

Abstract

The ground-airborne frequency-domain electromagnetic (GAFDEM) method exhibits high efficiency and low cost compared to conventional ground electromagnetic methods. It is applicable to electromagnetic sounding in complex topographic and geomorphic settings, demonstrating promising application potential. Despite the development and preliminary application of GAFDEM-related instrumentation and equipment, the interpretation methods for GAFDEM data remain under-studied. By investigating the resistivity-varying patterns of three components of the magnetic field in a homogeneous half-space, this study proposed an iterative method based on Taylor series expansion to calculate the global apparent resistivity. Through the calculation of a typical stratigraphic model, this study analyzed the characteristics of global apparent resistivity under different components, frequency domains, flight altitudes, and offsets. The results demonstrate that the definition method of global apparent resistivity in this study, subjected to minimal impacts from parameters like receiver-transmitter distance and flight altitude, can effectively reflect the variations of formation resistivity. Therefore, this study provides a theoretical guide for the processing and interpretation of GAFDEM data.

Keywords： frequency domain; ground-airborne electromagnetic system; global apparent resistivity; three components of a magnetic field

PDF (2587KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

罗姣, 郭文波, 刘长生, 张继锋, 王伟, 徐毅, 张鑫鑫, 陈靖. 频率域地空电磁法磁场三分量全域视电阻率的定义[J]. 物探与化探, 2025, 49(3): 679-686 doi:10.11720/wtyht.2025.1204

LUO Jiao, GUO Wen-Bo, LIU Chang-Sheng, ZHANG Ji-Feng, WANG Wei, XU Yi, ZHANG Xin-Xin, CHEN Jing. Definition of global apparent resistivity based on three components of the magnetic field for the interpretation of the ground-airborne frequency-domain electromagnetic data[J]. Geophysical and Geochemical Exploration, 2025, 49(3): 679-686 doi:10.11720/wtyht.2025.1204

0 引言

地空电磁法以电磁感应原理为基础,是通过在地面布设发射脉冲或不同频域的电磁信号源,利用飞行装置在空中接收电磁感应信号的一种地球物理勘探方法。该技术具有工作效率快、勘探深度大、信噪比高、可以在地形复杂且勘探难度大的地区开展作业等优势。电磁法主要分为时间域和频率域两种,频率域是通过人工改变供电电源的电流频率,产生不同频率的电磁波,观测不同频率的远区电磁波信号的方法。由于不同频率电磁波信号可以反应不同深度介质的电磁特性,因此可以通过分析不同频率的视电阻率来探测地下目标体。

频率域电磁法最早是采用卡尼亚视电阻率来定性解释地下介质的电性结构,但卡尼亚视电阻率在过渡区及近场区常会发生畸变,不能反应地下真实的电阻率变化规律,因此殷长春等^[1]计算了电偶源的全波视电阻率,研究了全区视电阻率定义的思想与方法;方文藻等^[2]通过对均匀半空间场的近区公式与远区公式进行比较,引入了校正系数K,将远区定义的视电阻率乘以校正系数得到了全区视电阻值;黄皓平等^[3]利用磁场3个分量分段计算了垂直磁偶极子全区视电阻率;毛先进等^[4]提出了水平电偶源频率域电磁测深全区视电阻率直接算法;陈明生等^[5]研究了电偶源频率电磁测深中的E_x分量,得出电场E_x分量具有分辨率高、观测信噪比高、不需做近场改正的优点。汤井田等^[6]计算了CSAMT水平电场y分量E_y定义的全区视电阻率,通过模拟计算得出E_y全区视电阻率可以明显改善非波区的畸变效应。2011年,戚志鹏等^[7]提出了在频率域内利用多项式拟合来计算非中心点的垂直分量,用最小二乘原理建立与偏移距有关的视电阻率表达式;郝延松等^[8]研究了隧道及矿井中瞬变电磁的全空间视电阻率计算;柳建新等^[9]、王启等^[10]、王宏宇等^[11]讨论了E_x分量、E_φ分量定义的广域视电阻率,并对两者定义的广域电阻率进行对比,发现利用水平电场E_φ分量定义的广域视电阻率可以增大电磁法野外工作的测量范围;刘长胜等^[12]研究了地空频率域电磁法的探测范围与探测深度;罗维斌等^[13]给出了比值法计算H_y全区视电阻率公式,对比了不同视电阻率定义法获得的电阻率对模型的响应能力,发现H_y全区视电阻率在赤道装置和轴向装置的广大区域,对地电模型均有较好地响应;张继峰等^[14]采用非结构化有限元数值模拟,研究了多源地空三维电磁垂直磁场的响应特征;秦西社等^[15]给出了基于反函数原理的可控源电磁法全域视电阻率定义;钱威州等^[16]从垂直磁偶极子Z方向磁场公式推导了在低感应系数下的视电导率公式,实现了垂直磁偶源频率域电磁测深的一维正演。

目前,国内外电磁法的研究多侧重于时间域,采集数据大多为单一分量的响应信号。由于在接收点可以同时接收X、Y、Z三个方向上的磁场分量,并且实际生产中多种接收设备已具备三分量数据采集能力,相关学者已开展了对磁场各分量的研究。McNeill等^[17-18]对导电半空间中埋藏导体的瞬变电磁各分量响应进行了近似计算,分析了不同分量对异常体的反映,并研究了在瞬变电磁测量中测量电磁场各分量的必要性;刘金涛等^[19]通过对瞬变电磁三分量深度研究发现瞬变电磁三分量解释可对异常体的空间特性进行综合解释和精确定位;席振铢等^[20]对瞬变电磁三分量测量方法进行了研究,发现X分量可以用来确定异常体的中心,而Y、Z分量可以定性确定异常体的倾向;戚志鹏等^[21]研究了瞬变电磁水平分量的视电阻率,用实测数据验证了水平分量可以较好地确定异常体的边界;Sun等^[22]研究了多分量、多阵列瞬变电磁方法的实际应用,发现磁场垂直分量的纵向分辨率较高,而水平分量的横向分辨率也较高;Meng等^[23]研究了地井瞬变电磁多分量响应的数值分析;张莹莹等^[24-25]研究了多辐射场源地空瞬变电磁法多分量全域视电阻率定义,以及多分量的响应特征;张继锋等^[26-27]研究了地空电磁法在煤矿水害隐患探测方面应用效果,发明了“一种多源频率域地空电磁探测采集系统及方法”;徐晶等^[28]采用有限单元法,分析了半航空频率域电磁场电偶源与长导线源的感应磁场三分量在距地面20 m高度的磁场特征,当场源为电偶极源时,H_y对异常不敏感,而H_x和H_z对异常敏感,而三分量对长导线源均有反应。

经过综上研究可知,磁场各分量对解释地下介质的电性特征均有效,为更好地研究磁场多分量信息,本文基于地空电磁场磁场三分量给出了全域视电阻率的计算方法。

1 频率域地空电磁法基本原理

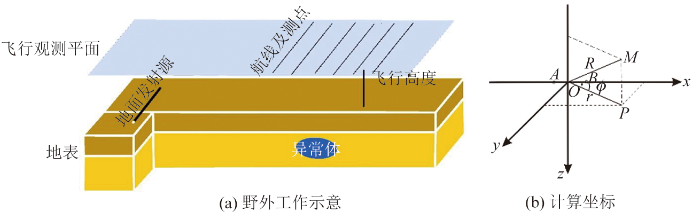
频率域地空电磁法采用电偶源地面供电,通过发射一系列不同频率的电磁波,以无人机搭载接收机在空中进行数据的采集,工作效率大大提升。图1是水平电偶源地空电磁法示意,AB是位于地表的电偶极源,坐标轴原点O位于AB中点,x方向为AB方向,z方向垂直向下,整个坐标轴满足右手准则。M表示空中的任一测点,P是测点M在地表的投影,R是测点M到原点O的距离,r表示投影P到原点的距离,即偏移距,φ为r和x轴正方向的夹角。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 水平电偶源频率域地空电磁法

Fig.1 Frequency domain ground-to-air electromagnetic method for horizontal couple sources

由于地表电偶极子在y方向上的电矢量位是对称的,即A_y=0,所以只存在A_x、A_z两个分量。根据磁场分量和电矢量位之间的关系,可得磁场各分量的表达式:

(1)

\{\begin{array}{l} H_{x} (ω) = \frac{P_{E}}{2 π} s i n ϕ c o s ϕ \int_{0}^{\infty} \frac{λ^{2}}{λ + u_{1} / R_{1}} e^{λ z} J_{0} (λ r) d λ - \frac{P_{E}}{2 π} \frac{s i n ϕ c o s ϕ}{r} \int_{0}^{\infty} \frac{2 λ}{λ + u_{1} / R_{1}} e^{λ z} J_{1} (λ r) d λ, \\ H_{y} (ω) = \frac{P_{E}}{2 π} s i n^{2} ϕ \int_{0}^{\infty} \frac{λ^{2}}{λ + u_{1} / R_{1}} e^{λ z} J_{0} (λ r) d λ + \frac{P_{E}}{2 π} \frac{(c o s^{2} ϕ - s i n^{2} ϕ)}{r} \int_{0}^{\infty} \frac{λ}{λ + u_{1} / R_{1}} e^{λ z} J_{1} (λ r) d λ, \\ H_{z} (ω) = \frac{P_{E}}{2 π} s i n ϕ \int_{0}^{\infty} \frac{λ^{2}}{λ + u_{1} / R_{1}} e^{λ z} J_{1} (λ r) d λ 。 \end{array}

其中:R₁迭代计算量为:

(2)

R_{1} = c t h [u_{1} h_{1} + a r c t h \frac{u_{1}}{u_{2}} c t h (u_{2} h_{2} + \dots + a r c t h \frac{u_{n - 1}}{u_{n}})]

其中:P_E=Id_s为点偶极矩;I为电流强度;d_s为电偶极子长度;u_i= $\sqrt{λ^{2} + k_{i}^{2}}$ ; $k_{i}^{2}$ =-iωμσ_i-ω²με;角频率ω=2πf,频率f,单位为Hz;磁导率μ,单位为H/m,一般取真空磁导率μ₀,即μ=μ₀=4π×10^-7 H/m;σ为介质电导率;ε为介质介电系数,若在导电介质中忽略位移电流,则 $k_{i}^{2}$ =-iωμσ_i;h_i为第i层厚度。

2 频率域地空电磁法视电阻率的定义

2.1 均匀半空间下频率域磁场各分量随电阻率的变化

建立均匀半空间模型,电偶源位于地表,长度为1 m,电流强度为1 A,即P_E=Id_s=1 A·m。分别计算偏移距为5 000 m、500 m,飞行高度为30 m、100 m的磁场响应,即以电偶源中点为原点,对应图1坐标系中的测点坐标分别为(300 m,400 m,-30 m)、(300 m,400 m,-100 m)和(3 000 m,4 000 m,-100 m)时的磁场各分量响应。

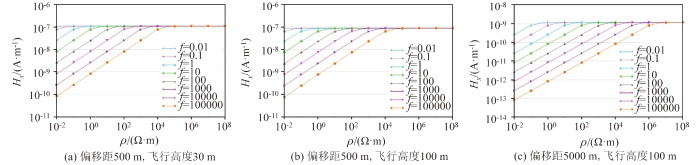
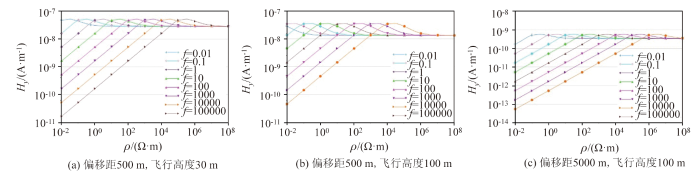
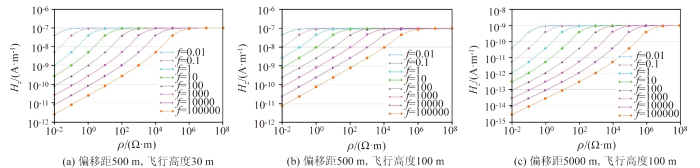
图2~图4是不同频率时,磁场强度x分量、y分量、z分量随地层电阻率变化的曲线,可以看出各个频率下H_x、H_z随地层电阻率的变大而增大,最后趋于一定值。而H_y变化曲线的形态比较复杂,呈现先增后减然后趋于一定值的形态。通过比较不同频率的曲线可以看出,高频的分辨率要大于低频的分辨率。对比磁场强度x、y、z 3个分量随地层电阻率变化的曲线可以发现H_x和H_z曲线形态相似,都比较简单,单调递增,在迭代计算全域视电阻率时只有1个解,而H_y曲线形态复杂,不具备单调性,在迭代计算全域视电阻率时具有多解性,需要特别注意。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 均匀半空间下磁场强度H_x响应随模型电阻率变化

Fig.2 Magnetic field strength in uniform half-space, H_x response varying with model resistivity

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 均匀半空间下磁场强度H_y响应随模型电阻率变化

Fig.3 Magnetic field strength in uniform half-space, H_y response varying with model resistivity

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 均匀半空间下磁场强度H_z响应随模型电阻率变化

Fig.4 Magnetic field strength in uniform half-space, H_z response varying with model resistivity

2.2 频率地空电磁法全域视电阻率定义

鉴于H_x和H_z迭代计算地层电阻率有唯一的地层电阻率ρ与之对应,而H_y曲线不单调,且具有多解性,我们分别对磁场强度x分量、y分量、z分量进行全域电阻率定义。

2.2.1 用频率域磁场强度x和z分量定义全域视电阻率

不同频率下H_x、H_z随地层电阻率的变大而增大,最后趋于一定值,具有单调性。以磁场强度z分量为例,将H_z记为H_z(ρ,C,ω),C为测点坐标参数。给定 $ρ_{τ}^{(0)}$ 为初值,在 $ρ_{τ}^{(0)}$ 的邻域内对H_z(ρ,C,ω)进行泰勒展开:

(3)

\begin{array}{l} H_{z} (ρ, C, ω) = H_{z} (ρ_{τ}^{(0)}, C, ω) + H'_{z} (ρ_{τ}^{(0)}, C, ω) \cdot \\ (ρ - ρ_{τ}^{(0)}) + \frac{H ″_{z} (ρ_{τ}^{(0)}, C, ω)}{2!} (ρ - ρ_{τ}^{(0)})^{2} + \dots + \\ \frac{H_{z}^{(n)} (ρ_{τ}^{(0)}, C, ω)}{n!} (ρ - ρ_{τ}^{(0)})^{n} \end{array}

保留线性部分及前两项:

(4)

\begin{array}{l} H_{z} (ρ, C, ω) \approx H_{z} (ρ_{τ}^{(0)}, C, ω) + H'_{z} (ρ_{τ}^{(0)}, C, ω) \cdot \\ (ρ - ρ_{τ}^{(0)}) \end{array}

对式(4)进行变换,得到关于ρ的近似表达:

(5)

ρ = \frac{H_{z} (ρ, C, ω) - H_{z} (ρ_{τ}^{(0)}, C, ω)}{H'_{z} (ρ_{τ}^{(0)}, C, ω)} + ρ_{τ}^{(0)}

将式(5)转换为迭代形式,得到地空系统频率域视电阻率迭代定义式:

(6)

ρ_{τ}^{(i + 1)} \approx Δ ρ_{τ}^{(i)} + ρ_{τ}^{(i)} (i = 0,1, 2, \dots)

其中:

(7)

Δ ρ_{τ}^{(i)} = \frac{H_{z} (ρ, C, ω) - H_{z} (ρ_{τ}^{(i - 1)}, C, ω)}{H'_{z} (ρ_{τ}^{(i - 1)}, C, ω)}

当满足式(8)时,停止迭代

(8)

|\frac{H_{z} (ρ, C, ω) - H_{z} (ρ_{τ}^{(i)}, C, ω)}{H_{z} (ρ, C, ω)}| < ε

其中:ε=10^-6~10^-4,是迭代终止误差限,H_z(ρ,C,ω)是空中某一测点的某一频率对应的频率域磁场强度垂直分量,H_z( $ρ_{τ}^{(i)}$ ,C,ω)是电阻率为 $ρ_{τ}^{(i)}$ 的均匀半空间在同一测点、同一频率产生的频率域磁场强度垂直分量。磁场强度x分量定义全域视电阻率的方法和z分量相同。

2.2.2 用频率域磁场强度H_y分量定义全域视电阻率

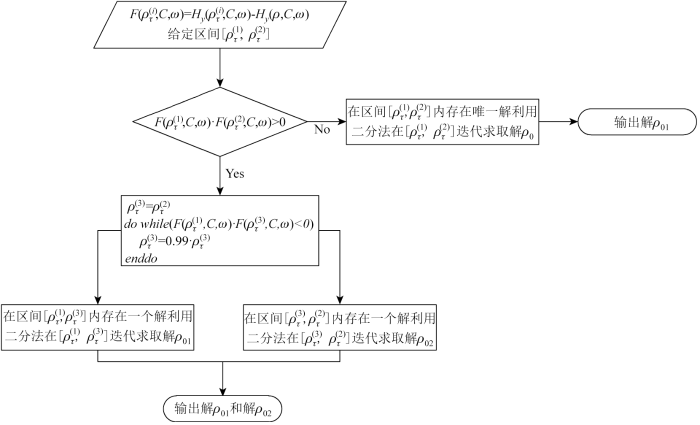
考虑到H_y的不单调存在多解性,我们选择使用二分法^[29]来逼近两个解,并选择其中更合适的解进行输出。由二分法原理可知:当函数F(x)在区间[a,b]上单调连续且存在零点,即F(a)·F(b)<0时,令c= $\frac{a + b}{2}$ ,则F(x)的零点必在[a,c]或[c,b]之间,将零点所在区间继续二分,不断重复,最后区间越来越小,区间边界逼近零点。当区间足够小时,即可近似将区间边界视为零点。

H_y随地层电阻率变化曲线不单调,并且利用H_y迭代求取视电阻率最多只存在两个解。令

(9)

F (ρ_{τ}^{(i)}, C, ω) = H_{y} (ρ_{τ}^{(i)}, C, ω) - H_{y} (ρ, C, ω)

给定区间[ρ₁,ρ₂],当F $(_{τ}^{(1)}$ ,C,ω)·F( $ρ_{τ}^{(2)}$ ,C,ω)<0,时,令ρ₃=ρ₂,利用二分法在区间[ρ₃,ρ₂]进行迭代,具体流程如图5所示。输出相邻频率的视电阻率值,选择合适的解作为y分量的视电阻率值。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 磁场强度y分量二分法求取全域视电阻率算法流程

Fig.5 Flow chart of global apparent resistivity algorithm by magnetic field intensity y-component dichotomy

2.2.3 均匀半空间各分量计算全域电阻率对比分析

建立均匀半空间模型,给定参数I=1 A,d_s=1 m,电阻率ρ=200 Ω·m,计算不同偏移距r和不同飞行高度h的各分量磁场强度并计算地层视电阻率。

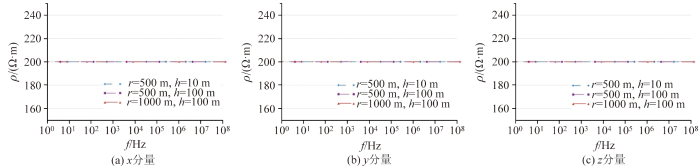
由图6可知,均匀半空间下不同偏移距、不同高度频率域磁场强度x、y、z三分量计算的地层全域视电阻率曲线可以看出,无论是偏移距500 m还是偏移距1 000 m,无论飞行高度是10 m还是100 m,无论是x分量、y分量还是z分量,计算得到的全域视电阻率都能很好地反应模型的地层电阻率。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 均匀半空间不同偏移距r、不同飞行高度h磁场各分量全域视电阻率

Fig. 6 Global apparent resistivity of magnetic components in a uniform half-space

3 模型验证

为验证各分量全域视电阻率的正确性,建立层状模型,计算x、y、z分量定义的全域视电阻率。分别建立二层和三层层状模型进行计算。

建立二层模型,给定参数I=1 A,d_s=1 m,第一层深度h₁=20 m,电阻率ρ₁=200 Ω·m,ρ₂依次等于50、100、150、200、250、300、350 Ω·m,偏移距分别为1 000、500 m,飞行高度为100、50 m,计算频率f=10⁸~10 Hz时的磁场强度并计算地层视电阻率。

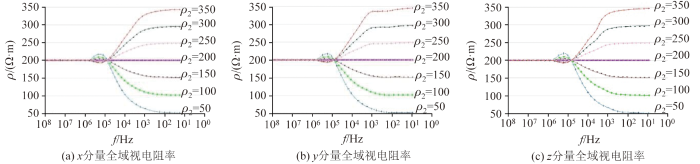
图7给出了二层模型磁场强度各分量随着频率的变化曲线。通过改变第二层模型的电阻率,计算出的全域视电阻率随着电阻率值的变化,整体呈现二层模型D或G型电阻率曲线形态。通过对比发现,x、y、z三分量的曲线差异不大,低频时接近第二层视电阻率,随频率升高,向第一层电阻率靠近,在汇于一点后出现反冲效应,随后趋近第一层电阻率。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 偏移距1 500 m,飞行高度100 m全域视电阻率

Fig.7 Global apparent resistivity for offset 1 500 m and flight altitude 100 m

整个曲线能很好地反映二层模型的地层电阻率变化情况。从不同偏移距及飞行高度对比可知,偏移距大或小,飞行高度高或低,3个分量计算得到的全域视电阻率曲线都能很好地反映地层电阻率变化。

建立典型三层电模型H型和K型地层,第一层电阻率为ρ₁,深度h₁=20 m,第二层电阻率为ρ₂,深度h₂=70 m,第三层电阻率为ρ₃,为向下半无限空间。假设偏移距r=1 500 m,飞行高度z=-100 m,频率f=10~10⁸ Hz,改变第二层电阻率ρ₂,分别计算两种模型的全域视电阻率。

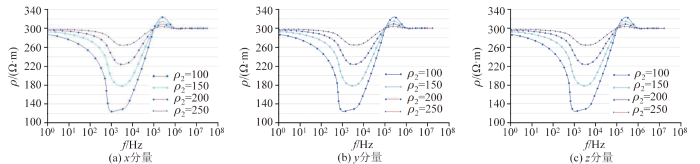
H型模型,ρ₁=300 Ω·m,ρ₃=300 Ω·m,ρ₂依次等于100、150、200、250 Ω·m。从图2~8可知,频率较低时全域视电阻率趋于第三层电阻率,高频时趋于第一层电阻率,由于中间层为低阻层,曲线整体呈一个下凹形态,中间低阻层电阻率越低,曲线越“凹”,但总是保持在低阻层实际电阻率之上,同样存在反冲效应。总体上都能反映地层电阻率变化情况。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 H型模型磁场各分量全域视电阻率随频率变化曲线

Fig.8 H model global apparent resistivity curves with frequency for each component of magnetic field

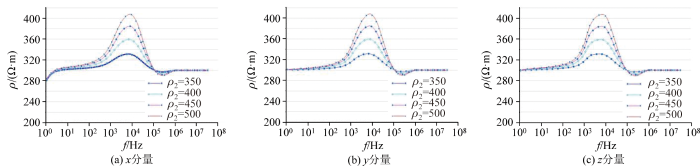
K型模型,ρ₁=300 Ω·m,ρ₃=300 Ω·m,ρ₂依次等于350、400、450、500 Ω·m,从图9可知,x、y、z三分量曲线形态差异不大,频率较低时全域视电阻率趋于第三层电阻率,高频时趋于第一层电阻率,曲线整体呈一个上凸形态,反映出了中间高阻层的存在,且中间高阻层电阻率越高,曲线越“凸”,但总是保持在高阻层实际电阻率之下,同样存在反冲效应,总体上都能反映地层电阻率变化情况。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 K型模型磁场各分量全域视电阻率随频率变化曲线

Fig.9 K model global apparent resistivity curves with frequency for each component of magnetic field

对比H、K两种类型的三层模型的全域视电阻率曲线,我们发现不论哪种类型,全域视电阻率曲线都能反映出电下层电阻率变化。通过对比发现,相比于K型模型,三分量全域视电阻率计算对H型更加敏感,比如在H型模型计算中,低阻层电阻率为100 Ω·m时,全域视电阻率曲线最低可以达到130 Ω·m,而在K型模型计算中,高阻层为500 Ω·m时,全域视电阻率最高没有超过400 Ω·m。横向对比频率域磁场强度x、y、z三分量可以发现,频率域磁场强度x、z分量的计算全域视电阻率效果要优于y分量。

4 结论

1)均匀半空间频率域地空电磁法中,磁场x和z分量是电阻率的单调函数,可依据其反函数关系得到全域视电阻率的定义,其结果具有单调性。

2)均匀半空间下频率域地空电磁法中,磁场y分量不是电阻率的单调函数,具有极值,采用二分法把计算区间分为两个单调区间,然后分别计算其视电阻率,可得到全域视电阻率。

3)经典层状模型的全域视电阻率随频率变化的曲线形态基本和地层电阻率变化相吻合,H型三层模型,受中间低阻层影响,曲线下凹,K型三层模型受高阻层影响,曲线上凸,首支趋向于第一层电阻率,尾支趋向于最后一层电阻率。

4)采用磁场强度x、y、z三分量对全域视电阻率进行了定义,计算结果表明:无论偏移距大小、飞行高低和收发距远近,全域视电阻率都能很好地吻合地层电阻率。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

殷长春, 朴化荣.

电磁测深法视电阻率定义问题的研究

[J]. 物探与化探, 1991, 15(4):290-299.