0 引言
基于岩石电性与激励频率的响应特征差异,衍生出了探地雷达法、可控源电磁法、频谱激电法等不同的地球物理电磁或电探测方法。其中采用低频(10-2~104 Hz)交变激励源的可控源电磁法,是通过电流源作用于岩石内部产生电传导和电磁感应,对应观测地表电磁场幅值和相位的频率响应,来推测地下电阻率或电导率结构的空间分布。而同样在该频段范围内,较多的岩矿石在交变电流源激励下不仅会产生瞬时的电传导和电磁感应效应,还能够观测到明显的随时间缓慢变化的充放电现象,即激发极化(induced polarization, IP)效应,简称激电效应。含激电效应的岩矿石在交变电流源激励下的电性响应等效是在电导(电阻)、电感和电容的共同作用,用来表征岩矿石电性的电阻率参数为随频率变化的复数[1],它的实部分量主要表征岩石电阻或电损耗能力,虚部分量主要表征储存电荷的能力。利用岩石的复电阻率频散及其差异特性,对岩石矿物含量、含水率等特征进行详细评价的探测方法为频谱激电法或复电阻率法[2-
频率域可控源电磁法与频谱激电法均是以低频交变电流源作为激励源,且观测频率大部分重合,但前者重点关注岩石中电传导与电磁感应作用下的电性响应,后者主要关注岩石中电传导与电容效应作用下的电性响应。由于自然界岩矿石普遍存在或强或弱的IP效应[5],对应含IP效应岩石在低频交变电流源激励下采集的电场响应数据是电传导、电磁感应和电容效应综合作用的结果,因此只从频率域可控源电磁法或频谱激电法单一观测视角,通常无法全面、准确地捕捉岩石的电性特征。要充分理解岩石复杂的电性,准确探测其结构,有必要对这两种方法进行整合,即同时考虑电感、电导与电容效应的综合影响。实际上在当前无论是可控源电磁法还是频谱激电法的数值模拟、数据处理解释等研究中,已逐渐开始关注电传导、电感效应与电容效应的综合影响,如研究可控源电磁观测法中激电效应的影响[6-7],以及如何提取激电效应[8-9]或模拟频谱激电法中的电磁响应[10],分析电磁感应的影响[11]。此外伴随着观测技术水平的提升,能够采集到更晚期、更低频的数据,激电效应引起时域电磁响应曲线符号反转现象越来越显著,激电效应对航空电磁等时域电磁法的影响也越来越被重视[12-13]。
无论是以电磁法观测视角来考虑激电效应,还是以频谱激电法观测视角来分析电磁效应的影响,均是以能够准确、全面地探测地下电性信息为目标。因此,要能够同时获得激电目标体的电损耗能力和储存电荷的能力,进而对其矿物含量或含水饱和度等进行准确评价,还需加深对人工源激励下电磁响应中所含有的激电效应和电磁效应特征认识,特别是系统分析目标含激电效应后对电磁响应的影响,这就需要对人工源激励下激电介质的电磁场进行准确模拟。其中在正演中是否考虑电磁效应,是准确模拟激电介质的人工源频率域电磁场的重要因素之一。传统方法以直流电阻率法为正演基础,通过求解复电位满足的Poisson方程来得到相应的电场值[14-15],忽略了电磁效应的作用,在大收发距或较高观测频率情况下,较难真实地反映电磁响应特征。而在理论上,从频率域电磁场满足的Maxwell方程出发,建立复电阻率法的Helmholtz控制方程,考虑了电磁效应的作用,能够更真实地模拟激电介质的电磁响应[16]。但相比求解Poisson方程,求解Helmholtz方程的复电阻率法三维模拟的计算复杂度及计算量显著增加,因此如何快速地进行计算,是复电阻率法三维正演必须要解决的问题。特别是频谱激电法需通过多次变换发射和接收的位置来达到探测的目的,即需同时完成多发射源的计算,这对计算效率提出了更高的要求。除可采用OpenMP+MPI的分布式并行计算来提高多源问题的计算效率[17]外,就单个源的计算而言,在有限的计算内存条件下,对离散线性方程组的预处理及迭代求解算法的选择,是影响正演计算效率的关键因素。参考可控源电磁法等频率域电磁法的Helmholtz方程求解,进行数值离散后,采用不完全LU分解预处理,并结合拟对称最小残差法求解线性方程组[18],能够在较少的内存消耗下快速完成正演计算,这给基于频率域Maxwell方程的复电阻率法的三维正演计算提供了研究基础。
为分析人工源激励下激电介质频率域电场响应中激电效应与电磁效应特征,探讨二者对电场响应的影响,本文开展了激电介质的人工源频率域电磁响应三维模拟研究。首先从频率域电磁场满足的Maxwell方程出发,建立同时考虑电磁效应与激电效应的复电阻率三维Helmholtz控制方程,其中激电介质电阻与电容特性以随频率变化的复电导率来体现,以分别求解背景场和二次场的方式,解决直接模拟发射源导致源区奇异性的问题。然后对控制方程以交错网格有限差分法进行差分离散,同时引入复全局拟最小残差法(QMR)求解离散复线性方程组,得到同时包含激电与电磁信息的电场响应,并建立可同时计算多发射源电场响应的正演计算框架。结合正演计算框架,通过建立典型激电模型,分析不同收发距激励下电磁响应中的激电效应与电磁效应的影响。
1 基于复全局QMR算法的复电阻率三维正演
1.1 控制方程及数值离散
针对基于频率Maxwell方程的复电阻法正演,首先考虑介质不存在激电效应时的情况,此时求解的问题退化为频率域人工源电磁法的正演问题。在一般人工源频率域电磁法中,考虑到数值模拟过程中发射源处的奇异性,采取分别求解背景场和二次场的方式。通过Maxwell方程得到频率域人工源电磁法的二次场控制方程如下:
式中:ω为角频率;对于地球大部分介质,μ可视为真空中的磁导率,即在本研究中μ=4π×10-7 H/m;σ为介质电导率,为与频率无关的实数;σp与Ep分别为背景电导率和对应的背景电场;Es为待求解的二次场,背景电导率为均匀半空间或层状模型,背景电场可通过半解析的方式进行求解,总场为背景场与二次场的和。
当介质具有激电特性时,电导率是随频率变化的复变函数σ*,那么由式(1)可得到关于含激电效应的控制方程:
式(2)中复电阻率法控制方程的形式与频域人工源电磁法的控制方程一致,但介质的电性参数发生改变,即介质的电导率在不同频率的人工源激发下具有相应的频谱特征:
式中:σr(iω)与σq(iω)分别为相应频率下复电导率参数的实部和虚部。通过求解方程(2)可得到频谱激电法中同时包含激电效应与电磁效应的电场响应。由于在数值求解过程中使用Krylov子空间迭代解存在零空间及误差积累,会导致残差收敛变缓等情况,在计算中引入电流密度散度为零条件进行散度校正,可起到加快收敛的目的[19]。
将式(2)通过交错网格有限差分方法离散,采用不均匀网格剖分离散后可得到如下线性方程组:
式中:K为大型稀疏复系数矩阵;e为待求解的未知电场值;b为由背景场及边界条件组成的向量。设定计算域的范围远大于三维异常体范围,可满足二次场在外边界为零的条件,达到简化计算的目的。
1.2 复全局QMR算法
1)对于初始值e(0),计算r(0)=b-Ke(0),令g1=
2)令
3)令γ0=1,η0=-1;
开始循环 i=1, 2, …,
如果ρi=0或ξi=0,退出;
计算Vi=
计算δi=zTy,如果δi=0,退出;
分别求解K2
如果i=1,则pi=
否则pi=
(ρiδi/εi-1)qi-1;
计算
计算εi=
计算βi=εi/δi,如果βi=0,退出;
计算
求解K1y=
KTqi-βiWi;
求解
计算θi=ρi+1/(γi-1|βi|);计算γi=1/
计算ηi=-ηi-1ρi
如果i=1,则di=ηipi,si=ηi
否则di=ηipi+(θi-1γi)2di-1,si=ηi
(θi-1γi)2si-1;
计算xi=xi-1+di,ri=ri-1-si;
判断是否达到收敛条件(残差范数‖r‖2/‖b‖2≤小量),若达到结束循环,否则继续。
1.3 计算精度检验
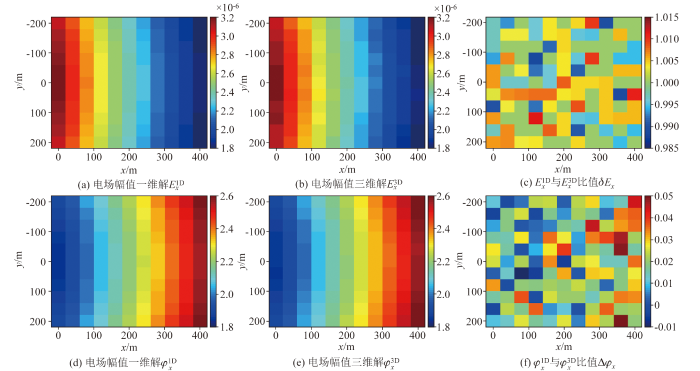
通过与一维半解析解计算结果对比,来检验三维数值模拟计算结果的准确性。地电模型为三层层状模型,第一、二层厚度分别为100、200 m,第一、二、三层电阻率依次为200、(200+20i)、200 Ω·m。另外发射源中心位置坐标为(-2 000,0,0),源长度为200 m,电流大小为2 A,在y轴方向上-200~200 m范围、x轴方向上0~400 m范围内,布设点距为40 m的测网。分别采用一维半解析计算[23]与三维数值计算,获得频率为1 Hz下共121个测点的电场Ex幅值和相位。其中三维离散模型沿x、y、z方向的网格数分别为66、66、42,x、y方向最小网格均为50 m,最大网格均为5 000 m,z方向上最小网格为50 m,最大网格为3 000 m。取一维半解析计算的电场幅值和相位分别为
图1
图1
层状模型一维半解析解与三维数值解对比
Fig.1
Comparison of 1D semi-analytical solution and 3D numerical solution for the layered model
2 三维激电模型电场响应特征
地下介质在人工源激发下的激电现象主要由电子导体和离子导体产生,其中电子导体的激电效应源于其与溶液界面上的电荷形成的双电层,在外电流的作用下发生定向移动,典型如黄铁矿等,可在宏观上表现出低电阻和较强激电效应特征[5,12]。而以离子导体主导的激电效应主要是由于岩石颗粒与其周围溶液中离子形成的双电层,在外电流作用下引起电荷分布的重新排列,同时引起溶液中离子的定向移动,典型的如具有一定水饱和度或被矿渣及有机质等污染的土壤,在宏观上多表现为一定的低电阻和激电效应特征[24
2.1 含激电效应的矿体模型
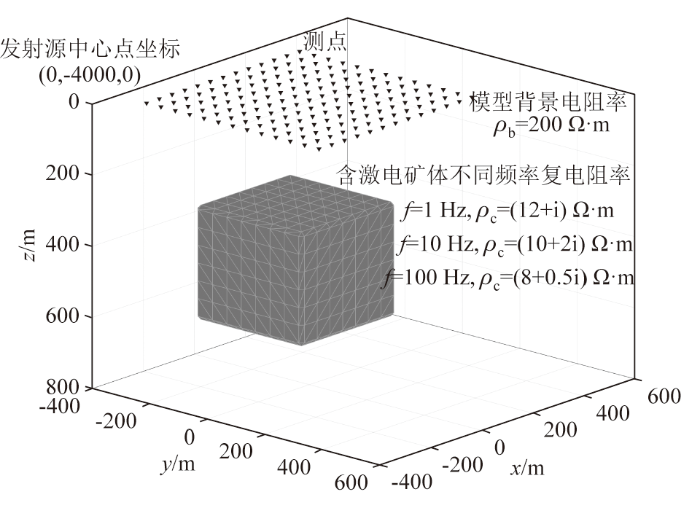
矿体模型及人工源电磁法观测系统如图2所示,设定矿体规模为400 m×400 m×350 m,顶面埋深为300 m。采用规则六面体网格进行剖分,沿坐标轴x、y、z方向的网格数分别为66、66、42,其中x、y方向最小网格间距均为50 m,最大网格间距均为5 000 m,z方向上最小网格间距为50 m,最大网格间距为3 000 m。如图2所示,在矿体正上方的地表布设等间距为50 m的测网,共169个测点,发射源沿着x轴方向,源长度为400 m,电流大小为2 A,源中心位置坐标为(0,-4 000,0)。围岩电阻率为200 Ω·m,为检验不同频率的计算效果,本文考虑并计算了1、10、100 Hz 3种不同量级频率的电场响应,同时由于激电介质复电阻率具有频散特征,复电阻率值随频率变化,3种频率对应矿体复电阻率值依次为(12+i) Ω·m、(10+2i) Ω·m、(8+0.5i) Ω·m,设定在频率为10 Hz时激电效应相对强,其次是频率1 Hz,频率为100 Hz时激电效应相对弱。
图2
图2
矿体三维模型及人工源电磁法观测系统
Fig.2
Three-dimensional model of the ore body and the artificial source electromagnetic observation system
图3
图3
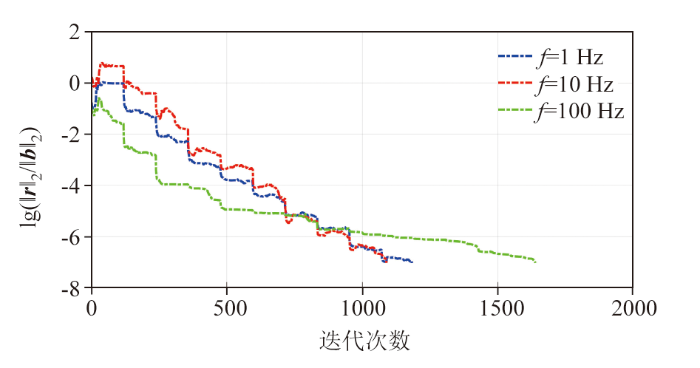
图2中矿体模型不同频率计算的残差范数随迭代次数变化曲线
Fig.3
The curve depicting the change of residual norm with iteration number for different frequency calculations of the ore body model in Figure 2
图4
图4
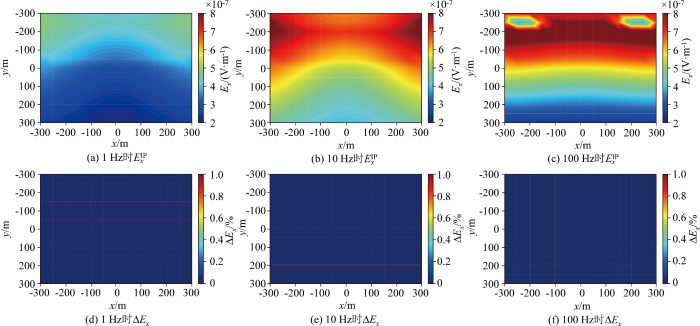
含激电矿体模型的不同频率电场幅值
Fig.4
The variation in electric field amplitude(
图5
图5
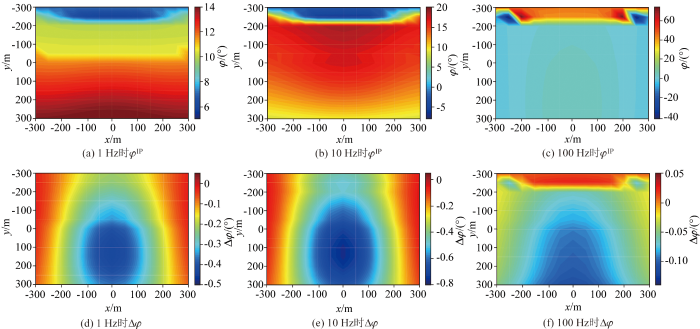
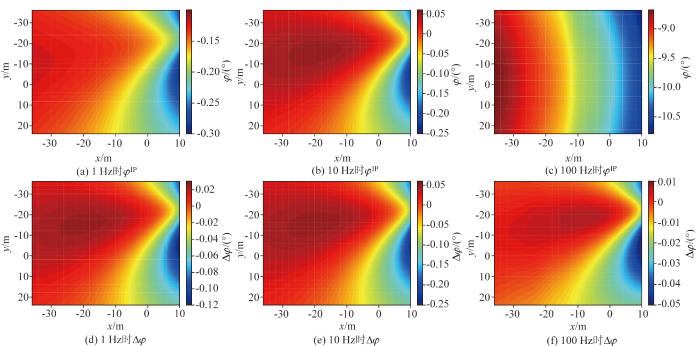
含激电矿体模型的不同频率电场相位φIP及相对不含激电矿体模型电场相位φNoIP的变化量Δφ
Fig.5
The variation in electric field phase(φIP) at different frequencies for the ore body model with induced polarization and the relative change in electric field amplitude(Δφ) compared to the model without induced polarization
同时进一步探讨了介质激电效应对电场响应的影响,在计算上述含激电效应矿体模型的电场Ex幅值
2.2 含激电效应的有机质渗漏模型
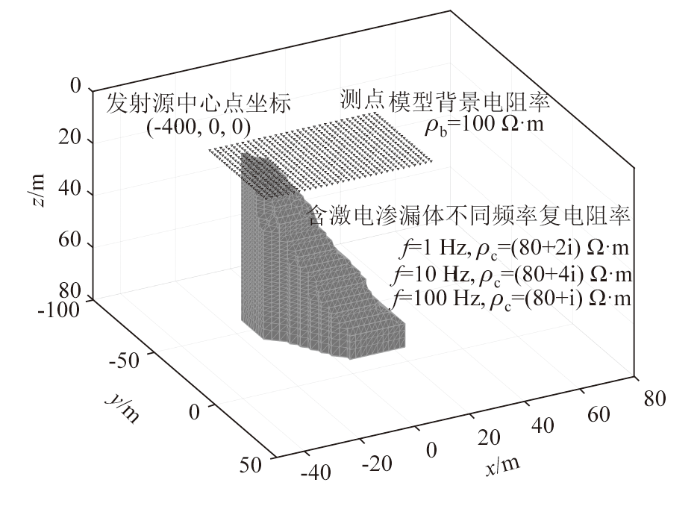
地表有机质渗漏模型及人工源电磁法观测系统如图6所示,设定渗漏液从地表向地下深处逐步扩散,扩散到地下60 m深处。模型同样采用规则六面体网格进行剖分,沿坐标轴x、y、z方向的网格数分别为80、80、60,x、y方向最小网格间距为2 m,最大网格间距为200 m,z方向上最小网格间距为1 m,最大网格间距为200 m。如图6所示,在渗漏体正上方的地表布设等间距为2 m的测网,共744个测点,发射源沿着x轴方向,源长度为40 m,电流大小为2 A,源中心位置为(-400,0,0)。围岩电阻率为100 Ω·m,同样考虑并计算了1、10、100 Hz 3种不同量级频率的电场响应,对应复电阻率依次为(80+2i) Ω·m、(80+4i) Ω·m、(80+i) Ω·m,设定在频率为10 Hz时激电效应相对强,其次是频率为1 Hz时,频率为100 Hz时激电效应相对弱,但与模型一不同的是,设定渗漏模型的复电阻率实部不随频率变化。
图6
图6
地表污染渗漏三维模型及人工源电磁观测系统
Fig.6
Three-dimensional model of surface pollutant leakage and artificial source electromagnetic observation system
图7
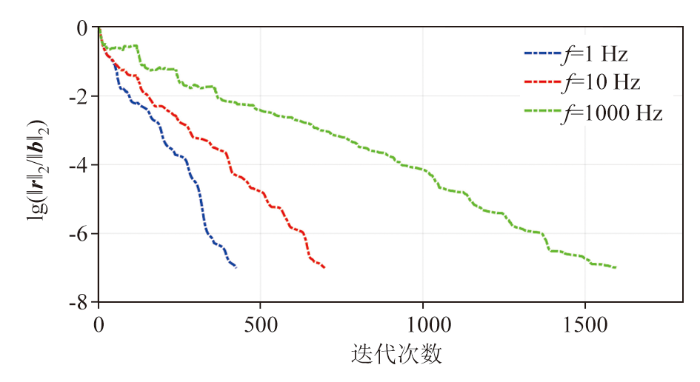
图7
Fig.7
The curve depicting the change of residual norm with iteration number for different frequency calculations of the ore body model in
图8
图8
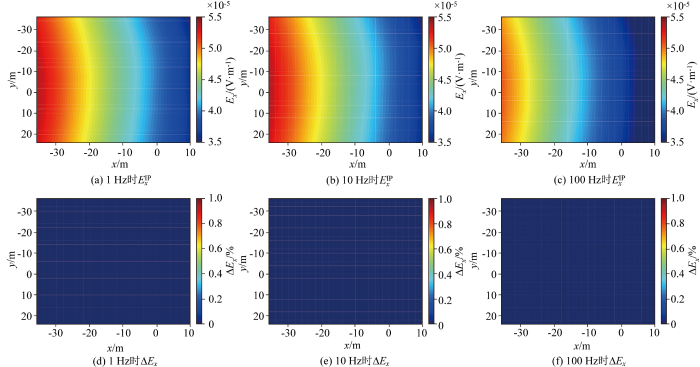
含激电渗漏模型的不同频率电场幅值
Fig.8
The variation in electric field amplitude(
图9
图9
含激电渗漏模型的不同频率电场相位φIP及相对不含激电矿体模型电场相位φNoIP的变化量Δφ
Fig.9
The variation in electric field phase(φIP) at different frequencies for the pollutant leakage model with induced polarization and the relative change in electric field amplitude(Δφ) compared to the model without induced polarization
3 结论与讨论
复电阻率参数可以同时描述介质的电阻和电容特性,有助于对地下目标体进行详细评价。本研究通过建立复电阻率法三维正演控制方程,并结合交错网格有限差分法和复全局QMR求解技术,进行了人工源激发下激电介质的电磁模拟研究,并分析了电场响应特性。依据简单层状模型以及不同规模和深度的激电异常模型的数值模拟测试,验证了算法的有效性和适用性进。本文计算结果表明,采用复全局QMR求解离散复线性方程组时,计算残差范数能够随迭代次数快速收敛。最后,对比了激电介质电容特性对电场幅值和相位的影响,结果显示介质电容特性对电场幅值的影响较小,但对相位的影响非常显著,即激电效应越强,对电场相位的影响越明显,这对于解释和理解激电介质的电磁响应具有重要意义。
综上所述,本研究提供了一种高效的复电阻率法三维正演模拟方法,深化了激电介质的电磁响应特性的认识,对地下资源勘探、环境监测和工程应用等领域具有潜在的重要应用前景。但如何准确地提取地下三维激电体的激电信息,还有待于进一步开发准确、稳定的三维反演算法。
参考文献
Complex conductivity signatures of microbial induced calcite precipitation,field and laboratory scales
[J].
激发极化法在覆盖区矿产勘查中的应用——以内蒙古昌图锡力锰银铅锌多金属矿勘查为例
[J].
Exploration in coverage area:A case study of the Changtuxili Mn-Ag-Pb-Zn polymetallic ore deposit,Inner Mongolia
[J].
Spectral induced polarization survey with distributed array system for mineral exploration:Case study in Saudi Arabia
[J].
Experimental study on hydrate saturation evaluation based on complex electrical conductivity of porous media
[J].
Induced polarization as a tool to assess mineral deposits:A review
[J].
激电效应对海洋可控源电磁响应的影响
[J].
Influence of IP Effecs on marine controlled-source electromagnetic responses
[J].
CSAMT一维正演可视化设计与激发极化效应
[J].
Visualization design of 1D CSAMT forward modeling and research on the induced polarization effect
[J].
改进混合蛙跳算法的CSAMT信号激电信息提取研究
[J].
DOI:10.6038/cjg20170831
[本文引用: 1]

从CSAMT信号中提取激电信息有利于提高频率域电磁法反演与解释的精度.目前的研究多以线性反演方法为主,存在依赖初始模型、易陷入局部极值的问题.针对CSAMT信号IP提取问题的非线性和非凸特征,本文提出了一种基于柯西分布和惯性权重的二阶段最小构造混合蛙跳反演方法来提取IP 信息.该方法首先利用柯西算子取代随机算子来提高算法的全局搜索能力,并通过引入混沌震荡惯性权重来均衡进化过程中的个体经验和群体经验,保证算法后期的稳定收敛;然后通过引入第二阶段反演过程来强化极化率对观测数据的影响,同时将正则化参数引入混合蛙跳算法的适应度函数来改善反演的多解性问题;最后利用CPU并行计算加速了算法的模因组搜索过程.反演结果表明,上述方法能够较好地重构地电结构和提取激电信息,在加噪环境下具有较强的鲁棒性.相比其他非线性算法(标准混合蛙跳算法SFLA,差分进化算法DE和粒子群优化算法PSO)的反演结果,本文算法具有更强的全局搜索能力和更高的计算效率,适合对微弱的激电信息进行提取.
A new methond based on improved SFLA for IP information extraction from CSAMT signal
[J].
3D complex resistivity imaging using controlled source electromagnetic data:A multistage procedure using a second order polynomial parametrization
[J].
基于自适应有限元的复电阻率法2.5维复杂构造电磁场模拟
[J].
DOI:10.6038/cjg2018L0321
[本文引用: 1]

复电阻率法在矿产、油气勘探调查中发挥着重要作用.为了认识复杂构造的复电阻率法电磁场的变化规律,本文基于自适应有限元方法,采用非结构化网格,引入Cole-Cole模型,实现了电偶源2.5D复电阻率法电磁场正演,可以模拟复杂地形和地电结构,正演结果更符合野外实际地质情况.通过将本文的计算结果与半空间模型解析解、层状介质和起伏模型结果进行对比,验证了本文算法的正确性.最后,基于复杂地电模型,通过正演模拟,系统分析了地形、激电参数、复杂构造对复电阻率法电磁场的影响特征.
2.5D simulation of the electromagnetic field with complicated structure in the complex resistivity method using adaptive finite element
[J].
激电和电磁效应对三维复电阻率正演结果的影响研究
[J].
Study on the influence of IP and EM effects of 3D resistivity modeling results
[J].
时间域航空电磁法激电效应对电磁扩散的影响
[J].
DOI:10.6038/cjg20161230
[本文引用: 2]

由于激发极化效应的影响,时间域航空电磁晚期道信号经常会出现变号现象.基于电阻率的传统反演方法无法对变号数据进行正确反演,因此通常在数据处理中予以剔除.为深入了解极化介质的电磁扩散特征,认识航空瞬变电磁负响应的产生机理,本文研究时间域航空电磁系统的电磁扩散特征.我们以均匀极化、非极化半空间及层状介质模型为例,通过直接积分的方法求解频率域电场响应,并由欧姆定律得到电流响应,再经过汉克尔变换得到时间域电流响应.通过研究电流随时间在地下极化介质中的传播特征研究电磁扩散过程;通过对比不同激电参数对电磁扩散的影响,研究极化介质中感应电流与极化电流的扩散规律,从而合理地解释极化介质中负响应的产生机理.基于本文研究和分析结果,可加深对时间域航空电磁法中激电效应的认识.
The effect of induced polarization on time-domain airborne EM diffusion
[J].
Modeling induced polarization effects in helicopter time-domain electromagnetic data:Field case studies
[J].
Spectral two-dimensional inversion of frequency-domain induced polarisation data from a mining slag heap
[J].
基于Fractal模型的复电阻率法2.5D有限元数值模拟
[J].
Fractal model-based 2.5D finite element modeling of complex resistivity method
[J].
3D induced-polarization data inversion for complex resistivity
[J].
基于Lanczos-模型降阶算法的三维频率域可控源电磁快速正演
[J].
Fast 3D forward modeling of frequency domain controlled-source electromagnetic method using Lanczos-model order reduction algorithm
[J].
三维频率域可控源电磁反演研究
[J].
DOI:10.6038/cjg20160128
[本文引用: 1]

对于三维可控源电磁,反演计算效率、张量测量、旁侧效应以及阴影效应是目前研究的热点.本文正演采用基于库仑规范条件的耦合势有限体积算法,反演采用有限内存BFGS(L-BFGS)算法.合成数据反演结果表明:(1)有限内存BFGS法比非线性共轭梯度法,在反演计算效率上具有一定的优势,更适合求解大规模三维可控源电磁反演问题.(2)张量可控源电磁法相对于标量可控源电磁法,前者在模型分辨率上优于后者.(3)在某个区域无法布置测网的情况下,我们可利用旁侧效应在异常体周围布置测网进行三维反演,从而获得真实异常体的信息.同时,为避免阴影效应,我们应在测网外增加可控源电磁控制点,使得三维反演的数据更加完备.
3D frequency-domain CSEM inversion
[J].
Conservative modeling of 3D electromagnetic fields,Part II,biconjugate gradient solution and an accelerator
[J].
A2ILU:Auto-accelerated ILU Preconditioner for Sparse Linear Systems
[J].
QMR:A quasi-minimal residual method for non-Hermitian linear systems
[J].
复矩阵方程的复全局QMR算法
[J].
Complex global QMR Algorithm for the complex matrix equations
[J].
1D inversion of multicomponent,multifrequency marine CSEM data:Methodology and synthetic studies for resolving thin resistive layers
[J].
海滨垃圾填埋场渗滤液污染土壤的复电阻率特性
[J].
Complex resistivity properties of leachate-contaminated soil coastal landfill
[J].
三氯乙烯污染土壤的复电阻率特征和频谱参数研究
[J].
DOI:10.13745/j.esf.sf.2021.2.4

复电阻率法(complex resistivity, CR)由于其对孔隙水化学性质、固-液界面和流体含量的敏感性已成为具有良好前景的污染物识别工具。本研究选取三氯乙烯(trichloroethylene, TCE)作为典型有机污染物,利用频谱激电仪对TCE污染土壤进行了复电阻率测量,讨论孔隙水盐度、水饱和度和土壤类型对污染土壤的复电阻率特征和频谱参数影响。试验结果表明:污染土样的复电阻率均随水饱和度的降低和孔隙水盐度的减小而增大;土壤黏土含量影响孔隙水连续性,当孔隙水出现不连续状态时,实部和虚部出现大幅度变化。总充电率M随着孔隙水盐度的增加而增加,随水饱和度的降低先减后增。黏土颗粒重排导致的比表面积减小使得总充电率M减小,双电层极化加强使总充电率M升高;平均弛豫时间常数随孔隙水盐度的升高而降低,二者呈对数相关,随水饱和度变化的主要原因为可极化孔隙尺寸的变化。本研究探讨了地球物理参数与水文地质参数间的关系,为SIP方法在实际有机污染场地调查与评估提供了理论依据。
Complecx resistivity properties and spectral parameters of TCE contaminated soils
[J].
Complex conductivity of soils
[J].