E-mail Alert Rss
 

物探与化探, 2025, 49(3): 653-660 doi: 10.11720/wtyht.2025.0039

方法研究信息处理仪器研制

基于阈值迭代法和加速线性Bregman联合的多震源地震数据同时分离和重建

莫子奋,1, 邱达星2, 张华,2, 张春雷2, 何承峻2, 杨熙熙2,3

1.江西省地质局 第六地质大队,江西 南昌 330011

2.东华理工大学 铀资源探采与核遥感全国重点实验,江西 南昌 330013

3.中国电建集团 江西省电力设计院有限公司,江西 南昌 330096

Simultaneous separation and reconstruction of multisource seismic data based on the iterative shrinkage-thresholding algorithm and the accelerated linearized Bregman method

MO Zi-Fen,1, QIU Da-Xing2, ZHANG Hua,2, ZHANG Chun-Lei2, HE Cheng-Jun2, YANG Xi-Xi2,3

1. The Sixth Geological Brigade of Jiangxi Geological Bureau,Nanchang 330011,China

2. National Key Laboratory of Uranium Resources Exploration-Mining and Nuclear Remote Sensing,East China University of Technology,Nanchang 330013,China

3. PowerChina Jiangxi Electric Power Engineering Co.,Ltd.,Nanchang 330096,China

通讯作者: 张华(1979-),男,博士生导师,研究方向为地震数据处理方法技术以及自然灾害探测与评估。Email:zhhua1979@163.com

第一作者: 莫子奋(1981-),男,海南定安人,在江西省地质局第六地质大队工作,主要从事地球物理勘探的科研工作。Email:160561728@qq.com

责任编辑: 叶佩

收稿日期: 2025-01-9   修回日期: 2025-04-12  

基金资助: 江西省自然科学基金重点项目(20242BAB26051)
铀资源探采与核遥感全国重点实验室项目(2024QZ-TD-13)

Received: 2025-01-9   Revised: 2025-04-12  

摘要

多震源技术极大地提高了地震数据的采集效率,但采集到的数据存在严重的混叠和缺失现象,需要在分离的过程中有效地对缺失道进行重建。由于单一的分离和重建算法在精度和速度上不能同时提高。为此,本文提出将阈值迭代法和加速线性Bregman方法进行联合,充分利用阈值迭代法后期处理精度高和加速线性Bregman方法前期收敛速度快的优势,用于多震源数据的同时分离和重建。在此过程中,选择曲波变换为稀疏基,引入硬阈值函数、指数阈值因子和加速因子,并提出新型指数加权因子,最终分离和重建出单震源数据,并且与单独的阈值迭代法和加速线性Bregman方法进行对比分析。此外,本文还对该联合方法的抗噪性和去噪能力进行了研究。理论模拟和实际应用表明,在分离和重建出完整的单震源信号方面,联合方法具有更高的精度和更快的计算效率。

关键词： 多震源; 地震数据分离; 重建; 阈值迭代法; 加速线性Bregman算法

Abstract

Multisource technology has significantly improved the acquisition efficiency of seismic data.However,the acquired data often suffer from severe aliasing and channel missing,necessitating effective reconstruction of missing channels during data separation.Since an individual separation and reconstruction algorithm cannot improve accuracy and computational efficiency simultaneously,this study proposed a method combining the iterative shrinkage-thresholding algorithm(ISTA) and the accelerated linearized Bregman method(ALBM) to leverage ISTA's high post-processing accuracy and ALBM's fast convergence speed for simultaneous separation and reconstruction of multisource data.The simultaneous separation and reconstruction process employed curvelet transform(as a sparse basis),hard threshold function,exponential threshold and acceleration factors,and a novel exponential weighting factor.Finally,the single-source data were separated and reconstructed.The results obtained from the combined method were compared with those obtained using ISTA and ALBM,respectively.Additionally,the noise robustness and denoising capability of the combined method were examined.Both theoretical simulation and practical application demonstrate that the combined method achieves higher accuracy and faster computational efficiency in separating and reconstructing complete single-source signals.

Keywords： multisource; seismic data separation; reconstruction; iterative shrinkage-thresholding algorithm(ISTA); accelerated linearized Bregman method(ALBM)

PDF (5445KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

莫子奋, 邱达星, 张华, 张春雷, 何承峻, 杨熙熙. 基于阈值迭代法和加速线性Bregman联合的多震源地震数据同时分离和重建[J]. 物探与化探, 2025, 49(3): 653-660 doi:10.11720/wtyht.2025.0039

MO Zi-Fen, QIU Da-Xing, ZHANG Hua, ZHANG Chun-Lei, HE Cheng-Jun, YANG Xi-Xi. Simultaneous separation and reconstruction of multisource seismic data based on the iterative shrinkage-thresholding algorithm and the accelerated linearized Bregman method[J]. Geophysical and Geochemical Exploration, 2025, 49(3): 653-660 doi:10.11720/wtyht.2025.0039

0 引言

传统地震数据采集是逐炮激发,多个检波器接收,工作效率低且成本高。1980年,Silverman提出了多震源采集技术[1],该技术允许同时或延时激发两个或两个以上的震源,在相同时间有了更高的采集密度,极大地缩短了采集时间、降低了采集成本[2]。然而,由于多个震源同时激发,检波器记录的数据存在严重的混叠噪声。目前针对多震源混合数据处理的方法主要有直接成像法和分离法[3]。直接成像法不考虑混叠噪声的影响,适合较简单的地形数据,处理复杂地形时则会有较大误差。分离法将混合数据分离成单个震源数据,再进行常规处理;该方法虽然计算量大,但误差小,有更高的成像精度,是目前主要应用的方法。此外,由于野外工作受地形、仪器、成本等限制,采集的数据通常不完整、不规则,为了提高地震数据的质量,重建亦是地震数据处理过程中不可或缺的步骤[4]。

目前,对多震源混合数据进行分离或者重建的方法较多,无论是分离还是重建均可将混合数据进行稀疏变换到稀疏域,然后用优化算法进行约束,从而实现基于稀疏反演的重建或者分离。常用的稀疏变换有Radon变换[5-8]、Curvelet变换[9-12]、Seislet变换[13-16]等。优化算法常用阈值迭代法(iterative shrinkage thresholding algorithm,ISTA)[17],阈值迭代法实现相对简单,但收敛速度慢,需要经过多次迭代才能达到较高的精度,时间成本高。2013年,Huang等[18]提出了加速线性Bregman算法(accelerated linearized Bregman method,ALBM ),有更快的迭代速度,但收敛精度较低。庞洋等[19]将ISTA方法和ALBM方法联合,在重建中获得了较好的效果。2022年,魏亚杰等[20]基于稀疏反演的方法,在简单层状模型合成欠采样混合地震数据,实现了同时分离和重建,证明了实现同时分离和重建的可行性和有效性。

在多震源混合数据处理中,单独分离或重建含缺失的多震源混合数据,会产生较大的误差,影响最终结果的精度,目前能实现同时分离和重建处理的方法较少。为此,本文基于稀疏反演方法,提出将阈值迭代法和加速线性Bregman方法进行联合,应用于多震源数据的同时分离和重建。以Curvelet变换为稀疏基,在Curvelet域采用硬阈值函数和指数阈值因子对Curvelet系数进行约束,并选择新型指数作为加权因子。将处理结果与传统的ISTA和ALBM方法得到的结果进行对比。理论数据模拟和实际数据检验表明,联合方法比传统方法具有更高的精度和更快的迭代速度,具有一定的抗噪性,在含随机噪声的数据中仍能有效地分离混叠噪声,重建出完整的单震源数据。

1 理论基础

1.1 多震源数据分离和重建原理

多震源采集的数据可假设为如下数学模型:

d=M1d1+ΓM2d2,

式中:d为采集的数据;d1、d2分别为主震源数据和辅震源数据;M1、M2为采样矩阵;Γ为时间延迟算子,其表达式为:

Γ=F-1diag(e-iωt1, e-iωt2,…, e-iωtN)F 。

式中:F和F-1分别为傅里叶正变换和逆变换;tN为辅震源中第N炮的随机延迟算子。在式(1)两端同时乘以时间随机延迟算子的逆,得到下式:

Γ-1d=Γ-1M1d1+M2d2 。

将式(1)和式(3)联合得到增广方程:

Lm= d~,

其中:

L=M1ΓM2 Γ-1M1M2,m=d1d2,d~=dΓ-1d。

由于实际观测的数据包含来自不同震源的混合信息,式(4)是一个欠定方程,稀疏性约束可以有效地限制解的空间,使得在众多可能的解中找到符合实际情况且有意义的解。这种约束不仅可以提高信号恢复的准确性,还能有效抑制混叠噪声。为此,采用以下优化目标函数来解决分离和重建问题:

m~= 12argmin‖Lm- d~‖22+λ‖Cm‖1,

式中:m~为m的估计值;λ是一个正则化参数,用于调整第一项和第二项的权重;C为稀疏Curvelet(曲波)变换。通过优化算法来计算最优的稀疏系数m~,再进行Curvelet逆变换得到真实数据dz=CHm~。

1.2 阈值迭代法

求解式(6)常用迭代的方法,阈值迭代法参数设置简单,在每次迭代后会更新阈值,能有效处理稀疏优化问题。迭代公式如下:

xn+1=Tλ[xn+AT(d-Axn)], n=1,2,…,N

式中:n表示迭代次数;N为最大迭代次数;上标“T”表示转置,Tλ为阈值因子为λ的函数。阈值函数分为硬阈值Th和软阈值Ts两种,公式分别如下:

Th(x)= 0x≤λxx>λ,
Ts(x)=sign(x)·max(|x|-λ,0) 。

软阈值函数会对大于阈值的元素进行缩小,信号具有连续性,但可能导致一些重要的信号特征被削弱或丢失。同时导致信号的锐利度下降,在边缘检测等需要高分辨率的应用中,会使信号变得模糊产生“伪影”现象。硬阈值函数保留绝对值大于阈值的系数,可以更好地保留信号的原始特征,不会损失重要信息,能精确识别特征。且硬阈值函数的实现逻辑相对简单,仅需判断系数是否大于阈值,在处理大量数据时,计算量更小。因此,本文选择硬阈值函数。为了加快收敛速度,提高计算效率,选择呈指数变化的阈值因子,公式如下:

λ=Max×exp n-1N-1[ln(ε)-ln(Max)],

式中:Max为最大阈值;ε为最小阈值;n为迭代次数。

1.3 加速线性Bregman算法

加速线性Bregman迭代公式如下:

zn+1=zn+AT(d-Axn) ,zn+1=αnzn+1+(1-αn)zn,xn+1=Tλ(zn+1) 。

式中:αn为加速因子,取值范围在1~2,一般选择为αn=1+n-1n+2。加速线性Bregman算法由于直接使用未阈值的数据zn,前期保留更多的有效信号,信噪比相对较高,但最终收敛精度会降低。

1.4 联合算法

阈值迭代法与加速线性Bregman联合的公式:

zn+1=βzn+(1-β)xn+AT(d-Axn),zn+1=αnzn+1+(1-αn)zn,xn+1=T(zn+1)。

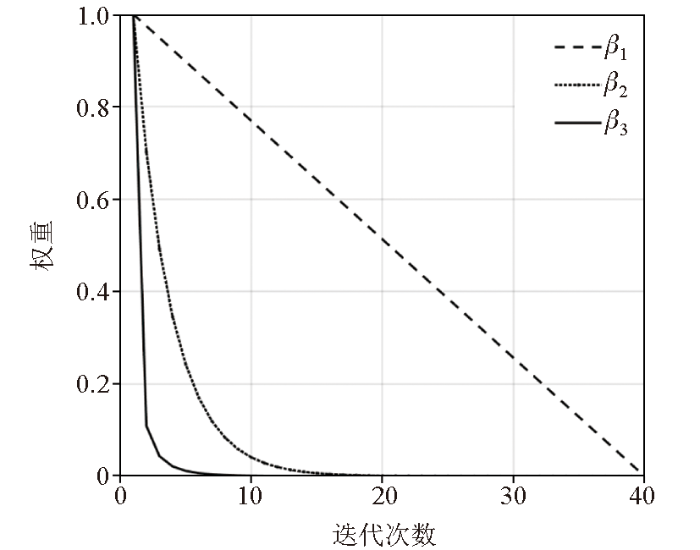
式中:β为加权因子,用于调节ISTA和ALBM之间的权重。传统加权因子β有线性β1和指数β2两种形式:

β1=1- n-1N-1,
β2= en-1N-1ln(ε),

式中:ε=10-6,加权因子随着迭代次数增加,从1~0不断减小。所以,在式(12)中,前期βzn项有更高的权重,能加快迭代速度,后期(1-β)xn项有更高的权重,分离的结果zn+1包含未阈值化的系数zn,在此阶段可以获得更多的有效信号,保证有较高的收敛精度。为了进一步提高计算效率,本文提出具有更快迭代速度的新型指数加权因子,如下式所示:

β3= en-1N-1ln(ε) 。

3种不同加权因子随迭代次数变化关系如图1所示。从图中可以看出,随着迭代次数增加,新型指数加权因子β3有更快的下降速度,能让阈值迭代法所占的比重更大。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   不同加权因子曲线

Fig.1   Different weighting factor curves


2 理论数据

2.1 数据混合

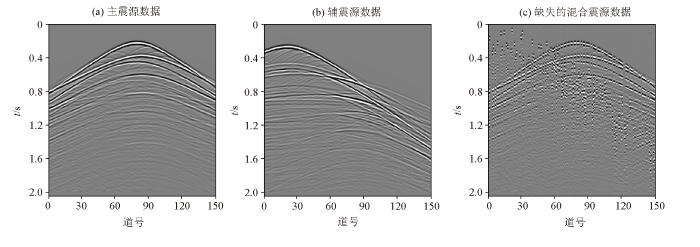
理论数据由两个单震源数据合成,如图2a和2b所示。两个单震源数据均为150道,每道512个时间采样点,采样间隔为4 ms。首先对主震源和辅震源都进行30%的随机道集缺失,再对辅震源在 [-150 150] ms进行随机时间延迟,进行混合后得到的数据如图2c所示。可以看出,主震源和辅震源由于道集缺失不具有连续性,辅震源随机时间延迟后分布散乱,表现为随机噪声。处理的目的就是从混合数据中分离并重建出完整的主震源数据。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   混合前后的地震数据

Fig.2   Seismic data before and after mixing


2.2 理论数据同时分离和重建

为了对比不同算法处理后的效果,定义信噪比公式:

SNR=20lg ‖f0‖2f-f0‖2,

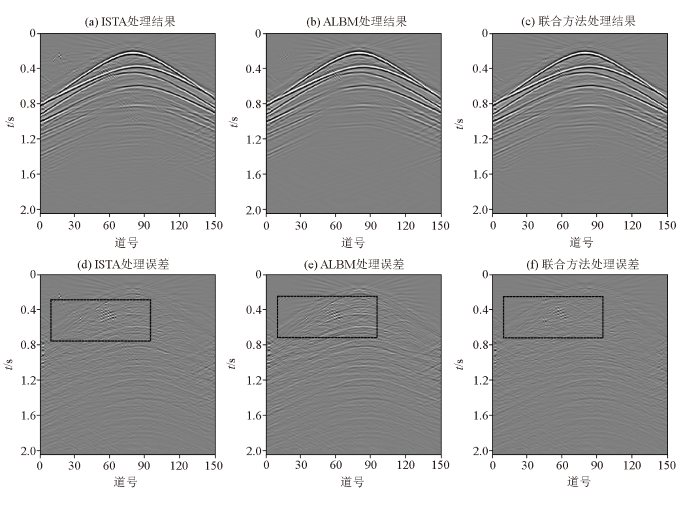
式中:f0表示原始主震源数据;f表示同时分离和重建后的主震源数据。信噪比越高,表示处理的效果就越好。曲波变换的尺度选择为5,第二尺度上的方向为16,将联合方法与ISTA、ALBM进行对比。以10次迭代次数为例,分离和重建后的结果如图3a~c所示, ISTA、ALBM和联合方法处理后的信噪比分别为12.65、11.89、15.13 dB,3种方法都能从混合数据中分离和重建得到主震源数据,但联合方法的信噪比明显高于ISTA和ALBM。图3d~f分别是3种方法分离和重建后的误差。从图中可以看出,ISTA和ALBM处理后还存在较大的误差,尤其是两震源混合相交处。同时,在黑框左上角处还存在较明显的噪声未分离,而联合方法在相交处存在的混合误差更小,且在其他地方没有明显的噪声残留。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   不同方法处理的结果和误差

Fig.3   The results and errors of different algorithms


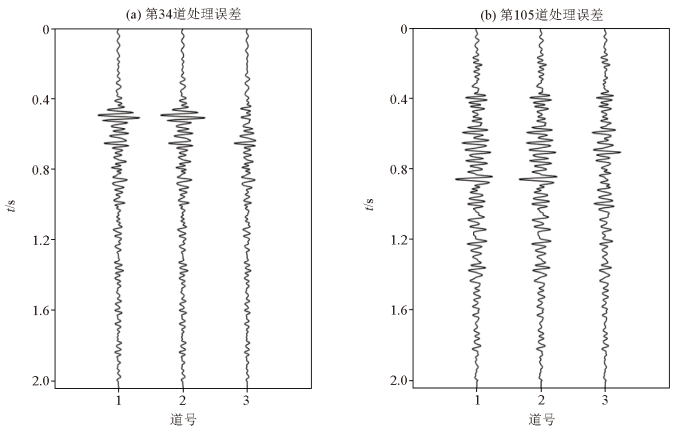
为了能在细节上对比这3种方法同时分离和重建的效果,随机选取了两个单道地震记录在分离和重建前后的误差。图4a和图4b分别为第34道和第105道分离和重建的误差曲线,图中的1~3道分别是ISTA、ALBM和联合算法的处理误差。曲线幅值越大代表得到的结果与原始主震源数据的误差越大。可以看出,联合方法的误差最小,说明对有效信号的损失也较小。综上,联合方法在多震源数据同时分离和重建处理中信噪比更高,能更高精度得到完整的主震源数据。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   单道地震记录处理后的误差

Fig.4   Errors after single-channel seismic record processing


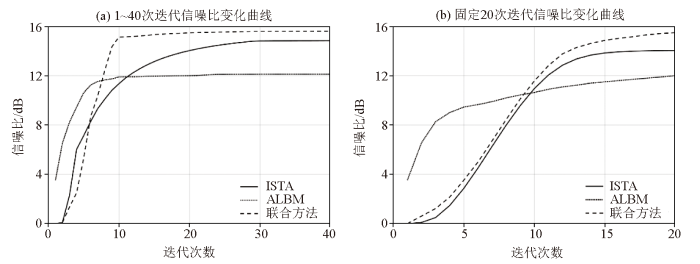
此外,为了进一步了解3种方法在不同迭代次数下的处理效果,将最大迭代次数从1逐渐增加到40,绘制出信噪比随迭代次数变化的曲线图,如图5a所示。联合方法有更快的迭代速度,经11次迭代达到收敛,且精度更高。图5b为最大迭代次数20时,信噪比随迭代次数的变化曲线图。可以看出,ALBM由于直接引入了未阈值的数据,在前期保留了较多的有效信号,有相对较高的信噪比和上升速率,但随迭代次数增加,上升速率降低,并且收敛后的信噪比较低。ISTA和联合方法前期有较快的上升速率,但随着迭代次数增加,ISTA的上升速率逐渐缓慢,需要更多的迭代次数才能达到收敛;而联合方法仍能保持较快的上升速率,达到收敛时有更高的信噪比。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   信噪比随迭代次数变化曲线

Fig.5   The curve of signal-to-noise ratio changing with the number of iterations


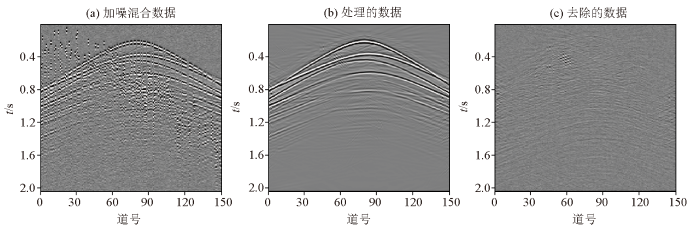
由于实际工作环境中通常含有大量的随机噪声,需检验联合方法的抗噪性和去噪能力。在混合数据加入高斯随机噪声,如图6a所示。为了能更好分离和重建完整的主震源数据,压制随机噪声,经过多次试验,选取合适的最小阈值。图6b和6c分别为联合方法处理的结果和去除的噪声。可以看出,联合算法在含随机噪声的情况下,仍可以有效地分离和重建出完整的主震源数据,混合噪声和随机噪声也基本滤除,因此,联合算法在分离和重建处理中不仅具有较强的抗噪性, 还具有较好的去噪能力。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   加噪混合地震数据处理结果

Fig.6   Seismic data processing map with noise


3 实际数据

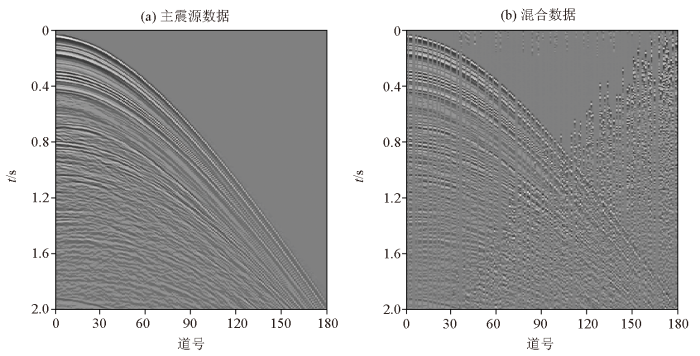
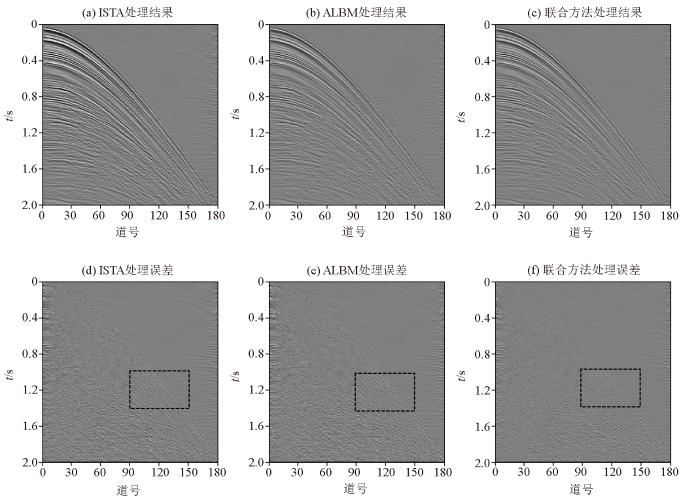
为了检验联合方法在实际中的应用效果,将实测数据进行缺失和混合处理,模拟野外多震源采集过程。实测数据有180道,采样时长为2 s,采样间隔4 ms,且都进行30%的随机道集缺失,辅震源在[-200 200] ms进行随机时间延迟,得到的混合数据如图7a和7b所示。用3种方法分别对其进行同时分离和重建,迭代次数选择10次,其他参数设置一致。处理后的结果如图8a~c所示,ISTA、ALBM和联合方法的信噪比分别是7.32、6.74和8.23 dB。说明实际数据处理中,联合方法相对ISTA和ALBM具有更高的精度。图8d~f是3种方法处理后的误差。ISTA和ALBM在右侧存在较多的混合误差,对有效信号的损伤更大(黑框处)。联合方法能更好地去除混叠噪声,保留更多的有效信号。因此,在实测数据的同时分离和重建中,联合方法的处理效果仍然优于传统单一方法。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   实际混合数据的同时分离和重建

Fig.7   Simultaneous separation and reconstruction of real mixed data


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   3种方法处理实际混合数据的结果和误差

Fig.8   The results and errors of three methods for processing actual mixed data


4 结论

多震源采集技术极大地提高了野外工作效率,但采集的数据存在严重缺失和混叠现象,如何对多震源混合数据进行快速高精度的分离和重建,是该技术能否应用推广的关键。本文以Curvelet变换作为稀疏基,提出将阈值迭代法和加速线性Bregman进行联合,充分利用了阈值迭代法后期精度高和线性Bregman法前期效率快的优点。在此过程中,引入了指数阈值因子和加速因子,提出了新的加权因子,从而得到了一种快速高精度联合方法,并将其应用于多震源混合数据的同时分离和重建中,取得了较好的效果。与传统的阈值迭代法和加速线性Bregman对比,联合方法有更高的信噪比,能更好地去除混合噪声,对有效信号的损伤更小。在不同迭代次数下的同时分离和重建结果也证实了本文提出的联合方法具有快速收敛和高精度的特点。此外,还对其进行抗噪性能研究,联合方法在随机噪声下仍能分离重建出较高质量的单震源数据,将混合噪声和随机噪声去除。

参考文献

Silverman D.

Method of three dimensional seismic prospecting

[J]. Journal of the Acoustical Society of America, 1980,67:365.

[本文引用: 1]

郭建宏, 成景旺, 陈芷若, 等.

基于改进迭代去噪法的多震源地震数据分离

[J]. 物探与化探, 2019, 43(5):1054-1063.

[本文引用: 1]

Guo J H, Cheng J W, Chen Z R, et al.

Seismic data separation of simultaneous source based on an improved iterative denoising method

[J]. Geophysical and Geochemical Exploration, 2019, 43(5):1054-1063.

[本文引用: 1]

石太昆, 徐海, 黄亮, 等.

混采地震数据高效高精度分离处理方法研究进展

[J]. 石油物探, 2020, 59(5):703-712.

DOI:10.3969/j.issn.1000-1441.2020.05.      [本文引用: 1]

高效率采集是提高“两宽一高”采集效率的有效方式。对高效率地震数据采集和处理方法进行了综述,着重介绍了混采地震数据的高效高精度分离方法研究进展,包括:噪声压制类方法、反演类方法和预测相减类方法,并对各类方法的发展进行了评述。噪声压制类方法效率高、较稳定、易实现;反演类方法可以获得比噪声压制类方法更高信噪比和保真度的结果,但计算效率有待提高;预测相减类方法可以获得精度很高的分离效果,但算法受预测波场精度的影响,稳定性较差。基于3类方法的特点,分析认为多方法联合是混采地震数据分离处理的主要发展方向,多方法联合将进一步提高数据分离的精度和效率,并且适用于复杂地区的混采地震数据分离,从而拓宽“两宽一高”采集方式的应用范围,提高勘探精度,推动行业发展。

Shi T K, Xu H, Huang L, et al.

Progress in high-efficiency and high-precision separation of blended seismic data

[J]. Geophysical Prospecting for Petroleum, 2020, 59(5):703-712.

DOI:10.3969/j.issn.1000-1441.2020.05.      [本文引用: 1]

<p>Technology for the acquisition of &ldquo;Broadband,wide-azimuth and high-density&rdquo; data has significant advantages in improving the quality of seismic data and accuracy of subsurface imaging.In this paper,methods for acquiring and processing high-efficiency seismic data are summarized,and progress in separation methods for blended seismic data are discussed,including denoising,inversion and prediction-subtraction.Denoising methods are stable,exhibit high efficiency,and are easy to implement.Inversion methods can obtain higher signal-to-noise ratios and fidelity than denoising method but incur more expensive computation costs.Prediction-subtraction methods can obtain relatively accurate separation results,but are easily affected by the accuracy of the predicted wave field and have poor stability.Because of the relative advantages and disadvantages of all three approaches,future developments in separation of blended seismic data may be through the combination of several methods.The combined method will improve the accuracy and efficiency of blended seismic data separation and be more robust in complex areas,thus extending the implementation of the technology for the acquisition of broadband,wide-azimuth and high density data.</p>

朱义坤, 赵景怀, 缪旭煌, 等.

综合物探方法在蚌埠隆起金多金属矿勘查中的应用——以怀远双沟勘查区为例

[J]. 华东地质, 2023, 44(1):82-92.

[本文引用: 1]

Zhu Y K, Zhao J H, Miao X H, et al.

Application of comprehensive geophysical survey in Bengbu uplift gold polymetallic ore exploration:A case study of Huaiyuan Shuanggou exploration area

[J]. East China Geology, 2023, 44(1):82-92.

[本文引用: 1]

唐欢欢, 毛伟建.

基于多路径 Radon变换的地震数据噪声压制和波型分离方法研究

[J]. 地球物理学报, 2022, 65(1):333-348.

DOI:10.6038/cjg2022P0102      [本文引用: 1]

Radon变换是一种稀疏变换，被广泛应用于地震数据处理，其中线性Radon和抛物Radon最为常用.在实际地震数据中，直达波和面波的同相轴形态为线性，反射波为双曲型，单独使用线性Radon或抛物Radon变换时，不能确保所有同相轴在变换域的系数都是稀疏的，影响地震数据处理效果.本文提出的多路径Radon变换联合了线性Radon变换和抛物Radon变换，每个同相轴都有两种不同的变换参数来与积分路径相适应，能够兼顾不同形态的同相轴；然后利用最小二乘稀疏反演方法对不同形态同相轴匹配最佳积分路径，使其自动分离到两个不同的Radon域剖面且保持系数同时稀疏.从多路径Radon域剖面上，能够很容易地识别不同系数所对应的同相轴形态、时间截距以及速度，这些特征有利于提高利用Radon变换方法进行随机噪声压制、面波压制以及波型分离等技术的处理效果，该变换在模型数据和实际数据中的应用结果证明了本文方法有效性.

Tang H H, Mao W J.

Multi-path Radon transform and its application in denoising and wave field separation

[J]. Chinese Journal of Geophysics, 2022, 65(1):333-348.

[本文引用: 1]

司艳欣. 基于鲁棒双曲Radon变换稀疏反演的多震源地震数据分离方法研究[D]. 北京: 中国石油大学(北京), 2023.

Si Y X. Multi-source seismic data separation method via robust hyperbolic Radon transform sparse inversion[D]. Beijing: China University of Petroleum(Beijing), 2023.

薛亚茹, 唐欢欢, 陈小宏, 等.

高阶高分辨率Radon变换地震数据重建方法

[J]. 石油地球物理勘探, 2014, 49(1):95-100,131.

Xue Y R, Tang H H, Chen X H, et al.

Seismic data reconstruction based on high order high resolution Radon transform

[J]. Oil Geophysical Prospecting, 2014, 49(1):95-100,131.

魏亚杰, 张盼, 许卓.

基于稀疏约束反演的三维混采数据分离

[J]. 地球物理学报, 2019, 62(10):4000-4009.

DOI:10.6038/cjg2019M0501      [本文引用: 1]

混合震源采集技术相对于传统的地震数据采集，在极大提高采集效率的同时引入了混叠噪声，很大程度上影响了成像结果的精度.二维混采数据中，我们通常利用混叠噪声在非共炮域呈非相干分布这一特点来压制混叠噪声，从而实现混合震源数据分离.相对于二维混采数据，三维混采数据具有数据量巨大，构建混合震源算子困难，混合度的增加引入了高强度混叠噪声的特点.针对上述问题，本文采用稀疏约束反演方法在Radon域实现混采数据分离，混叠噪声强度比较大的情况下，稀疏约束反演方法能够得到更高精度的分离结果；利用震源激发的GPS时间通过长记录的方式在共接收点道集对上一次迭代分离结果做混合、伪分离，实现了单个共接收点道集自身混合、伪分离，避免了对整个数据做运算，同时不需要构建混合震源算子.通过模拟数据和实际数据计算来验证上述方法的适用性.

Wei Y J, Zhang P, Xu Z.

Separation of 3D blending seismic data based on sparse constrained inversion

[J]. Chinese Journal of Geophysics, 2019, 62(10):4000-4009.

[本文引用: 1]

陈红灵. 基于稀疏反演的多震源地震数据分离方法研究[D]. 北京: 中国石油大学(北京), 2018.

[本文引用: 1]

Chen H L. Research on the separation of simultaneous sources data based on sparse inversion method[D]. Beijing: China University of Petroleum(Beijing), 2018.

[本文引用: 1]

白兰淑, 刘伊克, 卢回忆, 等.

基于压缩感知的Curvelet域联合迭代地震数据重建

[J]. 地球物理学报, 2014, 57(9):2937-2945.

DOI:10.6038/cjg20140919     

由于野外采集环境的限制，常常无法采集得到完整规则的野外地震数据，为了后续地震处理、解释工作的顺利进行，地震数据重建工作被广泛的研究.自压缩感知理论的提出，相继出现了基于该理论的多种迭代阈值方法，如CRSI方法（Curvelet Recovery by Sparsity-promoting Inversion method）、Bregman迭代阈值算法（the linearized Bregman method）等.CSRI方法利用地震波形在Curvelet的稀疏特性，通过一种基于最速下降的迭代算法在Curvelet变换域恢复出高信噪比地震数据，该迭代算法稳定，收敛，但其收敛速度慢.Bregman迭代阈值法与CRSI最大区别在于每次迭代时把上一次恢复结果中的阈值前所有能量都保留到本次恢复结果中，从而加快了收敛速度，但随着迭代的进行重构数据中噪声干扰越来越严重，导致最终恢复出的数据信噪比低.综合两种经典方法的优缺点，本文构造了一种新的联合迭代算法框架，在每次迭代中将CRSI和Bregman的恢复量加权并同时加回本次迭代结果中，从而加快了迭代初期的收敛速度，又避免了迭代后期噪声干扰的影响.合成数据和实际数据试算结果表明，我们提出的新方法不仅迭代快速收敛稳定，且能得到高信噪比的重建结果.

Bai L S, Liu Y K, Lu H Y, et al.

Curvelet-domian joint iterative seismic date reconstruction based on compressed sensing

[J]. Chinese Journal of Geophysics, 2014, 57(9):2937-2945.

杨熙熙, 张华, 武召祺, 等.

基于曲波变换与快速指数阈值迭代的多震源地震数据分离

[J]. 科学技术与工程, 2024, 24(13):5296-5303.

Yang X X, Zhang H, Wu Z Q, et al.

Separation of multi-source seismic data based on curvelet-transfrom and fast exponential threshold iteration method

[J]. Science Technology and Engineering, 2024, 24(13):5296-5303.

张华, 陈小宏.

基于jitter采样和曲波变换的三维地震数据重建

[J]. 地球物理学报, 2013, 56(5):1637-1649.

[本文引用: 1]

Zhang H, Chen X H.

Seismic data reconstruction based on jittered sampling and curvelet transform

[J]. Chinese Journal of Geophysics, 2013, 56(5):1637-1649.

[本文引用: 1]

温睿. 基于Seislet变换的地震数据重建方法研究[D]. 北京: 中国石油大学(北京), 2018.

[本文引用: 1]

Wen R. Study on seismic data reconstruction methods based on seislet transform[D]. Beijing China University of Petroleum(Beijing), 2018.

[本文引用: 1]

董烈乾, 周恒, 郭善力, 等.

一种改进型 seislet 域迭代阈值压制混叠噪声方法

[J]. 物探与化探, 2020, 44(3):568-572.

Dong L Q, Zhou H, Guo S L, et al.

An optimized blending noise suppression based on seislet domain iterative threshold denoising approach

[J]. Geophysical and Geochemical Exploration, 2020, 44(3):568-572.

吴庚. 不同地震数据缺失情况下数据插值方法研究[D]. 长春: 吉林大学, 2023.

Wu G. Research on seismic data interpolation methods for different data missing cases[D]. Changchun: Jilin University, 2023.

王凯. 基于 Seislet 域的混叠数据分离方法研究[D]. 青岛: 中国石油大学(华东), 2021.

[本文引用: 1]

Wang K. Research on separation method of blended data using seislet domain[D]. Qingdao: China University of Petroleum(East China), 2021.

[本文引用: 1]

王大为, 周寒, 李列, 等.

Seislet变换在海上拖缆多震源采集数据分离中的应用

[J]. 地质科技情报, 2018, 37(5):247-253.

[本文引用: 1]

Wang D W, Zhou H, Li L, et al.

Application of Seislet transform in separation of multi-source acquisition data of offshore streamer

[J]. Geological Science and Technology Information, 2018, 37(5):247-253.

[本文引用: 1]

Huang B, Ma S, Goldfarb D.

Accelerated linearized Bregman method

[J]. Journal of Scientific Computing, 2012, 54(2-3):428-453.

[本文引用: 1]

庞洋, 张华, 郝亚炬, 等.

基于加速 Bregman方法和阈值迭代法的联合地震数据重建法

[J]. 石油地球物理勘探, 2022, 57(5):1035-1045.

[本文引用: 1]

Pang Y, Zhang H, Hao Y J, et al.

Joint seismic data reconstruction based on the accelerated Bregman method and threshold iteration method

[J]. Oil Geophysical Prospecting, 2022, 57(5):10351045.

[本文引用: 1]

魏亚杰, 曹静杰.

欠采样混合震源数据同时分离和重建研究

[C]// 中国地球科学联合学术年会论文集(二十九): 2022.

[本文引用: 1]

Wei Y J, Cao J J.

Research on simultaneous separation and reconstruction of under sampled mixed source data

[C]// Proceedings of the Annual Conference of China Earth Sciences Union(29):2022.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com