基于非平稳褶积模型的泊松阻抗及裂缝参数叠前地震各向异性高分辨率直接反演方法

doi:10.11720/wtyht.2025.1432

基于非平稳褶积模型的泊松阻抗及裂缝参数叠前地震各向异性高分辨率直接反演方法

汪舒^,¹, 王锐¹, 杨家义¹, 赵卫升¹, 廖建^,²

1.中国石油塔里木油田公司博大采油气管理区油气藏地质研究所,新疆库尔勒 841000

2.成都西南石大石油工程技术有限公司,四川成都 610500

High-resolution direct inversion of Poisson's impedance and fracture parameters using prestack seismic anisotropy data based on the non-stationary convolution model

WANG Shu^,¹, WANG Rui¹, YANG Jia-Yi¹, ZHAO Wei-Sheng¹, LIAO Jian^,²

1. Boda Oil and Gas Management Area Oil and Gas Reservoir Geology Institute, Tarim Oilfield Company, PetroChina, Korla 841000, China

2. Chengdu Southwest Petroleum Engineering Technology Co., Ltd., Chengdu 610500, China

通讯作者: 廖建(1997-),男,主要从事开发地质方面的研究工作。Email:1061347029@qq.com

第一作者: 汪舒(1994-),男,硕士学位,工程师,从事开发地质方面的研究工作。Email:wangshu-txn@petrochina.com.cn

责任编辑: 沈效群

收稿日期: 2024-10-30 修回日期: 2024-12-27

基金资助:

中国石油天然气股份有限公司重大专项“超深层油气藏开发关键技术研究与应用”(2023ZZ14YJ03)

Received: 2024-10-30 Revised: 2024-12-27

摘要

目前利用地震反演方法对复杂砂、泥岩储层的预测缺乏有针对性的研究,在砂、泥岩互层或存在水平裂缝发育的情况下,常规的反演方法难以给出准确的砂体预测结果。为此,结合实际工区的测井岩石物理交会,优选了泊松阻抗作为储层预测的敏感参数,同时考虑储层存在裂缝发育的特征,推导了含泊松阻抗的VTI各向异性反射系数方程。在此基础上,采用非平稳褶积模型设计了正演算子改善砂、泥岩互层产生的地震波强衰减特性,保护深层薄储层的反射特征,提出了一种叠前地震各向异性高分辨率直接反演泊松阻抗及裂缝参数的方法,为砂、泥岩储层高分辨率展布、刻画以及含裂缝性评价开辟了新的思路。模型测试与实际资料测试结果证明了本方法的可行性和适应性。

关键词： 泊松阻抗; 裂缝参数; 直接反演; 非平稳; 各向异性; 储层预测

Abstract

Since no targeted seismic inversion techniques are available for the prediction of complex sandstone-mudstone reservoirs, conventional inversion methods struggle to provide accurate sand body predictions in the presence of sandstone-mudstone interbeds or horizontal fractures. Hence, this study selected Poisson's impedance as the sensitive parameter for reservoir prediction based on the petrophysical parameter cross plots using log data from the study area. Considering the characteristics of fracture development in the reservoirs, this study derived the equation of anisotropic reflection coefficients in vertical transverse isotropy (VTI) media, incorporating Poisson's impedance. Furthermore, this study designed a forward modeling operator using a non-stationary convolution model to improve the strong attenuation characteristics of seismic waves generated by sandstone-mudstone interbeds and protect the reflection characteristics of deep thin reservoirs. Finally, this study proposed a high-resolution direct inversion of Poisson's impedance and fracture parameters using prestack seismic anisotropy data, providing a novel approach for high-resolution characterization of the distribution of sandstone-mudstone reservoirs and the assessment of fracture-bearing properties. Both model and field data tests validate the feasibility and adaptability of the proposed method.

Keywords： Poisson's impedance; fracture parameter; direct inversion; non-stationary; anisotropy; reservoir prediction

PDF (6166KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

汪舒, 王锐, 杨家义, 赵卫升, 廖建. 基于非平稳褶积模型的泊松阻抗及裂缝参数叠前地震各向异性高分辨率直接反演方法[J]. 物探与化探, 2025, 49(3): 642-652 doi:10.11720/wtyht.2025.1432

WANG Shu, WANG Rui, YANG Jia-Yi, ZHAO Wei-Sheng, LIAO Jian. High-resolution direct inversion of Poisson's impedance and fracture parameters using prestack seismic anisotropy data based on the non-stationary convolution model[J]. Geophysical and Geochemical Exploration, 2025, 49(3): 642-652 doi:10.11720/wtyht.2025.1432

0 引言

叠前地震反演作为利用地震振幅信息来描述地下弹性、物性变化的一种有效手段,已经逐渐成为地震岩石物理领域储层表征及流体识别研究的热点话题之一^[1-3]。基于贝叶斯框架的叠前反演方法通过合理引入先验信息,有效解决了常规AVO反演中的不适定性问题,可提高反演的精度和稳定性^[4-6]。

随着油气勘探需求的不断增加,不同类型的复杂储层也开始被地球物理学家进行探索和研究。当地下介质由于裂缝、断块或砂泥互层的存在而表现出各向异性特征时,常规储层的地震岩石物理理论不足以对地下油气藏给予准确描述,因此,基于VTI或HTI理论的各向异性非常规岩石物理及地震反演理论逐渐发展起来,并为非常规油气藏的储层识别提供了指导^[7-10]。为充分利用各向异性介质中的多波探测信息,侯栋甲等^[11]提出了一种基于贝叶斯理论的多波联合叠前反演方法,此方法采用Ruger近似来描述各向异性介质中的反射系数,并利用最小二乘优化算法反演地层纵横波速度、密度和Thomsen各向异性参数^[12]。针对发育垂直裂缝而产生方位各向异性的地层,陈怀震等^[13]从各向异性岩石物理模型出发,引入流体因子指标来研究不同流体填充下的地震响应特征,并在此基础上提出了一种用于估算流体因子的AVAZ(振幅与方位角)反演方法。在VTI各向异性介质研究的基础上,王波等^[14]提出了一种改进的 VTI介质 SH-SH 波地震反演方法,相比常规 PP 波反演具有更低的不确定性,并减少了 PP 波各向异性反演中对大角度数据的需求。此外,为了获得独立的剪切波各向异性参数,进一步提出了一种基于岩石物理关系,准确预测横波阻抗、水平SH波速度和各向异性参数的新方法,为各向异性地层的岩性解释和油气藏预测提供可靠的解决方案,拓展了横波地震勘探的应用潜力。

针对砂、泥岩沉积工区的砂岩储层预测,学者们通常采用叠前地震反演弹性阻抗、纵横波速度比等参数进行地下砂岩储层的展布刻画。肖张波等^[15]提出了一种宽带叠前扩展弹性阻抗的地震反演方法,以扩展弹性阻抗为基础进一步建立储层弹性参数与物性参数(总有机碳、孔隙度)之间的量化关系,并用转换之后的物性参数预测了高品质源岩和有利储集层发育区域的分布。石亚兰等^[16]采用叠前地震反演地层的纵波阻抗以及纵横波速度比,对较为疏松的砂、泥岩沉积工区的砂体储层进行了可靠预测。在此基础上,张德明等^[17]使用叠前地震反演地层纵波阻抗以及纵横波速度比参数,在具有致密特征的砂、泥岩工区开展了储层预测方法研究。然而,上述地震反演储层敏感参数的方法仍然存在许多不足:首先,敏感参数的选择较为简单,多为弹性阻抗或者纵横波速度比,而其他物性参数的获取则依靠参数转换,在转换过程中容易产生累积误差;其次,叠前地震反演并未考虑地层裂缝存在时表现出的各向异性特征,在裂缝型储层中的应用受到限制;最后,在深层或者砂、泥岩互层的沉积岩工区,地震波的传播具有较强的衰减性,使得深层薄层弱反射砂体预测的分辨率较低。

Robinsion褶积理论将地震波的传播过程总结为地震子波与反射系数的褶积过程,是用于描述地震波场随时间及空间变化的理想模型。在此基础上,Margrave^[18]提出了将卷积方法推广到非平稳过程这样一种广义的线性理论,该理论可应用于任何线性的、非平稳的滤波器,并且在时间域、频率域或混合域中具有任意的时频变化。该方法为分析非平稳褶积提供了直观的解释,也为处理非平稳信号提供了新的理论基础和实施方案。基于非平稳褶积理论,高静怀等^[19]提出了一个用于描述地震波形谱变化的小波模型的数学表达式,并研究了不同情况下地震波形谱的内容和结构,为改善地震记录分辨率提供了新的思路和有效手段。此外,Margrave等^[20]提出了一种用于处理非平稳地震数据的Gabor变换反褶积方法,利用Gabor 变换近似地将非平稳卷积模型分解为源波形、衰减函数和反射率的Gabor 变换的乘积,同时可以将源波形和衰减函数直接从地震波形的 Gabor 频谱中计算出来。该方法的提出将平稳的脉冲反卷积推广到了非平稳信号的情况,同时还考虑了衰减过程对波形的影响,可为更好地恢复地层反射率提供帮助。为解决地震反演中的地震波非平稳传播问题,Chai等^[21]提出了非平稳稀疏反射率反演(NSRI)方法,该方法可直接从非平稳地震数据中提取反射率序列,避免了存在不稳定性的反Q滤波方法的使用,为非平稳褶积模型用于叠前地震反演奠定了基础。非平稳褶积模型的提出和应用,为叠前地震反演分辨率的提升提供了新的解决方案。

考虑到上述叠前地震反演储层敏感参数及储层预测研究中所涉及到的问题,针对复杂砂、泥岩储层工区的实际概况,结合VTI介质的Ruger近似反射系数方程,本文利用测井岩石物理参数的交会,优选了泊松阻抗作为识别砂岩储层的敏感参数,推导了含泊松阻抗的VTI介质反射系数方程;在叠前反演的过程中,采用了非平稳褶积模型用于改善砂、泥岩互层导致的地震波衰减进而带来的薄层分辨率不足的情况。精度测试验证了所推导方程的准确性,模型测试和实际资料测试的结果为本文提出的高分辨率直接反演方法的可行性和实用性提供了坚实的依据。

1 理论与方法

1.1 复杂砂、泥岩沉积区储层岩石物理敏感参数分析

复杂砂、泥岩沉积区储层具有孔隙类型复杂、非均质性强等特征,使得常规的叠前反演获取的储层敏感参数(纵波阻抗、纵横波速度比等)难以适用于此类区块砂岩的岩性识别。因此,针对复杂砂、泥岩沉积区储层进行岩石物理敏感参数分析,优选砂岩储层敏感参数,是复杂砂、泥岩沉积区储层可靠和有效识别的理论基础。

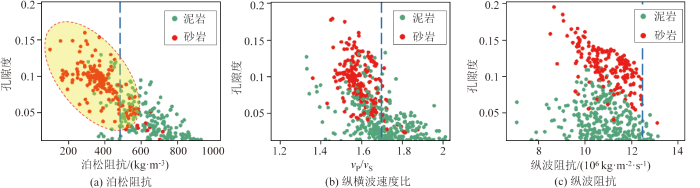
图1展示了工区内多口探井的岩石物理交会结果。可以观察到,在图中蓝色虚线位置处,泊松阻抗的交会结果能够对砂、泥岩进行更为清晰地区分,特别是在黄色椭圆形区域内,砂岩能够明显地与泥岩区区分开,而纵波阻抗与纵横波速度比的区分效果较差。出现这一结果的原因在于泊松阻抗为泊松比与密度的乘积,同时耦合了纵波速度、横波速度以及密度三种弹性参数的信息,能够在不同角度下更丰富、更全面地反映储层砂、泥岩的性质,而常规纵横波速度比与纵波阻抗所包含的弹性性质较为单一,未能同时考虑多种因素的影响,使得其用于区分砂、泥岩储层的效果较差。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 复杂砂、泥岩沉积区砂岩敏感参数测井岩石物理交会图

Fig.1 Petrophysical cross plots of sandstone sensitive parameter logging in complex sand and mudstone sedimentary area

1.2 VTI介质含泊松阻抗反射系数方程推导

在砂、泥岩沉积工区,由于地层水平展布且具有砂、泥岩互层的特性,在一定程度上会使地层存在VTI介质各向异性的特征,除此之外,本文将针对含有水平裂缝的砂、泥岩互层的储层进行反演方法的测试。因此,本研究将推导含有水平对称轴的VTI介质含泊松阻抗反射系数方程,并开展泊松阻抗及裂缝参数的反演工作。

线性化后的VTI介质各向异性反射系数方程通常由两部分组成:表征各向同性背景性质的各向同性项以及反映裂隙发育程度的各向异性参数项^[22]。根据潘新朋^[23]给出的含纵波模量M_b、横波模量μ_b、密度ρ_b这3个背景弹性参数的VTI介质反射系数方程,以及Zong等^[24]给出的杨氏模量反射系数 $\frac{Δ E}{E}$ 、泊松比反射系数 $\frac{Δ σ}{σ}$ 与纵横波模量反射系数 $(\frac{Δ M_{b}}{M_{b}}, \frac{Δ μ_{b}}{μ_{b}})$ 的关系,推导后可得到VTI介质含泊松阻抗反射系数( $R_{p p}^{V T I}$ (θ))方程:

(1)

R_{p p}^{V T I}

(θ)=a_E(θ)

\frac{Δ E_{b}}{E_{b}}

+a_σρ(θ)

\frac{Δ σ ρ_{b}}{σ ρ_{b}}

+a_ρ(θ)

\frac{Δ ρ_{b}}{ρ_{b}}

+b_ε(θ)Δε+b_δ(θ)Δδ;

(2)a_E(θ)=

[\frac{1}{4 c o s^{2} θ} - (1 - \frac{λ_{b}}{M_{b}}) s i n^{2} θ]

(3)a_σρ(θ)=

\{(1 - \frac{λ_{b}}{M_{b}}) s i n^{2} θ \frac{σ}{1 + σ} + \frac{1}{4 c o s^{2} θ} \cdot [\frac{σ}{(2 σ - 1) (σ - 1)} - \frac{σ}{1 + σ}]\}

(4)a_ρ(θ)=

\{\frac{1}{2} - \frac{1}{4 c o s^{2} θ} [\frac{σ}{(2 σ - 1) (σ - 1)} - \frac{σ}{1 + σ} + 1] - (1 - \frac{λ_{b}}{M_{b}}) \frac{σ}{1 + σ}\}

(5)b_ε(θ)=

\frac{s i n^{2} θ t a n^{2} θ}{2}

(6)b_δ(θ)=

\frac{s i n^{2} θ}{2}

。

式中:θ为入射角;Δ表示差分;λ_b为背景拉梅参数;ε与δ分别为表征裂隙发育程度的各向异性参数; $\frac{Δ σ ρ}{σ ρ}$ 为泊松阻抗反射系数; σ= $\frac{1 - 2 k}{2 - 2 k}$ ,k= $\frac{v_{S}^{2}}{v_{P}^{2}}$ ,v_S、v_P分别为横波速度和纵波速度。

作为参与反演并用于获取地下砂、泥岩储层信息的核心方程,其反射系数的精度是评价其能否合理、准确地提取储层敏感参数及描述裂缝发育状态的一项重要指标,因此,设计了一套砂、泥岩模型对其进行精度测试,模型参数由表1所示。

表1 砂、泥岩储层双层模型参数

Table 1 The parameters of sand and mudstone reservoir two-layer model

	v_P /(m·s^-1)	v_S /(m·s^-1)	ρ /(kg·m^-3)	σρ /(kg·m^-3)	E /10¹⁰Pa	ε	δ
砂岩	3450	2310	3020	282	3.52	0.07	0.45
泥岩	4025	2680	3630	369	5.75	0.02	0.005

新窗口打开| 下载CSV

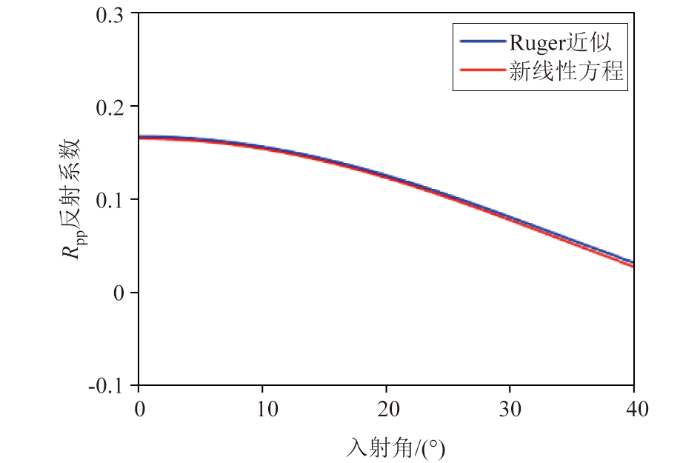
图2展示了反射系数方程的精度分析结果。从反射系数随入射角的变化情况可以看出,新推导的反射系数方程与Ruger近似具有很高的吻合度,直至大角度入射的情况下,吻合度依然保持了较高的水准。精度分析的结果证实了新方程在精度方面的可靠性,为新方程能够应用于叠前直接反演、进而合理准确地获取储层砂体以及裂缝敏感参数(σρ、ε、δ)奠定了基础。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 反射系数方程精度分析

Fig.2 The precision analysis of reflection coefficient equations

1.3 基于非平稳褶积模型的叠前直接反演

由于复杂砂、泥岩沉积区域的砂、泥岩互层性质以及储层非均质性特征,导致地震波在传播过程中产生了较强的衰减作用,因此常规的时间域稳态褶积模型难以满足对实际地震波传播过程的描述,使得基于常规褶积模型的叠前反演结果的分辨率较低。为此,非平稳褶积模型将用于复杂砂、泥岩沉积区域的砂泥岩储层正演建模并开展贝叶斯框架下的叠前地震直接反演,以此来提高反演结果的分辨率与可靠性。

首先推导非平稳褶积模型下的地震正演算子。根据非平稳反褶积理论,结合Kolsky-Futterman Q模型,地层中沿z轴传播的平面波表达式为

(7)u(z,ω,t)=eⁱ^ωtexp

[- i ω τ_{t} (z) - \frac{ω τ_{t} (z)}{2 Q_{e f f} (z)} + \frac{i}{π} l n (\frac{ω}{ω_{r}}) \frac{ω τ_{t} (z)}{Q_{e f f} (z)}]

式中:i为虚数单位;z为深度;t为时间;ω与ω_r分别为频率与参考频率;Q_eff为不同深度下的等效Q值,反映地层的Q滤波效应的累积。

定义

α(ω,τ_z,Q_z)=exp $(- \frac{ω τ_{t} (z)}{2 Q_{e f f} (z)})$ exp $(i \frac{1}{π} l n (\frac{ω}{ω_{r}}) \frac{ω τ_{t} (z)}{Q_{e f f} (z)})$

为与频率和时间相关的粘弹性衰减指示函数,基于地震波的叠加原理,推导后可得到实际的时间域非稳态褶积模型最终表达式:

(8)s(t)=

\frac{1}{2 π} \int_{0}^{+ \infty}

W(ω)

[\int_{0}^{+ \infty} r (z) e^{- i ω τ_{t} (z)} α (ω, τ_{z}, Q_{z}) d z]

·eⁱ^ωtdω+n(t)。

式中:W(ω)为频率域的地震子波,由时间域地震子波w(t)傅里叶变换得到;r(z)表示不同深度位置处的反射系数;n(t)代表地震记录含有的随机噪声。

式(8)在反映了地层Q滤波效应的同时,也囊括了地震子波的滤波效应。为便于反演,将该式两边进行傅里叶变换并化简,可得频率域非稳态褶积模型表达式:

(9)S(ω)=W(ω)·

[\overset{J}{\sum_{j = 1}} r_{j} e^{- i ω τ_{j}} α (ω, τ_{j}, Q_{j})]

+N(ω)。

式中:j代表时间采样点;J代表时间采样点的总数;S(ω)与N(ω)分别为频率域的地震记录与随机噪声,分别由s(t)与n(t)的傅里叶变换得到。

在实际反演的应用过程中,将采用离散矩阵形式的非稳态褶积模型,因此,式(9)可以改写并展开为离散矩阵形式:

(10)

[\begin{array}{l} S (ω_{1}) \\ S (ω_{2}) \\ ︙ \\ S (ω_{L}) \end{array}]

[\begin{array}{l} W (ω_{1}) α (ω_{1}, τ_{1}, Q_{1}) e^{- i ω_{1} τ_{1}} & W (ω_{1}) α (ω_{1}, τ_{2}, Q_{2}) e^{- i ω_{1} τ_{2}} & \dots & W (ω_{1}) α (ω_{1}, τ_{J}, Q_{j}) e^{- i ω_{1} τ_{J}} \\ W (ω_{2}) α (ω_{2}, τ_{1}, Q_{1}) e^{- i ω_{2} τ_{1}} & W (ω_{2}) α (ω_{2}, τ_{2}, Q_{2}) e^{- i ω_{2} τ_{2}} & \dots & W (ω_{2}) α (ω_{2}, τ_{J}, Q_{j}) e^{- i ω_{2} τ_{J}} \\ ︙ & ︙ & ⋱ & ︙ \\ W (ω_{L}) α (ω_{2}, τ_{L}, Q_{1}) e^{- i ω_{L} τ_{1}} & W (ω_{L}) α (ω_{L}, τ_{2}, Q_{2}) e^{- i ω_{L} τ_{2}} & \dots & W (ω_{L}) α (ω_{L}, τ_{J}, Q_{j}) e^{- i ω_{L} τ_{J}} \end{array}]

[\begin{array}{l} r_{1} \\ r_{2} \\ ︙ \\ r_{J} \end{array}]

[\begin{array}{l} N (ω_{1}) \\ N (ω_{2}) \\ ︙ \\ N (ω_{L}) \end{array}]

式中:L为所选取的频率分量的个数。

由于实际地震记录的带限特征以及随机噪声的宽频谱特征,在反演过程中选取合理的频率分量范围也是不可忽视的一项重要内容。在频率分量的选取中,最小截频ω_low一般选取地震记录所能达到的最小频率,而最高截频ω_high则一般选取不超过地震频带所能达到的最高频率,具体的最高截频将参考随机噪声的频带,选取随机噪声占比较少的优势频带。

基于上述非平稳褶积模型正演算子,即可开展贝叶斯框架下的非平稳叠前地震各向异性直接反演。贝叶斯理论建立了模型参数后验概率分布p(m'|S')与似然函数p(S'|m')以及先验分布p(m')之间的定量关系,当似然函数服从高斯分布且先验分布服从柯西分布时,其后验概率的具体表达式为

(11)p(m'|S')=

\frac{p_{C a u c h y} (m') p_{G a u s s} (S' | m')}{\int p_{C a u c h y} (m') p_{G a u s s} (S' | m') d m}

∝p_Cauchy(m')p_Gauss(S'|m')。

在叠前反演过程中,根据贝叶斯反演理论,似然函数旨在通过背景噪声的概率密度分布来描述反演结果m'与实际地震数据S'之间的匹配程度,先验分布用于描述待反演的模型参数m'的先验信息,后验分布则是将似然函数与先验分布的概率密度同时考虑,用于建立先验模型约束下的叠前反演目标泛函。根据式(11)的描述,可得似然函数表达式:

(12)p_Gauss(S'|m')=

\frac{1}{(2 π σ_{n}^{2})^{J / 2}}

·exp

[\frac{- {(S' - G' m')}^{T} (S' - G' m')}{2 σ_{n}^{2}}]

式中: $σ_{n}^{2}$ 为噪声的方差;G'为正演算子。同理,可得先验分布的表达式:

(13)p_Cauchy(m')=

\frac{1}{(π σ_{m})^{N}} \overset{N}{\prod_{i = 1}} \frac{1}{1 + m'_{i}^{2} / σ_{m}^{2}}

式中: $σ_{m}^{2}$ 为待反演参数得协方差;N为待反演模型的采样点的个数。结合式(12)与式(13),可以建立贝叶斯框架下的反演目标函数:

(14)F(m')=(S'-G'm')^T(S'-G'm')+2

σ_{n}^{2} \overset{N}{\sum_{i = 1}}

ln(1+m

'_{i}^{2}

σ_{m}^{2}

)。

根据式(9),结合式(1~6)的含泊松阻抗VTI介质反射系数方程,并加入平滑背景约束对地震数据的低频缺失作为补充以提高反演结果的稳定性,可得最终的叠前地震直接反演的目标函数:

(15)F(m)=(S-Gm)^T(S-Gm)+2

σ_{n}^{2} \overset{K}{\sum_{i = 1}}

ln(1+

m_{i}^{2}

σ_{m}^{2}

)+λT,

式中:λ为控制平滑背景约束参与权重的系数。式(15)中的剩余项的离散矩阵展开式为

(16)$\begin{array}{l}\boldsymbol{S}=\left[\begin{array}{llll}S_{1}(\omega) & S_{2}(\omega) & \cdots & S_{U}(\omega)\end{array}\right]^{\mathrm{T}}= \\{\left[\begin{array}{llllllll}S_{1}\left(\omega_{1}\right) & \cdots & S_{1}\left(\omega_{L}\right) & S_{2}\left(\omega_{1}\right) & \cdots & S_{2}\left(\omega_{L}\right) & \cdots & S_{U}\left(\omega_{1}\right)\end{array} \cdots e S_{U}\left(\omega_{L}\right)\right]^{\mathrm{T}},}\end{array}$

(17)G=

[\begin{array}{l} W_{1} (ω, α) \\ W_{2} (ω, α) \\ ⋱ \\ W_{U} (ω, α) \end{array}]

[\begin{array}{l} a_{E 1} (θ) & a_{σ ρ 1} (θ) & a_{ρ 1} (θ) & b_{ε 1} (θ) & b_{δ 1} (θ) \\ a_{E 2} (θ) & a_{σ ρ 2} (θ) & a_{ρ 2} (θ) & b_{ε 2} (θ) & b_{δ 2} (θ) \\ ︙ & ︙ & ︙ & ︙ & ︙ \\ a_{E U} (θ) & a_{σ ρ U} (θ) & a_{ρ U} (θ) & b_{ε U} (θ) & b_{δ U} (θ) \end{array}]

(18)W_U(ω,α)=

[\begin{array}{l} W_{U} (ω_{1}) α (ω_{1}, τ_{1}, Q_{1}) e^{- i ω_{1} τ_{1}} & W_{U} (ω_{1}) α (ω_{1}, τ_{2}, Q_{2}) e^{- i ω_{1} τ_{2}} & \dots & W_{U} (ω_{1}) α (ω_{1}, τ_{J}, Q_{j}) e^{- i ω_{1} τ_{J}} \\ W_{U} (ω_{2}) α (ω_{2}, τ_{1}, Q_{1}) e^{- i ω_{2} τ_{1}} & W_{U} (ω_{2}) α (ω_{2}, τ_{2}, Q_{2}) e^{- i ω_{2} τ_{2}} & \dots & W_{U} (ω_{2}) α (ω_{2}, τ_{J}, Q_{j}) e^{- i ω_{2} τ_{J}} \\ ︙ & ︙ & ⋱ & ︙ \\ W_{U} (ω_{L}) α (ω_{2}, τ_{L}, Q_{1}) e^{- i ω_{L} τ_{1}} & W_{U} (ω_{L}) α (ω_{L}, τ_{2}, Q_{2}) e^{- i ω_{L} τ_{2}} & \dots & W_{U} (ω_{L}) α (ω_{L}, τ_{J}, Q_{j}) e^{- i ω_{L} τ_{J}} \end{array}]

(19)m=

{[\begin{array}{l} \frac{Δ E_{b}}{E_{b}} & \frac{Δ σ ρ_{b}}{σ ρ_{b}} & \frac{Δ ρ}{ρ} & Δ ε & Δ δ \end{array}]}^{T}

{[\begin{array}{l} \frac{Δ E_{b 1}}{E_{b 1}} & \dots & \frac{Δ E_{b J}}{E_{b J}} & \frac{Δ σ ρ_{b 1}}{σ ρ_{b 1}} & \dots & \frac{Δ σ ρ_{b J}}{σ ρ_{b J}} & \frac{Δ ρ_{1}}{ρ_{1}} & \dots & \frac{Δ ρ_{J}}{ρ_{J}} & Δ ε_{1} & \dots & Δ ε_{J} & Δ δ_{1} & \dots & Δ δ_{J} \end{array}]}^{T}

(20)T=(η_i-l_im_i)^T(η_i-l_im_i),

(21)η_i=1/2×ln(m_i/m_i₀),

(22)l_i=

\int_{t_{0}}^{t_{i}}

dτ。

目标函数的求解将通过迭代最小二乘的求解方法进行,当目标函数取得极小值时,将获得与之对应的待反演参数m的数值解。

2 模型测试

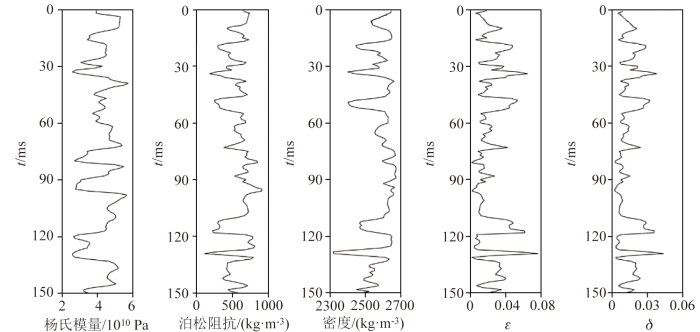
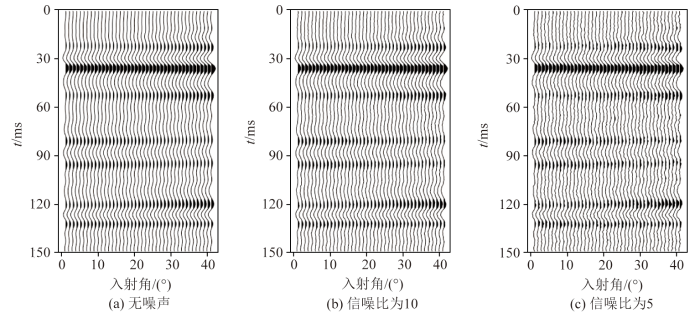
为评价本文所提方法的合理性与可行性,将采用图3所示的岩石物理参数模型对本文所提出的反演方法进行模型测试。图3展示了杨氏模量、泊松阻抗、密度3个各向同性背景参数,以及ε和δ这2个表征裂缝发育程度的各向异性参数的模型值。图4为以图3中的模型参数作为输入,基于非平稳褶积模型的无噪声、信噪比为10和信噪比为5的正演合成地震记录。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 岩石物理参数模型

Fig.3 The petrophysical models

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同信噪比下基于非平稳褶积模型的正演合成地震记录

Fig.4 The forward synthesized seismogram based on non-stationary convolution model with different signal-to-noise ratios

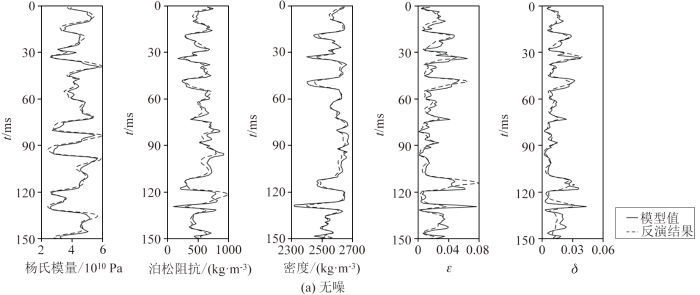
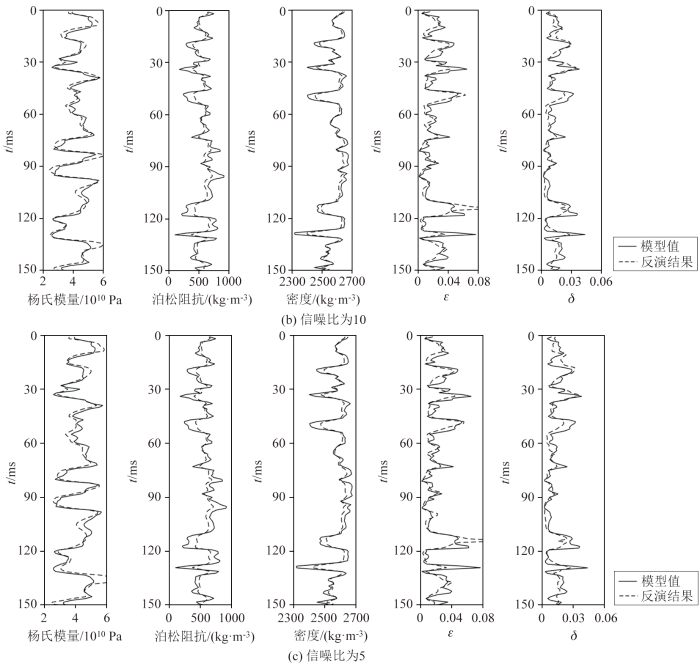
采用图4所示的合成地震记录作为观测数据输入,图5给出了合成地震记录不同信噪比下各岩石物理参数的叠前地震各向异性直接反演结果。从图5a看,无论是各向同性背景的参数还是各向异性参数,无噪声反演结果都能与真实模型有较高的吻合度;相比之下,图5b、c所示的含噪声反演结果与模型值的吻合度有所下降,但是仍然保持了较好的抗噪性和稳定性,能够较好描述参数的变化情况。

图5-1

新窗口打开| 下载原图ZIP| 生成PPT

图5-1 不同信噪比合成地震记录的叠前地震反演结果

Fig.5-1 The pre-stack seismic inversion results of the synthesized seismogram with different signal-to-noise ratios

图5-2

新窗口打开| 下载原图ZIP| 生成PPT

图5-2 不同信噪比合成地震记录的叠前地震反演结果

Fig.5-2 The pre-stack seismic inversion results of the synthesized seismogram with different signal-to-noise ratios

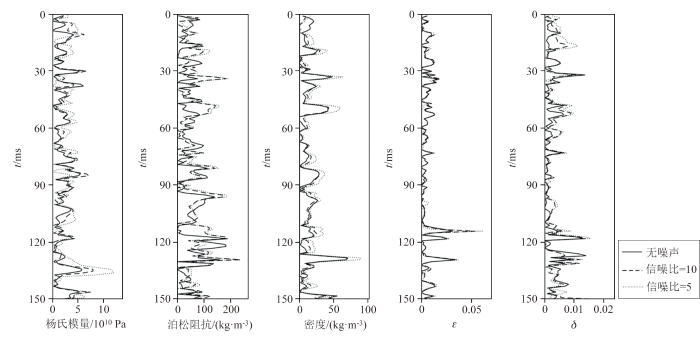
图6从定量、直观的角度展示了反演结果与真实模型值的误差绝对值对比情况。不难看出,无噪声的反演结果拥有较少的反演误差;随着合成地震记录信噪比的降低,反演结果的误差逐渐增大,但是仍然控制在较少的范围内,效果比较理想。模型测试结果在理论模型层面验证了所提方法的合理性与可行性,为该方法在实际工区的应用奠定了基础。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同参数的反演结果与真实模型的误差绝对值对比

Fig.6 Comparison of absolute error between inversion results and actual models with different parameters

3 实际资料测试

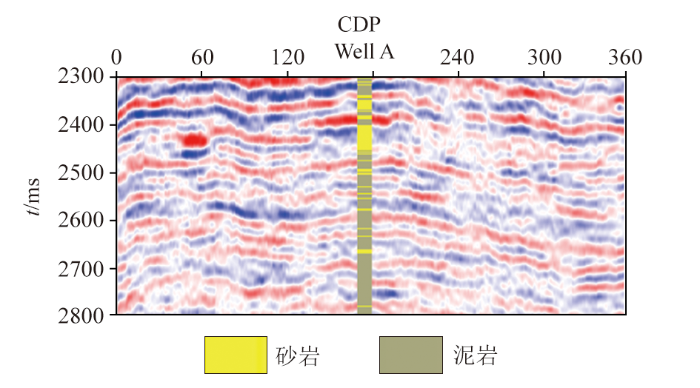
本文选用某砂泥岩沉积岩工区的过测井剖面对所提方法开展了实际资料测试。图7展示了所选择剖面的全叠加地震数据,其中的测井(Well A)位于CDP=175处,从测井记录中不难看到储层存在一定的砂、泥岩互层情况,这也导致了地震剖面由于衰减作用在整体上振幅随旅行时的增加而逐渐减弱。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 实际工区叠后过井地震剖面

Fig.7 Post stack well-cross seismic profile of actual working area

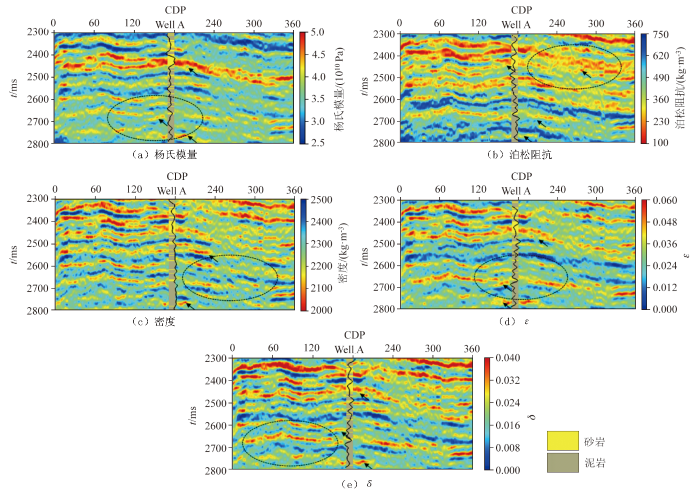
以图7中所示剖面的多个部分角度叠加数据作为观测数据输入,图8展示了实际地震资料的非平稳叠前各向异性直接反演的杨氏模量、泊松阻抗、密度以及ε和δ结果。可以看出,图中的各个参数都能够有效地描述地层性质的纵向变化以及横向展布,在测井位置处,反演结果也能够与测井曲线有较高的吻合度。特别是在测井解释中泥岩里夹杂砂岩的储层位置处,泊松阻抗的低值异常能够比较精确地对砂体的存在进行预测,尤其是在剖面的中下部位置,即使由于砂、泥岩互层的衰减作用使得地震振幅强度减弱,泊松阻抗的砂岩储层识别能力依旧能够保持较高的水准。考虑到地层各向异性参数(ε和δ)的绝对值将随着地层裂缝发育程度的增加而逐渐增大,通过图中裂缝参数反演的高值异常区域,能够对含有水平裂缝发育程度较高的地层进行有效的预测。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 实际资料非平稳叠前各向异性高分辨率直接反演结果

Fig.8 High resolution direct inversion results of non-stationary pre-stack anisotropy method in actual data

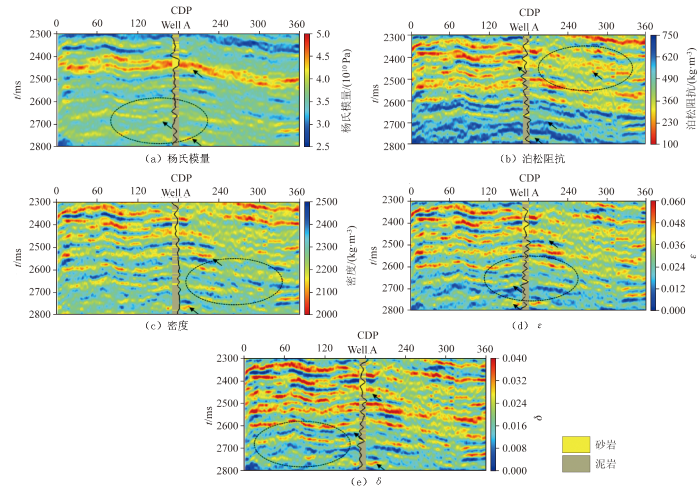
图9展示了以图7所示的以多个部分角度叠加数据为观测数据输入,基于常规平稳褶积模型的叠前地震各向异性直接反演的各参数结果。从结果来看,各个参数都能够与测井解释结果有较好的吻合度,但是相比于图8所示的采用本文所提方法的反演结果,其吻合度较低。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 实际资料常规叠前各向异性直接反演结果

Fig.9 Direct inversion results of conventional prestack anisotropy method in actual data

对比图8与图9中黑色箭头所指示的地层位置,本文所提方法在砂体的识别和刻画能力以及地层的裂缝发育程度描述方面,相比于常规反演方法具有明显的优势,分辨率更高。由于常规反演方法并未考虑到地震波传播的衰减作用,使得其对于薄层弱反射的保护能力较低,也导致了常规反演结果的砂岩储层识别和展布描述能力以及储层含裂缝表征能力相比于新方法有所下降,这一结果在图8、9中所圈位置处可得到有力证明。

实际资料的反演结果从应用层面验证了所提方法的适应性和有效性,通过不同方法之间的对比,进一步证实了本研究所提方法在复杂砂、泥岩储层进行泊松阻抗以及在裂缝参数的高分辨率反演预测中的优越性及可靠性。

4 结论

本文基于砂、泥岩互层工区的测井解释结果,通过岩石物理交会优选了用于区分砂、泥岩储层的敏感参数泊松阻抗,通过针对复杂区砂、泥岩沉积区储层的裂缝发育特征,推导了含泊松阻抗以及裂缝参数ε和δ的VTI介质反射系数方程,考虑砂、泥岩储层存在的强衰减特征,结合非平稳褶积模型,利用非平稳叠前各向异性地震直接反演方法对地层泊松阻抗和裂缝参数进行了估计。本文所提方法在常规平稳褶积模型反演方法的基础上,提高了复杂砂、泥岩工区泊松阻抗以及裂缝参数预测的分辨率,同时也为发育水平裂缝储层的含裂缝性评价提供了技术支持,各向异性参数的直接获取也能够为油气藏的勘探开发、储层含裂缝性的评价以及储层的产能评价提供指导作用。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

, Yang

, Wang

, et al.

Joint PP and PS AVA seismic inversion using exact Zoeppritz equations

[J]. Geophysics, 2015, 80(5):R239-R250.