基于L1-2范数约束的叠前多分量地震数据直接反演纵横波速度比方法

doi:10.11720/wtyht.2025.1365

基于L_1-2范数约束的叠前多分量地震数据直接反演纵横波速度比方法

韩磊^,¹, 李景叶¹, 耿伟恒², 王永平¹, 杨骐羽¹, 张宇宁¹

1.中国石油大学(北京) 地球物理学院,北京 102249

2.清华大学信息科学与技术学院,北京 100084

A method for calculating the P-to-S-wave velocity ratio through direct inversion of prestack multi-component seismic data based on the L_1-2 norm constraint

HAN Lei^,¹, LI Jing-Ye¹, GENG Wei-Heng², WANG Yong-Ping¹, YANG Qi-Yu¹, ZHANG Yu-Ning¹

1. College of Geophysics,China University of Petroleum(Beijing),Beijing 102249,China

2. School of Information Science and Technology,Tsinghua University,Beijing 100084,China

第一作者: 韩磊(1998-),男,中国石油大学(北京)博士在读,主要研究方向为地震反演。Email:hl981019@163.com

责任编辑: 叶佩

收稿日期: 2024-10-25 修回日期: 2025-02-13

基金资助:

中国石油天然气集团有限公司项目“物探应用基础实验和前沿理论方法研究”(2022DO0604-04)

Received: 2024-10-25 Revised: 2025-02-13

摘要

纵横波速度比是判别岩性、描述储层特征、识别气藏的重要工具。通过PP波地震数据直接反演纵波速度和横波速度的技术已经相对成熟,但分别反演纵横波速度后再求取其比值会产生累积误差。相比之下,PS波中包含横波速度信息,联合反演能够提高纵横波速度比的反演精度。本文引入了L_1-2范数以提高反演结果的分辨率。相较于L₁范数和L₂范数,L_1-2范数更稀疏,可以得到分辨率更高的反演结果。首先,通过推导线性化的PP波和PS波正演近似公式并分析其精度。然后,基于贝叶斯理论,引入L_1-2范数构建直接反演纵横波速度比的目标函数,通过求解该目标函数,获得纵横波速度比的反演结果。定量对比相关系数表明,基于L_1-2范数的反演结果优于L₁范数和L₂范数,直接反演结果优于间接反演结果,联合反演的结果优于单独反演的结果。合成数据和实际资料的反演验证了所提方法的有效性和可行性。

关键词： 纵横波速度比; L_1-2范数; 多波多分量地震数据; 直接反演

Abstract

The ratio of compressional to shear wave velocities(hereafter referred to as the P-to-S-wave velocity ratio) is an essential parameter for lithology discrimination,reservoir characterization,and gas reservoir identification.Direct inversion of PP-wave seismic data to derive the P- and S-wave velocities has been a well-established technique.However,calculating the P-to-S-wave velocity ratio using the P- and S-wave velocities obtained through individual inversion may lead to cumulative errors.In contrast,since PS-wave data inherently contain S-wave velocity information,the joint inversion of PS-wave data can significantly improve the accuracy of the P-to-S-wave velocity ratio.This study employed the L_1-2 norm to enhance the resolution of inversion results.Compared to the L₁ and L₂ norms,the L_1-2 norm yielded sparser solutions with higher resolution.First,this study derived and assessed the accuracy of linearized forward modeling approximate formulas for PP- and PS-waves.Second,based on Bayesian theory,this study incorporated the L_1-2 norm to construct an objective function for the direct inversion of the P-to-S-wave velocity ratio.Third,the objective function was solved to obtain the inversion result for the P-to-S-wave velocity ratio.The quantitative comparison of the correlation coefficients demonstrates that the inversion results based on the L_1-2 norm outperform those based on the L₁ or L₂ norm,direct inversion is superior to indirect inversion,and joint inversion provides better results than individual inversion.Finally, the effectiveness and feasibility of the proposed method in this study were validated through inversions of synthetic and field data.

Keywords： P-to-S-wave velocity ratio; L_1-2 norm; multi-wave multi-component seismic data; direct inversion

PDF (7321KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

韩磊, 李景叶, 耿伟恒, 王永平, 杨骐羽, 张宇宁. 基于L_1-2范数约束的叠前多分量地震数据直接反演纵横波速度比方法[J]. 物探与化探, 2025, 49(3): 620-630 doi:10.11720/wtyht.2025.1365

HAN Lei, LI Jing-Ye, GENG Wei-Heng, WANG Yong-Ping, YANG Qi-Yu, ZHANG Yu-Ning. A method for calculating the P-to-S-wave velocity ratio through direct inversion of prestack multi-component seismic data based on the L_1-2 norm constraint[J]. Geophysical and Geochemical Exploration, 2025, 49(3): 620-630 doi:10.11720/wtyht.2025.1365

0 引言

叠前多分量地震反演是地震勘探中一种重要的解释工具,多波多分量地震采集技术日趋完善,纵波与转换横波联合AVO/AVA反演已发展为储层表征和流体识别的基本技术。相较于PP波单独反演,PP与PS波联合反演能够获取更加精确的地下介质的纵横波速度信息。根据挪威海Tommeliten油田的勘探发现,当地下存在“气烟囱”构造时,纵波数据的成像结果较差,相比之下,PS波由于受流体情况影响较小,可以获得更加清晰的成像结果^[1]。由于P波与S波在地下介质中传播速度的差异,在地面接收到的PP波和PS波地震记录存在时差,需要进行匹配处理^[2],本文采用DTW(dynamic time warping,DTW)算法^[3]对地震数据进行匹配处理。匹配处理的方法是将转换波压缩到纵波时间域。压缩转换波会使得原本稳态的转换波数据变成非稳态。子波不再统一,而是随着时间和空间位置的变化而变化。这时,如果再对转换波提取一个统一的子波进行后续的联合反演,势必会影响到反演结果的精度。因此,在联合反演之前,必须要对转换波的波形进行校正。利用一个自适应时频域整形滤波器^[4]进行波形校正。

利用纵横波速度比能够有效的进行储层的表征以及岩性区分^[5]。该参数能够直接用于表示泊松比,泊松比是一个重要的流体因子,因为相较于S波,P波对流体更加敏感,纵横波速度比在储层含气性评价中起着重要的作用^[6]。含气砂岩随着含气饱和度升高,纵波速度和横波速度都降低,但是纵波速度比横波速度变化大,因此,纵横波速度比降低。近年来纵横波速度比反演技术发展迅速,Compton等 ^[7]利用DIW技术来估算纵横波速度比,但是该方法计算得到的纵横波速度比分辨率较低,无法准确地指示气藏。Zhi等^[8]提出了利用精确Zoeppritz方程的两步法PP-PS波联合反演方法,两步法计算会产生累计误差,降低纵横波速度比的反演精度。

Donoho^[9]、Zhang等^[10]、Yin等^[11]许多学者致力于研究从线性测量中恢复稀疏信号,稀疏重建是从欠定的线性系统中,通过施加合适的正则化项,利用反演方法来估计出稀疏解的过程。L₀范数是最稀疏的度量,理论上,向反演的目标函数中施加L₀范数约束项即可获得一个最稀疏的解。然而,L₀最小化问题是一个NP-Hard(nondeterministic polynomial-time hard,NP-Hard)问题,在实际应用中想要求解L₀范数是非常困难的。为此,学者们提出了各式各样的稀疏度量来近似L₀范数,例如L_p范数、L₁范数等。近几年,L_1-2范数^[12]被广泛地应用于稀疏重建,相比于L₁范数,它更加地近似L₀范数,并且也更易于求解。利用L_1-2范数进行约束,可以得到稀疏的反射系数反演结果^[13]。本文将L_1-2范数应用于纵横波速度比反演,合成数据和实际数据表明该方法在指示气藏以及储层表征方面的可行性和有效性。

1 PP与PS波联合反演纵横波速度比方法

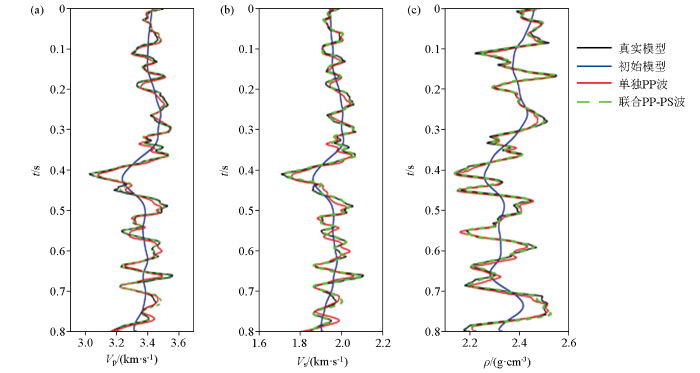
由于PS波地震数据相较于PP波包含更加丰富的地层信息,PP波与PS波进行联合反演可以更好地描述储层边界,提出储层预测精度(图1)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 单独PP波、联合PP-PS波直接反演纵波速度(a)、横波速度(b)、密度(c)

Fig.1 Direct inversion of P-wave velocity (a), S-wave velocity (b) and density (c) by PP and PP-PS wave

为了更加直观体现出联合反演的精度,通过计算相关系数来进行精度对比:

(1)C=

\frac{c (X, Y)}{\sqrt{c (X, X) \times c (Y, Y)}}

式中:c(X,X)、c(Y,Y)分别为序列X、Y的方差,c(X,Y)为序列X、Y的协方差。

联合反演的纵波速度、横波速度、密度相较于单独反演都得到了显著提高(表1)。

表1 不同数据类型反演结果的相关系数

Table 1 Correlation coefficients of inversion results of different data types m/s

数据类型	单独PP反演			联合PP+PS联合反演
反演参数	纵波速度	横波速度	密度	纵波速度	横波速度	密度
相关系数	0.8723	0.8259	0.9067	0.9423	0.8697	0.9619

新窗口打开| 下载CSV

20世纪80年代出版的《Quantitative seismology theory and methods》一书中提出了一种反射系数的近似方程^[14]:

(2)R_pp(θ)≈

\frac{1}{2} \frac{Δ V_{p}}{V_{p}}

(1+tan²θ)-4

\frac{V_{s}^{2}}{V_{p}^{2}} \frac{Δ V_{s}}{V_{s}}

sin²θ+

\frac{1}{2} \frac{Δ ρ}{ρ} (1 - 4 \frac{V_{s}^{2}}{V_{p}^{2}} s i n^{2} θ)

我们对该式进行重新表达:

(3)R_pp(θ)≈

\frac{1}{2} \frac{Δ V_{p}}{V_{p}}

(1+tan²θ)-4k

\frac{Δ V_{s}}{V_{s}}

sin²θ+

\frac{1}{2} \frac{Δ ρ}{ρ}

(1-4ksin²θ),

式中:k为背景参数,实际生产应用中选择井数据计算:

(4)k=(

V_{s 1}^{2}

V_{p 1}^{2}

V_{s 2}^{2}

V_{p 2}^{2}

)/2 。

通过数学推导,建立起纵横波速度积、纵横波速度比与上下界面纵横波速度的关系^[15]:

(5)

\frac{Δ V_{p}}{V_{p}}

\frac{1}{2} (\frac{Δ (V_{p} V_{s})}{V_{p} V_{s}} + \frac{Δ (\frac{V_{p}}{V_{s}})}{\frac{V_{p}}{V_{s}}})

(6)

\frac{Δ V_{s}}{V_{s}}

\frac{1}{2} (\frac{Δ (V_{p} V_{s})}{V_{p} V_{s}} - \frac{Δ (\frac{V_{p}}{V_{s}})}{\frac{V_{p}}{V_{s}}})

式中:

(7)Δ(V_pV_s)/V_pV_s=2(V_p2V_s2-V_p1V_s1)/(V_p2V_s2+V_p1V_s1),

(8)

Δ (\frac{V_{p}}{V_{s}}) / \frac{V_{p}}{V_{s}}

2 (\frac{V_{p 2}}{V_{s 2}} - \frac{V_{p 1}}{V_{s 1}}) / (\frac{V_{p 2}}{V_{s 2}} + \frac{V_{p 1}}{V_{s 1}})

将式(4)、(5)代入式(2)中得到式(8),建立起反射系数与纵横波速度比之间的联系:

(9)R_pp(θ)≈

(\frac{1}{4} + \frac{1}{4} t a n^{2} θ + 2 k s i n^{2} θ) (\frac{Δ (\frac{V_{p}}{V_{s}})}{\frac{V_{p}}{V_{s}}})

(\frac{1}{4} + \frac{1}{4} t a n^{2} θ - 2 k s i n^{2} θ) (\frac{Δ (V_{p} V_{s})}{V_{p} V_{s}})

(\frac{1}{2} - 2 k s i n^{2} θ) \frac{Δ ρ}{ρ}

。

相较于传统的PP波,PS波对于横波速度更加敏感,采用纵横波联合反演能够有效地提高弹性参数的预测精度,提高气藏边界刻画能力。

Wang等^[16]采用与Ramos等^[17]相似的方法推导了一种新的P-SV波的反射系数近似表达式,该表达式在一定程度上克服了对大入射角适应性差的缺点,而且在工程应用中实际采集到的PS波入射角通常大于30°。Wang的近似式可以表示为:

(10)R_ps(θ)≈Asinθ+Bsin³(θ)+C₂sin⁵(θ),

(11)$\begin{array}{l}\left\{\begin{array}{l}A=\left[-2 \frac{V_{\mathrm{s}}}{V_{\mathrm{p}}} \frac{\Delta V_{\mathrm{s}}}{V_{\mathrm{s}}}\right]-\left[\left(\frac{1}{2}+\frac{V_{\mathrm{s}}}{V_{\mathrm{p}}}\right) \frac{\Delta \rho}{\rho}\right] \\B=\left[\left(2\left(\frac{V_{\mathrm{s}}}{V_{\mathrm{p}}}\right)^{2}+\left(\frac{V_{\mathrm{s}}}{V_{\mathrm{p}}}\right)\right) \frac{\Delta V_{\mathrm{s}}}{V_{\mathrm{s}}}\right]+\left[\left(\frac{3}{4}\left(\frac{V_{\mathrm{s}}}{V_{\mathrm{p}}}\right)^{2}+\right.\right.\end{array}\right. \\\left\{\begin{array}{l}\left.\left.\left(\frac{V_{\mathrm{s}}}{2 V_{\mathrm{p}}}\right)\right) \frac{\Delta \rho}{\rho}\right] \\C_{2}=\left(\frac{V_{\mathrm{s}}}{V_{\mathrm{p}}}\right)^{2} \frac{\Delta V_{\mathrm{s}}}{V_{\mathrm{s}}}+\frac{5}{16}\left(\frac{V_{\mathrm{s}}}{V_{\mathrm{p}}}\right)^{4} \frac{\Delta \rho}{\rho}+\frac{1}{8} \frac{V_{\mathrm{s}}}{V_{\mathrm{p}}} \frac{\Delta \rho}{\rho}+ \\\frac{1}{8} \frac{V_{\mathrm{s}}}{V_{\mathrm{p}}} \frac{\Delta V_{\mathrm{s}}}{V_{\mathrm{s}}}\end{array}\right.\end{array}$

同样将式(4)、(5)代入式(11)中得到式(12):

(12)R_ps(θ)≈

[- 2 \frac{V_{s}}{V_{p}} \frac{Δ V_{s}}{V_{s}}]

[(\frac{1}{2} + \frac{V_{s}}{V_{p}}) \frac{Δ ρ}{ρ}]

sinθ+

[(2 {(\frac{V_{s}}{V_{p}})}^{2} + (\frac{V_{s}}{V_{p}})) \frac{Δ V_{s}}{V_{s}}]

[(\frac{3}{4} {(\frac{V_{s}}{V_{p}})}^{2} + (\frac{V_{s}}{2 V_{p}})) \frac{Δ ρ}{ρ}]

sin³(θ)

(13)R_ps(θ)=

\frac{1}{2} (- 2 k^{- \frac{1}{2}} s i n θ + 2 k s i n^{3} θ + k^{- \frac{1}{2}} s i n^{3} θ + k s i n^{5} θ + \frac{1}{8} k^{- \frac{1}{2}} s i n^{5} θ) \frac{Δ (V_{p} V_{s})}{V_{p} V_{s}}

\frac{1}{2} (- 2 k^{- \frac{1}{2}} s i n θ + 2 k s i n^{3} θ + k^{- \frac{1}{2}} s i n^{3} θ + k s i n^{5} θ + \frac{1}{8} k^{- \frac{1}{2}} s i n^{5} θ) \frac{Δ (\frac{V_{p}}{V_{s}})}{\frac{V_{p}}{V_{s}}}

(- \frac{1}{2} s i n θ - k^{- \frac{1}{2}} s i n θ + \frac{3}{4} k s i n^{3} θ + \frac{1}{2} k^{- \frac{1}{2}} s i n^{3} θ + \frac{5}{16} k s i n^{5} θ + \frac{1}{8} k^{- \frac{1}{2}} s i n^{5} θ) \frac{Δ ρ}{ρ}

。

由此我们成功构建了用纵横波速度比来表示的PP波反射系数方程以及PS波反射系数方程。正演模型的正确与否将会直接影响反演结果的精度,接下来进行正演模拟分析对比,来检验我们新推导的反射系数方程与精确的Zoeppritz方程之间的误差。

建立了3种典型的AVO模型,来验证新构建的PP与PS波反射系数方程的正确性(表2~4)。

表2 第一类典型AVO模型

Table 2 The first type of typical AVO model

地层	V_p/(m·s^-1)	V_s/(m·s^-1)	ρ/(g·cm^-3)
页岩	2540	1250	2.30
含气砂岩	2980	1525	2.42

新窗口打开| 下载CSV

表3 第二类典型AVO模型

Table 3 The second type of typical AVO model

地层	V_p/(m·s^-1)	V_s/(m·s^-1)	ρ/(g·cm^-3)
页岩	2776	1780	2.35
含气砂岩	2700	1740	2.34

新窗口打开| 下载CSV

表4 第三类典型AVO模型

Table 4 The third type of typical AVO model

地层	V_p/(m·s^-1)	V_s/(m·s^-1)	ρ/(g·cm^-3)
页岩	3000	1280	2.30
含气砂岩	2450	1265	2.12

新窗口打开| 下载CSV

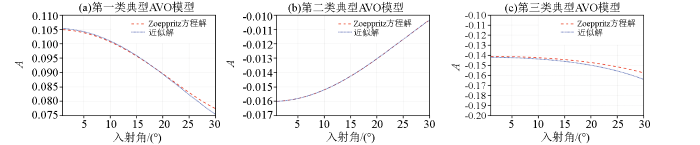
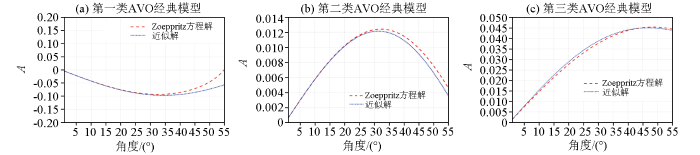
通过3种经典的AVO模型的验证,新构建的PP波、PS波反射系数表达式与精确Zoeppritz方程计算得到的反射系数拟合度较高,在一定程度上克服了大角度入射情况下PS波反射系数计算误差较大的缺点。说明本文所构建的反射系数方程的可行性,为直接反演纵横波速度比做好正演算子的准备。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 3种典型AVO模型的PP波反射系数对比

Fig.2 Comparison of PP wave reflection coefficients of three typical AVO models

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 3种典型AVO模型的PS波反射系数对比

Fig.3 Comparison of PS wave reflection coefficients of three typical AVO models

图4

新窗口打开| 下载原图ZIP| 生成PPT

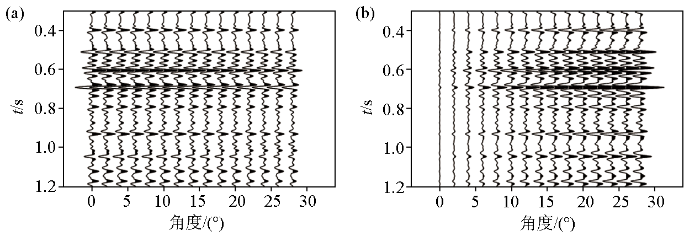
图4 无噪正演合成的PP波(a)和PS波(b)地震记录

Fig.4 Noise-free forward-modeled PP-wave(a) and PS-wave(b) seismic records

2 构造添加L_1-2范数约束的目标函数

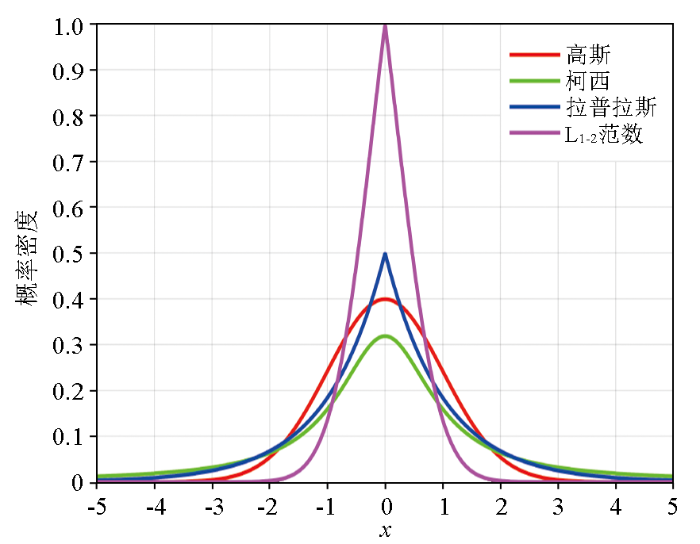
基于高斯先验分布的反演结果一般比较光滑,为此前人利用其他分布来提高反演结果的分辨率,如柯西分布^[18]、拉普拉斯分布^[19]。图5为不同分布的一维概率密度函数对比,由图可见:①高斯分布的峰值最宽,且没有“长尾”分布(“长尾”保证了反演结果中允许存在某些“大”值,即保证“稀疏”),所以基于高斯分布的反演结果较光滑且抗噪性差。②柯西分布和拉普拉斯分布在提升反演结果稀疏度方面明显优于高斯分布,二者的概率密度函数的峰值更尖锐且有明显的“长尾”现象。③L_1-2范数的概率密度函数的峰值更尖锐,且“长尾”现象更明显,因此在理论上可以获得更稀疏的反演结果。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同分布的一维概率密度函数对比

Fig.5 Comparison of one-dimensional probability density functions with different distributions

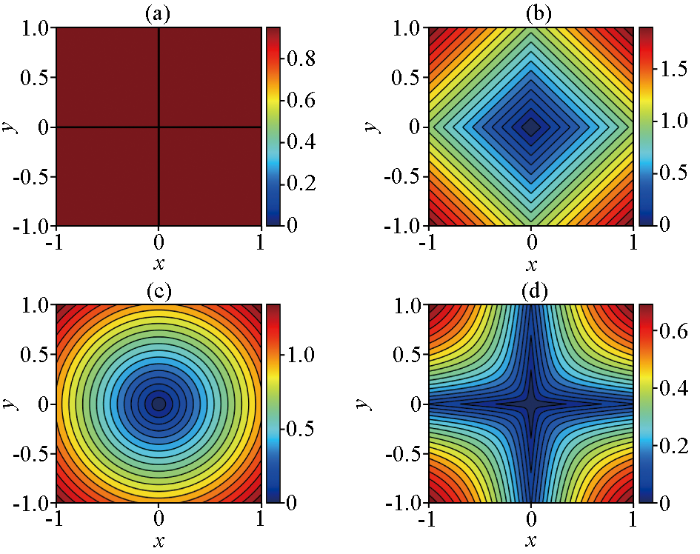
为了更直观地对比几种不同范数的分布特征,绘制了L₀范数、L₁范数(对应拉普拉斯分布)、L₂范数(对应高斯分布)以及L_1-2范数的二维图像(图6)。可见,相比于L₂范数和L₁范数,L_1-2范数与L₀范数更相似,因此,理论上基于L_1-2范数约束可以获得比L₂范数和L₁范数约束更稀疏、分辨率更高的反演结果。

(14)

\{\begin{array}{l} L_{0} = \{\begin{array}{l} 0 & (x, y) = 0 \\ 2 & x \neq 0, y \neq 0 \\ 1 & e l s e \end{array}\} \\ L_{2} = \sqrt{|x |^{2} + |y |^{2}} \\ L_{1} = |x| + |y| \\ L_{1 - 2} = |x| + |y| - \sqrt{|x |^{2} + |y |^{2}} \end{array}

式中:x、y为二维向量的分量。L₀范数定义为计算模型中非零项的个数,也被认为是最稀疏的度量。因此可通过对比其他范数图像与L₀范数图像的相似程度来判断范数的稀疏性。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 L₀范数(a)、L₁范数(b)、L₂范数(c)、L_1-2范数(d)的二维图像

Fig.6 Two-dimensional images of L₀ norm (a), L₁ norm (b), L₂ norm (c), and L_1-2 norm (d)

通过对正演算子正确性的验证以及正则化约束能够提高分辨率的理论进行的阐述,接下来进行目标函数的构建,由于L₂范数本质是一种高斯分布,根据贝叶斯框架构建L₂范数约束的反演纵横波速度比的目标函数^[20]:

(15)J(m)=‖d_pp-G_ppm‖²+α‖d_ps-G_psm‖²+β(m-μ)

C_{m}^{- 1}

(m-μ)

式中:d_pp表示PP波地震记录;d_ps表示PS波地震记录;G_pp示PP波的正演算子;G_ps表示PS波的正演算子;m表示待反演参数;C_m是模型参数的协方差矩阵与单位阵的Kronecker内积。

在反演过程中,通常需要多次试验反演结果与真实值的相关系数来获得合适的参数及迭代次数,以保证最终获得较满意的反演结果。

由于L₁范数与L_1-2范数不易求导,采用ADMM算法进行求解:

(16)J(m)=‖d_pp-G_ppm‖²+α‖d_ps-G_psm‖²+β‖m‖₁,

(17)J(m)=‖d_pp-G_ppm‖²+α‖d_ps-G_psm‖²+λ(‖m‖₁-β‖m‖₂),

具体求解过程见附录。

3 模型测试

利用单道模型,分别对比、分析基于L₂范数、L₁范数以及L_1-2范数约束的PP波反演结果和基于L₂范数、L₁范数以及L_1-2范数约束的联合PP-PS波的反演结果,以验证所提方法的效果。图7为无噪地震数据的反演结果,可以观察到,由于没有噪声的干扰均可得到较为准确的反演结果,其中L_1-2范数约束的联合反演的相关系数最高,达到0.999 68。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 无噪数据反演结果

a—PP单独反演;b—PP+PS联合反演

Fig.7 Noise-free data inversion results

a—PP only inversion;b—PP+PS joint inversion

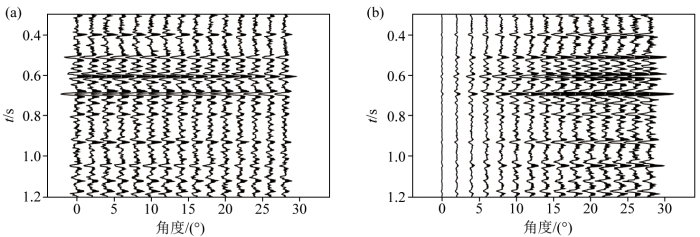
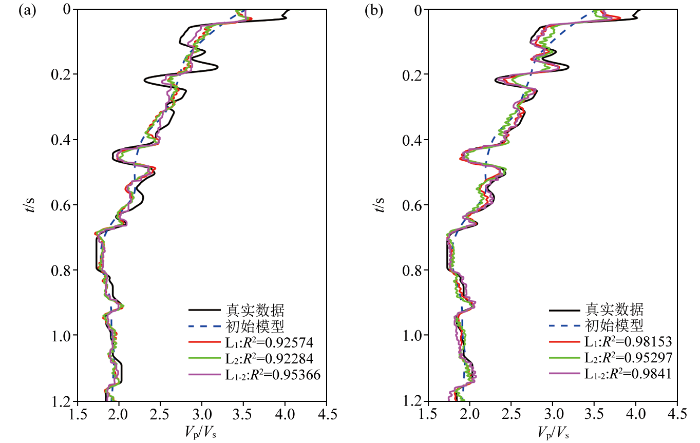
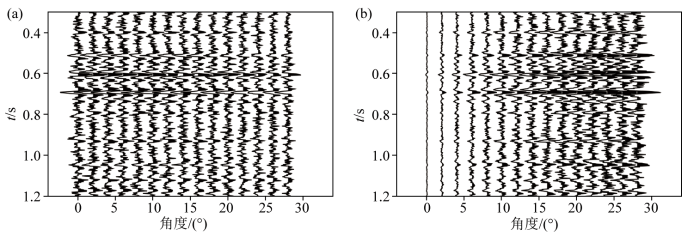
为了验证该方法的抗噪性,通过正演分别得到信噪比SNR=4和SNR=10的地震数据,如图8~10所示。当地震记录的SNR=10时,纵横波速度比的反演结果如图9所示,使用L_1-2范数约束的联合反演方法得到的纵横波速度比与真实结果的相关系数最高,在表5可以对比观察达到0.984 1,图9中0.4~0.6 s、0.2 s所示,该方法在边界刻画能力方面更加准确。由于联合反演添加了PS波地震记录,将地层中的横波信息得到充分应用,提高了纵横波速度比的反演精度。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 SNR=10正演合成地震记录

a—PP波地震记录;b—PS波地震记录

Fig.8 Forward modeling synthetic seismic record with SNR=10

a—PP wave seismic record;b—PS wave seismic record

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 SNR=10数据反演结果

a—PP单独反演;b—PP+PS联合反演

Fig.9 SNR=10 data inversion results

a—PP only inversion;b—PP+PS joint inversion

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 SNR=4正演合成地震记录

a—PP波地震记录;b—PS波地震记录

Fig.10 Forward modeling synthetic seismic record with SNR=4

a—PP wave seismic record;b—PS wave seismic record

表5 反演结果相关系数对比

Table 5 Comparison of correlation coefficients of inversion results

	联合PP+PS直接反演			单独PP直接反演			联合PP+PS间接反演
	L₁	L₂	L_1-2	L₁	L₂	L_1-2	L₁	L₂	L_1-2
SNR=4	0.9326	0.9300	0.9592	0.9123	0.9050	0.9454	0.9073	0.9017	0.9342
SNR=10	0.9815	0.9529	0.9841	0.9257	0.9228	0.9536	0.9219	0.9162	0.9425

新窗口打开| 下载CSV

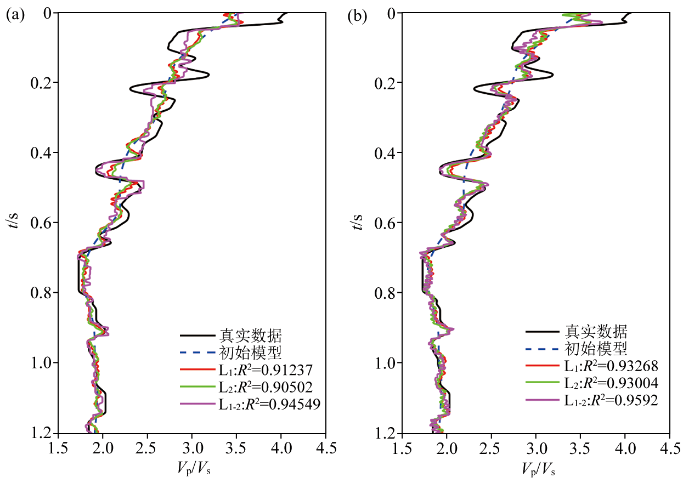
随着噪声的增强,相较于地震记录的SNR=10,SNR=4的反演结果的精度都会降低(图11),主要是由于线性反演易受到噪声的影响导致的。通过添加PS波地震信息,反演结果的精度和稳定性都得到改善。L_1-2范数约束由于更好地压制了“小值”,同时也保护了大值,纵横波速度比的反演结果在噪声较强的条件下,仍能够提高反演结果的分辨率。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 SNR=4数据反演结果

a—PP单独反演;b—PP+PS联合反演

Fig.11 SNR=4 data inversion results

a—PP only inversion;b—PP+PS joint inversion

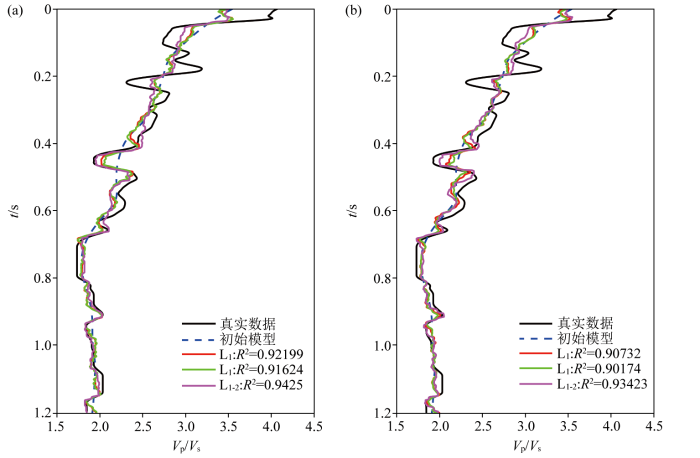
相较于本文所提出的利用叠前多分量地震资料直接反演纵横波速度比,常规方法仅利用PP波地震数据单独反演纵波速度、横波速度,间接计算得到的纵横波速度比精度较低。如图12所示,为常规的间接反演得到的纵横波速度比。SNR=10时,常规联合反演结果与真实结果的相关系数为0.942 5,低于本文提出直接反演结果与真实结果的相关系数0.984 1。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 SNR=10(a)和SNR=4(b)数据PP单独反演结果

Fig.12 PP only inversion results with SNR=10(a) and SNR=4(b) data

合成数据的反演结果表明本文提出的基于L_1-2范数约束的叠前多分量地震数据直接反演纵横波速度比,反演结果的精度和抗噪性都得改善,证明了该方法的可行性。

4 实际数据应用

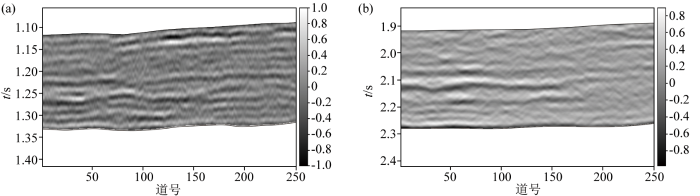
为了进一步验证该方法的有效性,利用S区实际地震资料测试本文方法。该工区目的层的岩性以致密砂岩为主,主要油藏类型为致密砂岩气。利用纵横波速度比能够较好地指示“甜点”。由于该工区河道砂岩具有期次多、砂体叠置的地质特征,传统的纵波勘探难以精细刻画砂体及其叠置关系。因此在研究区开展了多分量地震采集探索。多分量地震资料采用炸药震源激发、DSU3数字三分量检波器接收。在纵波剖面上反射特征不明显;在转换波剖面上反射特征能够清晰地识别。纵波数据对砂体变化不敏感,地震波形难以反映砂体的叠置关系。转换波虽然主频低于纵波,但对岩性变化敏感,地震波形与砂体变化有很好的对应关系。图13为该地区的叠后地震剖面。通过DTW算法对地震数据进行匹配处理,对匹配处理后的地震数据利用自适应滤波器进行整形滤波,为纵横波速度比做好数据准备。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 PP波(a)和PS波(b)部分叠加地震剖面

Fig.13 Part-stack seismic profile of PP waves(a) and PS waves(b)

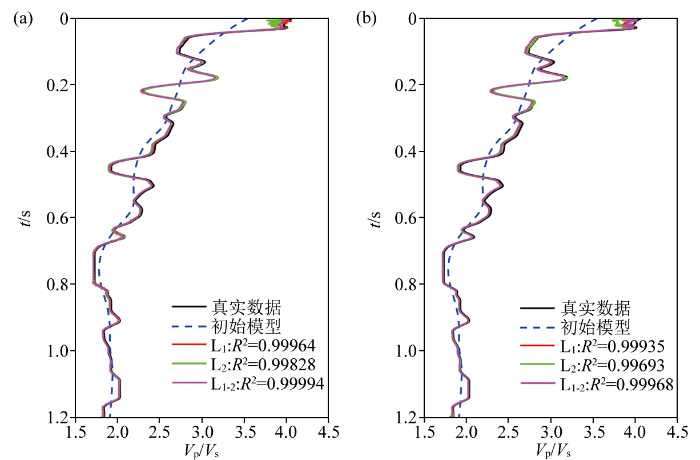
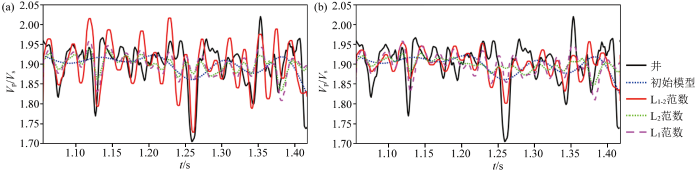
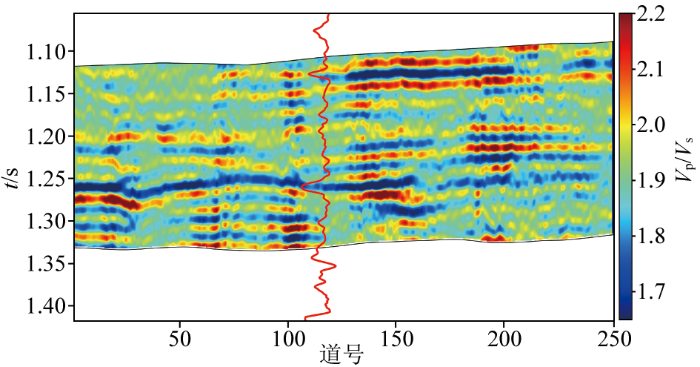
通过井旁道的反演结果与测井数据的分析对比(图14~16),L_1-2范数约束的联合反演结果与测井数据的相关系数最高,达到0.653 5,在1.25 s左右纵横波速度比明显降低,实际生产也证明该段为主要的产气层,进一步从地质解释上证明了本文所提出的反演方法的有效性。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 井旁道PP波单独反演结果(a)和井旁道PP波、PS波联合反演结果(b)

Fig.14 Comparison between offset well log inversion results inversion results of PP waves alone(a) joint inversion results of PP-PS waves(b)

图15

新窗口打开| 下载原图ZIP| 生成PPT

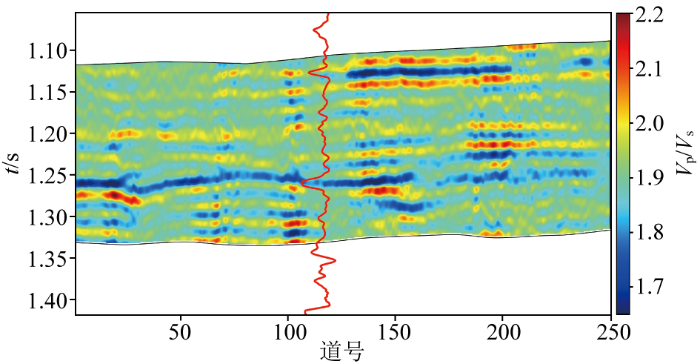
图15 L_1-2范数约束的叠前单独PP波地震数据直接反演纵横波速度比

Fig.15 Direct inversion of P-to-S wave velocity ratio using L_1-2 norm constraint for single PP waves seismic data

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 L_1-2范数约束的叠前联合PP波、PS波地震数据直接反演纵横波速度比

Fig.16 Direct inversion of P-to-S wave velocity ratio using L_1-2 norm constraint for joint PP waves and PS waves seismic data

表6 反演结果相关系数对比

Table 6 Comparison of correlation coefficients of inversion results

数据类型	单独PP反演			联合PP+PS联合反演
约束方法	L₁范数	L₂范数	L_1-2范数	L₁范数	L₂范数	L_1-2范数
相关系数	0.3133	0.3019	0.5350	0.4514	0.4359	0.6535

新窗口打开| 下载CSV

5 结论及讨论

本文提出了一种利用叠前多分量地震数据直接反演纵横波速度比,并添加L_1-2范数约束的技术,通过合成数据和实际数据验证了该方法的可行性和有效性。利用该方法直接反演得到的纵横波速度比分辨率高,提高了气藏识别的精度,并且该方法具有一定的抗噪性。然而,该方法仍存在一些缺点,由于PP波与PS波具有走时的差异,本文所采用的正演模拟方法并没有考虑波的走时信息,因此需要匹配处理,这个过程会存在一定的误差,进而影响纵横波速度比的反演结果。

附录:

1 L₂范数约束的目标函数求解

J(m)= ${‖d - G m‖}^{2}$ +β(m-μ) $C_{m}^{- 1}$ (m-μ)

γ= $\frac{\partial J (m)}{\partial m}$ =G^Td+βQm,Q=kron(invCMR,eye(n_t)),n_t为采样点数,invCMR为由纵横波速度比、纵横波速度积、密度组成的协方差矩阵的逆。

Hessian≈ ${(\frac{\partial J (m)}{\partial m})}^{T} (\frac{\partial J (m)}{\partial m})$ +βQ,

则Δm=Hessian/γ,m^k⁺¹=m^k+λΔm 。

2 L₁范数约束的目标函数求解(ADMM算法)

J(m)= ${‖d - G m‖}^{2}$ +β ${‖m‖}_{1}$

重新表述目标函数: $\underset{m}{m i n} {‖d - G m‖}^{2}$ +β ${‖m‖}_{1}$ , s.t. z=m

增广拉格朗日函数为:L(m,z,u)= ${‖d - G m‖}^{2}$ +β ${‖m‖}_{1}$ + $\frac{ρ}{2} {‖z - m + u‖}_{2}^{2}$ 。

1)更新m: m^k⁺¹= $(G^{T} {G + ρ I)}^{- 1}$ [G^Td+ρ(z^k+u^k)];

2)更新z: z^k⁺¹=soft $(m^{k + 1} + u^{k}, \frac{β}{ρ})$ ;

3)更新拉格朗日算子u: u^k⁺¹=u^k+z^k⁺¹-m^k⁺¹。

3 L_1-2范数约束的目标函数求解

J(m)= ${‖d - G m‖}^{2}$ +λ( ${‖m‖}_{1}$ -α ${‖m‖}_{2}$ )

重新表述目标函数: $\underset{m}{m i n} {‖d - G m‖}^{2}$ +λ ${‖z‖}_{1}$ + $({‖z‖}_{1} - α {‖m‖}_{2})$ ,s.t. z=m。

L(m,z,u)= ${‖d - G m‖}^{2}$ +λ ${‖z‖}_{1}$ -λα ${‖m‖}_{2}$ + $\frac{η}{2} ‖z - m + u‖$ ,其中η>0为惩罚参数。

1)初始化,设置初始值m₀、z₀、u₀,设置超参数η、λ、α以及最大迭代次数;

2)迭代循环,更新m: m^k⁺¹= ${(G^{T} G + ρ I)}^{- 1} (G^{T} d + η (z^{k} - u^{k}) - λ α \frac{m^{k}}{{‖m^{k}‖}_{2}})$ ,

更新z: z^k⁺¹=soft $(m^{k + 1} + u^{k}, \frac{λ}{η})$ ,

更新u: u^k⁺¹=u^k+m^k⁺¹-z^k⁺¹;

3)收敛检查: $‖m^{k + 1} - z^{k + 1}‖$ <tol,停止迭代;

4)输出结果:返回m^k⁺¹作为最优解。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Granli

J R

, Arntsen

, Sollid

, et al.

Imaging through gas-filled sediments using marine shear-wave data

[J]. Geophysics, 1999, 64(3):668-677.