基于BP神经网络的时域激电谱Cole-Cole模型参数反演及应用

doi:10.11720/wtyht.2025.1422

基于BP神经网络的时域激电谱Cole-Cole模型参数反演及应用

杨海明^,¹, 姚卫星^,¹, 唐塑¹, 潘展超¹^,², 关力伟¹^,²

1.中国地质调查局乌鲁木齐自然资源综合调查中心,新疆乌鲁木齐 830057

2.中亚造山带成矿预测与找矿示范创新基地,新疆乌鲁木齐 830057

Parameter inversion and application of the Cole-Cole model for time-domain induced polarization spectra based on the backpropagation neural network

YANG Hai-Ming^,¹, YAO Wei-Xing^,¹, TANG Su¹, PAN Zhan-Chao¹^,², GUAN Li-Wei¹^,²

1. China Geological Survey Urumqi Comprehensive Survey Center on Natural Resources, Urumqi 830057, China

2. Innovation Base of Metallogenic Prediction and Prospecting in Central Asia Orogenic Belt, Urumqi 830057, China

通讯作者: 姚卫星(1986-),男,高级工程师,主要从事金属矿山物探方法研究工作。Email:wtyaoweixing@163.com

第一作者: 杨海明(1991-),男,工程师,硕士,主要从事电法勘探正反演研究工作。Email:yanghaiming009@163.com

责任编辑: 朱晓颖

收稿日期: 2024-10-21 修回日期: 2025-01-2

基金资助:

中国地质调查局矿产资源评价项目“新疆阿勒泰清水泉—昌吉双泉金矿重点调查区调查评价”(DD20230380)

Received: 2024-10-21 Revised: 2025-01-2

摘要

Cole-Cole模型的频谱参数可以提升时间域激电数据综合解释的分辨率,对于寻找金属矿有一定的潜力。利用BP神经网络模型预测反演频谱参数,不仅能够避免复杂的计算量提升反演速度,还可以充分挖掘时间域激电数据的使用效率来丰富地下矿体特征信息。基于此,本文利用数字滤波算法获得时间域视极化率衰减曲线表达式,以此表达式为正反演模型,对比探究训练集样本数、输入神经元个数、隐含层节点数和隐含层层数4种因素对BP神经网络模型训练及反演效果的影响,并筛选出最合适模型;进一步采用8个时间窗口的时间域激电数据,将训练好的BP神经网络模型应用在野外实测的时间域激电数据进行预测反演。研究结果表明,BP神经网络模型在理论数据集和实测数据集反演频谱参数均是可行的,反演效果具有精度高、误差小的特征,对于区分共生、伴生矿,减少误判有所帮助,具有一定的研究意义。

关键词： Cole-Cole模型; 时间域激电; BP神经网络; 反演

Abstract

The spectral parameters of the Cole-Cole model can improve the resolution of comprehensive interpretation of time-domain induced polarization (IP) data, contributing somewhat to the exploration of metal deposits. Applying the backpropagation neural network (BPNN) model to the prediction and inversion of spectral parameters can avoid high computational complexity to improve the inversion speed. Moreover, the BPNN model can fully explore the utilization efficiency of time-domain IP data to enrich the characteristic information of subsurface ore bodies. Based on this, this study derived the mathematical expression of the time-domain apparent polarizability attenuation curve using the digital filtering algorithm. With the mathematical expression as the forward/inverse model, this study comparatively analyzed the impacts of four factors-the sample size of the training set, the number of neurons in the input layer, the node number of hidden layers, and the number of hidden layers-on the training and inversion effects of the BPNN model, determining the optimal model. Furthermore, this study trained the BPNN model using time-domain IP data from eight time windows. Finally, this study applied the trained BPNN model for prediction and inversion based on the measured time-domain IP data. The results indicate that the BPNN model is feasible in inverting spectral parameters based on both theoretical and measured datasets, manifesting high inversion accuracy and minor errors. Overall, the results of this study can assist in distinguishing paragenetic and associated minerals and reducing misinterpretation.

Keywords： Cole-Cole model; time-domain induced polarization; backpropagation neural network; inversion

PDF (3859KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨海明, 姚卫星, 唐塑, 潘展超, 关力伟. 基于BP神经网络的时域激电谱Cole-Cole模型参数反演及应用[J]. 物探与化探, 2025, 49(2): 433-440 doi:10.11720/wtyht.2025.1422

YANG Hai-Ming, YAO Wei-Xing, TANG Su, PAN Zhan-Chao, GUAN Li-Wei. Parameter inversion and application of the Cole-Cole model for time-domain induced polarization spectra based on the backpropagation neural network[J]. Geophysical and Geochemical Exploration, 2025, 49(2): 433-440 doi:10.11720/wtyht.2025.1422

0 引言

Cole-Cole模型可以近似描述激电效应,其模型中的多个频谱参数在地球物理勘探中均有明确的意义。Grissemann等^[1]发现充电率m能够反映可极化物质的含量,时间常数τ与可极化颗粒和孔隙大小有密切关系,频率相关系数c则表征极化体颗粒均匀性。以往频谱参数大多从频谱激电(或复电阻率)获取^{[2⇓⇓⇓⇓-7]}。然而频谱激电存在野外探测效率低、受电磁耦合影响较大等缺陷,应用不如时间域激电广泛。时间域激电法目前仅能直接利用到视极化率和视电阻率两个电性参数,观测数据得不到充分挖掘,使得激电异常解释往往存在分辨率不高、异常误判漏判的问题。近年来,从时间域激电观测数据获取频谱参数引起了许多学者的关注。Mark等^[8]采用马奎特法反演得到频谱参数并实现了1D和2D 频谱参数成像。罗润林等^[9]采用最小二乘法从时域激电数据中得出频谱参数信息,并应用于实践。彭伟等^[10]利用阻尼最小二乘法实现时间响应与Cole-Cole模型的最佳拟合,实现对激电异常的正确推断解释,提高了时间域激电在深部找矿的应用。李密^[11]和岑海波^[12]利用BP神经网络反演频谱参数,并应用到野外测量得到地质体更综合的电性信息。以上两位学者主要是利用4个时间窗口的观测数据进行训练,预测反演 Cole-Cole 模型频谱参数的准确性可能不够高。本文在前人的研究基础上,进一步利用全波形采样的激电仪获得任意时间段的视极化率这一优势,增加输入神经元个数至8个,对比发现,增加输入神经元个数后,3个隐含层BP(Back-Propagation)神经网络结构模型预测的频谱参数和原来正演模型输出的频谱参数总均方误差函数的值从0.05降至0.01,由此可见预测反演的精确度有所提升。

人工神经网络是一种非线性反演方法,具有高度自学习和自适应能力,泛化能力强,被广泛应用在地球物理领域。李健等^[13]利用深度卷积神经网络方法来解决震相拾取问题,构建了多任务卷积神经网络模型。杨凯等^[14]将人工神经网络应用于大地电磁时间序列分类中,实现对噪声高效率的识别和分类。赵军等^[15] 利用前馈神经网络融合属性预测断裂,综合不同尺度特征的断裂信息,有效提升了预测准确度和可靠性。

本文利用数字滤波算法^[16],联合复电阻率公式得出时域激电二次场的衰减电位,计算出各观测时窗的视极化率的表达式,该方法绘制出的时谱曲线平滑、完整、无突变情况,预测反演过程能够避免出现收敛性不好、误差较大等问题,降低了计算难度。基于Matlab软件平台,编写了Cole-Cole频谱参数训练集正演和BP神经网络反演程序,对比探究训练集样本数、输入神经元个数、隐含层节点数和隐含层层数4种因素对频谱参数训练结果的影响,筛选出最适BP神经网络。用500组随机样本进行测试,结果验证了BP神经网络学习对于理论上反演预测频谱参数是可行、有效的。最后将训练好的BP神经网络应用于野外实测数据反演频谱参数,开展多种电性参数解释。

1 理论基础

当通过岩、矿石的供电电流密度不大时, 岩、矿石的激电效应具有线性规律, 并且在时间范围内可以用不变的参数来描述,是一个线性不变系统^[17]。Pelton在柯尔兄弟的电介质极化特性的数学模型基础上,提出介质激电效应复阻抗的经验公式来描述复电阻率频谱的性质, 将等效电路模型称之为Cole-Cole模型:

(1)

Z (ω) = Z (0) [1 - m (1 - \frac{1}{1 + {(j ω τ)}^{c}})]

。

根据上式可得到在频率域中的复电阻率Cole-Cole表达式:

(2)

ρ (ω) = ρ_{0} [1 - m (1 - \frac{1}{1 + {(j ω τ)}^{c}})]

。

式(2)经傅里叶逆变换后,得到时间域响应^[18]:

(3)

V (t) = m R_{0} I_{0} \overset{\infty}{\sum_{n = 0}} \frac{{(- 1)}^{n} {(t / τ)}^{n c}}{Γ (n c + 1)}

。

式中:ω是角频率;Z(0)是频率为0时的阻抗;ρ₀是频率为0时的电阻率;V(t)是二次场电位差;I₀是一次场电流;R₀是零频电阻;Γ是伽马函数;m是充电率;τ是时间常数;c是频率相关系数;t是响应时间;n是实测衰减曲线上取样点总数。

根据李金铭^[19]对时间域激电视极化率定义:

(4)

η_{i} = \frac{1}{t_{i} - t_{i - 1}} \int_{t_{i - 1}}^{t_{i}} V (t) d t / V_{0} 。

(5)再结合Guptasarma提出的数字滤波算法,整理可得视极化率衰减曲线公式:

\begin{array}{l} \{\begin{array}{l} η (t) = \overset{21}{\sum_{i = 1}} Φ_{i} m [x_{i} (t + T_{P}) - x_{i} (t)] \\ x_{i} = \frac{1 + (ω_{i} {τ)}^{c} c o s π c / 2}{1 + (ω_{i} {τ)}^{2 c} + 2 (ω_{i} {τ)}^{c} c o s π c / 2} \\ ω_{i} = \frac{10^{a_{i}}}{t} \end{array} 。 \end{array}

式中:T_P是窗口时间;a_i是滤波系数对应的横坐标;Φ_i是与a_i对应的滤波系数;x_i是传递函数。

根据随机的Cole-Cole模型参数m、τ、c可计算出理论上的视极化率衰减曲线(图1a),根据野外实际观测的全波形数据可得到视极化率衰减曲线(图1b)。对比图1可以看出,理论数据和实测数据衰减趋势具有较好的一致性,为后续实测数据反演频谱参数奠定了理论基础。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 两类视极化率衰减曲线对比

Fig.1 Comparison of two types of polarization attenuation curves

2 BP神经网络训练

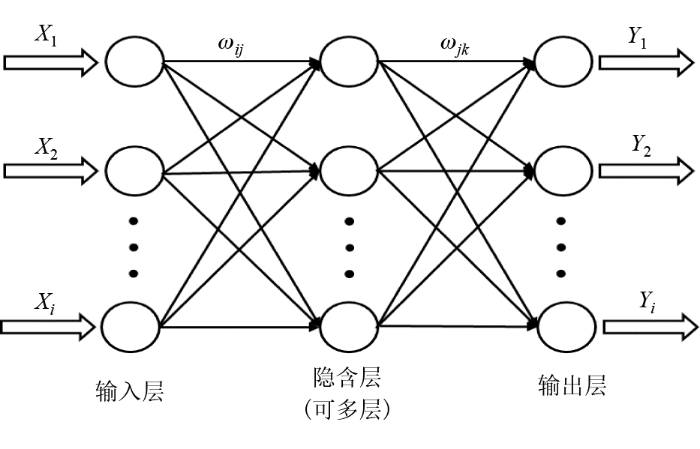
BP神经网络是基于误差反向传播算法的一种具有非线性连续转移函数的多层前馈网络(图2),其核心思想是利用梯度下降法,以期使网络的实际输出值和期望输出值的误差均方差为最小,适用于对复杂非线性数据进行建模处理。BP神经网络是具有一个输入层、单个或多个隐含层和一个输出层的多层网络,隐含层和输出层上的每个神经元都对应于一个激发函数和一个阀值,每一层上的神经元都通过权重与其相邻层上的神经元互相连接(图中X_i是输入值,Y_i是输出值,ω_ij是输入层到隐含层的连接权重,ω_jk是隐含层到输出层的连接权重)。将BP算法用于具有非线性转移函数的多层前馈网,可以以任意精度逼近任何非线性函数,这一巨大优势使BP神经网络得到广泛应用。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 BP神经网络模型

Fig.2 Back-Propagation neural network model

对于简单或者线性数据集,通常选择单个隐含层;对于非线性函数,则需要多个隐含层。文中对于隐含层分别选择单层、两层和三层进行预测反演。输入神经元数量分别为3、5、8和10,输出神经元数量为3。神经元隐含层节点数过多或者过少,会出现过拟合或者欠拟合现象,根据经验公式(6)获取单个隐含层神经元节点数N_h,文中单个隐含层的神经元节点分别设为3、5、10和15进行对比训练。

(6)

N_{h} = \frac{N_{s}}{(a * (N_{i} + N_{0}))}

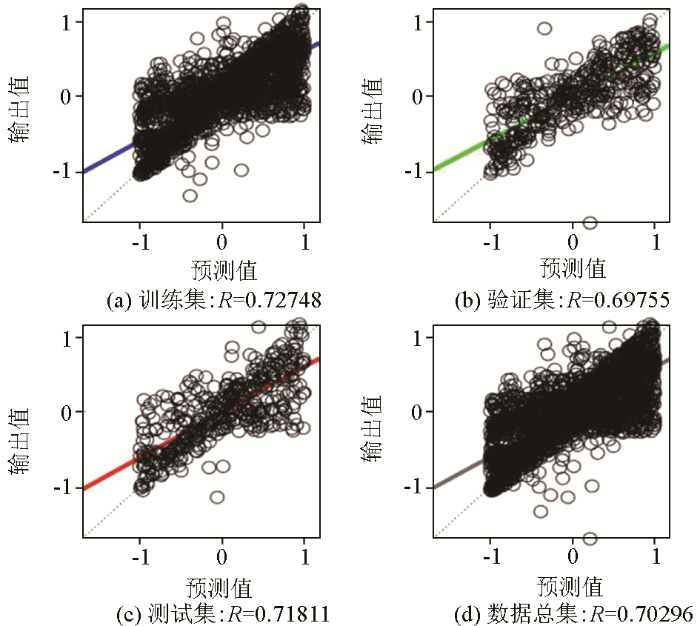
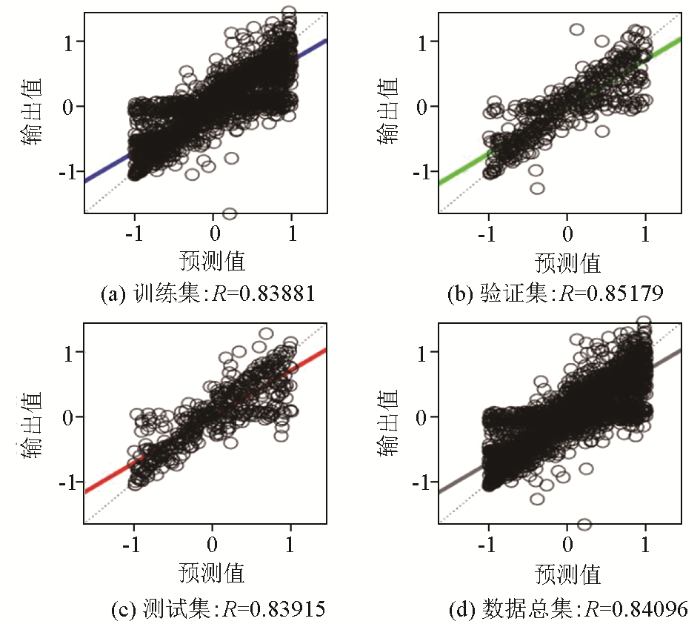
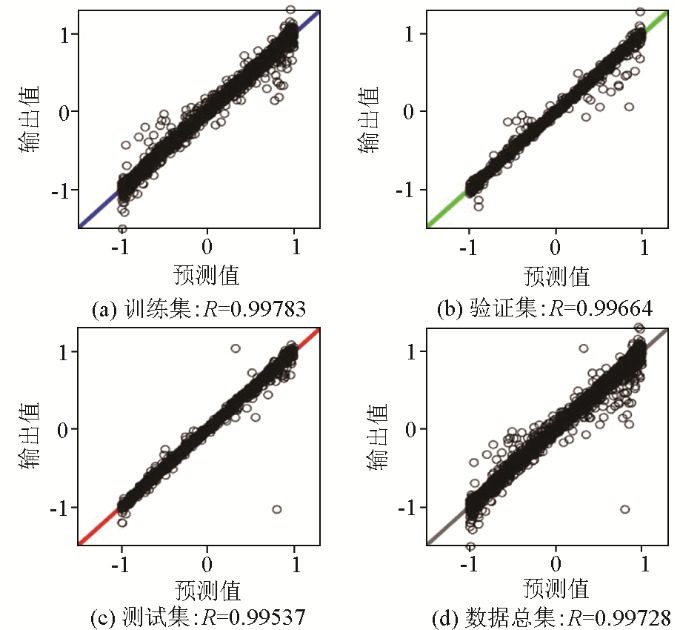
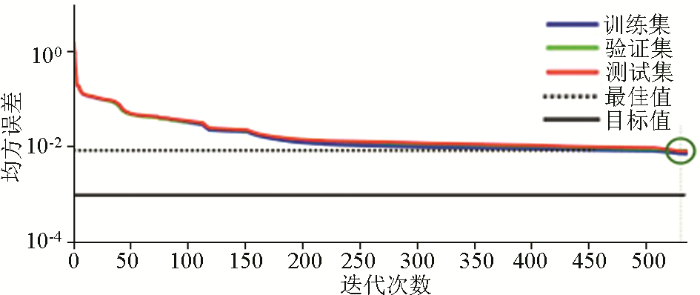
式中:N_s是训练集样本数;N_i是输入层神经元个数;N₀是输出层神经元个数;a通常取值是2~10。一个具有8个输入神经元、2个隐含层、单个隐含层节点数为3、3个输出神经元的神经网络模型简要记作8-[3 3]-3型,其他类型以此类推。随机生成1 000组、3 000组、8 000组、10 000组4个样本集进行训练,按照模型结构从简单到复杂原则,共设计52组模型结构开展对比研究,筛选最合适模型。图3~图5分别是以8 000组样本集为基础的单层3-[5]-3、双层8-[3 3]-3和三层8-[10 10 10]-3模型结构得出的训练集、验证集、测试集、总数据集的回归曲线。回归值R越接近1表示预测和输出数据之间的关系越密切,反之则随机性越大。图3中单隐含层R均值为0.711 53,图4中双隐含层R均值为0.842 68,图5中三隐含层R均值则达到0.996 78,由此得出,增加输入神经元数量、隐含层数、神经元节点数可以明显提高神经网络性能,其中8-[10 10 10]-3结构训练集、验证集、测试集的均方误差随训练迭代次数逐渐降低,当迭代次数达到536次时,达到最佳值(图6)。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 3-[5]-3模型结构的训练集(a)、验证集(b)、测试集(c)、数据总集(d)回归曲线

Fig.3 Regression curves for the training set(a)、validation set(b)、testing set (c) and total dataset(d) of Model 3-[5]-3 structure

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 8-[3 3]-3模型结构的训练集(a)、验证集(b)、测试集(c)、数据总集(d)回归曲线

Fig.4 Regression curves for the training set(a)、validation set(b)、testing set(c) and total dataset(d) of Model 8-[3 3]-3 structure

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 8-[10 10 10]-3模型结构的训练集(a)、验证集(b)、测试集(c)、数据总集(d)回归曲线

Fig.5 Regression curves for the training set(a)、validation set(b)、testing set(c) and total dataset(d) of Model 8-[10 10 10]-3 structure

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 8-[10 10 10]-3模型传递误差随训练次数变化曲线

Fig.6 Transmission error variation curve with training times of Model 8-[10 10 10]-3

影响模型预测精度的参数包括样本训练数、输入值数量、隐含层层数、隐含层节点数等,本文对这些主要参数做了测试优化,最终确定了最适神经网络模型。参数测试优化过程中,利用网络模型预测的和正演输出的频谱参数均方误差(Mse)以及相关系数R作为评价指标来判断预测模型的有效性,均方误差越小,相关系数越接近1,代表拟合效果越好,网络模型有效性越高。

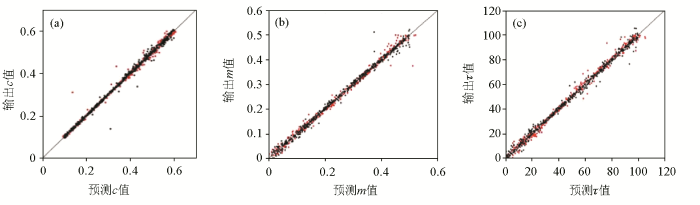
筛选最合适的BP神经网络模型通常采用试凑方法,步骤如下:首先,设置神经网络结构为单隐含层,逐步增加输入值数量和隐含层节点数来提升神经网络的性能,得出在8-[10]-3模型结构下,c值、m值和τ值相关系数R达到最大值,分别为0.883 236、0.869 024、0.853 044,总均方误差(即分别算出3个参数的预测值和正演输出值的均方误差,再取平均值)为:0.132 834,继续增加隐含层节点数,在8-[15]-3模型结构下频谱参数相关性降低,可能是节点数较多,导致出现过拟合现象。第二步,选择双隐含层层数且节点数较低时,在8-[3 3]-3模型结构下,c值、m值和τ值相关系数R仅达到0.826 257、0.840 143、0.804 028,总均方误差为:0.127 816,表明BP神经网络训练反演频谱参数精度较低,误差较大(图7),逐步增加隐含层节点数,得出在8-[10 10]-3模型结构下,c值、m值和τ值相关系数R达到最大,分别为0.956 072、0.965 203、0.924 37,总均方误差为:0.060 440,表明该模型结构精度较好,误差较小。继续增大隐含层节点数,8-[15 15]-3模型结构的频谱参数相关性变化不明显,但神经网络训练时间明显增加。第三步,选择3个隐含层层数训练,可以看出随着隐含层层数增加,神经网络的性能在逐步提升,且频谱参数的相关性趋于稳定,结构模型为8-[10 10 10]-3型的c值、m值和τ值相关系数R达到最大,分别为0.992 135、0.997 192、0.996 653,总均方误差减小为0.018 477,表明该模型训练效果好,反演精确度高,误差小,结果可信(图8),对比筛选该模型结构作为本文最合适BP神经网络结构(表1)。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 8-[3 3]-3模型结构的频谱参数回归曲线:(a)频率相关系数、(b)充电率、(c)时间常数

Fig.7 Spectral parameter regression curve of Model 8-[3 3]-3 structure:(a) Frequency correlation coefficient、(b) charge rate、(c) time constant

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 8-[10 10 10]-3模型结构的频谱参数回归曲线:(a)频率相关系数、(b)充电率、(c)时间常数

Fig.8 Spectral parameter regression curve of Model 8-[10 10 10]-3 structure:(a) Frequency correlation coefficient、(b) charge rate、(c) time constant

表1 BP神经网络训练频谱参数的相关系数R及均方误差Mse(8 000样本集)

Table 1 Correlation coefficient and mean square error of spectral parameters in BP neural network training (8,000 sample set)

参数	c		m		τ
模型结构	R	Mse	R	Mse	R	Mse
3-[3]-3	0.686 672	0.164 371	0.659 548	0.178 509	0.616 054	0.226 556
3-[5]-3	0.703 721	0.158 974	0.699 014	0.177 708	0.680 032	0.190 873
5-[5]-3	0.825 955	0.105 401	0.833 382	0.090 517	0.726 354	0.209 827
8-[10]-3	0.883 236	0.124 673	0.869 024	0.120 921	0.853 044	0.152 909
8-[15]-3	0.833 561	0.165 781	0.812 135	0.143 291	0.752 719	0.190 345
8-[3 3]-3	0.826 257	0.095 627	0.840 143	0.100 481	0.804 028	0.187 341
8-[5 5]-3	0.945 304	0.038 803	0.953 647	0.046 215	0.873 556	0.180 023
8-[10 10]-3	0.956 072	0.035 238	0.965 203	0.026 610	0.924 37	0.119 473
8-[15 15]-3	0.943 289	0.424 467	0.949 861	0.058 321	0.879 808	0.130 944
8-[3 3 3]-3	0.955 658	0.043 565	0.980 468	0.028 764	0.915 581	0.125 348
8-[5 5 5]-3	0.975 376	0.032 639	0.982 149	0.027 649	0.973 748	0.071 334
8-[10 10 10]-3	0.992 135	0.018 607	0.997 192	0.011 095	0.996 653	0.025 730
8-[15 15 15]-3	0.979 347	0.033 456	0.969 457	0.037 855	0.968 965	0.085 321

新窗口打开| 下载CSV

3 实例应用

红柳沟矿区位于卡拉麦里深断裂与其北部的次一级构造清水—苏吉泉大断裂之间,褶皱强烈,断裂构造发育,岩石多已蚀变破碎,沿断裂带有大量的超基性岩脉、岩株分布。部分断裂带构成了超基性岩浆上升和赋存的有利部位,是成矿的有利地段。工作区矿化类型以蚀变岩夹石英细脉为主,构造由NW-SE向展布,呈强应变构造带与弱变形区域强弱相间的格局。

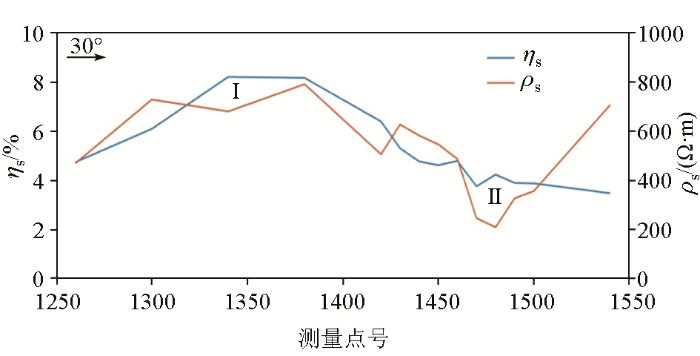
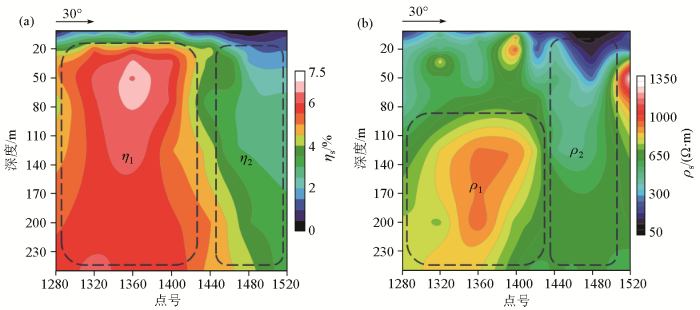
图9是测区一条测线(1 280~1 540点之间)的激电中梯扫面异常曲线。视极化率背景值约为3.3%,该测线在1 280~1 400点之间η_s>4.8%、ρ_s>550 Ω·m,呈高极化率、高电阻率异常(图9中Ⅰ异常),在1 460~1 520点之间η_s<4.0%、ρ_s<430 Ω·m,呈低极化率、低电阻率异常(图9中Ⅱ异常)。结合激电测深视极化率和视电阻率等值线断面(图10),Ⅰ异常与η₁、ρ₁, Ⅱ异常与η₂、ρ₂都具有较好的对应性,由地质学认识可以推断:即Ⅰ异常为高极化高阻特征,对应硅化较强的金属硫化物地质体,Ⅱ异常为处于破碎带的含星点状黄铁矿、导电矿物连通较差的凝灰质砂岩,只能分析出该测线有2~3种极化体,可以区分较明显的激电异常特征,对于弱激电异常无法进一步提高分辨率。利用该网络模型对野外实测数据的频谱参数预测反演,得到频谱参数等值线(图11),可以看出实际对应的异常可以细化分为5种,意味着存在至少有5类不同的极化体。结合钻孔标本测量结果验证,可以给出相应的推断结果。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 视极化率和视电阻率异常曲线

Fig.9 Abnormal curves of apparent polarization and apparent resistivity

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 激电测深视极化率(a)、视电阻率(b)等值线断面

Fig.10 Cross section of apparent polarization rate (a) and apparent resistivity (b) contour lines in induced polarization depth measurement

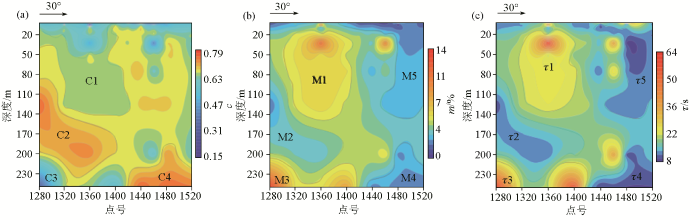
不同的频谱参数对应不同的极化异常现象,频谱参数能够反映弱激电异常特征。m值随导电矿物含量的增大而增大。c值受导电矿物颗粒的含量和颗粒均匀性影响,导电矿物含量越高,c值越小,矿化程度较高的岩石内部矿化颗粒往往不均匀,c值较小;零星或稀疏浸染矿化的背景地段岩石一般颗粒较均匀,c值较大;至于矿化或石墨化程度很高、导电矿物连通极好的网脉状或致密状矿(化)体,已接近于面极化体,其c值都在0.5以上^[20]。τ值的大小主要受导电矿物颗粒大小和导电矿物连通的程度控制,颗粒越大,连通程度越好,则τ值越大。将该测区实测数据代入最适BP神经网络,频谱参数预测反演结果如图11a~c所示,可以看出c值、m值、τ值具有较好的一致性,依据频谱参数异常重新细分激电异常区域,可划分为C1~C4的频率相关系数异常、M1~M5的充电率异常、τ1~τ5的时间常数异常。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 实测数据代入BP神经网络中训练与预测反演频谱参数等值线图:(a)频率相关系数、(b)充电率、(c)时间常数

Fig.11 Contour map of inverted spectral parameters for training and prediction using measured data input into BP neural network:(a) Frequency correlation coefficient、(b) charge rate、(c) time constant

C1、M1、τ1为同一异常,属于中高频率相关系数(0.66左右)、高充电率(大于5%)、中高时间常数(25~40)、高极化率、低电阻率异常,推测该地层是导电矿物连通性较好,矿化程度较高的金属硫化物地质体。此处经浅钻孔验证后,大部分岩心是含黄铁矿的凝灰质粉砂岩,黄铁矿呈脉状或薄膜状分布,个别岩心是导电矿物连通较好的网脉状矿化体,推测与钻探验证结果对应比较吻合。C2、M2、τ2为同一异常,属于高频率相关系数(0.70以上)、低充电率(4%以下)、低时间常数(16以下)、高极化率、高电阻异常,推测该地层矿物连通程度较差,呈零星、稀疏浸染状金属硫化物矿化体或者是具有高阻高极化特征硅化较强的金属硫化物地质体。C3、M3、τ3为同一异常,属于低频率相关系数(0.50以下)、高充电率(5%以上)、高时间常数(30以上)、高极化率、低电阻率异常,推测是矿化程度较高、金属矿物含量较多、矿化颗粒不均匀且导电矿物连通程度较好的金属硫化物矿化体。C4、M4、τ4为同一异常,属于高频率相关系数(0.70以上)、低充电率(3%以下)、低时间常数(15以下)、低极化率、中低电阻率异常,推测是无矿化或矿物含量稀少的凝灰岩围岩地质体。M5、τ5为同一异常,属于低充电率(3%以下)、低时间常数(15以下)、低极化率、高电阻率异常,依据地表出露情况推断是硅化程度较强、导电矿物连通较差、含星点状黄铁矿的凝灰质砂岩。

对弱激电异常区域,该区域中存在的相对高极化率的局部异常体。由图10a可以看出,在测线1 280~1 400点之间,深度20~250 m的范围内,实测出的视极化率值整体呈高极化特征,图10b视电阻率在0~90 m呈低阻特征,在90~250 m呈高阻特征,由此只能得出2种极化体的解释。然而实际并非如此,结合反演的Cole-Cole模型参数分析,实际在1 280~1 400点之间,地下存在至少3类极化体异常。尤其在深度110~200 m和200~250 m均为高极化高阻,仅根据这一特征,可以推断这两处异常为同一种地质体引起的,而从频谱参数异常特征分析,是由两种不同的地质体,分别为图11中C2、M2、τ2异常体和C3、M3、τ3异常体。

4 结论

本文基于BP神经网络结构模型,实现对理论数据集和野外实测时间域激电数据的频谱参数预测反演研究,获得以下几点认识:

1)利用数字滤波算法对Cole-Cole模型变换得到其时域表达式,进一步得到视极化率衰减曲线谱,同一时窗内,不同谱特征参数所对应的衰减曲线不相同,结合采集到的全波形数据所反映的时变特征,能够较精准区分出极化异常体特征。

2)通过改变训练集样本数、输入神经元个数、隐含层层数、隐含层节点数4个影响因素,多次训练对比,得到最适BP神经网络训练结构模型,理论上证明了BP神经网络反演频谱参数是可行的。测试数据集反演结果精度高、误差小,反演所需计算时间短,提升了反演效率,但如何约束BP神经网络模型反演的稳定性还需要进一步研究。

3)从预测反演效果来看,整个测区预测出的c值平均高于0.5,主要由于矿化程度较低,矿化颗粒较均匀,这与钻孔岩心验证相吻合。随着极化体在地下深度的增加,对τ值稀释作用较小,测区τ值的变化范围在3~65 s之间,更具有主导作用。τ值大于1 s表明测区没有无矿化的纯离子导电岩石和互不相连的岩矿石。

4)基于实际测量的放电过程中8个时间窗口的观测数据预测反演,从红柳沟矿区应用实例来看,利用时间域激电数据反演的频谱参数能够进一步区分出视极化率和视电阻率不能测出的弱激电异常特征,反演数据的可靠性通过钻探得到进一步验证,对于频谱参数的综合解释,提升了时间域激电勘探数据在找矿上的应用潜力。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Grissemann

, Rammlmair

, Siegwart

, et al.

Spectral induced polarisation linked to image analyses:A new approach

[C]// Applied mineralogy:In research,economy,technology,ecology and culture,vol.2:Sixth international congress on applied mineralogy, 2000.