E-mail Alert Rss
 

物探与化探, 2025, 49(2): 422-432 doi: 10.11720/wtyht.2025.1286

方法研究信息处理仪器研制

最小二乘配置在磁力异常数据网格化中的应用

高小伟,1, 李雄伟1, 庞少东1, 李文刚1, 姚伟华1, 杜劲松,2,3

1.中煤科工西安研究院(集团)有限公司,陕西 西安 710077

2.中国地质大学(武汉) 地球物理与空间信息学院 地球内部多尺度成像湖北省重点实验室,湖北 武汉 430074

3.中国地质大学(武汉) 地质过程与成矿预测全国重点实验室,湖北 武汉 430074

Application of least-squares collocation to the gridding of magnetic anomaly data

GAO Xiao-Wei,1, LI Xiong-Wei1, PANG Shao-Dong1, LI Wen-Gang1, YAO Wei-Hua1, DU Jin-Song,2,3

1. CCTEG Xi'an Research Institute (Group) Co., Ltd., Xi'an 710077, China

2. Hubei Subsurface Multi-scale Imaging Key Laboratory, School of Geophysics and Geomatics, China University of Geosciences (Wuhan), Wuhan 430074, China

3. State Key Laboratory of Geological Processes and Mineral Resources, China University of Geosciences (Wuhan), Wuhan 430074, China

通讯作者: 杜劲松(1985-),男,副教授,长期从事地磁场与磁法勘探方面的教学与研究工作。Email:jinsongdu@cug.edu.cn

第一作者: 高小伟(1977-),男,高级工程师,主要从事煤田水文物探方面的研究工作。Email: 26930319@qq.com

责任编辑: 朱晓颖

收稿日期: 2024-07-10   修回日期: 2024-12-25  

基金资助: 中煤科工西安研究院(集团)有限公司科技创新基金项目(2022XAYJS06)
陕西省自然科学基金重点研发计划项目(2022SF-046)
国家自然科学基金面上项目(42174090)

Received: 2024-07-10   Revised: 2024-12-25  

摘要

为了解决传统网格化方法在处理不规则分布的磁力异常数据时难以同时兼顾计算精度与计算效率的问题,本文将大地测量学领域经典的最小二乘配置法应用于地面磁力异常数据的网格化处理中。仿真数据和煤田实测数据的测试与分析结果表明:最小二乘配置网格化方法的计算精度取决于离散观测数据的误差估计、协方差函数的选取与拟合,误差估计越准确插值计算精度越高;采用多项式函数作为磁力异常数据处理的经验协方差函数是简单、有效的;相较于克里金法、最小曲率法和径向基函数法,最小二乘配置法在网格化处理时对噪声具有更好的压制能力。应用最小二乘配置方法进行磁力异常数据的网格化处理,能够提高数据处理的精度与计算效率。

关键词： 最小二乘配置; 磁力异常; 网格化; 插值; 协方差函数

Abstract

Traditional gridding methods struggle to balance computational accuracy and efficiency when processing irregularly distributed magnetic anomaly data. To address this issue, this study applied the classic least-squares collocation method from geodesy to the gridding of ground-based magnetic anomaly data. This application was verified through the test and analysis of the simulation data and the actual coalfield data. The results indicate that the computational accuracy of gridding based on least-squares collocation is dictated by the error estimation of discrete observational data and the selection and fitting of the covariance function. More accurate error estimation contributes to higher-accuracy interpolation. A polynomial function is a simple and effective empirical covariance function for processing magnetic anomaly data. The least-squares collocation method demonstrates more effective noise suppression compared to the Kriging, minimum curvature, and radial basis function methods. Overall, applying the least-squares collocation to the gridding of magnetic anomaly data can enhance the accuracy and efficiency of data processing.

Keywords： least-squares collocation; magnetic anomaly; gridding; interpolation; covariance function

PDF (9890KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

高小伟, 李雄伟, 庞少东, 李文刚, 姚伟华, 杜劲松. 最小二乘配置在磁力异常数据网格化中的应用[J]. 物探与化探, 2025, 49(2): 422-432 doi:10.11720/wtyht.2025.1286

GAO Xiao-Wei, LI Xiong-Wei, PANG Shao-Dong, LI Wen-Gang, YAO Wei-Hua, DU Jin-Song. Application of least-squares collocation to the gridding of magnetic anomaly data[J]. Geophysical and Geochemical Exploration, 2025, 49(2): 422-432 doi:10.11720/wtyht.2025.1286

0 引言

针对不规则分布重磁异常数据的网格化方法众多[1⇓⇓⇓⇓⇓⇓-8],有克里金法[9⇓-11]、最小二乘配置法[12-13]、最小曲率法[14-15]、径向基函数法[16]、谐分析法[17]和等效源法[18-19]。其中,谐分析法与等效源法虽然满足位场的物理性质,插值与网格化的计算精度较高,但具有较大的计算量;最小曲率法常用于重磁异常数据的网格化处理[20-21],尽管其网格化结果能够保证二阶导数连续性,但是依然缺乏重磁场本身物理性质的约束,而且在数据空区受初值给定结果的影响较大;径向基函数法对于重力数据的网格计算效果最佳[22],但其插值参数繁多,还需求解方程组,虽然最优插值参数可以采用交叉验证法进行选取[23],但大大降低了计算效率;克里金法与最小二乘配置法均是基于随机过程统计的线性最优无偏估计方法,都是通过已测点信号推估未测点的待求量。而最小二乘配置法在理论上更严密,其关键即协方差函数表达了不同距离重磁异常之间的相关性,这反映了重磁异常的空间变化物理特性,若信号的方差—协方差已知,其估值也是最优的[24],并且能够融合处理重磁场的不同分量[25];另外,最小二乘配置方法从原理上可以对噪声信号滤波,按照噪声影响最小的原则确定待估信号[26]。

最小二乘配置是在Moritz[27]提出的协方差估计的基础上发展而来的,是物理大地测量学中的一个基础与经典的方法,已被广泛地应用于重力、高程与形变等空间离散数据的插值、网格化与多源数据融合等处理中。但是,在地磁数据的插值与网格化应用中还比较少见,且缺乏仿真数据测试与实际应用的对比研究[28⇓⇓-31]。此外,尽管磁力异常与重力异常均属于位场,但是,两者起源的物理机制不同,而且从重磁异常泊松方程角度而言磁力异常可以视为重力扰动位二阶梯度张量不同元素的组合量。

为此,本文将最小二乘配置法应用于磁力异常数据的插值与网格化处理中,通过仿真数据测试与分析,研究了该方法的计算精度以及参数设置与数据噪声的影响。由于高精度磁法是煤田火烧岩探测与煤层自燃监测的重要手段[32-33],受到地形地貌与环境干扰等诸多因素影响,实测离散磁力异常数据均存在不同程度的分布不规则性。因此,将本文方法应用于煤层火烧岩探测的地面高精度磁力异常数据的网格化处理中,并与传统网格化方法计算结果进行了对比与分析,旨在拓展最小二乘配置法的应用领域,作为可选方法之一推广其在磁力异常离散数据的插值、网格化与多源数据融合等处理中的应用。

1 方法原理

观测数据不可避免地包含测量误差,而测量误差M一般包括系统误差B、随机误差N与粗差G,即:

M=B+N+G。

一般而言,粗差G可以通过探测方法进行识别与剔除,而观测数据量较大时随机误差N可被视为零均值的白噪声。相对而言,信号S则是某种物理量P的一个分量且其算数平均值也为零值,例如重力异常和磁力异常。一般情况下,信号成分的幅值较小且被视为物理量P相对其参考模型R或趋势成分的异常或剩余成分,即:

P=R+S。

某种物理量的观测量L可以视为真实物理量P与测量误差M之和,即:

L=P+M。

若不考虑粗差,将式(1)与式(2)代入式(3)得到:

L=R+S+B+N。

其中,系统误差B很难被完全校正或消除,因此可将参考模型R与系统误差B组合为数学模型AX,即:

AX=R+B。

式中:A表示模型的核矩阵;X表示模型对应的系数向量。

将式(5)代入式(4),可得:

L=AX+S+N。

若数学模型已知,例如正常重力公式或主磁场模型,则可将其从观测量L中去除,从而仅得到信号S与随机误差N,此时由于信号与随机误差均具有零均值统计特征,因而将数学模型校正之后的物理观测量称之为中心化后的观测量C,即:

C=S+N。

若再忽略随机误差N的影响,式(7)则可写为

C=S。

1.1 最小二乘配置插值的基本原理

基于式(6),最小二乘配置法(least squares collocation)的估值遵循高斯给出的最小二乘和最小方差原则,利用拉格朗日乘子法(lagrange multiplier method),可推导出模型系数向量X、信号向量S和随机误差向量N分别表示为[34]

X=[ATcov(L,L)-1A]-1ATcov(L,L)-1L,
S=cov(S,L)cov(L,L)-1(L-AX),
N=cov(N,L)cov(L,L)-1(L-AX),
cov(L,L)=cov(S,S)+cov(N,N)。

式中,cov()表示协方差函数。

在特殊情况下,当观测量L中不存在非随机的系统成分时,即A=0,则对于重、磁异常,可将这些观测量L视为空间平稳随机场的随机量,在仅考虑含有观测随机误差的情况下得到[33]:

S=cov(S,L)cov(L,L)-1L,
N=cov(N,L)cov(L,L)-1L。

如前所述,若观测数据量较大则其随机误差N可视为零均值的白噪声,则随机误差的协方差矩阵为

cov(N,N)=αI。

式中:α为随机误差的方差;I为单位矩阵。

将式(12)代入式(10),再将式(10)代入式(11)得到:

S=cov(S,L)[cov(S,S)+αI]-1L,
N=cov(N,L)[cov(S,S)+αI]-1L。

对于最小二乘配置插值,可将式(13a)改写为

S'm×1=cov(S'm×n,L)[cov(Sn×n,S)+α In×n]-1Ln×1。

式中:信号待插值点个数为m个;观测数据个数为n个;S'为待插值点处的信号矢量;S为观测位置处的信号矢量。一般情况下,可以根据实际观测数据拟合常用协方差函数的系数,计算出研究区域的信号与观测量之间的互协方差矩阵cov(S',L)、信号自协方差矩阵cov(S,S),则待推估信号S'可根据式(14)最终求出。通过式(14)可以看出,每个待插值点处的信号实际上均是所有观测数据的一个加权平均值。

1.2 经验协方差函数及其参数拟合方法

由式(14)可知,最小二乘配置插值的关键之一在于根据实际观测数据拟合常用协方差函数的系数。常用的协方差函数包括Hirvonen(西尔沃宁)协方差函数、Gauss(高斯)协方差函数、Moritz协方差函数、Tscherning/Rapp(简称T-R)协方差函数、多次幂函数等。其中,Hirvonen协方差函数与Gauss协方差函数经常被用于构建区域应变场与速度场[26],Moritz协方差函数与T-R协方差函数常被用于重力数据处理[13]。本文根据仿真数据和实测数据计算的协方差观测数据的变化特征,选取了N阶多项式函数[28⇓⇓-31]作为经验协方差函数,其表达式如下:

CNor(l)=1+a1l+a2l2+…+aNlN。

式中:l为距离;CNor(l)=C(l)/C0为归一化协方差;C0为距离为0时的协方差,即自协方差;a1、a2、…、aN为待求系数(N为正整数),本文采用最小二乘法对其进行求解。

1.3 计算流程

最小二乘配置插值与网格化的计算流程如下:

1)识别并剔除观测数据中的粗差;

2)最小二乘配置推估要求待测点信号和已测点信号均为零均值的随机过程,若信号的均值不为零,则在实际应用中通常需要进行中心化处理,此外系统(长波)分量(或趋势场)必须被去除;

3)计算已知点之间的距离对,按照距离远近分类为等间隔区段,计算每一个区段的协方差C(l)以及中心距离l,并根据观测数据计算距离为0时的自协方差C0;

4)对观测的C(l)数据进行归一化处理,计算CNor(l)=C(l)/C0数据;

5)选择合适的协方差函数模型,对CNor(l)数据进行最小二乘拟合得到未知系数;

6)根据拟合得到的协方差函数以及观测点坐标和待插值点坐标计算信号与观测量之间的互协方差矩阵cov(S', L)、信号自协方差矩阵cov(S, S)、噪声协方差矩阵cov(N, N);

7)根据式(14)计算待插值点处的信号向量S'。

2 仿真测试

首先采用仿真模拟数据测试最小二乘配置网格化方法的有效性并分析了其计算精度的影响因素,然后与其他网格化方法计算结果进行对比与分析。

2.1 方法有效性测试与影响因素分析

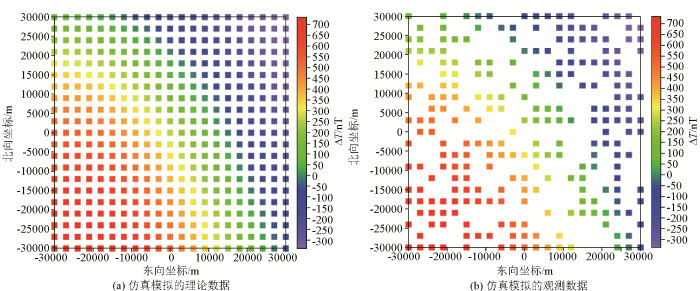
采用均匀磁化的直立长方体模型正演计算出总磁场强度异常(ΔT)[35],选取(-30 000 m, 30 000 m)范围内21×21个规则格网测点(噪声标准差为0 nT)作为仿真模拟的理论数据(图1a)。由于实际观测点位受地形、地貌等多种因素限制,因此将正演计算的原始数据随机抽取50%的测点作为待插值点,剩余测点作为仿真模拟的观测数据(图1b)。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   仿真模拟的理论数据(a)与仿真模拟的观测数据(b)

Fig.1   Simulated theoretical data (a) and observation data (b)


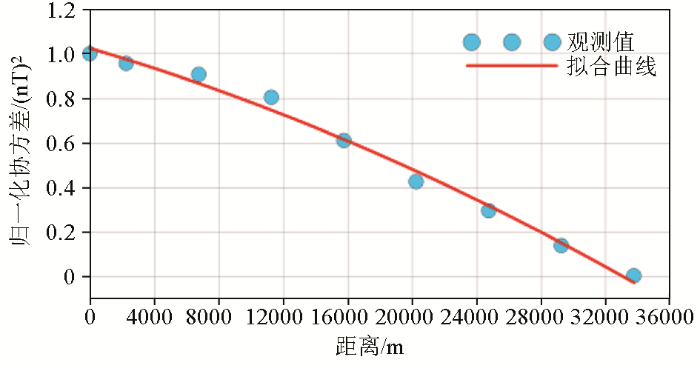
将已知点坐标以及观测数据带入计算程序中,计算出任意两点之间的所有距离,然后按照从小到大划分区间,区间大小一般取距离的平均值,计算每一段区间的数据协方差,将距离段中心点坐标与计算的协方差绘制成散点图(图2)。进而,采用各向同性的二阶多项式类型的经验协方差函数拟合观测协方差,得到如图2红色实线所示的协方差函数的拟合曲线,可见其拟合效果较好。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   计算的观测协方差值及拟合曲线

Fig.2   Calculated covariance values and fitted covariance function


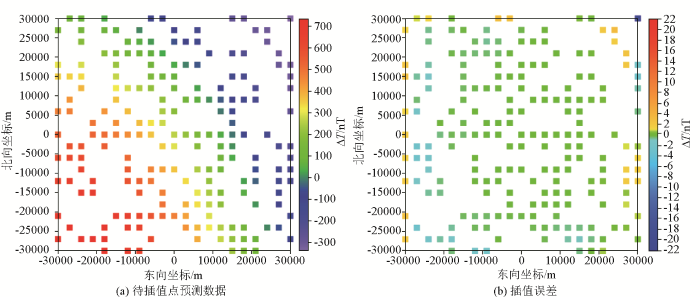
根据拟合的协方差函数即二阶多项式,发现当距离接近34 000 m时,协方差接近0(nT)2,因此认为超过这个距离的两点之间几乎无相关性。根据拟合得到的协方差函数以及观测点坐标和待插值点坐标计算信号与观测量之间的互协方差矩阵cov(S', L)、信号自协方差矩阵cov(S, S)、噪声协方差矩阵cov(N, N),进而代入式(14),计算得到待插点处的预测数据(图3a),并将插值点预测值与图1a所示的理论值作差,得到预测残差(图3b)。由图3b可以看出,待插点预测数据与待插点理论数据之差异大部分均集中于零值附近,最大值3.1 449 nT,最小值-22.0 778 nT,均方根为±1.8 267 nT,相较于理论值的幅值范围,插值计算误差较低。因此,通过该仿真数据测试证明基于最小二乘配置的磁力异常数据插值与网格方法是有效的。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   待插点预测数据(a)与插值误差(b)

Fig.3   Predicted data (a) and interpolation errors (b)


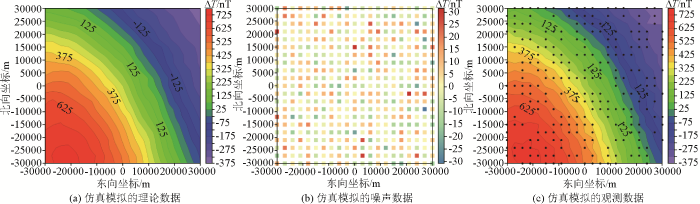
由式(14)可知,数据噪声估计对最小二乘配置插值计算精度存在影响。在实际应用中准确估计数据噪声水平往往较难,因此,需要测试数据噪声水平估计对插值计算精度的影响。首先在仿真模拟的理论数据(图4a)的基础上添加均值为0 nT、标准差为±10 nT的高斯白噪声(图4b),得到模拟的实际观测数据(图4c);其次将噪声标准差估值设置为0、±10与±20 nT,分别代入式(14)进行插值计算;最后将插值计算结果与不含噪声的理论数据进行对比。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   仿真模拟的理论数据(a)、仿真模拟的噪声数据(b)与仿真模拟的观测数据(c)

(图中黑点表示模拟的观测点位置)

Fig.4   Simulated theoretical data (a), noises (b) and practical observation data (c)

(black dots represent synthetic observation locations)


从不同噪声标准差设置情况下的计算精度统计参数(表1)可以看出:在插值计算时,当输入真实的数据噪声标准差可以更加准确地计算出待插值点的磁力异常值;但是,数据噪声估计对插值计算结果的影响并不大。

表1   不同噪声标准差设置情况下的计算精度统计参数

Table 1  Statistic parameters of calculation accuracy in cases of setting different levels of data noisesnT

输入的噪声
标准差		残差均方根平均残差最大残差最小残差
±0±8.879 01.129 540.800 0-24.370 0
±10±7.338 30.074 935.390 0-33.490 0
±20±8.854 21.126 941.260 0-24.810 0

新窗口打开| 下载CSV


2.2 与其他网格化方法计算结果的对比分析

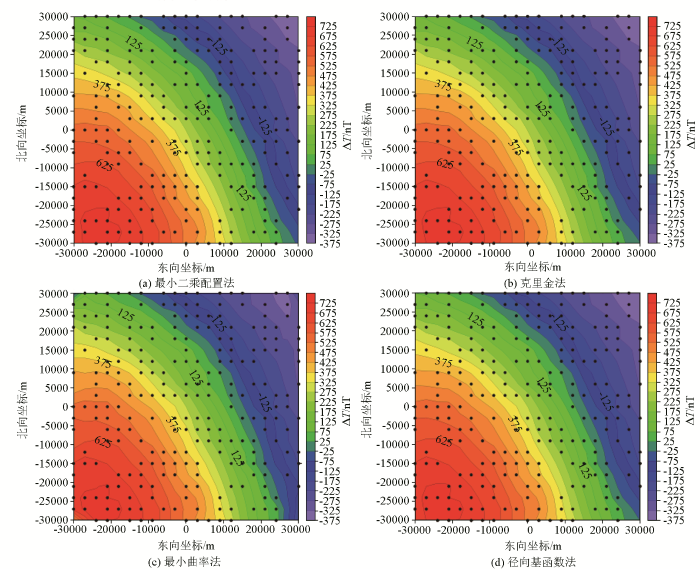
对模拟的实际观测数据(图4c),通过使用交叉验证法[23]选取最佳参数后,分别采用最小二乘配置法、克里金法、最小曲率法、径向基函数法对离散观测数据进行网格化处理(图5)。对比图4与图5可以看出,4种插值方法均具有一定的去噪能力,插值效果相差不大,均能够较好地恢复出磁力异常的空间变化趋势。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   不同插值方法的计算结果

Fig.5   Calculating results by using different interpolation methods


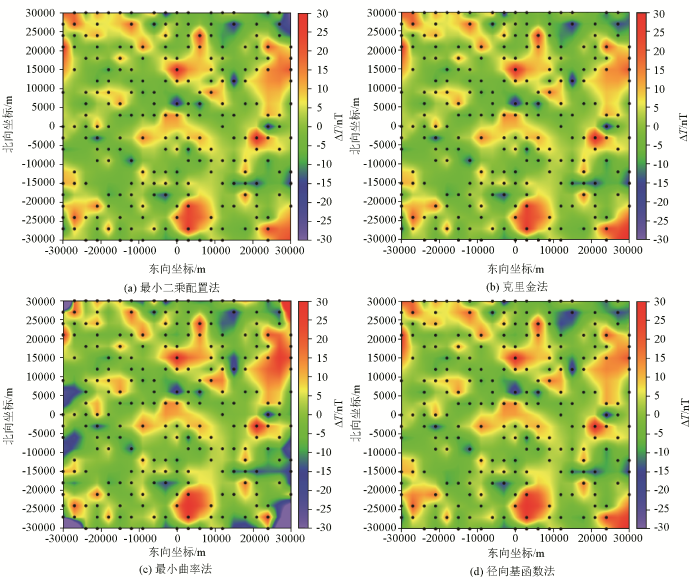
为进一步对比各种插值方法计算结果之间的差异特征,分别对图5中不同插值计算结果与图4a仿真模拟的理论磁力异常数据作差,得到图6所示的残差分布。从图6中可以看出,4种插值方法计算误差的分布形态比较一致,这说明插值计算精度主要与观测数据的误差及点位空间分布有关,但是最小二乘配置插值计算误差的幅值相比其他方法最弱,克里金与径向基函数的残差信号大致相同,而最小曲率法在边界处产生了较大的插值误差(尤其在计算区域的4个角部)。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   不同插值方法计算结果与理论值的偏差

Fig.6   Differences between calculating results and theoretical data by using different interpolation methods


由表2可见,最小二乘配置法、克里金法、最小曲率法与径向基函数法的插值结果的均方根误差分别为±8.56、±8.68、±19.21、±9.00 nT。因此,可以初步判断插值计算精度最好的是最小二乘配置法,克里金法较优,径向基函数法次之,最小曲率法较差。

表2   4种插值方法的计算精度统计参数

Table 2  Statistic parameters of calculating accuracy of four interpolation methodsnT

网格化方法残差均方根平均残差最大残差最小残差
最小二乘配置法±8.559 21.594 330.940 0-32.890 0
克里金法±8.676 21.698 336.110 0-20.990 0
最小曲率法±19.212 9-0.671 3123.100 0-218.300 0
径向基函数法±8.996 61.714 832.970 0-20.990 0

新窗口打开| 下载CSV


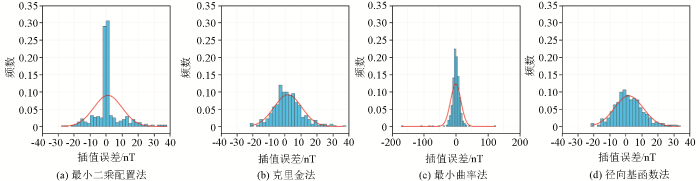
从残差数据的柱状统计(图7)中可以看出,最小二乘配置法、克里金法和径向基函数法的残差分布范围较为集中,但最小二乘配置法的残差为零值的数据总量占比更高;最小曲率法插值结果出现了误差较大的插值点,产生了不稳定的插值结果。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   不同插值方法计算的残差数据的柱状统计

Fig.7   Columnar statistical charts of residual data by using different interpolation methods


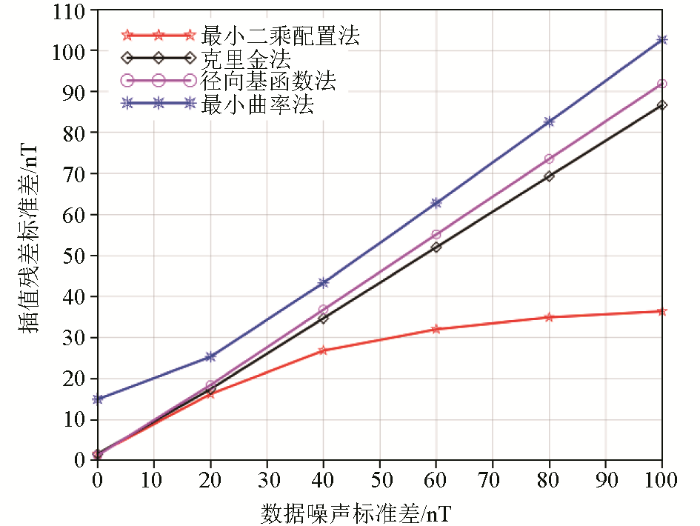
进一步地,为了测试不同插值方法对噪声的压制能力,在图4a的仿真磁力异常网格节点中随机抽取50%的测点并添加标准差分别为0、±20、±40、±60、±80、±100 nT的高斯噪声得到仿真观测数据,进而获得不同噪声水平下各种插值方法计算结果的残差标准差(图8)。可以看出,在不同噪声水平下,最小二乘配置法的残差标准差最小,随着噪声水平增大,残差标准差具有减缓的趋势,说明其插值效果最优且抑制噪声的能力更强;对于克里金插值方法,在噪声较小的情况下其插值效果和最小二乘配置法的相同,可是随着噪声水平增加,残差标准差呈现线性增高;径向基函数方法在噪声水平较低的时候插值效果较好,但是随着噪声水平增加,残差标准差呈现增加趋势,且增加幅度和克里金法的类似;最小曲率插值方法的残差标准差随噪声水平增加呈现大幅度增高,这说明噪声越高最小曲率法抑制噪声的能力最弱。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   不同插值方法在不同噪声水平情况下的残差标准差

Fig.8   Standard deviation values of calculating residuals in cases of different noise levels by using different interpolation methods


通过上述分析认为,在4种插值方法中,最小二乘配置法的插值效果最好、最小曲率法的插值效果相比最差;最小二乘配置法、克里金法、径向基函数法在噪声标准差为0~20 nT的范围内相差不大,但是随着噪声水平增高,最小二乘配置法的残差标准差均小于克里金法和径向基函数法,这说明最小二乘配置法对噪声的抑制效果最好,其本质原因在于最小二乘配置法是按照噪声影响的最小原则来确定待估信号[24,26]。

3 实际应用

本节使用张家峁井田西部的火烧岩地面磁法探测数据,测试最小二乘配置插值与网格化方法的实际应用效果。

3.1 研究区域概况

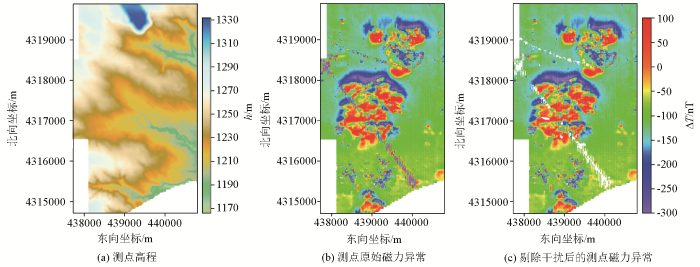
张家峁煤矿位于陕北黄土高原与毛乌素沙漠的接壤地带,地形(图9a)总的趋势为西南、西北高,中东部低[36]。本煤矿地表大部分为第四系沙层、黄土和新近系红土层所覆盖,基岩大多出露于较大的沟谷之中[36]。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   磁力测点高程(a)、原始ΔT磁力异常数据(b)与剔除干扰之后的ΔT磁力异常数据(c)

Fig.9   Elevation (a), original (b) and interference removed (c) ΔT magnetic anomaly data


张家峁井田延安组的2-2煤层位于延安组第四段顶部,埋藏深度0~146.3 m,平均88.18 m,见煤孔中煤层厚度1.13~10.60 m,66个见煤点平均厚度7.58 m;岩性以泥岩和粉砂岩为主,次为炭质泥岩;该煤层区内大面积自燃,于煤矿西部局部保留于矿井西部,呈狭长条状分布,煤层自燃边界线以东煤层自燃或剥蚀,与下伏煤层间距极值23.68~43.04 m,平均间距为30.94 m;2-2煤层为沉积稳定、结构复杂、煤类单一的赋存范围内全部可采的厚—特厚煤层,可采面积11.247 km2。

3.2 地面磁测数据及其预处理

为了探测2-2煤层的火烧岩分布范围,采用加拿大GEM公司生产的GSM-19T型质子磁力仪进行地面高精度总磁场强度测量,线距20 m、点距20 m。经过日变校正、基点值改正与正常场改正之后,获得地面总磁场强度异常(即ΔT磁异常)离散数据分布(图9b)。由于高压电线等影响,存在两条明显的干扰条带。因此,结合高压电线的位置与磁力异常幅值特征,手动删除了干扰较大的测点,得到剔除严重干扰之后的ΔT磁力异常数据(图9c)。

3.3 网格化处理结果

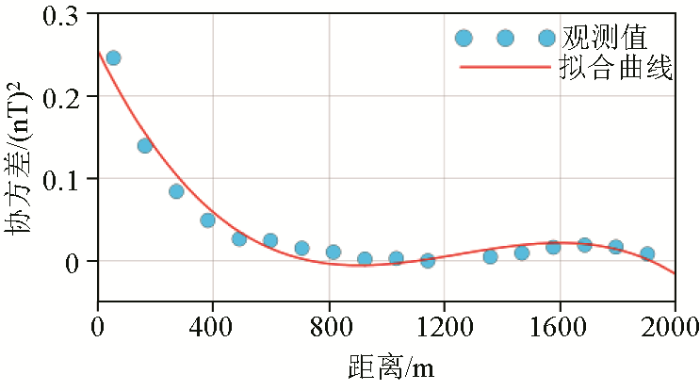
首先采用实测数据根据其点位坐标与磁力异常值,计算得到观测的协方差值(图10中蓝色圆点);然后采用3阶多项式函数拟合观测协方差,得到协方差函数(图10中红色实线)。根据拟合得到的协方差函数即3阶多项式函数以及观测点坐标和待插值点坐标计算信号与观测量之间的互协方差矩阵cov(S', L)、信号自协方差矩阵cov(S, S)、噪声协方差矩阵cov(N, N),进而代入式(14),计算得到待网格化点处的预测数据(图11a)。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   由实测数据计算的协方差以及拟合的协方差函数曲线

Fig.10   Calculated covariance values and fitted covariance function curve by practical observation data


图11

新窗口打开| 下载原图ZIP| 生成PPT

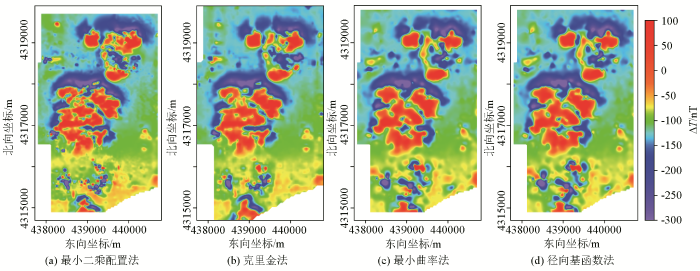
图11   采用不同插值方法计算的网格化结果

Fig.11   Calculated grid results by using different interpolation methods


同时,为了对比网格化效果,采用克里金法、最小曲率法和径向基函数法对图9c所示的实测ΔT磁力异常数据进行了网格化处理,将其绘制成彩色影像图分别如图11b~d所示。

对比不同插值方法的网格化结果可以看出:最小二乘配置法与克里金法的计算结果比较接近,但是最小二乘配置法的计算结果保留的异常细节更丰富;最小曲率法与径向基函数法的计算结果比较一致,但是均损失了较多的异常细节,整体显得更为平滑。

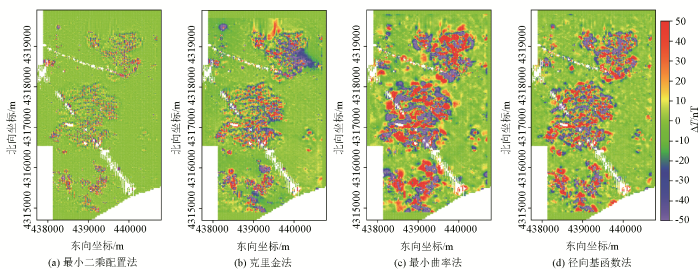
进一步地,为了定量评价每种网格化方法的计算精度,采用Surfer软件中的“Residuals”功能,计算网格化结果与实测数据之间的偏差散点分布(图12)。可见,最小二乘配置网格化方法的计算精度最高,克里金法次之,最小曲率法的计算误差最大,径向基函数的计算精度稍微优于最小曲率法,这与4种网格化方法计算结果的残差均方根值(表3)的结论相符合。4种网格化方法计算结果与实测数据之间的偏差均存在一些绝对值超过1 000 nT的较大值。但是,最小二乘配置法所得的偏差较大的测点相比而言更加稀疏、比较离散,这些偏差较大的测点往往是磁力异常奇异点或粗差,主要由电线与村庄等人类活动干扰或可能的仪器操作失误所致;而其他3种方法所得的偏差较大的测点,不仅存在奇异点,还包括大量的由于插值计算不准确从而引入的有效数据信息,这些测点空间分布比较连续,呈现大尺度分布特征。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   不同网格化方法计算结果与实测数据之间的偏差

Fig.12   Differences between calculated results and practical data by using different interpolation methods


表3   4种网格化方法的计算误差统计参数

Table 3  Statistic parameters of calculating error of four gridding methodsnT

网格化方法均方根值平均值最大值最小值
最小二乘配置法±29.465 4-0.018 01.175 4×10+03-1.496 4×10+03
克里金法±44.854 6-2.791 21.539 3×10+03-2.362 1×10+03
最小曲率法±62.034 40.044 31.826 9×10+03-2.462 5×10+03
径向基函数法±55.273 60.679 21.844 4×10+03-2.508 2×10+03

新窗口打开| 下载CSV


为了了解4种网格化方法计算结果与实测数据之间偏差的统计分布特征,绘制了柱状统计图(图13)。为了更好地展示偏差的统计特征,仅绘制的-200~200 nT之内的偏差数据显示,4种网格化方法计算结果与实测数据之间的偏差均满足正态分布特征。通过对比,最小二乘配置法所得的偏差更加集中于0 nT,这说明最小二乘配置法的插值与网格化的计算精度较高,其本质原因在于最小二乘配置法的关键即协方差函数表达了不同距离磁力异常之间的相关性,这反映了磁力异常的空间变化物理特性,同时也是其他数学类插值方法不具备的重要优势[12-13];另外,最小二乘配置方法按照噪声影响最小的原则确定待估信号,从原理上可以对噪声信号进行滤波与压制。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   不同网格化方法计算误差的柱状统计

Fig.13   Columnar statistical charts of calculating errors by different gridding methods


4 结论与展望

本文针对不规则分布的磁力异常数据网格化处理,引入了最小二乘配置法,通过仿真模拟数据测试以及在煤田地面实测磁力异常数据中的应用与分析,得到如下结论:

1)基于最小二乘配置的磁力异常数据插值与网格化方法的计算精度取决于离散观测数据的误差估计、协方差函数的选取与拟合,误差估计越准确插值计算精度越高,但是数据噪声估计对插值计算结果的影响并不大。此外本文研究表明采用多项式函数作为磁力异常数据处理的经验协方差函数是简单、有效的。

2)通过仿真模拟数据的对比分析表明,最小二乘配置插值与网格化方法是有效的,其计算精度优于克里金法、最小曲率法和径向基函数法,而且最小二乘配置插值与网格化方法可以更好地抑制噪声干扰,且噪声水平越高其抗噪能力越强。

3)在张家峁煤矿实测数据的网格化处理上,相比克里金法、最小曲率法和径向基函数法,最小二乘配置法得到了更好的应用效果,即在尽量排除干扰与误差影响的同时能够更好地保留磁力异常数据中的有效信号。

基于最小二乘配置法的磁力异常数据插值与网格化处理还可在如下3个方面进行改进与拓展:一是,可以通过不同参量之间协方差函数关系的推导从而融合不同的磁力异常分量(如标量、三分量、空间差分梯度以及梯度张量)以及多来源(例如航空与无人机、地面与船载等)的磁测数据;二是,可以采用相应的经验协方差函数将该方法由平面直角坐标系“移植”至球坐标系;三是,本文仅考虑了各向同性插值,可进一步将该方法拓展至各向异性插值问题。

致谢

感谢中国地质大学(武汉)董亚楠在插值与网格化计算方面提供的协助。

参考文献

郭良辉, 孟小红, 郭志宏, 等.

地球物理不规则分布数据的空间网格化法

[J]. 物探与化探, 2005, 29(5):438-442.

[本文引用: 1]

Guo L H, Meng X H, Guo Z H, et al.

Gridding methods of geophysical irregular data in space domain

[J]. Geophysical and Geochemical Exploration, 2005, 29(5):438-442.

[本文引用: 1]

陈欢欢, 李星, 丁文秀.

Surfer 8.0等值线绘制中的十二种插值方法

[J]. 工程地球物理学报, 2007, 4(1):52-57.

[本文引用: 1]

Chen H H, Li X, Ding W X.

Twelve kinds of gridding methods of surfer 8.0 in isoline drawing

[J]. Chinese Journal of Engineering Geophysics, 2007, 4(1):52-57.

[本文引用: 1]

刘兆平, 杨进, 武炜.

地球物理数据网格化方法的选取

[J]. 物探与化探, 2010, 34(1):93-97.

[本文引用: 1]

Liu Z P, Yang J, Wu W.

The choice of gridding methods for geophysical data

[J]. Geophysical and Geochemical Exploration, 2010, 34(1):93-97.

[本文引用: 1]

李小东, 金胜, 王阳玲, 等.

散乱离散点数据的三角形网格化快速成图

[J]. 物探与化探, 2015, 39(1):156-160.

[本文引用: 1]

Li X D, Jin S, Wang Y L, et al.

Triangular grid-based rapid mapping of scattered data

[J]. Geophysical and Geochemical Exploration, 2015, 39(1):156-160.

[本文引用: 1]

孟小红, 侯建全, 梁宏英, 等.

离散光滑插值方法在地球物理位场中的快速实现

[J]. 物探与化探, 2002, 26(4):302-306.

[本文引用: 1]

Meng X H, Hou J Q, Liang H Y, et al.

The fast realization of discrete smooth interpolation in the interpolation of potential data

[J]. Geophysical and Geochemical Exploration, 2002, 26(4):302-306.

[本文引用: 1]

郭志宏.

一种实用的等值线型数据网格化方法

[J]. 物探与化探, 2001, 25(3):203-208.

[本文引用: 1]

Guo Z H.

A practical contour type data gridding technique

[J]. Geophysical and Geochemical Exploration, 2001, 25(3):203-208.

[本文引用: 1]

闫永利, 陈本池, 周凤桐.

提高航空物探网格化精度的一种方法

[J]. 物探与化探, 1997, 21(2):81-90.

[本文引用: 1]

Yan Y L, Chen B C, Zhou F T.

A method for improving gridded precision of airborne geophysical survey

[J]. Geophysical and Geochemical Exploration, 1997, 21(2):81-90.

[本文引用: 1]

张冕, 张春灌, 赵敏, 等.

地球磁异常EMAG2v3与全球重力数据库V29数据质量综合评估——以北极地区Aegir脊为例

[J]. 物探与化探, 2023, 47(6):1410-1416.

[本文引用: 1]

Zhang M, Zhang C G, Zhao M, et al.

An integrated data quality evaluation of Earth magnetic anomaly grid EMAG2v3 and global gravimetric database V29:A case study of the Aegir ridge in the Arctic

[J]. Geophysical and Geochemical Exploration, 2023, 47(6):1410-1416.

[本文引用: 1]

Matheron G.

Principles of geostatistics

[J]. Economic Geology, 1963, 58(8):1246-1266.

[本文引用: 1]

孙洪泉. 地质统计学及其应用[M]. 徐州: 中国矿业大学出版社, 1990.

[本文引用: 1]

Sun H Q. Geostatistics and its application[M]. Xuzhou: University of Mining & Technology Press, 1990.

[本文引用: 1]

Hansen R O.

Interpretive gridding by anisotropic Kriging

[J]. Geophysics, 1993, 58(10):1491-1497.

[本文引用: 1]

彭泽辉, 李辉, 申重阳, 等.

基于最小二乘配置的重力变化插值方法

[J]. 大地测量与地球动力学, 2010, 30(3):43-46.

[本文引用: 2]

Peng Z H, Li H, Shen C Y, et al.

Interpolation method based on least squares collocation for dynamic gravity changes

[J]. Journal of Geodesy and Geodynamics, 2010, 30(3):43-46.

[本文引用: 2]

阮明明, 陈石, 韩建成.

用最小二乘配置法构建局部重力场模型

[J]. 地震学报, 2020, 42(1):53-65,120.

[本文引用: 3]

Ruan M M, Chen S, Han J C.

Regional gravity field model constructed by the least squares collocation

[J]. Acta Seismologica Sinica, 2020, 42(1):53-65,120.

[本文引用: 3]

Briggs I C.

Machine contouring using minimum curvature

[J]. Geophysics, 1974, 39(1):39-48.

[本文引用: 1]

Smith W H F, Wessel P.

Gridding with continuous curvature splines in tension

[J]. Geophysics, 1990, 55(3):293-305.

[本文引用: 1]

许海红, 韩小锋, 袁炳强, 等.

基于径向基函数的1:5万规则分布重力数据插值参数优选

[J]. 物探与化探, 2021, 45(6):1539-1552.

[本文引用: 1]

Xu H H, Han X F, Yuan B Q, et al.

Optimization of interpolation parameters for 1:50,000 regular distribution gravity data based on radial basis function

[J]. Geophysical and Geochemical Exploration, 2021, 45(6):1539-1552.

[本文引用: 1]

Alldredge L R.

Rectangular harmonic analysis applied to the geomagnetic field

[J]. Journal of Geophysical Research:Solid Earth, 1981, 86(B4):3021-3026.

[本文引用: 1]

Cordell L.

A scattered equivalent-source method for interpolation and gridding of potential-field data in three dimensions

[J]. Geophysics, 1992, 57(4):629-636.

[本文引用: 1]

Mendonca C A, Silva J B C.

The equivalent data concept applied to the interpolation of potential field data

[J]. Geophysics, 1994, 59(5):722-732.

[本文引用: 1]

王万银, 邱之云.

一种稳定的位场数据最小曲率网格化方法研究

[J]. 地球物理学进展, 2011, 26(6):2003-2010.

[本文引用: 1]

Wang W Y, Qiu Z Y.

The research to a stable minimum curvature gridding method in potential data processing

[J]. Progress in Geophysics, 2011, 26(6):2003-2010.

[本文引用: 1]

Li X, Götze H J.

Comparison of some gridding methods

[J]. The Leading Edge, 1999, 18(8):898-900.

[本文引用: 1]

许海红, 卢进才, 李玉宏, 等.

基于Surfer的1:50 000规则测网重力数据网格化方法选取——以银额盆地赛汉陶来区块重力资料为例

[J]. 地球物理学进展, 2015, 30(6):2566-2573.

[本文引用: 1]

Xu H H, Lu J C, Li Y H, et al.

Selection of gridding methods for 1:50,000 regular-grid gravity data based on surfer — A case from gravity data in Saihantaolai Block of Yin’e Basin

[J]. Progress in Geophysics, 2015, 30(6):2566-2573.

[本文引用: 1]

高艳芳, 陈实, 冯斌.

交叉验证在离散数据网格化时的应用

[J]. 物探化探计算技术, 2012, 34(5):619-621,504.

[本文引用: 2]

Gao Y F, Chen S, Feng B.

Using cross validation in gridding

[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2012, 34(5):619-621,504.

[本文引用: 2]

姚道荣, 钟波, 汪海洪, 等.

最小二乘配置与普通Kriging法的比较

[J]. 大地测量与地球动力学, 2008, 28(3):77-82.

[本文引用: 2]

Yao D R, Zhong B, Wang H H, et al.

Comparison between least square collocation and ordinary Kriging

[J]. Journal of Geodesy and Geodynamics, 2008, 28(3):77-82.

[本文引用: 2]

刘晓刚, 吴晓平, 王凯.

扰动重力梯度张量单分量和组合分量最小二乘配置法模型的建立

[J]. 地球物理学报, 2012, 55(5):1572-1580.

[本文引用: 1]

Liu X G, Wu X P, Wang K.

Construction of the least squares collocation models for single component and composite components of disturbed gravity gradients

[J]. Chinese Journal of Geophysics, 2012, 55(5):1572-1580.

[本文引用: 1]

Wu Y Q, Jiang Z S, Liu X X, et al.

A comprehensive study of gridding methods for GPS horizontal velocity fields

[J]. Pure and Applied Geophysics, 2017, 174(3):1201-1217.

[本文引用: 3]

Moritz H. Advanced physical geodesy[M]. Karlsruhe: Herbert Wichmann, 1980.

[本文引用: 1]

Goyal H K, von Frese R R B, Hinze W J, et al.

Statistical prediction of satellite magnetic anomalies

[J]. Geophysical Journal International, 1990, 102(1):101-111.

[本文引用: 2]

Langel R A, Hinze W J. The magnetic field of the earth’s lithosphere:The satellite perspective[M]. Cambridge: Cambridge University Press, 1998.

[本文引用: 2]

Maus S, Sazonova T, Hemant K, et al.

National geophysical data center candidate for the world digital magnetic anomaly map

[J]. Geochemistry,Geophysics,Geosystems, 2007, 8(6):Q06017.

[本文引用: 2]

Maus S, Barckhausen U, Berkenbosch H, et al.

EMAG2:A 2-arc Min resolution Earth Magnetic Anomaly Grid compiled from satellite,airborne,and marine magnetic measurements

[J]. Geochemistry,Geophysics,Geosystems, 2009, 10(8):Q08005.

[本文引用: 2]

朱晓颖, 于长春, 熊盛青, 等.

磁法在煤火探测中的应用

[J]. 物探与化探, 2007, 31(2):115-119.

[本文引用: 1]

Zhu X Y, Yu C C, Xiong S Q, et al.

The application of the magnetic method to the detection of underground coal fires

[J]. Geophysical and Geochemical Exploration, 2007, 31(2):115-119.

[本文引用: 1]

熊盛青, 于长春.

地下煤层自燃区岩石磁性增强特征及机理研究——以内蒙古乌达和宁夏汝萁沟煤矿为例

[J]. 地球物理学报, 2013, 56(8):2827-2836.

[本文引用: 2]

Xiong S Q, Yu C C.

Characteristics and mechanisms of rock magnetic increasing in underground coal spontaneous combustion area—Take Wuda coal mine of Inner Mongolia and Ruqigou coal mine in Ningxia as examples

[J]. Chinese Journal of Geophysics, 2013, 56(8):2827-2836.

[本文引用: 2]

Ruffhead A.

An introduction to least-squares collocation

[J]. Survey Review, 1987, 29(224):85-94.

[本文引用: 1]

郭志宏, 管志宁, 熊盛青.

长方体ΔT场及其梯度场无解析奇点理论表达式

[J]. 地球物理学报, 2004, 47(6):1131-1138.

[本文引用: 1]

Guo Z H, Guan Z N, Xiong S Q.

Cuboid ΔT and its gradient forward theoretical expressions without analytic odd points

[J]. Chinese Journal of Geophysics, 2004, 47(6):1131-1138.

[本文引用: 1]

王家乐. 张家峁井田2-2煤烧变岩地下水流场数值模拟[D]. 西安: 西安科技大学, 2017.

[本文引用: 2]

Wang J L. Numerical simulation of groundwater flow field of 2-2 coal-burnt metamorphic rock in Zhangjiamao mine field[D]. Xi’'an: Xi’an University of Science and Technology, 2017.

[本文引用: 2]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com