基于Res-UNet网络的井地电阻率法反演

doi:10.11720/wtyht.2025.1126

基于Res-UNet网络的井地电阻率法反演

周楠^,¹, 王智^,¹, 方思南², 张宇哲¹

1.长江大学电子信息与电气工程学院,湖北荆州 434023

2.长江大学地球物理与石油资源学院,湖北武汉 430100

A Res-UNet network-based method for borehole-to-surface electrical resistivity inversion

ZHOU Nan^,¹, WANG Zhi^,¹, FANG Si-Nan², ZHANG Yu-Zhe¹

1. School of Electronic Information and Electrical Engineering, Yangtze University, Jingzhou 434023, China

2. College of Geophysics and Petroleum Resources, Yangtze University, Wuhan 430100, China

通讯作者: 王智(1985-),男,博士,副教授,主要研究方向为电磁法数值模拟和图像处理工作。Email:1324385898@qq.com

第一作者: 周楠(1997-),男,硕士研究生,主要从事电磁法数值研究工作。Email:18140649212@163.com

责任编辑: 朱晓颖

收稿日期: 2024-04-1 修回日期: 2024-10-31

基金资助:

国家自然科学基金(41604093)
国家自然科学基金青年项目(42204127)

Received: 2024-04-1 Revised: 2024-10-31

摘要

为了解决传统电阻率反演方法依赖反演初始模型的选择、反演过程容易陷入局部极小且反演耗时较长的缺点,本文提出了一种基于Res-UNet神经网络的井地电阻率实时反演方法,通过Gmsh软件获得大幅扩展的正演响应数据集,并针对数据特性选取合适的网络参数进行反演实验。实验结果表明,Res-UNet算法能充分挖掘数据特性,快速获得符合地层电性特征的电阻率成像结果,在电阻率正演数据集上的预测值和正演响应的均方误差为0.019 44,在测试集上的均方根误差为0.075 8,与传统反演方法相比,成像结果有显著提升。基于Res-UNet网络的井地电阻率反演方法在仿真模型的反演计算中得到了较好的结果,能快速、准确地反演出地下异常体的位置和形态,且具有较好的抗噪声能力,为电阻率数据和真实地电结构之间的映射关系提供了一种新的方法和思路。

关键词： Res-UNet; Gmsh; 残差块; 批量建模; 井地电阻率反演

Abstract

Traditional resistivity inversion methods tend to rely on the initial inversion model selected, get stuck in local minima, and be time-consuming. To address these issues, this study proposed a real-time resistivity inversion method based on the Res-UNet neural network. First, a significantly expanded forward response dataset was generated using the Gmsh software. Then, inversion experiments were carried out based on appropriate network parameters determined according to data characteristics. The experimental results indicate that the Res-UNet algorithm can fully dig the data characteristics and rapidly produce resistivity images that align with the electrical properties of strata. The experiments on the dataset for resistivity forward modeling yielded a mean squared error between the predicted values and the forward responses of 0.019 44, and those on the test set yielded a mean squared error of 0.075 8, suggesting improved imaging results compared to traditional inversion methods. Furthermore, the proposed method achieved encouraging results in the inversion calculations of simulation models, enabling rapid and accurate inversion of the location and morphologies of subsurface anomalies while exhibiting a strong noise resistance. This study provides a new method and philosophy for mapping the relationship between resistivity data and the actual geoelectric structures.

Keywords： Res-UNet; Gmsh; residual block; batch modeling; borehole-to-surface resistivity method inversion

PDF (4671KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

周楠, 王智, 方思南, 张宇哲. 基于Res-UNet网络的井地电阻率法反演[J]. 物探与化探, 2025, 49(1): 73-81 doi:10.11720/wtyht.2025.1126

ZHOU Nan, WANG Zhi, FANG Si-Nan, ZHANG Yu-Zhe. A Res-UNet network-based method for borehole-to-surface electrical resistivity inversion[J]. Geophysical and Geochemical Exploration, 2025, 49(1): 73-81 doi:10.11720/wtyht.2025.1126

0 引言

井地电阻率法是一种通过测量地下电流与电压关系来探测地下介质电阻率分布的地球物理勘探技术。该方法通过在地面或井下布设电极,并通过电流注入地下介质,测量电流与电压之间的关系,进而推算出地下介质的电阻率分布,广泛应用于矿产勘探、地下水调查等领域。基于深度学习的井地电阻率反演方法依赖于高精度的正演响应数据,正演结果直接影响反演算法的收敛性^[1⇓-3]。为提高正演模拟的精度,任政勇等^[4]总结了目前常用的结构化网格及其局限性,并分析了非结构化网格对复杂地质体边界的适应性;Tang等^[5]使用非结构化网格来拟合复杂地形的电阻率模型。近期,张宇哲等^[6]采用Gmsh软件对起伏地形下的异常体模型进行建模和不规则网格剖分,证明了该软件在地球物理有限单元法正演建模方面具有良好的应用价值。因此,本文采用了有限单元法进行电阻率正演数值模拟,并使用 Gmsh 软件对复杂地形进行非结构化网格剖分,以确保正演计算的准确性。

在井地电阻率反演方面,早期对于勘探数据的反演解释,通常采用在初始模型附近线性近似的迭代反演方法,其中包括OCCAM反演^[7]、快速松弛反演^[8]、自适应正则化反演^[9]等。黄俊革等^[10]实现了二维、三维有限元最小二乘法反演。刘斌等^[11]在最小二乘反演引入不等式约束作为其先验信息,有效地改善了反演结果的精度。王智等^[12]在井地电阻率反演中引入不等式约束项,降低了反演的多解性问题。由于电阻率反演是一个复杂的非线性问题,将非线性问题在初始模型附近进行线性化时,反演易陷入局部极小、依赖初始模型的选择等问题。近年来,随着计算机技术的进步,采用神经网络进行电阻率反演,不依赖于初始模型,不需要求解偏导数矩阵且反演速度快,取得了较好的反演效果^{[13⇓⇓⇓~17]}。张凌云等^[18]将蚁群算法结合BP(back propagation)神经网络进行电阻率反演,改善了神经网络容易陷入局部极小的问题,但网络收敛速度慢;高明亮等^[19]利用免疫遗传算法优化BP神经网络,缩短了反演时间,但反演精度仍有待提高。Phueakim等^[20]将卷积神经网络应用于电阻率反演中,反演分辨率明显优于BP网络,但深层网络容易出现网络退化现象。针对以上问题,本文尝试将Res-UNet网络应用于井地电阻率反演。通过残差块引入的残差连接^[21],使网络更易于训练和优化,并且可以有效地解决网络退化的问题;U形的网络结构^[22]能够更好地保留输入数据的空间信息,同时提取到不同尺度的特征,通过跳跃连接的方式,将编码器中的特征图与解码器中相应尺度的特征图进行连接,使得解码器可以获得更丰富的特征信息。Res-UNet网络克服了BP网络结构不稳定的问题,确保快速收敛于全局最优解,同时可以获得更好的电阻率反演结果,实现了高精度反演。

1 方法原理

1.1 正演理论

在三维无限半空间Ω中,点电源A的坐标为(x_A,y_A,z_A),若求解直流电法点源2.5D边值问题,可以通过傅里叶变换将空间域电位u(x,y,z)转为波数域电位U(x,k,z)。对应波数域电位U满足的偏微分方程:

(1)

\begin{array}{l} \{\begin{array}{l} - Δ \cdot [σ (x, z) Δ U (x, k, z)] + k^{2} σ (x, z) \cdot \\ U (x, k, z) = \frac{1}{2} I δ (r - r_{A}) \\ \frac{\partial U}{\partial n} = 0 \in Γ_{S} \\ \frac{\partial U}{\partial n} + U k c o s (r, n) \frac{K_{1} (k r)}{K_{0} (k r)} = 0 \in Γ_{\infty} \end{array} 。 \end{array}

式中:σ是地下介质电导率;k为波数;I是供电电流强度;δ是Delta脉冲函数;Γ_s和 $Γ_{\infty}$ 分别为三维无限半空间的地表边界和无穷远边界;n代表边界的外法向向量;r是 $Γ_{\infty}$ 上任意一点到点电源的向量;r_A是观测点到点电源的向量;K₁和K₀分别为一阶和零阶修正贝塞尔函数。该偏微分方程的地表边界满足New-man边界条件,无穷远边界满足混合边界条件。有限单元法解决上述边值问题时,需推导边值问题对应的变分问题,式(1)对应的变分问题为

(2)

\begin{array}{l} \{\begin{array}{l} F (u) = \int_{Ω} [\frac{1}{2} {(Δ U)}^{2} + \frac{1}{2} k^{2} σ U^{2} - I δ (r - r_{A})] \cdot d Ω \\ + \frac{1}{2} \int_{Γ_{\infty}} σ k c o s (r, n) \frac{K_{1} (k r)}{K_{0} (k r)} U^{2} d Γ \\ δ F (u) = 0 \end{array} 。 \end{array}

在转换为对应的变分问题后,首先将2.5D井地电阻率法正演模拟程序中基于Gmsh三角形单元剖分的求解区域进行离散化;然后在每个离散单元e上用多项式函数和对应的形函数来近似待求量;最后将每个单元合并,求解大型稀疏线性方程组,得到各个节点处的波数域电位值U,进行傅里叶反变换便可得到空间中的电位值u。

1.2 基于Res-UNet网络模型的反演理论

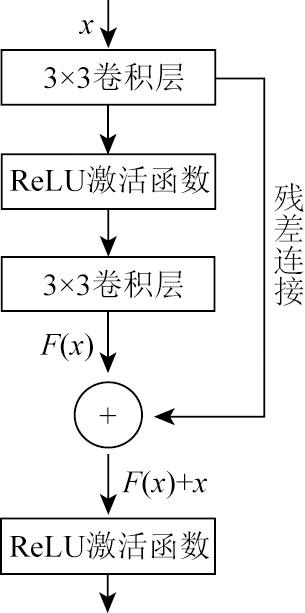
本文所采用的Res-UNet网络是在经典U-Net的基础上进行改进的,U-Net是一种典型的U型网络结构,最早用于解决医学图像的分割任务。该结构具有编码器解码器结构,其中编码器用于捕捉数据的上下文信息,解码器用于还原特征信息,并通过跳跃连接将编码器中的特征图与解码器中的特征图进行连接。Res-UNet网络的井地电阻率反演方法是基于残差块构建模块进行反演训练。残差块构建的模块可以解决深层神经网络训练过程中的梯度消失和梯度爆炸问题,提高网络的训练效果。本文使用如图1所示的残差块结构,其中x代表神经网络输入,F(x)为网络的学习目标,残差连接会直接将输入x传到输出作为输出结果,当x代表的特征达到最为合理的状态时,F(x)会趋近于0。残差网络通过这种跳跃结构简化了学习目标,避免了信息在传递过程中出现丢失、损耗等问题,并且在网络进行前向传播的过程中,有助于缓解网络过深而导致的模型退化现象。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 残差块结构

Fig.1 The diagram of residual block

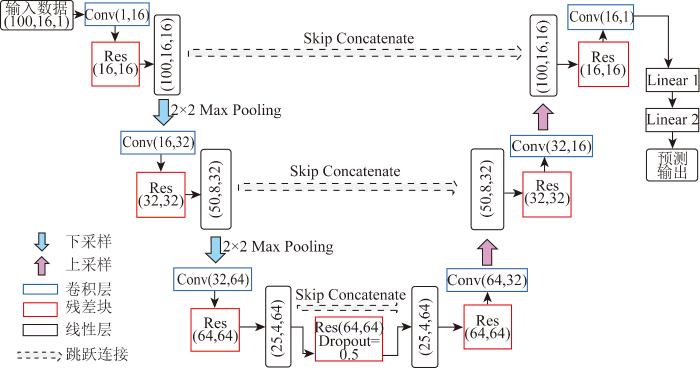
为了实现井地电阻率的反演,本文在每个残差块(Res)使用两个3×3的卷积层,同时填充值为1,以确保特征图的尺寸保持不变。残差连接后,采用ReLU激活函数输出,以增强网络的非线性表达能力。编码器部分由3个卷积层(Conv)、3个残差块和2个最大池化层(Max Pooling)组成,经过卷积层后特征通道增加,以完成特征信息更高层次的抽象表达(图2)。每两次残差计算中间使用池化核大小为2×2的最大池化层对卷积块输出的图像特征进行下采样,下采样可以减少过拟合的风险和计算量,并增加感受野的大小;在经过中间层的残差块后引入Dropout层^[23],取dropout=0.5。Dropout层是一种常用的正则化技术,在训练过程中,它会随机“丢弃”一定比例的神经元,即将其输出置为0。这种做法迫使神经网络不依赖于某些特定的神经元,从而降低了过拟合的风险,提高了网络的泛化能。解码器部分与编码器基本对称,通过最近邻插值快速上采样恢复数据的原始尺寸,并通过跳跃连接(skip concatenate)将编码器的特征图与解码器的特征图连接起来。跳跃连接允许底层的特征直接传递到高层,从而保留了更丰富的信息,防止多次池化下采样造成的部分特征丢失而影响最终的预测精度,且有助于防止梯度消失问题。最后将解码器的输出数据拉伸为一维数组,通过两次全连接层将预测数据与标签维度相匹配。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 Res-UNet网络结构

Fig.2 Res-UNet network structure

由于电阻率法正演数据有限,实验中网络输入仅为(16, 100)的二维矩阵,为了找到最合适该数据集的网络参数,以编码器部分为例,对比不同通道数(表1)在训练500轮时的均方误差MSE值(图3)用于确定合适的网络参数。表1中,Conv1代表编码器部分第一个卷积层,Res1代表第一个残差块;Conv(x,y)和Res(x,y)中x为输入通道数,y为输出通道数。

表1 编码器部分不同通道数

Table 1 Encoder section with different channel numbers

	Conv1	Res1	Conv2	Res2	Conv3	Res3
1	Conv(1,4)	Res(4,4)	Conv(4,16)	Res(16,16)	Conv(16,32)	Res(32,32)
2	Conv(1,16)	Res(16,16)	Conv(16,32)	Res(32,32)	Conv(32,64)	Res(64,64)
3	Conv(1,32)	Res(32,32)	Conv(32,64)	Res(64,64)	Conv(64,128)	Res(128,128)
4	Conv(1,64)	Res(64,64)	Conv(64,128)	Res(128,128)	Conv(128,256)	Res(256,256)

新窗口打开| 下载CSV

图3

新窗口打开| 下载原图ZIP| 生成PPT

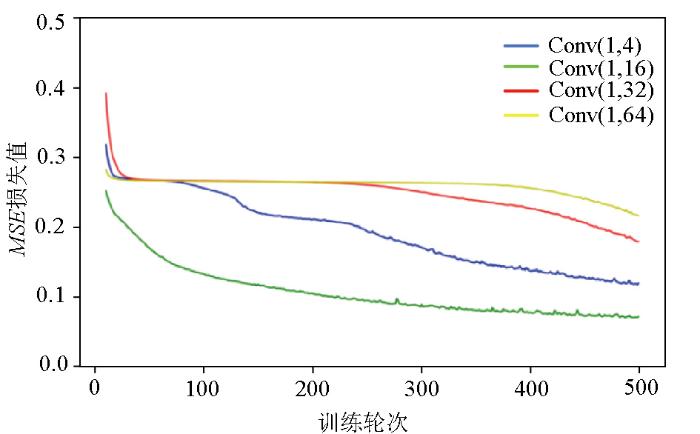
图3 对比不同通道数的MSE值

Fig.3 Compare mean squared error (MSE) values for different channel numbers

2 数据集建立

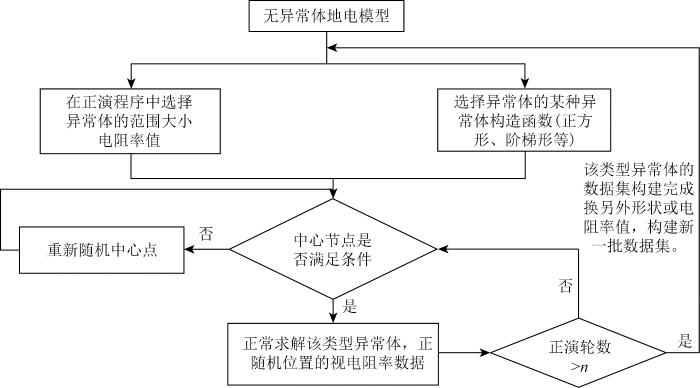
深度学习在井地电阻率法反演中的应用依赖于大量的数据支持。传统的数据集构建方法通常要求预先设计不同位置、大小和电阻率值的异常体模型,并针对每个模型进行计算以获取相应的正演数据。本实验采用不预设异常体的通用井地模型,在每次正演计算前动态赋值异常体参数,以获得不同异常体模型的正演响应。

2.1 训练数据模型的建立

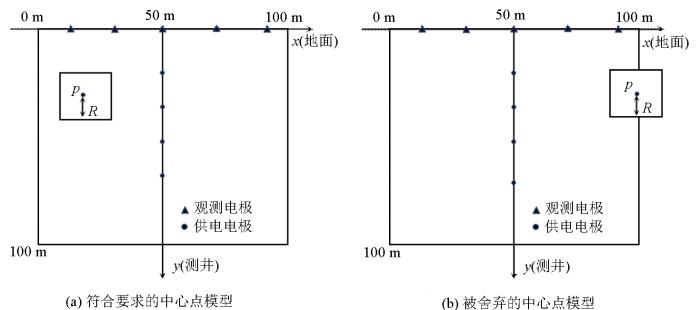
本文以构建正方形异常体井地二级装置模型为例,具体步骤如:①采用Gmsh脚本语言构建图4所示地电模型,待测范围100 m×100 m;测线上均匀部署100个测量电极,范围从0~99 m,间距为1 m;井口位于地面50 m处,井下部署16个供电电极,埋深10~85 m,间距为5 m。读取Gmsh网格剖分数据并整理,同时将所有剖分三角形赋予背景电阻率值。②以随机选取的某网格节点p为中心,通过控制点p到正方形边长的距离R,确定正方形四个顶点的坐标。如果4个顶点都在待求区间范围内(图4a),则该中心点符合条件,反之,该点会被舍弃(图4b),并重新选取符合条件的随机节点p。③利用网格剖分数据定位上述正方形区域内的所有剖分三角,并将其电阻率修改为异常体电阻率的预设值ρ。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 正方形异常体井地二级装置模型示意

Fig.4 Schematic diagram of square anomaly body well-earth secondary device model

对于不同形状的异常体模型,可以选用不同的异常体构造函数,包括正方形、阶梯型、层状模型等;控制异常体大小的R值和电阻率ρ值均可在正演数值模拟程序中设置。随机批量建模流程框图见图5。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 基于Gmsh的随机批量建模流程框架

Fig.5 Flow Chart of Random Batch Modeling Based on Gmsh

井地模型采用Gmsh提供的Delaunay非结构性剖分算法生成网格节点2 4361个、剖分三角形 48 222个。正演模拟程序采用CSR格式储存大型稀疏矩阵,选用Eigen库的LLT(Lower Triangular Cholesky)求解器求解,每次正演计算耗时约87 s。

数据集共包含6 000组样本,其中3 800组用于训练,1 200组用于验证,1 000组用于测试。低阻异常体的电阻率包括10 Ω·m、50 Ω·m、100 Ω·m,高阻异常体的电阻率包括300 Ω·m、500 Ω·m、1 000 Ω·m。数据集中包含的样本类型、以及该类型的样本数量等参数如表2所示。

表2 异常体模型参数

Table 2 Parameters of anomalous body models

异常体类型	异常体尺寸/m	样本数量/个	异常体电率/ (Ω·m)	围岩电阻率/ (Ω·m)
正方形异常体	12×12	1 000	10~100 300~1 000	200
长方形异常体	16×8	1 000
阶梯型异常体	3层9×3	1 000
正方形	12×12	1 500
阶梯型	3层9×3	1 500
层状	100×20	1 500
阶梯型	3层9×3	1 500

新窗口打开| 下载CSV

2.2 数据预处理

正演样本输入神经网络前,通过归一化处理,使其均值为0、标准差为1,从而加速模型的收敛。网络标签是网格剖分后所有节点的电阻率值,但由于剖分节点数量远超正演数据量,输入与输出之间存在显著维度差异。为减少输出空间的维度,实验选择每3个剖分节点中选取1个节点作为预测标签,最终输出的预测标签数量为8 120个。同时,标签数据在输入模型前归一化至[0,1]区间,并在输出最终预测结果前进行反归一化处理,以保持标签数据的相对比例关系,并提升模型在大规模输出情况下的预测效果。

2.3 Res-UNet网络训练流程

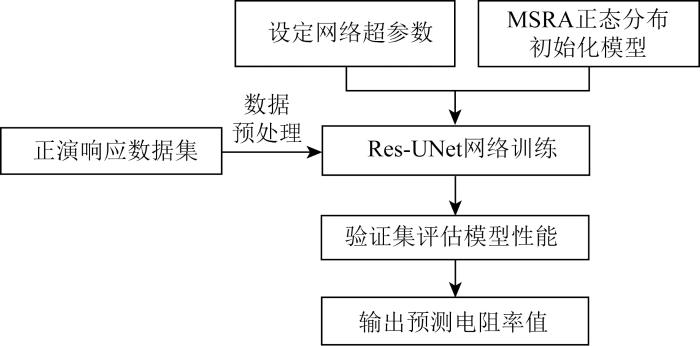
RRes-UNet网络训练和电阻率值预测工作流程如图6所示,具体步骤如下:

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 Res-UNet网络反演流程

Fig.6 Res-UNet network inversion process

1)以Gmsh批量生成2.5D井地模型训练样本为输入数据进行预处理。

2)设定网络超参数,训练采用自适应矩估计(Adaptive moment estimation,Adam)优化函数,该优化器利用梯度的一阶矩估计和二阶矩估计来计算每个参数的学习率,可以更好地适应不同参数的特性有助于克服局部最优解。

3)使用MSRA正态分布初始化网络模型^[24],MSRA正态分布初始化方法解决了传统的正态分布初始化在使用ReLU激活函数时可能导致的梯度消失问题,有助于提高网络的训练效果。

4)使用图3所示的Res-UNet网络对训练集进行训练,通过反向传播算法来调整模型的参数,使得损失函数尽可能地减小。在训练周期结束后,使用验证集来评估模型的性能,以便及时调整模型的超参数。

5)在模型训练完成后,使用测试集来评估模型的泛化能力和性能,计算预测结果与真实电阻率值之间的均方误差来评估模型的准确性。

3 理论数据反演实验

3.1 模型性能

本文采用均方误差MSE作为网络的性能指标,以评估预测模型的准确性,即

(3)

\begin{array}{l} \begin{matrix} M S E = \frac{1}{N} \sum_{i = 1}^{N} (y_{p r e} - y_{t r u e})^{2} 。 \end{matrix} \end{array}

式中:y_true为剖分网格第i个节点的真实电阻率值;y_pre表示网络预测该节点的电阻率值;N为节点总个数,本文中N=8 120。

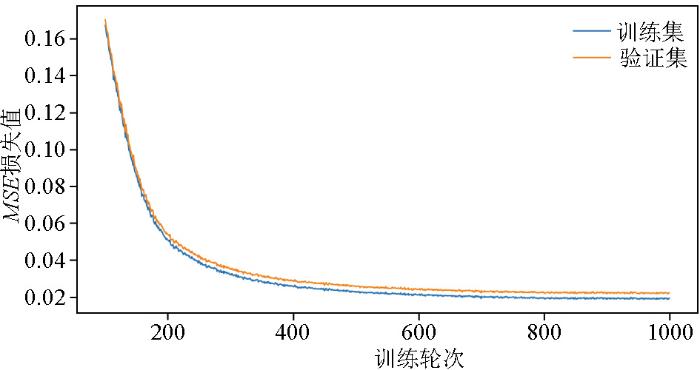
Res-UNet神经网络模型训练的损失曲线如图7所示,实验共训练1 000轮,batch_size为32,初始学习率为10^-4。随着训练的进行,损失曲线趋于收敛。训练过程在800轮左右时,损失曲线的变化幅度减小,但仍在不断地优化,此处调用学习率调度器,使学习率降为10^-5以保证网络收敛更稳定。最终训练集的MSE为0.019 44,验证集的MSE值为0.022 43。损失曲线图呈现出整体平滑的收敛趋势,表明模型在给定的数据集上能够有效地学习到数据的特征,并且在训练过程中没有受到过度拟合或者欠拟合的影响。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 Res-UNet损失曲线

Fig.7 Res-UNet network loss curve graph

3.2 Res-UNet反演结果

为了测试所开发的反演算法对于不同模型的有效性,设计了4组模型,包括低阻单异常体模型一、高阻单异常体模型二、一低阻一高阻双异常体模型三、以及双高阻异常体模型四(具体参数见表3)。以Gmsh批量生成的地电模型(图8a),整个模型的研究区域(目标区域与边界区域)x、z方向的剖分范围分别是(-200 m,300 m)和(0 m,-300 m);目标区域x、z方向的剖分范围在(0 m,100 m)和(0 m,-100 m)之间。测线沿x轴方向上共布置100个测点,间距为1 m;井口坐标为(50 m,0 m),点源移动范围在井下-15~-90 m,间隔为5 m,一共设置16个供电电极。

表3 异常体模型参数

Table 3 Single anomaly model parameters

	异常体大小	异常体中心节点坐标	异常体电阻率/(Ω·m)	背景电阻率/ (Ω·m)
模型一	正方形12 m×12 m	(39,-29)	ρ=500	200
模型二	长方形16 m×8 m	(42,-42)	ρ=100
模型三	正方形12 m×12 m 阶梯形3层9 m×3 m	(20,-30) (80,-50)	ρ₁=100 ρ₂=1 000
模型四	层状100 m×20 m 阶梯形3层9 m×3 m	(50,-70) (43,-39)	ρ₁=500 ρ₂=1 000

新窗口打开| 下载CSV

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 反演结果对比

Fig.8 Inversion result comparison chart

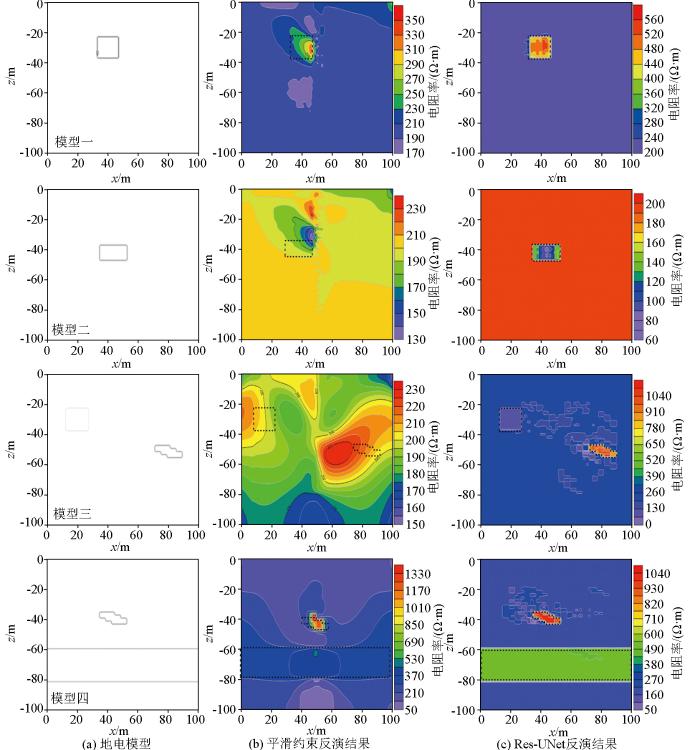
平滑约束反演结果(图8b)显示,基于平滑约束项的传统反演方法通过在模型中引入正则化,增强反演结果的稳定性和连续性,从而减少模型在空间上的剧烈波动,但这种平滑化处理也抑制了模型对地下结构复杂细节的敏感度,使得模型难以精确捕捉其真实形态和尺度。相比传统的反演方法,基于Res-UNet网络的反演结果(图8c)是通过大量的样本数据来学习地下结构的特征,因此可以更好地恢复地下的真实情况。而Res-UNet网络利用残差块允许信息直接在网络中进行传递的特性,减少了信息丢失;且基于跳跃连接使得编码器和解码器部分能够共享特征,这样不仅保留了高分辨率的空间信息,还融合了不同尺度的特征,使其反演结果与原模型在位置、形状、大小等特征方面均基本一致。

由于均方根误差(root mean square error,RMSE)相比于均方误差对离群值的拟合效果更加敏感,可以更好地反映异常体电阻率预测的准确性,因此用RMSE值表示预测模型和真实模型之间的误差大小,计算公式如下:

(4)

R M S E = \sqrt{\frac{\sum_{i = 1}^{N} (y_{p r e} - y_{t r u e})^{2}}{\sum_{i = 1}^{N} (y_{t r u e})^{2}}} 。

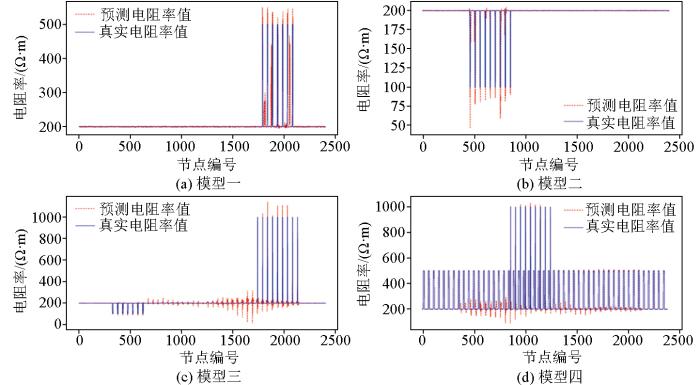
通过Res-UNet网络预测电阻率值和真实电阻率值的对比图(图9)可以看出,模型二的RMSE值仅为0.054 4,模型三和模型四的RMSE值分别为0.110 3和0.072 1。虽然双异常体的RMSE值相对较高,但是偏差主要集中于高阻异常体附近的区域,对于低阻异常体的预测仍较为准确。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 Res-UNet预测值和真视电阻率值对比

Fig.9 Comparison chart of res-UNet predicted values and true apparent resistivity values

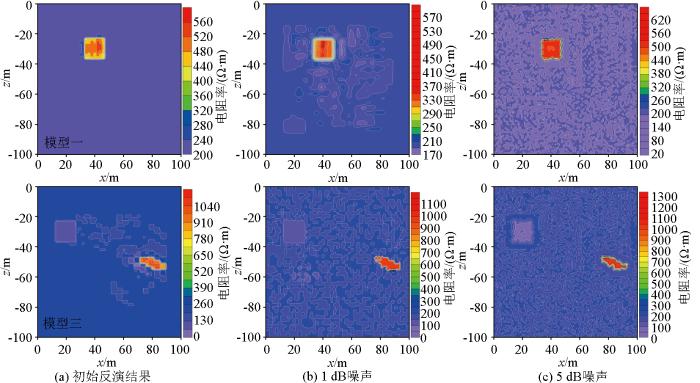
在真实的环境中,直流电法数据通常受噪声等因素的影响。因此抗噪能力分析是评估网络质量的重要步骤。本文选用模型一和模型三的样本,同时对该数据分别加入1 dB 和5 dB的高斯白噪声,得到的反演结果如图10所示。从实验结果可以看出,反演结果受噪声的影响较小,虽然反演准确度有所下降,但反演出异常体的范围和位置都接近于真实模型,说明基于Res-UNet网络的电阻率反演方法,具有较好的抗噪声能力。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 添加高斯白噪声后的反演结果

Fig.10 Adding Gaussian white noise to the inversion results

4 总结

本文使用Gmsh实现了2.5D井地电法正演响应数据的批量生成,该方法可以节约大量建模的时间成本,为网络训练提供了充足的数据集。在基于Res-UNet网络的反演任务中,实验通过比较残差块不同通道数对预测值的影响,对网络结构进行调整和优化,确保其能够有效地学习地下结构与电阻率之间的复杂关系。实验结果表明,该方法可以快速准确地反演出异常体的位置和电阻率值,具有较好的抗噪声能力,证明了该方法在2.5D井地电阻率反演中的可用性。

对于复杂的非规则异常体模型,可以通过更加密集的网格剖分来模拟,但也导致了输入数据和预测数据之间更大的维度差异,这个问题还有待进一步研究。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

蔡军涛, 阮百尧, 赵国泽, 等.

复电阻率法二维有限元数值模拟

[J]. 地球物理学报, 2007, 50(6):1869-1876.