随着勘探技术和计算机技术的进步,大范围密集采样的地球物理勘探得到了发展和普及,如航空地球物理等,随之兴起的大规模勘探数据处理反演解释技术逐渐成为热点研究领域之一。在航空重磁勘探数据物性三维反演中,通常将地下研究区域离散成大量立体网格,而大范围的密集采样数据必然将导致时间成本和存储成本的迅猛增加,提高了大规模位场数据三维反演技术的门槛,难以在实际资料解释中得到应用。

由于物性参数和数据间的线性特征,传统的位场反演技术是通过存储核矩阵来避免不断重复的正演计算过程,这为反演计算节省了大量时间。但随着数据规模和网格数量的急剧增加,核矩阵的计算和存储成本使反演过程难以在普通计算机上实施,尽管提升计算机硬件条件可以暂时解决该问题,但随着数据量的进一步增加,这一问题仍难以避免。针对这一问题,不同学者提出了很多不同的建设性方案。例如通过矩阵压缩技术,减少核矩阵计算量和所需存储空间^[1⇓⇓-4],或者在频率域/波数域进行正演计算^{[5⇓⇓⇓⇓⇓-11]}。还有一些学者通过引入数值计算来简化复杂的位场正演解析计算过程,如有限元法^[12],有限差分法^[13]和有限体积法^[12],但这些方法需要在精度和计算效率上进行权衡,且内存需求仍未减少。Zhdanov^[14]通过将每个网格等效成质点,简化了正演计算过程,在保证精度的同时提高了航空重磁正反演效率,但该方法仅适用于飞行高度远大于网格尺寸的情况。cˇuma 等^[15]将footprint的概念引入到重磁正演中,实现了大范围数据的快速反演。同时,利用并行计算技术搭配强大的计算机配置也是很多大规模位场数据反演所采取的有效手段^{[3,16⇓⇓⇓-20]}。此外,一些特殊的网格剖分方式也被用来减少网格数量,如八叉树离散^[2],非结构网格剖分^[4]和自适应网格剖分^[21]等。采用快速多极算法的重磁正演也展现出高效高精度的优势^[22⇓-24]。

除以上方法外,核矩阵的一些特殊性质也被用来实现位场正演过程的快速计算。Boulanger等^[25]发现规则网格下重力核矩阵具有对称性,并用这一性质来减小核矩阵的存储需求;姚长利等^[26]利用规则网格下重力核矩阵的对称性和平移不变性实现重力正演过程的快速计算;此外,核矩阵的一种特殊结构——分块托普利兹结构(BTTB)被发现,利用该结构特性,可实现核矩阵的大幅度压缩,结合快速傅里叶变换(FFT),可实现位场的快速正演^{[27⇓⇓⇓-31]}。Sun等^[32]基于重力位的球对称性,推导了位场核矩阵的对称性、奇偶性和互相转换关系,解释了以上核矩阵的特殊结构及现象,从而进一步改善了位场正演效率和成本。

在Sun等^[32]提出的位场方法基础上,本文尝试结合footprint技术和FFT技术,进一步提高超大规模正演计算的效率,降低正演对计算机配置的要求,为超大规模位场数据反演奠定基础。随着快速三维正反演技术的发展,“footprint”概念在地球物理勘探领域中得到广泛应用^{[33⇓⇓-36]}。在位场勘探领域,cˇuma 等^[15,34]采用集成灵敏度矩阵的方式对重磁及重力张量的footprint进行了分析,实现了大规模重力张量数据快速反演,但该论文结论仅对特定模型有效,且研究区域当范围较大时,该方法确定footprint的计算量和时间成本均较大。石泽玉等^[36]分析了理论模型在几种footprint尺寸下的正演结果,实现了计算速度的提升,但该分析不够深入全面,仅讨论了特定模型在几种footprint大小下的正演结果,不具有代表性。

本文首先提出位场中footprint的定义方法,再通过理论模型分析位场footprint的范围和影响因素,将有限的影响范围footprint和FFT算法结合,提出footprint-FFT策略,实现超大规模模型的位场快速正演计算。本文通过算例来说明算法的有效性和高效性,所有算例均在一台1.80 GHz CPU和16 GB 内存的笔记本上完成,模型网格数量达到了18亿,计算在数分钟内完成。利用本文提出的方法,超大规模模型的正演计算全程只用存储footprint子空间范围内的核矩阵,同时核矩阵的时间和存储成本也极低,而不同footprint子空间所对应的观测值也会由于FFT算法取代逐点计算,计算十分快捷。Footprint的确定决定了正演精度和计算效率,为精度和计算效率间的平衡提供一种参考依据。理论算例表明该方法效率高,同时对计算机的配置要求不高,在大规模位场数据正反演和基于等效源法的数据处理技术上潜力巨大。

位场正演通常是通过将计算区域地下空间划分为规则网格,并假定网格内的物性均匀分布,通过计算每个网格在观测点处的位场贡献并求和相加。根据位场理论,位场数据和物性之间呈线性关系,因此位场正演过程可表示为:

其中:d表示位场数据;m表示网格物性参数;A则为核矩阵。传统核矩阵大小与地下空间范围和观测点数量息息相关,当数据量和计算区域增加时,核矩阵的大小急剧增加,导致计算耗时严重,甚至导致计算机内存不足。因此,在数据规模较大时,位场核矩阵的计算和存储则成为制约大规模位场三维正反演的关键因素之一。

本文中采用Sun等^[32]提出的位场核矩阵快速计算方法,提高位场正演中大型核矩阵的计算效率和成本。Sun等^[32]根据重力位的球对称特性,推导了位场核矩阵的对称性、奇偶性和互相转换关系等衍生性质。这些性质表明,传统核矩阵中存在大量的冗余信息和冗余计算,解决这个问题不仅可大幅减少单个传统核矩阵的计算量和存储量,还可减少多个分量同时正反演时(如联合反演等)需要存储的核矩阵数量,进一步改善了位场正演模拟的效率和成本。此外,这些衍生性质从本质上解释了重力核矩阵的BTTB结构存在的原因,也解释了姚长利等^[26]提到的平移不变性现象。

该算法不仅适用于重力场核矩阵,还适用于重力位二阶导数和三阶导数的核矩阵计算,这意味着以上性质对磁场和磁梯度、磁张量的正演核矩阵计算同样有效。

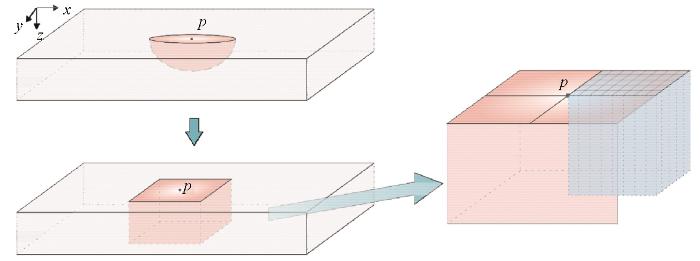
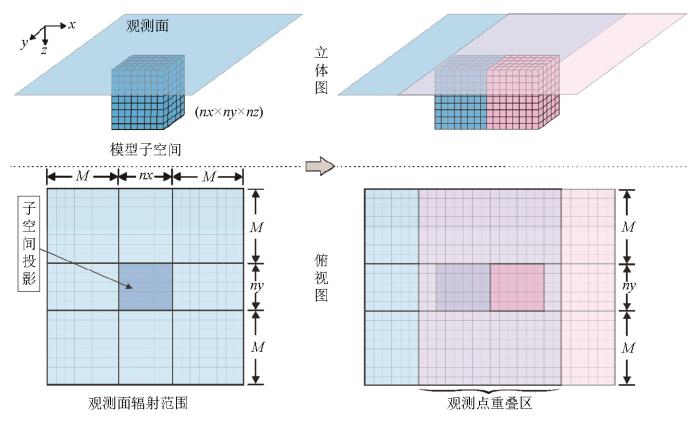
尽管位场的衍生性质能大幅减小核矩阵的计算量和存储量,但是核矩阵仍会随着计算区域的增大而不断增大,对于配置不高的计算机,亦会很快触及其性能上限。本文引入”footprint”概念来解决这一问题。Footprint是指一个观测点周围的地下空间,且该空间的物性对该观测点处的地球物理场产生的影响无法忽视,如图1左上所示,红色区域表示观测点p的footprint范围,该范围内的剖分网格对p点场值的影响不可忽视,而footprint外的网格对观测点的影响有限。该方法可将无限大的地下区域缩减到仅观测点附近的有限影响范围,在保证精度的同时,大幅减少参与计算的网格量,从而减少计算量、提高效率。本文在前人工作基础上,提出一种快速简单的位场footprint确定方法,通过设计理论模型,对位场footprint进行全面分析,掌握不同因素对footprint的影响规律。

不同于航空电磁法,对于位场数据来说,其包含的地下信息深度范围可从地表深至莫霍面,因此不能简单地使用统一固定的footprint范围进行所有正反演的计算,需要针对不同研究深度,进行响应的针对性分析。为了便于分析和计算,我们将图1左上中的footprint简化为长方体形态(如图1左下所示),且footprint水平两个方向宽度相同,深度与所研究区域的深度一致,此时只需要研究footprint水平范围变化,即为该目标深度下footprint水平范围。之所以固定目标深度来研究footprint水平范围,是因为通常研究区域的深度范围远小于水平范围,且水平范围优化所带来的效率提升更为显著。

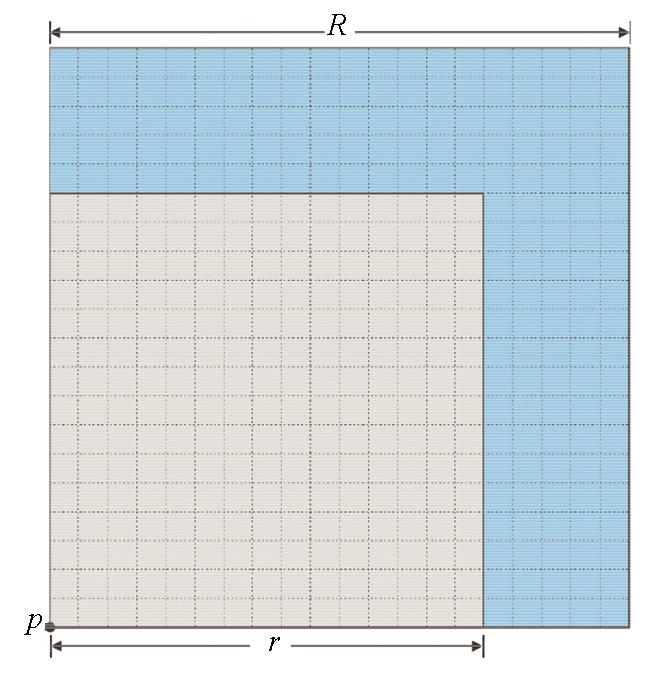
为了定量计算和分析位场的footprint范围,这里定义其判定方法:在以任意观测点为中心的地下长方体空间范围内,当某个范围内,其外围50%的区域体积对该观测点的位场贡献占比小于某个设定阈值ε(足够小),此时的范围即定义为观测点的footprint范围。为了简化footprint定量计算过程和减少计算量,根据1.1节所推出的位场对称性和奇偶性,我们在计算贡献占比时,只需计算以观测点为原点的1/4象限区域(如图1右所示),即只需计算p点右上角蓝色区域。此外,贡献占比计算时,只需根据网格间距进行水平方向上的剖分,在深度方向上网格只设置一层,即每个网格的厚度与研究深度一致。这是由于网格处于观测点下方时,网格深度方向上的剖分方式不影响贡献占比计算,采用单层模式可以大幅减少计算网格的数量,提高footprint分析效率。

为了便于理解本文提出的位场footprint判定方法,以图2为例对判定方法进行解释。图2中蓝色区域为图1右侧中p点左上角空间的俯视图,蓝色区域长度为R,灰色区域长度为r,虚线表示网格。当r=2R/2时,灰色区域占蓝色区域体积比为50%,记灰色区域对p点的位场贡献为V^r,蓝色区域对p点位场贡献为V^R,当满足:

即蓝色外围区域对p点位场贡献之比小于ε时,则认为R为该研究深度下的footprint半径,footprint范围为2R。根据位场性质,离观测点越远的网格体对观测点的贡献越小,因此当ε足够小时,footprint外的区域对观测点的影响很小;同时ε越小,精度越高。以V^R为例,给出位场贡献计算方式如下:

其中:i表示p点左上角空间的网格剖分数量;g_i则表示第i个网格在p点的位场灵敏度。从式(3)可知,蓝色区域对p点的位场贡献为该区域所有网格灵敏度绝对值的和。

由footprint判定方法可知,ε越小,footprint越大,计算精度将越高,但footprint越大,其计算量将迅速增加,因此需要权衡ε取值,使在尽可能保证计算精度满足要求的前提下,减少footprint大小。以将ε设置为1%为例,根据判定方法,在满足式(2)条件时,即使再将footprint空间增加1倍,新增区域网格对观测点的贡献占比将不超过2%,新增区域带来的精度提升有限,但因此而增加的计算量则将成倍增长。因此,根据以该判定方法确定的footprint范围外区域对观测点的影响很小。该方法在尽可能大幅减小计算量的同时,将计算误差保持在一个较低且可接受的水平。需要额外指出的是,footprint定义中的50%比例可以根据实际情况进行调整和修改,在相同阈值情况下,该比例越大,footprint越大,精度越高;该比例越小,footprint越小,精度越低。

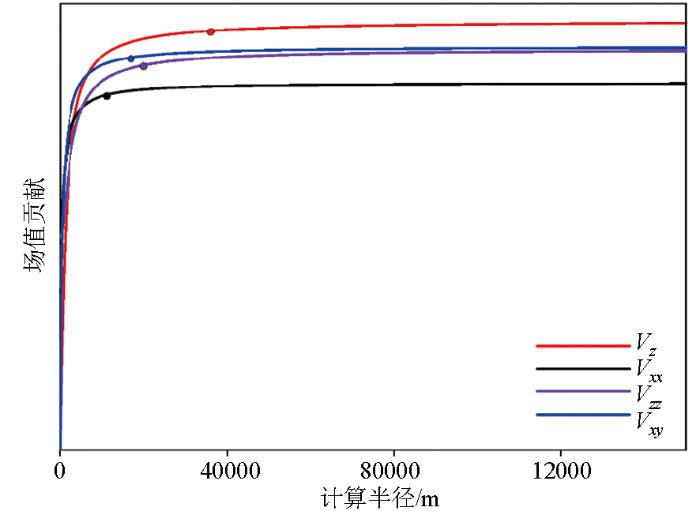
根据本文判定方法,下面对位场footprint的影响因素进行定量分析。设定ε为1%,区域深度为2 km,网格大小为25 m×25 m×2 km,网格厚度与区域深度一致,计算半径最大为150 km。本文计算了包括V_z、V_xx、V_zz和V_xy等位场贡献随计算半径的变化,如图3所示。为了将各场值贡献统一绘制在一个图中,将纵坐标设置为无数值刻度,各曲线仅代表该场值贡献的变化趋势,各曲线间的位置关系不代表场值贡献大小关系。曲线上的圆点表示由式(2)所计算出的footprint半径,V_z、V_xx、V_xy和V_zz的footprint半径分别是36.10 km、11.43 km、20.20 km、14.93 km,重力场的footprint半径最大,符合理论预期。

从图3可知,随着计算半径的增加,各场值贡献不断增大,且呈现前快后慢的形态,计算半径大到一定程度后,场值贡献曲线基本呈现水平趋势,即半径的增大、网格的增多,对场值贡献的影响微乎其微。通过本文方法计算出的footprint半径,曲线均处于接近水平阶段,footprint半径之前,场值贡献变化较快;而footprint半径之后,场值贡献变化基本趋于水平。因此,本文footprint判定方法可以有效界定对位场起主要贡献和作用的区域边界,在减小网格数量的同时为保证计算精度提供保障。此外,当我们认为适当减少footprint半径,对精度影响并不大,但能大幅减少参与计算的网格数量时,减小ε是经济和合适的。例如当我们将ε设为1.5%时,计算得到的重力场的footprint半径为17.80 km,从图3可以看出,该半径仍然处于场值贡献增长趋于水平阶段,即精度影响较少,但半径减少了将近一半。因此,本文方法在平衡精度和计算效率上,提供了一种快速、有效的依据。

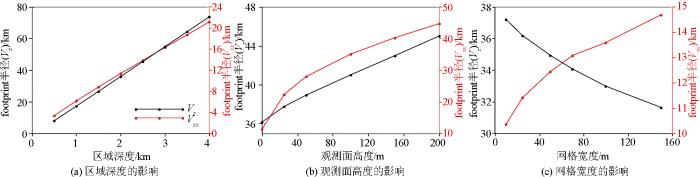
在此基础上,以V_z和V_xx为例,研究了不同区域深度、网格大小、观测面高度等因素对footprint的影响,结果如下图4所示,图中黑色点线表示V_z,红色点线表示V_xx,左侧y轴表示V_z的footprint半径大小,右侧y轴表示V_xx的footprint半径大小。

从上图可知,随着区域深度的增加,V_z和V_xx的footprint半径均呈线性增加趋势;随着观测面高度的增加,V_z和V_xx的footprint半径均增加,但不再呈现线性特征;随着网格宽度的增加,V_z的footprint半径增加,但V_xx的footprint半径却呈现减小趋势。综合以上分析得出,目标深度越大,位场footprint越大;观测面高度越大,位场footprint越大,区域深度和观测面高度对footprint的影响呈正相关关系,但网格大小对不同位场的影响存在差异性。

footprint虽然减少了所需网格数量,但需逐个对观测点计算footprint范围内网格在该观测点处的场值,当数据量过多、计算区域过大时,效率仍不够高。基于FFT的位场正演算法,利用FFT代替卷积过程,实现所有观测点同步计算,可大幅提升计算效率。本文结合两者的优点,提出footprint-FFT正演策略,实现批量观测点的同时计算,配合本文的位场特性,可大幅提高大规模数据正演计算效率和规模上限。

首先将地下区域分成N个互不重叠的模型子空间,每个子空间网格数量为nx×ny×nz,并假定此时位场footprint水平方向半径为R(对应可剖分网格数为M)。如图5所示,左上立体图表示单一模型子空间及观测面,左下俯视图中深蓝色区域表示模型子空间在地表的投影。与传统位场的FFT正演计算不同,单一模型子空间的位场计算不再仅局限于子空间在地表投影的范围。由于footprint的引入,子空间内网格的影响外溢且不可忽略,即投影区邻近的测点同样受到子空间的影响,如图5左下俯视图所示,浅蓝色表示子空间的观测面辐射范围,其辐射范围的网格数量为(nx+2M)×(ny+2M)。

针对这一现象,本文提出一种footprint-FFT策略,在计算子空间正演时,不仅计算子空间网格在地表投影内的位场贡献,还需同时计算在子空间外、footprint范围内的观测点的贡献,即测点计算数量扩大到(nx+2M)×(ny+2M)。

图5中右图表示两个相邻模型子空间及其观测面辐射范围。从图中可知,相邻模型子空间的观测辐射范围存在互相重叠的现象,表示重叠区的测点同时受到这两个子空间内网格的影响。根据位场的可叠加性原理,对不同子空间在重叠测点上的贡献,采取叠加求和计算,这样就能实现任意测点都能反映和累计footprint范围内的网格的影响的目的。

以重力张量中的g_zz为例,说明footprint-FFT方法的实施过程。以m_i表示第i个模型子空间的物性参数(密度或磁化率),数组大小为nx×ny×nz,以U_zz表示g_zz的正演核矩阵,根据位场的衍生性质和以上footprint范围分析,核矩阵的大小为M×M×nz。需要注意的是,核矩阵的大小仅与footprint大小和深度方向的网格剖分有关,而与整个地下空间和模型子空间无关,因此当目标研究深度一定时,该方法的核矩阵不会随着数据规模的增大而不断增大;而且所有模型子空间的核矩阵相同,即该核矩阵仅需要计算一次并保存就可以在所有子空间的计算中直接使用。因此,该方法的核矩阵不仅计算效率高、计算量少,而且所需存储量也很少。

接下来采用二维FFT对物性参数和核矩阵进行逐层卷积,过程如下:

1) 对第i个模型子空间的第k层物性参数mik进行快速傅里叶变换,得到第i个子空间第k层频率域参数m∧ik:

式中:FFT2()表示二维快速傅里叶变换运算,m∧ik大小为nx×ny。

2) 对第k层核函数Uzzk进行快速傅里叶变换,得到频率域核函数U∧zzk,大小为M×M:

3) 拓展m∧ik、U∧zzk矩阵为m∧ik、U∧zzk,扩充元素全部填0,大小增至(nx+2M)×(ny+2M)。

4) 以频率域乘积代替空间域卷积,得到该子空间第k层在测点处的频率域场值g∧zz^ik:

5) 对g∧zzik进行反傅里叶变换,获得该子空间第k层在测点处的频率域场值gzzik:

式中,g∧zzik和gzzik数组大小均为(nx+M)×(ny+M),由子空间及footprint大小决定。

6) 更新k,循环步骤1)~5),逐层计算第i子空间第k层的g_zz^ik并叠加,获得子空间在footprint范围内观测点的场值gzzi:

7) 更新i,循环步骤1)~5),计算不同子空间在相应测点处的场值gzzi并整合,即重叠测点上的场值直接叠加,即可获得整个测区的位场数据g_zz。

与传统方法不同,由于footprint的引入,在3)中对核矩阵和子空间模型参数进行了拓展处理,并在步骤6)中对重叠区域场值进行了叠加,卷积计算的测点不再是子空间地表投影范围,同时对划分的所有子空间进行了遍历。该方法中核矩阵的大小只与footprint大小和深度方向网格数量有关,而与数据规模无关。利用该方法,可实现超大规模位场数据正演,对计算机性能要求大幅降低,同时计算效率也显著提升。

综合来看,footprint-FFT法的作用在于:①引入footprint,来确定子区网格的有效影响范围,并衔接和整合子区对测点的综合影响,避免因分区而带来的各子区间割裂的问题;②通过引入和改变FFT的实施过程与矩阵拓展方式,解决footprint引入后,单一子区对应位场需要逐点计算的低效问题,实现子区内及其外溢效应影响的所有测点同时计算。

需要指出的是,所有子区共用一个核矩阵,而该核矩阵由Sun等^[32]提出的方法来计算,即核矩阵各元素通过解析的位场积分公式求解,因此计算的误差主要由footprint法舍弃的网格所引起,通过1.2节的分析可知,当ε足够小时,这部分引入误差很小,算法精度较高。

本节采用理论模型算例来说明算法的准确性和效率。为了便于进行精度验证,首先采用简单的双长方体异常进行正演,利用解析解和本文方法进行对比,证明方法有效性。

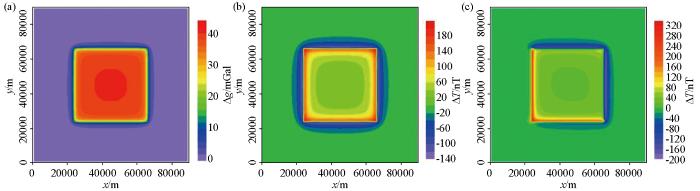
设定模型地下区域范围为90 km×90 km×2 km,单个网格大小为30 m×30 m×10 m,整个地下区域被剖分为18亿个网格(3 000×3 000×200)。设置一个长方体异常,大小为42 km×42 km×1 km,顶部埋深0.3 km,剩余密度为1.0 g/cm³,磁化强度为1 A/m,设置两种磁化模式,分别为垂直磁化(磁化偏角0°,磁化倾角90°)和斜磁化(磁化偏角30°,磁化倾角60°),地磁场与异常体磁化方向相同。

根据之前的footprint分析,取ε为1.5%,区域深度为2 km时,重力场的footprint半径为17.80 km,子空间大小设为30 km×30 km×2 km,即单一子空间所需计算网格数量为1 000×1 000×200,对应需计算的测点范围为65.60 km×65.60 km(子空间范围+2×footprint半径)。整个地下区域被划分为9个子空间,每个子空间按照本文提出的方法分别计算,子空间之间的测点重叠区域进行叠加处理。计算平台为Windows 10系统的联想笔记本,配置为1.80 GHz CPU和16 GB 内存,处理器为Intel Core i7-8550U。得到如图6所示的重力场和磁总场正演计算结果,重力场正演计算耗时约4.62 min;垂直磁化和斜磁化模式下,磁异常场正演计算耗时分别约为7.07 min、9.25 min。

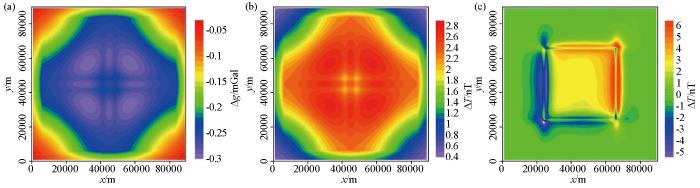
为了验证算法准确性,本文采用不对地下区域进行剖分网格,直接利用长方体解析公式计算整个异常体在相同观测点上的重力场和磁异常场,并于本文方法计算的结果相减,获得绝对误差分布,如图7所示。

从图7中可知,相对误差呈现一种规则性分布,这主要是由于本文选取了一种较为极端模型,即异常体宽度很大,且大小超过了footprint半径,导致超过footprint区域的异常体网格对场的影响被忽略,从而相对误差表现出与场分布较强的相关性。从不同磁化模式来看,倾斜磁化绝对误差相比垂直磁化模式虽然有一定程度增大,但其占磁异常场的百分比没有明显增加,footprint计算结果精度最大相对偏差仍不超过3%,可以满足实际数据精度要求。由于观测点的场值主要受观测点附近网格的影响,虽然增大footprint半径能进一步提高计算精度,但精度提升有限,而所带来的时间成本将迅速增加。

为了进一步说明本文方法的效果,我们在更为复杂的模型上进行了正演模拟计算。Bishop三维基底模型,是以美国加利福尼亚州Bishop以北的部分火山高原地区的地形数据为原型,通过缩放和深度调节,生成的公开测试模型,已被广泛应用于重磁场理论研究和算法验证中^[37-38]。该模型可通过SEG Wiki网站免费获得,该网站致力于向地球科学界和公众提供科学数据和模型。

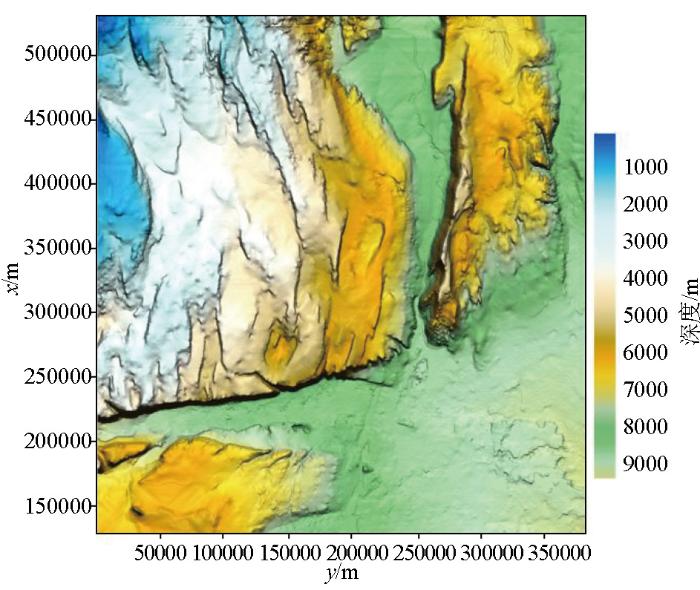
该模型水平范围接近380 km×400 km,基底深度变化范围为地下100~9 300 m,基底变化趋势如图8所示,整体在西北侧偏浅,东南侧较深,且大多数基底区域深度小于5 000 m,西北偏浅的基底被两条沟壑分割成3部分。

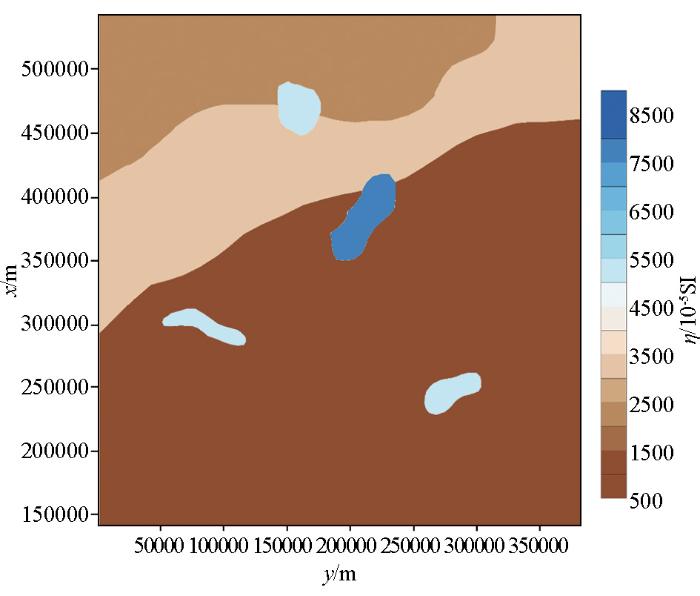
本文将该模型剖分成约27.75亿个长方体网格(2 850×3 015×320),每个网格大小为130 m×130 m×30 m。设定基底以浅的岩层剩余密度为0 g/cm³,且无磁性;而基底面及其深部岩层剩余密度为1.0 g/cm³,且在磁性特征上基底面及以下出现磁性变化,其趋势如图9所示,从西北至东南方向,磁化率逐渐减小,并且存在4个高磁化率的侵入体,均为垂直磁化。

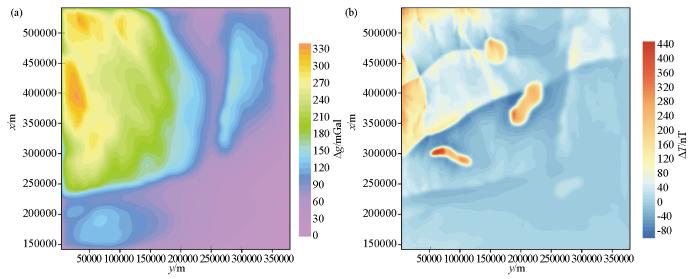
取footprint阈值ε为1.5%,区域深度为9.6 km时,重力场的footprint半径约为81 km,子空间大小设为127 km×133 km×9.6 km,即单一子空间所需计算网格数量为977×1 023×320,整个地下区域被划分为9个子空间,每个子空间按照本文提出的方法分别计算,子空间之间的测点重叠区域进行叠加处理。在与上文相同的计算平台下,得到如图10所示的正演结果,重力场正演计算耗时约4.87 min,磁异常场正演计算耗时约为7.78 min。

从结果分析可知,重力异常主要由基底形态所决定,浅部表现出明显的高场值,且高值部分亦被分割为3部分。磁异常与基底磁化率趋势基本一致,呈现西北高、东南低的特征;受基底深度变化的影响,4个侵入体表现各不相同,3个较浅的侵入体在磁异常场中表现较为明显,而深部的侵入体基本没有反映。以上重磁场特征与预期吻合,体现了本文方法的效果、效率和实用性。

为了改善大规模位场正演的计算效率和硬件成本,解决核矩阵大小随数据规模的变大而无限增加的问题,本文提出了一种footprint-FFT位场正演策略。

首先,本文定义了一种位场footprint的判定算法,并分析了不同因素对位场footprint的影响。其中,网格大小对footprint会产生一定影响,不同场分量对其影响趋势不尽相同;同时,位场的研究深度越大,footprint则越大;此外,飞行高度越大,footprint也越大,但其影响不及研究深度的变化。

在此基础上,本文结合footprint、位场衍生性质和FFT方法,构建了footprint-FFT位场正演算法,实现核矩阵的大幅精简和观测点的批量计算,从而在保证精度的同时提高大规模位场正演模拟的效率。该方法简单快速,在正演计算精度和计算效率间提供一种合理平衡,为大规模高精度的位场正反演奠定基础。算法计算过程表明,该算法的核矩阵大小与数据规模和网格数量无关,只与footprint范围有关,footprint范围越大,正演精度越高,且正演精度与子空间大小无关。子空间大小将影响正演计算效率,子空间数量越多,效率越低。

算例表明,利用该方法,在笔记本上可实现十多亿网格规模的高精度快速正演,且计算时间在数分钟内完成,同时精度可通过调节footprint得到保证。该方法将为大规模位场数据的反演、地形校正,以及基于等效源的延拓、异常转换等处理技术上提供一种高效算法,潜力巨大。