E-mail Alert Rss
 

物探与化探, 2025, 49(1): 52-62 doi: 10.11720/wtyht.2025.1213

方法研究信息处理仪器研制

基于Marchenko理论的层间多次波压制方法

廖震,, 马继涛, 陈小宏, 李文瑾

中国石油大学(北京) 地球物理学院,北京 102249

A Marchenko theory-based method for internal multiple suppression

LIAO Zhen,, MA Ji-Tao, CHEN Xiao-Hong, LI Wen-Jin

College of Geophysics,China University of Petroleum (Beijing),Beijing 102249,China

第一作者: 廖震(1997-),男,2019年毕业于中国石油大学(北京)地球物理学院勘查技术与工程专业,2022年毕业于中国石油大学(北京)地球物理学院地质资源与地质工程专业,目前于中国石油大学(北京)地球物理学院地质资源与地质工程专业攻读博士,主要从事地震资料处理、地球物理勘探等研究工作。Email:3213451131@qq.com

责任编辑: 叶佩

收稿日期: 2024-05-16   修回日期: 2024-11-4  

基金资助: 中国石油天然气集团有限公司科技管理部项目(2022DQ0604-03)

Received: 2024-05-16   Revised: 2024-11-4  

摘要

在地震数据处理流程中,层间多次波的形成机理异常复杂,如何对其准确识别与有效压制一直是地球物理勘探领域中的一个难题。传统的层间多次波压制方法往往需要人工识别地下反射层,在地下介质结构复杂的情况下较难适用。而且这类方法不仅过程繁琐,在预测层间多次波时,通常只能保证时间位置一致,振幅大小往往与实际数据中的观测值不符,一般需要借助自适应匹配相减算法来消除层间多次波。基于Marchenko理论的层间多次波压制方法在处理过程中,通过格林函数的褶积相关互易定理构建聚焦函数与格林函数的波场关系,利用聚焦函数基于波场关系求解得到格林函数,最终得到格林函数构建的多次波或一次波,该方法在迭代进行多维相关和褶积计算过程中只需提供背景速度或原始数据本身作为算子,步骤简便,计算效率高。本文基于Marchenko方程利用格林函数构建一次波场的表达式,通过SMAART模型和墨西哥湾实际数据的测试证明了Marchenko方法能够有效压制复杂地下介质条件下的层间多次波,迭代计算过程中无须速度信息,相比常规方法具有较大优势,在处理难以区分层位的复杂地下环境时具有很好的应用前景。

关键词： 层间多次波; 格林函数; 数据驱动; Marchenko方程; 地震资料处理

Abstract

Seismic data processing reveals that internal multiples exhibit highly complex formation mechanisms,making their accurate identification and effective suppression a persistent challenge in geophysical exploration.Traditional methods for internal multiple suppression frequently require manual identification of subsurface reflection interfaces,making them difficult to apply to complex underground medium structures.Moreover,these methods are not only computationally cumbersome but also typically ensure only temporal and positional consistency when predicting internal multiples.The amplitude often deviates from observed values,requiring adaptive matching subtraction algorithms for effective suppression.This study developed an internal multiple suppression method based on Marchenko theory.Specifically,the wavefield relationships between the focusing function and Green’s function were constructed using the convolution and correlation reciprocity theorem of the Green’s function during data processing.The Green’s function was then solved using the focusing function,yielding either multiples or primaries constructed from the Green’s function.This method requires only the background velocity or the original data as operators during the iterative multidimensional correlation and convolution process,rendering it simple and computationally efficient. This study constructed an expression for the primary wave field using the Green’s function and the Marchenko equation.The tests using the SMAART model and actual data from the Gulf of Mexico demonstrate that the Marchenko method can effectively suppress internal multiples under the conditions of complex subsurface media.The iterative process requires no velocity information,providing significant advantages over conventional methods and great potential for application in complex underground environments where layers are difficult to distinguish.

Keywords： internal multiple; Green’s function; data driven; Marchenko equation; seismic data processing

PDF (5190KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

廖震, 马继涛, 陈小宏, 李文瑾. 基于Marchenko理论的层间多次波压制方法[J]. 物探与化探, 2025, 49(1): 52-62 doi:10.11720/wtyht.2025.1213

LIAO Zhen, MA Ji-Tao, CHEN Xiao-Hong, LI Wen-Jin. A Marchenko theory-based method for internal multiple suppression[J]. Geophysical and Geochemical Exploration, 2025, 49(1): 52-62 doi:10.11720/wtyht.2025.1213

0 引言

在地震资料的处理流程中,多次波的压制一直是非常关键的一环。而层间多次波由于其相对振幅较弱,且速度特性与一次波相似,其识别与压制相较于表层相关多次波更为困难,尤其是在地下介质横向速度变化剧烈或存在低速带的区域,若多次波的消除不彻底,将对速度分析、偏移成像和反演等后续处理步骤产生不利影响。因此,层间多次波的准确识别和有效消除成为地球物理勘探工作中的一个重大挑战。

与表层多次波相比,层间多次波的形成机理更复杂,因此更难被识别和消除。目前主要的压制方法可分为滤波和波动方程两类。滤波类包括FK变换、Radon变换、聚束滤波等,当一次波和多次波之间的时差差异较大时,滤波法计算效率较高,且可以取得较好的压制效果。如Ryu[1]在CDP道集上用FK变换成功分离出一次波记录;Hampson[2]将Radon变换应用于实际数据以压制多次波;张亚伟等[3]联合FK变换与Radon变换对地震合成记录的层间多次波和表层多次波进行压制;White[4]应用MVU聚束滤波法提取出实际数据中的一次波记录;胡天跃等[5]提出了自适应聚束滤波方法,后续成功应用于海上和陆上实际资料处理。然而,滤波类方法在一次波与多次波动校时差差异较小时难以取得较好的压制效果。

波动方程类方法主要根据输入的速度模型或地震记录对层间多次波进行预测。典型的如共聚焦点CFP(common focus point)层间多次波压制方法,这是Berkhout和Verschuur提出的SRME理论的延伸,由Berkhout[6]提出,基于Berkhout等[7]的WRW模型理论,借助CFP道集将炮点和检波点延拓到地下,对层间多次波进行预测。随后,Hadidi等[8]利用CFP方法对实际数据层间多次波进行压制;Kelamis等[9]应用边界算法和层算法对叠后的CMP层间多次波进行压制;王成祥等[10]利用CFP技术处理地下复杂介质的地震资料;王锡文[11]应用CFP对共聚焦点进行成像;辛可锋等[12]基于共聚焦点技术的成像速度进行建模;李振春等[13]利用CFP理论解决复杂近地表问题;马继涛等[14]基于SRME理论对OBC多次波进行压制;包培楠等[15]在CFP的基础上提出了基于迭代反演的层间多次波压制方法。在CFP的基础上,Jakubowicz[16]基于SRME理论提出基于地表数据分离的层间多次波预测方法,基于一次波的逆时形态对层间多次波进行压制,这是目前工业界主流的层间多次波压制算法。Berkhout等[17]进一步提出了基于CFP的扩展SRME层间多次波预测方法,将SRME理论与CFP理论相结合用于预测层间多次波。Ikelle[18]提出了虚同相轴压制层间多次波,利用虚同相轴与原始数据相互褶积预测层间多次波。吴静等[19]基于构建虚同相轴压制层间多次波。然而,基于CFP理论压制层间多次波的方法都十分依赖速度模型,另一种波动方程类的压制层间多次波理论是基于逆散射级数的层间多次波压制技术。Araújo等[20]利用逆散射级数推导了层间多次波的表达式。在此基础上,Weglein等[21]提出了逆散射级数技术ISS(inverse scattering series)压制层间多次波;Malcolm等[22]利用逆散射理论去除CIP(common imaging point)中的层间多次波;Löer等[23]基于逆散射理论预测层间多次波;金德刚等[24]对一维ISS和1.5维ISS算法进行了改进,从而显著提高了这些方法的计算效率;李翔等[25]利用逆散射级数法去除表层多次波;陈小宏等[26]应用逆散射级数理论衰减海上多次波;叶月明等[27]利用地震干涉法衰减海底层间多次波;杨金龙等[28]对去子波化的数据进行逆散射级数计算,提高了算法精度;毕丽飞等[29]应用逆散射级数和2D卷积盲分离压制层间多次波,该方法不需要任何地下信息,但由于涉及到各项级数计算,需要较大的计算资源。

近年来,一种基于Marchenko方程求解格林函数从而对层间多次波进行压制的理论方法在国际上受到了广泛的关注。该方法无需人工选择产生多次波的反射层面,只需提供背景速度或使用原始数据本身,通过对计算的格林函数波场进行相关和褶积计算得到一次波,这是一种完全数据驱动的层间多次波压制方法,能实现对层间多次波“外科手术式”精准压制。在Rose[30]提出单边自聚焦(single-sided autofocusing)概念后,Broggini等[31]将Marchenko理论引入地球物理领域,展示了如何从地表获得地下的虚拟响应;Broggini等[32]提出地震超越干涉法(beyond seismic interferometry)后,将Marchenko理论推广应用到二维和三维;Wapenaar等[33]解释了Marchenko单边自聚焦算法中聚焦函数与格林函数之间的对应关系,通过Marchenko方程求解格林函数,将地下某一点看作聚焦点,也就是产生聚焦函数的虚拟点源,把地下虚拟源到地表的直达波记录看作初始聚焦函数,基于单程波互易性定理用聚焦函数迭代求解波场的格林函数;Wapenaar等[34]基于Marchenko理论对地震数据进行成像。在此基础上,Slob等[35]讨论了Marchenko方程中聚焦函数与格林函数的关系,基于平面波和一维介质实现了层间多次波压制;Meles等[36]首次基于Marchenko自聚焦方法压制层间多次波。然而,该方法需要选定多层的参考基准面计算格林函数,需要多次对预估得到的多次波模型进行匹配相减,可能会对一次波能量造成损伤。van der Neut等[37]研究了Marchenko方程在层间多次波压制方面的应用,为后续MME(marchenko multiple elimination)理论的提出奠定了基础;Zhang等[38]将Marchenko基准面重建方法用于实际资料处理并在此基础上提出了MME,通过格林函数构建一次波场,无需速度模型直接预测一次波,避免了自适应相减对一次波的损伤。

Marchenko理论方程通过格林函数场的褶积相关互易定理构建实际介质与参考均匀半空间介质的波场关系,基于格林函数的因果性和互易性求解得到格林函数与聚焦函数的关系式,从而通过求解参考介质中的聚焦函数得到对应的格林函数。

而基于此理论的层间多次波压制方法则是利用格林函数构建地下真实一次波场的函数表达式,直接对一次波进行求取。但是该方法需要输入去子波化的原始数据波场,但一般情况下很难获得地下的准确反射系数,因此需要先预估数据的子波,对原始数据做反褶积获得去子波的地震数据。本文通过地震道预估子波,基于预估子波对原数据进行反褶积获得反射系数,再将输入的反射系数与自身做多维互相关和褶积迭代更新层间多次波模型,此时的多次波振幅大小与原始数据中的层间多次波振幅一致,极性相反,与原始数据相加即可得到一次波。复杂模型和实际资料的测试结果均证明了该方法的有效性和实用性。

1 方法原理

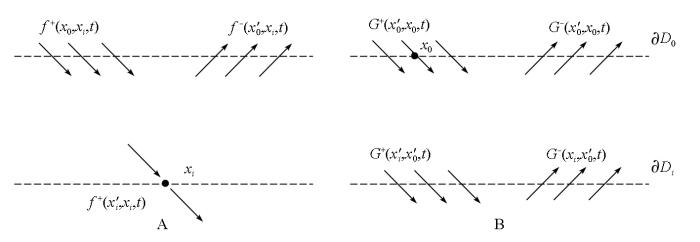
Marchenko层间多次波压制不需要识别地下反射界面,是用数据驱动方式对层间多次波进行压制。用参考半空间均匀介质替代实际均匀介质求解真实格林函数,参考介质和实际介质的波场如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   参考介质和实际介质波场

Fig.1   Reference medium and real medium wave fields


图1中,∂D0表示地表接收点所在的面,∂Di表示地下虚源点所在的面;A为参考介质,B为实际介质;f为参考介质中引入的聚焦函数,其中f+为下行波场,f-为上行波场;G+表示下行格林函数波场,G-表示格林函数上行波场,两者相加即为完整的格林函数G;x'0表示检波点所在的空间位置,x0表示震源点所在位置,xi表示聚焦点。对于格林函数,物理量后面括号中第一个坐标表示虚源点,第二个坐标表示接收点;对于聚焦函数,括号中第一个坐标表示记录波场的位置,第二个坐标表示聚焦点位置。参考介质∂D0平面和∂Di平面之间的区域与实际介质是一致的,但在接收点平面上和虚源点下都为均匀介质,没有反射波。B介质为实际介质,且假设只有地表上为均匀介质,即没有地表反射。则根据卷积型互易定理和相关型互易定理,参考介质A和实际介质B两种介质状态下的波场关系在频率域可以表示成下式:

∫∂D0ρ-1(x)(∂pB+)pA-+(∂pB-)pA+dx0=-∫∂Diρ-1(x)pB+(∂pA-)+pB-(∂pA+)dxi
∫∂D0ρ-1(x)(∂pB+)*pA++(∂pB-)*pA-dx0=-∫∂Diρ-1(x)(pB+)*(∂pA+)+(pB-)*(∂pA-)dxi

式中:p表示压力场,ρ为密度。利用互易定理求解格林函数G,可以将其定义为在∂D0平面上点x0的脉冲点源响应,遵循标量波动方程,格林函数可以写成:

ρ∇1ρ∇G-1c2∂2G∂t2=-ρδ(x-x0)∂δ(t)∂t

式(3)变换到频率域表示可以写成:

ρ∇1ρ∇G+ω2c2G=-jωρδ(x-x0) 。

因为上述是利用单程波的互易定理,格林函数G可以表示成上行格林函数下行格林函数:

G(x,x' 0,ω)=G+(x,x' 0,ω)+G-(x,x' 0,ω)

式中:x表示观测点。单程波的格林函数在观测点x处被分解为下行格林函数G+和上行格林函数G-。

根据波场的传播方向,介质A中的波场可以表示成:

pA+=f+(x0,x' i,ω)
pA-=f-(x0,x' i,ω) 。

聚焦函数在∂Di平面上的导数可以表示为:

∂f+(x' 0,xi,ω)=-12jωρ(xi)δ(xh-x' h)
∂f-(x' 0,xi,ω)=0 。

介质B的波场可以表示为:

pB+=G+(xi,x' 0,ω)
pB-=f+(xi,x' i,ω) 。

格林函数G±在∂D0平面上的导数可以表示为:

∂G-(x,x' 0,ω)=12jωρ(x0)R(x' 0,x0,ω)
∂G+(x,x' 0,ω)=-12jωρ(x0)δ(xh-x' h) 。

将从A、B介质中得到的式(6)~(13)代入式(1)、(2)中可以得到聚焦函数与格林函数的计算关系,如下式所示:

G-(xi,x' 0,ω)=R(x' 0,x0,ω)×　　　　　f+(x0,xi,ω)-f-(x' 0,xi,ω),

G+(xi,x' 0,ω)=-R(x' 0,x0,ω)×　　　　　f-(x0,xi,ω)+f+(x' 0,xi,ω)

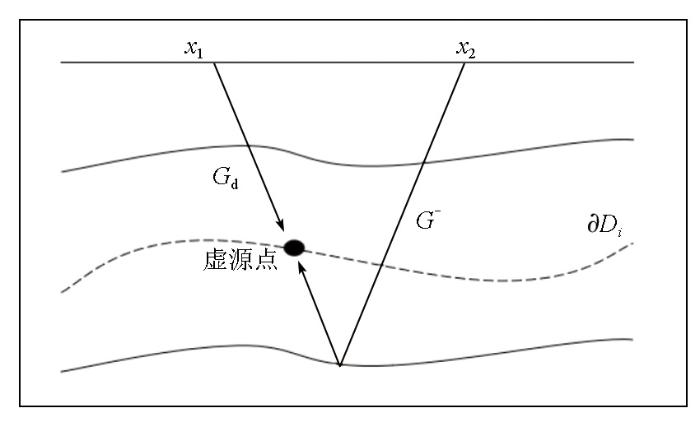
式中:G±表示上下行格林函数,f±表示上下行聚焦函数,R为去子波化的原始数据,x'0表示检波点所在的空间位置,x0表示震源点所在位置,xi表示聚焦点,w为频率。图2中表示了格林函数构建一次波波场,通过直达波Gd与上行格林函数G-做褶积能够得到地下真实反射面的一次波场U-。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   利用格林函数构建一次波场

Fig.2   The employment of Green’s functions for the construction of the primary wavefield


将式(13)、(14)两边同时与Gd做褶积可得:

U-=Gd×G-=Gd×R(x' 0,x0,ω)f+(x0,xi,ω)-　　　Gd×f-(x' 0,xi,ω)
U+=Gd×G+=-Gd×R(x' 0,x0,ω)f-(x0,xi,ω)+　　　Gd*f+(x' 0,xi,ω)

式中:U±表示直达波Gd与上下行格林函数的褶积结果,与格林函数类似,上下行聚焦函数与直达波Gd的褶积可以定义为v±:

v-(x' 0,x″ 0,ω)=Gd(xi,x″ 0,ω)×f-(x' 0,xi,ω)
v+(x' 0,x″ 0,ω)=Gd(xi,x″ 0,ω)×f+(x' 0,xi,ω) 。

根据格林函数的因果性,当初至波还没到达时,格林函数值为0,即在时间区间(0,t2)里,U±的值为0,式(15)、(16)可以改写成v±的表达式:

v-(x' 0,x″ 0,ω)=R(x' 0,x0,ω)×　　　[δ(ω)δ(xh-x″ h)+v+(x0,x″ 0,ω)]
v+(x' 0,x″ 0,ω)=R(x' 0,x0,ω)×v-(x0,x″ 0,ω)

将式(19)代入到式(20)中,可以得到v+的表达式:

v+(x' 0,x″ 0,ω)=R(x' 0,x0,ω)⊗R(x' 0,x0,ω)×δ(ω)δ(xh-x″ h)+R(x' 0,x0,ω)⊗R(x' 0,x0,ω)×　　vm+(x' 0,x″ 0,ω)

用Θ0t2表示时窗(0,t2),式(20)可以简化为:

　　vm+=(I-Θ0t2R*Θ0t2R)-1(Θ0t2R*Θ0t2Rδ)

这里R和R*表示地震数据R与任意波场的多维褶积和多维互相关计算,式(22)根据诺依曼级数展开可对矩阵求逆得:

(I-Θ0t2R*Θ0t2R)-1=I+Θ0t2R*Θ0t2R+(Θ0t2R*Θ0t2R)2+…=∑k=0∞(Θ0t2R*Θ0t2R)k

由式(23)求得的矩阵逆可以化简式(22)得到v+的最终表达式:

vm+=∑k=0∞(Θ0t2R*Θ0t2R)kδ

根据式(15)、(17)、(18)和(24)可以求得U-的表达式:

U-=Θ0t2R+∑k=1∞Θ0t2R(Θ0t2R*Θ0t2R)kδ

式中:Θ为时间窗函数,R为数据R与任意波场做多维褶积运算,R*为数据R与任意波场做多维相关运算,δ为脉冲函数。

等式两边同时略去时窗函数,不改变函数值,可得:

Rt(x' 0,x″ 0,ω)=R(x' 0,x″ 0,ω)+∑m=1∞M2m(x' 0,x″ 0,ω)

式中:Rt为所求解的一次波场,R为去子波化的原始数据,∑M2m为层间多次波,振幅与数据中的层间多次波相等,极性相反。Mm项计算可分为奇数项和偶数项:

M2m(x' 0,x″ 0,ω)=R(x‴ 0,x″ 0,ω)H(ω)×　　　　M2m-1(x‴ 0,x″ 0,ω)
M2m-1x‴ 0,x″ 0,ω)=R(x0,x‴ 0,ω)H(ω)×　　　　M2(m-1)(x0,x″ 0,ω)

Mm项的初值可以从原始数据中通过时窗截取。通过迭代计算,可以求得Mm的所有偶数项和,将其与原始数据相加即可得到一次波记录。

2 模型试算与应用实例

2.1 简单层状模型

本文给出一个简单的合成地震数据验证方法的有效性。所用的速度模型由3个倾斜界面构成。震源和检波点的间隔为10 m,主频为20 Hz,共模拟了401炮,每炮401道。

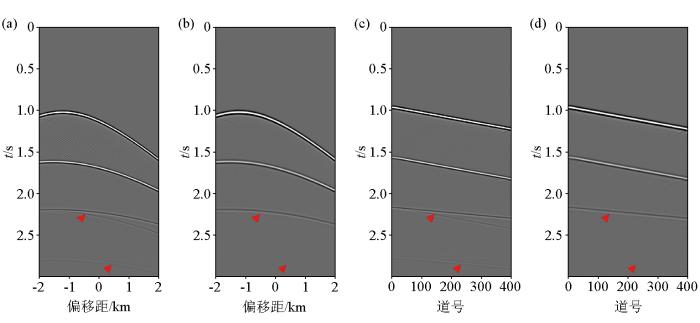
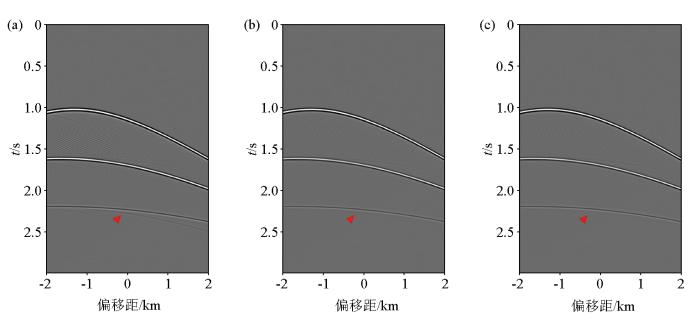
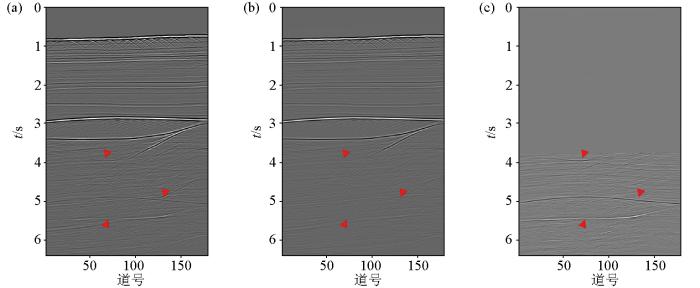
图3a和图3b显示的是模拟的单炮数据压制层间多次波的前后对比;图3c和图3d进一步展示了处理后的模拟数据在零偏移距剖面上的层间多次波压制效果。由这些结果对比可以看出,经过Marchenko层间多次波压制方法处理后,图3中2.1 s和2.7 s处的红色三角标示的层间多次波均被彻底压制,有效信号更加清晰突出。为更详细地显示Marchekno层间多次波压制方法的处理过程,图4和图5展示了根据式(26)计算的一次波Rt和M2m项。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   简单斜层模型的层间多次波压制结果

a—单炮数据;b—单炮压制层间多次波后的结果;c—模型的零偏移距剖面;d—压制层间多次波后的零偏移距剖面

Fig.3   Results of internal multiple elimination in a simple dipping layer model

a—single-shot data;b—the result of eliminating internal multiple in a single shot;c—the zero-offset profile of the model;d—the zero-offset profile after eliminating internal multiple


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   M2m项迭代计算结果

a—迭代2次的M2m项;b—迭代4次的M2m项;c—迭代10次的M2m项

Fig.4   Iterative calculation results for the M2m term

a—the M2m term after twice iterations;b—the M2m term after fource iterations;c—the M2m term after tenth iterations


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   一次波Rt迭代计算结果

a—迭代2次的一次波Rt;b—迭代4次的一次波Rt;c—迭代10次的一次波Rt

Fig.5   Iterative calculation results of the primary wave Rt

a—Rt after twice iterations;b—Rt after fourth iterations;c—Rt after tenth iterations


图4a~图4c显示的是层间多次波∑M2m每一项的迭代结果,可以看到,随着迭代次数的增减,M2m项中的层间多次波同相轴振幅能量越弱,说明累加的和越接近层间多次波的真实值,从下面的一次波Rt迭代结果中也可以看出,∑M2m的累加项越多,层间多次波的压制效果越好,10次迭代后层间多次波已经得到彻底压制。

图5a~图5c显示的是一次波Rt的迭代结果,从迭代结果中可以看出,随着迭代进行,层间多次波的能量逐渐削弱,第10次的一次波迭代结果中已经基本将层间多次波压制。而且图5中红色三角标示的层间多次波与一次波的振幅极性关系和图4中的正好相反,因此在式(26)中的原始数据R与层间多次波∑M2m的相加阶段,可以在不损伤一次波的前提下消除层间多次波。

简单模型的测试结果表面了Marchenko理论在倾斜地层中仍能够较为准确地从数据中识别出层间多次波对其进行压制,受到地下构造信息的影响较小,且完全数据驱动,无需任何的速度信息,操作简便,处理效率和质量较高。

2.2 SMAART模型

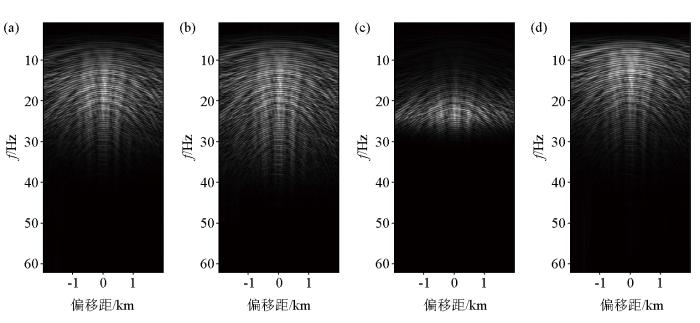
为进一步验证Marchenko层间多次波压制方法的适用性,使用复杂模型SMAART数据进行方法测试。SMAART模型中包含较深的海水和高速盐丘体,受海水和高速盐丘体的影响,海表面、海底和高速盐丘体上下均是较强的反射界面,数据中包含明显的自由表面多次波和层间多次波。Marchenko层间多次波压制方法要求在进行层间多次波压制时,数据中没有表层相关多次波,因此需要提前将SMAART数据中的表层相关多次波压制,这里使用的是SRME方法。Marchenko方法需要输入去子波化后的数据,因此在进行层间多次波压制前需要对SMAART数据压制表层相关多次波后的数据进行反褶积处理,这里选用的是15 Hz的雷克子波。图6是SMAART单炮数据经不同子波反褶积处理后的频谱图。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   SMAART单炮数据不同子波的反褶积频谱

a—原始单炮数据频谱;b—15 Hz雷克子波反褶积频谱;c—10 Hz雷克子波反褶积频谱;d—20 Hz雷克子波反褶积频谱

Fig.6   Deconvolution spectra of different wavelets in SMAART single-shot data

a—original single shot data spectrum;b—15 Hz ricker wavelet deconvolution spectrum;c—10 Hz ricker wavelet deconvolution spectrum;d—20 Hz ricker wavelet deconvolution spectrum


图6b~图6d为不同主频的雷克子波反褶积后的频谱,可以看到,只有图6b子波主频为15 Hz的反褶积频谱相比图6a原始数据主频得到提高,且频谱整体拓宽;图6c中子波主频过小时,反褶积后的主频并未提高,同时数据整体的频谱宽度反而更窄;图6d中的子波主频过大时,反褶积后的频宽与原数据一致,并未有明显的拓频效果。而Marchenko方法由于涉及到大量的多维褶积和相关计算,需要去除子波造成的影响,得到尽可能宽的频带。当子波去除不准时会导致迭代褶积和相关计算过程中生成周期性的图像假象,影响后续层间多次波累加项M2m的计算结果,最终影响层间多次波的压制效果。图7是Marchenko方法准确去子波化后的单炮数据层间多次波压制结果。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   SMAART单炮数据的层间多次波压制

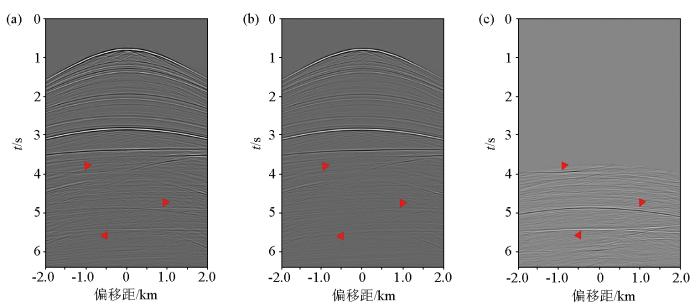
a—单炮数据;b—单炮数据的层间多次波压制;c—压制的层间多次波

Fig.7   Results of SMAART single-shot data after internal multiple elimination

a—single-shot data;b—the result of eliminating internal multiple in a single shot;c—eliminatd internal multiples


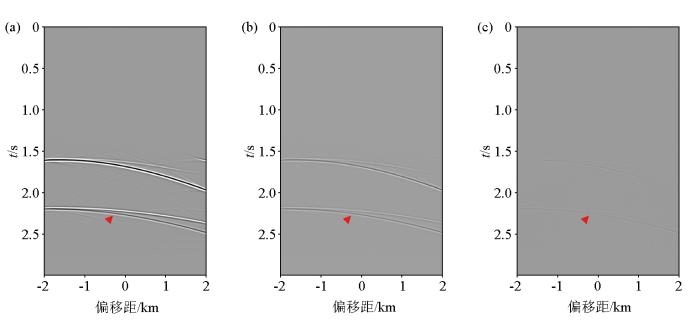
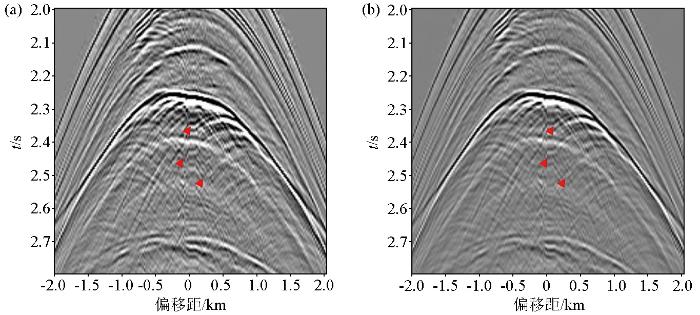
图7a为SMAART单炮数据,图7b为Marchenko层间多次波压制方法处理后的单炮数据,图7c为Marchenko方法压制的层间多次波。从中可以看到4 s、5 s和5.4 s附近的层间多次波被压制,说明在复杂介质下Marchenko方法依然能够压制层间多次波。由于本文测试的SMAART数据中的层间多次波多集中在3 s以下,为了更清晰地显示复杂模型中的层间多次波压制情况,将其时间窗设置在2.8~5.6 s区间进行对比,图8是单炮压制前后2.8~5.6 s的局部放大结果。

图8

新窗口打开| 下载原图ZIP| 生成PPT

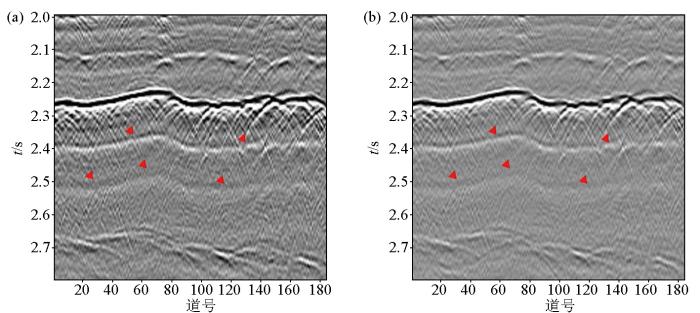
图8   图7在2.8~5.6 s的局部放大结果

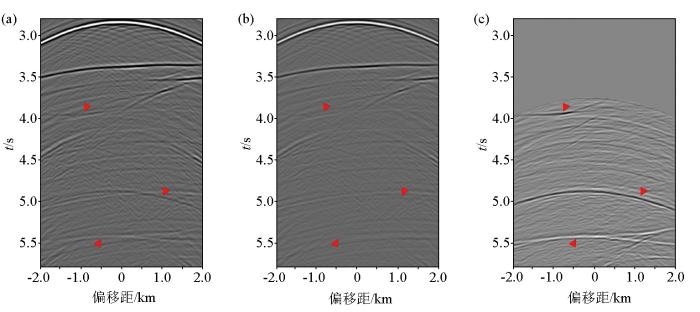
a—单炮数据2.8~5.6 s;b—单炮压制2.8~5.6 s;c—消除的层间多次波2.8~5.6 s

Fig.8   Zoomed section of figure 7 between 2.8 s and 5.6 s

a—single-shot data between 2.8 to 5.6 s;b—the result of eliminating internal multiple between 2.8 to 5.6 s;c—eliminatd internal multiples between 2.8 to 5.6 s


图8a~图8c为单炮层间多次波压制前后2.8~5.6 s的局部放大显示。与图8a对比,在图8b中可以清楚地看到原数据中红色三角标记的层间多次波在图8c中被压制,且与多次波相交的一次波振幅并未被损伤,同相轴相比原数据反而更加清晰可见。图8b单炮记录经过MME方法压制后整体较为干净,一次波形态清晰。图9展示了SMMART数据经Marchenko层间多次波压制方法处理前后的零偏移距剖面。总体来看,剖面整体的压制效果较显著。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   SMAART零偏移距剖面

a—原数据的零偏移距剖面;b—压制层间多次波后的零偏移距剖面;c—压制的层间多次波零偏移距剖面

Fig.9   SMAART zero-offset profile

a—zero-offset profile of the original data;b—zero-offset profile after eliminating internal multiple;c—zero-offset profile of the eliminated internal multiple


图9a~图9c为层间多次波压制前后的零偏移距剖面显示。通过对比可以看出,在图8单炮上显示的4 s、5 s和5.4 s处的层间多次波也被压制干净,且经过方法压制后的剖面(图9b)相较于原始剖面(图9a)具有更能反映地下真实构造的波场特征。地下构造的细节和分辨率得到了显著提升,同相轴的连续性和可追踪性也得到了改善。图7~图9的结果表明了层间多次波压制技术在复杂地质条件下依然适用,证明了Marchenko层间多次波压制方法的有效性和实用性。

2.3 实际数据

复杂模型SMAART数据试验证明了Marchenko层间多次波压制方法在复杂地质环境下依然能对层间多次波进行压制。为进一步说明方法的实用性,本文用部分墨西哥湾数据进行方法测试。这里同样需要先对墨西哥湾数据进行表层相关多次波的压制以及去子波化处理,做反褶积的子波从数据中提取得到。该数据震源和检波点的间隔为26 m,从中抽取了共184炮,每炮184道。图10~图11为Marchenko层间多次波压制方法处理墨西哥湾数据结果。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   墨西哥湾单炮的层间多次波压制

a—单炮数据;b—单炮数据的层间多次波压制

Fig.10   Results of Gulf of Mexico single-shot data after internal multiple elimination

a—single shot data;b—internal multiple elimination of single shot data


图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   墨西哥湾层间多次波压制的零偏移距剖面

a—原始数据零偏移距剖面;b—压制层间多次波后的零偏移距剖面

Fig.11   Zero-offset profile of internal multiple elimination in the Gulf of Mexico

a—zero-offset profile of original data; b—zero-offset profile after eliminating internal multiple


图10a为墨西哥湾单炮数据,图10b为单炮数据经Marchenko层间多次波方法处理后的结果。对比可以看到图中红色三角标示的2.35 s和2.45 s处的层间多次波能量被衰减。

图11a和图11b显示了Marchenko层间多次波方法处理前后的墨西哥湾零偏移距剖面对比,相比单炮结果,零偏移距剖面的对比结果中可以明显的看见箭头所示的2.35 s处的层间多次波能量大部分被压制,2.45 s处的层间多次波被彻底消除。墨西哥湾数据的成功应用证明了该方法在实际数据中也有一定的应用前景。

3 结论和讨论

本文研究了Marchenko层间多次波压制方法,通过求解格林函数并利用格林函数的单程波特性构建地下真实的一次波场。计算过程中涉及大量的多维褶积和多维互相关计算,因此需要每次迭代后设置时窗切除多余的事件轴,整个迭代压制层间多次波过程完全数据驱动。模型数据和实际数据的测试均证明了该方法的有效性和实用性。综合分析,可以得出以下结论:

1)Marchenko层间多次波压制方法基于Marchenko理论方程组求解格林函数,之后根据格林函数构建一次波场的表达式得到地下真实波场。在方法测试中,一般8~10次迭代即可达到较好的层间多次波压制效果,计算过程简单便捷。与常规的层间多次波压制算法相比,Marchenko层间多次波压制方法处理的过程中仅需要输入去子波化的原始数据,无须人为选择反射地层的步骤。对于较难区分地层层位的复杂地下环境可以考虑试用Marchenko层间多次波压制方法去除层间多次波。

2)Marchenko层间多次波压制方法由于涉及大量的多维褶积和相关计算,子波效应会影响褶积和相关计算后的振幅,所以需要输入去子波化的原始数据,而且子波的准确与否同样也会影响方法的压制效果。如何降低Marchenko层间多次波压制方法对子波的敏感性也是我们下一步的研究方向。

参考文献

Ryu J V.

Decomposition(DECOM) approach applied to wave field analysis with seismic reflection records

[J]. Geophysics, 1982, 47(6):869-883.

[本文引用: 1]

Hampson D.

Inverse velocity stacking for multiple elimination

[C]// SEG Technical Program Expanded Abstracts,1986.

[本文引用: 1]

张亚伟, 严加永, 刘振东, 等.

基于F-K和Radon变换的多次波衰减方法

[J]. 中国地质调查, 2015, 2(3):22-27.

[本文引用: 1]

Zhang Y W, Yan J Y, Liu Z D, et al.

Multiples attenuation approach by F-K and radon transform

[J]. Geological Survey of China, 2015, 2(3):22-27.

[本文引用: 1]

White R E.

A multichannel method of multiple attenuation based on hyperbolic moveout curves

[C]// 50th EAEG meeting,Extended Abstracts,1988:1-22.

[本文引用: 1]

胡天跃, 王润秋, White R E.

地震资料处理中的聚束滤波方法

[J]. 地球物理学报, 2000, 43(1):105-115.

[本文引用: 1]

Hu T Y, Wang R Q, White R E.

Beamforming in seismic data processing

[J]. Chinese Journal of Geophysics, 2000, 43(1):105-115.

[本文引用: 1]

Berkhout A J.

Pushing the limits of seismic imaging,Part I:Prestack migration in terms of double dynamic focusing

[J]. Geophysics, 1997, 62(3):937.

[本文引用: 1]

Berkhout A J, Verschuur D J, Romijn R.

Reconstruction of seismic data using the focal transformation

[C]// SEG Technical Program Expanded Abstracts 2004,Society of Exploration Geophysicists,2004.

[本文引用: 1]

Hadidi M T, Verschuur D J.

Removal of internal multiples-field data examples

[C]//Geneva:59th EAGE Conference & Exhibition. European Association of Geoscientists & Engineers,1997.

[本文引用: 1]

Kelamis P G, Erickson K E, Verschuur D J, et al.

Velocity-independent redatuming:A new approach to the near-surface problem in land seismic data processing

[J]. The Leading Edge, 2002, 21(8):730-735.

[本文引用: 1]

王成祥, 赵波, 张关泉, 等.

地下复杂介质地震处理中的CFP技术

[J]. 地球物理学进展, 2003, 18(1):30-34.

[本文引用: 1]

Wang C X, Zhao B, Zhang G Q, et al.

The CFP technology in seismic processing of complex media

[J]. Progress in Geophysics, 2003, 18(1):30-34.

[本文引用: 1]

王锡文.

利用共聚焦点方法消除复杂的近地表效应

[J]. 勘探地球物理进展, 2004, 27(4):260-265.

[本文引用: 1]

Wang X W.

Common focus-point method for elimination of complex near surface effect

[J]. Progress in Exploration Geophysics, 2004, 27(4):260-265.

[本文引用: 1]

辛可锋, 王华忠, 马在田, 等.

共聚焦点层析速度建模方法

[J]. 石油物探, 2005, 44(4):329-333,15-16.

[本文引用: 1]

讨论了基于双聚焦成像理论的层析速度反演方法的基本原理,利用该反演方法实现成像速度模型的迭代更新,使最终模型速度更接近于实际地层速度。由双聚焦成像产生的共聚焦点(CFP)道集是一个部分偏移过的道集,借助于反射层析思想,利用逆时聚焦算子和共聚焦点响应两者之间的时移,通过算子的更新来反演地层速度的更新量。该方法用向量参数化来描述速度模型,用摄动法来更新模型参数,因此提高了计算的稳定性。利用大庆油田的模型数据和胜利油田的实际地震数据对该方法进行了验证。结果表明,用该方法得到的速度模型进行叠前深度偏移,成像效果得到了改善。

Xin K F, Wang H Z, Ma Z T, et al.

Tomographic velocity modeling based on CFP technology

[J]. Geophysical Prospecting for Petroleum, 2005, 44(4):329-333,15-16.

[本文引用: 1]

Based on the fundament of inversion tomography, the method calculates imaging velocity update by operator update, which got from time difference between CFP response and inverse operator. The method uses vector parameterization to characterize velocity model and perturbation to update the model parameters to improve the stability of the inversion. To applied the velocity modeling for synthetic data sets and the real data sets and obtain satisfied results. The tests proved that the imaging effect of prestack depth migration have improved with the method.

李振春, 艾秀娟.

利用CFP技术解决复杂近地表问题综述

[J]. 地球物理学进展, 2008, 23(2):464-469.

[本文引用: 1]

Li Z C, Ai X J.

Review of using CFP technology to resovle complex near surface problems

[J]. Progress in Geophysics, 2008, 23(2):464-469.

[本文引用: 1]

马继涛, Sen Mrinal K, 陈小宏, 等.

海底电缆多次波压制方法研究

[J]. 地球物理学报, 2011, 54(11):2960-2966.

[本文引用: 1]

Ma J T, Sen M K, Chen X H, et al.

OBC multiple attenuation technique using SRME theory

[J]. Chinese Journal of Geophysics, 2011, 54(11):2960-2966.

[本文引用: 1]

包培楠, 王孝, 谢俊法, 等.

基于迭代反演的层间多次波压制方法

[J]. 地球物理学报, 2021, 64(6):2061-2072.

DOI:10.6038/cjg2021O0285      [本文引用: 1]

层间多次波与有效波在走时、频率和叠加速度上差异较小，因此层间多次波压制常难以获得理想效果.本文提出一种基于迭代反演的层间多次波压制方法（MSI，Multiple Suppression Inversion），该方法以共聚焦点（CFP，Common Focus Point）层间多次波压制理论为基础，通过构建卷积因子，将层间多次波压制转变为迭代反演的问题，直接利用观测的地震数据进行迭代反演计算，进而完成多次波压制.MSI方法避免了共聚焦点方法中构建CFP道集的聚焦运算，大幅降低层间多次波预测的计算成本；同时该方法为全数据驱动方法，无需地下介质任何先验信息，算法容易实现.模型数据测试表明，本文提出的方法可有效压制层间多次波，而且对有效波也具有很好的保幅性.

Bao P N, Wang X, Xie J F, et al.

Internal multiple suppression method based on iterative inversion

[J]. Chinese Journal of Geophysics, 2021, 64(6):2061-2072.

[本文引用: 1]

Jakubowicz H.

Wave equation prediction and removal of interbed multiples

[C]// SEG Technical Program Expanded Abstracts 1998.Society of Exploration Geophysicists,1998.

[本文引用: 1]

Berkhout A J, Verschuur D J.

Removal of internal multiples with the common-focus-point (CFP) approach:Part 1—Explanation of the theory

[J]. Geophysics, 2005, 70(3):V45-V60.

[本文引用: 1]

Ikelle L T.

A construct of internal multiples from surface data only:The concept of virtual seismic events

[J]. Geophysical Journal International, 2006, 164(2):383-393.

[本文引用: 1]

吴静, 吴志强, 胡天跃, 等.

基于构建虚同相轴压制地震层间多次波

[J]. 地球物理学报, 2013, 56(3):985-994.

[本文引用: 1]

Wu J, Wu Z Q, Hu T Y, et al.

Seismic internal multiple attenuation based on constructing virtual events

[J]. Chinese Journal of Geophysics, 2013, 56(3):985-994.

[本文引用: 1]

Araújo F V, Weglein A B, Carvalho P M, et al.

Inverse scattering series for multiple attenuation:An example with surface and internal multiples

[C]// SEG Technical Program Expanded Abstracts 1994.Society of Exploration Geophysicists,1994.

[本文引用: 1]

Weglein A B, Gasparotto F A, Carvalho P M, et al.

An inverse-scattering series method for attenuating multiples in seismic reflection data

[J]. Geophysics, 1997, 62(6):1975-1989.

[本文引用: 1]

Malcolm A E, de Hoop M V.

A method for inverse scattering based on the generalized Bremmer coupling series

[J]. Inverse Problems, 2005, 21(3):1137-1167.

[本文引用: 1]

Löer K, Curtis A,

Angelo Meles G.Relating source-receiver interferometry to an inverse-scattering series to derive a new method to estimate internal multiples

[J]. Geophysics, 2016, 81(3):Q27-Q40.

[本文引用: 1]

金德刚, 常旭, 刘伊克.

逆散射级数法预测层间多次波的算法改进及其策略

[J]. 地球物理学报, 2008, 51(4):1209-1217.

[本文引用: 1]

Jin D G, Chang X, Liu Y K.

Algorithm improvement and strategy of internal multiples prediction based on inverse scattering series method

[J]. Chinese Journal of Geophysics, 2008, 51(4):1209-1217.

[本文引用: 1]

李翔, 胡天跃.

逆散射级数法去除自由表面多次波

[J]. 地球物理学报, 2008, 52(6):1633-1640.

[本文引用: 1]

Li X, Hu T Y.

Surface-related multiple removal with inverse scattering series method

[J]. Chinese Journal of Geophysics, 2008, 52(6):1633-1640.

[本文引用: 1]

陈小宏, 刘华锋.

预测多次波的逆散射级数方法与SRME方法及比较

[J]. 地球物理学进展, 2012, 27(3):1040-1050.

[本文引用: 1]

Chen X H, Li H F.

Comparison between inverse scattering series method and SRME method in free surface related multiple prediction

[J]. Progress in Geophysics, 2012, 27(3):1040-1050.

[本文引用: 1]

叶月明, 姚根顺, 赵昌垒, 等.

利用地震干涉法衰减海底相关层间多次波

[J]. 石油地球物理勘探, 2015, 50(2):225-231.

[本文引用: 1]

Ye Y M, Yao G S, Zhao C L, et al.

Sea bottom peg-leg multiple suppression based on seismic interferometry

[J]. Oil Geophysical Prospecting, 2015, 50(2):225-231.

[本文引用: 1]

杨金龙, 朱立华.

逆散射级数层间多次波压制方法及其应用

[J]. 石油物探, 2018, 57(6):853-861.

DOI:10.3969/j.issn.1000-1441.2018.06.007      [本文引用: 1]

逆散射级数法在有效预测层间多次波的同时,面临着一次波和多次波叠加的干扰,为解决压制多次波时保护有效信号不被损伤的问题,开展了逆散射级数层间多次波压制方法的研究。首先从理论上推导并阐述了逆散射级数层间多次波压制方法的物理机制,然后改进常规层间多次波压制处理流程,在逆散射级数法预测层间多次波前、后去除和补偿子波来提高层间多次波预测的准确性,从而降低对自适应相减的依赖度。该方法完全由数据驱动,无需人工干预和先验信息,适用于复杂地形和地质情况的层间多次波压制。模型数据和实际数据应用结果证明了方法的有效性和适用性。

Yang J L, Zhu L H.

Inverse scattering series internal multiple attenuation method and its application

[J]. Geophysical Prospecting for Petroleum, 2018, 57(6):853-861.

DOI:10.3969/j.issn.1000-1441.2018.06.007      [本文引用: 1]

In seismic exploration,due to the interference and overlay of primaries and internal multiples,it is difficult to remove internal multiples,and sometimes,subtracting internal multiples will damage the effective signals.Hence,based on the scattering theory,the inverse scattering series internal multiple attenuation method is discussed,with a detailed demonstration of its physical and mathematical foundations.Moreover,the processing flow is modified by accommodating the source wavelet effect to improve the accuracy of the prediction of the internal multiple and reduce dependence on the adaptive subtraction.This method is completely data-driven and does not require any subsurface information.It is applicable to complex topography and geology.The numerical and field data tests show the validity and applicability of the inverse scattering series internal multiple attenuation method.

毕丽飞, 秦宁, 李钟晓, 等.

应用逆散射级数波场预测和2D卷积盲分离压制层间多次波

[J]. 石油地球物理勘探, 2020, 55(3):521-529.

[本文引用: 1]

Bi L F, Qing N, Li Z X, et al.

Wavefield prediction with inverse scattering series and 2D blind separation of convolved mixtures for suppressing internal multiples

[J]. Oil Geophysical Prospecting, 2020, 55(3):521-529.

[本文引用: 1]

Rose J H.

Single-sided autofocusing of sound in layered materials

[J]. Inverse Problems, 2002, 18(6):1923-1934.

[本文引用: 1]

Broggini F, Snieder R.

Connection of scattering principles:A visual and mathematical tour

[J]. European Journal of Physics, 2012, 33(3):593-613.

[本文引用: 1]

Broggini F, Snieder R, Wapenaar K.

Focusing the wavefield inside an unknown 1D medium:Beyond seismic interferometry

[J]. Geophysics, 2012, 77(5):A25-A28.

[本文引用: 1]

Wapenaar K, Broggini F, Slob E, et al.

Three-dimensional single-sided Marchenko inverse scattering,data-driven focusing,Green's function retrieval,and their mutual relations

[J]. Physical Review Letters, 2013, 110(8):084301.

[本文引用: 1]

Wapenaar K, Thorbecke J, van der Neut J, et al.

Marchenko imaging

[J]. Geophysics, 2014, 79(3):WA39-WA57.

[本文引用: 1]

Slob E, Wapenaar K, Broggini F, et al.

Seismic reflector imaging using internal multiples with Marchenko-type equations

[J]. Geophysics, 2014, 79(2):S63-S76.

[本文引用: 1]

Meles G A, Löer K, Ravasi M, et al.

Internal multiple prediction and removal using Marchenko autofocusing and seismic interferometry

[J]. Geophysics, 2015, 80(1):A7-A11.

[本文引用: 1]

van der Neut J, Wapenaar K.

Adaptive overburden elimination with the multidimensional Marchenko equation

[J]. Geophysics, 2016, 81(5):T265-T284.

[本文引用: 1]

Zhang L L, Staring M.

Marchenko scheme based internal multiple reflection elimination in acoustic wavefield

[J]. Journal of Applied Geophysics, 2018,159:429-433.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com