用于物化探测网布设的GPS航点生成方法与实现

doi:10.11720/wtyht.2025.1292

用于物化探测网布设的GPS航点生成方法与实现

张琪^,, 刘多朝, 张万仁^,

甘肃省地质调查院,甘肃兰州 730000

Method and achievement of GPS waypoint generation for survey grid layout in geophysical and geochemical exploration

ZHANG Qi^,, LIU Duo-Zhao, ZHANG Wan-Ren^,

Geological Survey of Gansu Province,Lanzhou 730000,China

通讯作者: 张万仁(1970-),男,高级工程师,长期从事地质矿产调查工作。Email:873609154@qq.com

第一作者: 张琪(1965-),男,高级工程师,主要从事地球物理勘查工作。Email:zqylzyx@163.com

责任编辑: 沈效群

收稿日期: 2024-07-10 修回日期: 2024-10-18

基金资助:

中国地质调查局地质调查项目(1212010781066)

Received: 2024-07-10 Revised: 2024-10-18

摘要

测网布设是物化探勘查的先行工作内容,手持GPS的广泛应用给中小比例尺物化探野外勘查的导航定位带来了极大的便利。本文从坐标系转换的基础理论出发,面向物化探勘查中规则和不规则两类设计测网,提出了一种可生成大批量航点的方法,并编制了相应的计算软件。该软件界面设计简洁,操作便利,无须借助第三方工具软件即可快捷地生成适合于重磁电测量、土壤测量、水系沉积物测量等方法的设计测网,用于野外作业时导航。

关键词： 坐标系; WGS-84; 手持GPS; 测网布设; 规则网; 不规则网

Abstract

Survey grid layout is a preliminary task of geophysical and geochemical exploration. The widespread use of handheld GPS has greatly facilitated navigation and positioning in small-to medium-scale geophysical and geochemical field surveys. This study, based on coordinate transformation theory, presented a method for generating large numbers of GPS waypoints for both regular and irregular survey grids for geophysical and geochemical exploration. Furthermore, an associated software program was developed. The software enjoys simple interfaces and convenient operations, enabling the quick generation of survey grids suitable for applications such as gravity, magnetic, and resistivity surveys, soil surveys, and stream sediment surveys. Therefore, this software can be used for field navigation.

Keywords： coordinate system; WGS-84; handheld GPS; survey grid layout; regular grid; irregular grid

PDF (3997KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张琪, 刘多朝, 张万仁. 用于物化探测网布设的GPS航点生成方法与实现[J]. 物探与化探, 2025, 49(1): 200-205 doi:10.11720/wtyht.2025.1292

ZHANG Qi, LIU Duo-Zhao, ZHANG Wan-Ren. Method and achievement of GPS waypoint generation for survey grid layout in geophysical and geochemical exploration[J]. Geophysical and Geochemical Exploration, 2025, 49(1): 200-205 doi:10.11720/wtyht.2025.1292

0 引言

在物化探勘查中,野外观测须在设计的规则网或自由网(不规则网)点位上进行,测量人员逐点观测以完成作业。GPS技术应用之前,测点的布设一般先于勘查工作,由地形测量专业人员测绘、定位、标记。GPS的应用使这一阶段工作的效率大大提高、成本大大降低,大大降低了野外工作者的劳动强度^[1]。

GPS(global positioning system)即全球定位系统,用户可利用该系统在全球范围内实现全天候、连续、实时的三维导航定位^[2]。随着3S技术应用和信息化的深入,各类GPS终端机在地质勘查野外作业中已是必需的装备,尤其是手持GPS,因其携带方便、使用简捷等特点更是深受广大野外技术人员的欢迎^[3]。手持GPS已广泛应用于中小比例尺地质、物探(不含重力等对高程要求较高的物探方法)、化探等工作中的定位及导航。

物化探勘查的测点往往较多,数量多以几千甚至上万计。将手持GPS用于定位和导航,当勘查点位数量较少时,航点坐标可手工输入GPS设备中,一旦点位较多,依靠传统的手工输入则是难以想象的。因此,需要一种能够自动生成准确的大批量航点的方法。

1 方法原理

1.1 方法与思路

物化探勘查的野外测网一般分为规则网和不规则网。规则网是在某个测量范围内,按固定的线距、点距、测线方位角排列的测量点网,多在中大比例尺的重磁电测量和化探工作的土壤测量中采用;不规则网则视地形条件的限制或工作方法本身的技术要求等情形而采用,呈自由散点式布设,比如中小比例尺的重力测量和水系沉积物测量。

无论采用哪种测网,在开展野外工作之前,均须在北京54、或西安80、或近年来要求的CGCS2000平面坐标下的底图上设计测点点位,野外测量在这些设计点位上进行。对规则网,根据起始点平面坐标以及测网要素信息,即可计算出所有测点的高斯平面坐标;对不规则网,则需准备包含所有设计测点的高斯平面坐标数据文件。将这些平面坐标数据通过一系列坐标转换,即能生成适于GPS的坐标数据集。

1.2 坐标系简介

长期以来,我国使用的两个国家大地坐标系是1954年北京坐标系和1980年国家大地坐标系(自2018年7月1日起全面使用2000国家大地坐标系),而GPS采用的是WGS-84大地坐标系。

1.2.1 1954年北京坐标系

20 世纪50年代,在我国天文大地网建立初期,鉴于当时的历史条件,采用了Krassovsky椭球,并与前苏联1942年Pulkovo坐标系进行联测,通过计算建立了我国大地坐标系,定名为1954年北京坐标系。几十年来我国按1954年北京坐标系完成了大量的测绘工作,在该坐标系上,通过Gauss-Kruger投影,得到点的平面坐标,测制了各种比例尺地形图。

1.2.2 1980年国家大地坐标系

1975年,第16届国际大地测量及地球物理联合会通过国际大地测量协会第一号决议,公布了被称为IUGG(1975)的地球椭球体。我国自1980年开始采用IUGG(1975)新参考椭球体系,建立了1980年国家大地坐标系,该坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇。

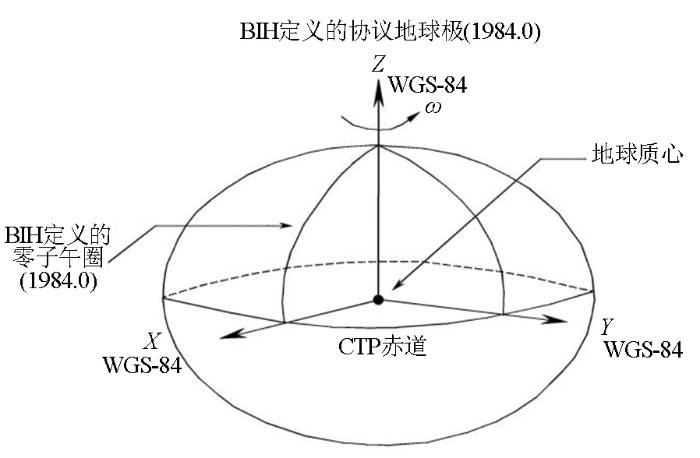
1.2.3 WGS-84大地坐标系

WGS-84大地坐标系的几何定义是(图1):原点位于地球质心,Z轴指向BIH1984.0定义的协议地球极(CTP)方向,X轴指向BIH1984.0的零度子午面和CTP赤道的交点,Y轴通过右手规则确定^[4]。对应地,有WGS-84椭球。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 WGS-84坐标系

Fig.1 WGS-84 coordinate system

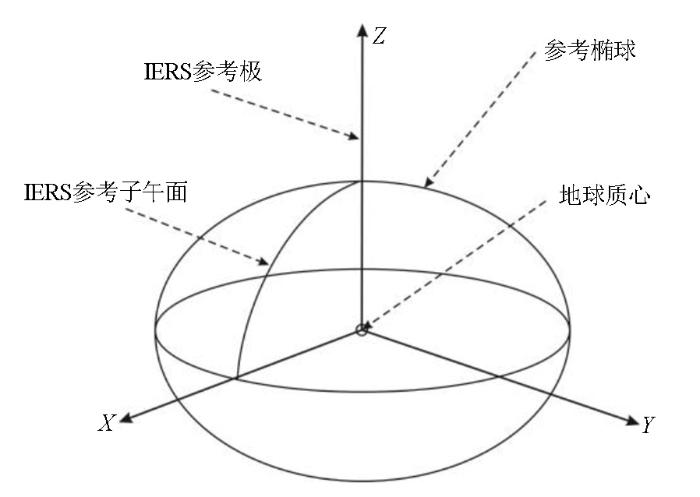
1.2.4 2000国家大地坐标系

2000国家大地坐标系是我国当前最新的国家大地坐标系,英文名称为China Geodetic Coordinate System 2000,英文缩写为CGCS2000。这是一个地心大地坐标系统,以ITRF97参考框架为基准,参考框架历元为2000.0。原点位于地球质量中心,Z轴指向IERS参考极方向,X轴为IERS参考子午面与通过原点且同Z轴正交的赤道面的交线,Y轴完成右手地心地固直角坐标系(图2)^[5]。四个椭球体参数见表1。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 CGCS2000定义

Fig.2 Definition for CGCS2000

表1 四个坐标系采用的椭球参数

Table 1 Ellipsoid parameters for four coordinate systems

椭球体	长半轴a/m	短半轴b/m	扁率f	采用情况
Krassovsky	6378245	6356863.018	1/298.300	北京54坐标系
IUGG 75	6378140	6356755.288	1/298.257	西安80坐标系
WGS 84	6378137	6356752.314	1/298.257	美国GPS
CGCS 2000	6378137	6356752.314	1/298.257	2000国家大地坐标系

新窗口打开| 下载CSV

1.3 坐标系之间的换算^[6⇓-8]

1.3.1 同一椭球内的坐标换算

常用的3种坐标表示方法是:①大地坐标系,用经度(L)、纬度(B)和高程(H)来表示;②空间大地直角坐标,用X、Y、Z来表示;③平面直角坐标系,用纵坐标x、横坐标y和高程h表示。

大地坐标(B、L、H)与空间大地直角坐标(X、Y、Z)的换算关系式是:

$\{\begin{array}{l} X = (N + H) c o s B c o s L, \\ Y = (N + H) c o s B s i n L, \\ Z = [N (1 - e^{2}) + H] s i n B; \end{array}$

式中:N为卯酉圈半径, $N = \frac{a}{\sqrt{1 - e^{2} s i n^{2} B}}$ ;e为第一偏心率, $e = \sqrt{\frac{a^{2} - b^{2}}{a^{2}}}$ ,其中a为椭球长半轴(径),b为椭球短半轴(径),下同。

大地坐标(B、L、H)变换到高斯投影平面直角坐标(x、y)的正算公式为

$\{\begin{array}{l} x = X + N t [\frac{1}{2} m^{2} + \frac{1}{24} (5 - t^{2} + 9 η^{2} + 4 η^{4}) m^{4} + \frac{1}{720} (61 - 58 t^{2} + t^{4}) m^{6}], \\ y = N [m + \frac{1}{6} (1 - t^{2} + η^{2}) m^{3} + \frac{1}{120} (5 - 18 t^{2} + t^{4} + 14 η^{2} - 58 η^{2} t^{2}) m^{5}], \end{array}$

式中: $m = c o s B \cdot l \frac{π}{180}$ ; $l = L - L_{0}$ ,L₀是中央子午线经度; $η = e' c o s B$ , $t = t a n B$ ,e'为第二偏心率: $e' = \sqrt{\frac{a^{2} - b^{2}}{b^{2}}}$ ;X 为子午线弧长,对于克拉索夫斯基(Krassovsky)椭球和IUGG1975椭球,分别按下式计算:

$\begin{array}{l} X_{54} = 111134.8611 B - 16036.4803 s i n 2 B + \\ 16.8281 s i n 4 B - 0.0220 s i n 6 B \end{array}$ ,

$\begin{array}{l} X_{80} = 111133.0047 B - 16038.5282 s i n 2 B + \\ 16.8326 s i n 4 B - 0.0220 s i n 6 B \end{array}$ 。

1.3.2 两个椭球间的坐标转换

两个椭球间的空间直角坐标转换用7参数来定义:3个平移参数ΔX、ΔY、ΔZ,表示两坐标原点的平移值;3个旋转参数w_x、w_y、w_z,表示当地坐标系分别绕地心坐标系空间直角坐标轴(X_t、Y_t、Z_t)旋转至与之平行时的旋转角;最后是比例校正因子m,用于调整椭球大小。

一般用的是布尔莎(Bursa)7参数变换公式:

$\begin{array}{l} [\begin{array}{l} X \\ Y \\ Z \end{array}] = [\begin{array}{l} Δ X \\ Δ Y \\ Δ Z \end{array}] + (1 + m) [\begin{array}{l} X' \\ Y' \\ Z' \end{array}] + \\ [\begin{array}{l} 0 & w_{z} & - w_{y} \\ - w_{z} & 0 & w_{x} \\ w_{y} & - w_{x} & 0 \end{array}] [\begin{array}{l} X' \\ Y' \\ Z' \end{array}] \end{array}$ 。

式中:X、Y、Z是转换后的空间直角坐标值;X'、Y'、Z'是转换前的空间直角坐标值。

如果区域范围不大,最远点间的距离不大于30 km(经验值)时,可以用三参数法,即只计算3个平移参数ΔX、ΔY、ΔZ,而令3个旋转参数和尺度变化参数w_x=w_y=w_z=m=0。

2 技术路线

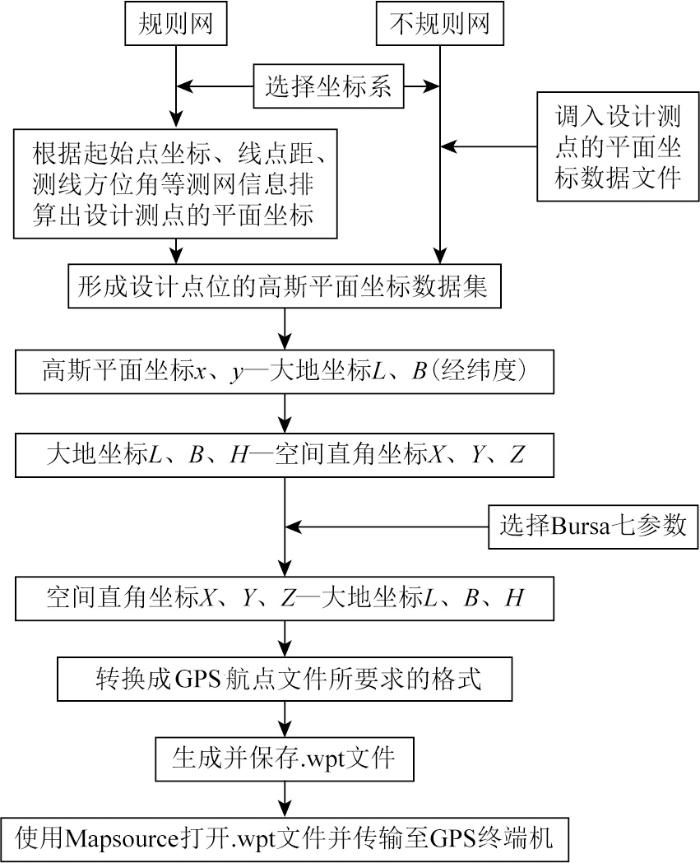
为找到一种将设计的高斯平面坐标点正确、精准地表达在GPS终端设备里(被GPS采用的坐标系认可)的方法,采取的技术路径如下(图3):将设计的高斯平面坐标(北京54或西安80系,或CGCS2000)反算成同椭球下的经纬度;再将此经纬度正算至WGS-84椭球的空间直角坐标X、Y、Z(以米或千米值表征);将X、Y、Z在同椭球参数内反算出WGS-84系的经纬度。当约束加载Bursa七参数改正时,如果3个旋转量和比例因子均赋零值时,则为三参数改正。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 技术流程

Fig.3 Technical flow chart

经过多种方法的验算对比^[9],空间直角坐标X、Y、Z反算成大地坐标L、B、H,采用Newton-Raphson迭代算法^[10]。

3 软件实现

3.1 程序编制

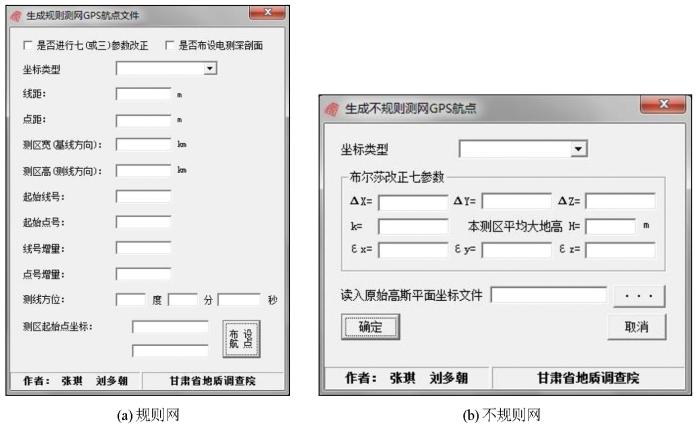
根据上述原理及技术路线,针对物化探勘查常采用的规则网和不规则网,以Visual BASIC 6.0编程语言为工具分别编制了计算程序,界面如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 生成测网GPS航点计算程序界面

Fig.4 GPS waypoint grid generation software interface

3.2 应用实例

3.2.1 规则网航点生成

在某地开展1∶10 000比例尺高精度磁测,测区宽(基线方向)4 km、高(测线方向)2.5 km、线距100 m、点距50 m、测线方位角28.35°。图5a为设计的规则测点网,利用图4a的规则网程序即能生成如图5b所示的可由MapSource调用并传输至GPS的航点文件。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 规则网的航点生成

Fig.5 Generated regular GPS waypoints in MapSource

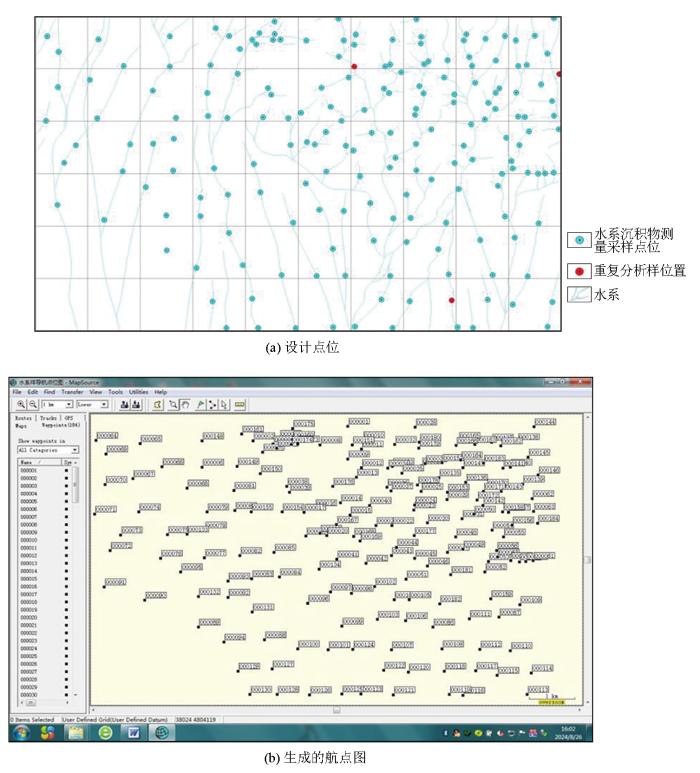
3.2.2 不规则网航点生成

在某地开展水系沉积物测量,采样点位依规范和水系布设(图6a)。此类不规则测点网用图4b所示的不规则网程序生成航点(图6b)。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不规则网的航点生成

Fig.6 Generated irregular GPS waypoints in MapSource

3.3 软件特点

1)本着人机友好的原则,软件界面设计简洁易懂,用户只需按照输入框标题键入设计测网的相应参数即可,并且鼠标在输入框悬停时会有相关数据格式的提示。

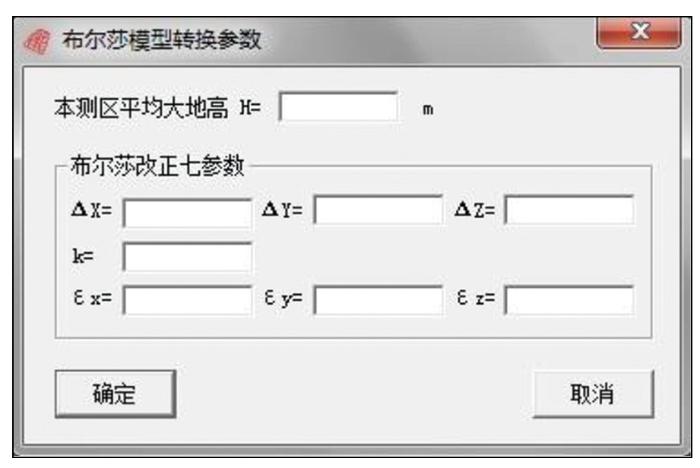
2)可根据是否拥有当地的三角点改正参数勾选“是否进行七(或三)参数改正”项。当勾选时,界面会弹出如图7所示的布尔莎模型转换(改正)参数的输入界面。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 布尔莎(Bursa)改正参数输入界面

Fig.7 Input interface for Bursa transformation parameters

3)如果还需进行激电测深剖面测量,则可勾选“是否布设电测深剖面”,程序即会生成温纳装置下A、B、M、N四极的点位。

4)程序计算生成“.wpt”航点文件,即可由MapSource软件识别调用,并可通过其通讯功能将设计航点传输到GPS终端机上,继而用于野外作业导航。

5)依据该原理及技术路线,程序仍可扩展,比如最终生成其他格式的航点文件。

6)该软件为野外物化探测量作业时的手持GPS机导航而设计,仍可用于其他采用WGS-84坐标系的GPS终端设备。

4 结论

本文提出了一种用于物化探测网布设的大批量GPS航点生成方法,并针对规则网和不规则网分别编制了软件。该方法从测量学基本原理和坐标转换理论出发,计算逻辑严谨、结果精确,无须借助第三方软件,其软件可用于物化探测量中规则网(比如电磁测量和土壤测量)及不规则网(比如水系沉积物测量)等设计点位的布设。

该方法不仅应用在物化探勘查中,也可用于大多数中小比例尺使用GPS的工作场景。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

王会锋, 彭立华, 安兴, 等.

GPS技术在化探工作中的应用

[J]. 物探与化探, 2008, 32(5):477-479.