0 引言
由于叠前地震数据蕴含丰富的地震波运动学和动力学信息,AVO(amplitude variation with offset)技术成为地震勘探中非常重要的方法。Zoeppritz方程[1]是AVO反演的基石,完整的Zoeppritz公式较复杂,学者们从简化公式、明确物理意义等角度展开研究,提出了一系列近似公式[2⇓⇓⇓⇓⇓⇓⇓-10]。随着油气勘探技术和计算机技术的发展,更多叠前正反演方法被应用于更复杂的勘探场景[11⇓-13]。但近似公式假设条件较多,易受噪声影响,而Zoeppritz方程没有多种假设条件限制,能够精确描述反射系数与弹性参数之间的关系,因此,业界学者逐渐开始就基于完全Zoeppritz方程的叠前反演方法展开研究[14⇓⇓-17]。
在基于Zoeppritz方程的叠前反演理论中,入射角是各类方程的基础要素,也是AVO公式计算的关键元素。但在实际应用中发现:叠前道集以不同炮检距数据记录,反演操作前需要实现从炮检距到角度的换算,这就容易产生计算误差;角度叠加资料中,角度会表示为一个范围值,这就导致三角函数计算受到影响,在不同工区、不同数据的适用性也会有所偏差;而精确Zoeppritz方程更加复杂,计算量更大。
随着人工智能技术的发展,深度学习技术凭借其强大的复杂特征表示能力,在地震数据处理、储层预测、流体识别、地震反演等方面已经得到了广泛应用[18⇓⇓-21]。在叠前反演领域,杨柳青等[22]利用Transformer的多任务学习架构,结合迁移学习策略实现叠前三参数反演;Biswas等[23]构建了回归卷积神经网络,通过两步预测向网络中加入物理约束,实现半监督叠前反演;孙宇航等[24]基于循环神经网络构建了一种无监督训练策略,利用纵、横波直接反演等效流体体积模量;Sun等[25]以无监督策略为动机,构建可逆神经网络,通过确定性前向建模降低了初始模型依赖,同时提高模型精度与可解释性,实现三参数叠前反演。深度学习技术不受具体数学公式及边界条件限制,可描述AVO公式中复杂的非线性关系。但在叠前反演领域,为了解决更加复杂的反演问题,提高模型预测精度,往往需要构建更庞大的神经网络,这就导致计算量显著增大,训练效率较低;一些无监督方法需要在训练过程中加入经验公式,计算误差仍然存在,影响反演精度。
1 方法原理
1.1 适应性叠前反演基本理论
适应性叠前反演从AVO公式出发,将实际测井数据和初始模型作为约束,利用神经网络学习其中的角度关系。
以Aki-Richards近似式为例,将包含角度的项简化,得到如下公式:
式中:
为从地震资料反演得到
为获得更具适用性的关系式,可将神经网络参数本身作为表达式的一部分,在每个工区训练不同的网络参数,特异性地抽取
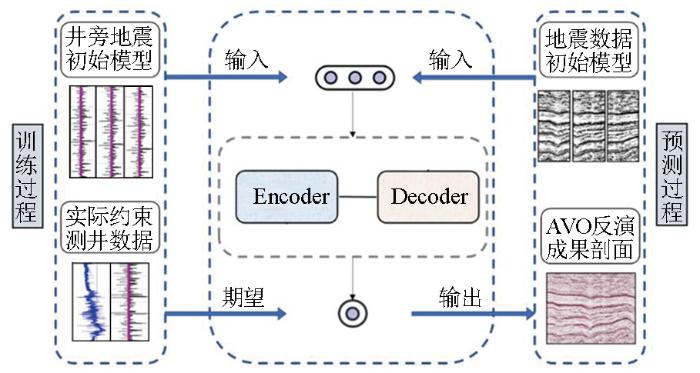
图1
图1
二次编解码网络叠前反演训练及预测流程
Fig.1
Pre-stack inversion training and prediction flow of quadratic Encoder-Decoder network
1.2 二次编解码网络模型
循环神经网络各节点按链式连接,在时序数据的非线性特征提取任务上有天然优势[29],适用于本文的适应性叠前反演数据集。但在实际应用中发现,此类网络在训练过程中经常出现损失不下降的问题。经过分析认为,循环神经网络中,信息在网络单元中依次传递,序列初始的几个采样点在训练时总是没有足够的前驱信息,即使构建双向LSTM(long short term memo)也会受序列长度制约导致效果不理想。此外,细胞态是LSTM中的信息记忆单元,较差的初始化会影响梯度传递,进而干扰网络训练结果。
由此,本文引入Encoder-Decoder结构缓解上述问题。该模型首先通过Encoder对输入序列编码得到中间结果,再通过Decoder解码生成一个新序列。标准Decoder结构只在第一个时间步有编码信息输入,此后每个网络单元的预测只与前一个单元有关。通过大量实践,发现此模式在序列生成任务上适用性更强,在序列预测任务上效果不理想,参数优化困难。其原因在于解码过程没有任何引导,一旦Decoder序列起始点预测结果出错,会导致误差逐步积累,出现误差爆炸的问题。另外,由Encoder-Decoder结构可知,Decode解码过程没有长度限制,在解决输入输出长度不等的任务中有明显优势,但本文序列预测任务要求输入和输出序列长度相等。
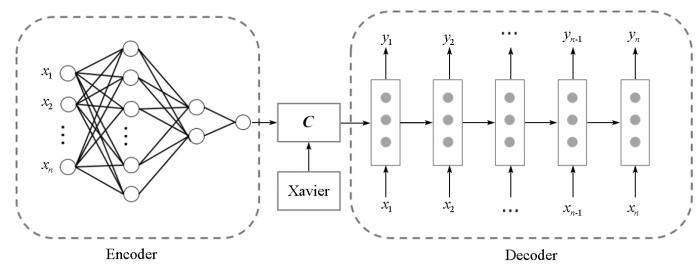
为解决上述问题,本文对标准Encoder-Decoder结构进行针对性改进,加入序列长度约束,更适用于本文序列预测任务。模型结构如图2所示。
图2
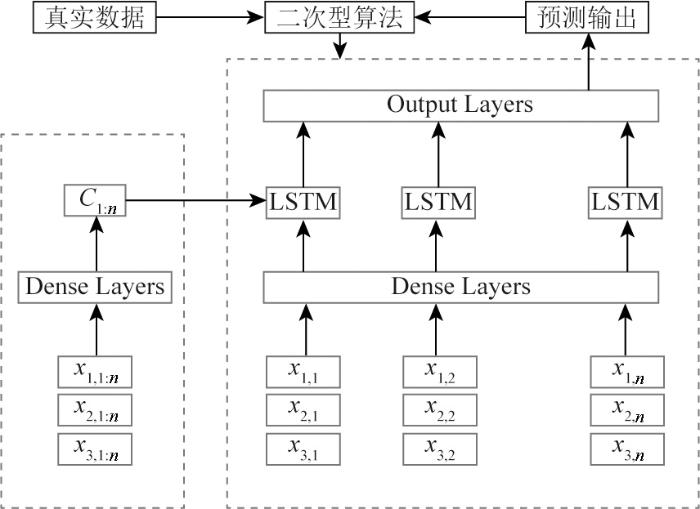
改进的编解码结构通过多模型串行融合的方式构造一个更强的学习器,为了融入全局信息,Encoder采用前馈神经网络进行编码,将多种序列叠加后输入网络,将整体序列信息融入中间网络单元C中。Decoder摒弃了生成式模型,采用循环神经网络结构,利用中间向量C为LSTM的细胞态初始化。该结构拥有较强的序列预测能力,可进行序列长度约束,在训练过程的每个时间步均有数据输入,防止网络单元在递推时产生较大偏差。以中间编码结果为Decoder细胞态初始化,目的是考虑全局特征,解决训练开始阶段没有足够前驱信息的问题。为了增加初始化的随机性,让模型拥有更好的抗干扰能力,在中间向量上叠加Xavier初始化参数,通过权重调整两者融合比例,模型训练细节如图3所示。
图3
二次编解码网络选用二次型算法进行寻优,该算法凭借其更快的收敛效率和更高的预测精度,在横波速度预测等任务中取得了较优的效果[26]。算法以均方误差作为损失函数:
式中:W为网络参数;m为样本个数;
二次编解码网络效率更高。表1展示了不同网络结构的时间复杂度对比。在本文所选的网络维度以及任务复杂度范围内,全连接网络和LSTM的时间复杂度相对较小,同时结合二次型优化算法收敛迅速的特点,让本文方法具有较高的运算效率。
表1 不同神经网络时间复杂度
Table 1
| 网络类型 | 单层时间复杂度 |
|---|---|
| 全连接神经网 | O(M×N) |
| LSTM | O(T×h2) |
| CNN | O(L2×K2×Cin×Cout) |
| Self-Attention | O(T2×d) |
注:M、N为全连接网络的单层神经元个数;T为序列长度;h为LSTM隐藏态维度;L为CNN卷积层输出维度;K为卷积核维度;Cin、Cout分别为卷积输入和输出的通道数;d为Self-Attention的向量维度。
2 参数试验及反演结果分析
2.1 数据准备
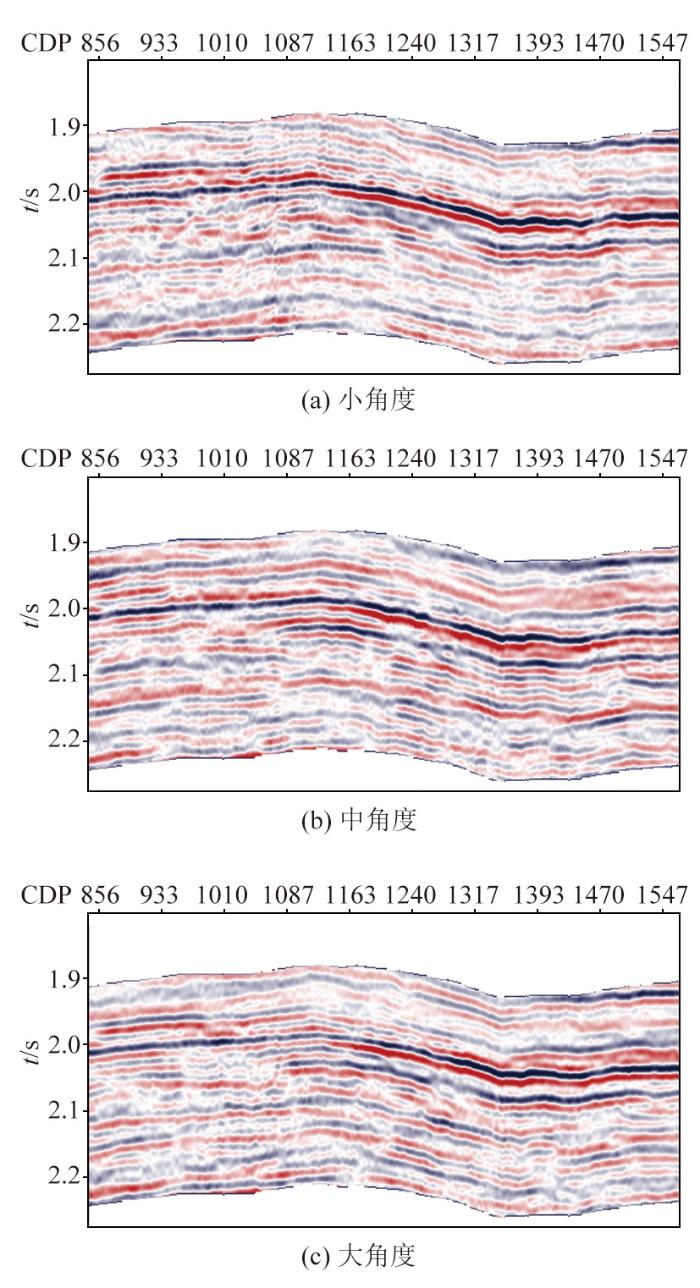
利用实际工区的部分角道集叠加数据进行实验,共划分为 3 个角度范围,包括0°~10°(小角度)、8°~17°(中角度)、15°~25°(大角度),如图4所示。利用18口井作为训练集参与反演训练,并选取Te1和Te2井作为测试井验证反演效果。
图4
初始模型作为反演的重要资料,对模型预测效果起着关键作用,本文利用深度学习方法将工区速度谱等数据利用起来,通过插值重构得到完整的初始模型[30],并作为先验数据一并加入训练。
2.2 二次编解码网络超参数优选
影响模型训练效果的超参数及训练策略包括Encoder参数量,Decoder细胞态维度、隐藏层数,优化算法以及是否加入Xavier初始化。利用正交试验优选超参数,将所有因子与水平填入因子水平表中,如表2所示。
表2 二次编解码网络反演因子水平
Table 2
| 因子 | 水平 | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| A)Encoder参数量 | 0.2 | 0.3 | 0.4 | 0.6 |
| B)Decoder层数 | 1 | 2 | 3 | 4 |
| C)Decoder维度 | 64 | 128 | 256 | 512 |
| D)优化算法 | Adam | 二次型 | ||
| E)Xavier初始化 | 是 | 否 | ||
选择均方误差作为网络评判标准,试验结果如表3所示。分析可得,Decoder中细胞态维度与Decoder隐藏层数分别位于因子主次序列的首位和第三位,说明Decoder结构的复杂程度能够显著影响AVO反演的效果,通过调整这两种因子的组合,可以达到联合控制Decoder复杂度的目的,即使隐藏层数较少,通过适量增大细胞态维度也能取得较好的效果。但当网络结构为4层Decoder隐藏层,细胞态维度为64时,误差远高于其他试验的平均水平,表明细胞态维度对模型预测精度的影响更大,当选取较少的维度时,即便增大隐藏层数,也不能保证模型预测效果,此结论与两因子在因子主次序列的位置相匹配。
表3 二次编解码网络反演试验结果分析
Table 3
| 因子 | |||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| 较优水平 | A3 | B2 | C3 | D2 | E1 |
| 因子主次 | 4 | 3 | 1 | 2 | 5 |
优化算法位于因子主次序列的第二位,应用二次型算法能够提高模型预测精度。Encoder模型参数量与Xavier初始化在因子主次序列上排名靠后,直觉上Encoder模型参数量与Decoder参数量同样能够抽取序列信息,应处于对等地位,但实际试验结果表明更复杂的Encoder带给模型的提升相对较小,这与Encoder结构在本任务的作用有关。与一般Encoder-Decoder结构不同,本文二次编解码网络中Encoder起到抽取全局信息的作用,为模型提供全局趋势,以便更有效地初始化Decoder参数,加入Xavier方法同样也是为了更好地实现初始化;而初始化任务相对简单,选用相对简单的模型即可达到任务需求。
最终神经网络参数及训练策略为:Encoder模型参数量0.4M,Decoder构建 2层隐藏层,细胞态维度为256,采用二次型优化算法更新网络参数,加入Xavier方法进行模型参数初始化。
2.3 实际研究区反演分析
2.3.1 模型效果分析
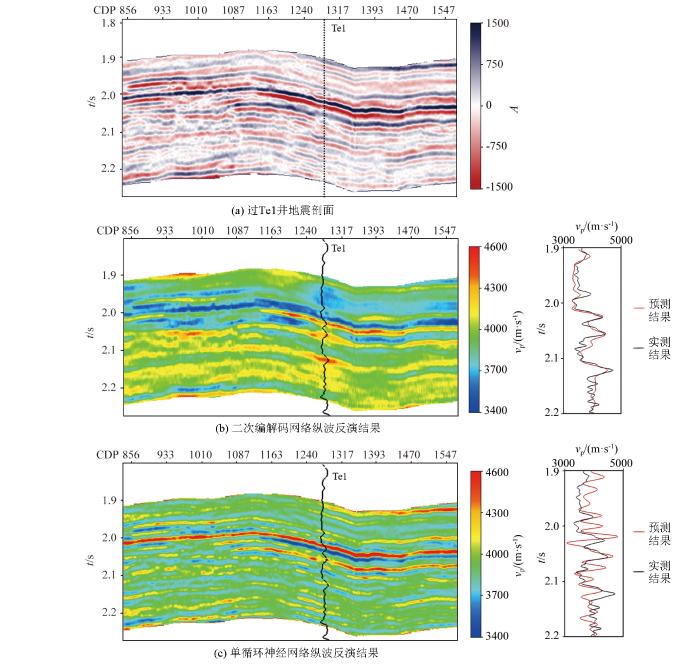
为了验证网络模型结构的有效性,将编解码网络与单解码循环神经网络进行对比,图5为过Te1井不同网络结构预测剖面及单井预测曲线。观察发现,二次编解码网络预测剖面与地震强连续反射界面走向相符,横向连续性强,符合研究区地震反射特征。通过对比不同网络结构单井预测曲线的反演精度与效率(表4)可知,二次编解码网络预测曲线与井曲线吻合程度更高,清晰预测了2.05~2.12 s处的速度变化,没有异常值干扰,相对误差和相关系数更低;循环神经网络预测曲线虽然也能在一定程度上反映速度变化,在2.05 s、2.12 s处呈现高值,但整体曲线不稳定,趋势预测不准确,出现如2s处和2.12s处的明显异常。相较而言,二次编解码网络的预测精度更高,证明了加入Encoder编码结构的必要性。在训练效率方面,串行的二次编解码网络与单循环神经网络平均训练时长相当,能够实现秒级运算,与理论论述相符,验证了本文方法的高效性。
图5
图5
过Te1井二次编解码网络与循环神经网络预测剖面及Te1井预测曲线
Fig.5
Prediction profile and prediction curve of quadratic Encoder-Decoder network and RNN through well Te1
表4 不同网络模型的反演精度与效率
Table 4
| 方法 | 相对误差/% | 相关系数 | 训练时长/s |
|---|---|---|---|
| 二次编解码网络 | 4.12 | 0.932 | 5.17 |
| 单解码循环神经网络 | 9.28 | 0.845 | 4.86 |
2.3.2 反演成果资料解释
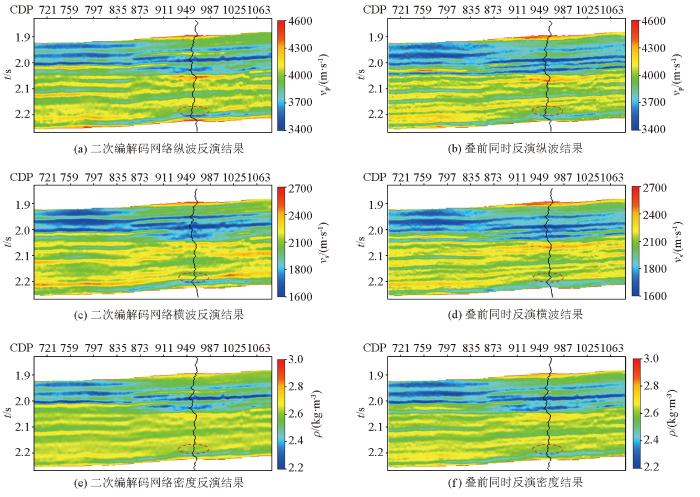
图6
图7
图7
过Te2井二次编解码网络与常规叠前同时反演结果对比
Fig.7
Results of quadratic Encoder-Decoder network and conventional prestack inversion through Te2 well
表5 不同方法反演结果的相关系数
Table 5
| 方法 | 纵波速度 /(m·s-1) | 横波速度 /(m·s-1) | 密度 /(kg·m-3) |
|---|---|---|---|
| 二次编解码网络 | 0.872 | 0.870 | 0.863 |
| 常规同时反演方法 | 0.883 | 0.879 | 0.871 |
此研究区为准噶尔盆地高速致密砂岩区,若存在致密油储层,则纵波速度和密度呈下降趋势,横波速度呈现高值。对比两种方法的反演成果剖面,由2.2 s处红色虚线圈出的位置可见,横波速度均显示为高值,纵波速度和密度均显示为低值,呈现出“横亮纵不亮”的剖面特征,与实际测井曲线相吻合,清晰反映了致密油储层的特征。综上所述,二次编解码网络能够区分研究区致密油的纵、横波速度与密度的差异,实现高效、高可靠的AVO反演。
3 结论
本文针对AVO公式中角度关系不准确的问题,构建了一种二次编解码网络,该网络将不同角度的地震数据、初始模型以及地层参数相互联系起来,实现了高效、高适应性叠前反演。根据实际数据的训练和预测结果,得到以下结论:
1)二次编解码网络可通过优化模型结构极大地提高模型训练效率,实现秒级运算。与单解码网络模型相比,编解码网络的反演结果与实际测井曲线符合程度更高,证明了加入编码层的必要性。通过实际工区数据测试,验证了二次编解码网络在具备最大效率的同时还保证了反演准确率,反演结果能够对致密油储层资料解释起到指导作用,反演效果与常规方法相当。
2)模型训练效率与预测精度很难并行不悖,在实际应用中如何进行取舍是需要优先考虑的问题。过于简单的神经网络可能在训练过程中陷入局部最优,可以考虑调整正则化方法或使用可变学习率进行缓解。Encoder-Decoder结构由两部分组成,平衡两者复杂度是优选模型的关键。本文通过正交试验法对此做出探索,认为由于两者作用不同,对复杂度的需求也不同。但此结论只针对二次编解码网络,其他网络结构是否也有此特点还需要进一步的理论验证。此外,本文方法需要用较为准确的初始模型进行约束,文中利用深度学习方法进行构建。如何获得更高质量的初始资料将是未来进一步研究方向。
参考文献
On the reflection and propagation of seismic waves at discontinuities
[J].
Approximations to the reflection and transmission coefficients of plane longitudinal and transverse WAVES
[J].
Detection of gas in sandstone reservoirs using AVO analysis:A 3-D seismic case history using the geostack technique
[J].
Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters; “λρ”,“μρ”,&“λ/μ fluid stack”,from P and S inversions
[C]//
Weighted stacking for rock property estimation and detection of gas
[J].
杨氏模量和泊松比反射系数近似方程及叠前地震反演
[J].
Reflection coefficient equation and pre-stack seismic inversion with Young’s modulus and Poisson ratio
[J].
Direct inversion for reservoir parameters from prestack seismic data
[J].
Robust AVO inversion for the fluid factor and shear modulus
[J].
剪切模量和密度反射系数近似方程及叠前地震反演
[J].
DOI:10.3969/j.issn.1000-1441.2022.05.008
[本文引用: 1]

地球物理反演的本质是利用物性和弹性参数揭示地下介质的属性和含油气特征。拉梅参数是储层预测和流体识别中最常用的弹性参数。根据纵、横波速度与拉梅参数的关系,基于Zoeppritz方程提出了一种新的以剪切模量、密度相对变化率为参量的反射系数方程,结合稀疏性原则和核模约束提高反演的横向连续性,添加先验信息约束,实现从叠前地震数据中直接提取剪切模量和密度信息,从而减少间接计算带来的累积误差,该反演方法比常规三参数反演具有更高的稳定性。建立4类AVO模型,分别利用该方法、Aki-Richards方程与Gray近似方程进行正演模拟、误差分析和条件数分析,结果表明了该方法的反演结果与原始数据吻合得更好且稳定性更高。基于最小二乘法对一维层状模型反演证明,该方法能更准确地反演μ、ρ,在井数据充裕的情况下,能够较准确获取拉梅常数λ。将该方法用于实际叠前地震数据反演,井位处的反演结果与测井曲线基本一致,能够准确识别岩性,为后续分析提供准确的弹性参数。
Approximate equations of shear modulus and density reflection coefficient and prestack seismic inversion
[J].
AVO inversion using the Zoeppritz equation for PP reflections
[C]//
基于佐普里兹方程的高精度叠前反演方法
[J].
High precision prestack inversion algorithm based on Zoeppritz equations
[J].
An improved strategy for exact Zoeppritz equations AVA inversion
[C]//
模型驱动的高精度叠前地震反演方法及应用
[J].
DOI:10.3969/j.issn.1000-1441.2020.06.011
[本文引用: 1]

线性化叠前地震反演方法由于具有高效率、低成本的特点,在叠前地震油气储层预测中得到广泛应用。为进一步提高线性化叠前地震反演方法的精度、稳定性及资料适应性,提出了模型驱动的高精度叠前地震反演方法。根据地震残差分布特点,采用最小二乘法构建目标函数,同时增加了L2范数正则化项确保反演解适定性,基于泰勒公式展开推导构建了反演迭代公式。反演计算中采用的雅克比矩阵是直接通过佐普里兹方程矩阵形式推导构建的,避免了小角度和弱反射界面假设,确保了雅克比矩阵的构建精度,从而提高了反演精度。在正则化参数选取方面,利用地震噪声和反演参数扰动量的高斯统计方差自动选取正则化参数。模型实验数据表明,模型驱动的高精度叠前地震反演方法在实现正则化参数自动化选取的同时确保了反演精度。胜利油田东部地区实际资料应用结果表明,该方法稳定性强,对复杂地震资料具有较强的适应能力,反演结果精度高,能够较好利用部分角度叠加数据体中的叠前地震振幅变化信息,提高了储层岩性和流体预测能力。
Model driven high-precision prestack seismic inversion
[J].
DOI:10.3969/j.issn.1000-1441.2020.06.011
[本文引用: 1]

Linear prestack seismic inversion has been widely used in prestack seismic reservoir prediction because of its high efficiency and low cost.A model-driven,high-precision,prestack seismic inversion method was proposed to further improve the accuracy,stability,and adaptability for application to complicated seismic conditions.Based on the characteristics of seismic residuals,the least-square method was used to construct the inversion objective function,with the L2 norm regularization term ensuring the inversion results were well posed.The inversion iteration formula was finally deduced using Taylors formula,based on the idea of linearization inversion.In this method,the Jacobian matrix was directly constructed by the matrix form of the Zeoppritz without the assumptions of a small incidence angle and weak reflection interface.This was done to ensure the accuracy of construction of the Jacobian matrix and improve the precision of inversion results.The regularization parameters were automatically selected using the Gaussian statistical variance of seismic noise and inversion parameter disturbances.Tests on model and field data from SL oilfield demonstrated that the method has good stability and high adaptability when applied to complicated seismic data,and it can improve the prediction of reservoir lithology and fluid by making full use of seismic partial angle stacked data.
深度学习在地球物理中的应用现状与前景
[J].
Current status and application prospect of deep learning in geophysics
[J].
Deep learning for geophysics:Current and future trends
[J].
基于BP神经网络的区域滑坡易发性评价
[J].
Evaluation of regional landslide susceptibility assessment based on BP neural network
[J].
基于BERT的三维地质建模约束信息抽取方法及意义
[J].
BERT-based method and significance of constraint information extraction for 3D geological modelling
[J].
多任务Transformer下的小样本叠前AVO反演方法研究
[J/OL].
Few-shot pre-stack AVO inversion using a multi-task Transformer
[J/OL].
Prestack and poststack inversion using a physics-guided convolutional neural network
[J].
基于无监督深度学习的多波AVO反演及储层流体识别
[J].
DOI:10.3969/j.issn.1000-1441.2021.03.004
[本文引用: 1]

流体因子是储层流体识别中的重要参数,传统的流体因子不能较为准确地识别储层流体,等效流体体积模量对储层流体的变化更加敏感。多波AVO反演是从地震道集中提取等效流体体积模量的重要手段之一。常规的多波AVO反演基于最小二乘或贝叶斯理论,反演精度强烈依赖于初始模型,但大多数实际工区很难建立高精度、高分辨率的初始模型。为了进一步提高储层流体识别的精度,并降低反演对初始模型的依赖程度,在AVO反演理论的指导下,构建基于无监督深度学习的纵波和转换波道集直接反演等效流体体积模量的方法,将该方法应用于X工区实际数据的反演并进行储层流体识别。X工区内井旁道地震道集的试算结果表明,该方法具有较高的精度,反演结果与测井数据的相对误差约为2.949%,绝对误差小于0.1GPa;X工区内反演得到的等效流体体积模量的剖面和时间切片与已知测井解释结果匹配度良好,说明该方法能够较为精确地识别储层流体,具有良好的实用价值。
Multi-wave amplitude-versus-offset inversion and reservoir fluid identification based on unsupervised deep learning
[J].
DOI:10.3969/j.issn.1000-1441.2021.03.004
[本文引用: 1]

Fluid factors are key parameters in reservoir fluid identification;however,traditional fluid factors are unable to precisely identify the reservoir fluid.Among these factors,the effective pore fluid modulus is the most sensitive to the fluid.Multi-wave amplitude-versus-offset (MW AVO) inversion is an effective tool for characterizing reservoir fluids.The inverted accuracy of conventional MW AVO inversion methods,which are based on the least squares theory or Bayesian theory,depend heavily on the models that define the initial conditions.However,building such models with high resolution and high precision is difficult in most field areas.To improve the accuracy of reservoir fluid identification and reduce the dependence of the inversion method on the initial models,an unsupervised deep-learning MW AVO inversion method was developed,which incorporates deep learning within a conventional pre-stack AVO.This allows the effective fluid bulk modulus to be inverted directly by using both P-and S-wave gathers.This method was used to perform field data inversion and fluid identification in the X work area and achieved high accuracy.The relative error between the inverted results and the logging data was 2.949%,and the absolute error was less than 0.1 GPa.The inverted profiles and time slices matched well with the log interpretation results,thereby demonstrating that the proposed method can identify reservoir fluid accurately and has a significant practical value.
Inversion of low-to medium-frequency velocities and densities from AVO data using invertible neural networks
[J].
利用二次型寻优网络预测砂泥岩地层横波速度
[J].
S-wave velocity prediction method for sand-shale formation based on quadratic optimization network
[J].
Understanding the difficulty of training deep feedforward neural networks
[C].