E-mail Alert Rss
 

物探与化探, 2025, 49(1): 129-137 doi: 10.11720/wtyht.2025.1157

方法研究信息处理仪器研制

岩石物理数据反演成像研究

苏本玉,1, 张佳琦1, 谭登攀2, 于景邨2, Li Zhixiong3

1.中国矿业大学 安全工程学院 煤矿瓦斯与火灾防治教育部重点实验室,江苏 徐州 221116

2.中国矿业大学 资源与地球科学学院,江苏 徐州 221116

3.Faculty of Mechanical Engineering, Opole University of Technology,Opole, Poland 45-758

Inversion imaging of petrophysical data

SU Ben-Yu,1, ZHANG Jia-Qi1, TAN Deng-Pan2, YU Jing-Cun2, LI Zhi-Xiong3

1. Key Laboratory of Gas and Fire Control for Coal Mines,China University of Mining and Technology, Xuzhou 221116, China

2. School of Resources and Geosciences, China University of Mining and Technology, Xuzhou 221116, China

3. Faculty of Mechanical Engineering, Opole University of Technology, 45-758 Opole, Poland

第一作者: 苏本玉(1981-),男,2012年10月毕业日本九州大学,博士,教授,目前主要从事地球物理反演成像与地质灾害监测的研究工作。Email:subenyu@gmail.com

责任编辑: 王萌

收稿日期: 2024-04-7   修回日期: 2024-05-12  

基金资助: 国家自然基金项目(42274179)
国家自然基金项目(42027801)
国家重点研发计划项目(2022YFC3003300)

Received: 2024-04-7   Revised: 2024-05-12  

摘要

岩石物理数据反演能对岩石内部微观裂隙结构进行成像,可洞察岩土内部裂隙的随外界环境变化演化规律,是研究深部岩土灾变机理直观可靠的方法。文章介绍了岩石物理数据的采集系统和电阻率正、反演算法。基于上述工作,分别开展了岩石物理二维和三维反演成像的数值模拟工作,二维反演成像的数值模拟结果表明,该方法可刻画充填高电阻率和低电阻率的毫米级岩石裂隙;三维数值模拟结果表明,该方法对充填高电阻率和低电阻率的毫米级缝洞可进行精确定位和有效识别。针对微波破裂岩石样本,开展了砂岩加热破坏前、砂岩加热至熔融状态和砂岩从熔融状态至冷却3种状态下的数据测量和反演成像工作,初步揭示了微波加热砂岩裂隙变化规律,为研究深部岩土灾变机理提供了一种新的方法。

关键词： 岩石物理; 反演成像; 岩石微观裂隙结构; 深部岩土灾变机理

Abstract

The inversion of petrophysical data can image the microscopic fracture structures inside rocks, revealing the evolutionary patterns of fractures within rocks and soil with changes in external environments. Hence, it is an intuitive and reliable method for investigating the mechanisms of deep geotechnical disasters. This study presented a petrophysical data acquisition system and resistivity-based forward modeling and inversion algorithms. Based on the above, this study conducted numerical simulations of 2D and 3D inversion imaging of petrophysical data. As indicated by the numerical simulation results, 2D inversion imaging can characterize millimeter-scale rock fractures with high/low resistivities, whereas 3D inversion imaging can accurately locate and effectively identify millimeter-scale fractures and vugs with high/low resistivities. Moreover, data measurement and inversion imaging were conducted on rock samples subjected to microwave-induced fracturing in three states: heated sandstone before failure, sandstone heated to a molten state, and molten sandstone in a cooled state, preliminarily revealing the variation patterns of sandstone fractures under microwave heating. Overall, this study provides a novel method for exploring the mechanisms of deep geotechnical disasters.

Keywords： petrophysics; inversion imaging; microscopic rock fracture structure; mechanism of a deep geotechnical disaster

PDF (5029KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

苏本玉, 张佳琦, 谭登攀, 于景邨, Li Zhixiong. 岩石物理数据反演成像研究[J]. 物探与化探, 2025, 49(1): 129-137 doi:10.11720/wtyht.2025.1157

SU Ben-Yu, ZHANG Jia-Qi, TAN Deng-Pan, YU Jing-Cun, LI Zhi-Xiong. Inversion imaging of petrophysical data[J]. Geophysical and Geochemical Exploration, 2025, 49(1): 129-137 doi:10.11720/wtyht.2025.1157

0 引言

电阻率法广泛应用于水文、工程、环境地质以及资源勘探与开发中,是解决地质问题的有力工具。针对油田注水开发的储层水淹问题,刘欢等[1]开展了水淹层原始电阻率反演,为水淹层定量解释与评价提供了数据资料支撑。针对煤层开采引发的采动覆岩垮落带和导水裂隙带难以定量表征的问题,高超等[2]采用三维电阻率反演技术,开展了工作面实测垮落带和导水裂缝带发育高度的实测研究,获得了较好的效果。杨志成等[3]应用电阻率反演方法,开展了深部地热资源的调查,结合地热地质条件,优选了地热钻探井位,经钻探最终验证,推测地层与实际钻探基本吻合,获得了理想的效果。Wahab等[4]研制了一个新的电阻率测量CDMT系统,可同时监测 24 个供电电极发射电流的情况,并记录了 24 个测量电极采集到的电位信息,针对伊东校区(日本福冈九州大学)北部研究了地下水含水层及其电阻率的变化情况,得出一些有意义的地质结论,为温泉的开发利用提供了地质信息。为实现定期监测地下电阻率的时间变化,Loke等[5]通过修改最小二乘优化方法,导出了最小化模型电阻率值随时间变化的数学表达式,实现了时移电阻率的反演,为电阻率监测研究奠定了基础。尽管电阻率反演成像方法已被证明是解决地质问题极有用的工具,具有反演高效和稳健特点,但传统的反演方法不能很好地解决尖锐界面问题,往往会减少和平滑电阻率的变化,使得地质的信息模糊化,不能得到真实的地质信息[6]。为改善电阻率成像的分辨率和提升其解释效果,Aleardi等[7]开发了PyMERRY软件,并用在了不丹中南部野外测量数据的处理中,成功揭示了小规模地质异常体电阻率的变化规律。但以上案例均是用于解决野外大尺度的地质探测问题。

近年来基于电阻率的岩石物理学在研究深度岩土破裂机理方面发挥了重要的作用,并得到了广泛的关注,其成为联系地球物理学、岩石学、水文地质学、工程地质学、岩土力学等学科的纽带和桥梁,也是研究岩石物性和各种地质灾害机理的重要工具。

杨永明等[8]以砂岩为研究对象,利用统计学原理和FLAC3D软件重构了三维孔隙模型,基于数值模型试验的方法研究了孔隙结构参数(孔隙率、孔径分布和空间位置分布)对孔隙砂岩力学性能的影响,证明了孔隙结构参数对岩石物理力学性能有一定影响,但该研究仅仅依赖数值模拟数据,说服力显然不强。2013年,孙强等[9]基于物理试验研究岩石内部结构随温度升高其物理力学性质的改变规律,利用MTS伺服试验机和高温炉,将温度加热至800℃,研究花岗岩物理力学参数随温度变化规律,得出了岩石强度和波速温度等参数在不同条件下的变化规律。但在实验中把整个岩心样本作为一个均匀介质进行考虑,仅仅对不同条件下测量得到的声波速度数据、温度数据和压力数据进行分析后得出的结论。显然,随着压力的增大,岩石样本将会破碎,此时再把岩心样本作为均匀介质考虑,不免有些欠妥。何国梁等[10]通过测量不同条件下煤岩样本的声波—时间数据,分析了煤系沉积岩石纵波和横波速度变化规律。在开放系统下,孟召平等[11]开展不同成岩作用程度下砂岩物理力学性质三轴试验研究,得出了砂岩随施加压力的变化规律,但这仅是表面现象,难以揭示岩石内部冻融劣化机理。

在传统电阻率探测理论的基础上,本研究开发了用于反演岩石样本尺度的二维和三维电阻率反演成像程序。同时,研发了岩石样本尺度级别的电阻率测量系统,可用于测量施加不同压力状态下的电阻率信号。在上述电阻率反演成像程序研发和岩石样本电阻率测量系统研制的基础上,本文完成了数值模拟和实际测量岩石样本二维和三维成像电阻率成像研究,可清晰、直观地显示随压力变化,岩石样本内部裂隙的变化规律,可为深部岩石灾变提供数据支撑。

1 岩石样本电阻率测量系统

中国矿业大学与企业联合开发研制的岩石样本数据采集系统包括主机、信息电缆、测量电极系、供电电极系和控制软件系统,如图1~3所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   岩样数据采集系统主机

Fig.1   Microelectrode rock sample acquisition system


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   采集控制界面

Fig.2   Acquisition control interface


图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   参数设置界面

Fig.3   Parameter setting interface


图1为岩样数据采集系统主机,主机接口有供电电极和测量电极,各192个,系统软件包里已经预备了4种常见的装置形式,可供用户选择。此外,用户可根据需要,选择供电电极和测量电极的耦合方式,采集以任何电极组合形式的电位数据。仪器采集使用自动循环配置的方法,一次配置即可循环采集,不需要每次都重新配置,方便用户操作;例如,供电电极选择1~192,采集电极选择1~192,那么采集时将自动配置,在同一个供电电极工作时,其他192个采集电极采集数据,采集完成后,自动更换下一个供电电极,重新开始采集。为方便在岩石样本室内或者保温箱内测量,岩样采集系统集成到智能手机中,与主机通过WiFi相连,测量数据将自动保存到智能手机中,控制系统与采集主机分离,确保可以对不同工作环境下的测量实施遥控操作。

图2为数据采集控制界面,该界面主要将采集结果以图表的形式显示在手机上,用户方便实时监控测量结果,每测量5道采集电极更新一次图表,并在界面中的表格中显示出测量的视电阻值和对应的误差。图3为参数设置界面,分为项目设置、测量控制和校准方法3部分。测量控制显示了本次测量的主要设置,采用输入框和下拉框两种方式进行配置设置,操作简单、界面简洁。此外还可设置最大测量次数和最小测量次数,进行相对误差计算,支持重复测量,在误差超过门限值时进行多次测量,保证数据的准确性。

2 有限元计算与电阻率正反演理论

2.1 有限元电阻率正演算法

点电流源的三维电场的边值问题为[12]:

Δ·(σΔu)=-Iδ(A)∈Ω ,∂u∂n+cos(r,n)ru=0∈Γ∞ ,

式中:σ为电导率;I为电流源电流;Ω为研究区域;Γ∞为无穷远边界,其对应的变分问题为:

δI(u)=∫ΩΔ·(σΔuδu)-[Δ·(σΔu)+Iδ(A)]δudΩ

将式(1)第一式代入式(2)得:

I(u)+12∫Γ∞σcos(r,u)ru2dΓ=0

三维电场边值问题等效于下列变分问题:

F(u)=∫Ω12σ(Δu)2-Iδ(A)udΩ+12∫Γ∞σcos(r,n)ru2dΓ ,δF(u)=0 。

采用四面体有限单元,积分可由非结构网格划分成各个小单元的单元积分,如图4所示,图中1、2、3、4为四面体单元节点序号,P为单元内任意一点,P点处的电位由四面体各个节点通过线性插值或高次插值获得[13]。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   非结构四面体单元

Fig.4   Unstructured tetrahedral element


对式(4)求变分并令其为0,可得下列线性方程组:

KU=P

其中:K是刚度矩阵,U节点电位,P与源项相关的1维数组。通过求解式(5)[14-15],可得研究域内各个节点得电位。

2.2 圆柱型岩石样本反演成像算法

构造反演目标函数可以通过式(6)表示[16⇓-18]:

Φ=(Δd→-Jm→)T(Δd→-Jm→)+λ(Rm→)T(Rm→)

式中:Δd→为观测数据与正演数据之差;m→为模型参量;J为雅可比系数矩阵;λ为拉格朗日因子,R为粗糙度矩阵,每次迭代后模型参数修正量为:

Δm→=(JTJ+λRTR)-1JΔd→

由均方根误差作为迭代判断依据,

RMS=1N∑i=1N(di-f(m→)idi)2×100

式中:N为观测数据的个数;di是第i个观测数据。

3 岩石样本电阻率反演与成像数值模拟研究

地下地质构造中含有一系列不同尺度的孔隙和裂缝,严重影响着岩石中物理场的传播[19]。特别是碳酸盐岩内部的孔隙结构非均质性强,次生改造作用强烈,使其储集空间多样,如铸模孔、溶蚀孔、粒内孔和裂缝等[20-21],致使含油气饱和度的精准计算和含油气性的准确评价成为储层储量评价的一大难题。岩石物性参数的精准计算在定量勘探预测中具有重要的地位[22-23],岩石物理模型是该研究的基础。此外,层状岩石属于典型的各向异性介质,在我国分布较为广泛,成岩环境特殊且长期受地质构造运动的作用,使岩石产生不同形状和大小的孔洞[24-25]。岩石的强度及变形特征与内部缺陷的几何形态有着密切联系[26],在层理面的影响下,岩石的力学特征变得更为复杂。因此,开展含孔洞缺陷层状岩石力学特性的研究,对了解其变形破坏机理有着重要的意义[27]。并且,弄清岩石内部裂隙结构分布规律和物性参数的精确数值,对含油气储层评价和岩石受力破坏机理的研究具有重要作用。基于此,建立了岩石样本尺度的含裂隙岩石模型,开展了数值模拟研究,探讨了电阻率反演方法在研究岩石内部裂隙结构分布规律和物性参数精确数值的可行性。

3.1 二维反演成像数值模拟研究

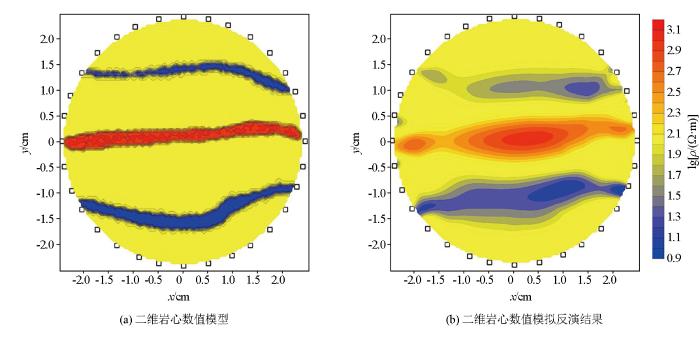
基于有限元计算与电阻率正反演理论,首先建立了有两条低阻裂隙和一条高阻裂隙发育的电阻率二维岩石模型,剖分网格单元为2 953个,模型尺寸半径2 cm,其内含有3条微米级别裂隙,设计圆形观测系统,围绕模型布设32个电极,采用偶极—偶极装置采集电位数据,一共采集数据204个数据。其中,模型如图5a所示,背景场电阻率为100 Ω·m;中间为高电阻率,大小为1 000 Ω·m,模拟裂隙中充填油气等高电阻率物质;两侧的两条裂隙为低电阻率,电阻率大小为10 Ω·m,模拟充填为水或导电金属矿等低电阻率物质。基于有限单元方法,开展数值模拟计算,对正演模拟数据添加2%白噪声来模拟探测数据,设电阻率为100 Ω·m的均匀模型为初始模型,采用Occam电阻率反演方法,迭代10次,共用时125 s,反演电阻率模型如图5b所示。对比二维电阻率模型和反演结果,可知反演结果基本可以反应模型电阻率分布的趋势,与模型裂隙分布趋势和形态基本吻合。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   中间高电阻率、两侧低电阻率的岩心裂隙模型数值模拟

Fig.5   Numerical simulation of core fracture model with high resistivity in the middle and low resistivity on both sides


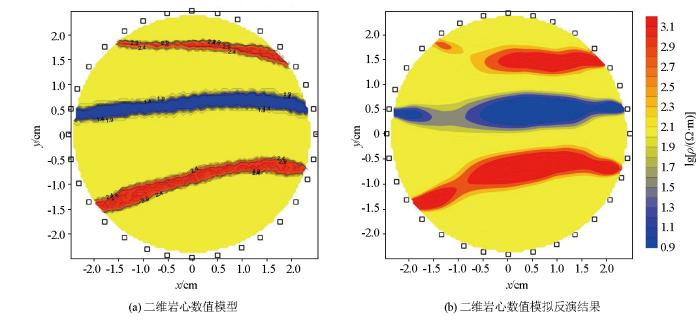
随后我们置了两侧高阻裂隙发育、中间低阻裂隙发育模型,如图6所示,设置模型中间裂隙为低电阻率,模拟充填为水或者导电金属矿等低电阻率物质,两侧的两条裂隙为高电阻率,模拟裂隙中充填油气等高电阻率物质。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   中间低电阻率两侧高电阻率的岩心裂隙模型数值模拟

Fig.6   Numerical simulation of core fracture model with low resistivity in the middle and high resistivity on both sides


与模拟模型图5相同,对正演模拟数据添加2%白噪声来模拟探测数据,设电阻率为100 Ω·m的均匀模型为初始模型,开展电阻率反演计算,反演结果如图6b所示,对比电阻率模型6a可知,反演结果基本可反应正演模型的电阻率分布模型趋势,与模型裂隙分布趋势和形态基本吻合。

3.2 三维反演成像数值模拟研究

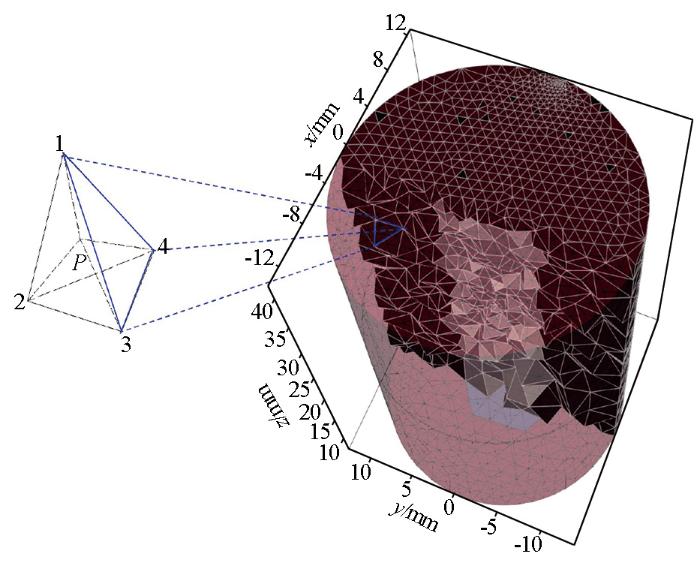
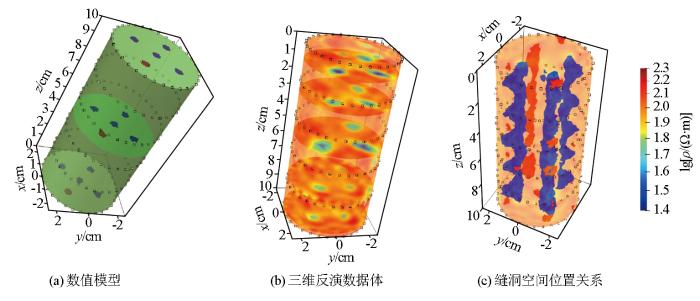
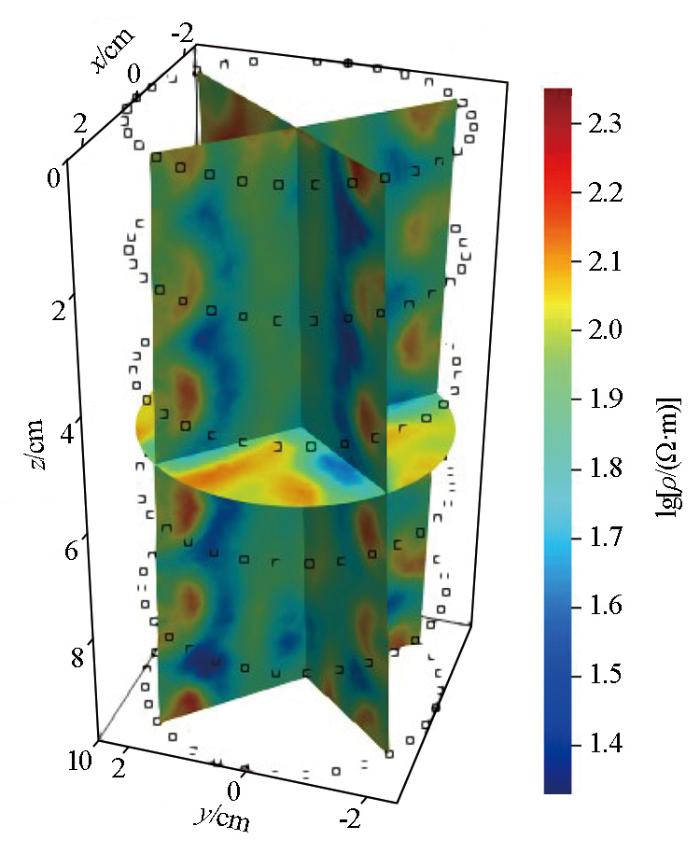
基于有限元计算与电阻率正反演理论,建立电阻率三维岩心样本模型,剖分网格单元为232 117个,如图7a所示,在模型中一共设置了5条圆柱形缝洞,半径大小为0.2 cm,其中,一条为高电阻率,来模拟缝洞中充填油气等高电阻率物质;其余4条缝洞设置为低电阻率,来模拟缝洞中充填为水或者导电金属矿等低电阻率物质。设计圆柱形电阻率观测系统,共有6组电极系列,每组电极系列由32个电极组成,分别环绕在岩心样本模型周围。每组电极系列均采用偶极—偶极装置形式采集电位数据,每次测量共获取1 224个数据。基于图7a三维岩心样本模型,开展三维正演计算,将正演计算数据添加2%的噪音来模拟探测数据。设电阻率为100 Ω·m的均匀模型为初始模型,开展反演计算,迭代20次后,最终迭代误差为4%,一共用时19 650 s。反演结果如图7b和7c所示。其中,图7b为反演结果三维数据体,从图中可看出高电阻率区域与模型中的高电阻率缝洞相吻合,而其余的3个低电阻率区域与模型中的位于相对边缘区的3个低阻率缝洞相吻合。为形象地显示高电阻率和低电阻率异常体的空间位置关系,从三维数据体中提取出了高电阻率和低电阻率异常区域,如图7c所示。图8为三维反演结果切片,可详细显示内部细节信息。然而,位于中心的低电阻率区域并没有清晰地反演出来,其原因与直流电法的体积效应和观测系统的设计有关,导致周围的低电阻率异常体对其屏蔽,后续将开展立体观测系统及相关约束反演研究,以期改善探测效果。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   缝洞型三维岩心样本模型数值模拟

Fig.7   Numerical simulation of fracture-cavity three-dimensional core sample model


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   缝洞型三维岩心样本模型数值反演结果切片

Fig.8   The inversion result slices of numerical simulation of fracture-cavity three-dimensional core sample model


4 实测数据岩石样本的电阻率反演与成像

我国95%的高瓦斯和突出矿井具有瓦斯渗透性较低[22]、吸附强和抽采过程中解吸难的特点[23],破煤卸压增透是提高瓦斯抽采量重要方法。微波加热也是高效弱化坚硬岩石的手段之一,可实现工程岩体的高效开挖。无论是微波破煤卸压增透还是微波硬岩弱化,微波参量、岩石物理属性和应力环境都是影响微波破岩的主要因素。微波注热后,岩体内部介质传热与应力演化内在联系等规律的研究成为研究煤岩的热点[24⇓⇓⇓⇓⇓⇓⇓-32]。为此,课题组开展电阻率反演成像监测微波破岩试验。首先,将岩心固定在实验台上,且加载上电阻率观测系统,如图9所示;然后,利用微波仪对岩心进行加热和破坏,同时采集电场数据;最后,对采集数据开展电阻率反演与成像。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   岩心电阻率数据采集系统

Fig.9   Core resistivity data acquisition system


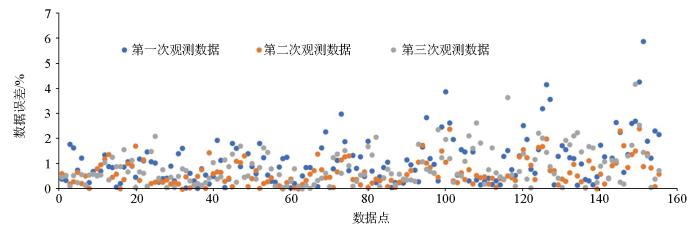
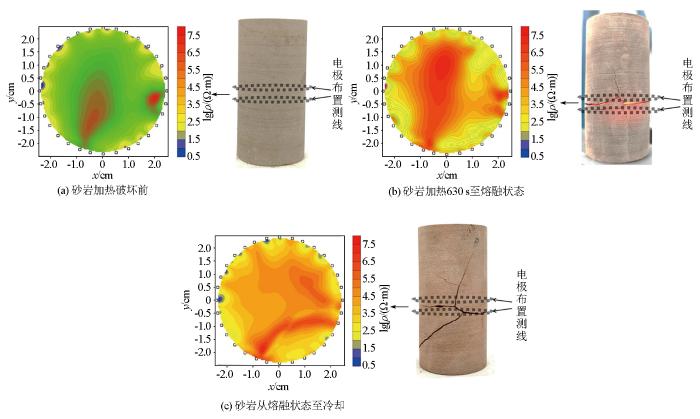
实验时将微波仪功率调整为2 kW,对硬质砂岩进行微波破岩,利用岩心电阻率测量系统采集电响应信号。对岩心加热破坏前、加热630 s至熔融状态和彻底冷却后3个状态分别进行电阻率响应测量,每次采集共获得155个数据,数据误差如图10所示,3次采集数据误差基本小于2%。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   岩心电阻率测试采集数据误差

Fig.10   The error of core resistivity data acquisition


利用3次测量数据开展电阻率二维反演成像,如图11所示,基于反演成像结果,对微波破岩效果进行分析和评估,为相关专业人员分析岩石微波弱化机理提供了直观、可信的数据资料。基于上述反演结果,可获得如下结论:砂岩加热破坏前,岩心未遭受到破坏,电阻率反演结果如图11a所示,但岩心内部有一定的非均质性,局部出现高电阻率,可能是原始岩心具有微小裂隙,裂隙充有空气,显示为高电阻率。随着微波加热岩心破坏,原始岩心裂隙区域变大,沿着原始裂隙向外扩张,岩心裂隙分布区域显示为高电阻率特征,如图11b所示。岩心受热膨胀,应力变大,脆性变强,忽然冷却,岩心局部发生错段,形成明显裂隙,如图11c所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   微波破岩物理实验与数据反演成像

Fig.11   Microwave rock breaking physical experiments and data inversion imaging


5 结论

传统的岩石物理相关研究通常是把岩石样本作为一个均匀介质,通过改变温度、压力等相关环境参数,测量相关速度和电阻率或者观测表面变化现象,例如脱落、破裂等,归纳总结岩石随环境的变化规律,总结地质灾变机理。事实上,随着环境的变化,岩石受到破损后不可作为均匀介质对待,而反观测岩石表面变化现象,也不能反映岩石内部真实的变化规律。基于此,本文提出了岩石样本尺度的三维反演成像方法研究岩石物理问题。基于不同状态下观测的响应信号信息,开展地球物理反演,对岩石样本进行二维或三维成像,直观地洞察随外界环境的变化岩石样本内部裂隙的变化规律,为研究深部岩土灾变机理提供了一种新的方法。

基于实际应用的角度,作者研发一套岩石样本电阻率测量系统,介绍了岩石样本电阻率测量设备和正反演理论、算法、数值模拟以及实际资料的反演与成像。后续将开展声波测量系统和反演与成像以及声、电联合反演相关工作。

参考文献

刘欢, 徐锦绣, 高文博, 等.

基于解释单元的水淹层原始电阻率反演及应用

[J]. 地球物理学进展, 2019, 34(1):144-150.

[本文引用: 1]

Liu H, Xu J X, Gao W B, et al.

Original resistivity inversion of water-flooded zones based on interpretation unit and its application

[J]. Progress in Geophysics, 2019, 34(1):144-150.

[本文引用: 1]

高超, 秦胜君, 安守学, 等.

基于三维电阻率反演技术的采动覆岩“两带” 发育特征研究

[J]. 山西煤炭, 2023, 43(1):109-118.

[本文引用: 1]

Gao C, Qin S J, An S X, et al. Development characteristics of the “two zones”

of mining overburden strata based on 3D resistivity inversion

[J]. Shanxi Coal, 2023, 43(1):109-118.

[本文引用: 1]

杨志成, 陈海宏, 周玲玲, 等.

时频电磁法在金牛湖地区深部地热资源勘查中的应用

[J]. 工程地球物理学报, 2024, 21(1):81-91.

[本文引用: 1]

Yang Z C, Chen H H, Zhou L L, et al.

Application of time-frequency electromagnetic method in exploration of deep geothermal resources in Jinniu Lake area

[J]. Chinese Journal of Engineering Geophysics, 2024, 21(1):81-91.

[本文引用: 1]

Wahab S, Saibi H, Mizunaga H.

Groundwater aquifer detection using the electrical resistivity method at Ito Campus,Kyushu University (Fukuoka,Japan)

[J]. Geoscience Letters, 2021, 8(1):15.

[本文引用: 1]

Loke M H, Rucker D F, Chambers J E, et al. Electrical resistivity surveys and data interpretation[M]. Cham: Springer International Publishing, 2020.

[本文引用: 1]

Tso C H M, Iglesias M, Wilkinson P, et al.

Efficient multiscale imaging of subsurface resistivity with uncertainty quantification using ensemble Kalman inversion

[J]. Geophysical Journal International, 2021, 225(2):887-905.

[本文引用: 1]

Aleardi M, Vinciguerra A, Hojat A.

A geostatistical Markov chain Monte Carlo inversion algorithm for electrical resistivity tomography

[J]. Near Surface Geophysics, 2021, 19(1):7-26.

DOI:10.1002/nsg.12133      [本文引用: 1]

Electrical resistivity tomography is an ill-posed and nonlinear inverse problem commonly solved through deterministic gradient-based methods. These methods guarantee a fast convergence towards the final solution, but the local linearization of the inverse operator impedes accurate uncertainty assessments. On the contrary, numerical Markov chain Monte Carlo algorithms allow for accurate uncertainty appraisals, but appropriate Markov chain Monte Carlo recipes are needed to reduce the computational effort and make these approaches suitable to be applied to field data. A key aspect of any probabilistic inversion is the definition of an appropriate prior distribution of the model parameters that can also incorporate spatial constraints to mitigate the ill conditioning of the inverse problem. Usually, Gaussian priors oversimplify the actual distribution of the model parameters that often exhibit multimodality due to the presence of multiple litho-fluid facies. In this work, we develop a novel probabilistic Markov chain Monte Carlo approach for inversion of electrical resistivity tomography data. This approach jointly estimates resistivity values, litho-fluid facies, along with the associated uncertainties from the measured apparent resistivity pseudosection. In our approach, the unknown parameters include the facies model as well as the continuous resistivity values. At each spatial location, the distribution of the resistivity value is assumed to be multimodal and non-parametric with as many modes as the number of facies. An advanced Markov chain Monte Carlo algorithm (the differential evolution Markov chain) is used to efficiently sample the posterior density in a high-dimensional parameter space. A Gaussian variogram model and a first-order Markov chain respectively account for the lateral continuity of the continuous and discrete model properties, thereby reducing the null-space of solutions. The direct sequential simulation geostatistical method allows the generation of sampled models that honour both the assumed marginal prior and spatial constraints. During the Markov chain Monte Carlo walk, we iteratively sample the facies, by moving from one mode to another, and the resistivity values, by sampling within the same mode. The proposed method is first validated by inverting the data calculated from synthetic models. Then, it is applied to field data and benchmarked against a standard local inversion algorithm. Our experiments prove that the proposed Markov chain Monte Carlo inversion retrieves reliable estimations and accurate uncertainty quantifications with a reasonable computational effort.

杨永明, 鞠杨, 刘红彬, 等.

孔隙结构特征及其对岩石力学性能的影响

[J]. 岩石力学与工程学报, 2009, 28(10):2031-2038.

[本文引用: 1]

Yang Y M, Ju Y, Liu H B, et al.

Influence of porous structure properties on mechanical performances of rock

[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(10):2031-2038.

[本文引用: 1]

孙强, 张志镇, 薛雷, 等.

岩石高温相变与物理力学性质变化

[J]. 岩石力学与工程学报, 2013, 32(5):935-942.

[本文引用: 1]

Sun Q, Zhang Z Z, Xue L, et al.

Physico-mechanical properties variation of rock with phase transformation under high temperature

[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(5):935-942.

[本文引用: 1]

何国梁, 张磊, 吴刚.

循环冻融条件下岩石物理特性的试验研究

[J]. 岩土力学, 2004, 25(S2):52-56.

[本文引用: 1]

He G L, Zhang L, Wu G.

Test study on physical characteristics of rock under freezing-thawing cycles

[J]. Rock and Soil Mechanics, 2004, 25(S2):52-56.

[本文引用: 1]

孟召平, 彭苏萍, 张慎河.

不同成岩作用程度砂岩物理力学性质三轴试验研究

[J]. 岩土工程学报, 2003, 25(2):140-143.

[本文引用: 1]

Meng Z P, Peng S P, Zhang S H.

Triaxial test on physical and mechanical properties of sandstone for different diagenesis degree

[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(2):140-143.

[本文引用: 1]

马炳镇, 李貅.

矿井直流电法超前探中巷道影响的数值模拟

[J]. 煤田地质与勘探, 2013, 41(1):78-81.

[本文引用: 1]

Ma B Z, Li X.

Roadway influences on advanced DC detection in underground mine

[J]. Coal Geology & Exploration, 2013, 41(1):78-81.

[本文引用: 1]

李毛飞, 刘树才, 姜志海, 等.

矿井直流电透视底板探测及三维反演解释

[J]. 煤炭学报, 2022, 47(7):2708-2721.

[本文引用: 1]

Li M F, Liu S C, Jiang Z H, et al.

Detecting floor geological information bymine DC perspective and 3D inversion

[J]. Journal of China Coal Society, 2022, 47(7):2708-2721.

[本文引用: 1]

Tang W W, Liu J X, Ma C Y, et al.

Fast iterative solver for 3D finite-element modeling of controlled-source electromagnetic responses with vector and scalar potentials

[J]. Geophysics, 2023, 88(3):E91-E105.

[本文引用: 1]

Yang Y, Wang P F, Brandenberg S J.

An algorithm for generating spatially correlated random fields using Cholesky decomposition and ordinary Kriging

[J]. Computers and Geotechnics, 2022,147:104783.

[本文引用: 1]

Neyamadpour A.

Application of joint inversion of electrical resistivity data to determine the geometric distribution of municipal sewage leaks:A case study in the Masjedsoleyman town

[J]. Advanced Applied Geology, 2023, 13(4):1105-1117.

[本文引用: 1]

Mohammadi Vizheh M, Bastani M, Kalscheuer T, et al.

Constrained 2D inversion of radio-magnetotelluric and controlled-source audio-magnetotelluric data using high-resolution reflection seismic data:An example in groundwater surveying from Heby,Sweden

[J]. Geophysics, 2023, 88(2):B79-B90.

[本文引用: 1]

Avseth P, Mukerji T, Mavko G. Quantitative seismic interpretation:Applying rock physics tools to reduce interpretation risk[M]. Cambridge: Cambridge University Press, 2005.

[本文引用: 1]

陈剑铭, 任启伟, 涂运中, 等.

基于孔裂隙理论的岩石物理实验研究与理论应用

[J]. 地质论评, 2023, 69(S1):585-587.

[本文引用: 1]

Chen J M, Ren Q W, Tu Y Z, et al.

Experimental study and theoretical application of rock physics based on pore and fracture theory

[J]. Geological Review, 2023, 69(S1):585-587.

[本文引用: 1]

Anselmetti F S, Eberli G P.

Controls on sonic velocity in carbonates

[J]. Pure and Applied Geophysics, 1993, 141(2):287-323.

[本文引用: 1]

Xu S Y, Payne M A.

Modeling elastic properties in carbonate rocks

[J]. The Leading Edge, 2009, 28(1):66-74.

[本文引用: 1]

印兴耀, 宗兆云, 吴国忱.

岩石物理驱动下地震流体识别研究

[J]. 中国科学:地球科学, 2015, 45(1):8-21.

[本文引用: 2]

Yin X Y, Zong Z Y, Wu G C.

Study on seismic fluid identification driven by petrophysics

[J]. Scientia Sinica:Terrae, 2015, 45(1):8-21.

[本文引用: 2]

何沛田, 黄志鹏.

层状岩石的强度和变形特性研究

[J]. 岩土力学, 2003, 24(S1):1-5.

[本文引用: 2]

He P T, Huang Z P.

Studies of strength and deformation characteristics for stratified rock

[J]. Rock and Soil Mechanics, 2003, 24(S1):1-5.

[本文引用: 2]

罗彦斌, 陈建勋, 王利宝, 等.

考虑层间黏聚力的水平层状围岩隧道顶板力学模型计算

[J]. 中国公路学报, 2018, 31(10):230-237,265.

[本文引用: 2]

水平层状岩体力学性质不仅受岩层组合和结构面控制，而且与层间黏聚力密切相关。水平层状围岩隧道在施工过程中对层间黏聚力考虑不当时，极易造成设计支护参数不合理，导致拱部掉块落石、离层、弯折，甚至局部坍塌、超欠挖等工程问题，严重影响工程安全、施工质量和建设进度。目前水平层状围岩隧道顶板一般简化为锚固梁和简支梁模型，但未考虑层间黏聚力。根据水平层状围岩隧道开挖的不同阶段，将隧道顶板分别简化为开挖初始阶段的锚固梁模型和施工扰动后的简支梁模型，并利用顶板梁体模型的协调变形条件，得出梁模型的层间黏聚力计算公式。以大梁峁隧道为工程依托，分别应用考虑层间黏聚力和不考虑层间黏聚力的梁模型进行隧道临界开挖跨度计算。结果表明：考虑层间黏聚力和不考虑层间黏聚力对水平层状围岩隧道临界开挖跨度影响较大。考虑层间黏聚力时，锚固梁模型临界开挖跨度为3.36~4.75 m，简支梁模型临界开挖跨度为2.74~3.88 m；不考虑层间黏聚力时，锚固梁模型临界开挖跨度为0.14~0.30 m，简支梁模型临界开挖跨度为0.12~0.24 m。结合大梁峁隧道工程现场，隧道开挖跨度3~6 m时，拱顶会出现平顶现象，产生离层和掉块，因此考虑层间黏聚力的水平层状围岩隧道顶板力学模型更符合工程实际情况。

Luo Y B, Chen J X, Wang L B, et al.

Mechanical model calculations of tunnel roof with horizontal StratifiedRock mass tunneling considering the interlayer cohesion

[J]. China Journal of Highway and Transport, 2018, 31(10):230-237,265.

[本文引用: 2]

刘平, 刘泉声, 夏明锬, 等.

孔洞形状对层状岩石力学特性影响的FDEM数值模拟研究

[J]. 中南大学学报:自然科学版, 2024, 55(2):595-606.

[本文引用: 2]

Liu P, Liu Q S, Xia M T, et al.

Effect of hole shapes on mechanical behavior of layered rocks using FDEM numerical method

[J]. Journal of Central South University:Science and Technology Edition, 2024, 55(2):595-606.

[本文引用: 2]

张茹, 吕游, 张泽天, 等.

深地工程多维信息感知与智能建造的发展与展望

[J]. 煤炭学报, 2024, 49(3):1259-1290.

[本文引用: 2]

Zhang R, Lyu Y, Zhang Z T, et al.

Development and prospect of multidimensional information perception and intelligent construction in deep earth engineering

[J]. Journal of China Coal Society, 2024, 49(3):1259-1290.

[本文引用: 2]

朱健, 胡国忠, 许家林, 等.

煤层层理对微波破煤增透效果的影响规律

[J]. 煤炭学报, 2024, 49(5):2324-2337.

[本文引用: 2]

Zhu J, Hu G Z, Xu J L, et al.

The influence law of coal seam bedding on the effect of microwave breaking coal and increasing permeability

[J]. Journal of Coal Science, 2024, 49(5):2324-2337.

[本文引用: 2]

许家林.

煤矿绿色开采20年研究及进展

[J]. 煤炭科学技术, 2020, 48(9):1-15.

[本文引用: 1]

Xu J L.

Research and progress of coal mine green mining in 20 years

[J]. Coal Science and Technology, 2020, 48(9):1-15.

[本文引用: 1]

王兆丰, 刘军.

我国煤矿瓦斯抽放存在的问题及对策探讨

[J]. 煤矿安全, 2005, 36(3):29-32,44.

[本文引用: 1]

Wang Z F, Liu J.

Problems existing in methane drainage in coal mines of China and probing into the countermeasures

[J]. Safety in Coal Mines, 2005, 36(3):29-32,44.

[本文引用: 1]

李贺. 微波辐射下煤体热力响应及其流—固耦合机制研究[D]. 徐州: 中国矿业大学, 2018.

[本文引用: 1]

Li H. Studyonthermalresponseand fluid-solidcoupling mechanismof coalunder microwave radiation[D]. Xuzhou: China University of Mining and Technology, 2018.

[本文引用: 1]

杨新乐, 任常在, 张永利, 等.

低渗透煤层气注热开采热—流—固耦合数学模型及数值模拟

[J]. 煤炭学报, 2013, 38(6):1044-1049.

[本文引用: 1]

Yang X L, Ren C Z, Zhang Y L, et al.

Numerical simulation of the coupled thermal-fluid-solid mathematical models during extracting methane in low-permeability coal bed by heat injection

[J]. Journal of China Coal Society, 2013, 38(6):1044-1049.

[本文引用: 1]

管伟明, 张紫昭.

微波加热煤岩裂隙变形的电—热—固耦合模型

[J]. 中国矿业, 2015, 24(7):133-136.

[本文引用: 1]

Guan W M, Zhang Z Z.

Numerical simulate for crack deformation of coal in microwave heated

[J]. China Mining Magazine, 2015, 24(7):133-136.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com