E-mail Alert Rss
 

物探与化探, 2024, 48(6): 1693-1701 doi: 10.11720/wtyht.2024.1526

方法研究·信息处理·仪器研制

基于共偏移距GPR信号包络和三维速度谱分析的介质电磁波速度估计方法

周鑫,, 王洪华,, 王欲成, 吴祺铭, 王浩林, 刘洪瑞

桂林理工大学 地球科学学院,广西 桂林 541004

A method for estimating electromagnetic wave velocities in subsurface media based on common-offset GPR signal envelope and 3D velocity spectrum analysis

ZHOU Xin,, WANG Hong-Hua,, WANG Yu-Cheng, WU Qi-Ming, WANG Hao-Lin, LIU Hong-Rui

School of Geosciences,Guilin University of Technology,Guilin 541004,China

通讯作者: 王洪华(1986-),男,博士,副教授,主要从事探地雷达理论方法及应用研究工作。Email:wanghonghua5@glut.edu.cn

第一作者: 周鑫(1999-),男,硕士研究生,主要从事探地雷达逆时偏移成像方面的研究工作。Email:2807433190@qq.com

责任编辑: 叶佩

收稿日期: 2024-02-22   修回日期: 2024-09-26  

基金资助: 广西自然科学基金项目(2022GXNSFAA035595)
广西自然科学基金项目(2020GXNSFAA159121)

Received: 2024-02-22   Revised: 2024-09-26  

摘要

目前广泛应用于探地雷达(ground penetrating radar,GPR)信号的速度谱分析方法大都通过叠加相干信号的振幅能量来构建速度谱,并估计地下介质电磁波速度;当信号子波出现多个波峰和波谷时,基于振幅的方法所构建的速度谱会出现多个能量团,不利于后续能量峰值的判别、拾取和速度估计。为此,提出了一种基于共偏移距GPR信号包络和三维速度谱分析的地下介质电磁波速度估计方法。该方法通过扫描GPR剖面中的双曲线绕射波信号包络来构建叠加能量随零偏双程走时、试速度以及测点位置变化的三维速度谱,并根据三维速度谱中双曲线顶点出现位置,提取二维速度谱切片。在此基础上,拾取二维速度谱切片中能量峰值对应的试速度并作为地下介质的电磁波速度。数值试验结果表明:与基于信号振幅的三维速度谱分析方法相比,基于信号包络的三维速度谱分析方法计算的速度谱中连续能量团更少、能量更集中、速度估计误差更小,且可更有效地构建逆时偏移的速度模型。

关键词： 三维速度谱分析; 信号包络; 共偏移距探地雷达信号; 速度估计

Abstract

Currently,velocity spectrum analysis methods widely used for ground-penetrating radar(GPR) signals mostly construct velocity spectra by superposing the amplitude energy of coherent signals to estimate electromagnetic wave velocities in subsurface media.In the case of multiple peaks and troughs in signal wavelets,velocity spectra constructed using these amplitude-based methods display multiple energy clusters,adversely affecting the identification,picking,and velocity estimation of subsequent energy peaks.Hence,this study proposed a method for estimating electromagnetic wave velocities in subsurface media based on common-offset GPR signal envelope and 3D velocity spectrum analysis.By scanning the signal envelope of hyperbolic diffracted waves in the GPR profile,the proposed method constructed the 3D velocity spectra of superimposed energy varying with zero-offset two-way travel time,test velocity,and measuring point position.Moreover,it extracted the slices of 2D velocity spectra according to the positions of hyperbolic vertices in the 3D velocity spectra.On this basis,the test velocities corresponding to the energy peaks in the slices of 2D velocity spectra were picked as the electromagnetic wave velocities in subsurface media.The numerical test results show that compared to the amplitude-based methods,the signal envelope-based 3D velocity spectrum analysis method obtained velocity spectra characterized by fewer continuous energy clusters,more concentrated energy,and minor velocity estimation errors,thus more effectively constructing the velocity model with inverse-time migration.

Keywords： three dimensional velocity spectrum analysis; signal envelope; common offset ground penetrating radar signal; velocity estimation

PDF (4846KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

周鑫, 王洪华, 王欲成, 吴祺铭, 王浩林, 刘洪瑞. 基于共偏移距GPR信号包络和三维速度谱分析的介质电磁波速度估计方法[J]. 物探与化探, 2024, 48(6): 1693-1701 doi:10.11720/wtyht.2024.1526

ZHOU Xin, WANG Hong-Hua, WANG Yu-Cheng, WU Qi-Ming, WANG Hao-Lin, LIU Hong-Rui. A method for estimating electromagnetic wave velocities in subsurface media based on common-offset GPR signal envelope and 3D velocity spectrum analysis[J]. Geophysical and Geochemical Exploration, 2024, 48(6): 1693-1701 doi:10.11720/wtyht.2024.1526

0 引言

探地雷达(ground penetrating radar,GPR)作为一种高分辨率无损探测方法,在工程检测、水文地质、考古调查中得到广泛应用[1⇓⇓⇓-5]。信号处理是利用GPR信号准确分析与解释地下介质结构分布的作用手段[6]。其中,地下介质电磁波速度是对GPR信号进行时深转换、偏移成像、全波形反演等处理的关键参数[7]。常规的介电常数法[8]、几何刻度法[9]、金属板反射法[10]等需要取心测量介质的相对介电常数、未考虑电磁波衰减、需要人工拾取信号的初至,一方面造成电磁波速度估计精度较低,另一方面存在以“点”盖“面”的局限,限制了其在实际GPR信号处理中的应用[11-12]。理论上,基于反演理论的GPR波形反演和层析成像可构建较为精确的速度模型,但上述两种方法都存在计算效率低,噪声影响大、且涉及多参数反演等问题,在实际应用中还较为困难[13⇓⇓-16]。

速度分析是利用实测数据估计地下介质电磁波速度的有效方法。常用的速度分析方法主要有:频率波数域偏移法速度估计[17]、互相关分析及最小二乘拟合速度估计[18]、绕射波孤立和偏移聚焦分析速度估计[19]、最小熵法[16]、K-means法速度谱估计[20]、多偏移距数据速度谱分析[21]等。其中,应用最广泛的是多偏移距数据速度谱分析法,其基本原理是通过叠加相干GPR信号的振幅来构建速度谱,以估计地下介质电磁波速度,通常用于共源观测、共中心点观测、阵列天线观测方式等采集的多偏移距GPR信号处理中。然而,现有的商业GPR系统大都采用剖面法观测,通常采集的是共偏移距GPR信号[22]。常规基于多偏移距GPR信号的速度谱分析方法,通常难以用于共偏移距GPR信号的电磁波速度估计。为此,Dong等[23]根据叠后地震信号构建速度谱的思想,构建了基于共偏移距GPR信号的速度谱分析方法,并应用于共偏移距探月雷达信号处理中,较为精确地估计了月壤分层结构的电磁波速度。随后,该方法被应用于共偏移距管线探测GPR信号的电磁波速度估计,准确定位了管线埋深[24]。然而,上述速度谱分析方法估计地下介质电磁波速度时,均以相干信号振幅的叠加为基础,当信号子波出现多个峰值时,构建的速度谱会出现多个能量团,不利于后续能量峰值的精确判别和拾取,从而导致电磁波速度估计精度较差。希尔伯特变换可将信号转换为其解析信号,获得只含有一个正峰值的包络信号,对信号包络进行速度谱分析,可避免原信号子波中的多个正峰值和负峰值共同作用对速度谱产生多个连续能量团问题,更有利于后续能量峰值的精确判别和拾取。目前该方法被应用于共源道集[25]和共中心点道集[26]信号的地下介质电磁波速度估计,并取得了较好的效果。

为此,本文将信号包络思想引入到共偏移距GPR信号的速度谱分析中,以解决常规基于信号振幅的速度谱分析方法构建的速度谱中连续能量团较多,能量峰值难以准确拾取的问题,为从共偏移距GPR信号中准确估计介质电磁波速度提供一种可行有效的方法。

1 共偏移距GPR信号包络的速度谱构建方法

1.1 信号包络的提取

根据希尔伯特变换,一个随时间t变化的解析信号y˜(t)可由实信号y(t)及其对应的希尔伯特变换yH(t)组成,可表示为[27]:

y˜(t)=y(t)+iyH(t)

yH(t)的表达式为:

yH(t)=Hy(t)=-1πP∫-∞∞y(τ)t-τdτ

式中:P代表柯西主值。此外,解析信号y˜(t)也可以通过瞬时振幅E(t)和瞬时相位Φ(t)来表示:

y˜(t)=E(t)eiΦ(t)

其中,瞬时振幅E(t)可表示为:

E(t)=y˜(t)|=y2(t)+yH2(t)

式(4)称为实信号y(t)的包络。可见,GPR信号的包络可通过求取解析信号的振幅获得。

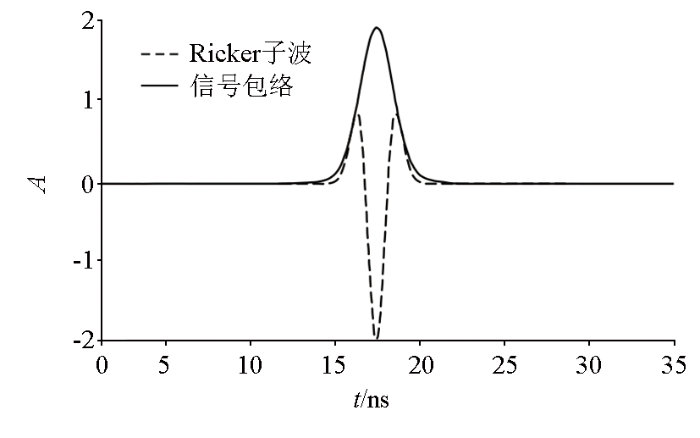
图1展示了时间域Ricker子波波形及其包络,与原始信号振幅中出现2个波峰和1个波谷相比,原信号包络均为正振幅值,只出现1个波峰,更有利于后续构建速度谱过程中信号能量的相干叠加。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   Ricker子波及其包络

Fig.1   Ricker wavelet and its envelope


1.2 共偏移距信号包络的三维速度谱构建

共偏移距三维速度谱分析方法是GPR信号处理中常用的电磁波速度估计方法,其基本原理是[28]:假定一系列可能的试速度,根据不同的零偏双程走时、试速度以及测点位置计算得到不同双曲线轨迹上各个点的双程走时,从而确定一系列双曲线。在此基础上,通过计算双曲线轨迹上不同测点位置的信号包络能量相干性,然后叠加相干度并构建信号能量随测点位置、试速度和零偏移距双程走时变化的三维速度谱。

图2展示了共偏移距GPR信号的三维速度谱分析示意。根据图2a所示的共偏移距测量示意,可采集到如图2b所示的共偏移GPR剖面。由图2b可知:根据零偏双程走时ti、试速度vk以及第j个测点位置与双曲线顶点位置之间的水平距离xj,可得到双曲线第j个点的双程走时ti,j,k为:

ti,j,k=ti2+4xj2/vk2 。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   共偏移距GPR信号的三维速度谱分析示意

a—共偏移距测量示意;b—共偏移距GPR剖面;c—三维速度谱示意

Fig.2   Diagram of three dimensional velocity spectrum analysis of common offset GPR signal

a—diagram of common offset measurement;b—profile of common offset GPR;c—diagram of three dimensional velocity spectrum


根据式(5)可生成一系列双曲线,随后在采集的共偏移GPR剖面图2b中,叠加双曲线位置处所有道的信号包络,可获得叠加能量,其表达式为[29]:

S(ti,xj,vk)=∑i=1NiE(ti,j,k,xj) 。

式中:i=1,2,…,nt;j=1,2,…,nx;k=1,2,…,nv;E表示共偏移距GPR信号包络。Ni为第i次计算时沿测点排列方向的水平窗口长度,nt、nx、nv分别为每道的采样点数、道数和试速度数。S(ti,xj,vk)为叠加能量随测点位置xj、试速度vk和零偏双程走时ti变化的三维速度谱,若试速度非常接近真实速度,则双曲线能量相干叠加后会在三维速度谱中出现一个能量团,如图2c所示。

然而,受地表杂波干扰,以及背景介质速度不均匀的影响,实测信号中双曲线绕射波形态会出现诸如不完整、歪曲、交错或振幅不均匀等现象,导致计算得到的叠加振幅效果较差。为此,对式(6)计算的叠加能量进行归一化处理[24,30]:

C(ti,xj,vk)=1NiL∑j=1L+i-1Si,j,k2∑j=1NE2(ti,j,k,xj)

式中:L为计算时的时间窗口长度。由于剖面中的双曲线绕射波在时间方向上具有一定宽度,利用时间窗口长度L对叠加能量进行归一化,来保证计算结果C(ti,xj,vk)不受信号包络变化的影响。重要的是,在式中增加1/Ni,以补偿沿测点零偏双程走时方向使用不同水平窗口Ni所引起的能量差异[24]。C(ti,xj,vk)是一个三维数据体,由于其能量最大值所对应的三维坐标可以确定双曲线绕射波顶点的双程走时、沿测点排列方向的位置以及电磁波在地下介质中的传播速度,因而可从三维速度谱试速度轴方向上的所有速度谱切片中,找到能量峰值,并提取该位置相应的二维速度谱切片,二维速度谱切片中能量峰值对应的试速度值即为电磁波在地下介质中的传播速度。

然而,由于干扰信号的存在,速度谱仍会受到其影响,从而影响峰值的拾取。因此,为了压制三维速度谱中的干扰响应,本文采用如式(8)所示的软阈值函数[24]:

Ci,j,k=Ci,j,k-a,　　Ci,j,k-aa0　　,　　Ci,j,k-a≤a

式中:a值通常为0.5~0.95,可以根据情况自行调节。

计算速度谱的参数包括水平窗口长度Ni,时窗长度L,试速度步长Δvk,可以根据实际共偏移距剖面的特征进行合理地选择。水平窗口长度Ni可以根据双曲线绕射波沿零偏双程走时的长度进行设定;时窗长度Li根据双曲线绕射波的持续时间进行设定,时窗的起点应该在直达波初至时间之下,以减小直达波的影响;试速度步长Δvk应该根据数据大小、所要估计的速度精度以及计算时间综合考虑进行选择。

2 数值模拟实验

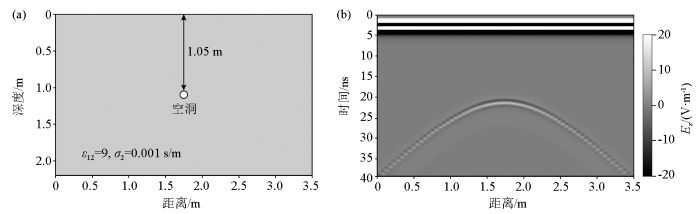
为验证基于共偏移距GPR信号包络和三维速度谱分析的地下介质电磁波速度估计方法的正确性和有效性,采用时域有限差分法对图3a所示的空洞模型进行模拟计算。空洞模型的大小为3.5 m×2.2 m,模型正中心(1.75 m,1.10 m)处埋有一个直径为0.1 m,埋深为1.05 m的空洞。背景介质的相对介电常数为9.0,电导率为0.001 s/m。模拟计算时的网格大小为0.005 m,激励源是中心频率为500 MHz的Ricker子波,时间长度为40 ns,收发天线间距为0.01 m,天线步长为0.05 m。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   空洞模型(a)及其GPR模拟剖面(b)

Fig.3   Model of cavity(a) and its GPR simulation profile(b)


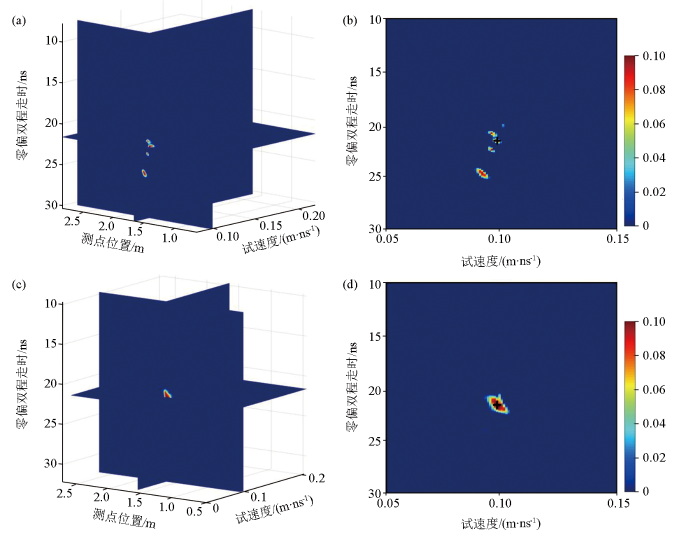
图3b为图3a所示的空洞模型的共偏移距GPR模拟剖面,空洞产生的双曲线绕射波在约21 ns开始出现,且清晰可见。去除图3b中的直达波后,分别利用基于信号振幅和包络的三维速度谱分析方法对其进行速度分析,获得的三维速度谱如图4a、c所示。从图4a、c试速度轴方向上的所有速度谱切片中,找到能量的最大值处,即为双曲线绕射波顶点出现位置,并分别提取出该位置处速度谱切片,获得的结果如图4b、d。由图可见:与图4a和图4b中出现4个明显的能量团相比,图4c和图4d中能量分别更集中,只有一个能量团,更易于速度值的拾取。根据双曲线绕射波出现时间和能量峰值(黑色十字标注),从图4b、d估计的电磁波速度分别为0.096 m/ns、0.098 m/ns,与真实速度0.1 m/ns相比,误差分别为4.0%、2.0%。由此可见,与基于信号振幅的三维速度谱分析结果相比,基于信号包络的三维速度谱分析方法不仅更易于根据能量峰值拾取速度,而且速度估计精度更高。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   图3b去直达波后的GPR信号构建的三维速度谱

a—基于振幅的三维速度谱;b—基于振幅的速度谱切片;c—基于包络的三维速度谱;d—基于包络的速度谱切片

Fig.4   Three dimensional velocity spectrum constructed by the GPR signal in figure 3b after removing the direct wave

a—three dimensional velocity spectrum based on amplitude;b—velocity spectrum slice based on amplitude;c—three dimensional velocity spectrum based on envelope;d—velocity spectrum slice based on envelope


3 实测信号测试

为验证基于共偏移距GPR信号包络和三维速度谱分析方法在实测信号中的应用效果,将其应用于实测信号中并与基于信号振幅的三维速度谱分析结果进行对比,以分析其优势。

图5a为利用GSSI-SIR-4000型GPR系统对某地下管道进行探测获得的原始GPR剖面一,主要采集参数如下:天线中心频率为1 600 MHz、叠加次数为50、点距为0.01 m,时间间隔为0.013 4 ns,时窗为8.66 ns。对其进行零时校正、背景去除、道间均衡、增益处理等常规处理后的GPR剖面如图5b所示。需要注意的是,零时校正导致剖面中双曲线位置发生了较为明显的上移。分别利用基于信号振幅和信号包络的三维速度谱分析方法对图5b中的GPR信号进行处理,获得的结果如图6所示。根据双曲线绕射波顶点出现位置,从图6a、c中分别提取出该位置处速度谱切片,获得的结果如图6b、d所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   实测原始GPR剖面一(a)及常规处理后的GPR剖面(b)

Fig.5   The original GPR profile 1 of measured data(a) and GPR profile after conventional processing(b)


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   图5b中的GPR信号构建的三维速度谱

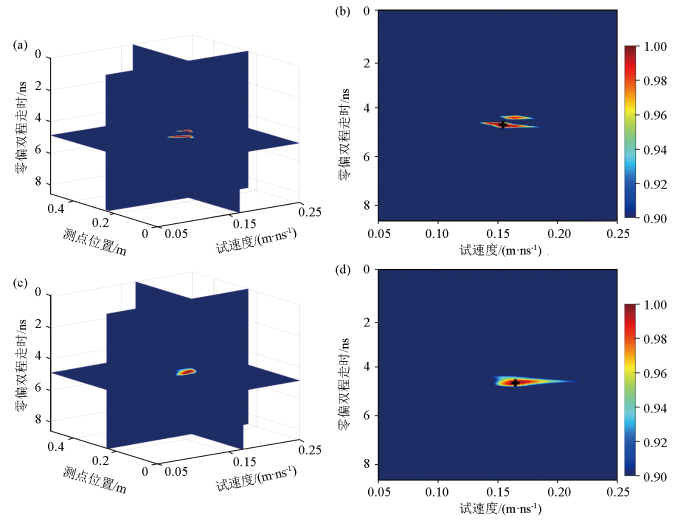
a—基于振幅的三维速度谱; b—基于振幅的速度谱切片;c—基于包络的三维速度谱; d—基于包络的速度谱切片

Fig.6   Three dimensional velocity spectrum constructed by the GPR signal in figure 5b

a—three dimensional velocity spectrum based on amplitude;b—velocity spectrum slice based on amplitude;c—three dimensional velocity spectrum based on envelope;d—velocity spectrum slice based on envelope


由图可见:与图6a和图6b中出现2个明显的能量团相比,图6c和图6d中能量分别更集中,只有一个能量团,更易于速度值的拾取。根据双曲线绕射波顶点出现时间和能量峰值(黑色“十字”标注),从图6b和图6d估计的电磁波速度分别为0.153 m/ns、0.163 m/ns。根据图6b和图6d中能量峰值,提取到对应的零偏双程走时分别为4.64 ns、4.70 ns,利用式(9)计算的地下管道埋深分别为0.355 m、0.383 m,与真实埋深0.370 m相比,误差分别约为4.1%、3.5%。

h=vt2

式中:v、t、h分别代表所估计的电磁波速度、双曲线绕射波顶点所对应时间以及所估计的埋深。实测结果表明,与基于信号振幅的三维速度谱分析方法结果相比,基于信号包络的三维速度谱分析方法不仅更易于根据能量峰值拾取速度,而且速度估计精度更高。

利用GSSI-SIR-4000型GPR系统对某地进行探测获得的GPR剖面二经常规处理后如图7所示。主要采集参数如下:天线中心频率为200 MHz、叠加次数为70、点距为0.05 m,时间间隔为0.046 9 ns,时窗为45.25 ns。对该GPR剖面中所含有的其中10条双曲线绕射波利用红色数字进行标记。10条双曲线的顶点出现时间和水平位置等信息如表1第2列和第3列所示。将基于信号振幅和信号包络的三维速度谱算法分别应用于图7中白色虚线所划分的7个子GPR数据,获得的速度谱切片如图8和图9所示。由于第1、2条双曲线绕射波的水平位置相同,其速度谱分析结果出现在一张速度谱切片中,如图8a和9a所示。同理,第4、5、6条双曲线绕射波的计算结果也出现在一张速度谱切片中,如图8c和9c所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   实测GPR剖面二处理结果

Fig.7   Processing result of measured GPR profile 2


表1   估计的速度值

Table 1  The estimated velocity value

双曲线
序号		顶点出现
时间/ns		顶点水平
位置/m		估计的速
度/(m·ns-1)		估计的
深度/m
14.640.80.0910.21
211.580.80.0850.49
334.692.90.0751.30
416.926.40.0800.67
523.726.60.0820.97
638.306.50.0721.37
732.918.20.0681.12
828.5510.70.0721.03
919.1712.70.0880.84
1022.3614.10.0850.95

新窗口打开| 下载CSV


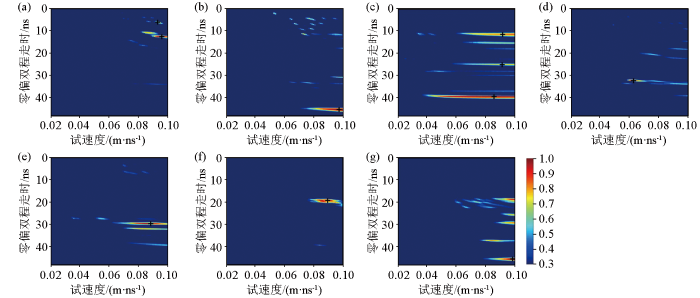
图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   图7中GPR信号所构建的基于振幅的速度谱切片

a—双曲线1和2;b—双曲线3;c—双曲线4、5和6;d—双曲线7;e—双曲线8;f—双曲线9;g—双曲线10

Fig.8   The amplitude-based velocity spectrum slice constructed by the GPR signal in figure 7

a—hyperbola 1 and 2;b—hyperbola 3;c—hyperbola 4,5 and 6;d—hyperbola 7;e—hyperbola 8;f—hyperbola 9;g—hyperbola 10


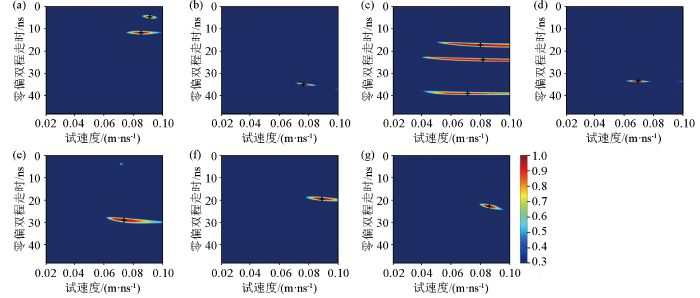
图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   图7中GPR信号所构建的基于包络的速度谱切片

a—双曲线1和2;b—双曲线3;c—双曲线4、5和6;d—双曲线7;e—双曲线8;f—双曲线9;g—双曲线10

Fig.9   The envelope-based velocity spectrum slice constructed by the GPR signal in figure 7

a—hyperbola 1 and 2;b—hyperbola 3;c—hyperbola 4,5 and 6;d—hyperbola 7;e—hyperbola 8;f—hyperbola 9;g—hyperbola 10


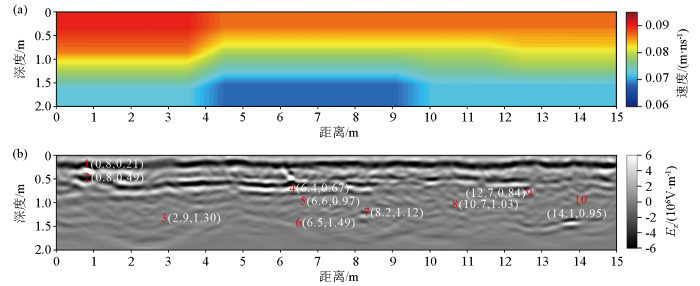
由图8可见,速度谱切片普遍出现多个连续能量团如图8a、c、e、f、g,能量团周围存在微弱信号的干扰如图8b、c、d、e、g,不利于速度的拾取。个别速度谱切片估计的速度值不在合理速度分布范围内如图8b、g。由图9可见,能量聚焦较好,能量团清晰可见,无多个连续能量团出现。对比可知:基于信号包络的三维速度谱分析方法相比基于信号振幅更容易拾取速度,且拾取的速度值更合理。分别提取图9能量峰值(黑色“十”字所示)对应的速度,如表1第4列所示,地下介质电磁波速度分布在0.068~0.091 m/ns之间,根据式(9)计算的双曲线顶点深度如表1第5列所示。在此基础上,利用表1中估计的速度和顶点深度值,并结合高斯圆滑,构建的二维电磁波速度模型如图10所示。由图可见:地下介质电磁波速度大致呈层状分布,埋深1.0 m以内的介质电磁速度约为0.086 m/ns;埋深1.0~1.5 m之间的介质电磁波速度约为0.076 m/ns;埋深1.5~2.0 m之间的介质电磁波速度约为0.071 m/ns,水平位置4~10 m出现局部低速异常。利用图10a所示的二维速度模型作为偏移速度模型,对图7中的实测GPR数据进行逆时偏移成像,获得结果如图10b所示。由图可见,双曲线绕射波能量收敛较好,成像结果有利于后续定位地下目标体位置。实测信号测试结果表明基于信号包络的三维速度谱方法可为后续的逆时偏移提供更为有效的速度模型。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   二维速度模型(a)及逆时偏移剖面(b)

Fig.10   The two dimensional velocity model(a) and reverse time migration profile(b)


4 结论

1)针对基于共偏移距GPR信号振幅的三维速度谱分析方法所构建的速度谱出现多个能量团,不利于后续能量峰值的准确拾取以及速度的准确估计问题,本文提出了一种基于共偏移距GPR信号包络和三维速度谱分析的地下介质电磁波速度估计方法。

2)数值测试结果表明:与基于信号振幅的三维速度谱分析方法相比,基于信号包络的三维速度谱分析方法计算的速度谱中连续能量团更少、能量更集中,估计的速度更合理、精确,可为逆时偏移提供更为有效的速度模型。

参考文献

韩佳明, 仲鑫, 景帅, 等.

探地雷达在黄土地区城市地质管线探测中的应用

[J]. 物探与化探, 2020, 44(6):1476-1481.

[本文引用: 1]

Han J M, Zhong X, Jing S, et al.

The application of geological radar to urban geological pipeline detection in the loess area

[J]. Geophysical and Geochemical Exploration, 2020, 44(6):1476-1481.

[本文引用: 1]

戴前伟, 宁晓斌, 张彬.

基于共中心点道集约束的探地雷达波阻抗反演

[J]. 煤田地质与勘探, 2020, 48(3):211-218.

[本文引用: 1]

Dai Q W, Ning X B, Zhang B.

Common midpoint gather constraint-based impedance inversion of ground penetrating radar

[J]. Coal Geology & Exploration, 2020, 48(3):211-218.

[本文引用: 1]

宗鑫, 王心源, 刘传胜, 等.

探地雷达在地下考古遗存探测中的实验与应用

[J]. 地球信息科学学报, 2016, 18(2):272-281.

DOI:10.3724/SP.J.1047.2016.00272      [本文引用: 1]

近年来,探地雷达被越来越多地应用于考古探查中。由于反演多解性问题的存在,雷达图像上的异常既可能是考古目标引起的,也可能是由于地下环境介质的不连续性引起的,所以探究不同类型的考古遗存在探地雷达图像上的典型异常响应,有助于准确识别雷达图像上的“真”异常,剔除一些“假”异常。首先,本文基于西北干旱-半干旱区文物埋藏环境,在河北省怀来县遥感综合试验站试验区设计实施了地下目标体探地雷达探测实验,分析了不同材质的小尺度目标体及夯土结构在探地雷达图像上的响应特征;然后,进一步将探地雷达应用于悬泉置遗址地下城墙基址的探测,对城墙在雷达图像上的响应特征进行了分析。实践表明,探地雷达技术在埋藏浅、小尺度、物性差异不大的考古探查中具有很好的效果,得到并解释了点状、线状、面状等不同考古目标体在探地雷达图像上的响应规律。

Zong X, Wang X Y, Liu C S, et al.

Experiments and applications of ground penetrating radar in the investigation of subsurface archaeological interest

[J]. Journal of Geo-Information Science, 2016, 18(2):272-281.

[本文引用: 1]

Lyu Y Z, Wang H H, Gong J B.

Application of GPR reverse time migration in tunnel lining cavity imaging

[J]. Applied Geophysics, 2020, 17(2):277-284.

[本文引用: 1]

江玉乐, 黄鑫, 张楠.

探地雷达在公路隧道衬砌检测中的应用

[J]. 煤田地质与勘探, 2008, 36(2):76-78.

[本文引用: 1]

Jiang Y L, Huang X, Zhang N.

Application of ground penetrating radar in the inspection of highroad tunnel lining

[J]. Coal Geology & Exploration, 2008, 36(2):76-78.

[本文引用: 1]

冯德山, 戴前伟, 余凯.

基于经验模态分解的低信噪比探地雷达数据处理

[J]. 中南大学学报:自然科学版, 2012, 43(2):596-604.

[本文引用: 1]

Feng D S, Dai Q W, Yu K.

GPR signal processing under low SNR based on empirical mode decomposition

[J]. Journal of Central South University:Science and Technology Edition, 2012, 43(2):596-604.

[本文引用: 1]

王敏玲, 梁值欢, 王洪华, 等.

探地雷达逆时偏移成像方法研究现状及进展

[J]. 地球物理学进展, 2019, 34(5):2087-2096.

[本文引用: 1]

Wang M L, Liang Z H, Wang H H, et al.

Review of reverse time migration in ground penetrating radar

[J]. Progress in Geophysics, 2019, 34(5):2087-2096.

[本文引用: 1]

王新静, 赵艳玲, 胡振琪, 等.

不同水分条件下探地雷达电磁波波速估算方法与对比分析

[J]. 煤炭学报, 2013, 38(S1):174-179.

[本文引用: 1]

Wang X J, Zhao Y L, Hu Z Q, et al.

Estimation method and comparative analysis of electromagnetic wave velocity of ground penetrating radar under different moisture conditions

[J]. Journal of China Coal Society, 2013, 38(S1):174-179.

[本文引用: 1]

牛富俊, 陈银城.

广州地区城市道路病害探测图谱与优化方法

[J]. 应用科技, 2022, 49(2):133-139.

[本文引用: 1]

Niu F J, Chen Y C.

The atlas and optimization method of urban road disease detection in Guangzhou area

[J]. Applied Science and Technology, 2022, 49(2):133-139.

[本文引用: 1]

孔令讲, 周正欧.

浅地层探地雷达波速测量方法的研究

[J]. 电子学报, 2002, 30(9):1330-1332.

[本文引用: 1]

波速的测量在探地雷达的研究中一直是一个至关重要的课题,尤其是对地下目标进行定位和成像时;本文针对浅地层探地雷达接收信号的特征,抛弃传统的过零点检测和其他的边缘轮廓检测方法,提出用极值进行边缘轮廓检测的方法,从而对目标的提取更准确并且有较少的数据,减少了霍夫变换的计算量;通过对霍夫变换算法的分析,针对传统霍夫变换的缺点,提出了一种加FIR低通滤波器的改进霍夫变换;同时应用算法对实测数据进行了计算,证明所提算法比传统的霍夫变换方法有更高的测速准确度.

Kong L J, Zhou Z O.

Research on measurement of wave speed for sub-surface penetrating radar

[J]. Acta Electronica Sinica, 2002, 30(9):1330-1332.

[本文引用: 1]

Leng Z, Al-Qadi I L.

An innovative method for measuring pavement dielectric constant using the extended CMP method with two air-coupled GPR systems

[J]. NDT & E International, 2014, 66:90-98.

[本文引用: 1]

李廷军, 周正欧.

探地雷达中双曲线的提取及在波速估计中的应用

[J]. 电波科学学报, 2008, 23(1):124-128.

[本文引用: 1]

Li T J, Zhou Z O.

Extraction of hyperbolic signatures and application for propagation velocity estimation in GPR

[J]. Chinese Journal of Radio Science, 2008, 23(1):124-128.

[本文引用: 1]

Guo X B, Liu H, Shi Y, et al.

Improving waveform inversion using modified interferometric imaging condition

[J]. Acta Geophysica, 2018, 66(1):71-80.

[本文引用: 1]

Seol S J, Kim J H, Cho S J, et al.

A radar survey at a granite quarry to delineate fractures and estimate fracture density

[J]. Journal of Environmental and Engineering Geophysics, 2004, 9(2):53-62.

[本文引用: 1]

Wang H H, Xi Y H, Lyu Y Z, et al.

Attenuation-compensated reverse time migration of GPR data constrained by resistivity

[J]. Applied Geophysics, 2022, 19(4):563-571.

[本文引用: 1]

席宇何, 王洪华, 王欲成, 等.

基于速度移动窗的最小熵法在GPR逆时偏移中的应用

[J]. 物探与化探, 2023, 47(5):1250-1260.

[本文引用: 2]

Xi Y H, Wang H H, Wang Y C, et al.

Application of the minimum entropy method based on a velocity-controlled moving window to the reverse time migration of ground-penetrating radars

[J]. Geophysical and Geochemical Exploration, 2023, 47(5):1250-1260.

[本文引用: 2]

张安学, 蒋延生, 汪文秉.

探地雷达频率波数域速度估计和成像方法的实验研究

[J]. 电子学报, 2001, 29(3):315-317.

[本文引用: 1]

探地雷达的分辨率和地下电磁波的速度估计是探地雷达应用中两个重要研究课题,类似地震信号处理中的频率波数域偏移处理,本文提出将频率波数域偏移方法应用到探地雷达的成像和速度估计中来,并用实验数据验证了该方法的可行性和有效性.

Zhang A X, Jiang Y S, Wang W B.

Experimental studies on GPR velocity estimation and imaging method using migration in frequency wavenumber domain

[J]. Acta Electronica Sinica, 2001, 29(3):315-317.

[本文引用: 1]

崔凡, 李思远, 王丽冰.

基于互相关分析及最小二乘拟合的GPR偏移速度估计

[J]. 地球物理学进展, 2018, 33(1):353-361.

[本文引用: 1]

Cui F, Li S Y, Wang L B.

Migration velocity estimation of GPR based on cross-correlation and least square fitting

[J]. Progress in Geophysics, 2018, 33(1):353-361.

[本文引用: 1]

吕文敏, 张金海. 基于绕射波孤立和偏移聚焦分析的探地雷达速度建模[M]. 北京: 北京伯通电子出版社, 2021.

[本文引用: 1]

Lyu W M, Zhang J H. Velocity modeling of ground-penetrating radar based on the analysis of isolated and offset focusing of wraparound waves[M]. Beijing: Beijing Botong Electronic Publishing House, 2021.

[本文引用: 1]

王天琪, 李静, 白利舸, 等.

基于速度分析的探地雷达阻抗介电常数反演

[J]. 吉林大学学报:地球科学版, 2021, 51(2):561-570.

[本文引用: 1]

Wang T Q, Li J, Bai L G, et al.

GPR impedance inversion of permittivity based on velocity analysis

[J]. Journal of Jilin University:Earth Science Edition, 2021, 51(2):561-570.

[本文引用: 1]

Wang H H, Liu H, Cui J, et al.

Velocity analysis of CMP gathers acquired by an array GPR system `Yakumo':Results from field application to tsunami deposits

[J]. Exploration Geophysics, 2018, 49(5):669-674.

[本文引用: 1]

刘钰. 探地雷达数据波阻抗反演方法及其应用研究[D]. 杭州: 浙江大学, 2018.

[本文引用: 1]

Liu Y. The study of ground penetrating radar impedance inversion method and its application[D]. Hangzhou: Zhejiang University, 2018.

[本文引用: 1]

Dong Z J, Feng X, Zhou H Q, et al.

Properties analysis of lunar regolith at Chang'E-4 landing site based on 3D velocity spectrum of lunar penetrating radar

[J]. Remote Sensing, 2020, 12(4):629.

[本文引用: 1]

彭建, 杨泽帆, 白洁, 等.

基于探地雷达的地下管线埋深估计方法

[J]. 雷达科学与技术, 2022, 20(1):79-86.

[本文引用: 4]

Peng J, Yang Z F, Bai J, et al.

Depth estimation of underground pipeline using ground penetrating radar

[J]. Radar Science and Technology, 2022, 20(1):79-86.

[本文引用: 4]

Liu H, Sato M.

In situ measurement of pavement thickness and dielectric permittivity by GPR using an antenna array

[J]. NDT & E International, 2014, 64:65-71.

[本文引用: 1]

Liu H, Xie X Y, Cui J, et al.

Groundwater level monitoring for hydraulic characterization of an unconfined aquifer by common mid-point measurements using GPR

[J]. Journal of Environmental and Engineering Geophysics, 2014, 19(4):259-268.

[本文引用: 1]

程乾生. 信号数字处理的数学原理[M]. 北京: 石油工业出版社, 1979.

[本文引用: 1]

Cheng Q S. Mathematical principle of signal digital processing[M]. Beijing: Petroleum Industry Press, 1979.

[本文引用: 1]

Liu H, Takahashi K, Sato M.

Measurement of dielectric permittivity and thickness of snow and ice on a brackish lagoon using GPR

[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(3):820-827.

[本文引用: 1]

陆基孟, 王永刚. 地震勘探原理(3版)[M]. 东营: 中国石油大学出版社, 2009.

[本文引用: 1]

Lu J M, Wang Y G. Principle of seismic exploration(3rd edition)[M]. Dongying: China University of Petroleum Press, 2009.

[本文引用: 1]

龚俊波. 三维多偏移距探地雷达数据的逆时偏移成像方法研究[D]. 桂林: 桂林理工大学, 2021.

[本文引用: 1]

Gong J B. Research on inverse time migration imaging method of 3D multi-offset ground penetrating radar data[D]. Guilin: Guilin University of Technology, 2021.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com