裂缝预测在储层勘探开发中具有重要意义,大尺度裂缝对钻井工程有重要影响^[1],对其发育位置及范围进行预测,可以减少钻井过程中可能产生的泥浆漏失,降低钻井施工的风险性,对页岩气地区的勘探开发具有十分重要的意义;中尺度裂缝提供了储层流体储集空间和渗透率;小尺度裂缝控制了储层的含气性,并对压裂效果有显著影响。地震断裂刻画主要依靠地震数据的几何学特征,常见的地震断裂刻画属性包括:相干属性、曲率属性、蚂蚁体属性、边缘检测属性、纹理属性、最大似然属性、混沌体属性、最优曲面投票属性以及振幅梯度凌乱性属性等。

相干属性在断裂检测发展历程中提出最早,发展最为成熟。自1955年Simpon在论文中提出了类似相干的想法,1995年Bahorich等^[2]将相干属性正式论证并应用于地震数据,引出了第一代相干算法(C1)。第一代相干算法是基于两点之间的相似性进行计算的,抗噪能力较差。1998年Marfurt等^[3]在第一代相干算法的基础上引入了地层倾角的概念,发展出了第二代多道相似性相干算法(C2),其抗噪能力以及地层产状刻画能力都得到了一定的增强,但是对于复杂构造的刻画精度依旧有限。1999年Gersztenkorn 等^[4]提出了第三代基于协方差矩阵的本征结构相干算法(C3),通过计算地震数据协方差矩阵的特征值进而表征地下地质构造。相比于第一代、第二代相干算法,第三代相干算法对地下复杂构造的辨识能力得到了一定的增强,但是对于倾角较大的断裂以及挠曲的刻画能力依旧有限。1999年Marfurt等^[3]在第三代相干算法的基础上加入了地层倾角概念,成功压制了第三代相干算法对倾角较大的断裂以及扰曲不敏感的缺陷。在此基础上,2002年国内学者王西文^[5]将时频分析算法和第三代相干算法结合,得到了比原始算法精度更高的结果,打开了多尺度断裂刻画的新思路,为多尺度断裂刻画奠定了一定的基础。2013年以及2016年,Hale^[6]和Wu等^[7⇓⇓-10]分别提出了fault likelihood以及最优曲面投票等属性,形成了断裂自动刻画的能力,通过这些属性可以自动表征断裂的走向以及规模,但是对于复杂构造以及微小裂缝的刻画能力有限。振幅梯度凌乱性属性是2014年由Ai-Dossary等^[11]提出的,它的核心思想是假设断层面在局部区域是一个面,通过在三维空间里各个方位角和倾角搜索地震振幅梯度向量的凌乱性,找出凌乱性最强的面便是断层位置^[1]。

在时间域中,单一属性无法准确刻画微小断裂,因此,将时间域地震数据通过高精度时频分析算法转换至时频域,根据不同频带表征的地质信息不同来刻画不同尺度的断裂信息。同步挤压变换是2011年Daubechies^[12]在经验模态分解(EMD)的思路上,结合小波变换提出的高分辨率时频分析算法。但是,由于小波变换本质上是表征尺度和时间的关系,和真实的频率并未建立直接的联系,因此,2016年黄忠来^[13-14]等提出了同步挤压S变换并应用于地震数据的解释中,使地震解释结果的分辨率得到了提高。2019年周怀来等^[15⇓-17]将同步挤压短时傅里叶变换和多道倾角导向相干算法综合应用于地震数据断裂刻画,得到了不同尺度的断裂信息。同步挤压变换是传统变换的后处理过程,能够在时间域转换至时频域时提高信号的时频聚焦能力;广义S变换能够满足时间分辨率和频率分辨率的同时调节,使得时频分辨率达到最佳,因此将同步挤压变换和广义S变换结合可以得到更为准确的时频变换结果。模型计算以及实际资料对比结果表明,基于振幅梯度凌乱性属性对于断裂的连续性好于相干算法,同时结合高精度的时频分析算法,对不同尺度的断裂都有着较好的表征能力。

同步挤压广义S变换可以提高信号时频分析中的噪声鲁棒性、频率分量的稳定性和连续性。对于信号h(t),如果h(t)∈L²(R)(L²(R)表示实数域中的平方可积函数空间),则h(t)的广义S变换表达式GST为:

式中:t为时间;f为频率;τ为时间窗口参数;r和σ为控制高斯窗函数伸缩和平移的常数。

鉴于 Hyssenburg 的不确定原理决定了广义S变换的时频分辨率,结合同步挤压的思想发展了同步挤压广义S变换。首先,对广义S变换后的时频谱求取其真实的瞬时频率,其次,对广义S变换的时频谱能量展开挤压并且重排于信号的瞬时频率处。根据式(1)计算可以得到信号的瞬时频率表达式f_h:

式中:δ为冲激函数;n为某一频率点常数。

根据求取得到的信号瞬时频率值,结合广义S变换所得到的时频能量值,对信号求取同步挤压广义S变换值。信号h(t)的同步挤压广义S变换值SGST为:

式中:f₀、f_m分别为同步挤压广义S变换后和变换前时频谱上的频率索引;Δf、Δf_m分别为同步挤压广义S变换后和变换前时频谱的离散频率之间的频率间隔。式(3)表示将同步挤压广义S变换后的时频谱上的频率区间fh-f02,fh+f02内的值进行挤压并且重排,放在频率f₀处^[16-17]。

假设沿着某个地震样点s的某个方位v(为法向向量)搜索振幅矢量的凌乱性,构建的梯度构造张量场T(s,v)为^[11]:

式中:D_x、D_y、D_t分别为地震振幅沿着坐标轴x、y以及时间t方向的变化率;SW_N(s,v)为沿着方位v的平滑因子,平滑函数为多点高斯函数,平滑半径由用户进行控制。在建立s方向的矩阵后,使用以下函数求取振幅矢量凌乱性F:

式中:λ₁、λ₂、λ₃分别为T的第一、第二、第三特征值。

该方法从地震振幅数据体出发,直接搜索断层在三维空间的展布规律,简洁高效,其结果无论是在水平切片还是垂向剖面上,断层的可解释性都很强,是一种较好的三维断层自动追踪方案^[1]。

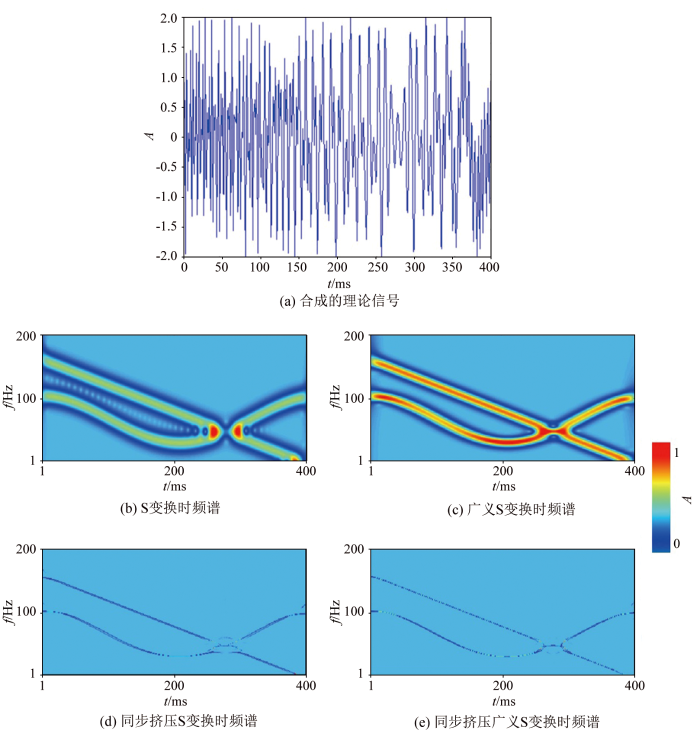
为了讨论S变换、广义S变换、同步挤压S变换、同步挤压广义S变换这4种变换的时频聚焦能力,合成了如图1a所示的理论信号来进行对比,信号长度为0.4 s,采样间隔为1 ms。对该理论信号分别使用4种变换进行时频变换处理,得到如图1b~e所示的检测结果。通过对比各时频谱发现:S变换由于受窗函数的制约,导致时频聚焦能力最差;而经过高斯窗控制参数的广义S变换时频谱中,时频聚焦能力有所提升,但是依旧无法满足高精度时频变换的目的;在同步挤压变换的时频谱中,同步挤压S变换以及同步挤压广义S变换都能表现出很高的时频分辨率,但同步挤压广义S变换由于存在高斯窗调节参数,使得在处理过程中可以灵活控制时间分辨率和频率分辨率,使其可以达到一个相对平衡的状态,因此同步挤压广义S变换的时频谱从时频能量分布以及时频连续性都较好于同步挤压S变换。

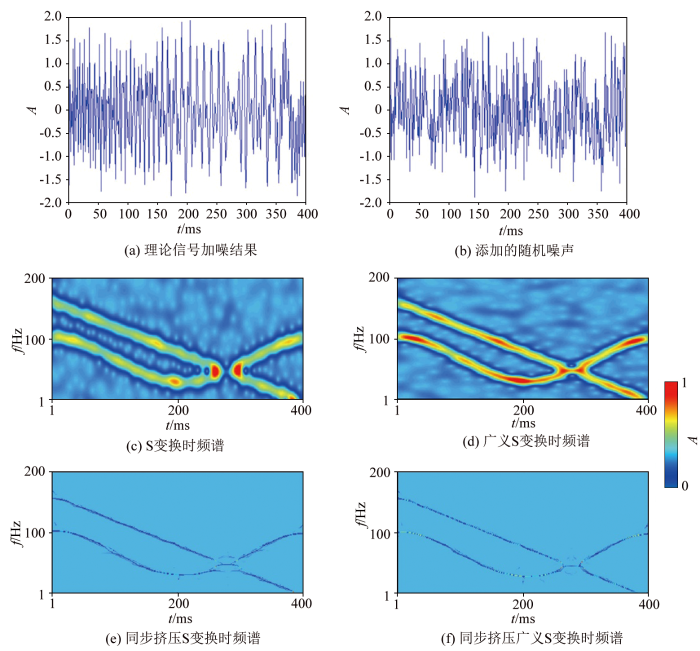
在地震资料采集处理过程中,存在许多噪声以及工业干扰等影响,因此需要处理解释算法具有一定的抗噪能力。为了验证并对比4种变换的抗噪能力以及在高噪声环境下对有效信号的高分辨识别能力,在合成的理论信号中加入如图2b所示的噪声信号,得到如图2a所示的持20%随机噪声的理论信号。对该信号分别使用4种变换进行时频分析,结果见图2c~f。可以发现,每一个时频结果与图1相对比都出现了一定的扰动,但是同步挤压广义S变换的结果受噪声的影响最小。

基于上述对单道信号的对比分析,同步挤压广义S变换对信号的时频聚焦能力最强,因此将该算法应用于正演模型进行验证,突出该算法对多尺度断裂预测的精度和准确性。

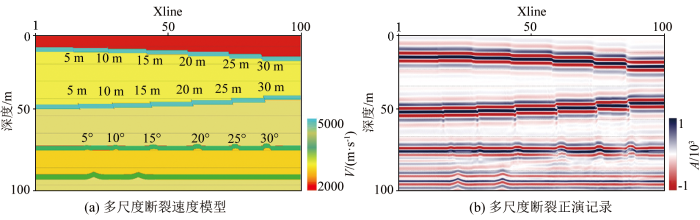
首先,建立5~30 m正断层、5~30 m逆断层以及0°~30°的挠曲模型,观测系统设置为炮点个数226,检波点个数301,偏移距6 000 m,炮点间距80 m,检波点间距40 m,子波主频25 Hz;其次,采用全波动方程方法进行断裂模型正演,并基于Kirchhoff积分法进行深度偏移,获得正演偏移剖面(图3)。

图3为建立的多尺度断裂速度模型以及多尺度断裂的正演记录,地震子波采用25 Hz主频的雷克子波。正演结果很好地反映了断裂的形态特征。

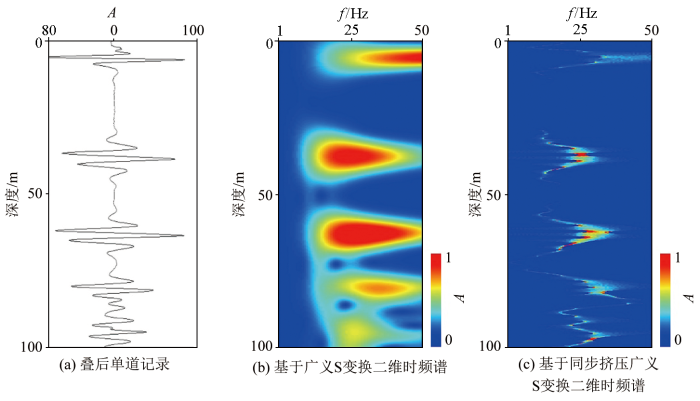
在进行同步挤压广义S变换振幅梯度凌乱性多尺度断裂预测前,首先需要对地震数据进行频谱分析,确定地震数据的频带范围,同时将频带按主频前后划分为低频、中频和高频,提取不同频带的地震数据进行多尺度断裂预测。图4为提取的模型叠后单道记录,总共4个反射界面,分别基于广义S变换和同步挤压广义S变换将时间域的单道记录转换至时频域。从时频域二维时频谱可知:同步挤压广义S变换的时频聚焦能力要高于广义S变换,因此基于同步挤压广义S变换得到的结果分辨率更高;数据整体优势频带范围为1~50 Hz,主频为25 Hz。

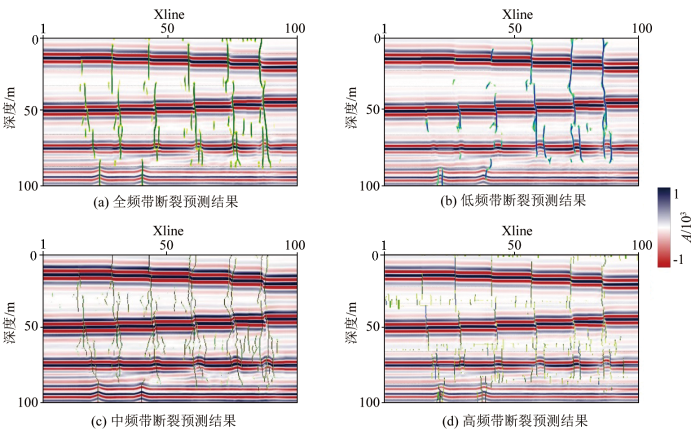
在基于上述单道记录时频分析的基础上,将地震数据频带等额划分为1~15 Hz、16~30 Hz、31~50 Hz的频带范围,进行多尺度的断裂分析(图5)。首先,基于全频带数据进行振幅梯度凌乱性断裂计算(图5a),然后分别对谱分解得到的不同频带数据进行振幅梯度凌乱性断裂计算,得到图5b~d所示的结果。图5显示:低频带计算的断裂结果对于大尺度断裂有较好的刻画能力;中频带计算的断裂结果对于中尺度断裂有较好的结果,同时对大尺度也有较好的刻画能力;相比于低频带和中频带,高频带计算得到的断裂对小尺度断裂有较好的表征能力。

从图5多尺度断裂预测结果中还可以发现,相比于图4速度模型及正演记录,每个频带均出现了较多的假断裂,这是由于上层的大尺度断裂导致了下层地质信息在偏移过程中引入了误差、子波旁瓣等因素造成的。但是,不同频带所得到的断裂结果和全频带计算得到的断裂结果有较高的相似性,分频断裂计算可以表征不同尺度的断裂,相较于全频带可以得到更多的断裂信息。

基于同步挤压广义S变换的高时频聚焦能力,在时频域可开展多种属性分析,对断裂具有更好的识别能力。

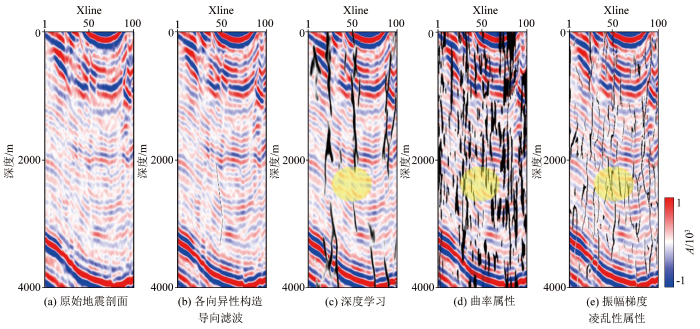
研究区紧邻二级断裂,构造特征复杂,钻遇率损失较多,同时受断裂预测算法精度限制,断裂预测吻合率有待提高。图6为对实际地震数据进行断裂识别的结果。分析原始的地震数据可知(图6a),两边地层的挤压造成了地层褶皱、断裂,但是原始地震剖面中断点不清晰,并且断裂不连续。基于此,通过各向异性构造导向滤波对原始数据进行处理,以增强断裂连续、突出断点信息。图6b为各向异性构造导向滤波结果,相对于原始剖面,表现为断裂连续,断点更为清晰。

为了验证空间3D振幅梯度凌乱性对断裂的刻画精度高于深度学习以及曲率属性,基于各向异性构造导向滤波的结果分别开展深度学习、曲率和空间3D振幅梯度凌乱性断裂计算。深度学习能够大体刻画断裂的基本信息,但是仅对大断裂有较好的刻画能力(图6c);曲率属性能够较好地刻画断裂,但是断裂不够连续并且断点刻画不够清晰(图6d);相比于深度学习、曲率属性,空间3D振幅梯度凌乱性检测结果(图6e)显示断裂连续性得到了加强,并且断点清晰,更符合地质规律(见图中黄色区域)。

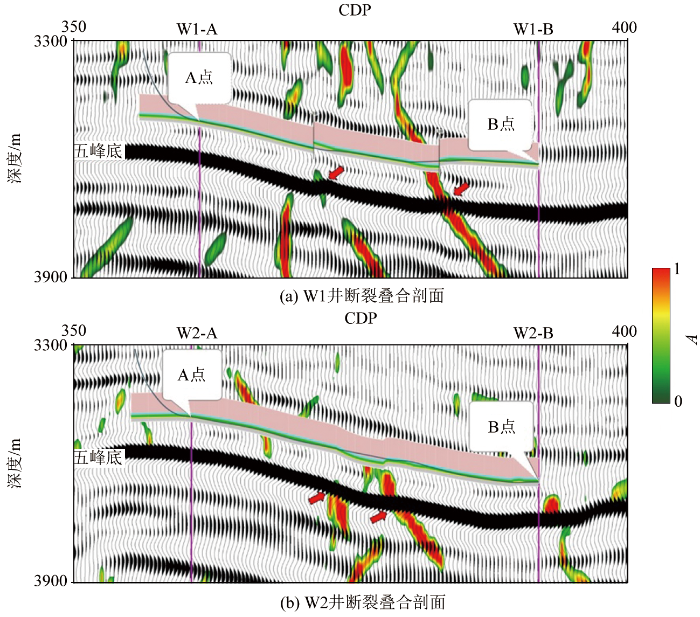
为了验证振幅梯度凌乱性属性的正确性,将断裂检测结果和实际地震剖面叠合并结合实钻结果进行对比分析(图7)。W1井实钻2条断层,断裂检测结果和实钻吻合;W2井实钻挠曲,断裂检测结果和实钻较为吻合,如图中红色箭头指示处。实钻结果和断裂检测结果验证了振幅梯度凌乱性方法结果的准确性。

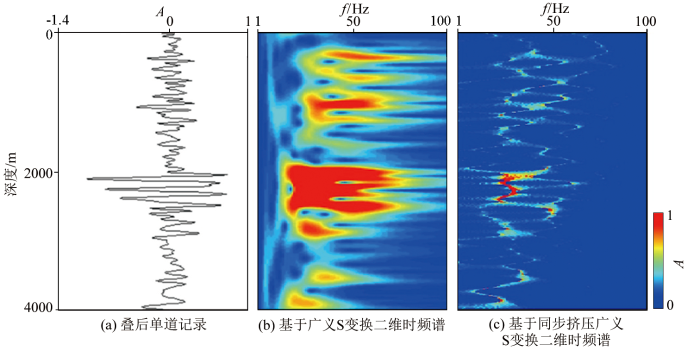
图8a为提取的叠后实际资料单道记录,分别基于广义S变换和同步挤压广义S变换,将时间域的单道记录转换至时频域(图8b、c)。从结果可知,同步挤压广义S变换的时频聚焦能力要高于广义S变换,因此基于同步挤压广义S变换得到的结果分辨率更高;同时,二维时频谱显示,数据整体优势频带范围为1~60 Hz,主频为25 Hz。

为探明该区域地层不同尺度断裂的分布范围,将同步挤压广义S变换和空间3D振幅梯度凌乱性断裂检测技术结合,开展了多尺度断裂计算。根据时频理论以及多尺度断裂模型研究成果,大尺度断裂和低频相关,断裂级数越小,则频率越高^[14],因此在开展大尺度断裂检测时,可将频带范围设置为低频段,进而突出刻画大尺度的断裂信息。在基于上述单道记录时频分析的基础上,将地震数据频带等额划分为1~20 Hz、21~40 Hz以及41~60 Hz的频带范围,进行多尺度的断裂分析。

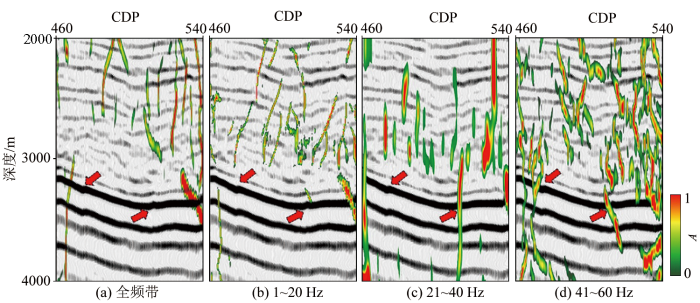
图9为任意线段不同频段的断裂检测结果和实际地震数据叠合显示。图9a显示,全频带断裂检测结果对于大断裂有较好的刻画能力,但是对于挠曲或者小断裂的识别能力有限。图9b显示,1~20 Hz断裂检测结果和全频带断裂检测结果有一定相似性,对大尺度断裂有较好的刻画能力,但是1~20 Hz的结果断裂信息更为丰富。图9c显示,21~40 Hz断裂检测,对于挠曲有一定的刻画能力,但是对于微小断裂的识别能力依旧有限。图9d显示,41~60 Hz断裂检测的信息更为丰富,对于小断裂、挠曲等都有较好的识别能力,同时对大断裂也有一定的响应。21~40 Hz检测的断裂特征与1~21 Hz的断裂信息类似,因此在实际应用中,为了提高计算效率,可直接计算1~20 Hz的断裂检测结果来指示大中尺度断裂的展布。

图10为基于振幅梯度凌乱属性的全频带断裂检测结果。全频带断裂检测结果对于大断裂的刻画较为清晰,但是对于大断裂所伴生的微小挠曲或者断裂识别能力较差,无法准确刻画挠曲、微小断裂的展布。

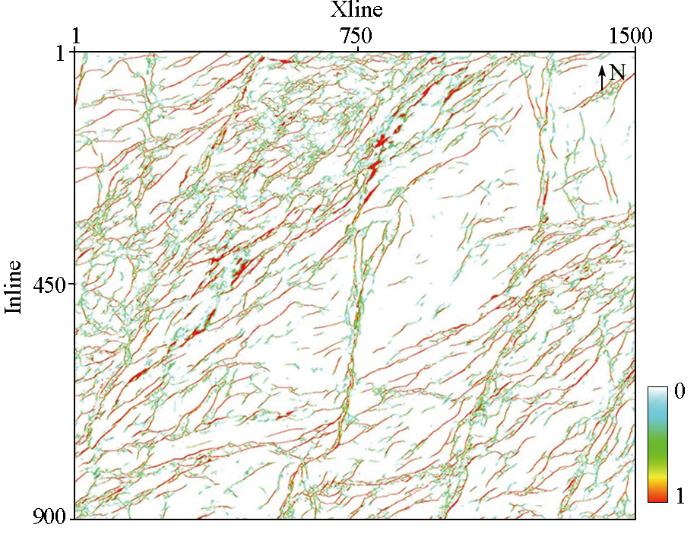
基于全频带断裂检测结果,将原始地震数据通过同步挤压广义S变换由时间域转换至时频域,同时提取不同频段的地震数据,开展振幅梯度凌乱性计算。依据图8所示,根据地震数据的时频谱特征,划分为1~20 Hz、41~60 Hz的地震数据,由低频端地震数据刻画的结果指示大中尺度断裂结果。图11显示,大尺度断裂检测结果对于大断层都有很好的刻画,但是对于大断层所衍生的小尺度断裂无法清晰地表征。

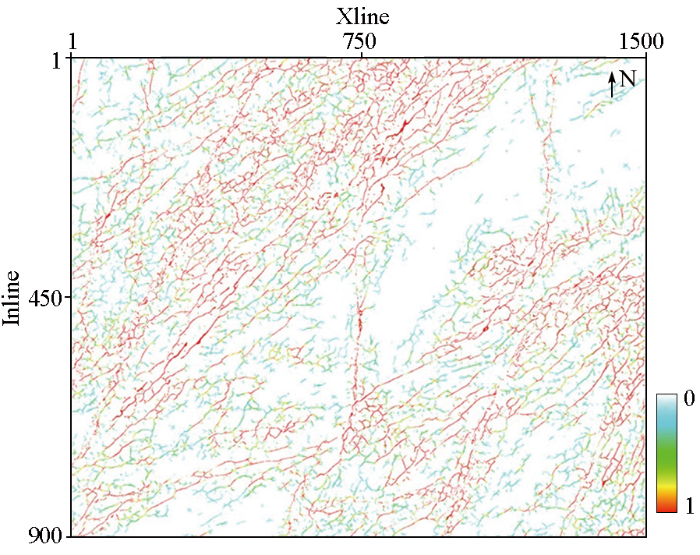
为探明该区域地层小尺度断裂的分布范围,为页岩气压裂开发奠定基础,将地震数据的时频谱范围设置为高频段,进而检测小尺度断裂。图12为小尺度断裂检测结果,可以发现:小尺度断裂检测结果与大尺度断裂检测结果(图11)具有较高的相似性,这是由于受地层挤压,地层应力发生变化,形成大尺度断裂,但是在大尺度断裂形成时,会伴生许多微小的裂缝和断层,即小尺度断裂和裂缝是受大尺度断裂影响的,因此大尺度断裂和小尺度的断裂具有较高的相似性。

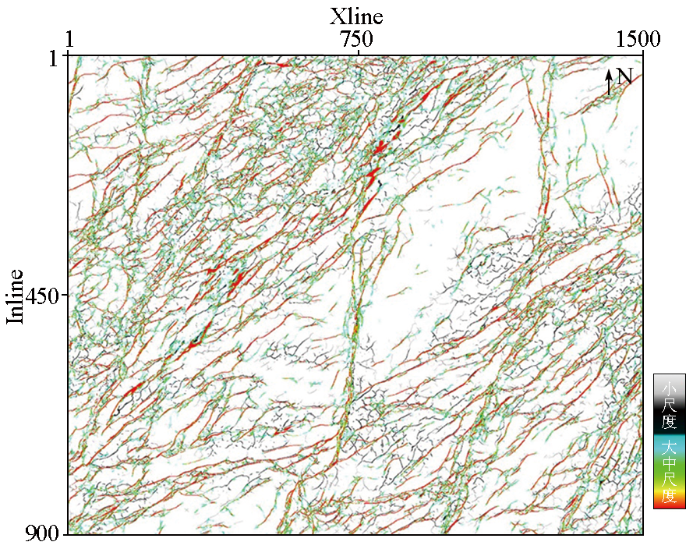
为了更清晰地刻画研究区域的不同尺度断裂信息,将大尺度断裂和小尺度断裂进行融合(图13)。由于小尺度断裂也能反映部分大尺度断裂信息,因此两者融合的比例以小尺度断裂为主,以全频带断裂结果作为监督,进而得到如图13所示的多尺度的断裂检测结果。

多尺度断裂检测结果明确了大尺度断层伴生小尺度断裂的发育模式。研究区域西北部断裂发育,主要以中、小尺度断裂为主,而研究区域东南部大尺度断裂较为发育。基于同步挤压广义S变换,结合空间3D振幅梯度凌乱性多尺度断裂检测技术,可以为页岩气勘探开发以及压裂改造提供信息,保证钻探的顺利,进而减少井漏量,降本增效。

从一维合成信号以及单道地震记录的二维时频谱对比分析可知,同步挤压广义S变换作为广义S变换的后处理技术,即在广义S变换的基础上对其时频谱值进行挤压,得到的结果分辨率更高,对于地震数据在时频域的处理解释能够发挥重要作用。

从断裂正演模型出发,验证了同步挤压广义S变换和振幅梯度凌乱性属性对不同尺度断裂的优秀刻画能力。从实际地震剖面对比中可以发现,空间3D振幅梯度凌乱性断裂检测技术对断层的刻画相对于深度学习、曲率技术更清晰,识别能力更强,结合同步挤压广义S变换的高时频聚焦能力,开展多尺度断裂检测更有效,可以更为准确地刻画不同尺度的断裂信息。相对于原始地震剖面,经过各向异性构造导向滤波后的地震数据,断点更为清晰,断裂也更连续,可以为断裂的准确识别奠定数据基础。同步挤压广义S变换振幅梯度凌乱性断裂检测技术可以实现不同尺度的断裂预测,并且得到了实际钻井验证。