地震信号倒谱分解技术及其在超深层碳酸盐岩储层烃类检测中的应用

doi:10.11720/wtyht.2024.1481

地震信号倒谱分解技术及其在超深层碳酸盐岩储层烃类检测中的应用

张永升^,¹, 黄超¹, 刘军¹, 张永恒², 王兴建², 薛雅娟³

1.中国石化西北油田分公司勘探开发研究院,新疆乌鲁木齐 830011

2.成都理工大学地球物理学院,四川成都 610059

3.成都信息工程大学通信与信息工程学院,四川成都 610059

Cepstrum decomposition of seismic signals and its application in hydrocarbon detection of ultradeep carbonate reservoirs

ZHANG Yong-Sheng^,¹, HUANG Chao¹, LIU Jun¹, ZHANG Yong-Heng², WANG Xing-Jian², XUE Ya-Juan³

1. Exploration and Development Research Institute,SINOPEC Northwest Oilfield Branch,Urumqi 830011,China

2. College of Geophysics,Chengdu University of Technology,Chengdu 610059,China

3. School of Communication and Information Engineering,Chengdu University of Information Technology,Chengdu 610059,China

第一作者: 张永升(1969-),男,高级工程师,主要从事油气物探方法研究工作。Email:zhangys.xbsj@sinopec.com

责任编辑: 叶佩

收稿日期: 2024-02-11 修回日期: 2024-09-26

基金资助:

国家自然科学基金项目“基于相干成像的测井远探测高精度成像理论研究”(42074163)

Received: 2024-02-11 Revised: 2024-09-26

摘要

地震信号倒谱分解技术是近年来发展起来的一种烃类检测方法,有利于突出宽频带地震信号内某些特定频段的弱流体信息。本文着重研究了基于傅里叶变换倒谱和基于小波包变换倒谱的地震信号倒谱分解技术,并应用于顺北地区超深层碳酸盐岩储层烃类检测。对比分析了共倒谱剖面与传统共频率剖面的特征,进一步详细对比分析了基于傅里叶变换倒谱和基于小波包变换倒谱的一阶和二阶共倒频剖面特征,在此基础上,对比研究了基于傅里叶变换倒谱和基于小波包变换倒谱的烃类检测效果。实际地震数据处理结果表明,倒谱分解技术较常规基于小波变换的谱分解技术时空分辨率更高,能给出更多的细节信息。小波包倒谱分解技术较傅里叶变换倒谱分解技术检测到的地震幅度异常剖面能给出更准确的含气性解释结果。

关键词： 倒谱分解; 傅里叶变换倒谱; 小波包倒谱; 超深层碳酸盐岩储层

Abstract

The cepstrum decomposition technology for seismic signals,recently developed for hydrocarbon detection,can highlight weak fluid information in some specific frequency bands of broadband seismic signals.This study explored the cepstrum decomposition technology for seismic signals using Fourier transform(FT)- and wavelet packet transform (WPT)-based cepstrum.Moreover,the technology was applied to the ultradeep carbonate reservoirs in the Shunbei area for hydrocarbon detection.A comparative analysis was conducted on the characteristics of common cepstrum profiles and conventional common frequency profiles.Furthermore,a detailed comparative analysis was conducted on the characteristics of the first- and second-order common cepstrum profiles of FT- and WPT-based cepstra.On this basis,the hydrocarbon detection effects were compared between FT- and WPT-based cepstra.The processing results of actual seismic data show that compared to the conventional spectral decomposition technology based on wavelet transform,the cepstrum decomposition technology manifested higher spatio-temporal resolution,providing more detailed information. Contrasting with FT-based cepstrum decomposition,WPT-based cepstrum decomposition provided a more accurate interpretation of gas-bearing properties through the seismic amplitude anomaly profiles.

Keywords： cepstrum decomposition; Fourier transform-based cepstrum; wavelet packet transform-based cepstrum; ultradeep carbonate reservoir

PDF (5595KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张永升, 黄超, 刘军, 张永恒, 王兴建, 薛雅娟. 地震信号倒谱分解技术及其在超深层碳酸盐岩储层烃类检测中的应用[J]. 物探与化探, 2024, 48(6): 1618-1625 doi:10.11720/wtyht.2024.1481

ZHANG Yong-Sheng, HUANG Chao, LIU Jun, ZHANG Yong-Heng, WANG Xing-Jian, XUE Ya-Juan. Cepstrum decomposition of seismic signals and its application in hydrocarbon detection of ultradeep carbonate reservoirs[J]. Geophysical and Geochemical Exploration, 2024, 48(6): 1618-1625 doi:10.11720/wtyht.2024.1481

0 引言

地震信号倒谱分解技术是一项基于倒谱的储层解释技术,通过在倒谱域分析每一个倒谱系数对应的振幅来最大限度地提高地震资料的分辨率,有利于突出深埋在宽带地震信号频带范围内特定频率段的烃类信息,可以揭示由于储层岩性和物性等变化引起的微小振幅变化^{[1⇓⇓⇓⇓-6]}。

倒谱分析自1963年由Bogert等^[7]用于识别核爆炸和地震信号以来,目前已被广泛应用于地震子波的恢复、地震道的去卷积、微地震和遥感事件分析、地层厚度预测以及烃类检测^{[4,6,8⇓⇓⇓⇓⇓-14]}。2011年,曹俊兴等^[1]借鉴声纹识别方法将倒谱分析应用于地震信号谱分解技术,并发展了基于倒谱分析算法的烃类检测方法,命名为地震纹分析法。近年来随着倒谱概念的发展,倒谱已经由早期的以傅里叶变换为核心运算的功率倒谱^[7,15],复倒谱^[16]和实倒谱拓展到核心运算为小波包变换的小波包倒谱^[17],从而,地震信号的倒谱分解技术也包括基于傅里叶变换的倒谱和基于小波包变换的倒谱几种形式。地震信号倒谱分解技术具有较常规频谱分解技术更高的时空分辨率,能够给出更好的成像效果和计算精度。

我们将基于傅里叶变换的倒谱分解技术和基于小波包变换的倒谱分解技术应用于顺北地区超深层碳酸盐岩储层地震数据,对比两种方法谱分解的特性,并对两种方法含气性检测的结果进行对比分析。

1 地震数据倒谱分解理论

1.1 基于傅里叶变换倒谱的地震倒谱分解技术

基于傅里叶变换倒谱的地震倒谱分解技术,主要利用如下倒谱定义公式^[1-2,6]:

(1)

c (n) = F^{- 1} {l n {|F [x (n)]|}},

式中:F、F^-1为傅里叶正、反变换;c(n)为倒谱序列;x(n)为地震信号。

基于傅里叶变换倒谱的地震数据倒谱分解技术流程如图1所示。地震数据首先进行分帧运算,设一帧数据长度为 $N$ ( $N$ 为偶数),则对每道原始地震数据前和后各补 $N / 2$ 个零。然后对每一帧地震数据,进行加窗并逐点移动。这里通常选汉明窗。再对加窗的信号进行傅里叶变换,对傅里叶变换的频谱值进行加“1”操作,这里主要是为了避免某些零或者是非常小的值对后续的取对数操作产生影响,并且这里的加“1”操作不改变信号的总体结构^[1,5-6]。然后再进行取对数,反傅里叶变换,得到的倒谱分解数据体中,提取每一帧的第一个点生成一阶共倒谱数据体,提取每一帧的第二个点生成二阶共倒谱数据体,以此类推,得到地震数据各阶的傅里叶变换倒谱分解数据体。

图1

新窗口打开| 下载原图ZIP| 生成PPT

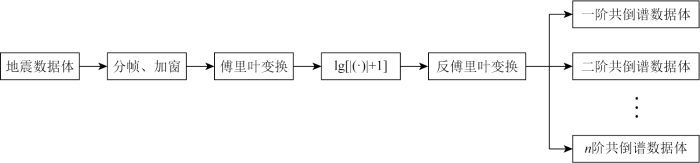
图1 基于傅里叶变换倒谱的地震数据倒谱分解技术流程

Fig.1 Flow chart of seismic data cepstrum decomposition technology based on Fourier-based cepstrum

1.2 基于小波包倒谱的地震倒谱分解技术

基于小波包变换倒谱的地震倒谱分解技术,主要利用如下倒谱定义公式^[5,17]:

(2)

c (n) = D W P T {l n {|D W P T [x (n)]|}},

式中: $D W P T$ 为离散小波包变换。

基于小波包变换的倒谱中,对输入信号进行滤波,使用对数函数对其进行缩放,再次进行滤波,然后计算每个子带的能量。与基于傅里叶变换的倒谱中最后一个步骤是傅里叶变换的反变换不同,这里,最后一个步骤是小波包变换,而不是小波包的反变换。在基于小波包变换的倒谱中,Symmlets或coiflet被发现是基于小波包变换的倒谱中小波函数的最佳选择^[5,17]。基于小波包变换的倒谱需要计算信号的长度为2的幂次方。每次分解,输入信号 $x (n)$ 被完全分解为 $m$ 级的离散小波包变换,其中 $m = l g (L) / l g (2)$ , $L$ 为输入信号 $x (n)$ 的长度。

基于小波包变换倒谱的地震数据倒谱分解技术流程如图2所示。对地震数据进行分帧加窗后,对每帧地震数据进行离散小波包变换,需要注意的是,离散小波包变换需要采用自然频率顺序,从而,每次离散小波包变换完全分解得到的结果需要利用格雷码交换滤波器对的顺序^[5,17]。然后再进行取对数和加“1”运算,再次进行离散小波包变换。得到的倒谱分解数据体中,提取每一帧的第一个点生成一阶共倒谱数据体,提取每一帧的第二个点生成二阶共倒谱数据体,以此类推,得到地震数据各阶的小波包倒谱分解数据体。

图2

新窗口打开| 下载原图ZIP| 生成PPT

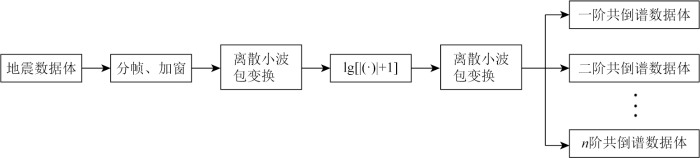
图2 基于小波包变换倒谱的地震数据倒谱分解技术流程

Fig.2 Flow chart of seismic data cepstrum decomposition technology based on wavelet-based cepstrum

由于在每个完整离散小波包变换中都采用了自然频率顺序,离散小波包变换分解树的每个叶子只包含一个样本,从而可以确定每个样本的频率范围。假设地震数据的采样频率为 $f_{s}$ ,那么,在第 $m$ 级离散小波包变换完全分解之后,基于小波包变换倒谱的 $k (k = 1,2, \dots)$ 阶倒谱系数数据体在 $(\frac{(k - 1) f_{s}}{2 N}, \frac{k f_{s}}{2 N})$ 频率范围^[5]。从而可知,基于小波包变换的倒谱的一阶共倒谱数据体在( $0, f_{s} / 2 N$ )频率范围内,二阶共倒谱数据体在( $f_{s} / 2 N, f_{s} / N$ )频率范围内。需要注意的是,这里滑动窗口的长度 $N$ 应该是2的幂次方,通常按照下式选择^[5]:

(3)

N = 2^{i} \approx \frac{f_{s}}{2 \times f_{d o m i n a n t}},

式中: $i$ 是整数, $i = 1,2, \dots$ 。 $f_{d o m i n a n t}$ 为地震数据的主频。

1.3 基于倒谱的烃类检测算法

基于倒谱的烃类检测算法主要利用了地震数据“低频能量增强,高频能量衰减”特征进行烃类检测。对于1条地震信号,倒谱幅度始终是按 $1 / |n|$ ( $n$ 是采样点)衰减的有界序列^[18]。倒谱的能量主要集中在信号的较低倒频部分。通常,一阶倒频剖面 $C_{w} (1)$ 和二阶倒频剖面 $C_{w} (2)$ 足以让我们进行储层表征和烃类检测^[1-2,5-6]。由倒谱检测的地震幅度异常剖面 $Δ C_{w}$ 定义为^[1-2,5-6]:

(4)

Δ C_{w} = |C'_{w} (1) - C'_{w} (2)|

式中: $C'_{w} (1)$ 表示一阶共倒频剖面中超过平均倒谱幅度的归一化幅度; $C'_{w} (2)$ 表示二阶共倒频剖面中超过平均倒谱幅度的归一化幅度,即:

(5)

C'_{w} (1) = N o r m a l i z e d {C_{w} (1) - a v e [C_{w} (1)]}

(6)

C'_{w} (2) = N o r m a l i z e d {C_{w} (2) - a v e [C_{w} (2)]}

式中: $N o r m a l i z e d ()$ 表示对结果归一化, $a v e ()$ 表示对信号取平均。

地震幅度异常剖面 $Δ C_{w}$ 可以识别深埋在宽带地震响应中的特定频段的强振幅异常。 $Δ C_{w}$ 可以反映目标层的许多地质特征,例如可能导致地震反射数据中的幅度异常的含气层或通道。因此,地震幅度异常剖面中的小振幅数据表示异常振幅较少,而较大的振幅数据表示异常振幅较大。

由于基于倒谱的烃类检测算法中包含了对数操作,它会增强弱孔隙流体响应,通过算法中去除平均振幅信息又抑制了骨架信息,因此,基于倒谱的烃类检测算法是一种弱信号检测方法,有利于超深层碳酸盐岩储层烃类检测。

2 模型测试

为了验证基于倒谱的烃类检测算法的有效性,说明不同倒谱烃类检测算法的特性,我们利用考虑流体在多孔介质中的粘滞性和扩散性的弥散粘滞波动方程^[19-20]进行正演模拟。这里,我们利用顺北地区超深层碳酸盐岩储层地震数据和储层测井参数生成正演模型,地质模型如图3a所示,包含6个地层,其中层④为含气层,与层④紧邻的层③为干层,各层参数如表1所示。含气层厚度为40 m,子波频率为20 Hz,采样频率为1 000 Hz。模型的地震响应如图3b所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

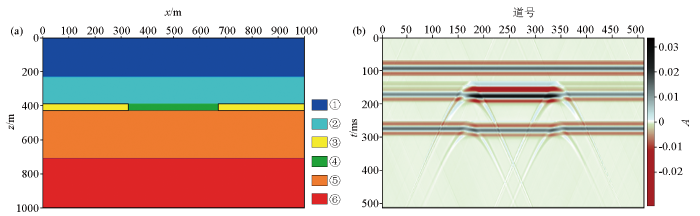
图3 地质模型(a)及其地震响应剖面(b)

Fig.3 Geological model(a) and its seismic response profile(b)

表1 地质模型参数

Table 1 Parameters for the geological model

层号	V_p $/$ (m·s^-1)	$ρ$ /(g·cm^-3)	$ζ$ /Hz	$η$ /(m²·s^-1)	$Q$
①	5000	2.500	1.0	1.0	200
②	5260	2.539	1.0	1.0	200
③	5320	2.548	1.0	1.0	200
④	5100	2.515	5	400	5
⑤	5550	2.583	1.0	1.0	200
⑥	5800	2.620	1.0	1.0	200

注: $ζ$ 是扩散系数, $η$ 为粘性系数

新窗口打开| 下载CSV

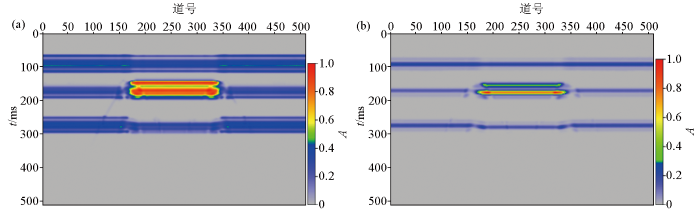
图4所示为基于傅里叶倒谱、小波包倒谱的烃类检测结果。从图中可以看到,基于傅里叶倒谱、小波包倒谱的烃类检测方法都能准确识别到含气层,但是,小波包倒谱检测到的含气层的上下界面区分更清晰,分辨率更高,而傅里叶倒谱检测到的含气层的上下界面区分不够清晰,分辨率较低。此外,小波包倒谱检测到的含气层异常振幅起始响应值较傅里叶倒谱的更低一些。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 地震振幅异常剖面

a—傅里叶倒谱;b—小波包倒谱

Fig.4 Seismic amplitude anomaly section

a—Fourier-based cepstrum;b—wavelet-based cepstrum

由于本模型采用的是顺北地区超深层碳酸盐岩储层地震数据和储层测井参数,本模型地震响应的烃类检测结果也表明基于倒谱的烃类检测方法适用于顺北地区超深层碳酸盐岩储层烃类检测。

3 实际地震数据应用

3.1 地震数据

这里,我们利用顺北地区超深层碳酸盐岩储层地震数据进行分析。该地区主要目的层为奥陶系碳酸盐岩储集层,目的层埋深大,有效储集空间类型主要为经过多期次构造挤压作用以及溶蚀改造等形成的柱状溶蚀孔、洞储集体,储层纵向、横向变化快,非均质性极强。研究区岩性主要为黄灰色泥晶灰岩、含砂屑泥晶灰岩、砂屑泥晶灰岩。研究区地震数据能量时强时弱,频率偏低。因此,缝洞型储集空间的空间预测是该地区超深层碳酸盐岩储层气藏勘探的关键。

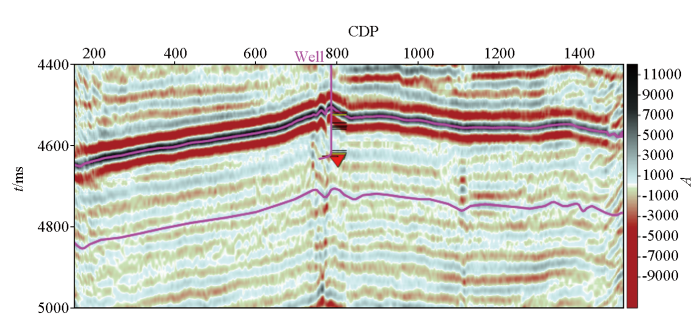
这里,我们利用该地区的过井叠后宽带偏移二维剖面(图5)分析基于倒谱的地震数据分解技术的应用特征和效果。该地震数据采样频率为2 ms。图中目标区为粉色上下层位线之间区域。该剖面过含气井Well。图中测井解释的含气区在井轨迹上进行了标识。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 过井剖面

Fig.5 The seismic section intersecting a known gas well

3.2 共倒谱剖面对比

首先,我们对过井剖面分别利用傅里叶变换倒谱和小波包倒谱进行分频处理,可以得到一系列共倒谱剖面。这里,我们首先对比分析共倒谱剖面和基于传统时频分析方法的共频率剖面的特征。

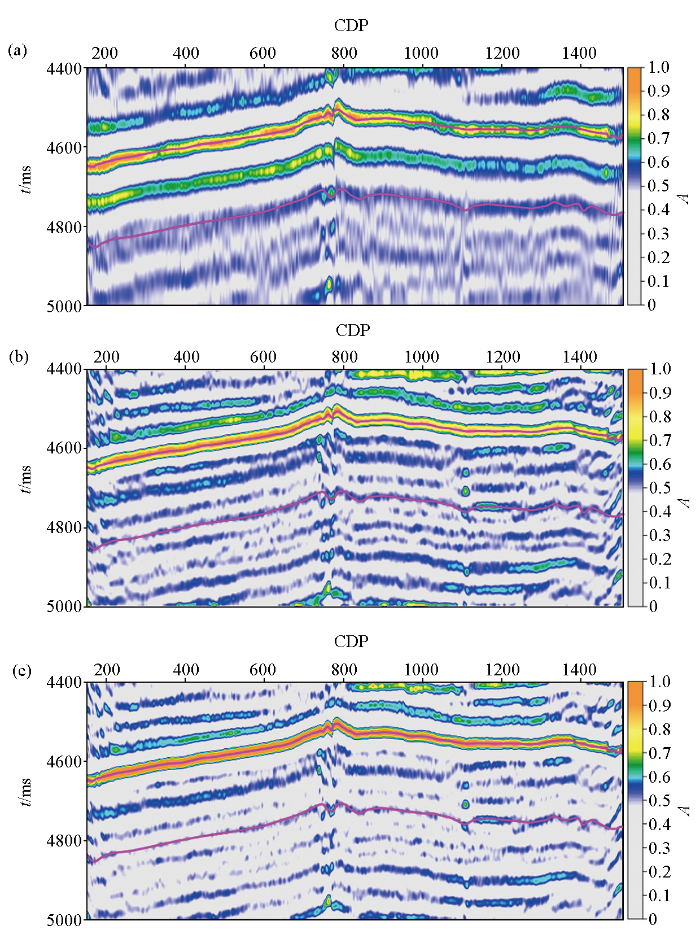
图6所示为过井剖面利用连续小波变换(CWT)获得的共频率剖面和利用傅里叶倒谱、小波包倒谱获得的共倒频剖面的对比。图4展示了共倒频剖面与共频率剖面的对应关系。该地震剖面数据主频约为20 Hz,采样频率为500 Hz。根据式(3),小波包倒谱中滑动窗的长度约为500/(2×20)=12.5,考虑到滑动窗需要为2的幂次方,所以我们选择滑动窗长度16进行计算。为了保持一致,傅里叶倒谱中滑动窗长度也选择为16。此时,一阶共倒频剖面(图6b、c)的频率范围为(0,500/(2×16)≈15.6 Hz)。为了对比,我们给出了使用CWT提取的8 Hz共频率剖面(图6a),注意,这里8 Hz是利用频率范围(0,16 Hz)计算的。注意这里为了对比,我们对所有结果进行了归一化。将图6b、c与图6a对比可知,一阶共倒谱剖面与CWT分别提取的8 Hz共频率剖面类似。这个事实说明了傅里叶倒谱、小波包倒谱的有效性及其与传统共频率剖面的关系。同时,我们可以发现,一阶共倒谱剖面的时空分辨率较CWT提取的8 Hz共频率剖面的时空分辨率更高,可以给出更多的细节信息。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 过井剖面的一阶共倒谱剖面和共频率剖面

a—CWT提取的8 Hz共频率剖面,小波变换中使用Morlet小波;b—傅里叶变换倒谱提取的一阶共倒谱剖面;c—小波包倒谱提取的一阶共倒谱剖面

Fig.6 First-order common quefrency and common frequency sections of the seismic section intersecting the known well

a—8 Hz common frequency section extracted by the CWT,Morlet wavelet is used in wavelet transform;b—first-order common quefrency section extracted by Fourier-based ceptrum;c—first-order common quefrency section extracted by the wavelet-based cepstrum

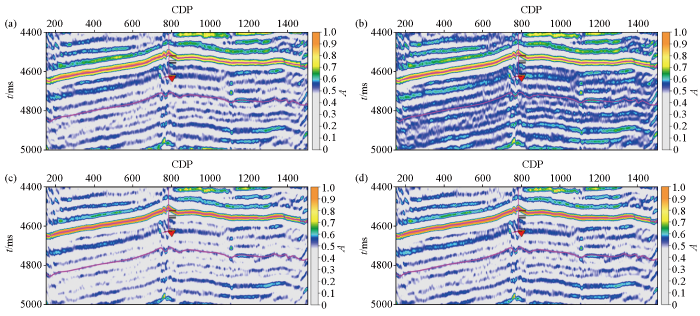
下面再对比分析傅里叶变换倒谱和小波包倒谱提取的一阶共倒谱剖面和二阶共倒谱剖面的特征差异。从图7可以看出,傅里叶变换倒谱和小波包倒谱提取的共倒谱剖面总体能量分布较为一致,但是在能量强弱分布上有差异,傅里叶变换倒谱提取的一阶共倒谱剖面和二阶共倒谱剖面中能量分布在中间部分区域,较小波包倒谱提取的结果更强,而小波包倒谱提取的一阶和二阶共倒谱剖面在上层位处能量分布较傅里叶变换倒谱更强,此外,傅里叶变换倒谱提取的二阶共倒谱剖面没有小波包倒谱提取的二阶共倒谱剖面时空分辨率高。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 傅里叶倒谱和小波包倒谱提取的一阶和二阶共倒谱剖面

a—傅里叶变换倒谱提取的一阶共倒谱剖面;b—傅里叶变换倒谱提取的二阶共倒谱剖面;c—小波包倒谱提取的一阶共倒谱剖面;d—小波包倒谱提取的二阶共倒谱剖面

Fig.7 First and second-order common quefrency sections extracted from Fourier-based cepstrum and wavelet-based cepstrum

a—first-order common quefrency section extracted by Fourier-based cepstrum;b—second-order common quefrency section extracted by Fourier-based cepstrum;c—first-order common quefrency section extracted from wavelet-based cepstrum;d—second-order common quefrency section extracted from wavelet-based cepstrum

3.3 烃类检测

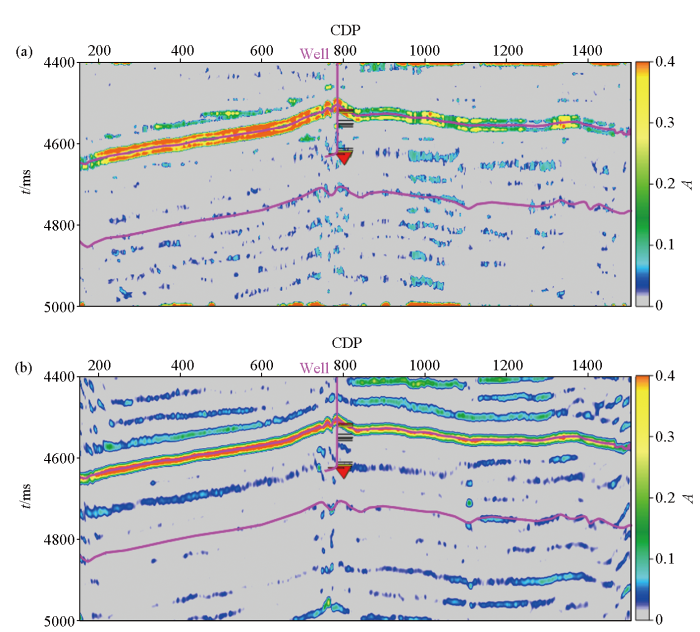
含烃类区域通常在基于倒谱的烃类检测技术检测到的地震幅度异常剖面中表现为强振幅异常特征区域,排除岩性、地层等其他因素影响,通常认为地震幅度异常剖面中的强振幅异常特征可以给出含烃类信息的解释结果。

图5所示的过井剖面基于傅里叶倒谱、小波包倒谱的烃类检测结果如图8所示。从地震振幅异常剖面图中可以看到,小波包倒谱检测到的含气井区域强振幅异常较傅里叶变换倒谱检测到的结果和测井含气解释结果吻合度更好,可以给出更好的含气性检测结果,表明小波包倒谱分解技术对弱含气响应更灵敏。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 地震振幅异常剖面

a—傅里叶倒谱;b—小波包倒谱

Fig.8 Seismic amplitude anomaly section

a—Fourier-based cepstrum;b—wavelet-based cepstrum

在过井剖面分析的基础上,进一步将基于傅里叶倒谱、小波包倒谱的烃类检测方法应用到三维区域的数据上。该地区有五口已知井(A、B、C、D、E),位于研究目标区上层位下移5 ms处,A、B、C井位于强含气层,D、E井位于弱含气层。倒谱分解烃类检测结果如图9所示。从图中可以看到,在含气井所处位置均有强振幅异常,且A、B、C井所处区域位置的强振幅异常能量大于D、E井所处区域位置。小波包倒谱给出的烃类解释结果(图9b)分辨率较傅里叶倒谱(图9a)更高,细节信息显示的更多。

图9

新窗口打开| 下载原图ZIP| 生成PPT

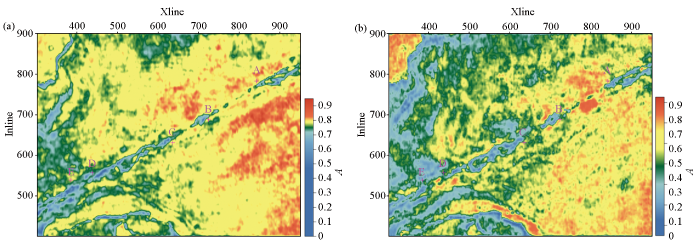
图9 地震振幅异常切片

a—傅里叶倒谱;b—小波包倒谱

Fig.9 Seismic amplitude anomaly slice

a—Fourier-based cepstrum;b—wavelet-based cepstrum

4 结论

本文对比研究了傅里叶变换倒谱和小波包倒谱分解技术。地震数据倒谱分解技术可以得到类似谱分解一样的系列分频数据体,能有效避免调谐效应,提高剖面的空间分辨率。模型分析表明小波包倒谱较傅里叶倒谱检测到的含气层的上下界面区分更清晰,分辨率更高。顺北实际地震数据处理结果表明,应用地震数据倒谱分解技术能有效地对该地区超深层碳酸盐岩储层进行很好的预测,且小波包倒谱分解技术较傅里叶变换倒谱分解技术具有更高的时空分辨率,能体现更多细节信息。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

曹俊兴, 刘树根, 田仁飞, 等.

龙门山前陆盆地深层海相碳酸盐岩储层地震预测研究

[J]. 岩石学报, 2011, 27(8):2423-2434.

[本文引用: 6]

Cao

J X

, Liu

S G

, Tian

R F

, et al.

Seismic prediction of carbonate reservoirs in the deep of Longmenshan foreland basin

[J]. Acta Petrologica Sinica, 2011, 27(8):2423-2434.

[本文引用: 6]

[2]

Cao

, Tian

, He

Seismic-print Analysis and Hydrocarbon Identification

[C]// AGU Fall Meeting Abstracts,AGUFM, 2011.

[本文引用: 4]

[3]

田仁飞, 曹俊兴.

地震分倒频处理技术

[J]. 地球物理学进展, 2012, 27(3):1183-1188.

[本文引用: 1]

Tian

R F

, Cao

J X

Seismic sub-inverted frequency processing technology

[J]. Progress in Geophysics, 2012, 27(3):1183-1188.

[本文引用: 1]

[4]

曹俊兴, 薛雅娟, 田仁飞, 等.

深层碳酸盐岩储层含气性检测方法技术研究

[J]. 石油物探, 2019, 58(1):9-16.

DOI:10.3969/j.issn.1000-1441.2019.01.002 [本文引用: 2]

我国深层海相碳酸盐岩地层蕴藏有丰富的天然气资源,但因演化历史长、埋深大等因素影响,储层含气性评价困难。评述了现有储层含气性地震检测技术(包括亮点、AVO异常、低频阴影等)在深层天然气储层识别中的适用性,认为亮点和AVO异常反映的是界面响应,而低频阴影反映的是储层的“体”响应。储层含气性检测不仅要确定储层是否含气,还要确定储层含气量。为此,介绍了一种新的基于地震纹倒谱分析的储层含气性检测方法,指出①雷克子波的地震纹倒谱参数随子波频率呈非线性变化;②地震纹倒谱参数对储层参数变化反应灵敏;③含气储层地震响应的1阶倒谱系数呈高值异常,而2阶倒谱系数呈低值异常,且二者呈镜像对称。地震纹倒谱对弱反射的敏感性使得该方法能够发现“暗点”型气藏,同时因与模型无关而克服了诸多建模带来的弊端,能够对深层超深层储层含气性进行较为可靠的检测。探讨了基于地震的深层碳酸盐岩储层产能评价问题,认为地震纹分析与频散分析相结合有望能确定储层的含气性并估算其可采储量。

Cao

J X

, Xue

Y J

, Tian

R F

, et al.

Advances in hydrocarbon detection in deep carbonate reservoirs

[J]. Geophysical Prospecting for Petroleum, 2019, 58(1):9-16.

DOI:10.3969/j.issn.1000-1441.2019.01.002 [本文引用: 2]

<p>There are abundant natural gas resources in deep marine carbonate strata onshore China.It is necessary but difficult to discover gas-bearing reservoirs and evaluate their gas content,due to their long evolutionary history and large buried depth.This paper reviews existing hydrocarbon detection techniques,such as bright spot,AVO,and low-frequency shadow,in the identification of deep gas carbonate reservoir.Bright spots and AVO anomalies reflect the interface response,while low-frequency shadows reflect the response of the “body” of the reservoir.In this paper a hydrocarbon detection technique is proposed based on seismic cepstrum analysis.The cepstrum of the Ricker wavelet varies nonlinearly with frequency and the seismic cepstrum is sensitive to reservoir parameters.In addition,the first-order cepstral coefficient of the seismic cepstrum of gas-bearing reservoirs is of a high-value anomaly,while the second-order cepstral coefficient represents a low-value anomaly,and the two anomalies are mirror-symmetric.The sensitivity of the seismic cepstrum to weak reflection enables the method to detect “dim spot” gas reservoirs.In addition,the method is independent of reservoir modeling.Discussion on capacity evaluation based on seismic data analysis suggested that combined analysis of seismic print and dispersion could effectively detect gas-bearing reservoir and estimate the recoverable reserves for a deep carbonate reservoir.</p>

[5]

Xue

Y J

, Cao

J X

, Tian

R F

, et al.

Wavelet-based cepstrum decomposition of seismic data and its application in hydrocarbon detection

[J]. Geophysical Prospecting, 2016, 64(6):1441-1453.

[本文引用: 9]

[6]

Cao

J X

, Jiang

X D

, Xue

Y J

, et al.

The state-of-the-art techniques of hydrocarbon detection and its application in ultra-deep carbonate reservoir characterization in the Sichuan Basin,China

[J]. Frontiers in Earth Science, 2022, 10:851828.

[本文引用: 6]

[7]

Bogert

B P

, Healy

M J R

, Tukey

J W

The quefrency analysis of time series for echoes:Cepstrum,pseudo-autocovariance,cross-cepstrum and saphe cracking

[G]// Rosenblatt M.Proceedings of the Symposium on Time Series Analysis, 1963:209-243.

[本文引用: 2]

[8]

Ulrych

T J

Application of homomorphic deconvolution to seismology

[J]. Geophysics, 1971, 36(4):650-660.

[本文引用: 1]

[9]

Ulrych

T J

, Jensen

O G

, Ellis

R M

, et al.

Homomorphic deconvolution of some teleseismic events

[J]. Bulletin of the Seismological Society of America, 1972, 62(5):1269-1281.

[本文引用: 1]

[10]

Tuetuencueoglu

, Sate

Cepstrum analysis for determination of rupture length of microearthquakes

[J]. IISEE Bulletin, 1974, 12:1-16.

[本文引用: 1]

[11]

Buhl

, Stoffa

P L

, Bryan

G M

The application of homomorphic deconvolution to shallow-water marine seismology:Part ii:Real data

[J]. Geophysics, 1974, 39(4):417-426.

[本文引用: 1]

[12]

Scheuer

T E

, Wagner

D E

Deconvolution by autocepstral windowing

[J]. Geophysics, 1985, 50(10):1533-1540.

[本文引用: 1]

[13]

Miah

K H

, Herrera

R H

, Van

Der Baan M

, et al.

Application of fractional Fourier transform in cepstrum analysis

[C]// Recovery-2011 CSPG CSEG CWLS Convention, 2011:1-4.

[本文引用: 1]

[14]

Hall

Predicting bed thickness with cepstral decomposition

[J]. The Leading Edge, 2006, 25(2):199-204.

[本文引用: 1]

[15]

Oppenheim

A V

, Schafer

R W

Discrete-time signal processing

[M]. Englewood Cliffs,NJ:Prentice Hall, 1989.

[本文引用: 1]

[16]

Oppenheim

A V

. Superposition in a class of nonlinear systems[D]. Cambridge: Massachusetts Institute of Technology, 1965.

[本文引用: 1]

[17]

Sanchez

F L

, Barbon

, Vieira

L S

, et al.

Wavelet-based cepstrum calculation

[J]. Journal of Computational and Applied Mathematics, 2009, 227(2):288-293.

[本文引用: 4]

[18]

Deng

, O'Shaughnessy

. Speech processing:A dynamic and optimization-oriented approach[M]. CRC Press, 2003:50-52.

[本文引用: 1]

[19]

Korneev

V A

, Goloshubin

G M

, Daley

T M

, et al.

Seismic low-frequency effects in monitoring fluid-saturated reservoirs

[J]. Geophysics, 2004, 69(2):522.

[本文引用: 1]

[20]

陈学华, 贺振华, 钟文丽.

低频阴影与储层特征关系的数值模拟

[J]. 中国矿业大学学报, 2011, 40(4):584-591.

[本文引用: 1]

Chen

X H

, He

Z H

, Zhong

W L

Numeric simulation in the relationship between low frequency shadow and reservoir characteristic

[J]. Journal of China University of Mining & Technology, 2011, 40(4):584-591.

[本文引用: 1]

龙门山前陆盆地深层海相碳酸盐岩储层地震预测研究

2011

... 地震信号倒谱分解技术是一项基于倒谱的储层解释技术,通过在倒谱域分析每一个倒谱系数对应的振幅来最大限度地提高地震资料的分辨率,有利于突出深埋在宽带地震信号频带范围内特定频率段的烃类信息,可以揭示由于储层岩性和物性等变化引起的微小振幅变化^{[1⇓⇓⇓⇓-6]}. ...

... 倒谱分析自1963年由Bogert等^[7]用于识别核爆炸和地震信号以来,目前已被广泛应用于地震子波的恢复、地震道的去卷积、微地震和遥感事件分析、地层厚度预测以及烃类检测^{[4,6,8⇓⇓⇓⇓⇓-14]}.2011年,曹俊兴等^[1]借鉴声纹识别方法将倒谱分析应用于地震信号谱分解技术,并发展了基于倒谱分析算法的烃类检测方法,命名为地震纹分析法.近年来随着倒谱概念的发展,倒谱已经由早期的以傅里叶变换为核心运算的功率倒谱^[7,15],复倒谱^[16]和实倒谱拓展到核心运算为小波包变换的小波包倒谱^[17],从而,地震信号的倒谱分解技术也包括基于傅里叶变换的倒谱和基于小波包变换的倒谱几种形式.地震信号倒谱分解技术具有较常规频谱分解技术更高的时空分辨率,能够给出更好的成像效果和计算精度. ...

... 基于傅里叶变换倒谱的地震倒谱分解技术,主要利用如下倒谱定义公式^[1-2,6]: ...

... 基于傅里叶变换倒谱的地震数据倒谱分解技术流程如图1所示.地震数据首先进行分帧运算,设一帧数据长度为

N

(

N

为偶数),则对每道原始地震数据前和后各补

N / 2

个零.然后对每一帧地震数据,进行加窗并逐点移动.这里通常选汉明窗.再对加窗的信号进行傅里叶变换,对傅里叶变换的频谱值进行加“1”操作,这里主要是为了避免某些零或者是非常小的值对后续的取对数操作产生影响,并且这里的加“1”操作不改变信号的总体结构^[1,5-6].然后再进行取对数,反傅里叶变换,得到的倒谱分解数据体中,提取每一帧的第一个点生成一阶共倒谱数据体,提取每一帧的第二个点生成二阶共倒谱数据体,以此类推,得到地震数据各阶的傅里叶变换倒谱分解数据体. ...

... 基于倒谱的烃类检测算法主要利用了地震数据“低频能量增强,高频能量衰减”特征进行烃类检测.对于1条地震信号,倒谱幅度始终是按

1 / |n|

(

n

是采样点)衰减的有界序列^[18].倒谱的能量主要集中在信号的较低倒频部分.通常,一阶倒频剖面

C_{w} (1)

和二阶倒频剖面

C_{w} (2)

足以让我们进行储层表征和烃类检测^[1-2,5-6].由倒谱检测的地震幅度异常剖面

Δ C_{w}

定义为^[1-2,5-6]: ...

... [1-2,5-6]: ...

龙门山前陆盆地深层海相碳酸盐岩储层地震预测研究

2011

... 基于傅里叶变换倒谱的地震倒谱分解技术,主要利用如下倒谱定义公式^[1-2,6]: ...

... 基于傅里叶变换倒谱的地震数据倒谱分解技术流程如图1所示.地震数据首先进行分帧运算,设一帧数据长度为

N

(

N

为偶数),则对每道原始地震数据前和后各补

N / 2

... 基于倒谱的烃类检测算法主要利用了地震数据“低频能量增强,高频能量衰减”特征进行烃类检测.对于1条地震信号,倒谱幅度始终是按

1 / |n|

(

n

是采样点)衰减的有界序列^[18].倒谱的能量主要集中在信号的较低倒频部分.通常,一阶倒频剖面

C_{w} (1)

和二阶倒频剖面

C_{w} (2)

足以让我们进行储层表征和烃类检测^[1-2,5-6].由倒谱检测的地震幅度异常剖面

Δ C_{w}

定义为^[1-2,5-6]: ...

... [1-2,5-6]: ...

Seismic-print Analysis and Hydrocarbon Identification

2011

... 基于傅里叶变换倒谱的地震倒谱分解技术,主要利用如下倒谱定义公式^[1-2,6]: ...

... 基于倒谱的烃类检测算法主要利用了地震数据“低频能量增强,高频能量衰减”特征进行烃类检测.对于1条地震信号,倒谱幅度始终是按

1 / |n|

(

n

是采样点)衰减的有界序列^[18].倒谱的能量主要集中在信号的较低倒频部分.通常,一阶倒频剖面

C_{w} (1)

和二阶倒频剖面

C_{w} (2)

足以让我们进行储层表征和烃类检测^[1-2,5-6].由倒谱检测的地震幅度异常剖面

Δ C_{w}

定义为^[1-2,5-6]: ...

... -2,5-6]: ...

地震分倒频处理技术

2012

地震分倒频处理技术

2012

深层碳酸盐岩储层含气性检测方法技术研究

2019

深层碳酸盐岩储层含气性检测方法技术研究

2019

Wavelet-based cepstrum decomposition of seismic data and its application in hydrocarbon detection

2016

... 基于傅里叶变换倒谱的地震数据倒谱分解技术流程如图1所示.地震数据首先进行分帧运算,设一帧数据长度为

N

(

N

为偶数),则对每道原始地震数据前和后各补

N / 2

... 基于小波包变换倒谱的地震倒谱分解技术,主要利用如下倒谱定义公式^[5,17]: ...

... 基于小波包变换的倒谱中,对输入信号进行滤波,使用对数函数对其进行缩放,再次进行滤波,然后计算每个子带的能量.与基于傅里叶变换的倒谱中最后一个步骤是傅里叶变换的反变换不同,这里,最后一个步骤是小波包变换,而不是小波包的反变换.在基于小波包变换的倒谱中,Symmlets或coiflet被发现是基于小波包变换的倒谱中小波函数的最佳选择^[5,17].基于小波包变换的倒谱需要计算信号的长度为2的幂次方.每次分解,输入信号

x (n)

被完全分解为

m

级的离散小波包变换,其中

m = l g (L) / l g (2)

L

为输入信号

x (n)

的长度. ...

... 基于小波包变换倒谱的地震数据倒谱分解技术流程如图2所示.对地震数据进行分帧加窗后,对每帧地震数据进行离散小波包变换,需要注意的是,离散小波包变换需要采用自然频率顺序,从而,每次离散小波包变换完全分解得到的结果需要利用格雷码交换滤波器对的顺序^[5,17].然后再进行取对数和加“1”运算,再次进行离散小波包变换.得到的倒谱分解数据体中,提取每一帧的第一个点生成一阶共倒谱数据体,提取每一帧的第二个点生成二阶共倒谱数据体,以此类推,得到地震数据各阶的小波包倒谱分解数据体. ...

... 由于在每个完整离散小波包变换中都采用了自然频率顺序,离散小波包变换分解树的每个叶子只包含一个样本,从而可以确定每个样本的频率范围.假设地震数据的采样频率为

f_{s}

,那么,在第

m

级离散小波包变换完全分解之后,基于小波包变换倒谱的

k (k = 1,2, \dots)

阶倒谱系数数据体在

(\frac{(k - 1) f_{s}}{2 N}, \frac{k f_{s}}{2 N})

频率范围^[5].从而可知,基于小波包变换的倒谱的一阶共倒谱数据体在(

0, f_{s} / 2 N

)频率范围内,二阶共倒谱数据体在(

f_{s} / 2 N, f_{s} / N

)频率范围内.需要注意的是,这里滑动窗口的长度

N

应该是2的幂次方,通常按照下式选择^[5]: ...

... [5]: ...

... 基于倒谱的烃类检测算法主要利用了地震数据“低频能量增强,高频能量衰减”特征进行烃类检测.对于1条地震信号,倒谱幅度始终是按

1 / |n|

(

n

是采样点)衰减的有界序列^[18].倒谱的能量主要集中在信号的较低倒频部分.通常,一阶倒频剖面

C_{w} (1)

和二阶倒频剖面

C_{w} (2)

足以让我们进行储层表征和烃类检测^[1-2,5-6].由倒谱检测的地震幅度异常剖面

Δ C_{w}

定义为^[1-2,5-6]: ...

... ,5-6]: ...

The state-of-the-art techniques of hydrocarbon detection and its application in ultra-deep carbonate reservoir characterization in the Sichuan Basin,China

2022

... 基于傅里叶变换倒谱的地震倒谱分解技术,主要利用如下倒谱定义公式^[1-2,6]: ...

... 基于傅里叶变换倒谱的地震数据倒谱分解技术流程如图1所示.地震数据首先进行分帧运算,设一帧数据长度为

N

(

N

为偶数),则对每道原始地震数据前和后各补

N / 2

... 基于倒谱的烃类检测算法主要利用了地震数据“低频能量增强,高频能量衰减”特征进行烃类检测.对于1条地震信号,倒谱幅度始终是按

1 / |n|

(

n

是采样点)衰减的有界序列^[18].倒谱的能量主要集中在信号的较低倒频部分.通常,一阶倒频剖面

C_{w} (1)

和二阶倒频剖面

C_{w} (2)

足以让我们进行储层表征和烃类检测^[1-2,5-6].由倒谱检测的地震幅度异常剖面

Δ C_{w}

定义为^[1-2,5-6]: ...

... -6]: ...

The quefrency analysis of time series for echoes:Cepstrum,pseudo-autocovariance,cross-cepstrum and saphe cracking

1963

... [7,15],复倒谱^[16]和实倒谱拓展到核心运算为小波包变换的小波包倒谱^[17],从而,地震信号的倒谱分解技术也包括基于傅里叶变换的倒谱和基于小波包变换的倒谱几种形式.地震信号倒谱分解技术具有较常规频谱分解技术更高的时空分辨率,能够给出更好的成像效果和计算精度. ...

Application of homomorphic deconvolution to seismology

1971

Homomorphic deconvolution of some teleseismic events

1972

Cepstrum analysis for determination of rupture length of microearthquakes

1974

The application of homomorphic deconvolution to shallow-water marine seismology:Part ii:Real data

1974

Deconvolution by autocepstral windowing

1985

Application of fractional Fourier transform in cepstrum analysis

2011

Predicting bed thickness with cepstral decomposition

2006

Discrete-time signal processing

1989

1965

Wavelet-based cepstrum calculation

2009

... 基于小波包变换倒谱的地震倒谱分解技术,主要利用如下倒谱定义公式^[5,17]: ...

x (n)

被完全分解为

m

级的离散小波包变换,其中

m = l g (L) / l g (2)

L

为输入信号

x (n)

的长度. ...

2003

... 基于倒谱的烃类检测算法主要利用了地震数据“低频能量增强,高频能量衰减”特征进行烃类检测.对于1条地震信号,倒谱幅度始终是按

1 / |n|

(

n

是采样点)衰减的有界序列^[18].倒谱的能量主要集中在信号的较低倒频部分.通常,一阶倒频剖面

C_{w} (1)

和二阶倒频剖面

C_{w} (2)

足以让我们进行储层表征和烃类检测^[1-2,5-6].由倒谱检测的地震幅度异常剖面

Δ C_{w}

定义为^[1-2,5-6]: ...

Seismic low-frequency effects in monitoring fluid-saturated reservoirs

2004

... 为了验证基于倒谱的烃类检测算法的有效性,说明不同倒谱烃类检测算法的特性,我们利用考虑流体在多孔介质中的粘滞性和扩散性的弥散粘滞波动方程^[19-20]进行正演模拟.这里,我们利用顺北地区超深层碳酸盐岩储层地震数据和储层测井参数生成正演模型,地质模型如图3a所示,包含6个地层,其中层④为含气层,与层④紧邻的层③为干层,各层参数如表1所示.含气层厚度为40 m,子波频率为20 Hz,采样频率为1 000 Hz.模型的地震响应如图3b所示. ...

低频阴影与储层特征关系的数值模拟

2011

低频阴影与储层特征关系的数值模拟

2011

〈

〉