0 引言
伴随着地下水动态监测技术的不断发展[3-4],在新场地段构建了技术先进的地下水长期动态监测网络,并由此获取了大量的地下水动态监测数据。然而研究发现,实际的监测数据中存在较多的异常值,严重干扰了对地下水动态过程的准确判断。如何从大量的监测数据中识别出水位异常值成为了地下水动态研究中亟待解决的热点问题。对此,部分学者将统计学方法或机器学习方法引入到长时间序列、大批量数据的异常值检测工作中,大幅提高了识别效率与检测结果的客观性[5⇓-7],验证了自动化方法的可行性。目前,被广泛应用的自动识别算法可归纳为基于数理统计[8]、基于预测模型[9-10]和基于距离[11⇓-13]3种类型。其中,基于距离的检测算法与其他两种算法相比,更加适用于对孤立异常值的检测[14],该方法已被应用到了城市排水管网液位监测[15]、地下水环境监测[16]、网络安全监测[17]、医疗数据评估[18]等领域异常事件的识别中。而最小协方差行列式方法(MCD)[19-20]因对局部异常值反映更加灵敏,适用于小样本异常事件的检测,在众多基于距离的算法中具有广泛的适用性,如:Sunderland等[18]通过对不同模型检测效果的对比,发现MCD方法对医疗领域错误诊断数据的识别具有更好的检测精度,能够辅助提高数据质量;孙杰[21]以MCD方法对教学成绩的异常值进行检测,认为其能够更快、更具有鲁棒性地识别学生成绩中的异常数据。此外,也有一些学者对检测算法进行了深入优化,提出了更为复杂的检测模型[22],如混合模型[23]、时域频域组合模型[24]和自适应模型[25]等,以提高模型的识别精度。但优化后的算法随着复杂度的提高,增加了参数的维度,难以快速获取最佳的参数组合[26],无法保障高频率、高精度监测背景下异常值检测的时效性。
1 研究区概况
新场候选场址位于甘肃省酒泉市肃北县。场址地形多为低山丘陵,海拔一般在1 650~1 800 m。所在区域气候条件属半沙漠大陆性气候,夏季酷热,冬季严寒。多年平均降雨量为60~80 mm[29],多年平均蒸发量大于3 000 mm。
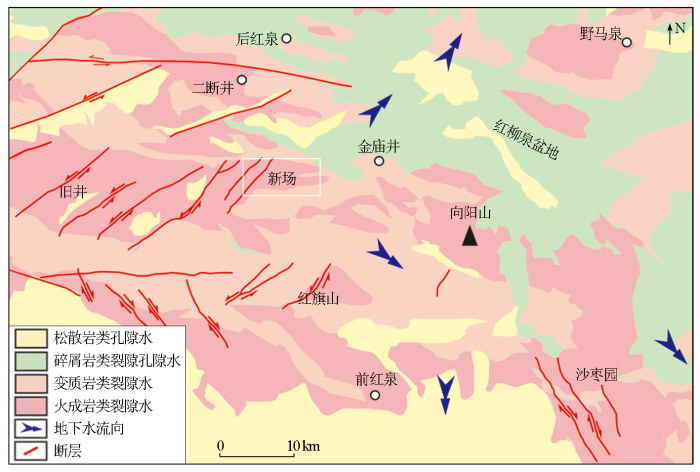
区域范围内地下水主要类型为松散岩类孔隙水、碎屑岩类裂隙孔隙水、变质岩类裂隙水及火成岩类裂隙水(图1)。其中,新场场址范围内以火成岩类裂隙水为主,钻孔揭露岩体渗透系数普遍小于10-8m·s-1,属于典型的低渗透性花岗岩裂隙岩体。区内地下水在断裂构造和地形的控制作用下,以新场场址中部南北分水岭为界向NE和SE方向径流。地下水系统的主要补给来源为大气降水的垂向入渗补给,并以侧向径流的方式向下游地区排泄。
图1
2 研究方法
2.1 数据准备
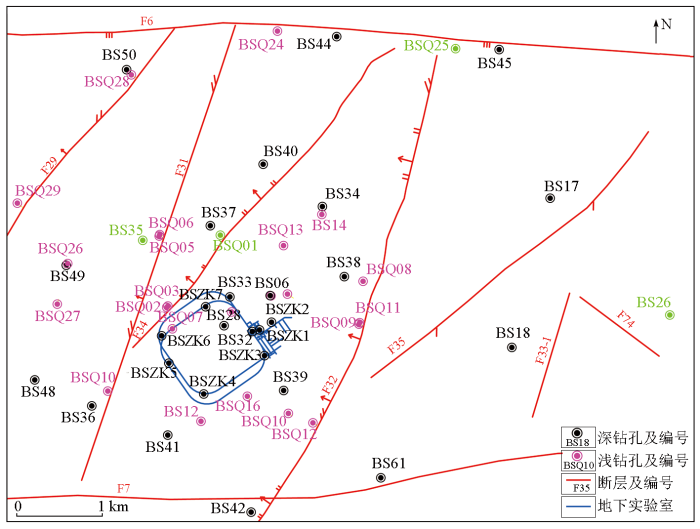
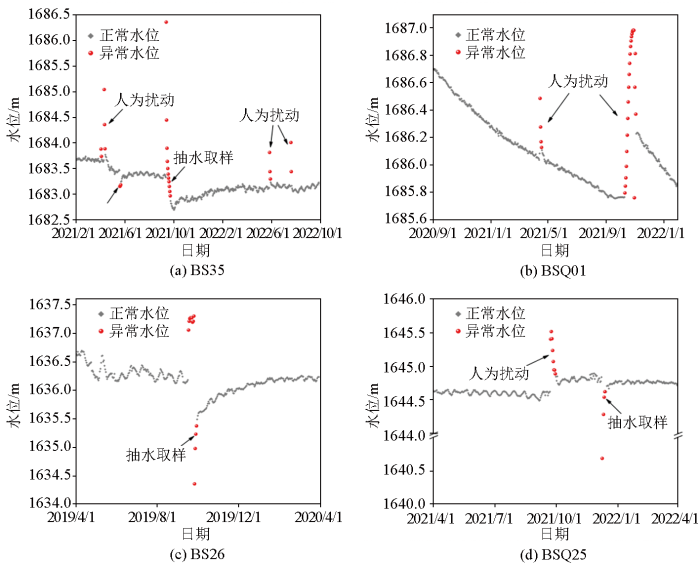
水位数据取自于研究区内的浅部(<100 m)和深部(约600 m)监测钻孔(图2),采用Solinst Levelogger 3001 或 Seametrics LevelScout 2X 型水位计自动获取监测数据,相应的传感器测量精度为0.1%FS。为保证数据分析结果的一致性,将水位数据样本间隔统一调整为1 d。考虑到监测数据中还同时包含固体潮、蒸散发等因素的影响,且地下水位在受上述因素影响下的微动态变化幅度一般小于10 cm。因此,通过比较相邻时刻的水位样本值来标注异常数据样本,将水位差大于15 cm的样本作为异常事件的起始时刻,并将其恢复至正常变化水平的时刻作为异常事件的结束时刻,以降低水位微动态效应的影响。起始和结束时刻内包含的超出正常水位变化范围的水位值则被标注为待检测的异常值。
图2
图2
新场地段内地下水位监测钻孔位置
Fig.2
Location map of monitoring boreholes around the Xinchang site
图3
图3
钻孔地下水位监测数据及异常值分布
Fig.3
Distribution of groundwater level monitoring data and anomaly values in boreholes
2.2 基于MCD方法的异常值检测单一模型
式中:
对获取的样本子集,计算其均值和协方差矩阵,并依据公式(2)[31]计算各个数据点到样本子集整体的距离,将偏离数据中心的样本标记为异常值;此外,通过不断调整模型阈值来优化检测结果,挑选出最优的阈值大小作为判别标准,完成最终的异常值检测工作。本研究选取pycaret模型库中的anomaly模型来实现此算法。
式中:RD(x)为样本x距离样本子集整体的距离;
2.3 结合STL分解与MCD方法的异常值检测组合模型
基于MCD方法的单一模型仅是对协方差行列式的估计,忽略了时间序列数据的时间依赖性和序列相关性,导致无法对异常值进行准确识别。因此,在传统MCD方法的基础上引入STL分解方法,用于处理数据的时间序列相关性,降低趋势性和微动态效应对检测结果的干扰,使MCD方法可以在更独立、相对无关的残差部分进行异常检测,增加模型对异常值的敏感程度,提高识别结果的准确性和可靠性。
STL分解方法作为异常值检测的预处理过程,其主要原理为基于局部加权回归的方法,将给定的时间序列数据分解为趋势项、周期项和残差项(式(3))[27]。在预处理过程中可分为内循环和外循环两个独立的迭代过程,其中,内循环主要处理数据序列的趋势性和周期性,外循环则是通过添加稳健性权重项,来抑制数据异常值对时间序列分解的影响。
式中:Yt为t时刻的数据的实际值;Tt为时间序列分解后的趋势项;St为时间序列分解后的周期项;Rt为时间序列分解后的残差项;t为数据样本的时间,t=1,2,…,N。
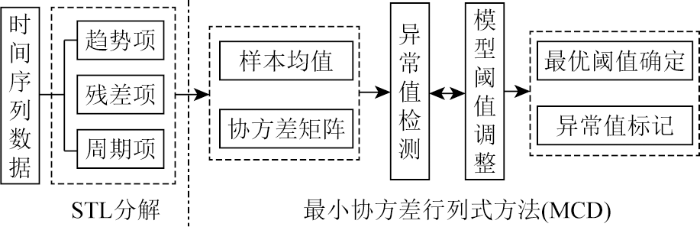
在完成STL分解后,依托单一MCD方法对拆分后的残差项序列执行异常值检测,其操作流程如图4所示。其中STL分解方法的实现选取了statsmodels统计分析库中的seasonal.STL模型算法,而MCD异常值检测算法则采取与单一模型相同的实现形式。
图4
图4
STL分解和最小协方差行列式方法组合的异常检测流程
Fig.4
Anomaly detection process for the combined STL decomposition and minimum covariance determinant method
3 研究结果
3.1 评价指标
为定量评价时间序列异常检测算法的精度,引入了精确率、召回率和F1值3个评价指标作为模型性能的判别标准,更全面地评价检测结果的可靠性。其中,精确率反映的是模型检测到的异常数据中实际异常值的占比;召回率是指模型正确识别的异常值占全部异常值的比例,反映模型对于异常值的查全率;而F1值则是精确率和召回率的加权平均值。求取的3个评价指标值越大,表明模型检测的精度越高。计算方法见式(4)~(6)[32]。
式中:P为精确率;R为召回率;TP为模型将实际的异常值预测为异常值的样本数量;FN为模型将实际的异常值预测为正常值的样本数量;FP为模型将实际的正常值预测为异常值的样本数量。
3.2 模型阈值确定
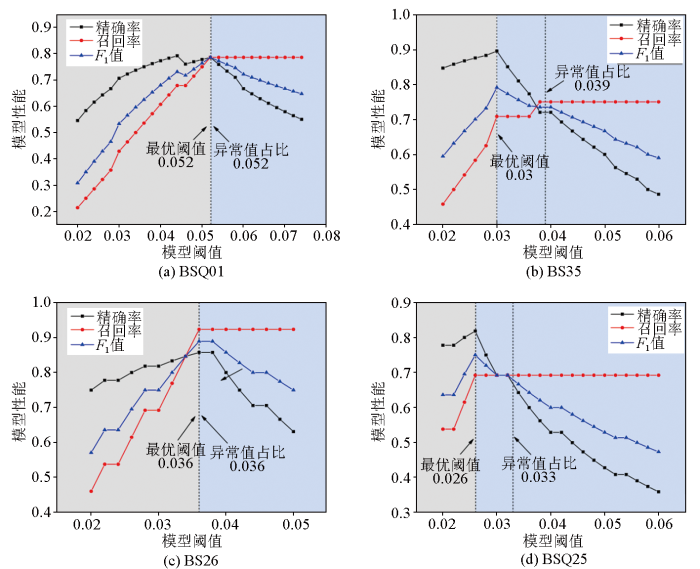
MCD方法中模型阈值的大小决定了数据序列中被判定为异常值的比例,合理的设置阈值可以帮助正确捕捉数据中的全部异常事件,提高模型的检测精度。考虑到选取的4个钻孔中异常值比例在3.4%~4.6%不等,为评价不同模型阈值情况下的检测效果,确定最优的模型阈值大小,将模型阈值设定在2.0%~8.0%区间范围内,并以精确率、召回率和F1值3个评价指标作为不同阈值条件下模型性能的判别标准。
图5 为以3个不同评价指标为标准反映的模型性能随阈值的变化情况。BSQ01、BSQ25、BS26和BS35钻孔的最优阈值分别为5.2%、2.6%、3.6%和3.0%,且模型性能的变化以最优阈值为界可分为两种不同的变化趋势。首先,当模型阈值小于最优阈值时,3个评价指标变化一致,均随着设定阈值的增大而增加,当达到最优阈值时模型性能最佳(图5灰色区域);其次,当模型阈值大于最优阈值时,精确率和F1值呈现降低趋势,召回率则呈现平稳变化趋势,表明当阈值增大到一定程度后,模型的宽容度也随之增大,将存在更多的正常样本被误判,造成模型的检测精度逐渐下降(图5蓝色区域)。此外,研究结果还表明,4个钻孔获取的最优阈值均小于或等于模型实际的异常值比例(图5),表明构建的模型能够较好地适应实际的数据特征,具有较高的稳定性,能够准确识别出混淆的异常值。
图5
3.3 组合模型与单一模型检测效果对比
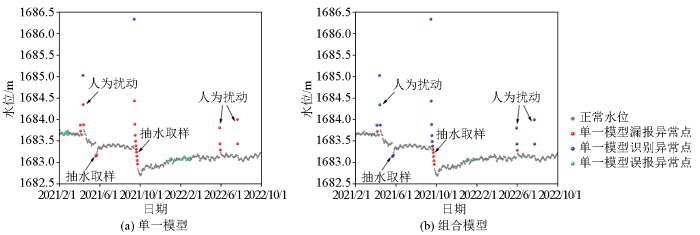
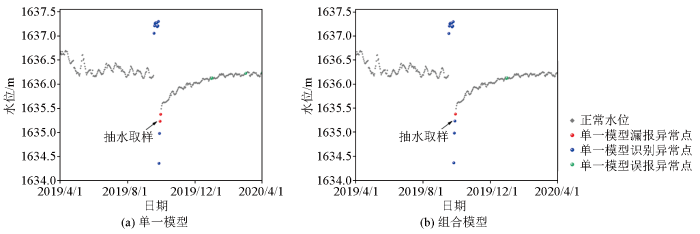
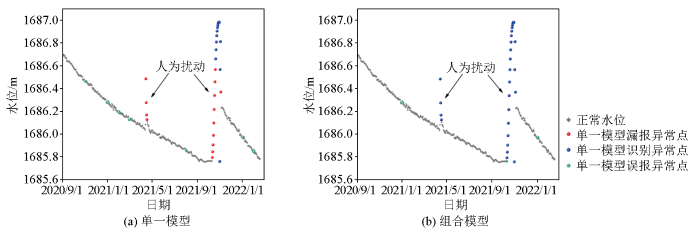
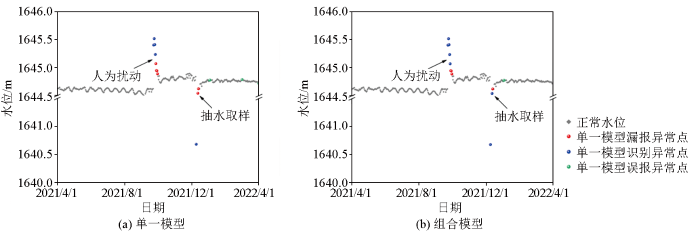
依托确定的最优阈值,将构建的组合模型与仅采用MCD方法的单一模型进行对比,评价不同模型的检测效果。整体上,组合模型能够有效地识别大部分水位异常值(图6b、7b、8b、9b),而单一模型仅可识别出两次水位大幅度上升的异常事件,模型漏报率较高(图6a、7a、8a、9a);且单一模型与组合模型相比,其识别的异常事件中包含了较多的正常值,模型误报率更高。分析原因,认为其检测精度较差可归因于模型仅采用了基于距离的处理方法,无法准确识别出地下水位数据中的微动态效应,在标注异常样本时错误处理了部分周期性变化特征,因而模型误报率较高。而组合模型在进行异常检测之前,首先应用STL分解剔除了数据中的趋势性和微动态效应,仅处理更独立、相对无关的残差部分,提高了模型对于一些小幅度水位异常事件的敏感性和检测精度。
图6
图6
BS35号孔组合模型与单一模型检测效果
Fig.6
Combined model and single model detection results in borehole BS35
图7
图7
BS26号孔组合模型与单一模型检测效果
Fig.7
Combined model and single model detection results in borehole BS26
图8
图8
BSQ01号孔组合模型与单一模型检测效果
Fig.8
Combined model and single model detection results in borehole BSQ01
图9
图9
BSQ25号孔组合模型与单一模型检测效果
Fig.9
Combined model and single model detection results in borehole BSQ25
此外,对于4个钻孔中几种不同类型异常事件的检测结果,组合模型基本能够对各种不同波动幅度的异常事件进行准确识别,仅在BS35号孔中对因抽水取样造成的水位骤然下降事件检测结果较差(图6b)。在对BS35号孔检测流程中的每个步骤进行单独分析时发现,产生这种偏差的原因是由于STL分解方法将未能识别的异常值错误处理为了具有下降趋势的正常水位,使得分解后的残差项中该部分异常值的差异特征与正常点相差不大,导致MCD方法无法对其进行准确识别。而单一模型因受到水位微观波动等因素的影响,仅能识别出部分水位波动在1 m以上的异常事件类型(图7a、8a),对于1 m以内的小幅度水位异常波动则均存在较大程度的漏报,模型的适用性较差。
基于此,计算了BSQ01、BSQ25、BS26、BS35这4个钻孔地下水位异常值检测结果的精确率、召回率和F1值(表1),以对组合模型的实际应用效果进行定量评价。可以看出,构建的组合模型与单一模型相比,在具有较高召回率的同时也能够兼顾良好的精确率。由此可见,构建的组合模型能够准确识别出混淆于大量正常水位数据中的异常值,在实际应用中取得了较好的检测效果,对于地下实验室场址周边地下水位监测数据中的异常值检测具有较好的适用性,并能够适用于不同类型地下水位异常事件的识别。
表1 场址周边钻孔地下水位异常值检测评价指标得分
Table 1
| 钻孔号 | 单一模型 | 组合模型 | ||||
|---|---|---|---|---|---|---|
| 精确率 | 召回率 | F1值 | 精确率 | 召回率 | F1值 | |
| BS26 | 0.71 | 0.76 | 0.74 | 0.85 | 0.92 | 0.88 |
| BS35 | 0.11 | 0.08 | 0.09 | 0.89 | 0.71 | 0.79 |
| BSQ01 | 0.50 | 0.50 | 0.50 | 0.78 | 0.64 | 0.71 |
| BSQ25 | 0.64 | 0.54 | 0.58 | 0.82 | 0.69 | 0.75 |
4 结论与展望
1)依托STL时间序列分解和基于距离的MCD方法构建了地下水位异常检测组合模型,使MCD方法可以在更独立、相对无关的残差部分进行异常值检测,提高了模型对异常数据的敏感性和检测精度;以精确率、召回率和F1值3个评价指标为标准,分析了模型性能随阈值的变化情况,表明模型阈值在接近实际异常值比例时,检测效果最佳。
2)将构建的组合模型应用到新场地段BSQ01、BSQ25、BS26、BS35等4口钻孔地下水位异常值的检测中,并通过与单一模型进行对比,证明其能够准确识别出混淆于大量正常水位数据中的异常值;且相比于单一模型,能够更好地适用于不同类型和不同水位波动幅度下地下水位异常事件的检测。
尽管现阶段已构建了适用于高放废物处置场址地下水位异常值的检测方法,并取得了较好的应用效果,但地下水动态监测是一个长期性工作,在未来的实际工作中仍存在当前研究未考虑的地下水位异常事件类型,仍需要进一步获取更新的水位监测数据,完善构建的异常值检测方法,提高模型的适用性。此外,还需要进一步构建适用于高放废物处置场址地下水位时间序列数据的缺失值处理方法,以保障地下水位监测数据的连续性。
参考文献
世界高放废物地质处置库选址研究概况及国内进展
[J].
The general situation of geological disposal repository siting in the world and research progress in China
[J].
The Beishan underground research laboratory for geological disposal of high-level radioactive waste in China:Planning,site selection,site characterization and in situ tests
[J].
Low-cost,open source wireless sensor network for real-time,scalable groundwater monitoring
[J].
Building a low-cost,internet-of-things,real-time groundwater level monitoring network
[J].
Machine learning approaches for anomaly detection of water quality on a real-world data set
[J].
Deep learning for anomaly detection:A review
[J].
Anomaly detection in time series:A comprehensive evaluation
[J].
Anomaly detection by robust statistics
[J].
Time series outlier detection based on sliding window prediction
[J].
Anomaly detection using a sliding window technique and data imputation with machine learning for hydrological time series
[J].
Multivariate outlier detection based on a robust Mahalanobis distance with shrinkage estimators
[J].
Robust distance measure to detect outliers for categorical data
[J].
Clustering-based anomaly detection in multivariate time series data
[J].
A critical overview of outlier detection methods
[J].
基于K-shape聚类的连续液位监测数据异常检测方法
[J].
Abnormal detection of continuous water level monitoring data based on K-shape clustering
[J].
Machine learning-based anomaly detection of groundwater microdynamics:Case study of Chengdu,China
[J].
Outlier detection approaches for wireless sensor networks:A survey
[J].
The utility of multivariate outlier detection techniques for data quality evaluation in large studies:An application within the ONDRI project
[J].
DOI:10.1186/s12874-019-0737-5
PMID:31092212
[本文引用: 2]

Large and complex studies are now routine, and quality assurance and quality control (QC) procedures ensure reliable results and conclusions. Standard procedures may comprise manual verification and double entry, but these labour-intensive methods often leave errors undetected. Outlier detection uses a data-driven approach to identify patterns exhibited by the majority of the data and highlights data points that deviate from these patterns. Univariate methods consider each variable independently, so observations that appear odd only when two or more variables are considered simultaneously remain undetected. We propose a data quality evaluation process that emphasizes the use of multivariate outlier detection for identifying errors, and show that univariate approaches alone are insufficient. Further, we establish an iterative process that uses multiple multivariate approaches, communication between teams, and visualization for other large-scale projects to follow.We illustrate this process with preliminary neuropsychology and gait data for the vascular cognitive impairment cohort from the Ontario Neurodegenerative Disease Research Initiative, a multi-cohort observational study that aims to characterize biomarkers within and between five neurodegenerative diseases. Each dataset was evaluated four times: with and without covariate adjustment using two validated multivariate methods - Minimum Covariance Determinant (MCD) and Candès' Robust Principal Component Analysis (RPCA) - and results were assessed in relation to two univariate methods. Outlying participants identified by multiple multivariate analyses were compiled and communicated to the data teams for verification.Of 161 and 148 participants in the neuropsychology and gait data, 44 and 43 were flagged by one or both multivariate methods and errors were identified for 8 and 5 participants, respectively. MCD identified all participants with errors, while RPCA identified 6/8 and 3/5 for the neuropsychology and gait data, respectively. Both outperformed univariate approaches. Adjusting for covariates had a minor effect on the participants identified as outliers, though did affect error detection.Manual QC procedures are insufficient for large studies as many errors remain undetected. In these data, the MCD outperforms the RPCA for identifying errors, and both are more successful than univariate approaches. Therefore, data-driven multivariate outlier techniques are essential tools for QC as data become more complex.
Outlier detection in the multiple cluster setting using the minimum covariance determinant estimator
[J].
Minimum covariance determinant and extensions
[J].
基于FAST-MCD算法的异常成绩检测研究
[J].
Research on the abnormal grade detection based on the FAST-MCD algorithm
[J].
Anomaly detection via a combination model in time series data
[J].
Anomaly detection for time series using VAE-LSTM hybrid model
[C]//
Anomaly detection using variational autoencoder with spectrum analysis for time series data
[C]//
Adaptive multivariate time-series anomaly detection
[J].
A comprehensive survey of anomaly detection algorithms
[J].
STL:A seasonal-trend decomposition procedure based on Loess
[J].
A fast algorithm for the minimum covariance determinant estimator
[J].
Using multiple isotopes to determine groundwater source,age,and renewal rate in the Beishan preselected area for geological disposal of high-level radioactive waste in China
[J].
Minimum covariance determinant
[J].
Robust statistics for outlier detection
[J].