0 引言
地质统计方法在资源储量评价和空间预测领域具有重要地位,该方法主要研究地质属性的空间相关性及其变化规律。变差函数是地质统计学中用于定量评价空间相关性的工具。通过建立空间距离与地质属性值的关系,变差函数揭示了空间属性变量的分布变化规律,为空间预测提供了可靠依据。基于地质统计学实施空间预测时,必须首先进行实验变差函数拟合,获取研究区的理论变差函数,如此才能获取任意距离的空间相关性。现有变差函数拟合方法包括最小二乘法[1]、加权多项式回归法[2]、线性规划法[3]和遗传算法[4]等,这些方法在实际使用中存在一定不足:例如当实验变差函数的数据点与理论模型存在较大偏差时,最小二乘法的拟合效果将不再稳定;遗传算法在求解非线性优化问题时具有寻找全局最优解的特点,但是需要调整多个参数,结构复杂且计算效率较低[5];粒子群优化算法虽能直接处理实数编码和连续可导问题,但同样需要进行参数调整,计算效率较低,容易陷入局部最优解[6]。由于传统机器学习方法在处理复杂的变差函数和包含噪声的数据时存在线性假设限制、局部极值问题等一定的局限性。深度学习采用多层神经网络[7],学习能力强,对噪声具有较强的容错性,可以充分逼近复杂的任意非线性关系函数[8],在分类与回归分析问题中表现优异。相比传统模型的滞后距与半变异函数学习,深度学习更适用于波动特征明显且不需要传统理论模型的情况,但对于强波动情况传统模型更合适[9]。因此本文在前人基础上,结合深度学习算法提出一种变差函数自动拟合方法。
1 方法原理
1.1 实验变差函数
其中:
1.2 理论变差函数模型
常用变差函数理论模型包括球状模型、高斯模型和指数模型等[13]。理论模型在描述储层参数在同一方向上的变化速度以及变化方式上存在差异。在实际应用中,根据地质属性的变异特征和数据分析的结果,选择合适的变差函数模型来描述地质属性的空间变异性至关重要。球状模型在空间上呈现出一种随距离递增而逐渐趋于平稳的趋势,其在空间上的变异性相对较小[5],对于实验数据的噪声和异常值具有一定的鲁棒性和稳定性[14],可有效地减少误差和干扰;球状模型到达基台值后其空间相关性不再随变程增加而显著变化,减少了变程对模型准确性的敏感度,且球状模型的参数较少,适合进行深度学习模型的拟合和优化,可以在保证拟合效果的同时,提高模型的训练速度和效率,本文选取球状模型作为理论变差函数模型开展研究。球状模型表达式如下:
式中:
1.3 新方法神经网络结构
除了图像识别、语音分析和自然语言处理等领域,将深度学习运用于储层建模和油气预测领域已成为当前研究热点[15]。深度学习通过大量样本数据的自主学习即可提取关键特征,取得了比传统指标更准确的识别效果。常用深度学习网络架构包括全连接神经网络(fully connected neural network,简称FCNN)、卷积神经网络(CNN)以及循环神经网络(RNN)等,其中FCNN属于一种多层感知机(MLP),FCNN中每个神经元都与前一层和后一层的所有神经元相连接,构成一个密集的连接结构,FCNN能够学习输入数据的复杂特征,并有效解决分类、回归等任务。根据实验变差函数进行拟合计算,得到最匹配的理论变差函数模型,属于典型的非线性回归问题,因此本文设计一种FCNN框架实现实验变差函数自动拟合。
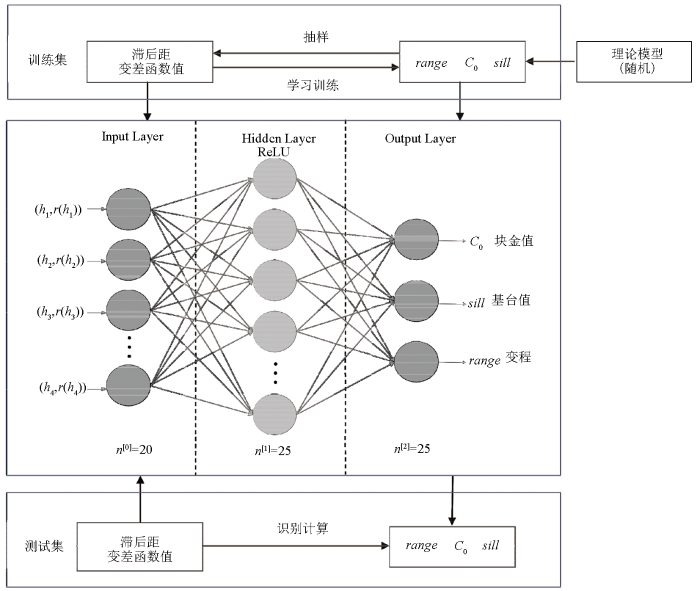
FCNN由输入层、隐藏层、输出层组成,通过激活函数引入非线性映射特征,使得神经网络具备拟合复杂非线性特征能力[16]。其中每个层包含多个神经元,多层神经元互相连接,使其能够捕捉输入层数据的复杂关系。本文采用的FCNN架构(见图1)输入层信息是实验变差函数的滞后距及其对应的变差函数值;输出层是拟合的理论变差函数模型参数,包括变差函数的变程、块金值和基台值;中间层为隐藏层,可由单个神经层或者多个神经层组成,每层包含大量神经元,这些神经元负责存储非线性权重信息。本次测试输入层的神经元数量设定为20,即包含20个不同滞后距及其对应的变差函数值,隐藏层神经元数量设定为25;输出层神经元数量为3,即变差函数的变程、块金值和基台值。
式中:
图1
损失函数则采用RMSE,定义如下:
式中:yi为真实值;
2 实例
2.1 训练样本
如表1所示,训练数据集由两部分组成:输入层数据(列名为v1~v20)和输出层数据(列名为C0 、range、sill)。输入层数据主要包括实验变差函数的滞后距离以及相应的变差函数值。输出层数据则包括理论变差函数的参数。以球状模型为例,这些参数为C0、range、sill。
表1 1 000×20 实验变差函数数据
Table 1
| v1 | v2 | v3 | v4 | … | v19 | v20 | C0 | range | sill |
|---|---|---|---|---|---|---|---|---|---|
| 13.04 | 23.73 | 36.66 | 41.25 | … | 85.43 | 87.01 | 5 | 44.14 | 84.75 |
| 6.04 | 16.99 | 43.76 | 45.61 | … | 77.48 | 82.78 | 5 | 35.89 | 79.97 |
| 14.45 | 17.54 | 33.05 | 39.66 | … | 78.51 | 76.79 | 5 | 43.64 | 75.19 |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
| 14.53 | 35.27 | 45.21 | 49.80 | … | 85.18 | 87.15 | 5 | 34.77 | 85.23 |
| 21.75 | 40.62 | 51.56 | 68.23 | … | 89.99 | 90.32 | 5 | 28.07 | 87.99 |
为对应各种不同参数的变差函数拟合情况,本文生成了一个包含20个随机且不等距分布的数据点的训练数据集。其中参数设置为C0 = 0,range = [20,45],sill = [70,85],数据集规模为1 000×20。设置训练次数为20 000次,经过不同数据集的多次实验验证,更改不同参数发现,当学习率为0.000 05时均方差损失最小,说明深度学习训练的结果与样本点数据相接近,拟合效果越好。
测试数据来源于理论变差函数,与训练数据来源类似,从表2中给定理论变差函数中随机抽取20个滞后距和变差函数值作为测试数据,将相应理论变差函数参数与测试结果进行对比,检验拟合效果。
表2 实验变差函数各数据参数
Table 2
| 分组 | C0 | range | sill |
|---|---|---|---|
| 第一组 | 0 | 20 ~ 45 | 70 ~ 85 |
| 第二组 | 10 | 25 ~ 50 | 75 ~ 90 |
| 第三组 | 15 | 30 ~ 55 | 80 ~ 95 |
| 第四组 | 20 | 35 ~ 60 | 85 ~ 100 |
2.2 方法比较
图2
图2
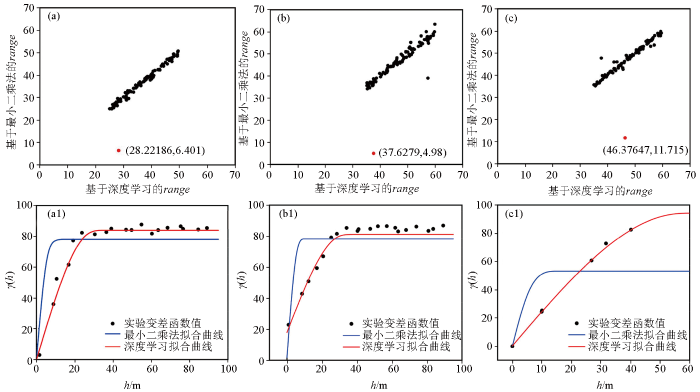
两种不同方法拟合效果对比
a—变差函数的range范围为25~50时最小二乘法和深度学习法range映射关系,红色点为异常点;b—变差函数的range范围为35~60时最小二乘法和深度学习法range映射关系,红色点为异常点;c—变差函数的range范围为35~60时最小二乘法和深度学习法range映射关系,红色点为异常点;a1—对应a红色异常点横纵坐标分别对应最小二乘法拟合曲线和深度学习曲线变程;b1—对应b红色异常点横纵坐标分别对应最小二乘法拟合曲线和深度学习曲线变程;c1—对应c红色异常点横纵坐标分别对应最小二乘法拟合曲线和深度学习曲线变程
Fig.2
Comparison of the fitting effect of the two different methods
a—range mapping relationship between the least squares method and the deep learning method when the variogram function's range is 25~50, with red points indicating outliers; b—range mapping relationship between the least squares method and the deep learning method when the variogram function's range is 35~60, with red points indicating outliers; c—range mapping relationship between the least squares method and the deep learning method when the variogram function's range is 35~60, with red points indicating outliers; a1—the x and y coordinates of the red outliers in a correspond to the values of the least squares fitting curve and the deep learning curve, respectively; b1—the x and y coordinates of the red outliers in b correspond to the range values of the least squares fitting curve and the deep learning curve, respectively; c1—the x and y coordinates of the red outliers in c correspond to the range values of the least squares fitting curve and the deep learning curve, respectively
将图2a~c中的异常点找出并标红,绘制出相应具体的变差函数拟合曲线对比图。如图2a1~c1所示,黑色点代表了实验变差函数的值,蓝线表示利用最小二乘法拟合得到的理论变差函数曲线,红线则表示使用深度学习拟合得到的理论变差函数曲线。表3为3组不同方法拟合参数结果对比,深度学习方法拟合结果更接近原始数据;通过拟合效果对比图2a1~c1可以明显看出,无论是参数不同还是实验数据点不同,深度学习方法拟合得到的曲线具有比最小二乘法拟合得到的曲线变程更贴近理论变差函数的变程,数据相关性越强,拟合曲线也更贴近实验数据点。与此相比,蓝色所代表的传统方法拟合结果在某些地方与实验数据存在较大偏差,变差范围更大,表明其在捕捉数据变异性方面的效果相对较差。因此本文所提出的深度学习方法对实验变差函数拟合具有更精确的效果。
表3 变差函数C0、range、sill参数对比
Table 3
| 参数 | 第一组 | 第二组 | 第三组 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 理论变差函数 | 最小二乘法 | 深度学习 | 理论变差函数 | 最小二乘法 | 深度学习 | 理论变差函数 | 最小二乘法 | 深度学习 | |
| C0 | 0 | 0 | -0.13 | 20.00 | 1.67 | 17.97 | 0 | 0 | 0.2 |
| range | 28.22 | 6.40 | 30.01 | 37.63 | 4.98 | 32.47 | 58.93 | 8.78 | 57.62 |
| sill | 84.27 | 78.11 | 83.86 | 85.17 | 78.25 | 81.24 | 96.83 | 53.18 | 94.37 |
本文利用均方根误差和平均绝对误差来对拟合结果进行评价,公式如下:
式中:RMSE和MAE分别为均方根误差和平均误差;
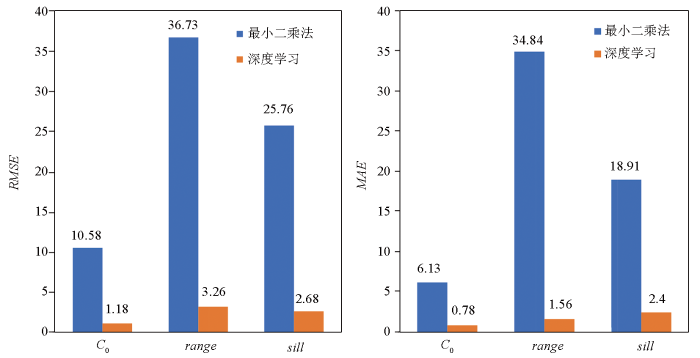
通过对图3中采用最小二乘方法和深度学习方法得到的理论变差函数值进行均方根误差和平均误差的比较,结果表明,采用深度学习方法得到的理论变差函数的均方根误差和平均误差均小于最小二乘方法得到的理论变差函数。因此,通过采用深度学习算法,得到的理论变差函数更符合实际数据,具有更小的拟合偏差,说明本文的方法在变差函数拟合方面具有更高的精度。
图3
图3
两种方法的均方根误差和平均误差对比
Fig.3
Comparison of root mean square error and average error of the two methods
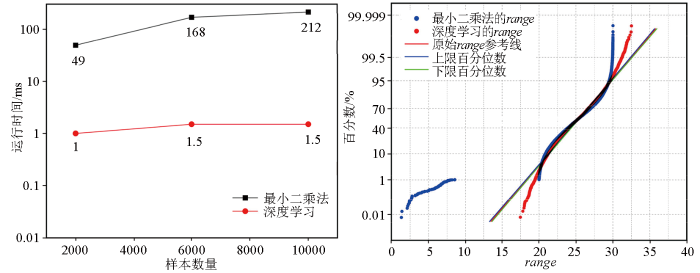
图4
总体来看,无论是从计算时间还是预测准确性的角度评估,深度学习方法在实验变差函数拟合方面的效率与效果均优于最小二乘法。
2.3 输入层的滞后距数量问题
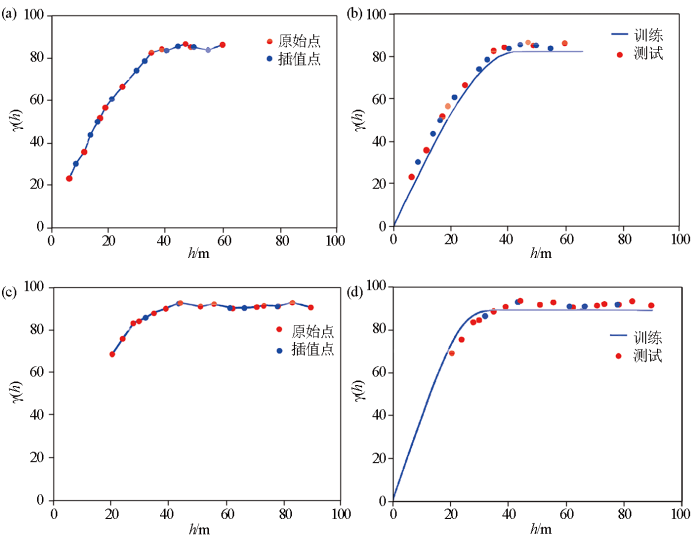
为了确保神经网络能够有效地接受、处理和表示输入数据,从而使神经网络能够在各种学习任务中发挥良好的性能,本文采用线性插值的方法[25],使输入特征数量与输入层神经元数量相匹配以实现输入层的神经元数量等于输入特征的数量[26]。为了在训练数据集中考虑不同的数据点数量和参数范围,我们对数据集进行了多样性的设计将数据点设置为10、15,对应参数范围如图5a中设置数据点的区间为[0,60],包含10个原始数据点的数据集;图5c数据点区间为[20,80],包含15个原始数据点的数据集。为匹配输入层的神经元数量,本文通过线性插值生成额外的数据点,以确保每个训练数据集都包含了20个数据点,与输入层的神经元数量相对应。图5中红色为原始数据点,蓝色为插值数据点,图5b、5d分别为插值训练后的拟合结果。训练数据集如表4所示,输入层数据为10个数据点和输出层数据。
图5
图5
深度学习插值拟合
a—数据点为10实验变差函数经插值后变为20个数据点红色为原始点蓝色为插值点;b—图a插值后的数据点拟合效果;c—数据点为15实验变差函数经插值后变为20个数据点红色为原始点蓝色为插值点;d—图c插值后数据点拟合效果
Fig.5
Depth learning interpolated fit plot
a—data points of 10 experimental variogram functions interpolated to 20 data points, with red indicating original points and blue indicating interpolated points; b—fitting effect diagram of fig.a interpolated data points; c—data points of 15 experimental variogram functions interpolated to 20 data points, with red indicating original points and blue indicating interpolated points; d—fitting effect diagram of fig.c interpolated data points.
表4 1 000×6 实验变差函数数据点
Table 4
| v1 | v2 | … | v10 | C0 | range | sill |
|---|---|---|---|---|---|---|
| 19.10 | 38.93 | … | 91.27 | 10 | 49.42 | 92.01 |
| 17.03 | 27.94 | … | 97.51 | 10 | 54.12 | 88.67 |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
| 11.36 | 30.05 | … | 94.78 | 10 | 58.91 | 94.25 |
| 17.68 | 35.53 | … | 92.45 | 10 | 54.42 | 93.44 |
为使输入特征数量与输入层神经元数量相匹配,对数据集进行插值能够充分利用有限的原始数据点,并确保输入数据与网络结构的匹配,从而提高了模型的性能和泛化能力。通过这种方式,可以更好地适应不同的数据集,并实现更好的拟合效果。
3 讨论
深度学习模型在拟合变差函数方面表现出色,经过20 000次迭代训练,模型的均方误差等性能指标表明,模型的预测与真实数据非常接近。并且模型在不同数据集上都表现出良好的泛化能力。将深度学习方法与最小二乘拟合方法进行对比,结果表明本文方法在变差函数拟合方面具有显著的优势,本文模型更能捕捉数据中的复杂关系,这在高度非线性的变差函数中尤为明显。但当前方法的主要局限在于仅针对球状模型对应的神经网络进行考虑。未来的工作将完善其他变差函数模型(如高斯模型和指数模型)相对应的神经网络,来扩展这一框架,形成一个完整体系更好地适应不同数据对模型选择的多样性需求。
通过深入研究模型在不同数据类型、地质结构和噪声水平下的表现,可以更全面地评估该方法适用性。其次,考虑到地质学中的不确定性,引入深度学习方法如贝叶斯神经网络[27],有助于更好地捕捉和量化地下结构的变异性和测量误差,提高地质模型的可靠性。扩充数据集、融合多源数据,引入更多地质信息,能够进一步提升模型性能。在处理大规模地质数据和复杂变差函数时,采用高性能计算和分布式计算技术,以加速训练和推理过程。将深度学习方法应用于实际地质问题,如矿产勘探、油气勘探和地震预测,可以验证方法的实际效益和可行性。
4 结论
根据实验变差函数自动拟合得到理论变差函数模型属于典型的非线性回归分析问题,深度学习模型具有强大的拟合能力,可以学习数据中的非线性关系和复杂规律,深度学习拟合实验变差函数在回归效果和鲁棒性以及运算效率方面都表现出优异性。经过大量数据测试深度学习模型具有较强的泛化能力,可以对未知数据进行良好的预测和推断,对于实验变差函数的预测具有较高的精度和可靠性。因此,本文提出的基于深度学习的变差函数自动拟合方法,能够更准确、高效地拟合实验变差函数,并且在波动特征明显的情况下不依赖于传统理论模型。这一新方法不仅提高了拟合的精度和稳定性,而且为地质统计学中的变差函数自动拟合提供了新的思路和解决方案,拓展了地质统计学在资源评估和空间预测方面的应用范围。
参考文献
Maximum likelihood estimation of models for residual covariance in spatial regression
[J].
线性规划法自动拟合变差函数的改进
[J].
Improvement of automatic fit of variation functions in linear programming
[J].
变差函数的参数模拟
[J].
Estimation of variation parameter
[J].
基于改进的量子粒子群算法的变差函数拟合方法及应用
[J].
Research on variogram fitting method and its application based on the improved quantum particle swarm algorithm
[J].
一种基于随机粒子群的变差函数优化方法
[J].
Based on the variogram of the random particle swarm optimization method
[J].
基于神经网络的脉搏波信号血压检测算法
[J].
Neural network-based blood pressure detection algorithms for pulse wave signals
[J].
Learning strict identity mappings in deep residual networks
[C]//
Application of a semivariogram based on a deep neural network to Ordinary Kriging interpolation of elevation data
[J].
用加权多项式回归进行球状模型变差图的最优拟合
[J].
On the best fitting of the spherical model variogram with the weighted polynomial regression
[J].
时空理论变异函数模型及其精度影响
[J].
Study of spatio-temporal theory model and its influence on the sptio-temporal prediction accuracy
[J].
A simulated annealing based optimization algorithm for automatic variogram model fitting
[J].
A fast learning algorithm for deep belief nets
[J].
DOI:10.1162/neco.2006.18.7.1527
PMID:16764513
[本文引用: 1]

We show how to use "complementary priors" to eliminate the explaining-away effects that make inference difficult in densely connected belief nets that have many hidden layers. Using complementary priors, we derive a fast, greedy algorithm that can learn deep, directed belief networks one layer at a time, provided the top two layers form an undirected associative memory. The fast, greedy algorithm is used to initialize a slower learning procedure that fine-tunes the weights using a contrastive version of the wake-sleep algorithm. After fine-tuning, a network with three hidden layers forms a very good generative model of the joint distribution of handwritten digit images and their labels. This generative model gives better digit classification than the best discriminative learning algorithms. The low-dimensional manifolds on which the digits lie are modeled by long ravines in the free-energy landscape of the top-level associative memory, and it is easy to explore these ravines by using the directed connections to display what the associative memory has in mind.
一种高精度LSTM-FC大气污染物浓度预测模型
[J].
A kind of high-precision LSTM-FC atmospheric contaminant concentrations forecasting model
[J].
基于深度全连接神经网络的储层有效砂体厚度预测
[J].
Thickness prediction of reservoir effective sand body by deep fully connected neural network
[J].
ImageNet classification with deep convolutional neural networks
[J].
Backpropagation and stochastic gradient descent method
[J].
Adam:A method for stochastic optimization
[C]//
地质统计学变差函数人机对话拟合
[J].
The study of variogram model fitting by interactive computer-aided program
[J].
Multivariate geostatistics
[J].
The Matérn function as a general model for soil variograms
[J].
线性插值算法研究
[J].
Research on linear interpolation algorithm
[J].
深度神经网络在EMD虚假分量识别中的应用
[J].
Application of deep neural networks in emd false component identification
[J].