基于虚拟波场的可控源三维电磁法正演

doi:10.11720/wtyht.2024.1124

基于虚拟波场的可控源三维电磁法正演

蒋志强^,¹, 林超^,²^,³, 杨庭伟²^,³^,⁴, 宁晓斌²

1.广西新发展交通集团有限公司,广西南宁 530029

2.广西交科集团有限公司,广西南宁 530007

3.广西壮族自治区公路隧道安全预警工程研究中心,广西南宁 530007

4.广西道路结构与材料重点实验室,广西南宁 530007

Forward modeling of a controllable-source 3D electromagnetic method based on fictitious wave field

JIANG Zhi-Qiang^,¹, LIN Chao^,²^,³, YANG Ting-Wei²^,³^,⁴, NING Xiao-Bin²

1. Guangxi XinFaZhan Communication Group Co.,Ltd.,Nanning 530029,China

2. Guangxi Transportation Science and Technology Group Co.,Ltd.,Nanning 530007,China

3. Guangxi Highway Tunnel Safety Warning Engineering Research Center,Nanning 530007,China

4. Guangxi Key Lab of Road Structure and Materials,Nanning 530007,China

通讯作者: 林超(1994-)男,硕士,主要从事公路试验检验检测工作。Email:1847107924@qq.com

第一作者: 蒋志强(1975-)男,本科,主要从事高速公路、市政项目建设管理工作。Email:495425386@qq.com

责任编辑: 叶佩

收稿日期: 2023-08-27 修回日期: 2024-01-2

基金资助:

广西自然科学基金项目(2021GXNSFAA196056)

Received: 2023-08-27 Revised: 2024-01-2

摘要

根据扩散场和虚拟波场的变换关系,将频率域电磁扩散方程转换成虚拟域的波动方程,实现了虚拟波场的电磁场数值计算。在边界的处理上,通过引入复频率完全匹配层吸收边界条件,降低了内存的存储量。将空气层包含在计算域中,避免了地—空界面的复杂处理。通过与均匀半空间解析解对比,其相对误差在3.5%以内,验证了算法的有效性和正确性。最后通过典型地电模型的数值模拟表明:通过一次正演可以获得多个频率的三维电磁响应,提高了计算效率。虚拟波场计算的视电阻率对场源效应不敏感且对异常体的边界具有较好的识别能力。

关键词： 可控源电磁法; 虚拟波场; 有限差分法; 三维正演

Abstract

This study converted the frequency-domain electromagnetic diffusion equation into the wave equation in the fictitious domain based on the transformation relationship between the diffusion field and the fictitious wave field,achieving the numerical calculation of the electromagnetic field in the fictitious wave field.By introducing the complex frequency shifted perfectly matched layer(CFPML) boundary condition,the storage capacity of the computer memory decreased.Furthermore,by encompassing the air layer in the calculation domain,the complex processing of the ground-air interfaces was avoided.Compared to the uniform half-space analytical solution,the algorithm proposed in this study had relative errors of less than 3.5% and thus is effective and correct.Finally,the numerical simulation of a typical geoelectric model indicated that the 3D electromagnetic responses of multiple frequencies can be obtained through single forward modeling,suggesting an elevated calculation efficiency.The numerical simulation results also exhibit that the apparent resistivity calculated based on the fictitious wave field is insensitive to the field source effect and thus can effectively identify anomaly boundaries.

Keywords： controlled-source electromagnetic method; fictitious wave field; finite difference method; 3D forward modeling

PDF (5381KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

蒋志强, 林超, 杨庭伟, 宁晓斌. 基于虚拟波场的可控源三维电磁法正演[J]. 物探与化探, 2024, 48(5): 1348-1358 doi:10.11720/wtyht.2024.1124

JIANG Zhi-Qiang, LIN Chao, YANG Ting-Wei, NING Xiao-Bin. Forward modeling of a controllable-source 3D electromagnetic method based on fictitious wave field[J]. Geophysical and Geochemical Exploration, 2024, 48(5): 1348-1358 doi:10.11720/wtyht.2024.1124

0 引言

可控源电磁法是一种利用远区测量相互正交的电、磁场切向分量并计算卡尼亚视电阻率,实现对地下电性结构测量的地球物理方法,具有工作效率高,观测范围大,勘探精度高,抗干扰能力强,适应性强等优点,在工程勘查、资源勘探、地下水探测、地质填图和矿井灾害预测等方面都有广泛的应用^{[1⇓⇓⇓⇓⇓-7]}。

数值分析在可控源电磁法数据的综合分析与解释中扮演着重要的角色,尤其是三维的数值模拟^[8]。目前,可控源电磁法数值分析主要在频率域进行,相应的数值模拟技术也发展比较成熟,提出了有限单元法^[8⇓-10]、有限体积法^{[11⇓⇓-14]}和有限差分法^{[15⇓⇓-18]}等数值模拟计算方法。频率域方法在三维分析中只能实现单频率的计算,即针对每一个频率就需要求解一次线型方程组,当计算的频率较多时,这将是耗时的。为了提高计算效率,根据扩散场和虚拟波场间的对应关系,将扩散场的电磁方程转换成波动场的电磁方程,求解得到虚拟波动域的电磁响应,然后通过积分变换恢复到真实的扩散场,实现宽频带的计算^[19⇓-21]。Lee等^[19] 通过在麦克斯韦方程组中引入“q函数”实现了扩散电磁场到虚拟波场的转换。Maaø^[20] 将麦克斯韦方程通过变换,转换到复频率域中,提出一种基于复频率域的虚拟波场变换方法,并将虚拟波场变换方法应用到电磁法的数值模拟之中。Mittet^[21]提出了一种更简单的虚拟波场变换方法,促进了虚拟波场方法在电磁法数值模拟中的应用。由于从虚拟波动域恢复到扩散域时,获得的是所有频谱的信息,因此,可以从频谱中同时提取出多个频率的电磁响应并进行分析。

吸收边界处理是影响有限区域电磁场数值分析的重要因素之一。良好的吸收边界条件和网格剖分技术可以有效地缩小计算区域。1994年Berenger^[22]通过在计算区域的外边界加载一层吸收媒质,使电磁波在边界中无反射的通过并按指数规律衰减,并把这种方法称这perfectly matched layer(PML)吸收边界条件。PML吸收边界条件的引入减少了电磁波在边界上的反射,同时由于对计算区域进行有效的截断,降低了计算存储量。然而PML吸收边界条件需要对电磁场进行分裂,增加了计算和数值实现的难度,且只对行波有较好的吸收效果,对隐失波、低频波、掠角波吸收效果不佳。徐正玉^[23]将PML吸收边界应用于三维的瞬变电磁有限差分数值模拟中,获得了比较好的处理效果。Kuzuoglu等^[24]提出了复频率完全匹配层(complex frequency-shifted perfectly matched layer,CFS-PML)吸收边界条件,加强了对低频隐失波、大角度掠射波的吸收。Ryhove等^[25]在研究基于虚拟波场的海洋大地电磁三维正演时,在求解过程中引入复频率完全匹配层(CFS-PML),对虚拟的倏逝波和低频波进行了有效的吸收。Li等^[26]实现了CFS-PML基于有限差分的频率域海洋可控源电磁法中的应用。

本文用显式有限差分方法实现了可控源电磁法虚拟波场变换并求解了虚拟波场的场分量。在空气层的处理上,将空气层作为有限高阻体加载在计算域中,简化了地—空界面的处理。在边界条件的处理上,通过引入CFS-PML吸收边界,对计算区域进行了有效的截断,降低了计算的储存,提高了计算效率;在源的加载上,采用一阶高斯脉冲函数的导数作为虚拟发射源的源函数。最后模拟了水平电偶极子源在均匀半空间模型的电磁响应,并与解析解对比,验证了算法的正确性和有效性;通过复杂的地电模型的测试,验证了本算法处理复杂模型的能力。

1 可控源电磁法的虚拟波场变换

虚拟波场变换一般用于低频电磁法方法中,对于准静态情况下的时域扩散场,麦克斯韦方程组可以表示为:

(1)▽×H(r,t)-σ(r)E(r,t)=-J(r,t),

(2)▽×E(r,t)+μ∂_tH(r,t)=-K(r,t),

频率域的麦克斯韦扩散方程表示为:

(3)▽×H(r,ω)-σ(r)E(r,ω)=-J(r,ω),

(4)▽×E(r,ω)-iωμH(r,ω)=-K(r,ω),

式中:H(r,ω)表示频率域磁场分量;E(r,ω)表示频率域电场分量;J(r,ω)表示外加电性源;K(r,ω)表示外加磁性源;r表示空间变量;σ(r)表示介质的电导率;μ表示介质的磁导率。

为了将扩散的电磁方程转换成虚拟的波动方程,2010年,Mittet^[21]通过引入了虚拟的介电常数ε',构造虚拟波场中各参数与实扩散场中相关参数的对应关系:

(5)ε'(r)=

\frac{σ (r)}{2 ω_{0}}

。

根据虚实的对应关系变换可得时域的虚拟波动方程:

(6)-▽×H'(r,t')+ε'(r)∂_t'E'(r,t')=-J'(r,t'),

(7)▽×E'(r,t')+∂_t'H'(r,t')=-K'(r,t'),

式(6)和式(7)在形式上和忽略了电导率项的波动方程相同,只是物理场不同,一个是真实的高频波动场,一个是虚拟的低频波动场。因此,可将在扩散场中的电磁场求解转换到时域虚拟波动场中求解,然后将虚拟波场中的时域电磁场响应变换到频率域扩散电磁场响应:

(8)E_i(r,ω)=

\int_{0}^{T}

dt'E'_i(r,t')eⁱ^ω't'=

\int_{0}^{T}

dt'E'_i(r,t')

e^{\sqrt{ω ω_{0}} t'} e^{i \sqrt{ω ω_{0}} t'}

(9)H_i(r,ω)=

\sqrt{\frac{- 2 ω_{0}}{i ω}} \int_{0}^{T}

dt'H'_i(r,t')eⁱ^ω't'=

\sqrt{\frac{- 2 ω_{0}}{i ω}} \int_{0}^{T}

dt'H'_i(r,t')

e^{\sqrt{ω ω_{0}} t'} e^{i \sqrt{ω ω_{0}} t'}

(10)

{J^{T}}_{n}

(r,ω)=

\sqrt{\frac{- 2 ω_{0}}{i ω}} \int_{0}^{T}

dt'J'

{^{T}}_{n}

(r,t')e^iω't'=

\sqrt{\frac{- 2 ω_{0}}{i ω}} \int_{0}^{T}

dt'J'

{^{T}}_{n}

(r,t')

e^{\sqrt{ω ω_{0}} t'} e^{i \sqrt{ω ω_{0}} t'}

式(8)、(9)为可控源电磁法虚拟波场变换的控制方程。由于虚拟波场中发射源激发的信号并不是真实的,需要根据发射场源类型来构造格林函数,对于电性源有:

(11)

\{\begin{array}{l} G_{i}^{E J} (r, ω) = E_{i}^{E J} (r, ω) = \frac{E_{i} (r, ω)}{{J^{T}}_{n} (r, ω)}, \\ G_{i}^{H J} (r, ω) = H_{i}^{H J} (r, ω) = \frac{H_{i} (r, ω)}{{J^{T}}_{n} (r, ω)} 。 \end{array}

利用格林函数获得频率域的电磁响应,并根据电磁场分量可求取视电阻率和阻抗相位:

(12)

\{\begin{array}{l} ρ_{i j} = \frac{1}{ω μ}| Z_{i j}^{E J} (r, ω) | = \frac{1}{ω μ} |\frac{E_{i}^{E J} (r, ω)}{H_{j}^{E J} (r, ω)}|, \\ θ_{i j} = A r g [Z_{i j}^{E J} (r, ω)] = A r g [\frac{E_{i j}^{E J} (r, ω)}{H_{i j}^{E J} (r, ω)}] 。 \end{array}

2 有限差分求解三维虚拟波动方程

2.1 虚拟波动方程有限差分离散

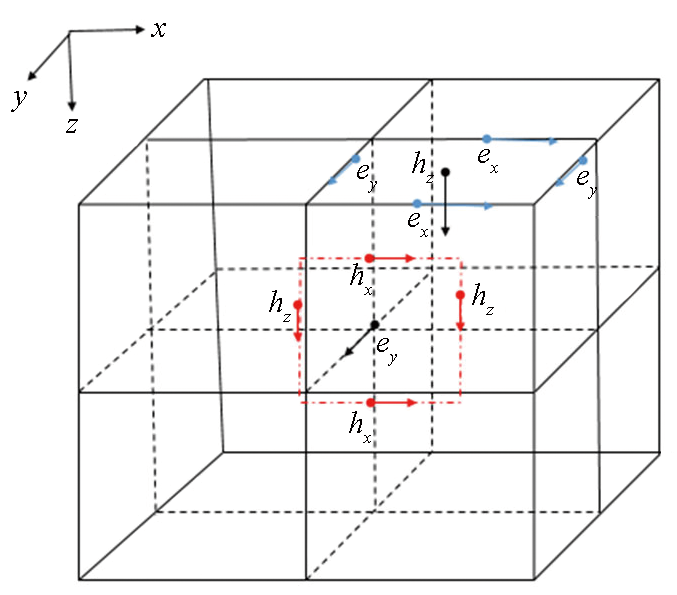
时域有限差分方法是最常用的求解时间偏微分方程的数值模拟方法,本文采用中心差分。在时域有限差分法对虚拟波动方程求解时,需要对控制方程进行空间上的离散。与时域电磁法在空间的离散一样,虚拟的电磁场在空间位置也需要满足安培环路定律和电磁感应定律。图1为Yee网格中虚拟电磁场的空间离散形式,电场在剖分网格的棱边中心,磁场在剖分网格面的中心,每个磁场周围存在4个电场,每个电场周围存在4个磁场。4个电场和4个磁场分别构成电回路和磁回路,相互交替着传播。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 虚拟波场中电磁场的空间离散示意

Fig.1 Spatial discretization of electromagnetic field in fictitious wave field

虚拟时间的离散上采用显示的Du Fort-Frankel方法^[27-28]。在虚拟时间轴上虚拟磁场在半整数的时刻采样,虚拟电场则在整数时刻采样,虚拟的电场和磁场的采样在虚拟时间轴上轮流进行。通过这种虚拟时间上的逐步迭代推进,实现虚拟波动场中电磁场在虚拟时间上的离散。式(6)和式(7)的电场差分迭代表达式表示为:

(13)E'_xⁿ⁺¹(i+

\frac{1}{2}

,j,k)=E'_xⁿ(i+

\frac{1}{2}

,j,k)+Δt

\frac{2 ω_{0}}{σ} [\partial_{y}^{-} H {'_{z}}^{n + \frac{1}{2}} (i + \frac{1}{2}, j + \frac{1}{2}, k) - \partial_{z}^{-} H {'_{y}}^{n + \frac{1}{2}} (i + \frac{1}{2}, j, k + \frac{1}{2})]

(14)E'_yⁿ⁺¹(i,j+

\frac{1}{2}

,k)=E'_yⁿ(i,j+

\frac{1}{2}

,k)+Δt

\frac{2 ω_{0}}{σ} [\partial_{z}^{-} H {'_{x}}^{n + \frac{1}{2}} (i, j + \frac{1}{2}, k + \frac{1}{2}) - \partial_{x}^{-} H {'_{z}}^{n + \frac{1}{2}} (i + \frac{1}{2}, j + \frac{1}{2}, k)]

(15)E'_zⁿ⁺¹(i,j,k+

\frac{1}{2}

)=E'_zⁿ(i,j,k+

\frac{1}{2}

)+Δt

\frac{2 ω_{0}}{σ} [\partial_{x}^{-} H {'_{y}}^{n + \frac{1}{2}} (i + \frac{1}{2}, j, k + \frac{1}{2}) - \partial_{y}^{-} H {'_{x}}^{n + \frac{1}{2}} (i, j + \frac{1}{2}, k + \frac{1}{2})]

。

同理,磁场的差分迭代计算式可得:

(16)H'_x

^{n + \frac{1}{2}}

(i,j+

\frac{1}{2}

,k+

\frac{1}{2}

)=H'_x

^{n - \frac{1}{2}}

(i,j+

\frac{1}{2}

,k+

\frac{1}{2}

\frac{Δ t}{μ} [\partial_{y}^{+} E'_{z}^{n} (i, j, k + \frac{1}{2}) - \partial_{z}^{+} E'_{y}^{n} (i, j + \frac{1}{2}, k)]

(17)H'_y

^{n + \frac{1}{2}}

(i+

\frac{1}{2}

,j,k+

\frac{1}{2}

)=H'_y

^{n - \frac{1}{2}}

(i+

\frac{1}{2}

,j,k+

\frac{1}{2}

\frac{Δ t}{μ} [\partial_{z}^{+} E'_{x}^{n} (i + \frac{1}{2}, j, k) - \partial_{x}^{+} E'_{z}^{n} (i, j, k + \frac{1}{2})]

(18)H'_z

^{n + \frac{1}{2}}

(i+

\frac{1}{2}

,j+

\frac{1}{2}

,k)=H'_z

^{n - \frac{1}{2}}

(i+

\frac{1}{2}

,j+

\frac{1}{2}

,k)-

\frac{Δ t}{μ} [\partial_{x}^{+} E'_{y}^{n} (i, j + \frac{1}{2}, k) - \partial_{y}^{+} E'_{x}^{n} (i + \frac{1}{2}, j, k)]

。

在三维情况下,时间步长应该满足Courant-Friedrichs-Lewy (CFL) 稳定性条件^[29]:

(19)Δt'≤

\frac{1}{c'_{m a x} \sqrt{\frac{1}{Δ x^{2}} + \frac{1}{Δ y^{2}} + \frac{1}{Δ z^{2}}}}

式中:c'_max= $\sqrt{\frac{2 ω_{0}}{μ σ_{m i n}}}$ 为虚拟波的最大波速;ω₀=2πf₀,为比例伸缩系数;f₀可根据模拟的实际情况取值,在本文的研究中f₀取1。从最大虚拟波的波速c'_max的求取公式可以看出,当最小电导率σ_min一定时,虚拟波的最大波速由ω₀决定,因此,可以通过改变ω₀来改变虚拟波的波速,进而改变虚拟的时间步长Δt'。

2.2 源的加载

在虚拟波场数值模拟时,需要加入发射源。源的加载上主要有两种方式,一种是利用解析解求取初始时刻均匀半空间的电场或者磁场值,代入到有限差分的迭代公式中进行计算,避免了源的直接加载,但这种方法需要经过复杂初始场的计算^[30]。第二种方法是加入一定带宽的高斯脉冲函数,如Ricker波、余弦函数、阶跃函数等,这种方法在源的加载上简单实用^[29]。本文采用第二种源加载方法。以高斯脉冲函数的一阶导数作为虚拟发射源的源函数:

(20)J(t')=-2β(t'-t₀)

\sqrt{\frac{β}{π}} e^{- β (t' - t_{0})^{2}}

式中:β=π $f_{m a x}^{2}$ ;t₀= $\frac{π}{f_{m a x}}$ ;f_max为虚拟波场中电磁波最大频率;t'为虚拟的时间变量;ω₀=2πf₀,为伸缩比例系数;f₀=1。

2.3 边界的处理

2.3.1 吸收边界的加载

在时域电磁法数值模拟中,边界的反射对数值模拟带来影响,为提高计算的准确性,需要对边界进行处理。虚拟电磁波具有低频、衰减较慢等特点,因此在边界条件的处理上采用复频率完全匹配层边界条件(CFS-PML)^[31],CFS-PML是在PML吸收边界的基础上,通过加入伸缩性坐标以及复数频率移位张量系数,增强了对低频电磁波和晚期的电磁波的吸收,在电磁法的数值模拟中被广泛的应用^[22-23]。

虚拟波场中坐标伸缩因子定义为:

(21)

\bar{s}

'_i=

k_{i}^{- 1}

\frac{σ_{i}}{k_{i}^{2} α_{i} + k_{i} σ_{i} + j ω' (ε' k_{i}^{2})}

式中:a_i>0,σ_i>0,k_i≥1。

使用拉普拉斯变换,将 $\bar{s}$ '_i转换为一个脉冲响应。

(22)

\{\begin{array}{l} \bar{s}'_{i} (t') = \frac{δ' (t')}{k_{i}} - \frac{σ_{i}}{ε'_{i}} e^{- \frac{α_{i}}{ε'_{i}} t'}, \\ u' (t') = \frac{δ' (t')}{k_{i}} + ζ'_{i} (t') 。 \end{array}

式中:u $(t')$ 和δ $(t')$ 分别为虚拟波场中的单位阶跃函数和单位脉冲函数。将式(22)代入式(21)中,经过变换可得时间域的虚拟坐标伸缩方程:

(23)ε'

\frac{\partial E'_{x} (t')}{\partial (t')}

+σE'_x

(t')

\bar{s}

'_y

(t')

×∂_yH'_z

(t')

\bar{s}

'_z

(t')

×∂_zH'_y

(t')

则虚拟波场中电场分量E'_x的离散形式为:

(24)ε'

\frac{E'_{x}^{n + 1} (I, j, k) - E'_{x}^{n} (I, j, k)}{Δ t'}

+σ

\frac{E'_{x}^{n + 1} (I, j, k) - E'_{x}^{n} (I, j, k)}{2}

\frac{H {'_{z}}^{n + 1 / 2} (I, J, k) - H {'_{z}}^{n + 1 / 2} (I, J - 1, k)}{k_{y} Δ_{y}}

\frac{H {'_{y}}^{n + 1 / 2} (I, j, K) - H'_{y} (I, j, K - 1)}{k_{z} Δ_{z}}

+ψ

'_{e_{x y}}

ⁿ⁺¹^/²(i,j,k)-ψ

'_{e_{x z}}

ⁿ⁺¹^/²(i,j,k),

式中:ψ $'_{e_{x y}}$ ⁿ⁺¹^/²(i,j,k)和ψ $'_{e_{x z}}$ ⁿ⁺¹^/²(i,j,k)为

(25)ψ

'_{e_{x y}}

ⁿ⁺¹^/²(i,j,k)=b_yψ

'_{e_{x y}}

ⁿ^-1^/²(i,j,k)+a_y

[\frac{H {'_{z}}^{n + 1 / 2} (I, J, k) - H {'_{z}}^{n + 1 / 2} (I, J - 1, k)}{Δ_{y}}]

(26)ψ

'_{e_{x z}}

ⁿ⁺¹^/²(i,j,k)=b_zψ

'_{e_{x z}}

ⁿ^-1^/²(i,j,k)+a_z

[\frac{H {'_{y}}^{n + 1 / 2} (I, j, K) - H {'_{y}}^{n + 1 / 2} (I, j, K - 1)}{Δ_{z}}]

式中:b_i= $e^{- (\frac{σ_{i}}{k_{i}} + α_{i}) \frac{Δ t'}{ε'}}$ 。

最后,将式(26)、(25)代入式(24)中可得:

(27)E'_xⁿ⁺¹(I,j,k)=E'_xⁿ(I,j,k)+Δt'

\frac{2 ω_{0}}{σ} [\partial_{y}^{-} H {'_{z}}^{n + 1 / 2} (I, J, k) - \partial_{z}^{-} H {'_{y}}^{n + 1 / 2} (I, j, K)]

+Δt'

\frac{2 ω_{0}}{σ} [ψ {'_{e_{x y}}}^{n + 1 / 2} (i, j, k) - ψ {'_{e_{x z}}}^{n + 1 / 2} (i, j, k)]

。

其他分量可依次类推得到。

2.3.2 地—空边界的处理

空气层的处理是时域电磁法数值模拟中需要着重考虑的问题,传统的方法是向上延拓,但是这种方法比较复杂,有自身的局限性等^[32-33]。 Hördt等^[34]、Commer等^[32,35]和Hu等^[36]在处理地—空边界时,将空气层作为有限高阻体直接加载在计算域中,取得了比较好的效果。该方法的关键在于空气电阻率的取值,如果空气层的电阻率设置过大,为了满足时域有限差分迭代计算的稳定性,迭代时间步长将会非常小,导致迭代次数的增多,计算将非常耗时,因此,需要在保证计算准确性情况下适当的减小空气层的电阻率,以提高计算效率。在时间域电磁法中,地—空的电导率比值范围一般设置为100:1到1 000:1。本文在进行数值模拟时,将地—空的电导率比值提高到1 000:1到10 000:1,保证了计算的准确性和计算效率。

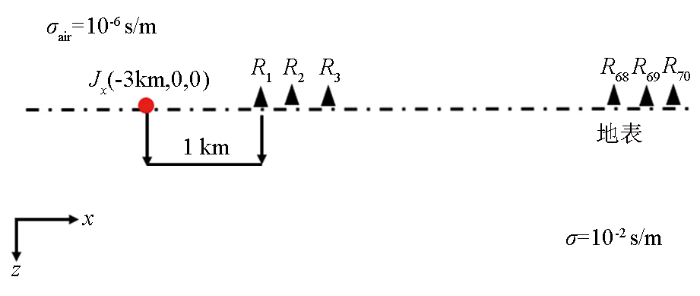
为了验证算法的可靠性和正确性,设均匀半空间模型如图2所示,模型计算区域为:10 km×10 km×10 km采用100 m×100 m×100 m的离散网格,沿x方向布置电偶极子源,场源坐标为(-3 km,0 km,0 km),源函数为式(20)。沿着x方向,距离源1 000 m处每隔100 m布置一个测点,一共布置了70个测点。大地的电导率为0.01 s/m,模型中空气层的电导率设置为10^-6 s/m (解析解空气层电导率设置为10^-10 s/m)。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 均匀半空间模型示意

Fig.2 Schematic diagram of a uniform half space model

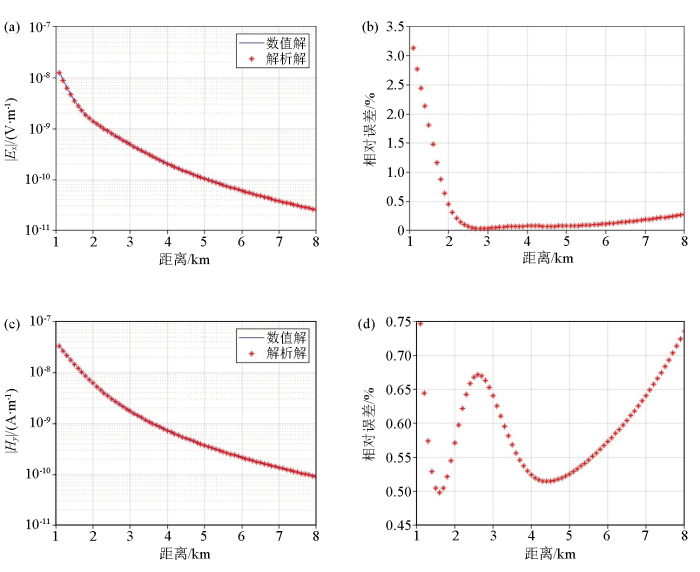
利用虚拟波场法及解析法分别计算电磁场分量,其结果如图3所示。从图3中可以看到当频率为100 Hz时,电场分量E_x的最大误差在3%左右;由于受源奇异性的影响,离源较近的测点误差比较大。磁场分量H_y的最大误差为0.75%左右。电场分量E_x和磁场分量H_y数值解和解析解的相对误差满足计算精度要求。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 均匀半空间中频率为100 Hz的电场分量E_x(a)和磁场分量H_y(c)的响应及相对误差(b、d)

Fig.3 Response and relative error plots of the electric field component E_x(a、b) and magnetic field component H_y(c、d) with a frequency of 100 Hz in a uniform half space

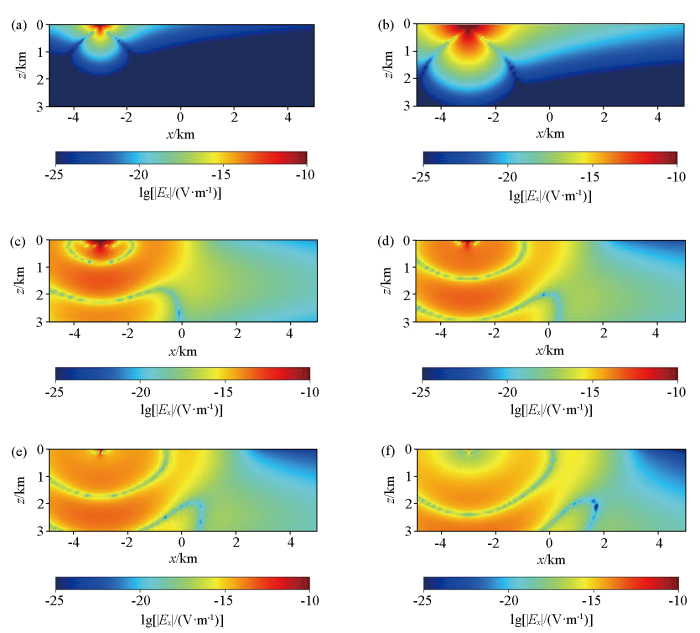
图4为不同时刻电场分量E'_x的虚拟波场快照,从图中可以看出,在整个虚拟电磁波传播过程中,在区域的边界处,CFS-PML使得电场幅值始终保持在比较小的值,对到达边界的虚拟电磁波进行了有效的吸收。图3和图4表明虚拟波场算法的正确性及空气层加载和边界条件处理在计算中的有效性。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 均匀半空间中不同时刻虚拟电场分量E'_x的xz面波场快照

Fig.4 xz surface wave field snapshot of fictitious electric field component E'_x at different times in a uniform half space

a—t=0.12 s;b—t=0.16 s;c—t=0.25 s;d—t=0.27 s;e—t=0.28 s;f—t=0.30 s

3 数值算例

3.1 均匀半空间中的低阻异常体

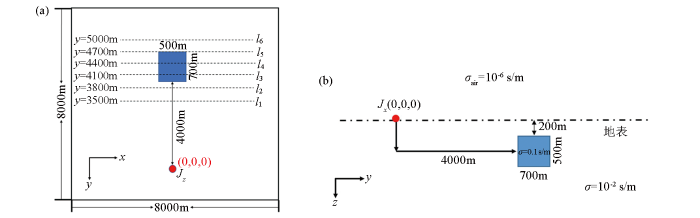
模型的区域为:8 km×8 km×5 km,进行均匀网格剖分,网格大小为100 m×100 m×100 m。发射源为沿x方向的电偶极子源,并设源的中心坐标为(0 m,0 m,0 m)。低阻异常体的大小为:700 m×500 m×500 m,异常体中心坐标为(0 m,4 350 m,450 m),虚拟波场中最大传输频率f_max为5 Hz,均匀半空间介质的电导率为0.01 s/m,低阻异常体的电导率为0.1 s/m,空气层电导率为1×10^-6 s/m。平行于场源方向布置6条4 km的观测线,测线的中心坐标为(0 m,3 500 m,0 m)、(0 m,3 800 m,0 m)、(0 m,4 100 m,0 m)、(0 m,4 400 m,0 m)、(0 m,4 700 m,0 m)、(0 m,5 000 m,0 m),测点之间的距离为100 m,如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 均匀半空间中低阻三维异常体模型示意

a—xy平面断面;b—yz平面断面

Fig.5 Schematic of low resistance 3D anomalous body model in uniform half space

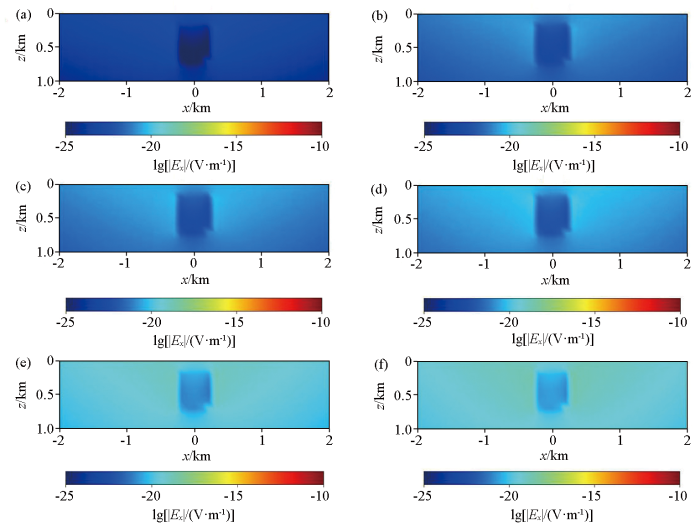
图6给出了y=4.4 km 剖面虚拟波场快照切片,从图中可以看出,当虚拟的电磁波到达异常体处时,由于低阻对电磁波的吸收作用,使得在其区域存在一个低值区,异常区的大小、埋深和模型中异常体的大小、埋深一致,通过不同时刻的波场快照切片可以看到虚拟电磁波在低阻异常体处的变化过程。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 低阻异常体不同时刻虚拟电场分量E'_x的xz面波场快照

Fig.6 xz surface wave field of fictitious electric field component E'_x at different times with one low resistance anomalous body

a—t=0.38 s;b—t=0.43 s;c—t=0.44 s;d—t=0.45 s;e—t=0.49 s;f—t=0.50 s

从图7和图8可以看出,16 Hz和64 Hz电场分量E_x等值线向场源方向弯曲,在异常体正上方弯曲的幅度最大,越靠近场源方向电场的幅值越大。随着频率的变大,电场等值线的幅值逐渐变小,并在异常体的上方变化明显。视电阻率等值曲线存在一个较为集中的低阻异常区,异常区的范围与异常体的位置相对应。可以看到利用虚拟波场计算的电场的场值及电阻率可以有效地反映介质的电性变化。通过计算,模型中16 Hz的趋肤深度约为1 200 m,对于4 km的收发距来说,观测点处于频率观测的近区或过渡区,但虚拟波场计算的卡尼亚电阻率并没有表现出场源效应的影响。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 低阻异常体16 Hz电场分量E_x和视电阻率等值线

a—视电阻率等值线;b—电场分量E_x等值线

Fig.7 Contour map of electric field component E_x and apparent resistivity of 16 Hz with one low resistance anomalous body

a—apparent resistivity contour line;b—electric field component E_x contour line

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 低阻异常体64 Hz电场分量E_x和视电阻率等值线

a—视电阻率等值线;b—电场分量E_x等值线

Fig.8 Contour map of electric field component E_x and apparent resistivity of 64 Hz with one low resistance anomalous body

a—apparent resistivity contour line;b—electric field component E_x contour line

3.2 均匀半空间包含低阻和高阻两个异常体

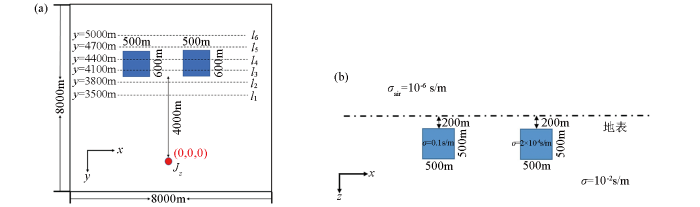
设均匀半空间含1个高阻和1个低阻异常体模型,高阻异常体的电导率为2×10^-4 s/m,低阻异常体的电导率为0.1 s/m,其他参数和均匀半空间低阻异常体模型中的一致,如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 均匀半空间含低阻和高阻三维异常体模型示意

a—xy平面断面;b—xz平面断面

Fig.9 Schematic of a 3D anomalous body model with one low resistance and one high resistance in a uniform half space

a—xy plane cross-section;b—xz plane cross-section

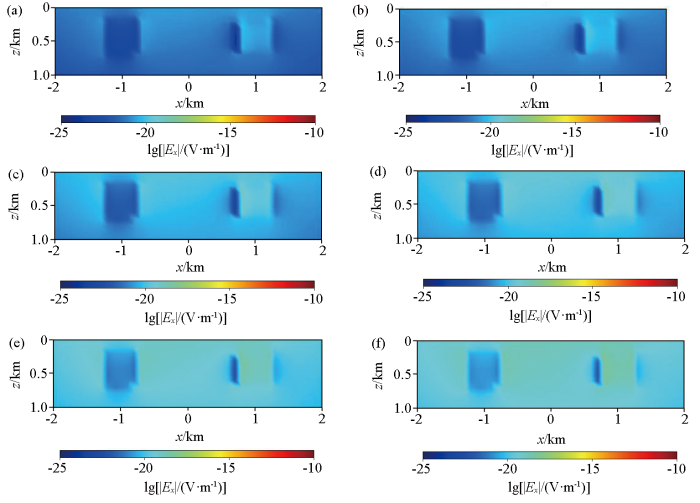
图10 给出了y=4.4 km不同时刻的虚拟波场快照切片,从图中可以看出,当虚拟电磁波到达异常体处时,由于低阻对电磁波的吸收较大,高阻对电磁波的吸收较小,在两个异常体区域形成明显电磁场异常区,异常区的大小、埋深和模型中异常体的大小、埋深基本一致。从不同时刻的波场快照中可以观察到虚拟电磁波在低阻异常体处和高阻异常体处的变化过程,低阻异常体的上下界面要比高阻异常体的清晰,说明在虚拟波动场中对低阻异常体的敏感度要优于高阻异常体。高阻异常体的左右边界比上下边界清晰。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 含低阻和高阻两个异常体不同时刻虚拟电场分量E'_x的xz面波场快照

Fig.10 xz surface wave field snapshot of fictitious electric field component E'_x at different times with one low resistance and one high resistance anomalous body

a—t=0.43 s;b—t=0.44 s;c—t=0.46 s;d—t=0.47 s;e—t=0.49 s;f—t=0.50 s

相比于扩散场,在虚拟波场中可以动态的观察到虚拟电磁波在地下随着时间的变化过程,特别是在异常体处的变化过程。由于异常体在波动过程产生的体积效应要比扩散过程小很多,在识别异常体上相比于扩散频率域更加清晰,能够大致地看到异常体的轮廓。

从图11和图12可以看出,16 Hz和64 Hz的视电阻率等值线中明显的发现一个较为集中的低阻异常区和一个较为集中的高阻异常区,异常区的曲线圈闭,异常区的范围与异常体的位置相对应;高阻异常区域的电场分量E_x的等值线向场源方向弯曲,低阻异常区域电场分量E_x的等值线向场源反方向弯曲,越靠近场源方向电场的幅值越大。随着频率的增高,电场等值线幅值逐渐变弱,并在异常体正上方变化明显。另外,从电场和视电阻率等值线图中可以明显看出,低阻异常体的等值线要比高阻异常体的等值线要密,表明对低阻体反应更灵敏。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 含低阻和高阻两个异常体16 Hz电场分量E_x和视电阻率等值线

a—视电阻率等值线;b—电场分量E_x等值线

Fig.11 Contour map of electric field component E_x and apparent resistivity of 16 Hz with one low resistance and one high resistance anomalous body

a—apparent resistivity contour line;b—electric field component E_x contour line

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 含低阻和高阻两个异常体64 Hz电场分量E_x和视电阻率等值线

a—视电阻率等值线;b—电场分量E_x等值线

Fig.12 Contour map of electric field component E_x and apparent resistivity of 64 Hz with one low resistance and one high resistance anomalous body

a—apparent resistivity contour line;b—electric field component E_x contour line

4 结论

将扩散场的电磁方程转换成虚拟域的波动方程,在虚拟域求解波动方程后利用积分变换转换到频率扩散场,实现了一次正演就可以同时计算多个频点的三维电磁场数值模拟方法,为可控源电磁法的快速数值模拟提供了新的思路。

导出了针对可控源电磁法的虚拟波场变换方法,利用显式有限差分法求解,采用复频率完全匹配层(简称CFS-PML)吸收边界,对边界进行了有效的截断,提高了计算的效率,通过与频率域解析解对比,验证了方法的正确性。

通过虚拟波场变换方法计算了多个模型的电磁响应,有效地反映了介质的电性变化,电性源的可控源电磁法对低阻异常体的敏感要优于高阻异常体;相比于扩散场,在虚拟波动场中能够观察到电磁波在地下介质传播的变化过程,这对根据虚拟电磁波的传播特性、研究分析一些实际问题是有意义的。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

吴璐苹, 李荫槐.

可控源音频大地电磁法在地下水勘查中的应用研究

[J]. 地球物理学报, 1996, 39(5):712-717.