电性源瞬变电磁法虚拟波场解析推导

doi:10.11720/wtyht.2024.1188

电性源瞬变电磁法虚拟波场解析推导

李海^,¹^,², 赵攀³, 李柯颖¹^,²^,⁴, 刘峥⁵

1.中国科学院地质与地球物理研究所中国科学院矿产资源研究重点实验室,北京 100029

2.中国科学院地球科学研究院,北京 100029

3.中国人民大学附属中学朝阳学校,北京 100028

4.中国科学院大学地球与行星科学学院,北京 100049

5.河北省地球物理勘查院,河北廊坊 065000

Deriving analytical solution of the pseudo wavefield from transient electromagnetic data

LI Hai^,¹^,², ZHAO Pan³, LI Ke-Ying¹^,²^,⁴, LIU Zheng⁵

1. Key Laboratory of Mineral Resources, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China

2. Institutions of Earth Science, Chinese Academy of Sciences, Beijing 100029, China

3. RDFZ Chaoyang School, Beijing 100028, China

4. College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

5. Hebei Geophysical Exploration Institute, Hebei Shallow Geothermal Energy Research Center, Langfang 065000, China

第一作者: 李海(1988-),男,2016年博士毕业于中国科学院地质与地球物理研究所,主要从事电磁法理论与应用研究工作。Email:lihai@mail.iggcas.ac.cn

责任编辑: 沈效群

收稿日期: 2023-05-4 修回日期: 2023-12-19

基金资助:

国家自然科学基金项目(XDA043020341804074)

Received: 2023-05-4 Revised: 2023-12-19

摘要

瞬变电磁场至虚拟波场的转换是瞬变电磁拟地震处理的基础,瞬变电磁场满足扩散方程,而虚拟波场满足波动方程,二者之间通过Q变换相互转换。将瞬变电磁数据转换成虚拟波场属于积分反变换,具有典型的不适定特性,以往主要采用数值方法求解该积分反变换。在数值求解中,需对求解方法和参数进行优化,以获得最佳求解效果。为此,本文推导了电性源瞬变电磁法电场响应的虚拟波场解析解。从均匀半空间电磁场响应的解析解出发,借助于拉普拉斯变换对,得到了阶跃响应和脉冲响应的解析表达式,从而建立起瞬变电磁场和虚拟波场的解析变换对。该解析变换对能够用于测试数值求解方法的准确性和稳定性,还能用于检验虚拟波场特性,从而形成有效的虚拟波成像方法。

关键词： 瞬变电磁; 电性源; 虚拟波场; 解析解

Abstract

The transform from transient electromagnetic (TEM) field to pseudo wavefield is the basis for using the imaging technique. The TEM field follows the diffusion equation, while the pseudo wavefield follows the wave equation. These two can be transformed into each other via the Q-transform. As the integral transformation from TEM field to pseudo wavefield is ill-posed, numerical method is used to get the desired pseudo wavefield. As a result, it is often the case that the methods and parameters are need to be optimized to get a optimal pseudo wavefield. Therefore, here in this paper, we derived the analytical solution of the pseudo wavefield from the TEM field. We start from the analytical formula of TEM field, and utilize the Laplace transform to establish the analytical solution pairs. The pairs can be used to test the accuracy and stability of the numerical method, as well as examining the features of the pseudo wavefield to get an effective imaging method.

Keywords： transient electromagnetic method; electrical source; pseudo wavefield; analytical solution

PDF (1705KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李海, 赵攀, 李柯颖, 刘峥. 电性源瞬变电磁法虚拟波场解析推导[J]. 物探与化探, 2024, 48(5): 1193-1198 doi:10.11720/wtyht.2024.1188

LI Hai, ZHAO Pan, LI Ke-Ying, LIU Zheng. Deriving analytical solution of the pseudo wavefield from transient electromagnetic data[J]. Geophysical and Geochemical Exploration, 2024, 48(5): 1193-1198 doi:10.11720/wtyht.2024.1188

0 引言

在地震勘探中,弹性波在地下介质中以波动方式传播。通过分析地震波在地下的传播时间,可以有效地对地下介质的反射界面进行成像。电磁波在真空中同样以波动方式传播,但是在地下介质中低频电磁场(满足准静态近似时)是以扩散方式进行传播的,这种扩散传播方式使得电磁脉冲的不同频率成分传播距离不同,且电磁脉冲的波形也会随着扩散的进行而变换。因此,在低频电磁法探测中,一般不用旅行时对电磁响应进行解释,而是采用迭代反演的方式进行解释^[1⇓-3]。但是,这种解释方式的计算量巨大,尤其是在高维情形下。

实际上,弹性波传播满足的波动方程和电磁场满足的扩散方程是能够等效转换的。波动方程与扩散方程的相互变换式被称为Q变换,该数学变换由Bragg建立,Lee等^[4]利用该变换式进行时间域电磁法的正演模拟工作,将该变换式引入瞬变电磁法领域。根据Lee等的研究工作,满足扩散方程的地下介质电磁场与满足波动方程的“波场值”可以相互转换,该“波场值”被称为虚拟波场。该转换关系所定义的扩散电磁场与波动虚拟波场值除各自满足扩散方程和波动方程外,还具有类似的源条件和边界条件。

由于虚拟波场满足波动方程,因此可以借鉴地震勘探的成像技术进行虚拟子波的成像。在此之前,需要将瞬变电磁场转换为虚拟子波。由于转换过程的不适定性,国内学者就虚拟子波的提取开展了大量研究^{[5⇓⇓⇓⇓-10]}。这些方法均为数值方法,针对该积分方程的特性而设计,旨在解决求解精度和稳定性方面的问题^[11]。在获得虚拟波场后,可以进行瞬变电磁数据的拟地震成像研究^[12⇓-14],也可以根据虚拟波动场本身的传播特性研究对应的成像方法^[15]。在此过程中,虚拟波场的求解和传播特性研究是基础。

本文针对虚拟波场和瞬变电磁场之间的转换展开研究。不同于以往的数值求解方法,本文采用解析推导的方式获得虚拟波场和瞬变电磁场的解析变换对,得到的变换对能够为数值方法的验证提供数据基础,也能够给出虚拟波场特征分析中各个量的物理关系。

1 下降沿阶跃响应的虚拟波场解析推导

波动方程与扩散方程的相互变换式被称为Q变换,具有如下积分形式^[4]:

(1)E(t)=

\frac{1}{2 \sqrt{π t^{3}}} \int_{0}^{\infty}

e^{- q^{2} / 4 t}

U(q)dq,

式中:E为电磁场分量;U为虚拟波场分量,单位m/ $\sqrt{s}$ ;q为虚拟时间,单位 $\sqrt{s}$ 。

虚拟波场解析推导的主要目标为建立瞬变电磁场与虚拟波场在上述积分变换下的解析变换对。由于式(1)表示的Q变换为第一类Fredholm积分方程,无法直接对其进行反变换以求取均匀半空间下与电磁场响应对应的波场值的解析解,因此,我们回归到Q变换式的推导过程,对解析解进行求解。推导步骤概括为以下3步:①将场值进行拉普拉斯变换,得到拉普拉斯变换域的场值 $\hat{F}$ (s),其中s为复变量;②令s=p²,根据虚拟波场与扩散电磁场在拉普拉斯变换域(p域)的关系式,得到虚拟波场在拉普拉斯变换域的表达式;③对虚拟波形的拉普拉斯域表达式进行反拉普拉斯变换,得到虚拟波场。

考虑电性源瞬变电磁法的轴向电场分量。在均匀半空间模型下,单位偶极源激发的轴向瞬变电磁的水平电场具有如下解析表达式^[16]:

(2)E(c,r,t)=

\frac{1}{2 π r^{3}} [e r f (\frac{r}{2 c \sqrt{t}}) - \frac{2}{\sqrt{π}} \frac{r}{2 c \sqrt{t}} e x p (- \frac{r^{2}}{4 c^{2} t})]

式中:r为源点与接收点之间的偏移距;t为源关断后的时间;erf为误差函数;变量c²=ρ/μ,其中,ρ为电阻率,μ=4π×10^-7 H/m,为真空中的磁导率。令

(3)F₁(t)=erf(

\frac{r}{2 c \sqrt{t}}

F₂(t)=

\frac{2}{\sqrt{π}} \frac{r}{2 c \sqrt{t}}

exp

(- \frac{r^{2}}{c^{2} 4 t})

则式(2)可以表示为:

(4)E(c,r,t)=

\frac{1}{2 π r^{3}} [F_{1} (t) - F_{2} (t)]

。

对F₁(t)关于时间t进行拉普拉斯变换,可得到 ${\hat{F}}_{1}$ (s):

(5)

{\hat{F}}_{1}

(s)=

\frac{1}{s} [1 - e x p (- \frac{r}{c} \sqrt{s})]

。

根据虚拟波场与扩散电磁场在拉普拉斯变换域的关系式 $\hat{U}$ (r,p)= $\hat{F}$ (r,p²)^[17],可得到与F₁(t)所对应的虚拟波场的拉普拉斯变换:

(6)

{\hat{U}}_{1}

(p)=

{\hat{F}}_{1}

(p²)=

\frac{1}{p^{2}} [1 - e x p (- \frac{r}{c} p)]

。

根据拉普拉斯变换恒等式

(7)

\{\begin{array}{l} L_{p \to q}^{- 1} [\frac{1}{p} (1 - e^{- a p})] = \{\begin{array}{l} 1 (0 < q < a) \\ 0 (q > a) \end{array} = Η (a - q), \\ L_{p \to q}^{- 1} [\frac{1}{p} \hat{u} (p)] = \int_{0}^{q} u (v) d v, \end{array}

式中H表示Heaviside函数。令a=r/c,对式(6)进行拉普拉斯反变换,可以得到

(8)U₁(q)=

[\frac{1}{p^{2}} 1 - e^{- a p}]

\int_{0}^{q}

(\frac{r}{c} - v)

dv=qΗ

(\frac{r}{c} - q)

\frac{r}{c}

(q - \frac{r}{c})

q>0 。

对式(4)中的F₂(t)进行同样处理,可以得到

(9)U₂

(q)

L_{p \to q}^{- 1} [{\hat{U}}_{2} (p)]

L_{p \to q}^{- 1} [\frac{r}{c p} e x p (- \frac{r}{c} p)]

\frac{r}{c}

(q - \frac{r}{c})

q>0 。

将式(8)和式(9)结合并化简,即可得到与式(2)所表示的均匀半空间下轴向电场解析式所对应的虚拟波场的解析表达式:

(10)U

(r, q)

\frac{ρ q}{2 π r^{3}}

(\frac{r}{c} - q)

。

式(10)表明,虚拟子波在q=r/c处存在极值点,源与接收之间的距离越远,虚拟子波极值点在虚拟时间轴上越晚。这个现象与电磁场随时间扩散是一致的,证实了虚拟时间仍然具备时间的度量。此外,虚拟波场的幅值与偏移距r成反比,也与电磁场的扩散衰减一致,而不同于常规纯波动场。

2 脉冲响应的虚拟波场解析推导

脉冲响应是单位脉冲源激发所产生的瞬变电磁场响应。基于脉冲响应和卷积技术,可以得到任意波形的瞬变电磁场响应。为此,本文对脉冲响应的虚拟波场解析解进行了推导。由于源波形的对应关系,对阶跃轴向电场响应进行求导并乘以-1,可得到脉冲响应。由式(1)可知,Q变换是非线性的,因此,大地脉冲响应的虚拟波场的解析解不能通过对式(10)直接求导获得。下面为大地脉冲响应的解析解的推导过程。

单位偶极源在均匀半空间下,其轴向电场具有如下解析表达式^[18]:

(11)g(ρ,r,t)=

\frac{ρ}{8 π \sqrt{π} c^{3}}

exp

(\frac{- r^{2}}{c^{2} 4 t})

t^-5^/² 。

根据以下拉普拉斯变换对

(12)

\{\begin{array}{l} L [t^{- 3 / 2} e x p (- \frac{a^{2}}{4 t})] = \frac{2}{a} \sqrt{π} e x p (- a \sqrt{s}), \\ L [(\frac{a^{2}}{4} - \frac{t}{2}) t^{- 5 / 2} e x p (- \frac{a^{2}}{4 t})] = \sqrt{s} \sqrt{π} e x p (- a \sqrt{s}), \end{array}

令a=c/r,并将式(12)所示拉普拉斯变换对应用于式(11),得到大地脉冲响应的拉普拉斯变换:

(13)

\hat{F} (s)

\frac{ρ}{2 π r^{3}} (\frac{r}{c} \sqrt{s} + 1)

exp

(- \frac{r}{c} \sqrt{s})

。

类似地,得到虚拟波场的拉普拉斯变换:

(14)

{\hat{U}}_{1}

(p)=

\hat{F}

(p²)=

\frac{ρ}{2 π r^{3}} (\frac{r}{c} p + 1)

exp

(- \frac{r}{c} p)

。

对式(14)进行反拉普拉斯变换,得到

(15)U

(r, q)

\frac{ρ}{2 π r^{3}} [\frac{r}{c} δ' (q - \frac{r}{c})

δ (q - \frac{r}{c})]

\frac{r}{c}

>0。

式中:δ为delta函数;δ'为delta函数的导数。由式(15)的结果可知,与大地脉冲响应对应的虚拟波场的连续性极差,因此在进行数值求解时极不稳定。

3 虚拟波场的数值求解分析

前面推导了均匀半空间下电磁场响应波场变换得到的虚拟子波的解析表达式。在更复杂的介质下,比如层状介质和高维模型下,需采用数值方法求解虚拟子波。本文所推导的解析变换对,能够验证瞬变电磁到虚拟子波变换方法的准确性和稳定性。为此,基于阶跃响应的虚拟变换对,对虚拟波场的数值求解方法开展了分析。

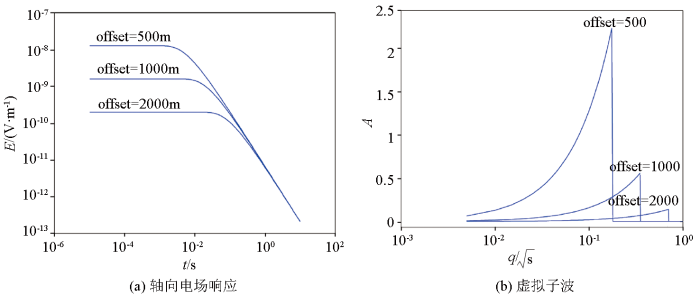
图1给出了电阻率为10 Ω·m的均匀半空间在偏移距为1 000 m时,计算出的轴向电场响应和虚拟子波。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 10 Ω·m均匀半空间1 000 m偏移距下电偶极源激发的电场及对应的虚拟子波

Fig.1 Analytical solution of the electrical field and the pseudo wavefield for 10 Ω·m half space with an offset of 1 000 m

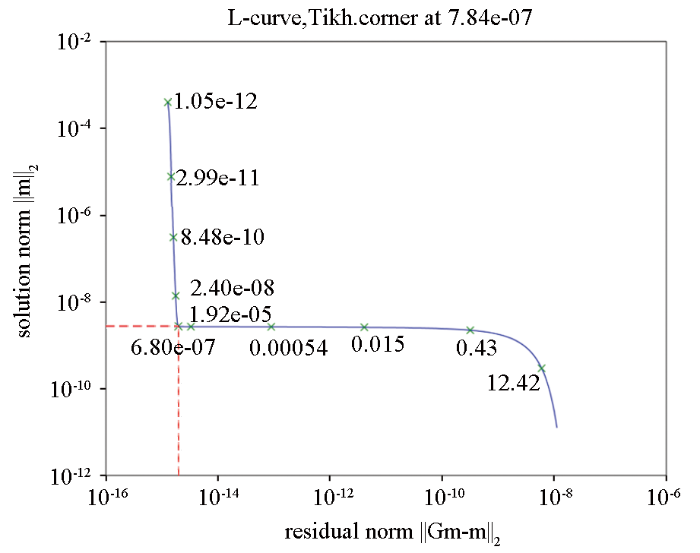
基于式(1)从瞬变电磁场数值求解虚拟波场是典型的不适定反问题,需要采用正则化方法求解,此处考虑Tikhonov正则化、TSVD(Truncated SVD,截断奇异值分解)和DSVD(Damped SVD,阻尼奇异值分解)三种方法。为了确定正则化参数的取值,采用L曲线法。在Tikhonov正则化方法中,采用二范数形式的正则化项。图2给出了Tikhonov正则化方法得到的L曲线,即模型向量的二范数随残差的二范数的变化。L曲线的转折点处正则化因子为7.84×10^-7,此时残差的二范数为1.98×10^-15,模型的二范数为2.73×10^-9。通过L曲线分析,认为正则化参数选择该值时,能够获得解的正则化项和残差的二范数之间的最佳平衡。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 Tikhonov正则化L曲线示意

Fig.2 Schematic of L-curve in Tikhonov regularization

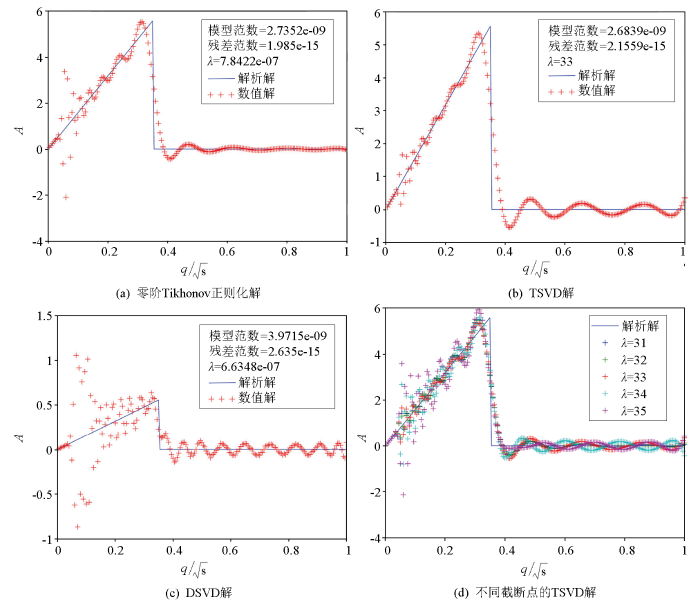
图3a~c给出了引入模型二范数作为正则化项,分别采用零阶Tikhonov正则化、TSVD和DSVD的求解结果,纵坐标A表示振幅。对于Tikhonov正则化和DSVD,正则化因子由L曲线获得,对于TSVD,其截断点的位置由L曲线获得;图中均以λ标识正则化因子。图3a中零阶Tikhonov正则化求解结果的晚期稳定,但是早期偏离真实值较大;图3c中DSVD求解结果在早期和晚期均不稳定;图3b中TSVD求解结果的稳定性要优于另外两种方法,由于奇异值的截断,早期解的不稳定性得到了压制,但是解的晚期出现了轻微振荡。为此,计算了由L曲线获得的最佳正则化参数附近的TSVD解,将其绘制于图3d中。计算结果显示:随着截断点后延,考虑的奇异值增多,所得到的TSVD解早期的稳定性降低,但所获得的虚拟子波的幅值更接近于真实值;相反,随着截断点提前,考虑的奇异值减小,得到的TSVD解的总体稳定性增加。总体而言,采用模型二范数作为正则化项时,所得到的正则化解早期的稳定性较差。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 采用模型二范数作为正则化项的求解结果

Fig.3 Solutions obtained from different regularizing method using L2-norm

4 结论及讨论

将瞬变电磁响应转换成虚拟波场,是瞬变电磁数据拟地震解释的基础。由于该转换是典型的具有病态特征的积分反变换,以往研究主要采用数值方法求解虚拟波场。数值求解时需要考虑稳定性和准确性,瞬变电磁场和虚拟波场的解析变换对能够为数值方法的验证提供数据基础。此外,虚拟波场的解析式具有更直观的物理意义,能够为虚拟波场成像方法的研究提供基础。

本文从Q变换的积分表达式和均匀半空间瞬变电磁响应的解析表达式出发,推导了电性源轴向电场响应的虚拟波场解析表达式,包括电场阶跃响应和脉冲响应的虚拟波场解析解。阶跃响应具有比较好的连续性,而脉冲响应包含脉冲函数及其导数,连续性较差,在数值求解时难以保证其稳定性。因此,阶跃响应能够作为虚拟波场验证和分析的基础。

基于电磁场响应与虚拟波场的解析变换对,对求解虚拟波场的正则化方法进行了对比性研究,分析了Tikhonov正则化、TSVD、DSVD等方法在求解虚拟子波时的准确性和正则化参数的选取问题。结果表明:三种方法中TSVD的准确性更高,尤其对于虚拟波场的早期响应。当选择不同的正则化参数时,由于积分反变换的不适定性,虚拟波场的准确度和稳定性相互制约。在进行虚拟波场求解时,应根据研究目标确定二者之间的平衡。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李海, 薛国强, 钟华森, 等.

多道瞬变电磁法共中心点道集数据联合反演

[J]. 地球物理学报, 2016, 59(12):4439-4447.

DOI:10.6038/cjg20161206 [本文引用: 1]

多道瞬变电磁法是目前地面资源勘查领域的研究热点，开展该方法观测数据的一维反演对完成装备研发及技术推广具有积极的推动作用.针对多道瞬变电磁法特殊的源波形和数据采集方式，本文对多道瞬变电磁数据的响应提取和一维反演进行了研究.首先，采用反卷积方法从伪随机二进制序列全波形响应数据中提取大地脉冲响应.为了避免脉冲响应中空气波的干扰，提出采用反向积分算法，把脉冲响应转换成下降沿阶跃响应，并将其整理成共中点道集.最后，为充分利用各个偏移距下的响应数据对不同深度范围目标体的分辨能力，采用基于OCCAM算法的联合反演方法对共中心点道集数据进行联合反演.结果表明在不同目标体深度以及有噪声干扰的情况下，共中心点道集数据联合反演计算均可获得较好的结果.

, Xue

G Q

, Zhong

H S

, et al.

Joint inversion of CMP gathers of multi-channel transient electromagnetic data

[J]. Chinese Journal of Geophysics, 2016, 59(12):4439-4447.