0 引言
在油气地震勘探中,面波及其泄漏模式的P—导波通常被认为是噪声被滤除掉,但也可以作为地震记录中的有用信号,用于反演近地表速度,解决各种实际的地球物理问题[1 ] 。通过正演模拟可以直观地展现面波和P—导波的传播规律,为反演和去噪研究奠定基础,也有助于更好地指导工程实践和提高勘探解释精度[2 ⇓ -4 ] 。
Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一。Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律。Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中。Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟。Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高。Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用。董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法。Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层。张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征。廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率。彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性。
P—导波与面波都属于近地表捕获波,这两种波都携带了无法从反射波和折射波中获得的近地表重要信息。
Pekeris[18 ] 在水声学的研究中发现声波也存在频散现象,他把这种频散波称之为P—导波,P—导波对于海洋中声波速度的研究有着重要意义。Robertsson等[19 ] 发现震源产生的大部分弹性能量可能被困在波导中,并以很小的损失长距离传播,这就是导波。Sheriff等[20 ] 研究发现导波常见的特征是高振幅和叠瓦状。Roth等[21 ] 认为自由表面和第一个主要地震不连续面之间的地层可以被视为一个有效的层状波导。为了区分面波和导波,Herman等[22 ] 也将导波称为面波到达前的频散波,在这种情况下,导波不包括面波。为了便于讨论,本文将P—导波和面波视为两种不同类型的频散波。Carcione等[23 ] 认为在固液耦合情况下的P—导波频散曲线和漏能振型理论上是一致的。Klein等[24 ] 在实际应用中通过海洋拖缆提取出的P—导波频散曲线有效地反演出海底P波速度。Ernst[25 ] 证明在反射地震学中,导波比初至波能更好地确定长波长近地表速度。
无论在理论研究还是实际应用中,P—导波的涉及都比面波要少一些,主要原因可能在于其频散曲线的复杂性[3 ,26 -27 ] 。此外,目前对同一震源下面波和导波产生机制和传播规律的研究和认识也不够充分和深入。本文基于高阶交错网格弹性波波动方程有限差分数值模拟的方法,有效地正演模拟出地震面波和P—导波波场。设计不同速度和厚度模型进行比较,从波场记录、频散成像等方面分析阐述了面波和P—导波的激发和传播规律。
1 基本原理
1.1 弹性波波动方程有限差分数值解法
根据弹性波动理论,已知在二维TI介质中,一阶速度—应力弹性波波动方程(假设体力为零)可以表示为[28 ] :
(1) ρ ∂ v x ∂ t = ∂ σ x x ∂ x + ∂ τ x z ∂ z , ρ ∂ v z ∂ t = ∂ τ z x ∂ x + ∂ σ z z ∂ z , ∂ σ x x ∂ t = ( λ + 2 μ ) ∂ v x ∂ x + λ ∂ v z ∂ z , ∂ σ z z ∂ t = λ ∂ v x ∂ x + ( λ + 2 μ ) ∂ v z ∂ z , ∂ τ x z ∂ t = μ ( ∂ v x ∂ z + ∂ v z ∂ x ) 。
式中:ρ λ 、 μ σ i i τ i j i , j = x , z v x 、 v z x 、 z
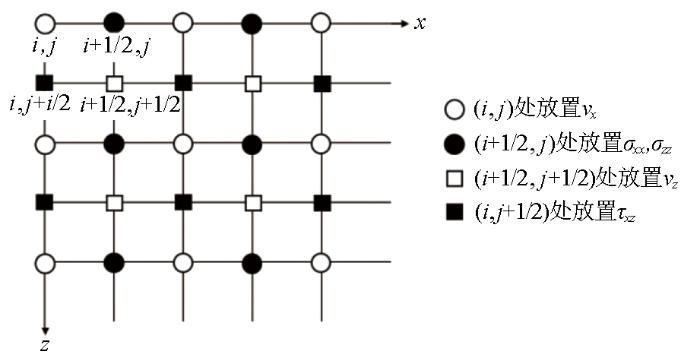
本文将一阶速度—应力波动方程中的应力分量和速度分量分别定义在两套相互交叉错动的网格系统上,各变量在空间的布置如图1 (对应的交错网格有限差分计算公式见附录A)所示。
图1
图1
交错网格差分示意
Fig.1
Diagram of stagger-grid difference
1.2 震源函数
在波动方程有限差分正演模拟过程中,使用的震源激发方式不同得到的波场也不同。本文选用具有频带宽、延续时间短、垂直分辨率高等优点的Ricker子波作为激发震源子波,其数学表达式如式(2)所示:
(2) w (t) = 1 - 2 π f m ( t - t 0 ) 2 e - π f m ( t - t 0 ) 2
本文采用垂向集中力源,把震源放置在自由表面的某个网格节点处,通过将式(2)Ricker子波函数加载在该网格节点处的垂直速度分量上,在时间为零的时刻激发,从而实现用数值计算的方式模拟波的传播。由于垂直集中力源的方向效益,震源附近介质受力不等,产生的P波和S波的能量相当,且两种波的振幅具有很强的方向性。
1.3 吸收边界条件
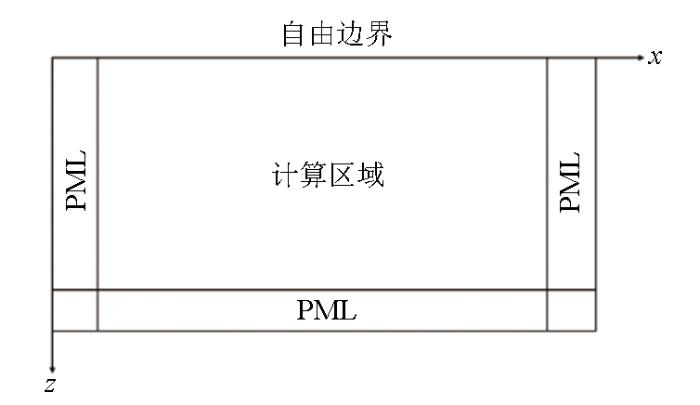
在使用波动方程有限差分法模拟地震波传播时,计算区域的有限性会导致计算区域边界处产生虚假反射,干扰正常波场的分析研究,所以必须设置合理的吸收边界条件对虚假反射进行吸收处理。本文选用吸收效果好、易实现、普遍使用的分裂式完全匹配层法(PML),在计算区域的左、右、下3处扩边设置吸收层(图2 )。该方法首先将质点处的速度分量和应力分量沿坐标轴分裂成垂直方向分量和水平方向分量两部分[29 ] ,然后利用前文介绍的交错网格差分离散化思路,推导出分裂式PML吸收边界条件差分方程[14 ] (见附录B)。吸收层内衰减因子设置方式为:
(3) d ( x ) = 3 v m a x 2 L l o g ( 1 R ) P x L 2 , d ( z ) = 3 v m a x 2 L l o g ( 1 R ) P z L 2 ,
图2
图2
模型设置示意
Fig.2
Diagram of model setting
式中: d x d z x z v m a x R 为理想边界反射系数(一般取0.001) ;P x 、 P z L 为吸收层厚度,本文设置为20 m,在吸收层内地震波按传播距离的指数规律衰减,不产生反射。
1.4 自由边界条件
在地震勘探中,导波由近地表多次反射产生[3 ] 。当相速度低于高速半空间横波速度时,导波的纵波分量和横波分量在波导结构中经过多次反射形成Rayleigh面波或Love面波。其中,Rayleigh 面波是由P波和SV波进行叠加干涉而成的,而Love面波则是由SH波构成。当相速度高于高速半空间横波速度且小于其纵波速度时,导波的横波分量会泄露到高速半空间中,剩余的由纵波分量主导的导波即为P—导波[26 ,30 ] 。
地球的自由表面和近地表下方高速层的顶界面之间可视为一种有效的层状波导[19 ] ,为了真实地模拟出面波和P—导波的波动现象,必须设置合理的自由地表边界条件。在水平自由表面上,应力分量必须满足如下条件:τ x z ( x , 0 , t ) = 0 , σ z z ( x , 0 , t ) = 0 [11 ,31 ] 处理自由边界,在自由界面上设置真空层(v p , v s σ z z τ x z σ z z N 阶交错网格有限差分自由边界在空间域中表示为:
(4) ( σ z z ) i , j k = 0 , ( σ z z ) i , j + n k = - ( σ z z ) i , j - n k , ( τ x z ) i , j + n k = - ( τ x z ) i , j - n + 1 k
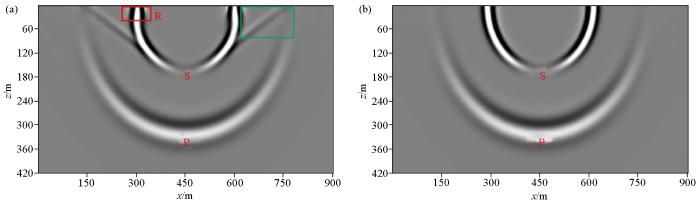
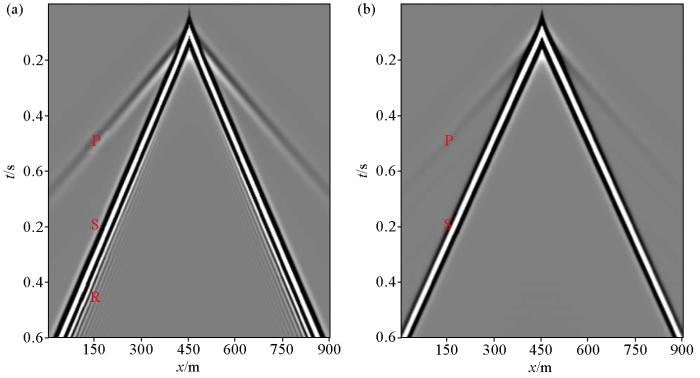
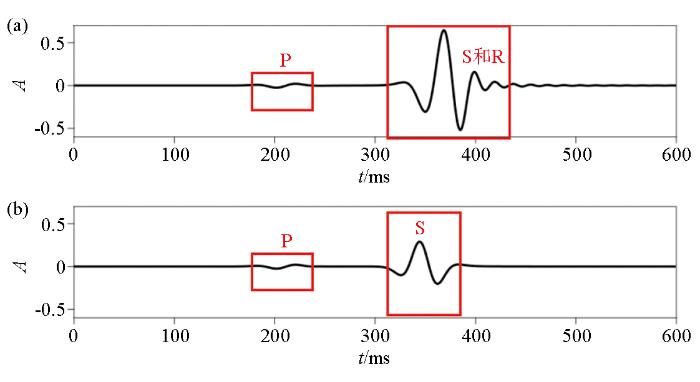
模型大小为900 m(宽)×600 m(深),网格大小Δ x = Δ z = 3 m v p = 1600 m / s , v s = 800 m / s , ρ = 2700 k g / m 3 d t = 0.2 m s 图3a 是在均匀半空间介质中表面处有自由边界条件时250 ms时刻的波场快照,图3b 为相同介质条件下表面处无自由边界条件时250 ms时刻的波场快照,图4 是地面地震记录,图5 是从图4 地震记录中抽取的第230道单道记录对比,图中标注R表示Rayleigh面波,P表示纵波,S表示横波。有自由地表边界条件时,除了纵波和横波外,还产生了波前与地面垂直的面波(如图3a 红色框线中所示)和Schmidt波(如图3a 绿色框线中所示);没有自由边界时,没有产生面波和Schmidt波,如图3b 所示;说明自由边界条件是产生Rayleigh面波的必要条件,同时也验证了本文所使用的设置自由边界条件方法的有效性。
图3
图3
波场快照
a—有自由边界时波场快照;b—无自由边界时波场快照
Fig.3
Wave field snapshot
a—wave field snapshot with free boundary;b—wave field snapshot without free boundary
图4
图4
地震记录
a—有自由边界时的地面地震记录;b—无自由边界时的地面地震记录
Fig.4
Seismic record
a—surface seismic records with free boundary;b—surface seismic records without free boundary
图5
图5
单道地震记录对比
a—有自由边界时第230道地震记录;b—无自由边界时第230道地震记录
Fig.5
Comparison of single-channel seismic records
a—230th seismic record with free boundary;b—230th seismic record without free boundary
1.5 数值频散
交错网格高阶差分算法是用有限的差分来代替微分,难免会存在误差项,这些误差项使计算结果振幅值衰减和相速度发生变化,得到的模拟结果不可避免地会出现数值频散现象,在波场快照中表现为一圈一圈的“小尾巴”,波的同相轴由一根分裂为好几根。数值频散虽然没有办法完全消除,但可以通过减小空间采样间距、减小时间采样步长、降低子波主频、提高差分精度等方法压制数值频散[13 ] 。为了最大可能削弱频散现象,本文限制的空间采样间隔条件为:
(5) Δ x = Δ z ≤ λ m i n 4
式中:λ m i n v m i n = 330 m/s,子波主频f m = 35 H z λ m i n = 3.14
综合考虑分析以上多方面因素的作用,同时在兼顾计算量、计算速度、内存的情况下,本文使用时间2阶、空间10阶的交错网格有限差分格式。实验表明在10阶精度条件下,每个最小波长上的采样只要不少于4个网格,就不会出现明显的频散。为此,网格大小不应大于0.785 m,实际计算中本文选取的网格为Δ x = Δ z = 0.5 m
1.6 解的稳定性
Jean[11 ] 、Levander[12 ] 、董良国等[32 ] 国内外许多专家都研究过交错网格差分格式下解的稳定性问题。总结前人研究成果得知均匀、完全弹性、各向同性介质中2N 阶精度的稳定性条件表达式为:
(6) Δ t v p 1 Δ x 2 + 1 Δ z 2 ≤ 1 ∑ n = 1 N a n
式中:Δ x Δ z Δ t v p 为纵波速度;a n N 阶差分系数。
2 正演模拟分析
2.1 均匀半空间介质模型
模型大小为300 m(宽)×300 m(深),网格大小Δ x = Δ z = 0.5 m v p = 1200 m / s , v s = 540 m / s , ρ = 2000 k g / m 3 d t = 0.1 m s
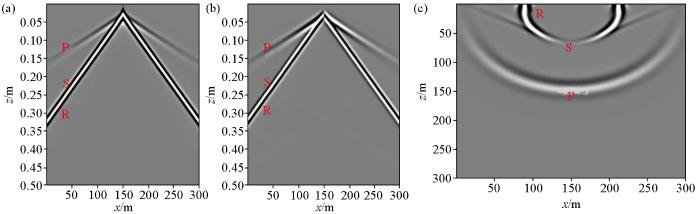
图6 为弹性波数值模拟的地震记录和150 ms时刻的波场快照。从波场记录中可以清晰地辨识出Rayleigh面波、纵波和横波,面波速度最低,紧随横波,由于垂向集中力源的方向效益,激发波场在垂直方向的能量强,在水平方向的能量弱,而由于面波是沿水平方向传播,所以在地表接收到的波场中横波能量比纵波强。正演记录中没有边界反射,也没有不稳定现象,波场模拟结果比较准确。图6 说明均匀半空间介质中同一震源激发可以产生Rayleigh面波而不产生P—导波。
图6
图6
弹性波正演模拟记录
a—地震记录(水平分量);b—地震记录(垂直分量);c—150 ms波场快照
Fig.6
Elastic wave forward modeling record
a—seismic record(horizontal component);b—seismic record(vertical component);c—150 ms wave field snapshot
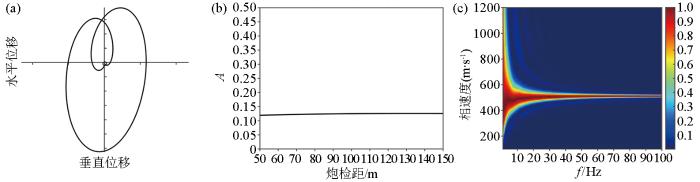
图7a 是在单炮记录图6a 和图6b 中炮检距为50 m处提取的0.2~0.256 s时的质点运动轨迹;图7b 是Rayleigh面波最大振幅随炮检距变化曲线;图7c 是用互相关相移法[33 ] 得到的频散成像。由图7a 可以看出Rayleigh面波是一种椭圆极化波。在二维直角坐标系下面波以平面形式传播,由于平面波没有几何扩散效应,所以随着炮检距增大面波振幅几乎不衰减[34 ] ,如图7b 所示。由图7c 可以看出均匀半空间介质中激发产生的面波不发生频散现象,频散谱近似是一条水平直线,其对应的相速度值与理论值506.6 m/s基本吻合,这也说明本文正演模拟和频散特征提取方法的准确性和有效性。
图7
图7
正演记录的分析结果
a—面波的质点运动轨迹;b—面波振幅随炮检距变化曲线;c—频散成像
Fig.7
Analysis results of forward record
a—the particle motion trajectory of surface wave;b—curve of surface wave amplitude changing with offset;c—dispersion imaging
2.2 两层介质模型
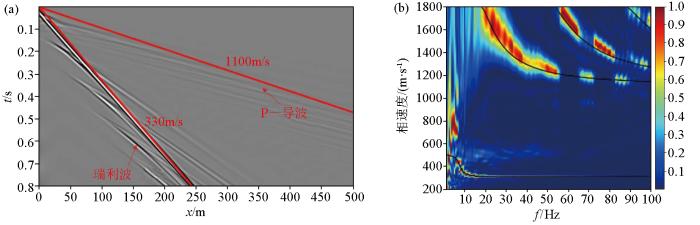
模型大小为500 m(宽)×100 m(深),网格大小Δ x = Δ z = 0.5 m d t = 0.1 m s 表1 所示,5个模型的纵波速度和密度都是固定的,横波速度和层厚变化。模型1、2、3泊松比相同,表层厚度不同;模型1、4、5表层厚度相同,泊松比不同。
图8
图8
模型1地震记录(a)与频散关系(b)
Fig.8
Model 1 seismic record(a) and dispersion relation(b)
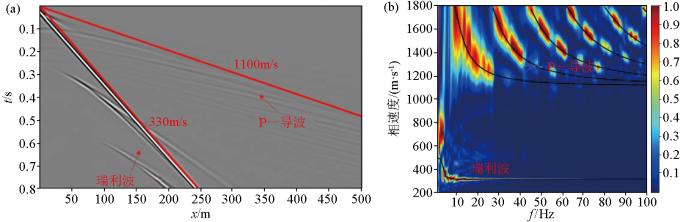
图9
图9
模型2地震记录(a)与频散关系(b)
Fig.9
Model 2 seismic record(a) and dispersion relation(b)
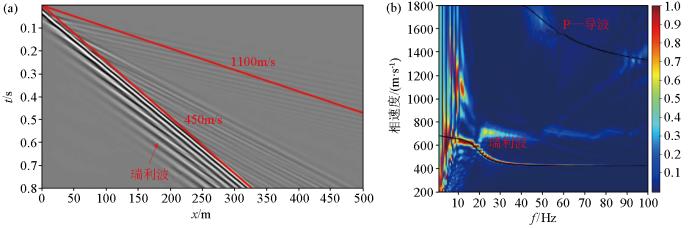
图10
图10
模型3地震记录(a)与频散关系(b)
Fig.10
Model 3 seismic record(a) and dispersion relation(b)
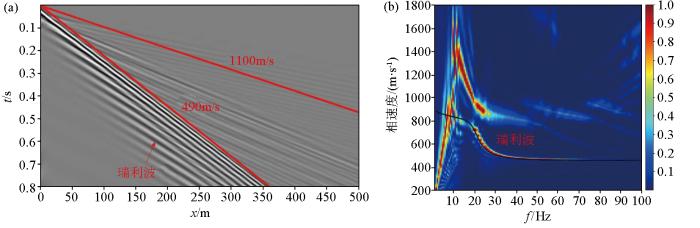
图11
图11
模型4地震记录(a)与频散关系(b)
Fig.11
Model 4 seismic record(a) and dispersion relation(b)
图12
图12
模型5地震记录(a)与频散关系(b)
Fig.12
Model 5 seismic record(a) and dispersion relation(b)
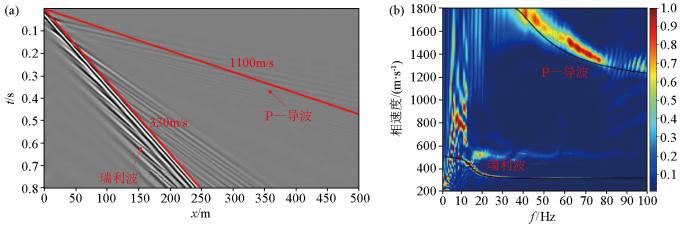
图8 、图9 、图10 说明了泊松比为0.45时近地表低速层厚度的影响。从地震记录上来看:面波在地震波场中占主导地位,能量最强,传播速度最慢。P—导波传播速度比面波快,常常尾随在折射波之后出现。层厚为10 m时,在地震记录中面波呈发散的“扫帚状”,P—导波呈“叠瓦状”,如图8a 所示。当层厚增加到20 m时,因为面波传播深度大约为一个波长,但横波的波长与层厚相比很小,所以面波主要集中在上层传播,此时面波的频散变弱,如图9a 所示。当层厚增加到40 m时,因为P波的主波长小于层厚,所以可以明显地辨别出多次P波反射,如图10a 所示。面波和P—导波的能量在频散图像中的分布范围也有明显差异,从频散图像上来看,面波主要分布在左下角的低频低速区域,P—导波主要分布在图像上方的高速区域。层厚为10 m时,如图8b 所示,面波和P—导波都表现出明显的频散。面波在低频部分的相速度和高频部分的相速度分别趋于均匀半空间S波速度540 m/s和表层S波速度330 m/s的0.92倍左右。P—导波的频率集中在40~80 Hz之间,波导的这种带通滤波效应与泄漏到半空间中的S波能量有关[30 ] 。P—导波和纯P波频散曲线两者的整体趋势基本一致但并不完全重合,这在一定程度上直观地表明P—导波频散曲线与纵波速度结构关系密切。另一方面也说明了 P—导波虽然主要由纵波分量主导,但仍然会受到横波分量的影响,这导致了其频散曲线比P波频散曲线更加复杂。当层厚增加到20 m时,如图9b 所示,P—导波表现出与相应的纯P波频散曲线相关的3个模态分支。层厚进一步增加到40 m时,如图10b 所示,P—导波出现6个模态分支,相速度大于1 800 m/s的部分表示能量泄漏到半空间中。
图8 、图11 、图12 说明了层厚为10 m时泊松比的影响。从地震记录上来看,面波和P—导波限制了最佳反射窗口大小,与泊松比为0.45(图8a )相比,泊松比为0.4时(图11a )面波和P—导波在地震记录中聚集从而缩小了最佳反射窗口,泊松比为0.3时(图12a )面波和P—导波几乎不能分开,此时最佳反射窗口消失。从频散图像上来看,P—导波常产生于高泊松比(大于0.4)的介质中。在高泊松比介质中,面波和P—导波的相速度分别对S波和P波速度敏感,P—导波主要由多次反射的P波能量组成,其频散特性可以用纯P波频散来近似。
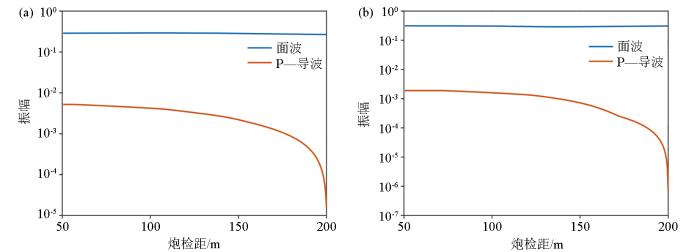
图13a 、图13b 分别是图8a 、图9a 地震记录中提取出来的面波、P—导波均方根振幅随炮检距变化曲线。可以看出,面波能量远强于P—导波,随着炮检距增大,二维直角坐标系下面波振幅几乎不衰减,P—导波振幅衰减很快,这是由于P—导波在传播过程中不断转换成S波并泄漏到高速半空间中。
图13
图13
振幅随炮检距变化曲线
a—从图8a地震记录提取的振幅曲线;b—从图9a地震记录提取的振幅曲线
Fig.13
Curve of amplitude changing with offset
a—amplitude curves extracted from seismic records in fig.8a;b—amplitude curves extracted from seismic records in fig.9a
P—导波频散数据不仅能够从石油地震数据资料中提取,在天然地震信号、背景噪声和工程勘探地震数据中同样能够观测到P—导波信号。P—导波频散信息对纵波速度结构的约束能力为地下纵波速度模型的构建提供了一个新的思路和手段。通过面波和P—导波一体化反演方法能够同时得到地下的纵横波速度模型,进一步计算可以得到泊松比模型[37 ] ,该方法可以广泛应用于岩石圈结构探测、资源勘探、地质灾害防治、环境调查、城市地下空间建设、岩土工程和无损检测等领域,具有广阔的应用前景。
3 结论
1)通过本文交错网格有限差分数值模拟方法可以成功地正演出面波和P—导波,在正演结果的基础上分析研究不同地质结构下面波和P—导波地震波场的产生机制和传播规律,得出一些规律性的认识,有助于指导实际地震资料的反演和去噪研究。
2)面波和P—导波都是与边界条件有关的波形现象。当地表存在低速薄层,且来自同一震源的P波和SV波的相速度大于高速层横波速度小于其纵波速度时,会产生P—导波。在地震记录上,面波的视速度相对于直达波明显要低很多,而P—导波的视速度通常介于直达波和折射波之间,尾随在直达波或折射波之后出现。
3)在频散关系上,层状介质中面波和P—导波都存在正频散现象。在高泊松比(大于0.4)介质中,面波和P—导波的相速度分别对S波和P波速度敏感,可以使用纯P波频散曲线来近似P—导波频散曲线。对于大约一个波长或更小的层厚度,P—导波主要由基阶模态组成,随着层厚度的增加,模态分支的数量增加。
附录A 交错网格有限差分
一阶速度—应力弹性波动方程在时间上二阶差分、空间上2N 阶差分的离散化方程组如下:
v x i , j k + 1 2 = v x i , j k - 1 2 + 1 ρ Δ t Δ x ∑ n = 1 N C n ( N ) σ x x i + n - 1 2 , j k - σ x x i - n + 1 2 , j k + 1 ρ Δ t Δ z ∑ n = 1 N C n ( N ) τ x z i , j + n - 1 2 k - τ x z i , j - n + 1 2 k v z i + 1 2 , j + 1 2 k + 1 2 = v z i + 1 2 , j + 1 2 k - 1 2 + 1 ρ Δ t Δ x ∑ n = 1 N C n ( N ) τ x z i + n , j + 1 2 k - τ x z i - n + 1 , j + 1 2 k + 1 ρ Δ t Δ z ∑ n = 1 N C n ( N ) τ x z i , j + n - 1 2 k - τ x z i , j - n + 1 2 k σ x x i + 1 2 , j k + 1 = σ x x i + 1 2 , j k + λ + 2 μ Δ t Δ x ∑ n = 1 N C n ( N ) v x i + n , j k + 1 2 - v x i - n + 1 , j k + 1 2 + λ Δ t Δ z ∑ n = 1 N C n ( N ) v z i + 1 2 , j + n - 1 2 k + 1 2 - v z i + 1 2 , j - n + 1 2 k + 1 2 σ z z i + 1 2 , j k + 1 = σ z z i + 1 2 , j k + λ Δ t Δ x ∑ n = 1 N C n ( N ) v x i + n , j k + 1 2 - v x i - n + 1 , j k + 1 2 + λ + 2 μ Δ t Δ z ∑ n = 1 N C n ( N ) v z i + 1 2 , j + n - 1 2 k + 1 2 - v z i + 1 2 , j - n + 1 2 k + 1 2 τ x z i , j + 1 2 k + 1 = τ x z i , j + 1 2 k + μ Δ t Δ x ∑ n = 1 N C n ( N ) v x i + n - 1 2 , j k + 1 2 - v x i - n + 1 2 , j k + 1 2 + μ Δ t Δ z ∑ n = 1 N C n ( N ) v z i , j + n k + 1 2 - v z i , i - n + 1 k + 1 2
式中:ρ 为弹性密度;λ、μ为拉梅常数; σii 为正应力, τij 为切应力,其中i ,j =x ,z ;vx 、vz 分别为质点在x 、z 方向的速度;上标k i , j Δ x Δ z x z Δ t 表2 给出了交错网格一阶导数对应于2 N N = 1 ~ 4
附录B PML吸收边界
∂ v x x ∂ t + d ( x ) v x x = 1 ρ ∂ σ x x ∂ x ∂ v x z ∂ t + d ( z ) v x z = 1 ρ ∂ τ x z ∂ z ∂ v z x ∂ t + d ( x ) v z x = 1 ρ ∂ τ x z ∂ x ∂ v z z ∂ t + d ( z ) v z z = 1 ρ ∂ σ z z ∂ z ∂ σ x x x ∂ t + d ( x ) σ x x x = ( λ + 2 μ ) ∂ v x ∂ x ∂ σ x x z ∂ t + d ( z ) σ x x z = λ ∂ v z ∂ z ∂ σ z z z ∂ t + d ( z ) σ z z z = ( λ + 2 μ ) ∂ v z ∂ z ∂ σ z z x ∂ t + d ( x ) σ z z x = λ ∂ v x ∂ x ∂ τ x z x ∂ t + d ( x ) τ x z x = μ ∂ v z ∂ x ∂ τ x z z ∂ t + d ( z ) τ x z z = μ ∂ v z ∂ x
式中:上标x z d ( x ) d ( z ) x z
参考文献
View Option
[1]
Roth M Holliger K Green A G Guided waves in near-surface seismic surveys
[J]. Geophysical Research Letters , 1998 , 25 (7 ):1071 -1074 .
[本文引用: 1]
[2]
吴华 , 李庆春 , 邵广周 . 瑞利波波形反演的发展现状及展望
[J]. 物探与化探 , 2018 , 42 (6 ):1103 -1111 .
[本文引用: 1]
Wu H Li Q C Shao G Z Development status and prospect of Rayleigh waveform inversion
[J]. Geophysical and Geochemical Exploration , 2018 , 42 (6 ):1103 -1111 .
[本文引用: 1]
[3]
Sun C Y Wang Z N Wu D S et al . A unified description of surface waves and guided waves with relative amplitude dispersion maps
[J]. Geophysical Journal International , 2021 , 227 (3 ):1480 -1495 .
[本文引用: 3]
[4]
Wang Z J Xiao J Y Li D et al . Full waveform inversion guided wave tomography with a recurrent neural network
[J]. Ultrasonics , 2023 , 133 :107043 .
[本文引用: 1]
[5]
Rayleigh L On waves propagated along the plane surface of an elastic solid
[J]. Proceedings of the London Mathematical Society , 1885 ,s1 - 17 (1 ):4 -11 .
[本文引用: 1]
[6]
Leslie D M Evans B The cause and effects of multilayer-generated guided-waves
[J]. Exploration Geophysics , 2000 , 31 (4 ):543 -551 .
[本文引用: 1]
[7]
Alterman Z S Karal F C J Propagation of elastic waves in layered media by finite difference methods
[J]. The Bulletin of the Seismological Society of America , 1969 , 59 (1 ):471 .
[本文引用: 1]
[8]
Boore D Finite difference methods for seismic wave propagation in heterogeneous materials [M]// Methods in computational physics : Advances in Research and Applications . Amsterdam:Elsevier, 1972 :1 -37 .
[本文引用: 1]
[9]
Madariaga R Dynamics of an expanding circular fault
[J]. The Bulletin of the Seismological Society of America , 1976 , 66 (3 ):639 -666 .
[本文引用: 1]
[10]
Jean V SH-wave propagation in heterogeneous media:Velocity-stress finite-difference method
[J]. Geophysics , 1984 , 49 (11 ):1933 .
[本文引用: 1]
[11]
Jean V P-SV wave propagation in heterogeneous media:Velocity-stress finite-difference method
[J]. Geophysics , 1986 , 51 (4 ):889 -901 .
[本文引用: 3]
[12]
Levander A R Fourth-order finite-difference P-SV seismograms
[J]. Geophysics , 1988 , 53 (11 ):1425 .
[本文引用: 2]
[13]
董良国 , 马在田 , 曹景忠 , 等 . 一阶弹性波方程交错网格高阶差分解法
[J]. 地球物理学报 , 2000 , 43 (3 ):411 -419 .
[本文引用: 2]
Dong L G Ma Z T Cao J Z et al . A staggered-grid high-order difference method of one-order elastic wave equation
[J]. Chinese Journal of Geophysics , 2000 , 43 (3 ):411 -419 .
[本文引用: 2]
[14]
Collino F Tsogka C Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media
[J]. Geophysics , 2001 , 66 (1 ):294 .
[本文引用: 2]
[15]
张伟 , 甘伏平 , 刘伟 , 等 . 双相介质瑞雷面波有限差分正演模拟
[J]. 物探与化探 , 2014 , 38 (6 ):1275 -1283 .
[本文引用: 1]
Zhang W Gan F P Liu W et al . Rayleigh surface wave modeling by finite difference method in biphasic media
[J]. Geophysical and Geochemical Exploration , 2014 , 38 (6 ):1275 -1283 .
[本文引用: 1]
[16]
廉西猛 , 张睿璇 . 基于GPU集群的大规模三维有限差分正演模拟并行策略
[J]. 物探与化探 , 2015 , 39 (3 ):615 -620 .
[本文引用: 1]
Lian X M Zhang R X Parallel strategy of large-scale 3D seismic forward by finite difference method on GPU cluster
[J]. Geophysical and Geochemical Exploration , 2015 , 39 (3 ):615 -620 .
[本文引用: 1]
[17]
彭更新 , 刘威 , 郭念民 , 等 . 基于时空域交错网格有限差分法的应力速度声波方程数值模拟
[J]. 石油物探 , 2022 , 61 (1 ):156 -165 ,173.
DOI:10.3969/j.issn.1000-1441.2022.01.016
[本文引用: 1]
目前应力速度声波方程数值模拟普遍采用时间二阶和空间2M阶交错网格差分法,相应的差分系数仅利用空间域频散关系和泰勒展开求解。但波动方程数值求解在时间和空间域同时进行,仅利用空间域频散关系计算差分系数,易产生数值频散,因而影响数值模拟精度。针对该问题,从差分离散波动方程和平面波理论出发,推导出了时间二阶、空间2M阶交错网格差分法的时空域频散关系,并进一步导出了基于时空域频散关系和泰勒展开的差分系数算法,该算法求解的差分系数随地震波的传播速度自适应变化。数值频散分析结果表明,新的差分系数算法能够有效减小数值频散进而提高模拟精度;稳定性分析结果表明,新的差分系数算法能够有效增强交错网格有限差分法的稳定性,使得该方法能采用更大的时间步长从而提高计算效率。层状介质模型和塔里木盆地典型复杂构造模型数值模拟实例进一步验证了基于新差分系数算法的交错网格有限差分法在提高模拟精度和计算效率方面的优越性。
Peng G X Liu W Guo N M et al . A time-space domain dispersion-relationship-based staggered-grid finite-difference scheme for modeling the stress-velocity acoustic wave equation
[J]. Geophysical Prospecting for Petroleum , 2022 , 61 (1 ):156 -165 ,173.
DOI:10.3969/j.issn.1000-1441.2022.01.016
[本文引用: 1]
Numerical simulations of the stress-velocity acoustic wave generally adopt a staggered grid difference with 2nd-order in time and 2M-order in space.The corresponding difference coefficients are calculated only based on the spatial domain dispersion relationship and the Taylor expansion.When the numerical solution of the wave equation is obtained in the time and space domains simultaneously,only the dispersion relationship in the space domain is used to calculate the difference coefficients.This easily causes numerical dispersion and affects the accuracy of the numerical simulation.To overcome this issue,we used the discrete difference wave equation and plane wave theory to derive the time-space domain dispersion relationship for calculating the staggered grid difference scheme of the second order in time and 2Mth order in space,and then developed an algorithm for calculating the difference coefficient based on the time-space domain dispersion relationship and the Taylor expansion.The so-obtained difference coefficient varies adaptively with the propagation speed of the seismic wave.Numerical dispersion analysis showed that the proposed algorithm can effectively reduce the numerical dispersion,thereby improving the simulation accuracy.Stability analysis showed that the proposed algorithm can effectively enhance the stability of the staggered grid difference scheme,making it can adopt a large time step to improve the calculation efficiency.Numerical simulation examples of a layered medium model and a complex structure model of the Tarim Basin further verified the superiority of the staggered grid finite difference scheme using the proposed difference coefficient algorithm in terms of simulation accuracy and calculation efficiency.
[18]
Pekeris C L Theory of propagation of explosive sound in shallow water
[J]. Geological Society of America Memoirs , 1948 , 27 (1 ):1 -116 .
[本文引用: 1]
[19]
Robertsson J O A Holliger K Green A G et al . Effects of near-surface waveguides on shallow high-resolution seismic refraction and reflection data
[J]. Geophysical Research Letters , 1996 , 23 (5 ):495 -498 .
[本文引用: 2]
[20]
Sheriff R E Geldart L P Exploration seismology(2nd ed) [M]. Cambridge : Cambridge University Press , 1995 .
[本文引用: 1]
[21]
Roth M Holliger K Joint inversion of Rayleigh and guided waves in high-resolution seismic data using a genetic algorithm
[C]// SEG Technical Program Expanded Abstracts 1998.Society of Exploration Geophysicists , 1998 :1570 -1573 .
[本文引用: 1]
[22]
Herman G C Milligan P A Huggins R J et al . Imaging shallow objects and heterogeneities with scattered guided waves
[J]. Geophysics , 2000 , 65 (1 ):247 .
[本文引用: 1]
[23]
Carcione J M Helle H B The physics and simulation of wave propagation at the ocean bottom
[J]. Geophysics , 2004 , 69 (3 ):825 -839 .
[本文引用: 1]
[24]
Klein G Bohlen T Theilen F et al . Acquisition and inversion of dispersive seismic waves in shallow marine environments
[J]. Marine Geophysical Researches , 2005 , 26 (2 ):287 -315 .
[本文引用: 1]
[25]
Ernst F E Long-wavelength statics estimation from guided waves
[C]// London:69th EAGE Conference and Exhibition incorporating SPE EUROPEC 2007,European Association of Geoscientists & Engineers , 2007 :1 -5 .
[本文引用: 1]
[26]
李正波 . 频率贝塞尔变换法提取地震记录中的频散信息 [D]. 合肥 : 中国科学技术大学 , 2020 .
[本文引用: 2]
Li Z B Frequency-Bessel transform method for extracting dispersion information from seismic records [D]. Hefei : University of Science and Technology of China , 2020 .
[本文引用: 2]
[27]
刘辉 , 李静 , 曾昭发 , 等 . 基于贝叶斯理论面波频散曲线随机反演
[J]. 物探与化探 , 2021 , 45 (4 ):951 -960 .
[本文引用: 1]
Liu H Li J Zeng Z F et al . Stochastic inversion of surface wave dispersion curves based on Bayesian theory
[J]. Geophysical and Geochemical Exploration , 2021 , 45 (4 ):951 -960 .
[本文引用: 1]
[28]
Boerner D E West G F A generalized representation of the electromagnetic fields in a layered earth
[J]. Geophysical Journal International , 1989 , 97 (3 ):529 -547 .
[本文引用: 1]
[29]
Collino F Perfectly matched absorbing layers for the paraxial equations
[J]. Journal of Computational Physics , 1997 , 131 (1 ):164 -180 .
[本文引用: 1]
[30]
Roth M Holliger K Inversion of source-generated noise in high-resolution seismic data
[J]. The Leading Edge , 1999 , 18 (12 ):1402 -1406 .
[本文引用: 2]
[31]
Robertsson J O A A numerical free-surface condition for elastic/viscoelastic finite-difference modeling in the presence of topography
[J]. Geophysics , 1996 , 61 (6 ):1921 -1934 .
[本文引用: 1]
[32]
董良国 , 马在田 . 一阶弹性波方程交错网格高阶差分解法稳定性研究
[J]. 地球物理学报 , 2000 , 43 (6 ):856 -864 .
[本文引用: 1]
Dong L G Ma Z T A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation
[J]. Chinese Journal of Geophysics , 2000 , 43 (6 ):856 -864 .
[本文引用: 1]
[33]
伍敦仕 , 孙成禹 , 林美言 . 基于互相关相移的主动源地震面波频散成像方法
[J]. 地球物理学进展 , 2017 , 32 (4 ):1693 -1700 .
[本文引用: 2]
Wu D S Sun C Y Lin M Y Activeseismic surface wave dispersion imaging method based on cross-correlation and phase-shifting
[J]. Progress in Geophysics , 2017 , 32 (4 ):1693 -1700 .
[本文引用: 2]
[34]
熊嫘 , 孙成禹 , 蔡瑞乾 . 柱对称条件下地震面波波场正演研究
[J]. 石油地球物理勘探 , 2023 , 58 (1 ):133 -144 .
[本文引用: 1]
Xiong L Sun C Y Cai R Q Forward wavefield modeling of seismic surface waves under cylindrical symmetry
[J]. Oil Geophysical Prospecting , 2023 , 58 (1 ):133 -144 .
[本文引用: 1]
[35]
Buchen P W Ben-Hador R Free-mode surface-wave computations
[J]. Geophysical Journal International , 1996 , 124 (3 ):869 -887 .
[本文引用: 1]
[36]
邱新明 , 王赟 , 韦永祥 , 等 . 多分量面波研究进展
[J]. 石油物探 , 2021 , 60 (1 ):46 -56 .
DOI:10.3969/j.issn.1000-1441.2021.01.005
[本文引用: 1]
随着多分量检波器和地震仪的广泛应用,针对地球壳幔结构成像、岩土工程探测、石油勘探等领域的多分量面波研究逐渐受到关注。在系统研究面波理论及相关方法技术的基础上,对多分量面波的研究现状进行了总结。首先简要介绍了面波相速度频散计算方法,列举了面波多模式频散曲线提取遇到的问题及相应的解决方法;然后重点介绍了多分量面波频散特征、偏振特征及多分量面波资料的处理和反演方法;接着介绍了旋转分量在面波分离和面波频散分析等方面的应用,最后讨论了多分量面波在石油勘探中的应用前景。不同分量的面波中包含了不同的速度频散信息,因此多分量面波反演有助于获得更准确的近地表速度结构,六分量观测能够更完备地刻画多分量面波频散及偏振特征,有助于识别和分离面波。目前多分量面波技术的研究在国内尚处于起步阶段,基于多分量面波频散及偏振等特征研发相应的面波处理和压制技术将是今后主要的研究方向之一。
Qiu X M Wang Y Wei Y X et al . Advancements in multi-component surface waves:A review
[J]. Geophysical Prospecting for Petroleum , 2021 , 60 (1 ):46 -56 .
DOI:10.3969/j.issn.1000-1441.2021.01.005
[本文引用: 1]
There has been widespread interest in multi-component surface-wave surveys in areas such as crustal and mantle research,engineering prospecting,and oil exploration.This study reviews the developments in multi-component surface waves,beginning with the computation methods of theoretical dispersion curves.Subsequently,the challenges associated with the extraction of multi-mode dispersion curves of vertical-component surface waves and their solutions are discussed.The dispersion characteristics,polarization characteristics,multi-component processing,and the inversion methods of multi-component surface-wave were also reviewed in detail,followed by the applications of rotational motion for surface-wave separation and dispersion analysis.Finally,the application prospects of multi-component surface waves in oil exploration were analyzed.It was found that more accurate dispersion curves may be obtained using multi-component surface waves,resulting in S-wave velocities of greater accuracy.Six-component surface-wave studies were found to be useful to learn the dispersion and polarization characteristics of surface waves.Six-component seismic data may also be utilized to separate surface waves from reflections.Multi-component surface wave methods continue to be developed in China.Future research will involve investigating new methods for surface-wave utilization and suppression,based on the multi-component surface-wave dispersion and polarization characteristics.
[37]
Shi C W Ren H X Chen X F Dispersion inversion for P- and S-wave velocities based on guided P and Scholte waves
[J]. Geophysics , 2023 , 88 (6 ):R721 -R736 .
[本文引用: 1]
Guided waves in near-surface seismic surveys
1
1998
... 在油气地震勘探中,面波及其泄漏模式的P—导波通常被认为是噪声被滤除掉,但也可以作为地震记录中的有用信号,用于反演近地表速度,解决各种实际的地球物理问题[1 ] .通过正演模拟可以直观地展现面波和P—导波的传播规律,为反演和去噪研究奠定基础,也有助于更好地指导工程实践和提高勘探解释精度[2 ⇓ -4 ] . ...
瑞利波波形反演的发展现状及展望
1
2018
... 在油气地震勘探中,面波及其泄漏模式的P—导波通常被认为是噪声被滤除掉,但也可以作为地震记录中的有用信号,用于反演近地表速度,解决各种实际的地球物理问题[1 ] .通过正演模拟可以直观地展现面波和P—导波的传播规律,为反演和去噪研究奠定基础,也有助于更好地指导工程实践和提高勘探解释精度[2 ⇓ -4 ] . ...
瑞利波波形反演的发展现状及展望
1
2018
... 在油气地震勘探中,面波及其泄漏模式的P—导波通常被认为是噪声被滤除掉,但也可以作为地震记录中的有用信号,用于反演近地表速度,解决各种实际的地球物理问题[1 ] .通过正演模拟可以直观地展现面波和P—导波的传播规律,为反演和去噪研究奠定基础,也有助于更好地指导工程实践和提高勘探解释精度[2 ⇓ -4 ] . ...
A unified description of surface waves and guided waves with relative amplitude dispersion maps
3
2021
... 在油气地震勘探中,面波及其泄漏模式的P—导波通常被认为是噪声被滤除掉,但也可以作为地震记录中的有用信号,用于反演近地表速度,解决各种实际的地球物理问题[1 ] .通过正演模拟可以直观地展现面波和P—导波的传播规律,为反演和去噪研究奠定基础,也有助于更好地指导工程实践和提高勘探解释精度[2 ⇓ -4 ] . ...
... 无论在理论研究还是实际应用中,P—导波的涉及都比面波要少一些,主要原因可能在于其频散曲线的复杂性[3 ,26 -27 ] .此外,目前对同一震源下面波和导波产生机制和传播规律的研究和认识也不够充分和深入.本文基于高阶交错网格弹性波波动方程有限差分数值模拟的方法,有效地正演模拟出地震面波和P—导波波场.设计不同速度和厚度模型进行比较,从波场记录、频散成像等方面分析阐述了面波和P—导波的激发和传播规律. ...
... 在地震勘探中,导波由近地表多次反射产生[3 ] .当相速度低于高速半空间横波速度时,导波的纵波分量和横波分量在波导结构中经过多次反射形成Rayleigh面波或Love面波.其中,Rayleigh 面波是由P波和SV波进行叠加干涉而成的,而Love面波则是由SH波构成.当相速度高于高速半空间横波速度且小于其纵波速度时,导波的横波分量会泄露到高速半空间中,剩余的由纵波分量主导的导波即为P—导波[26 ,30 ] . ...
Full waveform inversion guided wave tomography with a recurrent neural network
1
2023
... 在油气地震勘探中,面波及其泄漏模式的P—导波通常被认为是噪声被滤除掉,但也可以作为地震记录中的有用信号,用于反演近地表速度,解决各种实际的地球物理问题[1 ] .通过正演模拟可以直观地展现面波和P—导波的传播规律,为反演和去噪研究奠定基础,也有助于更好地指导工程实践和提高勘探解释精度[2 ⇓ -4 ] . ...
On waves propagated along the plane surface of an elastic solid
1
1885
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
The cause and effects of multilayer-generated guided-waves
1
2000
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
Propagation of elastic waves in layered media by finite difference methods
1
1969
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
1
1972
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
Dynamics of an expanding circular fault
1
1976
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
SH-wave propagation in heterogeneous media:Velocity-stress finite-difference method
1
1984
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
P-SV wave propagation in heterogeneous media:Velocity-stress finite-difference method
3
1986
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
... 地球的自由表面和近地表下方高速层的顶界面之间可视为一种有效的层状波导[19 ] ,为了真实地模拟出面波和P—导波的波动现象,必须设置合理的自由地表边界条件.在水平自由表面上,应力分量必须满足如下条件: τ x z ( x , 0 , t ) = 0 , σ z z ( x , 0 , t ) = 0 . 本文使用应力镜像法[11 ,31 ] 处理自由边界,在自由界面上设置真空层( v p , v s σ z z τ x z σ z z N 阶交错网格有限差分自由边界在空间域中表示为: ...
... Jean[11 ] 、Levander[12 ] 、董良国等[32 ] 国内外许多专家都研究过交错网格差分格式下解的稳定性问题.总结前人研究成果得知均匀、完全弹性、各向同性介质中2N 阶精度的稳定性条件表达式为: ...
Fourth-order finite-difference P-SV seismograms
2
1988
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
... Jean[11 ] 、Levander[12 ] 、董良国等[32 ] 国内外许多专家都研究过交错网格差分格式下解的稳定性问题.总结前人研究成果得知均匀、完全弹性、各向同性介质中2N 阶精度的稳定性条件表达式为: ...
一阶弹性波方程交错网格高阶差分解法
2
2000
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
... 交错网格高阶差分算法是用有限的差分来代替微分,难免会存在误差项,这些误差项使计算结果振幅值衰减和相速度发生变化,得到的模拟结果不可避免地会出现数值频散现象,在波场快照中表现为一圈一圈的“小尾巴”,波的同相轴由一根分裂为好几根.数值频散虽然没有办法完全消除,但可以通过减小空间采样间距、减小时间采样步长、降低子波主频、提高差分精度等方法压制数值频散[13 ] .为了最大可能削弱频散现象,本文限制的空间采样间隔条件为: ...
一阶弹性波方程交错网格高阶差分解法
2
2000
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
... 交错网格高阶差分算法是用有限的差分来代替微分,难免会存在误差项,这些误差项使计算结果振幅值衰减和相速度发生变化,得到的模拟结果不可避免地会出现数值频散现象,在波场快照中表现为一圈一圈的“小尾巴”,波的同相轴由一根分裂为好几根.数值频散虽然没有办法完全消除,但可以通过减小空间采样间距、减小时间采样步长、降低子波主频、提高差分精度等方法压制数值频散[13 ] .为了最大可能削弱频散现象,本文限制的空间采样间隔条件为: ...
Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media
2
2001
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
... 在使用波动方程有限差分法模拟地震波传播时,计算区域的有限性会导致计算区域边界处产生虚假反射,干扰正常波场的分析研究,所以必须设置合理的吸收边界条件对虚假反射进行吸收处理.本文选用吸收效果好、易实现、普遍使用的分裂式完全匹配层法(PML),在计算区域的左、右、下3处扩边设置吸收层(图2 ).该方法首先将质点处的速度分量和应力分量沿坐标轴分裂成垂直方向分量和水平方向分量两部分[29 ] ,然后利用前文介绍的交错网格差分离散化思路,推导出分裂式PML吸收边界条件差分方程[14 ] (见附录B).吸收层内衰减因子设置方式为: ...
双相介质瑞雷面波有限差分正演模拟
1
2014
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
双相介质瑞雷面波有限差分正演模拟
1
2014
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
基于GPU集群的大规模三维有限差分正演模拟并行策略
1
2015
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
基于GPU集群的大规模三维有限差分正演模拟并行策略
1
2015
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
基于时空域交错网格有限差分法的应力速度声波方程数值模拟
1
2022
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
基于时空域交错网格有限差分法的应力速度声波方程数值模拟
1
2022
... Rayleigh[5 ] 第一次在理论上证明了Rayleigh面波的存在,此后面波成为地球物理学家研究的热点之一.Leslie等[6 ] 推导了Rayleigh面波在层状均匀横向各向同性介质里传播的规律.Alterman等[7 ] 首先将有限差分运用到层状介质模型的地震波数值模拟中.Boore[8 ] 最早提出将自由边界上设置为真空层,从而实现地震面波数值模拟.Madariaga[9 ] 提出了非均匀介质应力—速度弹性波方程组交错网格有限差分法,Jean[10 -11 ] 利用这一格式实现了对弹性介质的SH和P-SV波的数值模拟,提高了模拟的稳定性与精度,并首次把交错网格差分格式和弹性波动方程数值模拟结合起来,相比于常规网格差分,交错网格在计算量和收敛速度方面有所提高.Levander[12 ] 提出了镜像法来实现自由边界的处理,取得了广泛的使用.董良国等[13 ] 利用高阶有限差分法和交错网格剖分相结合的方式,提出了高阶交错网格有限差分法.Collino等[14 ] 首次在弹性波的波场模拟的边界处添加匹配层.张伟等[15 ] 根据弹性波动方程交错网格有限差分算法详细地分析了双相介质瑞利面波的波场特征.廉西猛等[16 ] 通过使用GPU/CPU协同并行模式和区域分解方法,实现了该算法的多级并行策略,提高了计算效率.彭更新等[17 ] 实现基于时空域交错网格有限差分法的应力速度声波方程数值模拟,有效增强交错网格有限差分法的稳定性. ...
Theory of propagation of explosive sound in shallow water
1
1948
... Pekeris[18 ] 在水声学的研究中发现声波也存在频散现象,他把这种频散波称之为P—导波,P—导波对于海洋中声波速度的研究有着重要意义.Robertsson等[19 ] 发现震源产生的大部分弹性能量可能被困在波导中,并以很小的损失长距离传播,这就是导波.Sheriff等[20 ] 研究发现导波常见的特征是高振幅和叠瓦状.Roth等[21 ] 认为自由表面和第一个主要地震不连续面之间的地层可以被视为一个有效的层状波导.为了区分面波和导波,Herman等[22 ] 也将导波称为面波到达前的频散波,在这种情况下,导波不包括面波.为了便于讨论,本文将P—导波和面波视为两种不同类型的频散波.Carcione等[23 ] 认为在固液耦合情况下的P—导波频散曲线和漏能振型理论上是一致的.Klein等[24 ] 在实际应用中通过海洋拖缆提取出的P—导波频散曲线有效地反演出海底P波速度.Ernst[25 ] 证明在反射地震学中,导波比初至波能更好地确定长波长近地表速度. ...
Effects of near-surface waveguides on shallow high-resolution seismic refraction and reflection data
2
1996
... Pekeris[18 ] 在水声学的研究中发现声波也存在频散现象,他把这种频散波称之为P—导波,P—导波对于海洋中声波速度的研究有着重要意义.Robertsson等[19 ] 发现震源产生的大部分弹性能量可能被困在波导中,并以很小的损失长距离传播,这就是导波.Sheriff等[20 ] 研究发现导波常见的特征是高振幅和叠瓦状.Roth等[21 ] 认为自由表面和第一个主要地震不连续面之间的地层可以被视为一个有效的层状波导.为了区分面波和导波,Herman等[22 ] 也将导波称为面波到达前的频散波,在这种情况下,导波不包括面波.为了便于讨论,本文将P—导波和面波视为两种不同类型的频散波.Carcione等[23 ] 认为在固液耦合情况下的P—导波频散曲线和漏能振型理论上是一致的.Klein等[24 ] 在实际应用中通过海洋拖缆提取出的P—导波频散曲线有效地反演出海底P波速度.Ernst[25 ] 证明在反射地震学中,导波比初至波能更好地确定长波长近地表速度. ...
... 地球的自由表面和近地表下方高速层的顶界面之间可视为一种有效的层状波导[19 ] ,为了真实地模拟出面波和P—导波的波动现象,必须设置合理的自由地表边界条件.在水平自由表面上,应力分量必须满足如下条件: τ x z ( x , 0 , t ) = 0 , σ z z ( x , 0 , t ) = 0 . 本文使用应力镜像法[11 ,31 ] 处理自由边界,在自由界面上设置真空层( v p , v s σ z z τ x z σ z z N 阶交错网格有限差分自由边界在空间域中表示为: ...
1
1995
... Pekeris[18 ] 在水声学的研究中发现声波也存在频散现象,他把这种频散波称之为P—导波,P—导波对于海洋中声波速度的研究有着重要意义.Robertsson等[19 ] 发现震源产生的大部分弹性能量可能被困在波导中,并以很小的损失长距离传播,这就是导波.Sheriff等[20 ] 研究发现导波常见的特征是高振幅和叠瓦状.Roth等[21 ] 认为自由表面和第一个主要地震不连续面之间的地层可以被视为一个有效的层状波导.为了区分面波和导波,Herman等[22 ] 也将导波称为面波到达前的频散波,在这种情况下,导波不包括面波.为了便于讨论,本文将P—导波和面波视为两种不同类型的频散波.Carcione等[23 ] 认为在固液耦合情况下的P—导波频散曲线和漏能振型理论上是一致的.Klein等[24 ] 在实际应用中通过海洋拖缆提取出的P—导波频散曲线有效地反演出海底P波速度.Ernst[25 ] 证明在反射地震学中,导波比初至波能更好地确定长波长近地表速度. ...
Joint inversion of Rayleigh and guided waves in high-resolution seismic data using a genetic algorithm
1
1998
... Pekeris[18 ] 在水声学的研究中发现声波也存在频散现象,他把这种频散波称之为P—导波,P—导波对于海洋中声波速度的研究有着重要意义.Robertsson等[19 ] 发现震源产生的大部分弹性能量可能被困在波导中,并以很小的损失长距离传播,这就是导波.Sheriff等[20 ] 研究发现导波常见的特征是高振幅和叠瓦状.Roth等[21 ] 认为自由表面和第一个主要地震不连续面之间的地层可以被视为一个有效的层状波导.为了区分面波和导波,Herman等[22 ] 也将导波称为面波到达前的频散波,在这种情况下,导波不包括面波.为了便于讨论,本文将P—导波和面波视为两种不同类型的频散波.Carcione等[23 ] 认为在固液耦合情况下的P—导波频散曲线和漏能振型理论上是一致的.Klein等[24 ] 在实际应用中通过海洋拖缆提取出的P—导波频散曲线有效地反演出海底P波速度.Ernst[25 ] 证明在反射地震学中,导波比初至波能更好地确定长波长近地表速度. ...
Imaging shallow objects and heterogeneities with scattered guided waves
1
2000
... Pekeris[18 ] 在水声学的研究中发现声波也存在频散现象,他把这种频散波称之为P—导波,P—导波对于海洋中声波速度的研究有着重要意义.Robertsson等[19 ] 发现震源产生的大部分弹性能量可能被困在波导中,并以很小的损失长距离传播,这就是导波.Sheriff等[20 ] 研究发现导波常见的特征是高振幅和叠瓦状.Roth等[21 ] 认为自由表面和第一个主要地震不连续面之间的地层可以被视为一个有效的层状波导.为了区分面波和导波,Herman等[22 ] 也将导波称为面波到达前的频散波,在这种情况下,导波不包括面波.为了便于讨论,本文将P—导波和面波视为两种不同类型的频散波.Carcione等[23 ] 认为在固液耦合情况下的P—导波频散曲线和漏能振型理论上是一致的.Klein等[24 ] 在实际应用中通过海洋拖缆提取出的P—导波频散曲线有效地反演出海底P波速度.Ernst[25 ] 证明在反射地震学中,导波比初至波能更好地确定长波长近地表速度. ...
The physics and simulation of wave propagation at the ocean bottom
1
2004
... Pekeris[18 ] 在水声学的研究中发现声波也存在频散现象,他把这种频散波称之为P—导波,P—导波对于海洋中声波速度的研究有着重要意义.Robertsson等[19 ] 发现震源产生的大部分弹性能量可能被困在波导中,并以很小的损失长距离传播,这就是导波.Sheriff等[20 ] 研究发现导波常见的特征是高振幅和叠瓦状.Roth等[21 ] 认为自由表面和第一个主要地震不连续面之间的地层可以被视为一个有效的层状波导.为了区分面波和导波,Herman等[22 ] 也将导波称为面波到达前的频散波,在这种情况下,导波不包括面波.为了便于讨论,本文将P—导波和面波视为两种不同类型的频散波.Carcione等[23 ] 认为在固液耦合情况下的P—导波频散曲线和漏能振型理论上是一致的.Klein等[24 ] 在实际应用中通过海洋拖缆提取出的P—导波频散曲线有效地反演出海底P波速度.Ernst[25 ] 证明在反射地震学中,导波比初至波能更好地确定长波长近地表速度. ...
Acquisition and inversion of dispersive seismic waves in shallow marine environments
1
2005
... Pekeris[18 ] 在水声学的研究中发现声波也存在频散现象,他把这种频散波称之为P—导波,P—导波对于海洋中声波速度的研究有着重要意义.Robertsson等[19 ] 发现震源产生的大部分弹性能量可能被困在波导中,并以很小的损失长距离传播,这就是导波.Sheriff等[20 ] 研究发现导波常见的特征是高振幅和叠瓦状.Roth等[21 ] 认为自由表面和第一个主要地震不连续面之间的地层可以被视为一个有效的层状波导.为了区分面波和导波,Herman等[22 ] 也将导波称为面波到达前的频散波,在这种情况下,导波不包括面波.为了便于讨论,本文将P—导波和面波视为两种不同类型的频散波.Carcione等[23 ] 认为在固液耦合情况下的P—导波频散曲线和漏能振型理论上是一致的.Klein等[24 ] 在实际应用中通过海洋拖缆提取出的P—导波频散曲线有效地反演出海底P波速度.Ernst[25 ] 证明在反射地震学中,导波比初至波能更好地确定长波长近地表速度. ...
Long-wavelength statics estimation from guided waves
1
2007
... Pekeris[18 ] 在水声学的研究中发现声波也存在频散现象,他把这种频散波称之为P—导波,P—导波对于海洋中声波速度的研究有着重要意义.Robertsson等[19 ] 发现震源产生的大部分弹性能量可能被困在波导中,并以很小的损失长距离传播,这就是导波.Sheriff等[20 ] 研究发现导波常见的特征是高振幅和叠瓦状.Roth等[21 ] 认为自由表面和第一个主要地震不连续面之间的地层可以被视为一个有效的层状波导.为了区分面波和导波,Herman等[22 ] 也将导波称为面波到达前的频散波,在这种情况下,导波不包括面波.为了便于讨论,本文将P—导波和面波视为两种不同类型的频散波.Carcione等[23 ] 认为在固液耦合情况下的P—导波频散曲线和漏能振型理论上是一致的.Klein等[24 ] 在实际应用中通过海洋拖缆提取出的P—导波频散曲线有效地反演出海底P波速度.Ernst[25 ] 证明在反射地震学中,导波比初至波能更好地确定长波长近地表速度. ...
2
2020
... 无论在理论研究还是实际应用中,P—导波的涉及都比面波要少一些,主要原因可能在于其频散曲线的复杂性[3 ,26 -27 ] .此外,目前对同一震源下面波和导波产生机制和传播规律的研究和认识也不够充分和深入.本文基于高阶交错网格弹性波波动方程有限差分数值模拟的方法,有效地正演模拟出地震面波和P—导波波场.设计不同速度和厚度模型进行比较,从波场记录、频散成像等方面分析阐述了面波和P—导波的激发和传播规律. ...
... 在地震勘探中,导波由近地表多次反射产生[3 ] .当相速度低于高速半空间横波速度时,导波的纵波分量和横波分量在波导结构中经过多次反射形成Rayleigh面波或Love面波.其中,Rayleigh 面波是由P波和SV波进行叠加干涉而成的,而Love面波则是由SH波构成.当相速度高于高速半空间横波速度且小于其纵波速度时,导波的横波分量会泄露到高速半空间中,剩余的由纵波分量主导的导波即为P—导波[26 ,30 ] . ...
2
2020
... 无论在理论研究还是实际应用中,P—导波的涉及都比面波要少一些,主要原因可能在于其频散曲线的复杂性[3 ,26 -27 ] .此外,目前对同一震源下面波和导波产生机制和传播规律的研究和认识也不够充分和深入.本文基于高阶交错网格弹性波波动方程有限差分数值模拟的方法,有效地正演模拟出地震面波和P—导波波场.设计不同速度和厚度模型进行比较,从波场记录、频散成像等方面分析阐述了面波和P—导波的激发和传播规律. ...
... 在地震勘探中,导波由近地表多次反射产生[3 ] .当相速度低于高速半空间横波速度时,导波的纵波分量和横波分量在波导结构中经过多次反射形成Rayleigh面波或Love面波.其中,Rayleigh 面波是由P波和SV波进行叠加干涉而成的,而Love面波则是由SH波构成.当相速度高于高速半空间横波速度且小于其纵波速度时,导波的横波分量会泄露到高速半空间中,剩余的由纵波分量主导的导波即为P—导波[26 ,30 ] . ...
基于贝叶斯理论面波频散曲线随机反演
1
2021
... 无论在理论研究还是实际应用中,P—导波的涉及都比面波要少一些,主要原因可能在于其频散曲线的复杂性[3 ,26 -27 ] .此外,目前对同一震源下面波和导波产生机制和传播规律的研究和认识也不够充分和深入.本文基于高阶交错网格弹性波波动方程有限差分数值模拟的方法,有效地正演模拟出地震面波和P—导波波场.设计不同速度和厚度模型进行比较,从波场记录、频散成像等方面分析阐述了面波和P—导波的激发和传播规律. ...
基于贝叶斯理论面波频散曲线随机反演
1
2021
... 无论在理论研究还是实际应用中,P—导波的涉及都比面波要少一些,主要原因可能在于其频散曲线的复杂性[3 ,26 -27 ] .此外,目前对同一震源下面波和导波产生机制和传播规律的研究和认识也不够充分和深入.本文基于高阶交错网格弹性波波动方程有限差分数值模拟的方法,有效地正演模拟出地震面波和P—导波波场.设计不同速度和厚度模型进行比较,从波场记录、频散成像等方面分析阐述了面波和P—导波的激发和传播规律. ...
A generalized representation of the electromagnetic fields in a layered earth
1
1989
... 根据弹性波动理论,已知在二维TI介质中,一阶速度—应力弹性波波动方程(假设体力为零)可以表示为[28 ] : ...
Perfectly matched absorbing layers for the paraxial equations
1
1997
... 在使用波动方程有限差分法模拟地震波传播时,计算区域的有限性会导致计算区域边界处产生虚假反射,干扰正常波场的分析研究,所以必须设置合理的吸收边界条件对虚假反射进行吸收处理.本文选用吸收效果好、易实现、普遍使用的分裂式完全匹配层法(PML),在计算区域的左、右、下3处扩边设置吸收层(图2 ).该方法首先将质点处的速度分量和应力分量沿坐标轴分裂成垂直方向分量和水平方向分量两部分[29 ] ,然后利用前文介绍的交错网格差分离散化思路,推导出分裂式PML吸收边界条件差分方程[14 ] (见附录B).吸收层内衰减因子设置方式为: ...
Inversion of source-generated noise in high-resolution seismic data
2
1999
... 在地震勘探中,导波由近地表多次反射产生[3 ] .当相速度低于高速半空间横波速度时,导波的纵波分量和横波分量在波导结构中经过多次反射形成Rayleigh面波或Love面波.其中,Rayleigh 面波是由P波和SV波进行叠加干涉而成的,而Love面波则是由SH波构成.当相速度高于高速半空间横波速度且小于其纵波速度时,导波的横波分量会泄露到高速半空间中,剩余的由纵波分量主导的导波即为P—导波[26 ,30 ] . ...
... 图8 、图9 、图10 说明了泊松比为0.45时近地表低速层厚度的影响.从地震记录上来看:面波在地震波场中占主导地位,能量最强,传播速度最慢.P—导波传播速度比面波快,常常尾随在折射波之后出现.层厚为10 m时,在地震记录中面波呈发散的“扫帚状”,P—导波呈“叠瓦状”,如图8a 所示.当层厚增加到20 m时,因为面波传播深度大约为一个波长,但横波的波长与层厚相比很小,所以面波主要集中在上层传播,此时面波的频散变弱,如图9a 所示.当层厚增加到40 m时,因为P波的主波长小于层厚,所以可以明显地辨别出多次P波反射,如图10a 所示.面波和P—导波的能量在频散图像中的分布范围也有明显差异,从频散图像上来看,面波主要分布在左下角的低频低速区域,P—导波主要分布在图像上方的高速区域.层厚为10 m时,如图8b 所示,面波和P—导波都表现出明显的频散.面波在低频部分的相速度和高频部分的相速度分别趋于均匀半空间S波速度540 m/s和表层S波速度330 m/s的0.92倍左右.P—导波的频率集中在40~80 Hz之间,波导的这种带通滤波效应与泄漏到半空间中的S波能量有关[30 ] .P—导波和纯P波频散曲线两者的整体趋势基本一致但并不完全重合,这在一定程度上直观地表明P—导波频散曲线与纵波速度结构关系密切.另一方面也说明了 P—导波虽然主要由纵波分量主导,但仍然会受到横波分量的影响,这导致了其频散曲线比P波频散曲线更加复杂.当层厚增加到20 m时,如图9b 所示,P—导波表现出与相应的纯P波频散曲线相关的3个模态分支.层厚进一步增加到40 m时,如图10b 所示,P—导波出现6个模态分支,相速度大于1 800 m/s的部分表示能量泄漏到半空间中. ...
A numerical free-surface condition for elastic/viscoelastic finite-difference modeling in the presence of topography
1
1996
... 地球的自由表面和近地表下方高速层的顶界面之间可视为一种有效的层状波导[19 ] ,为了真实地模拟出面波和P—导波的波动现象,必须设置合理的自由地表边界条件.在水平自由表面上,应力分量必须满足如下条件: τ x z ( x , 0 , t ) = 0 , σ z z ( x , 0 , t ) = 0 . 本文使用应力镜像法[11 ,31 ] 处理自由边界,在自由界面上设置真空层( v p , v s σ z z τ x z σ z z N 阶交错网格有限差分自由边界在空间域中表示为: ...
一阶弹性波方程交错网格高阶差分解法稳定性研究
1
2000
... Jean[11 ] 、Levander[12 ] 、董良国等[32 ] 国内外许多专家都研究过交错网格差分格式下解的稳定性问题.总结前人研究成果得知均匀、完全弹性、各向同性介质中2N 阶精度的稳定性条件表达式为: ...
一阶弹性波方程交错网格高阶差分解法稳定性研究
1
2000
... Jean[11 ] 、Levander[12 ] 、董良国等[32 ] 国内外许多专家都研究过交错网格差分格式下解的稳定性问题.总结前人研究成果得知均匀、完全弹性、各向同性介质中2N 阶精度的稳定性条件表达式为: ...
基于互相关相移的主动源地震面波频散成像方法
2
2017
... 图7a 是在单炮记录图6a 和图6b 中炮检距为50 m处提取的0.2~0.256 s时的质点运动轨迹;图7b 是Rayleigh面波最大振幅随炮检距变化曲线;图7c 是用互相关相移法[33 ] 得到的频散成像.由图7a 可以看出Rayleigh面波是一种椭圆极化波.在二维直角坐标系下面波以平面形式传播,由于平面波没有几何扩散效应,所以随着炮检距增大面波振幅几乎不衰减[34 ] ,如图7b 所示.由图7c 可以看出均匀半空间介质中激发产生的面波不发生频散现象,频散谱近似是一条水平直线,其对应的相速度值与理论值506.6 m/s基本吻合,这也说明本文正演模拟和频散特征提取方法的准确性和有效性. ...
... 图8a 、9a 、10a 、11a 、12a 分别显示了模型1~5弹性波数值模拟的地震记录(垂直分量);图8b 、9b 、10b 、11b 、12b 分别显示了从图8a 、9a 、10a 、11a 、12a 中用互相关相移法[33 ] 提取的频散成像、用快速 δ [35 -36 ] 计算完全弹性介质中面波频散曲线和纯P波频散曲线. ...
基于互相关相移的主动源地震面波频散成像方法
2
2017
... 图7a 是在单炮记录图6a 和图6b 中炮检距为50 m处提取的0.2~0.256 s时的质点运动轨迹;图7b 是Rayleigh面波最大振幅随炮检距变化曲线;图7c 是用互相关相移法[33 ] 得到的频散成像.由图7a 可以看出Rayleigh面波是一种椭圆极化波.在二维直角坐标系下面波以平面形式传播,由于平面波没有几何扩散效应,所以随着炮检距增大面波振幅几乎不衰减[34 ] ,如图7b 所示.由图7c 可以看出均匀半空间介质中激发产生的面波不发生频散现象,频散谱近似是一条水平直线,其对应的相速度值与理论值506.6 m/s基本吻合,这也说明本文正演模拟和频散特征提取方法的准确性和有效性. ...
... 图8a 、9a 、10a 、11a 、12a 分别显示了模型1~5弹性波数值模拟的地震记录(垂直分量);图8b 、9b 、10b 、11b 、12b 分别显示了从图8a 、9a 、10a 、11a 、12a 中用互相关相移法[33 ] 提取的频散成像、用快速 δ [35 -36 ] 计算完全弹性介质中面波频散曲线和纯P波频散曲线. ...
柱对称条件下地震面波波场正演研究
1
2023
... 图7a 是在单炮记录图6a 和图6b 中炮检距为50 m处提取的0.2~0.256 s时的质点运动轨迹;图7b 是Rayleigh面波最大振幅随炮检距变化曲线;图7c 是用互相关相移法[33 ] 得到的频散成像.由图7a 可以看出Rayleigh面波是一种椭圆极化波.在二维直角坐标系下面波以平面形式传播,由于平面波没有几何扩散效应,所以随着炮检距增大面波振幅几乎不衰减[34 ] ,如图7b 所示.由图7c 可以看出均匀半空间介质中激发产生的面波不发生频散现象,频散谱近似是一条水平直线,其对应的相速度值与理论值506.6 m/s基本吻合,这也说明本文正演模拟和频散特征提取方法的准确性和有效性. ...
柱对称条件下地震面波波场正演研究
1
2023
... 图7a 是在单炮记录图6a 和图6b 中炮检距为50 m处提取的0.2~0.256 s时的质点运动轨迹;图7b 是Rayleigh面波最大振幅随炮检距变化曲线;图7c 是用互相关相移法[33 ] 得到的频散成像.由图7a 可以看出Rayleigh面波是一种椭圆极化波.在二维直角坐标系下面波以平面形式传播,由于平面波没有几何扩散效应,所以随着炮检距增大面波振幅几乎不衰减[34 ] ,如图7b 所示.由图7c 可以看出均匀半空间介质中激发产生的面波不发生频散现象,频散谱近似是一条水平直线,其对应的相速度值与理论值506.6 m/s基本吻合,这也说明本文正演模拟和频散特征提取方法的准确性和有效性. ...
Free-mode surface-wave computations
1
1996
... 图8a 、9a 、10a 、11a 、12a 分别显示了模型1~5弹性波数值模拟的地震记录(垂直分量);图8b 、9b 、10b 、11b 、12b 分别显示了从图8a 、9a 、10a 、11a 、12a 中用互相关相移法[33 ] 提取的频散成像、用快速 δ [35 -36 ] 计算完全弹性介质中面波频散曲线和纯P波频散曲线. ...
多分量面波研究进展
1
2021
... 图8a 、9a 、10a 、11a 、12a 分别显示了模型1~5弹性波数值模拟的地震记录(垂直分量);图8b 、9b 、10b 、11b 、12b 分别显示了从图8a 、9a 、10a 、11a 、12a 中用互相关相移法[33 ] 提取的频散成像、用快速 δ [35 -36 ] 计算完全弹性介质中面波频散曲线和纯P波频散曲线. ...
多分量面波研究进展
1
2021
... 图8a 、9a 、10a 、11a 、12a 分别显示了模型1~5弹性波数值模拟的地震记录(垂直分量);图8b 、9b 、10b 、11b 、12b 分别显示了从图8a 、9a 、10a 、11a 、12a 中用互相关相移法[33 ] 提取的频散成像、用快速 δ [35 -36 ] 计算完全弹性介质中面波频散曲线和纯P波频散曲线. ...
Dispersion inversion for P- and S-wave velocities based on guided P and Scholte waves
1
2023
... P—导波频散数据不仅能够从石油地震数据资料中提取,在天然地震信号、背景噪声和工程勘探地震数据中同样能够观测到P—导波信号.P—导波频散信息对纵波速度结构的约束能力为地下纵波速度模型的构建提供了一个新的思路和手段.通过面波和P—导波一体化反演方法能够同时得到地下的纵横波速度模型,进一步计算可以得到泊松比模型[37 ] ,该方法可以广泛应用于岩石圈结构探测、资源勘探、地质灾害防治、环境调查、城市地下空间建设、岩土工程和无损检测等领域,具有广阔的应用前景. ...