可控源音频大地电磁和微动资料的拟二维联合反演

doi:10.11720/wtyht.2024.1477

可控源音频大地电磁和微动资料的拟二维联合反演

张继伟^,, 谭慧

香港中文大学(深圳) 城市地下空间及能源研究院,广东深圳 518172

Quasi-two-dimensional joint inversion of the data from the controlled source audio-frequency magnetotellurics and the microtremor survey

ZHANG Ji-Wei^,, TAN Hui

Institute of Urban Underground Space and Energy Studies, The Chinese University of Hong Kong (Shenzhen), Shenzhen 518172, China

第一作者: 张继伟(1995-),男,硕士研究生,主要从事电磁法正反演和微动探测方法技术研究工作。Email:1064010459@qq.com

责任编辑: 朱晓颖

收稿日期: 2023-11-10 修回日期: 2023-12-29

基金资助:

云南省2023科技计划项目“云南省中深层地热能开发关键技术研究”(202302AF080001)
可控源电磁和微动探测数据联合反演及其在北京市地热勘探中的应用(8192041)

Received: 2023-11-10 Revised: 2023-12-29

摘要

可控源音频大地电磁(CSAMT)和微动探测在城市强干扰条件下均有较好的应用前景,但单一的地球物理反演具有多解性。为了实现不同地球物理方法优势的互补,同时解决单点反演横向不连续性的问题,本文开展了CSAMT和微动探测数据的拟二维联合反演研究。作者将横向约束矩阵引入联合反演的目标函数中,同时采用有限内存拟牛顿反演算法(LBFGS),实现了两种方法的联合反演。通过理论模型合成数据反演算例,验证了联合反演的可靠性和有效性。结果表明,联合反演相比单一数据反演能有效地提高反演结果的准确度,其电阻率模型和横波速度结构更加趋于一致,同时,横向约束能有效地降低相邻测点物性参数的不连续性。通过加入横向约束的拟二维联合反演以单点反演的效率,获得了更合理的物性参数和地下结构的剖面结果,提高了反演的可靠性。

关键词： 联合反演; 可控源音频大地电磁法; 微动探测; 横向约束反演

Abstract

Both the controlled source audio-frequency magnetotellurics (CSAMT) and the microtremor survey exhibit promising application prospectsunder strong urban interference. However,single geophysical inversion methods are challenged by a multiplicity of solutions. To achieve the complementary advantages of different geophysical methods, and address the lateral discontinuity of single-point inversion, this studyexplored the quasi-two-dimensional joint inversion of the CSAMTand microtremor survey data. It enabled the joint inversionby introducing a lateral constraint matrix into the objective function for joint inversion and employing the limited-memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) algorithm. The reliability and effectiveness of the joint inversion were verified using the inversion example of synthetic data from theoretical models. The results show that compared to single data inversion, the joint inversion can effectively improve the accuracy of inversion results, with the resistivity model more consistent with theshear-wave velocity structure. Moreover,lateral constraints can effectively reduce the discontinuity of the physical parameters of adjacentsurvey points. The quasi-two-dimensional joint inversion with lateral constraints enhances the inversion reliability by obtaining more reasonable profile results of physical parameters and structures with the efficiency of single-point inversion.

Keywords： joint inversion; controlled source audio-frequency magnetotellurics; microtremor survey; laterally constrained inversion

PDF (4316KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张继伟, 谭慧. 可控源音频大地电磁和微动资料的拟二维联合反演[J]. 物探与化探, 2024, 48(4): 1094-1102 doi:10.11720/wtyht.2024.1477

ZHANG Ji-Wei, TAN Hui. Quasi-two-dimensional joint inversion of the data from the controlled source audio-frequency magnetotellurics and the microtremor survey[J]. Geophysical and Geochemical Exploration, 2024, 48(4): 1094-1102 doi:10.11720/wtyht.2024.1477

0 引言

随着时代经济发展及环境保护的需要,如何在强干扰城镇地区或环境敏感型地区获得高分辨率的地球物理探测结果成为了当下研究热点^[1⇓-3]。可控源音频大地电磁法(controlled source audio frequency magnatelluric methods,CSAMT)是一种人工源电磁测深方法,具有抗干扰能力强、探测深度大的优点^[4-5]。但受趋肤效应的影响,电磁场强度随深度呈指数衰减,纵向分辨率降低;同时难以识别电阻率差异小的地质体。

微动探测是一种抗干扰能力强、探测深度大、施工效率高的天然源面波勘探方法,已广泛应用于城区和环境敏感型地区^[6-7]。但相对传统主动源地震勘探,存在信号强度弱的缺点,同时对于地下构造复杂的地区、尤其速度差异小的地区,很难获得可靠的结果。

联合反演充分利用不同地球物理数据,压制噪声对数据的影响,实现不同地球物理方法的优势互补,减小单一方法反演固有的非唯一性问题^[8]。电磁法与地震方法的一维、二维联合反演已有许多研究成果^{[9⇓⇓⇓⇓-14]},但对于电磁法与微动探测的联合反演的研究较少。考虑到电阻率和横波速度在空间分布具有相似性,本文采取了更新同一套厚度参数约束电阻率和横波速度更新从而实现了两种方法的联合反演。为消除传统一维反演结果相邻测点物性参数的突变,本文在联合反演基础之上引入了横向约束反演。虽然二、三维反演日趋成熟,但计算复杂,内存需求大,短时间难以得到准确结果。横向约束反演实质为一维反演,反演速度快,同时能够克服一维反演相邻测点间物性参数不连续的问题。对于地下层状沉积模型,二维反演结果在空间上平滑过度,反而无法分辨地层界面,横向约束反演取得了更好的效果^[15]。由于CSAMT和微动探测主要用于干扰较大的地区,如何去噪提高数据质量也是关键问题,据王颖^[16]研究表明横向约束反演加入使得抗噪性更好。

Auken等^[17]首先在直流电数据中引入了横向约束反演,之后又应用于二维电阻率数据^[15]、EM34剖面数据^[18]和三维瞬变电磁数据^[19]的反演。Siemon等^[20]和蔡晶^[21]将横向约束反演应用到了频率域航空电磁数据中,取得了很好的效果。殷长春等^[22]将横向约束反演应用到了时间域航空电磁数据反演中。本文将横向约束反演首次应用于CSAMT和微动探测的联合反演中。

1 层状介质单方法正演理论

1.1 可控源音频大地电磁法一维正演理论

由电磁场满足的麦克斯韦方程组,假设水平电偶极源沿x轴,引入矢量位 $A (A_{x}, 0, A_{z})$ 和标量位U,对于层状介质,参考考夫曼等^[23]求解矢量位和标量位得到柱坐标系下电磁场的表达式:

(1)

\begin{array}{l} \vec{H_{r}} = - \frac{I d x}{2 π r} s i n ϕ [\int_{0}^{\infty} \frac{m}{m + (n_{1} / R^{*})} J_{1} (m r) d m + \\ r \int_{0}^{\infty} \frac{n_{1}}{R^{*}} \frac{m}{m + (n_{1} / R^{*})} J_{0} (m r) d m] \end{array}

(2)

\vec{H_{ϕ}} = \frac{I d x}{2 π r} c o s ϕ [\int_{0}^{\infty} \frac{m}{m + n_{1} / R^{*}} J_{1} (m r) d m]

(3)

\vec{H_{z}} = \frac{I d x}{2 π} s i n ϕ [\int_{0}^{\infty} \frac{m^{2}}{m + n_{1} / R^{*}} J_{1} (m r) d m]

(4)$\overrightarrow{E_{r}}=\frac{I \mathrm{~d} x}{2 \pi} \cos \phi\left[\frac{i \omega \mu}{r} \int_{0}^{\infty} \frac{1}{m+\left(n_{1} / R^{*}\right)} J_{1}(m r) \mathrm{d} m-\rho_{1} \int_{0}^{\infty} \frac{m n_{1}}{R} J_{0}(m r) \mathrm{d} m+\frac{\rho_{1}}{r} \int_{0}^{\infty} \frac{n_{1}}{R} J_{1}(m r) \mathrm{d} m\right]$,

(5)$\overrightarrow{E_{\phi}}=\frac{I \mathrm{~d} x}{2 \pi} \sin \phi\left[\frac{\rho_{1}}{r} \int_{0}^{\infty} \frac{n_{1}}{R} J_{1}(m r) \mathrm{d} m-i \omega \mu \int_{0}^{\infty} \frac{m}{m+\left(n_{1} / R^{*}\right)} J_{0}(m r) \mathrm{d} m+\frac{i \omega \mu}{r} \int_{0}^{\infty} \frac{1}{m+\left(n_{1} / R^{*}\right)} J_{1}(m r) \mathrm{d} m\right] $。

其中: $\vec{H}$ 为磁场强度(A/m); $\vec{E}$ 为电场强度(V/m); $μ$ 为磁化率( $H / m$ );I为供电电流; $J_{0} (m r)$ 为第一类零阶贝塞尔函数; $J_{1} (m r)$ 为第一类一阶贝塞尔函数; $m$ 为分离常数; $r = \sqrt{x^{2} + y^{2}}$ 为柱坐标中的极径; $ϕ$ 为坐标轴x和径向 $r$ 之间的夹角; $n_{i} = \sqrt{m^{2} - k_{i}^{2}}$ , $k_{i}^{2}$ 为第 $i$ 层沿平行层面方向的波数, $k_{i}^{2} = i σ_{i} μ ω$ ; $d x$ 为偶极矩; $ρ_{N}$ 为第N层电阻率。

通过公式$\overrightarrow{E_{x}}= \ \overrightarrow{E_{r}} \cos \phi-\overrightarrow{E_{\phi}} \sin \phi$、 $\overrightarrow{E_{y}}=\overrightarrow{E_{r}} \sin \phi+ \ \overrightarrow{E_{\phi}} \cos \phi$、 $\overrightarrow{H_{x}}=\overrightarrow{H_{r}} \cos \phi-\overrightarrow{H_{\phi}} \sin \phi$ 和 $\overrightarrow{H_{y}}=\ \overrightarrow{H_{r}} \sin \phi+\overrightarrow{H_{\phi}} \cos \phi$将式(1)~(5)的柱坐标场值表达式化简得到直角坐标系下的电磁场分量表达式:

(6)

\begin{array}{l} \vec{E_{x}} = \frac{I d x}{2 π} (i ω μ_{0}) [\int_{0}^{\infty} \frac{m}{m + n_{1} / R^{*}} J_{0} (m r) d m + \frac{1}{r} \int_{0}^{\infty} (\frac{n_{1}}{k_{1}^{2} R} - \frac{1}{m + n_{1} / R^{*}}) J_{1} (m r) d m] s i n^{2} ϕ \\ + \frac{I d x}{2 π} (i ω μ_{0}) [\int_{0}^{\infty} \frac{m n_{1}}{k_{1}^{2} R} J_{0} (m r) d m - \frac{1}{r} \int_{0}^{\infty} (\frac{n_{1}}{k_{1}^{2} R} - \frac{1}{m + n_{1} / R^{*}}) J_{1} (m r) d m] c o s^{2} ϕ \end{array}

(7)

\begin{array}{l} \vec{H_{y}} = \frac{I d x}{2 π} [\int_{0}^{\infty} \frac{m}{m + n_{1} / R^{*}} \cdot \frac{n_{1}}{R^{*}} J_{0} (m r) d m - \frac{1}{r} \int_{0}^{\infty} \frac{m}{m + n_{1} / R^{*}} J_{1} (m r) d m] s i n^{2} ϕ \\ + \frac{I d x}{2 π} [\frac{1}{r} \int_{0}^{\infty} \frac{m}{m + n_{1} / R^{*}} J_{1} (m r) d m] c o s^{2} ϕ \end{array}

。

由卡尼亚视电阻率公式,可以求出不同频率范围的视电阻率值:

(8)

ρ_{w} = {|\vec{E_{x}} / \vec{H_{y}}|}^{2} / (ω μ)

其中, $R^{*}$ 和 $R$ 分别为:

(9)

R^{*} = c o t h [n_{1} H_{1} + a r c o t h \frac{n_{1}}{n_{2}} c o t h (n_{2} H_{2} + \dots + a r c o t h \frac{n_{N - t}}{n_{N}})]

(10)

R = c o t h [n_{1} H_{1} + a r c o t h (\frac{n_{1}}{n_{2}} \frac{ρ_{1}}{ρ_{2}}) c o t h (n_{2} H_{2} + \dots + a r c o t h (\frac{n_{N - 1}}{n_{N}} \frac{ρ_{N - 1}}{ρ_{N}}))]

。

1.2 微动探测一维正演理论

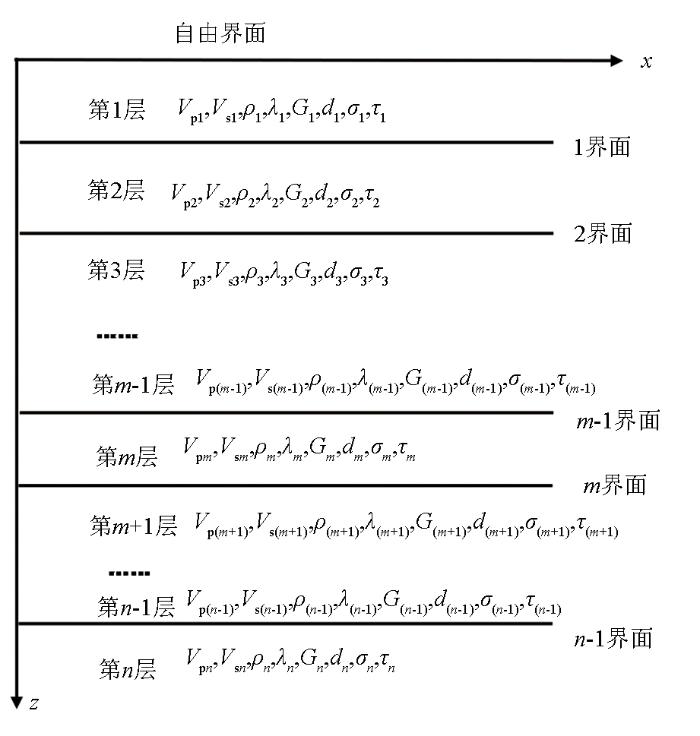
微动一维正演即是层状介质面波的频散。对于n层半无限空间介质,层状模型如图1所示,假设微动面波传播的方向为x轴,垂直向下为z轴,由knopoff快速算法^[24],借助行列式变换,第m层的位移与应力的分量为:

(11)

\{\begin{array}{l} V_{R} U_{x m} = c o s P_{m} A_{m} - i s i n P_{m} B_{m} + γ_{β_{m}} c o s Q_{m} C_{m} - i γ_{β_{m}} s i n Q_{m} D_{m} \\ V_{R} U_{z m} = - i γ_{α m} s i n P_{m} A_{m} + γ_{α m} c o s P_{m} B_{m} + i s i n Q_{m} C_{m} - c o s Q_{m} D_{m} \\ σ_{m} = ρ_{m} (γ_{m} - 1) c o s P_{m} A_{m} - i ρ_{m} (γ_{m} - 1) s i n P_{m} B_{m} \\ + ρ_{m} γ_{m} γ_{β_{m}} c o s Q_{m} C_{m} - i ρ_{m} γ_{m} γ_{β_{m}} s i n Q_{m} D_{m} \\ τ_{m} = i ρ_{m} γ_{m} γ_{α m} s i n P_{m} A_{m} - ρ_{m} γ_{m} γ_{α m} c o s P_{m} B_{m} \\ - i ρ_{m} (γ_{m} - 1) s i n Q_{m} C_{m} + ρ_{m} (γ_{m} - 1) c o s Q_{m} D_{m} \end{array}

。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 弹性介质层状模型

Fig.1 Layered model of elastic media

其中: $V_{P m}$ 是纵波速度; $V_{S m}$ 是横波速度; $V_{R}$ 是面波速度; $ρ_{m}$ 是介质密度; $λ_{m}$ 是拉梅常数; $G_{m}$ 是剪切模量; $d_{m}$ 是图1中各层厚度; $k = 2 π f / V_{R} = 2 π / λ_{R}$ 是波数; $U_{x m}$ 和 $U_{z m}$ 是x和z方向的位移; $σ_{m}$ 是法向的应力; $τ_{m}$ 是切向的应力。$A_{m}=-V_{\mathrm{P} m}^{2}\left(\mathrm{C}_{m}+\mathrm{D}_{m}\right)$,$B_{m}=-V_{\mathrm{P}_{m}}^{2}\left(\mathrm{C}_{m}-\mathrm{D}_{m}\right)$,$\mathrm{C}_{m}=-2 V_{\mathrm{S} m}^{2}\left(\mathrm{C}_{m}^{\prime}+\mathrm{D}_{m}^{\prime}\right)$,$\mathrm{D}_{m}=-2 V_{\mathrm{S} m}^{2}\left(\mathrm{C}_{m}^{\prime}+\mathrm{D}_{m}^{\prime}\right)$,
$P_{m}=k \gamma_{\alpha m} d_{m}, Q_{m}=k \gamma_{\beta m} d_{m}$,这里的$\mathrm{C}_{m}、\mathrm{D}_{m}、\mathrm{C}_{m}^{\prime}$和$\mathrm{D}_{m}^{\prime}$均为常数。 $γ_{m} = 2 (V_{S m} / V_{R})^{2}$ , $\begin{array}{l} γ_{α m} = \{\begin{array}{l} {[V_{R} / V_{P m} - 1]}^{1 / 2}, (V_{R} > V_{P m}) \\ - i {[1 - (V_{R} / V_{P m})^{2}]}^{1 / 2}, (V_{R} < V_{P m}) \end{array}, \\ γ_{β m} = \{\begin{array}{l} {[V_{R} / V_{S m} - 1]}^{1 / 2}, (V_{R} > V_{S m}) \\ - i {[1 - (V_{R} / V_{S m})^{2}]}^{1 / 2}, (V_{R} < V_{P m}) \end{array} \end{array}$ 。

对于第m层介面,由界面上位移与应力满足连续的条件,可以得到界面上满足的子矩阵,之后通过矩阵组合、Laplace分解和简化,得到n层介质的频散函数F(ω,V_R)。

当n为偶数时:

(12)

\begin{matrix} F (ω, V_{R}) = [V^{(n - 1)}, W^{(n - 1)}, R^{(n - 1)}, S^{(n - 1)}] \cdot [\begin{array}{l} - {(1 - V_{R}^{2} / V_{P n}^{2})}^{1 / 2} \\ - {(1 - V_{R}^{2} / V_{P n}^{2})}^{1 / 2} \cdot {(1 - V_{R}^{2} / V_{S n}^{2})}^{1 / 2} \\ 1 \\ - {(1 - V_{R}^{2} / V_{S n}^{2})}^{1 / 2} \end{array}] \cdot ε \end{matrix}

;

当n为奇数时:

(13)

\begin{matrix} F (ω, V_{R}) = [V^{(n - 1)}, W^{(n - 1)}, R^{(n - 1)}, S^{(n - 1)}] \cdot [\begin{array}{l} {(1 - V_{R}^{2} / V_{S n}^{2})}^{1 / 2} \\ 1 \\ - {(1 - V_{R}^{2} / V_{P n}^{2})}^{1 / 2} \cdot {(1 - V_{R}^{2} / V_{S n}^{2})}^{1 / 2} \\ {(1 - V_{R}^{2} / V_{P n}^{2})}^{1 / 2} \end{array}] \cdot ε \end{matrix}

。

其中: $V^{(n - 1)}$ 、 $W^{(n - 1)}$ 、 $R^{(n - 1)}$ 、 $S^{(n - 1)}$ 均为实数; $ε = {(- 1)}^{n - 1} ρ_{1}^{2} V_{R}^{2} / (γ_{α n} γ_{β n} γ_{n} ρ_{n}^{2} V_{P n}^{2})$ 。

2 横向约束联合反演

2.1 联合反演目标函数

由正则化反演理论^[25],联合反演目标函数由数据项和模型项组成。其中数据项包括两种方法的数据项,具体形式如下:

(14)

\begin{array}{l} φ (m) = ({W_{d}}^{c s} Δ d_{c s})^{T} ({W_{d}}^{c s} Δ d_{c s}) + \\ ({W_{d}}^{m s} Δ d_{m s})^{T} ({W_{d}}^{m s} Δ d_{m s}) + \\ λ_{1} (R_{P} {m)}^{T} (R_{P} m) + λ_{2} (R_{h} {m)}^{T} (R_{h} m) \end{array}

。

其中: ${W_{d}}^{c s}$ 和 ${W_{d}}^{m s}$ 分别为CSAMT与微动探测的数据协方差矩阵; $Δ d_{c s}$ 和 $Δ d_{m s}$ 分别为CSAMT模型正演理论响应数据与观测数据的差值、微动探测模型正演理论响应数据与观测数据的差值; $R_{P}$ 为电阻率、厚度、横波速度的横向约束矩阵, $R_{h}$ 为深度的横向约束矩阵;λ₁,λ₂为正则化因子;

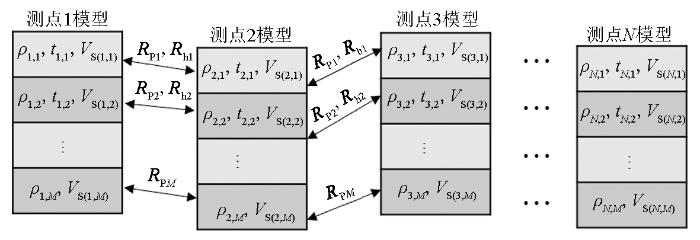
m = [l g (ρ_{1,1}), l g (ρ_{1,2}) \dots l g (ρ_{N, M}), l g (t_{1,1}), l g (t_{1,2}), \dots, l g (t_{N, (M - 1)}), l g (V_{S (1,1)}), l g (V_{S (1,2)}), \dots l g (V_{S (N, M)})]

为反演模型参数矩阵(图2),由电阻率 $ρ_{(N, M)}$ 、厚度 $t_{(N, M - 1)}$ 、横波速度 $V_{S (N, M)}$ 组成(M为层数,N为测点个数)。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 拟二维联合反演模型示意

Fig.2 Schematic of quasi two-dimensional joint inversion model

2.2 约束矩阵

2.2.1 电阻率、厚度和横波速度的横向约束矩阵

为了减小相邻测点间的电阻率、层厚度和横波速度参数的差异,引入了横向约束矩阵 $R_{p}$ 。参照Jackson^[26]获得主要模型参数的先验信息包含在额外的数据集 $m_{p r i o r}$ :

(15)

I m_{t r u e} = m_{p r i o r} + e_{p r i o r}

这里 $e_{p r i o r}$ 为先验模型误差项, $I$ 是模型维度的单位矩阵。

加入横向约束形式上类似的设为

(16)

R_{p} m_{t r u e} = r_{p} + e_{r p}

$e_{r p}$ 为相邻测点间电阻率、层厚度、横波速度的先验模型的误差项。当约束有效的情况下, $r_{p} = - R_{p} m_{r e f}$ ,则 $R_{p}$ 为1和-1构成的稀疏矩阵,形式为

R_{p} = [\begin{array}{l} 1 & 0 & \dots & 0 & - 1 & 0 & \dots & 0 & 0 & 0 \\ 0 & 1 & 0 & \dots & 0 & - 1 & 0 & \dots & 0 & 0 \\ ︙ & ︙ & ︙ \\ 0 & 0 & 0 & \dots & 0 & 1 & 0 & \dots & 0 & - 1 \end{array}]

。

2.2.2 深度横向约束矩阵

为了得到更为光滑的反演模型,引入约束矩阵 $R_{h}$ 实现深度的横向约束。类比横向约束矩阵 $R_{p}$ 的构建,把深度横向约束矩阵加入到真实模型里,即

(17)

R_{h} m_{t r u e} = r_{h} + e_{r h}

。

当约束有效情况下:

(18)

r_{h} = - R_{h} m_{r e f}

。

因加入了厚度的先验信息,需引入对厚度的导数得到深度的约束矩阵 $R_{h}$ 。该矩阵关于电阻率、横波速度的导数全为0,在水平位置x_k处关于厚度的导数^[15]为

(19)

\frac{\partial l g (h_{k, l})}{\partial l g (t_{i, j})} = \frac{t_{i, j}}{h_{k, l}} \cdot \frac{\partial h_{k, l}}{\partial t_{i, j}} = \frac{t_{i, j}}{h_{k, l}} \cdot \frac{\partial \overset{l}{\sum_{s = 1}} t_{k, s}}{\partial t_{i, j}} = \{\begin{array}{l} \frac{t_{i, j}}{h_{i, j}} & f o r i = k a n d j \leq l \\ 0 & 其 他 情 况 \end{array}

。

式中: $h_{k, l}$ 表示测点k处l层的深度; $t_{i, j}$ 表示测点i处第j层的厚度。因此,可以得出在x_k和x_k₊₁处深度横向约束矩阵如下:

$\boldsymbol{R}_{\mathrm{h}}=\left[\begin{array}{cccccccccccccccccccc} \cdots & 0 & \cdots & 0 & 1 & 0 & 0 & \cdots & 0 & \cdots & \cdots & 0 & \cdots & 0 & -1 & 0 & 0 & \cdots & 0 & \cdots \\ \cdots & 0 & \cdots & 0 & \frac{t_{k, 1}}{h_{k, 2}} & \frac{t_{k, 2}}{h_{k, 2}} & 0 & \cdots & 0 & \cdots & \cdots & 0 & \cdots & 0 & -\frac{t_{k+1,1}}{h_{k+1,2}} & -\frac{t_{k+1,2}}{h_{k+1,2}} & 0 & \cdots & 0 & \cdots \\ & \vdots & & \vdots & \vdots & \vdots & & & \vdots & & \vdots & & \vdots & \vdots & \vdots & & & \vdots & \\ \cdots & 0 & \cdots & 0 & \frac{t_{k, 1}}{h_{k, n}} & \frac{t_{k, 2}}{h_{k, n}} & \frac{t_{k, 3}}{h_{k, n}} & \cdots & \frac{t_{k, n}}{h_{k, n}} & \cdots & \cdots & 0 & \cdots & 0 & -\frac{t_{k+1,1}}{h_{k+1, n}} & -\frac{t_{k+1,2}}{h_{k+1, n}} & -\frac{t_{k+1,3}}{h_{k+1, n}} & \cdots & -\frac{t_{k+1, n}}{h_{k+1, n}} & \cdots \end{array}\right]$。

2.3 方程求解

由联合反演目标函数可求得梯度表达式:

(20)

\begin{array}{l} \nabla \cdot φ (m) = - 2 ({W_{d}}^{c s} J_{ρ})^{T} ({W_{d}}^{c s} Δ d_{c s}) - \\ 2 ({W_{d}}^{c s} J_{t h i}^{c s})^{T} ({W_{d}}^{c s} Δ d_{c s}) - 2 ({W_{d}}^{m s} J_{v s})^{T} ({W_{d}}^{m s} Δ d_{m s}) - \\ 2 ({W_{d}}^{m s} J_{t h i}^{m s})^{T} ({W_{d}}^{m s} Δ d_{m s}) + 2 λ_{1} ({R_{p}}^{T} R_{p} m) \\ \begin{matrix} + 2 λ_{2} ({R_{h}}^{T} R_{h} m) \end{matrix} \end{array}

。

式中: $J_{ρ}$ 为电阻率的雅可比矩阵; $J_{v s}$ 为横波速度的雅可比矩阵; $J_{t h i}^{c s}$ 为 CSAMT厚度的雅可比矩阵; $J_{t h i}^{m s}$ 为微动探测厚度雅可比矩阵。由于多参数求偏导公式过于繁琐,因此本文雅可比矩阵的求取采用的是扰动法。首先给定初始模型 $m_{0}$ ,由初始模型进行正演得到正演响应(本文采用的是视电阻率、相位和相速度) $d_{0}^{c s}$ 和 $d_{0}^{m s}$ ;由初始模型给出扰动量,这里记为 $Δ$ ;由初始模型对要反演的模型逐个加上扰动即可得到新的模型矩阵,记为 $m_{1}$ ;由新模型进行正演可得到新的正演响应 $d_{1}^{c s}$ 和 $d_{1}^{m s}$ ,通过 $(d_{1} - d_{0}) (m_{0}) / (Δ \cdot d_{0})$ 即可求得对应参数的雅可比矩阵 $J$ 。通过更新参考模型重复上述扰动法求雅可比矩阵过程,直到满足反演终止条件。得到雅可比矩阵后,进而求出梯度值,再采用LBFGS算法即可得到模型更新。

3 理论模型算例及讨论

基于以上正演数值模拟及反演理论,采用Fortran语言开发了CSAMT与微动探测的联合反演算法,并引入了横向约束反演。为了检验联合反演算法的有效性和优越性,本文进行了理论模型合成数据的反演研究,设计了倾斜层状模型和台阶层状模型。

3.1 倾斜层状模型

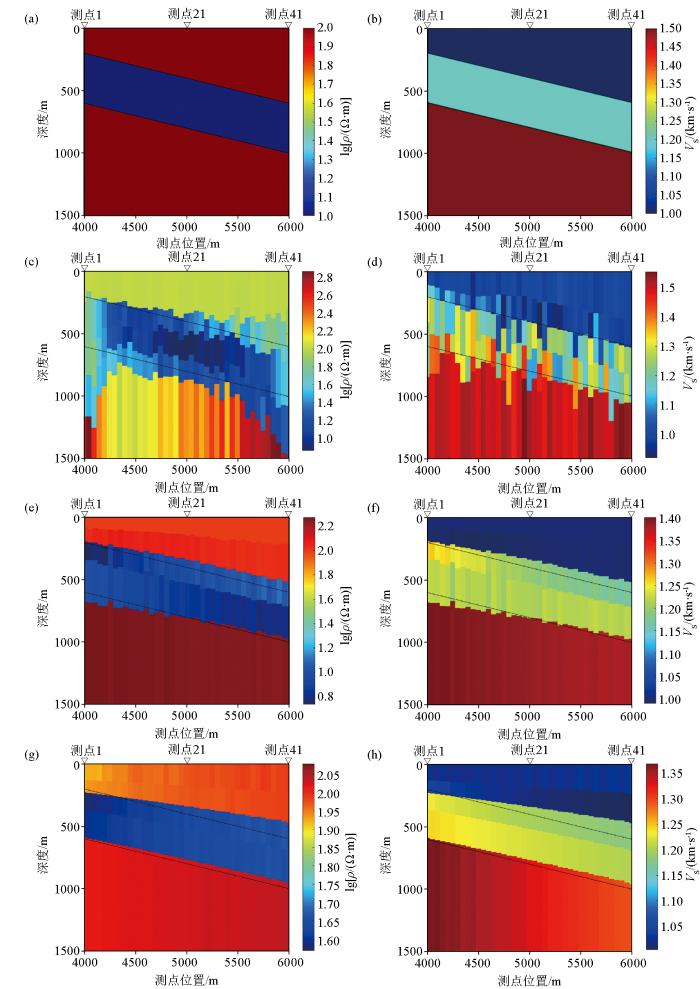
倾斜层状模型(图3a、3b)的3层电阻率分别为100、10、100 Ω·m,横波速度1.0、1.2、1.5 km/s。第一层测点1厚度200 m,测点41厚度600 m;第二层厚度400 m;第三层为均匀半空间。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 倾斜三层模型反演结果

a—倾斜三层电阻率模型;b—倾斜三层速度模型;c—电阻率反演结果;d—横波速度反演结果;e—无约束联合反演电阻率结果;f—无约束联合反演横波速度结果;g—横向约束联合反演电阻率结果;h—横向约束联合反演横波速度结果

Fig.3 Inversion results of the tilted three layer model

a—tilt three layer resistivity model; b—tilt three layer velocity model; c—single method inversion results (resistivity); d—single method inversion results (shear wave velocity); e—unconstrained joint inversion results (resistivity); f—unconstrained joint inversion results (shear wave velocity); g—lateral constraint joint inversion results (resistivity); h—lateral constraint joint inversion results (shear wave velocity)

CSAMT与微动探测均采用了41个测点,测点间隔为50 m,CSAMT收发距为4~6 km。CSAMT采用了2⁰~2¹³ Hz(指数间隔为1)之间的14个发射频率;微动探测采用了20个发射周期,在0.1~2.0 s(间隔0.1 s)之间。台阶模型采用了同样的发射接收参数。

其中CSAMT二维正演基于桂兵^[27]开发的张量CSAMT二维反演程序,该程序基于Siripunvaraporn等采用rebocc方法实现的大地电磁二维反演的程序发展而来;微动反演数据参考了方洪健^[28]、宓彬彬^[29]、吴萍萍^[10]等二、三维面波正演方法,采用一维正演频散数据拼凑得到的合成数据;一维正演程序采用Hermann和wang开发的Computer Program in Seismology 3.30开源程序。

反演初始模型设置为五层水平模型,每层电阻率为100 Ω·m,横波速度分别为0.8、0.9、1.0、1.2和1.3 km/s,厚度为200 m。合成数据加入5%的随机噪声(台阶模型合成数据同样加入5%随机噪声)。

电阻率、横波速度反演结果如图3c、3d所示,电阻率和横波速度反演结果在横向上“突变”现象都很严重,CSAMT方法在收发距首端与尾端异常体形态均偏离较严重,微动探测异常体形态也很紊乱;未加横向约束的电阻率、横波速度联合反演结果(图3e、3f)相比单方法反演在异常体形态恢复上有了很大提升,边界较为清晰,但存在小的“锯齿状”突变;加入横向约束的联合反演(图3g、3h)相比未加横向约束的反演结果,其“锯齿状”明显减小,层界面更连续光滑。

3.2 台阶模型

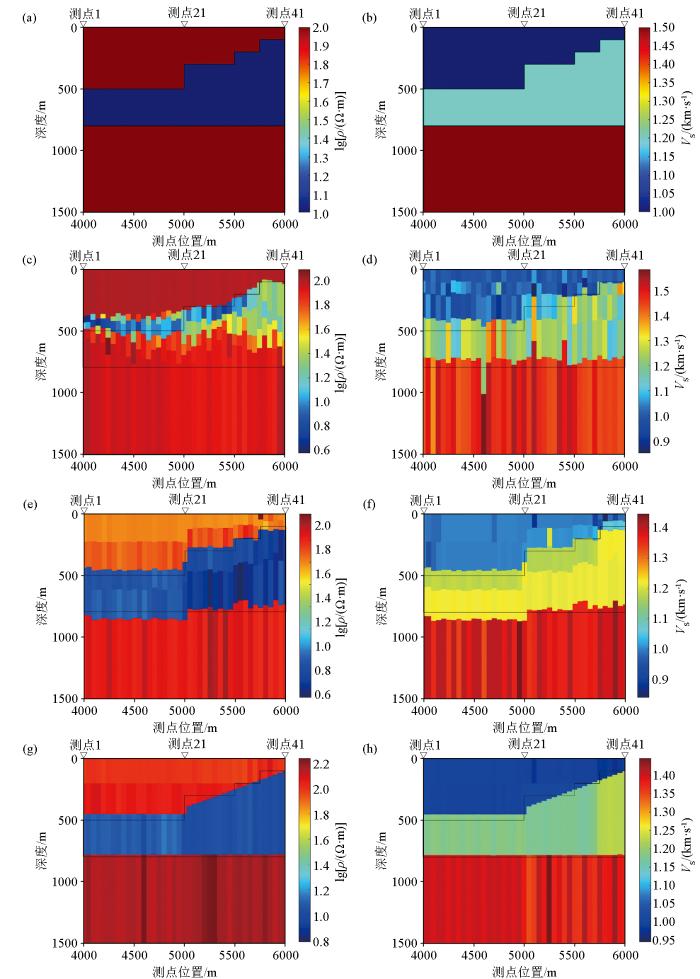
台阶模型如图4a、4b所示。三层的电阻率分别为100、10和100 Ω·m,横波速度分别为1.0、1.2、1.5 km/s。沿测线方向,四个台阶面顶层深度分别为500、300、200、100 m。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 台阶三层模型反演结果

a—台阶三层电阻率模型;b—台阶三层速度模型;c—电阻率反演结果;d—横波速度反演结果;e—无约束联合反演电阻率结果;f—无约束联合反演横波速度结果;g—横向约束联合反演电阻率结果;h—横向约束联合反演横波速度结果

Fig.4 Inversion results of step three layer model

a—step three layer resistivity model; b—step three layer velocity model; c—single method inversion results (resistivity); d—single method inversion results (shear wave velocity); e—unconstrained joint inversion results (resistivity); f—unconstrained joint inversion results (shear wave velocity); g—lateral constraint joint inversion results (resistivity); h—lateral constraint joint inversion results (shear wave velocity)

从电阻率、横波速度反演结果(图4c、4d)来看,在异常体结构上,CSAMT反演的上界面较清晰,微动探测反演的下界面较清晰,横向上电阻率值和横波速度值“突变”较严重。未加横向约束的联合反演(图4e、4f)显示台阶界面较清晰,电阻率和速度值恢复较好。加入横向约束的联合反演(图4g、4h)相比未加横向约束的联合反演,台阶形状更为连续,电阻率和速度值恢复较好,但棱角过于平滑,这可能是正则化形式的目标函数,模型项正则化因子选取较大而牺牲了部分数据拟合的缘故;但另一方面也反映出横向约束提升了相邻测点物性参数的连续性。

4 结论

本文介绍了CSAMT与微动探测横向约束拟二维联合反演的实施方法,并构建了两种方法的正演数值模拟、联合反演的目标函数形式及求解和横向约束矩阵,同时设计了理论模型算例对算法的有效性进行了验证。

1)理论模型反演结果表明:CSAMT采用一维反演剖面数据时,相邻测点间电阻率存在跳跃现象,结构也会发生一定程度的畸变;微动探测采用一维反演拟合一维正演拼凑的剖面数据时,结构反演结果比较清晰,但相邻测点间横波速度仍存在“突变”现象。

2)本文采用了厚度参数进行约束,实现了两种方法的联合反演,相比单方法反演的电阻率和横波速度值都更接近理论模型,也更加趋于一致。在联合反演中引入横向约束后,反演结果横向上连续性明显提高。对于倾斜模型,加入横向约束后更接近真实模型,但对于存在突变点的台阶模型,横向约束加入导致结构上也更加连续,与真实模型存在偏差。

总体来说,联合反演有助于消除单方法反演的多解性,在联合反演基础上加入横向约束反演,则有利于提高横向上物性参数和结构的连续性。该方法对于地下沉积模型的反演及数据量大的快速反演有重要意义。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

丁立锋, 徐佩芬, 凌苏群,

等.

微动勘探方法探测林南仓煤矿岩浆岩侵入体

[J]. 煤炭科学技术, 2010, 38(7):100-103.