模型反演和深度学习反演联合的地震波阻抗优化反演

doi:10.11720/wtyht.2024.1288

模型反演和深度学习反演联合的地震波阻抗优化反演

黄闻露^,, 阎建国, 任立龙, 谢锐

成都理工大学地球物理学院,四川成都 610059

Seismic impedance optimization inversion combining model inversion with deep learning inversion

HUANG Wen-Lu^,, YAN Jian-Guo, REN Li-Long, XIE Rui

College of Geophysics, Chengdu University of Technology, Chengdu 610059, China

第一作者: 黄闻露(1997-),女,硕士研究生,研究方向为油气地球物理勘探。Email:hwlcdut@163.com

责任编辑: 叶佩, 沈效群

收稿日期: 2023-07-7 修回日期: 2023-11-17

基金资助:

中国石油勘探开发研究院项目“油气地球物理前沿理论与新技术”(RPED-2020-JS-121)

Received: 2023-07-7 Revised: 2023-11-17

摘要

基于“数据驱动和模型驱动”相结合的思想,通过模型反演结果扩展标签训练集,并在深度学习算法中加入模型反演目标函数,对损失函数进行重构,提出了一种模型反演和深度学习反演联合的地震波阻抗优化反演。采用RNN网络结构实现了一种“伪标签”下的半监督深度学习网络反演,并用网络反演结果作为初始模型参与模型反演,最终优化反演由网络反演和模型反演不断迭代优化完成。通过合成Marmousi模型和实际资料,验证了所提出的方法具有较高的反演精度和实用性。

关键词： 数据驱动; 模型驱动; 伪标签; 半监督; 波阻抗反演

Abstract

Based on the combination ofdata- and model-driven approaches, this study expanded the labels of the training set through model inversion results, and added the model inversion objective function to the deep learning algorithm. By constructing a new loss function, this study proposed a seismic impedance optimization inversion method combining model inversion with deep learning inversion. The semi-supervised deep learning network inversion under a pseudo-label was achieved using the RNN network structure. The network inversion results were used as the initial model to participate in the model inversion. The final optimization inversion was completed by continuous iterative optimization of both network and model inversion. The method proposed in this study proves to possess high inversion accuracy and practicability, as demonstrated by the synthesis of the Marmousi model and the actual data.

Keywords： data-driven; model-driven; pseudo-label; semi-supervision; wave impedance inversion

PDF (7559KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

黄闻露, 阎建国, 任立龙, 谢锐. 模型反演和深度学习反演联合的地震波阻抗优化反演[J]. 物探与化探, 2024, 48(4): 1076-1085 doi:10.11720/wtyht.2024.1288

HUANG Wen-Lu, YAN Jian-Guo, REN Li-Long, XIE Rui. Seismic impedance optimization inversion combining model inversion with deep learning inversion[J]. Geophysical and Geochemical Exploration, 2024, 48(4): 1076-1085 doi:10.11720/wtyht.2024.1288

0 引言

地震反演是一种对地下层空间结构和物理性质进行求解的过程^[1]。常规地震反演方法的理论框架可以归结为“贝叶斯参数估计”^[2],虽然具体算法“种类繁多”,贝叶斯一序贯高斯模拟方法、基于谱反演方法、最优化方法等^[3⇓-5],但本质上是一种从初始模型出发的寻优算法,可以统称为“模型驱动”的反演方法。近年来,深度学习作为机器学习技术的最新延伸,在地震反演和储层解释等地球物理领域显现出了巨大的潜力。基于数据驱动的深度学习需要大量标记的数据集来实现良好的知识概括能力,将物理模型融合到机器学习算法中^[6],能减少算法对标签的依赖,地震反演技术也不再局限于物理模型或模型驱动^[7]。肖立志^[8]指出了3种数据驱动和物理模型融合的方式,分别为算法融合、评价方法融合和数据集融合。在地球物理反演方面,“数据驱动+物理模型驱动”比较有代表性的成果主要有:Das等^[9]结合阻抗标签训练卷积神经网络并测试分析该网络模型的稳健性;Alfarraj等^[10]提出了将物理模型引导的半监督学习模型应用在反演问题上;Biswas等^[11]提出物理引导的卷积神经网络对叠前和叠后数据进行反演研究;Luo等^[12]用数据增强策略使用地震数据,加强反演阻抗的准确性;Su等^[13]使用稀疏反射系数和地震正演模拟过程作为网络的地球物理约束,用Unet网络实现反演。

本文在前人研究的基础上,更注重于“算法融合”的实现,并结合3种融合思想,提出了一种模型反演和深度学习反演联合的地震波阻抗优化反演方法。首先,用数据驱动的方式得到初始反演结果,并将其作为模型反演的初始模型;再利用模型反演结果,对数据驱动方式下训练数据集进行扩充;同时,将模型反演的目标函数加入到网络反演的损失函数中,根据对数据驱动反演和模型反演结果的可靠性评价施加权重,共同约束深度学习网络的训练,不断迭代优化,最终得到一个融合了模型反演和数据驱动反演算法的优化反演结果。合成数据Moumasi模型的验证试验证明了所提出方法具有准确性以及更高的精确度。将本文提出的方法流程应用到新疆阜东研究区的实际资料反演中,得到了较高的反演分辨率和可靠度,验证了该方法的适用性。

1 方法原理

1.1 波阻抗联合优化反演原理

已知地质模型(构造、速度、密度等)求解地震响应的过程称为正演,也可叫做正演建模。正演建模可表示为实际地质模型m(阻抗)到地震记录d的映射:

(1)

d = F (m) + ε

。

式中: $F$ 表示正演算子; $ε$ 表示噪声。

反演是正演的逆过程,利用测量得到的地震和测井数据,反推地下的地质模型,并对地下岩层的岩性、物性和含油气性进行解释推断。反演问题可表示为从地震数据中获得地质模型 $m$ (阻抗)的过程:

(2)

m = F^{- 1} (d)

。

式中: $F^{- 1}$ 表示反演算子。

基于模型的地震波阻抗反演的一般性原理可表示为数学上的一种最优化问题:

(3)

Θ = ‖ d_{o b v} - d_{s y n} ‖

。

式中: $Θ$ 为目标函数; $d_{o b v}$ 为观测数据; $d_{s y n}$ 为正演计算得到的理论数据。

通过深度学习的方法实现反演的一般性原理,是通过构建一个深度神经网络DNN(deep neural network)训练神经网络的参数,获得地震数据和波阻抗的映射关系。网络参数的训练过程可看成式(4)的优化问题:

(4)

\begin{array}{l} Θ = ‖ F_{Θ} (x_{i}) - y_{i} (x) ‖ = \\ \underset{Θ}{a r g m i n} \frac{1}{N} \overset{N}{\sum_{i = 1}} L [y_{i} (x), F_{Θ} (x_{i})] 。 \end{array}

式中: $Θ$ 表示网络权重和偏重; $F_{Θ} (x)$ 为网络训练后的输出结果; $y (x)$ 表示标签; $a r g m i n$ 表示求极小; $L$ 为实际波阻抗和预测波阻抗的损失函数。

对比式(3)和式(4)可以看到,基于模型的反演与基于数据的深度学习反演,其算法的核心都可以看成是一个寻优的过程,只是实现方式不同。基于模型的反演方法是通过寻优过程直接修改模型参数,从初始模型开始迭代寻优;而深度学习算法主要是依据小样本的训练数据,在标签数据的约束下迭代训练网络参数,最终以最优的网络模型所代表的映射关系完成从地震数据到波阻抗的反演。

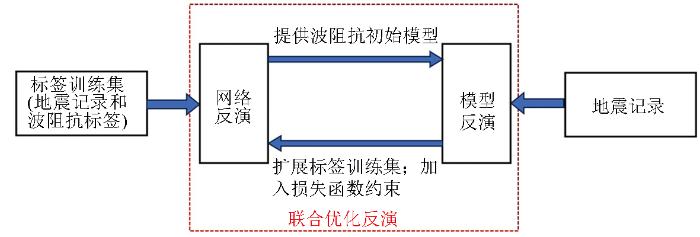
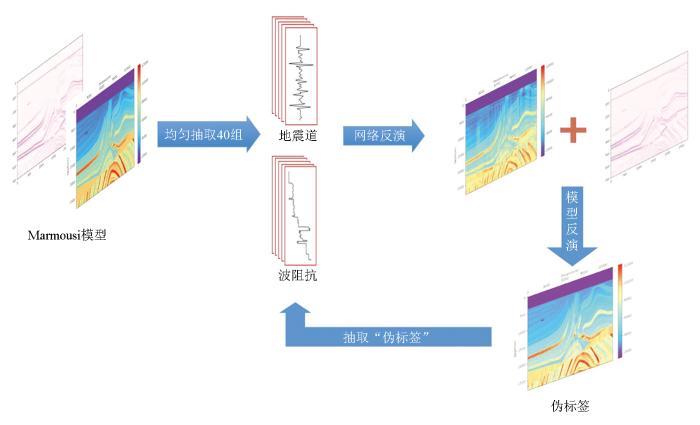
本文所提出的模型反演和深度学习反演联合的反演方法,其基本原理是在模型反演结果的约束下,不断迭代优化深度学习反演网络结构,最终得到一个融合了模型反演和数据驱动反演算法(简称网络反演)的优化反演结果。所提出方法的流程如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 优化反演流程示意

Fig.1 Schematic of the optimized inversion process

在本文所提出的方法中,网络反演算法采用的是一种基于伪标签的半监督算法,分为“训练和预测”两个主要步骤。在训练阶段,其输入数据为小样本的标签训练集,由作为标签的波阻抗数据道和与之对应的地震记录道组成;在预测阶段,其输入数据就是地震记录道,通过训练好的网络模型(地震记录与波阻抗的映射关系)得到波阻抗反演结果。在迭代训练的过程中,通过来自模型反演结果进行标签训练集的扩充以及构建新的损失函数实现半监督训练。

模型反演是用网络反演的结果作为初始模型,并不断寻优得到反演结果。将这种反演结果一方面作为“伪标签”用于网络训练的样本集,另一方面与网络反演结果一同按最小二乘方法求得目标函数并加入到网络训练的损失函数中,用于进一步优化网络结构。最后的优化反演是指在上述网络反演和模型反演联合运用下不断迭代优化,达到了一个最优的网络模型后,由输入的地震数据得到波阻抗的过程,并认为此时的反演结果为最优。

1.2 模型反演约束下的半监督网络反演方法原理

1.2.1 深度学习波阻抗反演网络结构

本文提出的联合优化反演方法主要由网络反演和模型反演两部分组成,其网络反演部分采用的是有监督的循环神经网络(recurrent neural networks, RNN),但结合模型反演结果的伪标签扩展,形成一种半监督的RNN网络反演(图2)。循环神经网络旨在处理时间序列数据和其他数据序列,已经成功应用于重力异常反演^[14]、雷达数据去噪^[15]等方面。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 RNN结构示意

Fig.2 Schematic of RNN structure

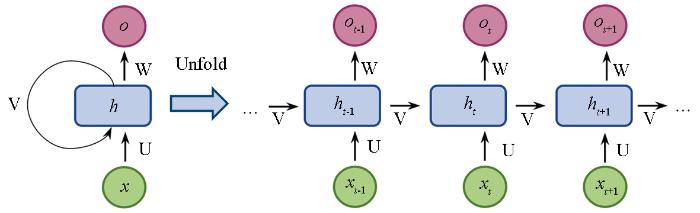
假设输入时间序列x₁, x₂,…, x_T,在时刻t的隐藏层用递归公式表示为:

(5)

h_{t} = t a n h (W_{h h} h_{t - 1} + W_{x h} x_{t} + b_{h}, x_{t})

。

式中: $t a n h (a) = \frac{e^{2 a} - 1}{e^{2 a} + 1}; W_{h h} 、 W_{x h}$ 是可训练的权重矩阵, $h$ 为隐藏层, $b$ 为偏置。

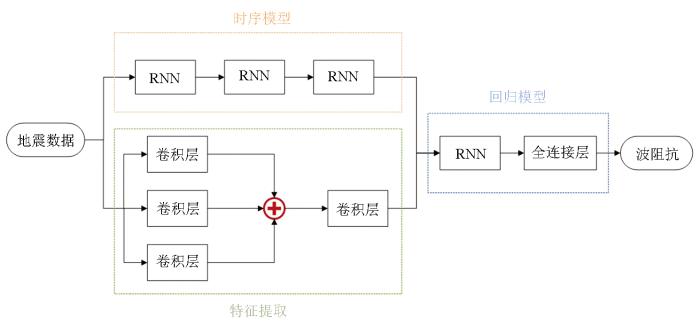
基于RNN深度学习的波阻抗反演网络结构由时序模型、特征提取和回归模型3部分组成(图3)。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 基于深度学习的波阻抗反演网络结构示意

Fig.3 Schematic of wave impedance inversion network structure based on deep learning

1)时序模型由3层RNN模块连接组成,RNN模块由输入层、隐藏层、输出层组成。隐藏层在时间步长上计算并输出隐藏状态,该隐藏状态作为后续输出层的输入。该模块的作用是提取地震数据的全局特征。

2)特征提取模块由卷积层组成。这里采用的卷积层由批标准化、卷积操作、ReLu激活函数组成。批标准化对每次批量输入数据进行标准化,缓解网络过拟合。卷积操作通过滑动窗口的卷积核,对输入数据做卷积操作,提取地震数据的多尺度特征。ReLu激活函数将非线性特征引入神经网络。该模块为地震数据并行输入时序模型和特征提取模块。

3)回归模型通过一层RNN层和一层全连接层将特征融合。全连接层将特征矩阵转化成一维的特征大向量,对数据进行降维处理。该部分一般放在网络结构的最后。

1.2.2 伪标签的产生和模型反演约束方法

有监督的深度学习算法是机器学习方法中解决问题能力较强的一类方法,这主要得益于标签样本数据集的监督作用,以及恰当的网络结构通过大量训练所具有的对数据特征的强大挖掘能力。但在实际应用中,特别是在地震反演中,经常遇到的是小样本、少标签数据集的情况。例如:测井资料约束下的地震波阻抗反演,可用于进行标签制作的数据是来自于几口或10几口钻井的测井资料的波阻抗数据,因此,神经网络反演结果会受到这一因素影响。另一方面,仅仅通过数据驱动来完成物理模型的反演,其效果在很多情况下并不尽如人意,常常需要用物理规律对反演结果进行评价和选择,或称为约束。因此,如何扩展标签数据集以及如何对网络反演施加适当的物理约束,成为了人们基于“数据驱动+模型驱动”相结合的思想来提高反演精度和可靠度的主要研究方向和拟解决的问题。

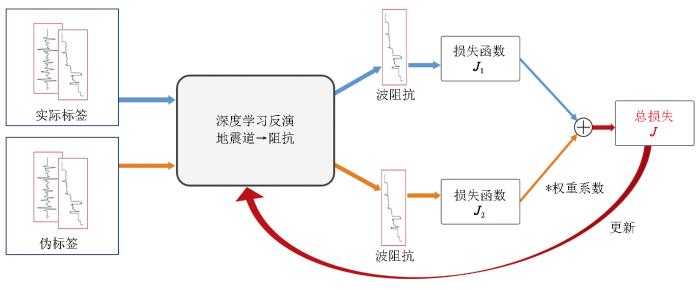
本文提出的优化反演方法也是基于这种“数据驱动+模型驱动”的思想优化的反演结果,通过扩充标签数据集和构建具有物理模型约束的损失函数两种手段来共同完成对深度学习网络的训练,并能得到一个优化的网络模型,从而提高反演的精度和可靠度。总体上可概述为:①通过模型反演得到波阻抗的初步反演结果,并将其作为“伪标签”与网络反演的真实标签一起,再继续对网络进行训练;②与此同时,在新的训练中构建原网络损失函数+模型反演目标函数,成为新的网络训练的损失函数;③不断迭代优化,得到优化反演的网络模型。

按照前述的优化反演方法原理,除扩充标签数据集外,还需要将模型反演结果与网络反演的结果进行最优化对比,构成新的目标函数 $(J_{2})$ ,并与原网络训练时的损失函数( $J_{1}$ )共同构成最终的损失函数J,重新约束网络训练过程。网络反演的损失函数的构成及约束原理见图4, $J_{1} 、 J_{2}$ 及 $J$ 的含义及相关表达式见式(6)~(8):

(6)

J (Θ) = λ_{1} \cdot J_{1} (Θ) + λ_{2} \cdot J_{2} (Θ)

(7)

J_{1} (Θ) = \underset{Θ}{a r g m i n} \frac{1}{N} \overset{N}{\sum_{i = 1}} L [m_{i}, G_{Θ}^{- 1} (d_{i})]

(8)

J_{2} (Θ) = \underset{Θ}{a r g m i n} \frac{1}{N} \overset{N}{\sum_{i = 1}} L [G_{B}^{- 1} (d_{i}), G_{Θ}^{- 1} (d_{i})]

。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 优化反演的损失函数构成

Fig.4 Optimize the loss function composition of the inversion

式中:λ₁、λ₂是人为控制的权系数; $G_{Θ}^{- 1}$ 表示网络反演; $G_{B}^{- 1}$ 表示模型反演;m_i是波阻抗模型标签;d_i是地震记录。

从式(6)可以看到:在新的损失函数中,可以根据对网络反演结果及模型反演结果的可信度,设置不同的权系数来调整网络反演结果或模型反演结果的约束程度;权系数λ是影响约束结果的重要因素,调整这些权系数可以改变损失函数的权值分布。

2 模型数据试算

以Mamousi模型为例,说明这种伪标签数据集的产生和扩展流程(图5)。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 伪标签的产生方式示意

Fig.5 Schematic of how pseudo-labels are generated

在模型实验中,选用2 721道作为研究范围(图6a、b)。首先,均匀选取40道、约总数据的1.5%作为标签数据集参与“训练”;将“预测”得到的2 721道网络反演结果作为初始模型(图6c)应用于模型反演,得到一个基于模型反演的结果(图6d);将模型反演结果按需要抽取一定数量的伪标签加到最初的40道真实标签中,得到扩充后的标签数据集;继续训练网络,不断迭代,直到满意为止。需要指出的是,这种伪标签扩充也是从少样本初步扩充的,实验中一般扩充到200道数据量,达到总数据量的8%左右就可以得到好的效果。

图6

新窗口打开| 下载原图ZIP| 生成PPT

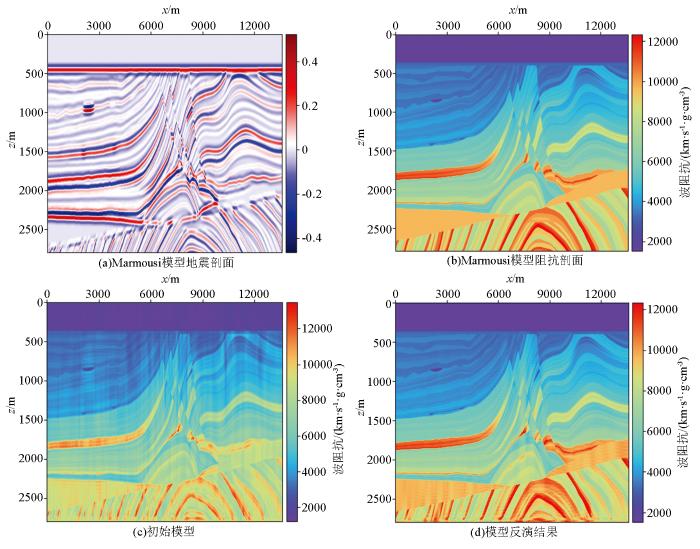
图6 模型反演的初始模型及反演结果

Fig.6 The initial model of model inversion and the results of the inversion

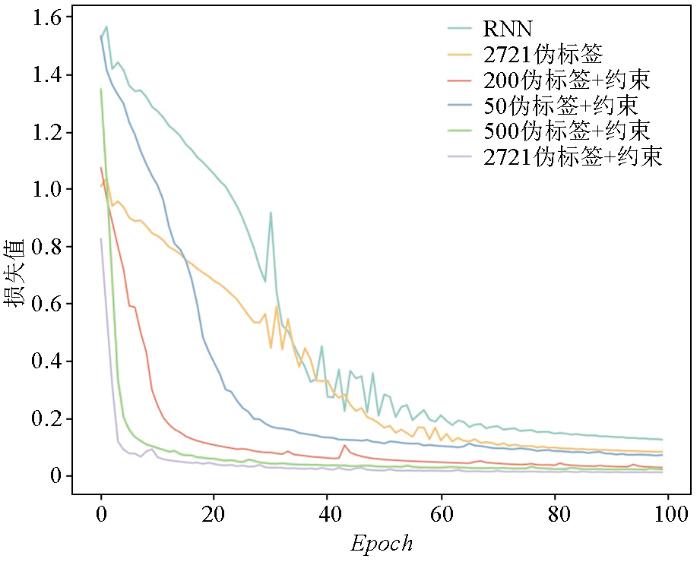
在RNN选取40组真实标签下,选择40组真实标签+50组伪标签模型约束、40组真实标签+200组伪标签模型约束、40组真实标签+500组伪标签模型约束和40组真实标签+2 721组伪标签模型约束下,RNN网络的训练误差进行对比,结果见图7。最终选择40组真实标签+200组伪标签模型约束RNN网络的方式进行网络训练。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 损失函数下降曲线

Fig.7 Decline of the loss function

按照本文提出的方法原理及流程,在进行了伪标签扩展和模型反演结果约束的各种实验后,最终结合这两种方法,完成了模型反演和深度学习反演联合的地震波阻抗优化反演。

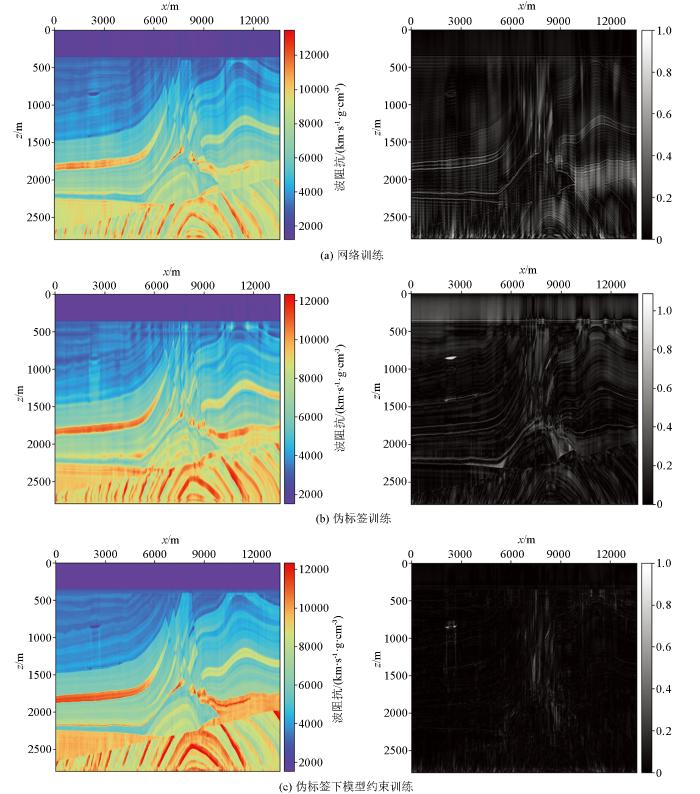
图8a左图是仅40组真实标签训练RNN网络的预测结果,图8b左图是200组伪标签未进行损失函数构建的训练RNN网络的预测结果,图8c左图是40组真实标签+200组伪标签并进行了损失函数约束(模型约束)的RNN网络的预测结果;右图为3种情况下预测结果与真实值之间的误差率。从阻抗预测结果可以看出,模型约束对“数据驱动”下的预测结果都有改进。网络训练选用40对标签训练时,波阻抗的预测结果在横向剖面上连续性很差,在地质情况起伏变化剧烈的地方预测精度低。伪标签下神经网络的预测结果,由于标签数据集的扩充而得到改善。伪标签+模型反演结果约束的预测结果最好,特别是对剖面深层的构造刻画清楚,横向连续性也有改进。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同反演方法的预测结果(左)及误差率(右)

Fig.8 Prediction results(left) and error rate(right) of different inversion methods

为了对比分析这几种不同条件下的反演结果,抽取了具有特征性的4道:第500道(2 500 m)、第1 400道(7 000 m)、第1 800道(9 000 m)和第2 400道(12 000 m)进行逐道对比,具体位置为各道深度位于1 400~2 800 km的部分(图9a)。从图9b可以更直观地看出反演约束预测结果的改进。

图9

新窗口打开| 下载原图ZIP| 生成PPT

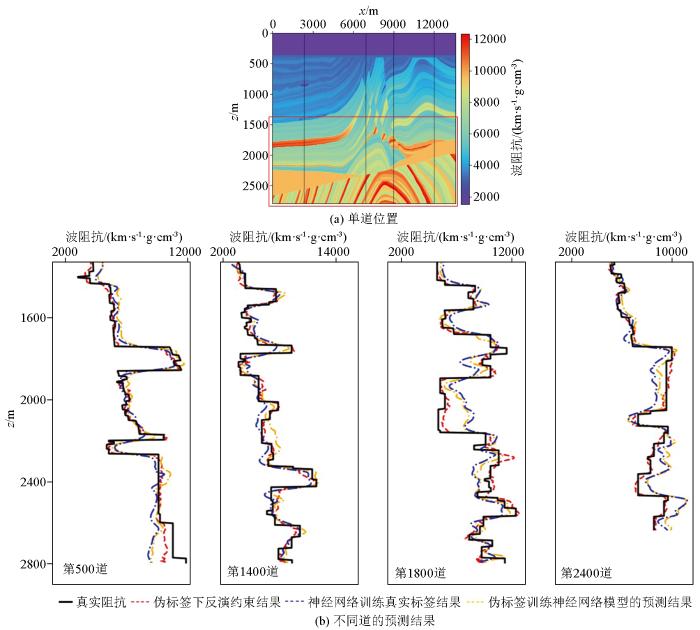
图9 不同反演方法网络模型单道预测结果对比

Fig.9 Single trace prediction results of network models with different inversion methods

表1中给出了不同反演方法预测结果的相对误差评价结果。可以看出:伪标签+模型反演约束结果的相对误差比RNN网络预测和伪标签约束RNN结果的相对误差;伪标签约束RNN虽然输入数据的数量比RNN多,但与实际标签仍存在差距,相对误差比RNN反演的略低。同一方法中,由于地震构造复杂程度不同,相对误差存在差异。

表1 不同反演方法的评价效果

Table 1 Evaluation effect of the relative error of one trace in the prediction results of different inversion methods

	RNN	伪标签	伪标签+ 反演约束
第500道相对第1400道误差第1800道第2400道	0.1296	0.1176	0.0547
	0.0671	0.0722	0.0490
	0.0988	0.1054	0.0493
	0.0877	0.0827	0.0441
MSE	0.0616	0.0573	0.0158
R₂	0.9378	0.9415	0.9839

新窗口打开| 下载CSV

为了定量评价本文提出的优化反演方法的性能,使用了均方误差(MSE)和决定系数(R₂)用于预测结果准确性的评价指标。评价指标主要分为两个方面:评估预测波阻抗与真实波阻抗的匹配程度和评估网络模型的拟合程度。从表1中给出的不同反演方法网络模型预测结果的MSE和R₂评价结果,可以看出:RNN能够学习到非线性地震数据以及波阻抗之间的映射关系,但因为没有足够的训练标签和地球物理约束,导致MSE误差值较高;伪标签增加了训练数据集,能够改善训练结果;在增加训练集和改进损失函数增加模型约束后,MSE误差明显减少,缓解了深度学习网络对标签的依赖。伪标签加的反演约束效果是最好的,大量无标签的地震数据经过模型反演生成阻抗伪标签,通过提取少量伪标签,在小样本训练下结合模型反演约束网络模型的训练,能得到明显的效果提升。

3 实际数据应用

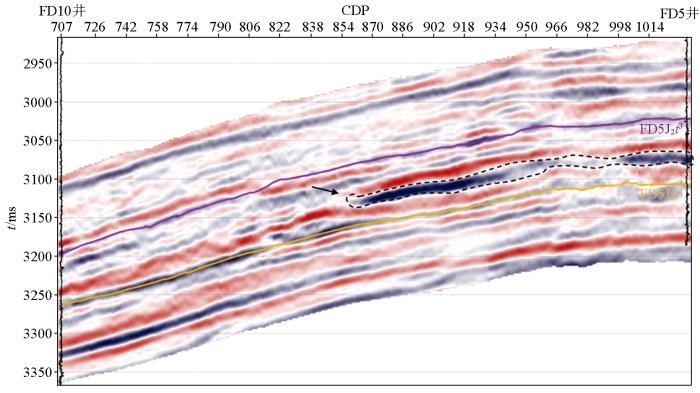
研究区位于新疆准噶尔盆地阜东5井区。根据前人的研究^[16],阜东5井区侏罗系头屯河组河道发育,且分流河道砂体网状交织,叠加样式多样,河道空间展布形态复杂。本次重点研究过FD5井与FD10井的连井线上河道储层分布情况(图10),目的层为中侏罗统头屯河组二段(J₂t²)与头屯河组三段(J₂t³)之间的河道砂岩储层。图10黑色虚线框范围目的层段间的“透镜体”反射体(剖面上的黑色箭头位置)是根据工区内测井资料(低波阻抗区域)井及地质地震综合特征分析得到的,可能是河道砂体的地震反射特征。根据目的层段J₂t²、J₂t³的地质解释结果,选用320道叠后数据进行反演,采样时间0.5 s,采样间隔2 ms。期望通过波阻抗反演更清晰地反映河道砂体的连续性和接触关系。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 研究区连井剖面

Fig.10 Connecting well profile in the research area

利用基于物理模型的反演方法与本文提出的模型反演约束下的半监督网络反演方法,对实际数据进行反演,其结果如图11所示。

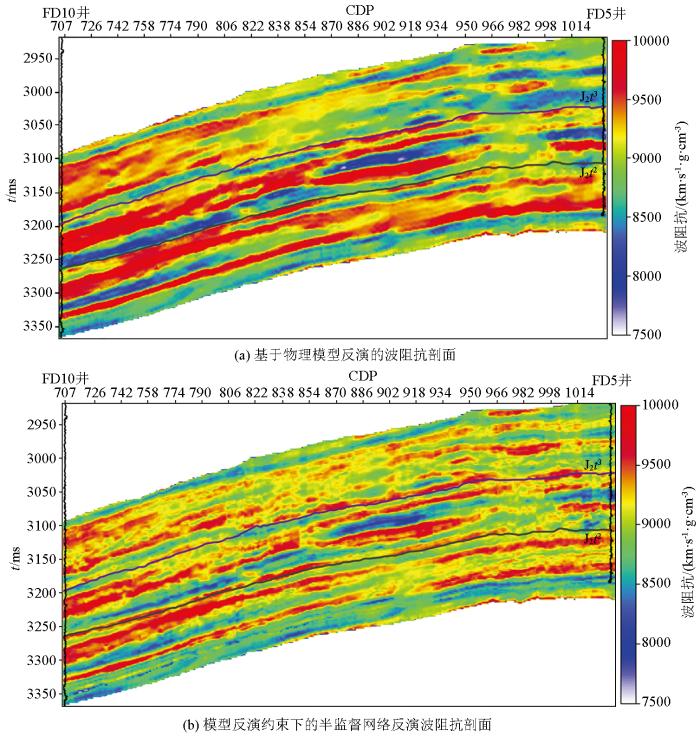
图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 基于不同反演方法的反演结果对比

Fig.11 Comparison of inversion results based on different inversion methods

基于物理模型的反演结果(图11a)是利用2口井(FD5井与FD10井)的波阻抗数据及地震构造解释结果进行初始模型创建,用常规的共轭梯度优化算法得到。图中显示,模型反演结果能大致反映地下河道砂体分布,但分辨率较低,河道砂体的连续性和接触关系可靠度不高。

图11b展示的是根据本文提出的反演方案所得到的反演结果。首先将2口井(FD5井与FD10井)的波阻抗数据作为真实标签进行网络反演,并以此作为模型反演的初始模型进行模型反演后,按照本文提出的方法流程,进行标签逐步扩充和损失函数约束的优化反演。本次实际资料试验结果表明,在2口真测井数据和100口“伪”测井数据(约30%的数据量)的标签集下,能够得到较好的预测结果。图11显示,本文提出的方法得到的实际资料反演结果比常规的模型反演结果分辨率更高,反映的河道砂体连续性及接触关系更加可靠。

4 结论

使用深度学习的方法,在地震反演时,由于井数量的限制,无法获得足够数量的标签数据用于神经网络的训练,并且深度学习模型直接应用在地震反演上容易出现网络不稳定、预测精确度较低的问题。因此,在合成数据Marmousi模型上,考虑对训练数据集扩充,通过模型反演给未标记的地震数据提供伪标签,并在深度学习模型中加入地球物理约束,将模型反演加入网络的训练中,更新网络参数。同时,比较了仅深度学习、增加伪标签、伪标签下模型约束3种反演方法的预测效果,认为伪标签下模型约束的反演方法可以预测得到更准确、精度更高的波阻抗。但是,该方法是建立在深度学习框架下的物理模型约束的反演,由于物理模型的计算繁琐,导致了网络训练耗时的增加。

此外,阜东5井区的实例表明,在较少井数据作为标签的情况下,模型反演约束下的半监督网络反演方法具有较高的反演精度和分辨率,能够较为准确地识别河道砂体,进一步证明了该方法的有效性和实用性。本次研究的框架流程并不局限于地震波阻抗反演,也可以扩展应用到地球物理学其他储层参数预测的研究中。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Chen

Y K

, Chen

H M

, Xiang

et al.

Geological structure guided well log interpolation for high-fidelity full waveform inversion

[J]. Geophysical Journal International, 2016, 207(2):1313-1331.