0 引言
裂隙储层的预测通常需要借助地球物理反演方法来实现,地震反演方法通过分析地震波在地下介质中传播的动力学特征来预测相关地质体的弹性参数和裂隙参数,以达到预测裂隙储层分布范围的目的[1 ] 。目前大多针对裂隙的地震反演将介质视为各向同性,实际地层中具有近似水平裂缝的介质可以被认为是VTI型(transversely isotropy with a vertical axis of symmetry,具有垂直对称轴的横向各向同性介质)。基于VTI介质的地震波反演,可得到裂隙相关的弹性参数,进一步探索裂隙中充填物的性质[2 ⇓ -4 ] 。
各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] 。Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式。Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算。Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析。Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式。Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程。孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度。Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征。李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征。Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据。Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性。陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测。陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度。针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性。
反演算法是实现地震反演的重要手段。目前,应用较为广泛的是线性反演算法以及非线性反演算法。相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解。Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率。在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高。Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计。乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析。张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层。李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法。张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演。优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能。
本文以VTI介质反射系数公式为基础,构建反演目标函数,将模拟退火算法中的Metropolis准则应用到粒子群标准算法中,设置跳出概率,有效减少陷入局部最优解的可能性,提高算法的稳定性和抗噪性,实现纵、横波速度和各向异性参数的反演;联合属性A、B、C和泊松比、泊松速度,对裂隙流体预测。
1 理论
在Rüger[8 ] 提出的VTI介质PP波反射系数公式基础上,Zhang等[36 ] 对Δ ρ V P 0 / ρ V P 0 _ Δ ρ V S 0 2 / ρ V S 0 2 _
(1) R P P ( θ ) = 1 2 l n A i + 1 A i - 2 V S 0 ¯ V P 0 ¯ 2 s i n 2 θ l n B i + 1 B i + 1 2 t a n 2 θ l n C i + 1 C i
(2) A = ρ V P 0
(3) B = ρ V S 0 2 e σ 4
(4) C = V P 0 e ε
V P0 、V S0 分别为垂向纵波速度、横波速度,ρ 为介质密度,θ 为入射角,ε 、δ 分别为表征各向异性的常数。· - Δ ( · ) A 为声波阻抗,属性B 为e σ 4 σ = (V P0 /V S0 )2 (ε -δ ),当e σ 4 B 即为在适当各向异性强度下的各向同性剪切模量。属性C 在ε <0.3时,近似等于水平传播的横向P波相速度。声波阻抗在岩体和流体中变化较大,剪切模量和横向P波相速度对流体较为敏感。因此,可先采用属性A 、B 、C 将含流体部分指明,再采用对不同性质流体更加敏感的物理量对含流体部分的类型进一步表征。
泊松比为纵波速度与横波速度比的函数,是反映声波传播时间或速度的物理量,在同一均质介质中为定值,其表达式如式(5)所示:
(5) σ = V P 2 - 2 V S 2 2 V P 2 - V S 2
式中:V P 、V S 分别为纵波速度、横波速度。不同介质中纵横波速度不同,尤其是储层中流体存在时,横波变化明显,泊松比的变化将会被放大。高孔隙度的含水饱和砂岩通常具有较高泊松比值,高孔隙气饱和砂岩泊松比值较低[37 ] 。实际测井资料中不同流体的泊松比值显示,泊松比最低对应气,次低对应含水,中高对应砂岩致密层,高值对应泥岩。因此,不同泊松比值对应不同地层介质,可将泊松比视作一种流体指示因子。
Quakenbush等[38 ] 使用坐标轴旋转构建泊松阻抗,主要方法是对纵、横波阻抗交会图选择合适旋转轴,将旋转后的参数定义为泊松阻抗,以识别区分流体类型。泊松阻抗表达式如下:
(6) P I = V σ ρ = V P - c V S ρ
式中:Vσ 为泊松速度,c为常数,决定了坐标轴的旋转程度,也决定所得泊松阻抗是否可以有效识别不同岩性和流体,常取岩性—流体趋势线的倒数。若定义c=2 , V P 、V S 表达如下:
(7) σ = V P 2 - 2 V S 2 2 V P 2 - V S 2 = V P + 2 V S 2 V P 2 - V S 2 V P - 2 V S = D V σ
(8) D = V P + 2 V S 2 V P 2 - V S 2
(9) V σ = V P - 2 V S
式中:D 为比例因子,减弱了纵、横波阻抗随深度增加而增加的背景值,而Vσ 不随地层深度的增加而变化,可削弱地层压实背景趋势的影响,且形式更为简单。
因此,文中首先选用属性A 、B 、C 指示出流体与岩体的差异。进而,利用泊松比对不同类型流体取值变化的不同,以及泊松速度在结合了纵横波速度变化的基础上,消除了随地层深度增加产生的变化,对流体类型进一步分析。综合根据5种参数变化,结合含流体时泊松比值的不同,可实现对裂缝中流体的识别。
2 改进后的粒子群算法反演过程
粒子群算法模拟鸟群觅食行为,每一个粒子被模拟为一只觅食的鸟,觅食过程中,鸟群中的每一只鸟共享目前已知最优位置,根据最优位置信息,每只鸟决定接下来的移动方向。模拟退火法模拟固体退火的物理过程(升温、等温、冷却),物体升温过程中,内能增大,粒子成无序状,冷却时,粒子逐渐有序,直至平衡状态内能达到最小。粒子群算法中随着进化次数的增加,鸟群的搜索能力会下降,易陷入局部最优。因此,引入模拟退火算法,通过调整温度,控制概率性跳出特性,进行新的随机搜索,有效避免陷入局部最优解。
采用式(1)作为反演的反射系数方程,假设待反演的弹性参数和各向异性参数符合粒子群分布,反演目标函数可定义为:
(10) F ( V P , V S , ρ , ε , δ , θ ) = ∑ i = 1 n R P P ( V P , V S , ρ , ε , δ , θ i ) - R P P _ M ( θ i ) 2
式中:θi 为P波入射角,R PP_M 为模型反射系数。
1)随机设置各个粒子的速度vi , j xi , j t 0 ;
2)评价每个粒子的适应度,将粒子的位置和适应度值存储在粒子的个体值P b (粒子自己发现的最好位置)中,将所有P b 中最优适用值的个体位置和适应度值保存在全局极值中;
(11) T F p i = e x p - f p i - f p g t ∑ i = 1 N e x p - f p i - f p g t
4)确定全局最优pi 值pi ' ,并更新各个粒子的位置和速度:
(12) x i , j ( t + 1 ) = x i , j ( t ) + v i , j ( i + 1 ) , j = 1,2 , … , n
(13) v i , j ( i + 1 ) = φ { v i , j ( i ) + c 1 r 1 p i , j - x i , j ( t ) + c 2 r 2 p g , j - x i , j ( t ) }
(14) φ = 2 2 - c 1 + c 2 - c 1 + c 2 2 - 4 c 1 + c 2
式中:vi , j k )为粒子在k 时刻的速度,xi , j k )为粒子在k 时刻的位置,c 1 为粒子局部学习能力学习因子,c 2 为粒子全局学习能力学习因子,粒子局部学习能力学习因子c 1 与全局学习能力学习因子c 2 之和大于4。r 1 和r 2 为[0,1]的随机数,pi , i k )、pg , j k )分别表示粒子i 和群体中其他粒子在t 时刻为止发现的最好位置,φ 为收缩因子。设置两组收缩因子,分别应用于前期迭代阶段(0~50)及后期迭代阶段(50~100),以提高搜索效率。
5)将每个粒子的适应度值与其经过最好位置的P b 的适应度值作比较,将每个粒子的适应度值与整个种群中的最好位置P bg 的适应度值作比较,如果更好则更新P b 和P bg 。
随后进行退火操作,Metropolis准则定义了某一温度T 下系统状态从状态i 到状态j 的能量概率为:
(15) P i j T = 1 , E j < E i e x p - E j - E i K T , E j ≥ E i
式中:P i j T Ei 和Ej 为固体在状态i 和状态j 下的能量,K为玻尔兹曼常数。
6)当算法达到迭代次数或无法找到新的最优解,则终止寻优搜索过程并输出计算结果;否则返回4)继续寻优过程。
3 模型试算
3.1 二层模型试算
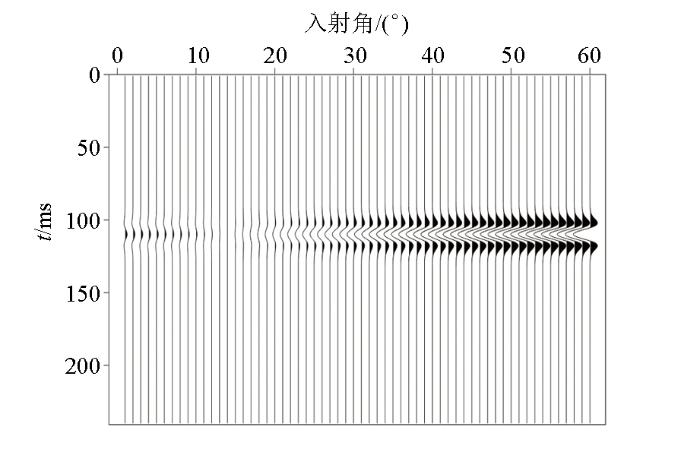
为了检验改进后的粒子群算法的反演效果,现建立二层地质模型(800 m×600 m),设置两种不同岩性地层A和B,地层A为各向同性层,地层B中含有横向含水裂隙,近似为VTI型各向异性介质,模型中各层的纵波、横波速度、密度各向异性参数如表1 所示。对模型采用主频50 Hz的雷克子波进行人工地震记录合成,得到角道集如图1 所示。
图1
图1
二层模型的角道集
Fig.1
Synthetic angle gathers for the two-layer model
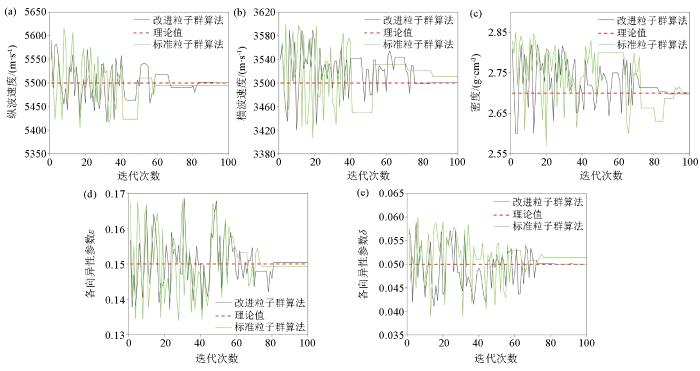
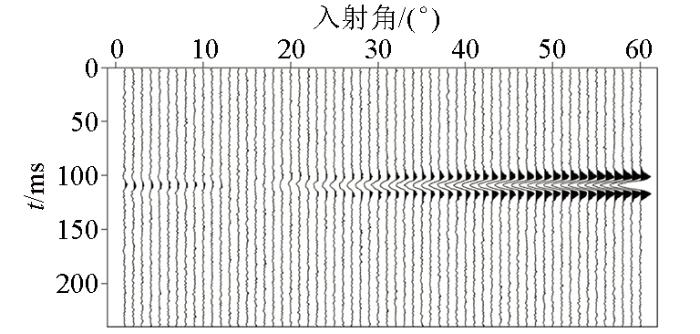
对二层模型采用标准粒子群算法和改进后的粒子群算法分别进行弹性参数和各向异性参数反演,迭代次数设置为100次,模型下层反演VTI介质物理参数及各向异性参数反演结果如图2 所示。反演结果表明,当反演达到一定迭代次数后,两种算法的反演结果都趋于稳定;相比之下,改进后的粒子群算法与先验值接近,误差较小。同时,对图1 所示的角道集加入10 dB的高斯随机噪声(图3 ),表2 为理想情况下与存在10 dB噪声情况下,采用不同算法反演后各向异性层的反演误差。结果表明:无噪声情况下,两种算法反演结果与理论值的误差均小于6%;增加10 dB噪声后,粒子群反演结果误差增大,最大至8.236%,改进后的粒子群算法误差变化较小,最大至6.667%,在反演合理误差范围之内。其中,无噪声与有噪声存在时,纵波速度反演误差均较小,ε值反演误差较大。
图2
图2
二层模型反演结果
Fig.2
Inverted results of the two-layer model
图3
图3
信噪比为10 dB时的角道集
Fig.3
Synthetic angle gathers for 10 dB signal-to-noise ratios
3.2 Marmousi2模型试算
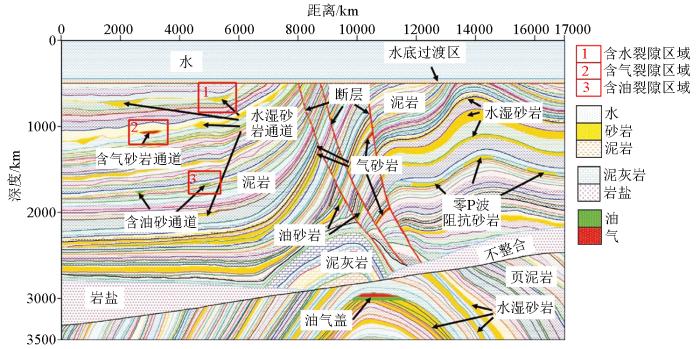
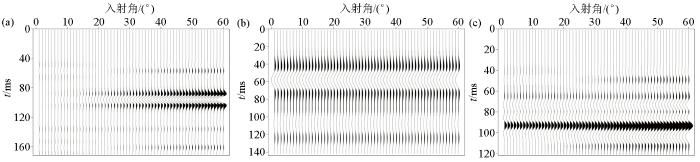
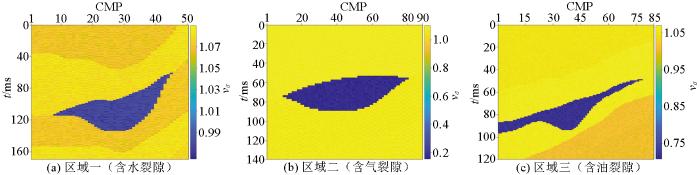
Marmousi2是复杂的二维各向同性地质—地球物理模型[40 ] 。本文选取模型中含水、含气、含油的3个部分(图4 红框圈出部分),根据不同岩层的特性赋予各向异性参数。假定含水、含气、含油区域横向裂隙发育,并将其近似等效为VTI介质。通过50 Hz的Ricker子波合成理论记录,对目标位置(含水区域:横向4 890~5 890 m,纵向538~674 m;含气区域:横向2 500~3 400 m,纵向1 153~1 265 m;含油区域:横向4 750~5 250 m,纵向1 585~1 681 m)提取角道集如图5 所示。
图4
图4
Marmousi2原始模型
Fig.4
Marmousi2 original model
图5
图5
对目标位置提取的角道集
a—含水区域;b—含气区域;c—含油区域
Fig.5
Corner gathers extracted from the target position
a—water-bearing fracture;b—gas-bearing fracture;c—oil-bearing fracture
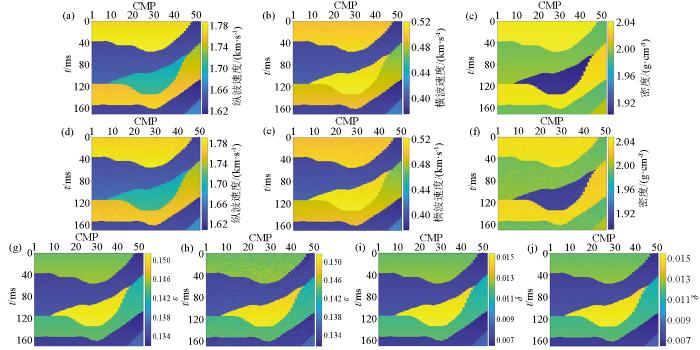
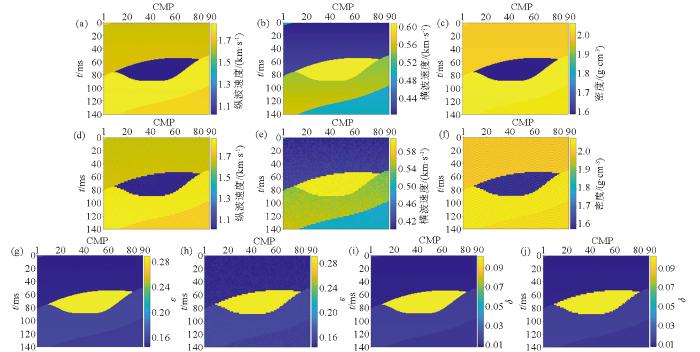
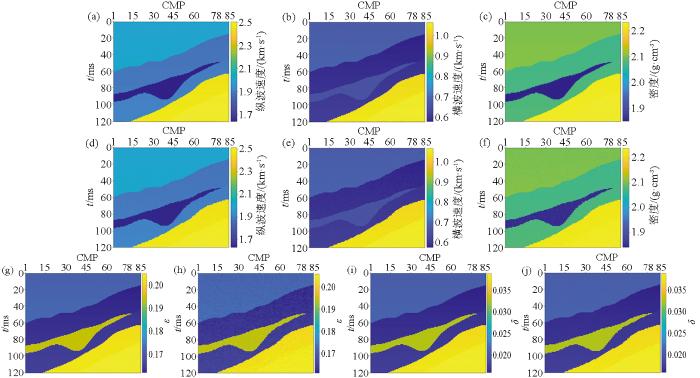
采用本文研究的改进后的粒子群算法,对Marmousi2模型中截取的3个含裂隙区域的物理参数及各向异性参数进行反演,所选区域的原始参数剖面与结果剖面如图6 ~8 所示。图6 ~8 为各区域纵波速度、横波速度、密度、ε 、δ 原始剖面与反演结果剖面的对比,从反演剖面可以看出各部分区域中地层的变化,填充物的裂隙形态与原模型吻合;纵波速度反演结果更为理想,横波速度、密度剖面反演结果较次于纵波剖面;各向异性参数反演结果合理,含裂隙的地层中ε 、δ 值升高,P波各向异性程度增强。
图6
图6
选定Marmousi2模型待反演区域一(图中裂隙为含水区域)的原始剖面与反演结果剖面
a、b、c、g、i—分别为纵波速度、横波速度、密度、ε 、δ 原始剖面; d、e、f、h、j—分别为纵波速度、横波速度、密度、ε 、δ 反演剖面
Fig.6
Original profiles and inverted results of region 1(water-bearing fracture) in Marmousi2 model
a,b,c,g,i—are original profiles of P-wave velocity,S-wave velocity,density,ε and δ respectively;d,e,f,h,j—are inverted profiles of P-wave velocity,S-wave velocity,density,ε and δ respectively
图7
图7
选定Marmousi2模型待反演区域二(图中裂隙为含气区域)的原始剖面与反演结果剖面
a、b、c、g、i—分别为纵波速度、横波速度、密度、ε 、δ 原始剖面;d、e、f、h、j—分别为纵波速度、横波速度、密度、ε 、δ 反演剖面
Fig.7
Original profiles and inverted results of region 2(gas-bearing fracture) in Marmousi2 model
a、b、c、g、i—are original profiles of P-wave velocity,S-wave velocity,density,ε and δ respectively;d、e、f、h、j—are inverted profiles of P-wave velocity,S-wave velocity,density,ε and δ respectively
图8
图8
选定Marmousi2模型待反演区域三(图中裂隙为含油区域)的原始剖面与反演结果剖面
a、b、c、g、i—分别为纵波速度、横波速度、密度、ε 、δ 原始剖面;d、e、f、h、j—分别为纵波速度、横波速度、密度、ε 、δ 反演剖面
Fig.8
Original profiles and inverted results of region 3(gas-bearing fracture) in Marmousi2 model
a、b、c、g、i—are original profiles of P-wave velocity,S-wave velocity,density,ε and δ respectively;d、e、f、h、j—are inverted profiles of P-wave velocity,S-wave velocity,density,ε and δ respectively
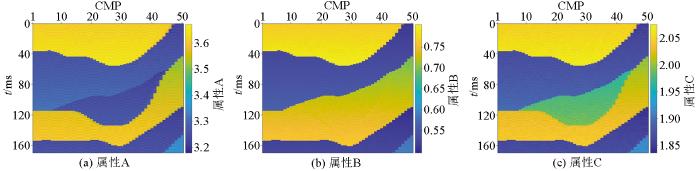
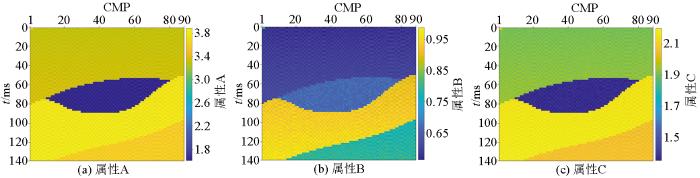
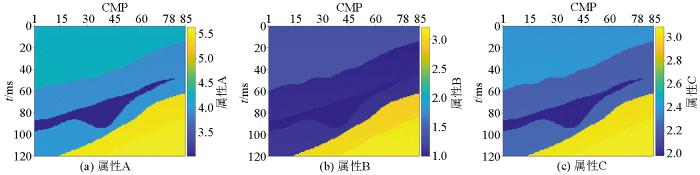
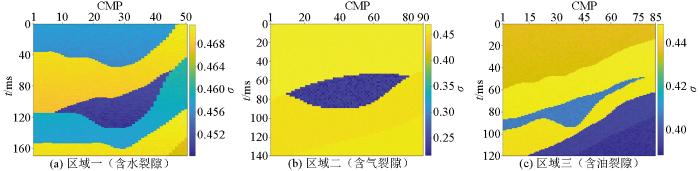
基于反演得到的纵、横波速度和各向异性参数等相关参数,得到A、B、C属性剖面(如图9 ~11 所示)以及泊松比、泊松速度剖面(如图12 ~13 所示)。从图9 ~11 可以看出,反演属性A、C在含流体裂隙区域明显下降,属性B在含流体裂隙区域变化微小(含水裂隙中属性B变化更小)。裂隙含有不同充填物时,地层的泊松比与泊松速度值会有不同程度降低,且有基本一致的变化趋势:含气裂隙泊松比变化最大,其次是含油裂隙,含水裂隙泊松比变化最小;泊松速度值不随深度变化而变化,联合属性A、B、C、泊松比以及泊松速度可用于裂隙识别。如图12 ~13 ,对于含气裂隙,裂隙处的泊松比和泊松速度值均有明显下降;其次是含油裂隙,降低幅度略有减小;对于含水裂隙,两参数变化幅度最小。
图9
图9
区域一(图中裂隙为含水区域)A、B、C属性剖面
Fig.9
Inverted results of attribute A、B、C in region 1(water-bearing fracture)
图10
图10
区域二(图中裂隙为含气区域)A、B、C属性剖面
Fig.10
Inverted results of attribute A、B、C in region 2(gas-bearing fracture)
图11
图11
区域三(图中裂隙为含油区域)A、B、C属性剖面
Fig.11
Inverted results of attribute A、B、C in region 3(oil-bearing fracture)
图12
图12
Marmousi2模型中截取的3个区域的泊松比
Fig.12
Poisson's ratio values of selected regions in Marmousi2 model
图13
图13
Marmousi2模型中截取的3个区域的泊松速度
Fig.13
Poisson velocity of selected regions in Marmousi2 model
4 实际数据应用
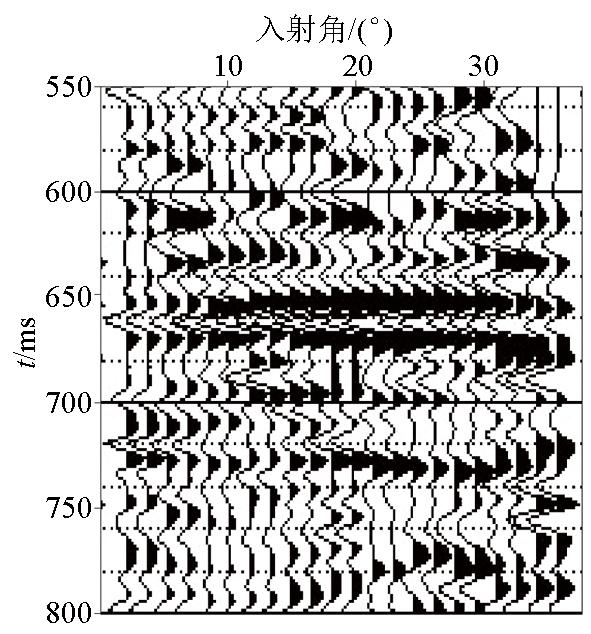
为了检验反演及预测方法在实际数据中的应用效果,将其应用于某煤田的实际地震资料。图14 为经过去噪、振幅补偿和动校正等一系列常规处理后得到的叠加剖面,剖面0.65 s附近存在煤层,煤层顶板上方有含水裂隙存在,红色箭头指示区域为目标反演区域。图15 为对CMP115,550~800 ms处提取的角道集。
图14
图14
叠加剖面(Inline317)
Fig.14
Post-stack profile(Inline 317)
图15
图15
角道集
Fig.15
Angle gathers
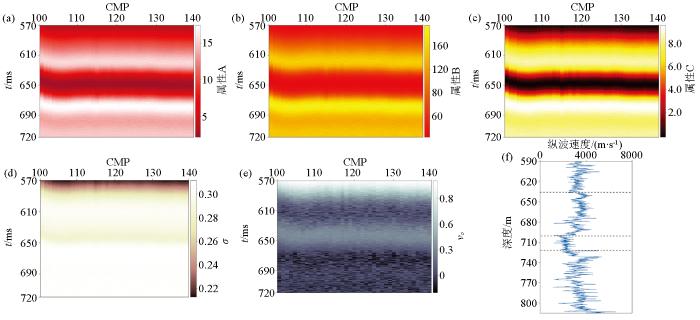
对目标区域进行反演,得到属性A、B、C与泊松比、泊松速度值。图16 为属性参数A、B、C与泊松比、泊松速度的结果剖面,煤层顶板上方出现属性A、C值的小幅下降,属性B未出现明显差异;泊松比和泊松速度剖面在煤层上部区域也出现下降,推断煤层顶板上方存在含水裂隙。图16f 为速度测井曲线,反演结果与测井曲线的速度变化特征相符;煤层上方波速增大,煤层顶板砂岩含水。预测结果与该地区的地质解释相符。
图16
图16
目标区域参数剖面
a—属性A;b—属性B;c—属性C;d—泊松比;e—泊松速度;f—测井曲线
Fig.16
Profiles of targeted area
a—attribute A;b—attribute B;c—attribute C;d—Poisson's ratio;e—Poisson velocity;f—log curve
5 结论
1)通过建立基于各向异性反射系数方程的目标函数,在标准粒子群算法中引入模拟退火算法,将粒子群算法的快速收敛性与模拟退火算法的概率性状态转换特征相结合,可以降低算法陷入局部最优解的可能性,实现对水平裂缝诱导的VTI介质的物理参数反演。
2)基于各向异性反演得到的纵、横波速度及各向异性参数,并进一步通过属性A、B、C以及泊松比和泊松速度,可以实现对裂隙填充物的预测。
3)通过对二层模型、Marmousi2模型和实际资料的应用,论证新的算法和反演参数的联合应用能在一定程度上提高反演算法的稳定性、抗噪性和预测的可靠性。
参考文献
View Option
[1]
刘世奇 , 王鹤 , 王冉 , 等 . 煤层孔隙与裂隙特征研究进展
[J]. 沉积学报 , 2021 , 39 (1 ):212 -230 .
[本文引用: 1]
Liu S Q Wang H Wang R et al . Research advances on characteristics of pores and fractures in coal seams
[J]. Acta Sedimentologica Sinica , 2021 , 39 (1 ):212 -230 .
[本文引用: 1]
[2]
唐杰 , 李聪 , 温雷 , 等 . 裂隙连通性对含流体介质剪切波分裂特征的影响
[J]. 物探与化探 , 2019 , 43 (4 ):859 -865 .
[本文引用: 1]
Tang J Li C Wen L et al . A study of influence of fracture connectivity on wave propagation characteristics
[J]. Geophysical and Geochemical Exploration , 2019 , 43 (4 ):859 -865 .
[本文引用: 1]
[3]
蔡刚 , 杨子玉 , 李双文 , 等 . 埕海潜山奥陶系碳酸盐岩裂缝预测
[J]. 地球物理学进展 , 2013 , 28 (2 ):945 -951 .
[本文引用: 1]
Cai G Yang Z Y Li S W et al . Fracture prediction of Ordovician carbonate rock in the buried hill of Chenghai
[J]. Progress in Geophysics , 2013 , 28 (2 ):945 -951 .
[本文引用: 1]
[4]
Liu S Q Sang S X Ma J S et al . Effects of supercritical CO2 on micropores in bituminous and anthracite coal
[J]. Fuel , 2019 , 242 :96 -108 .
[本文引用: 1]
[5]
张保卫 , 岳航羽 , 谢伟 , 等 . 反射地震在冀中坳陷保定凹陷精细地质结构探测中的应用
[J]. 物探与化探 , 2022 , 46 (6 ):1359 -1368 .
[本文引用: 1]
Zhang B W Yue H Y Xie W et al . Application of the seismic reflection method in detecting the fine-scale geological structure of the Baoding Sag,Jizhong depression
[J]. Geophysical and Geochemical Exploration , 2022 , 46 (6 ):1359 -1368 .
[本文引用: 1]
[6]
Thomsen L Weak elastic anisotropy
[J]. Geophysics , 1986 , 51 (10 ):1954 -1966 .
[本文引用: 1]
[7]
Thomsen L Reflection seismology over azimuthally anisotropic media
[J]. Geophysics , 1988 , 53 (3 ):304 -313 .
[本文引用: 1]
[8]
Rüger A Variation of P-wave reflectivity with offset and azimuth in anisotropic media
[J]. Geophysics , 1998 , 63 (3 ):935 -947 .
[本文引用: 2]
[9]
Hudson J A A higher order approximation to the wave propagation constants for a cracked solid
[J]. Geophysical Journal International , 1986 , 87 (1 ):265 -274 .
[本文引用: 1]
[10]
Crampin S A review of wave motion in anisotropic and cracked elastic-media
[J]. Wave Motion , 1981 , 3 (4 ):343 -391 .
[本文引用: 1]
[11]
Crampin S Chesnokov E M Hipkin R G Seismic anisotropy —the state of the art:II
[J]. Geophysical Journal International , 1984 , 76 (1 ):1 -16 .
[本文引用: 1]
[12]
Schoenberg M Orthorhombic media:Modeling elastic wave behavior in a vertically fractured earth
[J]. Geophysics , 1997 , 62 (6 ):1954 -1974 .
[本文引用: 1]
[13]
Bakulin A Grechka V Tsvankin I Estimation of fracture parameters from reflection seismic data:Part II:Fractured models with orthorhombic symmetry
[J]. Geophysics , 2000 , 65 (6 ):1803 -1817 .
[本文引用: 1]
[14]
Bakulin A Grechka V Tsvankin I Estimation of fracture parameters from reflection seismic data:Part III:Fractured models with monoclinic symmetry
[J]. Geophysics , 2000 , 65 (6 ):1818 -1830 .
[本文引用: 1]
[15]
Tsvankin I P-wave signatures and notation for transversely isotropic media:An overview
[J]. Geophysics , 1996 , 61 (2 ):467 -483 .
[本文引用: 1]
[16]
Tsvankin I Thomsen L Nonhyperbolic reflection moveout in anisotropic media
[J]. Geophysics , 1994 , 59 (8 ):1290 -1304 .
[本文引用: 1]
[17]
Pšenčík I Martins J L Properties of weak contrast PP reflection/transmission coefficients for weakly anisotropic elastic media
[J]. Studia Geophysica et Geodaetica , 2001 , 45 (2 ):176 -199 .
[本文引用: 1]
[18]
Russell B H Gray D Hampson D P Linearized AVO and poroelasticity
[J]. Geophysics , 2011 , 76 (3 ):C19 -C29 .
[本文引用: 1]
[19]
孟庆生 , 何樵登 , 王德利 . 均匀横向各向同性介质中P波及SV波的射线规律
[J]. 吉林大学学报:地球科学版 , 2002 , 32 (4 ):378 -381 .
[本文引用: 1]
Meng Q S He Q D Wang D L Study on P,SV-wave features in homogeneous transversely isotropic media
[J]. Journal of Changchun University of Science and Technology , 2002 , 32 (4 ):378 -381 .
[本文引用: 1]
[20]
Hao Z T Yao C Wang X The characteristics of velocities with azimuth variation for arbitrary spatial orientation TI media
[J]. Progress in Geophysics , 2006 , 21 (2 ):524 -530 .
[本文引用: 1]
[21]
李磊 . TI介质中的相速度和群速度及射线参数
[J]. 石油物探 , 2008 , 47 (4 ):334 -337 .
[本文引用: 1]
根据横向各向同性(TI)介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征。分析结果表明,随着各向异性参数所满足的条件不同,相速度曲线既可能单调递增,也可能单调递减,或在一定相角范围递增而在其它相角范围递减。相速度曲线的单调性决定群对相的偏离方向,当相速度递减时,群向TI对称轴方向偏离,群相偏离角为负;当相速度递增时,群向背离TI对称轴的方向偏离,群相偏离角为正。利用相表示的射线参数表达式和群相关系得出了群、相联合表示的射线参数表达式,并用数值算例进行了验证。
Li L Phase velocity,group velocity,and ray parameters in transversely isotropic media
[J]. Geophysical Prospecting for Petroleum , 2008 , 47 (4 ):334 -337 .
[本文引用: 1]
[22]
Farra V Pšenčík I Weak-anisotropy approximations of P-wave phase and ray velocities for anisotropy of arbitrary symmetry
[J]. Studia Geophysica et Geodaetica , 2016 , 60 (3 ):403 -418 .
[本文引用: 1]
[23]
Ding P B Di B R Wang D et al . P- and S-wave velocity and anisotropy in saturated rocks with aligned cracks
[J]. Wave Motion , 2018 , 81 :1 -14 .
[本文引用: 1]
[24]
陈同俊 , 崔若飞 , 刘恩儒 . VTI型构造煤AVO正演模拟
[J]. 煤炭学报 , 2009 , 34 (4 ):438 -442 .
[本文引用: 1]
Chen T J Cui R F Liu E R AVO forward modeling for VTI coal
[J]. Journal of China Coal Society , 2009 , 34 (4 ):438 -442 .
[本文引用: 1]
[25]
陈亮 , 黄建平 , 王自颖 , 等 . 应用自适应变网格紧致差分的地震波数值模拟及逆时偏移
[J]. 石油地球物理勘探 , 2023 , 58 (3 ):641 -650 .
[本文引用: 1]
Chen L Huang J P Wang Z Y et al . Seismic numerical simulation and reverse time migration with adaptive variable-grid and compact difference method
[J]. Oil Geophysical Prospecting , 2023 , 58 (3 ):641 -650 .
[本文引用: 1]
[26]
李红梅 . 弹性参数直接反演技术在储层流体识别中的应用
[J]. 物探与化探 , 2014 , 38 (5 ):970 -975 .
[本文引用: 1]
Li H M The application of elastic parameters direct inversion to reservoir fluid identification
[J]. Geophysical and Geochemical Exploration , 2014 , 38 (5 ):970 -975 .
[本文引用: 1]
[27]
Yan X S Zhang M Z Wu Q H Big-data-driven pre-stack seismic intelligent inversion
[J]. Information Sciences , 2021 , 549 :34 -52 .
[本文引用: 1]
[28]
陈志刚 , 刘雷颂 , 刘雅琴 , 等 . 煤系地层中薄砂岩储层预测
[J]. 石油地球物理勘探 , 2016 , 51 (S1 ):52 -57 .
[本文引用: 1]
Chen Z G Liu L S Liu Y Q et al . Thin-sandstone reservoir prediction in coal-bearing strata
[J]. Oil Geophysical Prospecting , 2016 , 51 (S1 ):52 -57 .
[本文引用: 1]
[29]
Pan X P Zhang G Z Fracture detection and fluid identification based on anisotropic Gassmann equation and linear-slip model
[J]. Geophysics , 2019 , 84 (1 ):R85 -R98 .
[本文引用: 1]
[30]
乔汉青 . 基于改进粒子群算法的横波速度预测方法研究 [D]. 长春 : 吉林大学 , 2017 .
[本文引用: 1]
Qiao H Q Shear wave velocity prediction method based on improved particle swarm algorithm [D]. Changchun : Jilin University , 2017 .
[本文引用: 1]
[31]
Li Q Wang W AVO inversion in orthotropic media based on SA-PSO
[J]. IEEE Transactions on Geoscience and Remote Sensing , 2021 , 59 (10 ):8903 -8912 .
[本文引用: 1]
[32]
张进 , 陈晓琦 , 邢磊 , 等 . 基于改进粒子群算法的叠前弹性阻抗反演
[J]. 物探化探计算技术 , 2016 , 38 (3 ):353 -360 .
[本文引用: 1]
Zhang J Chen X Q Xing L et al . Application of particle swarm optimization in prestack elastic impedance inversion
[J]. Computing Techniques for Geophysical and Geochemical Exploration , 2016 , 38 (3 ):353 -360 .
[本文引用: 1]
[33]
张晓阳 , 杜文凤 , 卢勇旭 , 等 . 粒子群算法在煤田地震面波频散曲线反演中的应用研究
[C]// 2015中国地球科学联合学术年会论文集(二十三)——专题55煤炭资源与矿山安全地球物理,北京 , 2015 :73 -74 .
[本文引用: 1]
[34]
李雅丽 , 王淑琴 , 陈倩茹 , 等 . 若干新型群智能优化算法的对比研究
[J]. 计算机工程与应用 , 2020 , 56 (22 ):1 -12 .
DOI:10.3778/j.issn.1002-8331.2006-0291
[本文引用: 1]
随着计算机技术的发展,算法技术也在不断交替更新。近年来,群体智能算法受到了广泛的关注和研究,并在诸如机器学习、过程控制、工程预测等领域取得了进展。群智能优化算法属于生物启发式方法,广泛应用在解决最优化问题上,传统的群智能算法为解决一些实际问题提供了新思路,但是也在一些实验中暴露出不足。近年来,许多学者相继提出了很多新型群智能优化算法,选取了最近几年国内外提出的比较典型的群智能算法,蝙蝠算法(Bat Algorithm,BA)、灰狼优化算法(Grey Wolf Optimization,GWO)、蜻蜓算法(Dragonfly Algorithm,DA)、鲸鱼优化算法(Whale Optimization Algorithm,WOA)、蝗虫优化算法(Grasshopper Optimization Algorithm,GOA)和麻雀搜索算法(Sparrow Search Algorithm,SSA),并进一步通过22个标准的CEC测试函数从收敛速度、精度和稳定性等方面对比了这些算法的实验性能,并对比分析了其相关的改进方法。最后总结了群智能优化算法的特点,探讨了其今后的发展潜力。
Li Y L Wang S Q Chen Q R et al . Comparative study of several new swarm intelligence optimization algorithms
[J]. Computer Engineering and Applications , 2020 , 56 (22 ):1 -12 .
DOI:10.3778/j.issn.1002-8331.2006-0291
[本文引用: 1]
With the development of computer technology, algorithm technology is constantly and alternately being updated. In recent years, swarm intelligence algorithm has become more and more popular and received extensive attention and research, and has made progress in such fields as machine learning, process control and engineering prediction. Swarm intelligence optimization algorithm is a biological heuristic method, which is widely used in solving optimization problems. The traditional swarm intelligence algorithm provides some new ideas for solving some practical problems, but it also exposes some shortcomings in some experiments. In recent years, many scholars have proposed many new types of intelligent optimization algorithms. This paper selects the more typical swarm intelligence algorithms at home and abroad in recent years, such as Bat Algorithm(BA), Grey Wolf Optimization Algorithm(GWO), Dragonfly Algorithm(DA), Whale Optimization Algorithm(WOA), Grasshopper Optimization Algorithm(GOA) and Sparrows Search Algorithm(SSA), and further compares the experimental performance of these algorithms and the development potential by 22 standard CEC test functions from the convergence speed and accuracy, stability and so on, and the refinement analysis is carried out to compare and analyze the relevant improvement methods. Finally, the characteristics of swarm intelligence optimization algorithm are summarized and its development potential is discussed.
[35]
张鹏飞 , 张世晖 . 西湖凹陷平湖组砂泥岩岩性神经网络地震预测
[J]. 物探与化探 , 2021 , 45 (4 ):1014 -1020 .
[本文引用: 1]
Zhang P F Zhang S H Neural network seismic prediction of sand and mudstone lithology of Pinghu Formation in Xihu Sag
[J]. Geophysical and Geochemical Exploration , 2021 , 45 (4 ):1014 -1020 .
[本文引用: 1]
[36]
Zhang F Zhang T Li X Y Seismic amplitude inversion for the transversely isotropic media with vertical axis of symmetry
[J]. Geophysical Prospecting , 2019 , 67 (9 ):2368 -2385 .
DOI:10.1111/1365-2478.12842
[本文引用: 1]
Transverse isotropy with a vertical axis of symmetry is a common form of anisotropy in sedimentary basins, and it has a significant influence on the seismic amplitude variation with offset. Although exact solutions and approximations of the PP-wave reflection coefficient for the transversely isotropic media with vertical axis of symmetry have been explicitly studied, it is difficult to apply these equations to amplitude inversion, because more than three parameters need to be estimated, and such an inverse problem is highly ill-posed. In this paper, we propose a seismic amplitude inversion method for the transversely isotropic media with a vertical axis of symmetry based on a modified approximation of the reflection coefficient. This new approximation consists of only three model parameters: attribute A, the impedance (vertical phase velocity multiplied by bulk density); attribute B, shear modulus proportional to an anellipticity parameter (Thomsen's parameter epsilon-delta); and attribute C, the approximate horizontal P-wave phase velocity, which can be well estimated by using a Bayesian-framework-based inversion method. Using numerical tests we show that the derived approximation has similar accuracy to the existing linear approximation and much higher accuracy than isotropic approximations, especially at large angles of incidence and for strong anisotropy. The new inversion method is validated by using both synthetic data and field seismic data. We show that the inverted attributes are robust for shale-gas reservoir characterization: the shale formation can be discriminated from surrounding formations by using the crossplot of the attributes A and C, and then the gas-bearing shale can be identified through the combination of the attributes A and B. We then propose a rock-physics-based method and a stepwise-inversion-based method to estimate the P-wave anisotropy parameter (Thomsen's parameter epsilon). The latter is more suitable when subsurface media are strongly heterogeneous. The stepwise inversion produces a stable and accurate Thomsen's parameter epsilon, which is proved by using both synthetic and field data.
[37]
吴大奎 , 张本全 , 戴勇 , 等 . 地震资料气水识别方法及其应用
[J]. 天然气工业 , 2011 , 31 (12 ):54 -58 .
[本文引用: 1]
Wu D K Zhang B Q Dai Y et al . Seismic identification methods for gas and water layers and their application
[J]. Natural Gas Industry , 2011 , 31 (12 ):54 -58 .
[本文引用: 1]
[38]
Quakenbush M Shang B Tuttle C Poisson impedance
[J]. The Leading Edge , 2006 , 25 (2 ):128 -138 .
[本文引用: 1]
[39]
Rutherford S R Williams R H Amplitude-versus-offset variations in gas sands
[J]. Geophysics , 1989 , 54 (6 ):680 -688 .
[本文引用: 2]
[40]
Martin G S Wiley R Marfurt K J Marmousi2:An elastic upgrade for Marmousi
[J]. The Leading Edge , 2006 , 25 (2 ):156 -166 .
[本文引用: 3]
煤层孔隙与裂隙特征研究进展
1
2021
... 裂隙储层的预测通常需要借助地球物理反演方法来实现,地震反演方法通过分析地震波在地下介质中传播的动力学特征来预测相关地质体的弹性参数和裂隙参数,以达到预测裂隙储层分布范围的目的[1 ] .目前大多针对裂隙的地震反演将介质视为各向同性,实际地层中具有近似水平裂缝的介质可以被认为是VTI型(transversely isotropy with a vertical axis of symmetry,具有垂直对称轴的横向各向同性介质).基于VTI介质的地震波反演,可得到裂隙相关的弹性参数,进一步探索裂隙中充填物的性质[2 ⇓ -4 ] . ...
煤层孔隙与裂隙特征研究进展
1
2021
... 裂隙储层的预测通常需要借助地球物理反演方法来实现,地震反演方法通过分析地震波在地下介质中传播的动力学特征来预测相关地质体的弹性参数和裂隙参数,以达到预测裂隙储层分布范围的目的[1 ] .目前大多针对裂隙的地震反演将介质视为各向同性,实际地层中具有近似水平裂缝的介质可以被认为是VTI型(transversely isotropy with a vertical axis of symmetry,具有垂直对称轴的横向各向同性介质).基于VTI介质的地震波反演,可得到裂隙相关的弹性参数,进一步探索裂隙中充填物的性质[2 ⇓ -4 ] . ...
裂隙连通性对含流体介质剪切波分裂特征的影响
1
2019
... 裂隙储层的预测通常需要借助地球物理反演方法来实现,地震反演方法通过分析地震波在地下介质中传播的动力学特征来预测相关地质体的弹性参数和裂隙参数,以达到预测裂隙储层分布范围的目的[1 ] .目前大多针对裂隙的地震反演将介质视为各向同性,实际地层中具有近似水平裂缝的介质可以被认为是VTI型(transversely isotropy with a vertical axis of symmetry,具有垂直对称轴的横向各向同性介质).基于VTI介质的地震波反演,可得到裂隙相关的弹性参数,进一步探索裂隙中充填物的性质[2 ⇓ -4 ] . ...
裂隙连通性对含流体介质剪切波分裂特征的影响
1
2019
... 裂隙储层的预测通常需要借助地球物理反演方法来实现,地震反演方法通过分析地震波在地下介质中传播的动力学特征来预测相关地质体的弹性参数和裂隙参数,以达到预测裂隙储层分布范围的目的[1 ] .目前大多针对裂隙的地震反演将介质视为各向同性,实际地层中具有近似水平裂缝的介质可以被认为是VTI型(transversely isotropy with a vertical axis of symmetry,具有垂直对称轴的横向各向同性介质).基于VTI介质的地震波反演,可得到裂隙相关的弹性参数,进一步探索裂隙中充填物的性质[2 ⇓ -4 ] . ...
埕海潜山奥陶系碳酸盐岩裂缝预测
1
2013
... 裂隙储层的预测通常需要借助地球物理反演方法来实现,地震反演方法通过分析地震波在地下介质中传播的动力学特征来预测相关地质体的弹性参数和裂隙参数,以达到预测裂隙储层分布范围的目的[1 ] .目前大多针对裂隙的地震反演将介质视为各向同性,实际地层中具有近似水平裂缝的介质可以被认为是VTI型(transversely isotropy with a vertical axis of symmetry,具有垂直对称轴的横向各向同性介质).基于VTI介质的地震波反演,可得到裂隙相关的弹性参数,进一步探索裂隙中充填物的性质[2 ⇓ -4 ] . ...
埕海潜山奥陶系碳酸盐岩裂缝预测
1
2013
... 裂隙储层的预测通常需要借助地球物理反演方法来实现,地震反演方法通过分析地震波在地下介质中传播的动力学特征来预测相关地质体的弹性参数和裂隙参数,以达到预测裂隙储层分布范围的目的[1 ] .目前大多针对裂隙的地震反演将介质视为各向同性,实际地层中具有近似水平裂缝的介质可以被认为是VTI型(transversely isotropy with a vertical axis of symmetry,具有垂直对称轴的横向各向同性介质).基于VTI介质的地震波反演,可得到裂隙相关的弹性参数,进一步探索裂隙中充填物的性质[2 ⇓ -4 ] . ...
Effects of supercritical CO2 on micropores in bituminous and anthracite coal
1
2019
... 裂隙储层的预测通常需要借助地球物理反演方法来实现,地震反演方法通过分析地震波在地下介质中传播的动力学特征来预测相关地质体的弹性参数和裂隙参数,以达到预测裂隙储层分布范围的目的[1 ] .目前大多针对裂隙的地震反演将介质视为各向同性,实际地层中具有近似水平裂缝的介质可以被认为是VTI型(transversely isotropy with a vertical axis of symmetry,具有垂直对称轴的横向各向同性介质).基于VTI介质的地震波反演,可得到裂隙相关的弹性参数,进一步探索裂隙中充填物的性质[2 ⇓ -4 ] . ...
反射地震在冀中坳陷保定凹陷精细地质结构探测中的应用
1
2022
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
反射地震在冀中坳陷保定凹陷精细地质结构探测中的应用
1
2022
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Weak elastic anisotropy
1
1986
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Reflection seismology over azimuthally anisotropic media
1
1988
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Variation of P-wave reflectivity with offset and azimuth in anisotropic media
2
1998
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
... 在Rüger[8 ] 提出的VTI介质PP波反射系数公式基础上,Zhang等[36 ] 对 Δ ρ V P 0 / ρ V P 0 _ Δ ρ V S 0 2 / ρ V S 0 2 _
A higher order approximation to the wave propagation constants for a cracked solid
1
1986
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
A review of wave motion in anisotropic and cracked elastic-media
1
1981
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Seismic anisotropy —the state of the art:II
1
1984
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Orthorhombic media:Modeling elastic wave behavior in a vertically fractured earth
1
1997
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Estimation of fracture parameters from reflection seismic data:Part II:Fractured models with orthorhombic symmetry
1
2000
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Estimation of fracture parameters from reflection seismic data:Part III:Fractured models with monoclinic symmetry
1
2000
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
P-wave signatures and notation for transversely isotropic media:An overview
1
1996
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Nonhyperbolic reflection moveout in anisotropic media
1
1994
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Properties of weak contrast PP reflection/transmission coefficients for weakly anisotropic elastic media
1
2001
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Linearized AVO and poroelasticity
1
2011
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
均匀横向各向同性介质中P波及SV波的射线规律
1
2002
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
均匀横向各向同性介质中P波及SV波的射线规律
1
2002
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
The characteristics of velocities with azimuth variation for arbitrary spatial orientation TI media
1
2006
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
TI介质中的相速度和群速度及射线参数
1
2008
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
TI介质中的相速度和群速度及射线参数
1
2008
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Weak-anisotropy approximations of P-wave phase and ray velocities for anisotropy of arbitrary symmetry
1
2016
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
P- and S-wave velocity and anisotropy in saturated rocks with aligned cracks
1
2018
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
VTI型构造煤AVO正演模拟
1
2009
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
VTI型构造煤AVO正演模拟
1
2009
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
应用自适应变网格紧致差分的地震波数值模拟及逆时偏移
1
2023
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
应用自适应变网格紧致差分的地震波数值模拟及逆时偏移
1
2023
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
弹性参数直接反演技术在储层流体识别中的应用
1
2014
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
弹性参数直接反演技术在储层流体识别中的应用
1
2014
... 各向异性响应是地震波各向异性研究的重要内容,加强参数与响应之间的理论模拟与分析,可以为进一步用于裂隙型储层各向异性研究提供理论基础[5 ] .Thomsen[6 -7 ] 通过VTI介质弹性矩阵,对弱各向异性介质中相位角和群角之间关系进行分析,推导出了弱各向异性介质中动校正速度的Thomson参数表示形式.Rüger[8 ] 利用Thomsen各向异性参数理论推导了TI介质的反射系数近似公式,随后,Hudson[9 ] 、Crampin等[10 -11 ] 、Schoenberg[12 ] 、Bakulin等[13 -14 ] 考虑了孔隙度、裂隙密度、裂隙填充物、裂隙尺寸等因素,提出不同的岩性参数与弹性系数矩阵间的表达式,实现了对各向异性介质多种裂隙参数计算.Tsvankin等[15 -16 ] 结合Hake的研究成果,进一步应用实际反射波数据进行了各向异性参数和速度参数的分析.Pšenčík等[17 ] 推导了包含入射角和方位角的弱各向异性介质反射系数公式.Russell等[18 ] 利用多孔弹性理论并结合链式求导法则和线性AVO近似方程推导了包含流体项、剪切模型和密度的线性AVO方程.孟庆生等[19 ] 研究得出地下介质中的Thomsen各向异性参数决定着P波波前面形状和传播射线密度.Hao等[20 ] 利用坐标变化法,研究了任意强弱TTI介质中体波速度的角散和方位变化特征.李磊[21 ] 根据横向各向同性介质中体波相速度的解析表达式,分析了不同各向异性参数条件下相速度曲线的特征.Farra等[22 ] 提出了P波相速度公式适用于任意对称轴和方向的弱或中等各向异性,为更好地研究速度各向异性提供了依据.Ding等[23 ] 分别在高频、低频和中频情况下分析预测了饱和裂隙岩石的剪切速度和各向异性.陈同俊等[24 ] 对VTI型构造煤进行了AVO正演模拟并尝试对裂隙进行预测.陈亮等[25 ] 利用自适应变网格差分方法进行地震波正演模拟,提高了逆时偏移成像效率与精度.针对各向异性介质的裂隙流体指示常采用单一参数,综合多种参数[26 ] 共同进行分析可以提高流体指示的有效性和可靠性. ...
Big-data-driven pre-stack seismic intelligent inversion
1
2021
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
煤系地层中薄砂岩储层预测
1
2016
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
煤系地层中薄砂岩储层预测
1
2016
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
Fracture detection and fluid identification based on anisotropic Gassmann equation and linear-slip model
1
2019
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
1
2017
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
1
2017
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
AVO inversion in orthotropic media based on SA-PSO
1
2021
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
基于改进粒子群算法的叠前弹性阻抗反演
1
2016
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
基于改进粒子群算法的叠前弹性阻抗反演
1
2016
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
粒子群算法在煤田地震面波频散曲线反演中的应用研究
1
2015
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
若干新型群智能优化算法的对比研究
1
2020
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
若干新型群智能优化算法的对比研究
1
2020
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
西湖凹陷平湖组砂泥岩岩性神经网络地震预测
1
2021
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
西湖凹陷平湖组砂泥岩岩性神经网络地震预测
1
2021
... 反演算法是实现地震反演的重要手段.目前,应用较为广泛的是线性反演算法以及非线性反演算法.相对于线性反演算法和局部非线性优化算法来说,全局非线性优化算法在对于TI介质地震反演以及裂隙预测中不依赖初始模拟、可获得全局最优解.Yan等[27 ] 针对地震资料反演储层参数是一个非线性问题,提出了利用遗传算法和MapReduce框架相结合的策略,改善了对于非线性问题容易陷入局部最优解这一缺陷,缩短了反演储层参数的时间,提高了效率.在煤系地层的预测中,陈志刚等[28 ] 也引入了贝叶斯估计来对反射系数进行估算,随后使用遗传算法来进行全局寻优,从而使得反演精度更高.Pan等[29 ] 利用Gassmann方程和线性滑移模型,在贝叶斯框架下对基于偏移距和方位角变化的逆问题进行迭代求解,最终得到了对流体模量和裂隙柔度的估计.乔汉青[30 ] 、Li等[31 ] 、张进等[32 ] 采用粒子群算法分别对不同岩石物理模型的横波速度、正交各向异性介质的各向异性参数以及弹性阻抗进行反演分析.张晓阳等[33 ] 采用粒子群算法对面波频散曲线进行反演,获得了近地表的横波速度结构和地质分层.李雅丽等[34 ] 对比了多种群体智能优化算法的实验性能,并对比分析了相关的改进方法.张鹏飞等[35 ] 将地震数据转换为与岩性关系更为密切的伽马数据体,利用神经网络进行砂泥岩岩性反演.优化算法易降低初始种群多样性、陷入局部最优,可以融合不同算法的优势来提高算法的性能. ...
Seismic amplitude inversion for the transversely isotropic media with vertical axis of symmetry
1
2019
... 在Rüger[8 ] 提出的VTI介质PP波反射系数公式基础上,Zhang等[36 ] 对 Δ ρ V P 0 / ρ V P 0 _ Δ ρ V S 0 2 / ρ V S 0 2 _
地震资料气水识别方法及其应用
1
2011
... 式中:V P 、V S 分别为纵波速度、横波速度.不同介质中纵横波速度不同,尤其是储层中流体存在时,横波变化明显,泊松比的变化将会被放大.高孔隙度的含水饱和砂岩通常具有较高泊松比值,高孔隙气饱和砂岩泊松比值较低[37 ] .实际测井资料中不同流体的泊松比值显示,泊松比最低对应气,次低对应含水,中高对应砂岩致密层,高值对应泥岩.因此,不同泊松比值对应不同地层介质,可将泊松比视作一种流体指示因子. ...
地震资料气水识别方法及其应用
1
2011
... 式中:V P 、V S 分别为纵波速度、横波速度.不同介质中纵横波速度不同,尤其是储层中流体存在时,横波变化明显,泊松比的变化将会被放大.高孔隙度的含水饱和砂岩通常具有较高泊松比值,高孔隙气饱和砂岩泊松比值较低[37 ] .实际测井资料中不同流体的泊松比值显示,泊松比最低对应气,次低对应含水,中高对应砂岩致密层,高值对应泥岩.因此,不同泊松比值对应不同地层介质,可将泊松比视作一种流体指示因子. ...
Poisson impedance
1
2006
... Quakenbush等[38 ] 使用坐标轴旋转构建泊松阻抗,主要方法是对纵、横波阻抗交会图选择合适旋转轴,将旋转后的参数定义为泊松阻抗,以识别区分流体类型.泊松阻抗表达式如下: ...
Amplitude-versus-offset variations in gas sands
2
1989
... 二层模型参数[39 -40 ] ...
... Parameters of the two-layer model[39 -40 ] ...
Marmousi2:An elastic upgrade for Marmousi
3
2006
... 二层模型参数[39 -40 ] ...
... Parameters of the two-layer model[39 -40 ] ...
... Marmousi2是复杂的二维各向同性地质—地球物理模型[40 ] .本文选取模型中含水、含气、含油的3个部分(图4 红框圈出部分),根据不同岩层的特性赋予各向异性参数.假定含水、含气、含油区域横向裂隙发育,并将其近似等效为VTI介质.通过50 Hz的Ricker子波合成理论记录,对目标位置(含水区域:横向4 890~5 890 m,纵向538~674 m;含气区域:横向2 500~3 400 m,纵向1 153~1 265 m;含油区域:横向4 750~5 250 m,纵向1 585~1 681 m)提取角道集如图5 所示. ...