DGS-AT1M型海洋重力仪静态观测结果分析与评估

doi:10.11720/wtyht.2024.1377

DGS-AT1M型海洋重力仪静态观测结果分析与评估

张彬彬^,¹, 万丽丽²

1.自然资源部第一海洋研究所,山东青岛 266061

2.天元建设集团有限公司,山东临沂 276002

Analysis and assessment of static measurement results from a DGS-AT1M marine gravimeter

ZHANG Bin-Bin^,¹, WAN Li-Li²

1. First Institute of Oceanography, MNR, Qingdao 266061, China

2. Tianyuan Construction Group Co., Ltd., Linyi 276002, China

第一作者: 张彬彬(1990-),男,工程师,主要从事海洋调查技术应用与研究工作。Email:zhangbinbin@fio.org.cn

责任编辑: 朱晓颖

收稿日期: 2023-09-5 修回日期: 2023-12-12

基金资助:

国家自然科学基金项目(42249902)

Received: 2023-09-5 Revised: 2023-12-12

摘要

海洋重力仪的性能直接决定测量数据的质量,而海洋重力仪稳定性则是反映仪器性能的关键性指标。本文结合DGS-AT1M型海洋重力仪静态试验,分析了静态试验过程中影响观测结果的主要因素,研讨了海洋重力仪静态试验稳定性评估方法及流程,对该型海洋重力仪稳定性进行了分析与评估。首先,计算了理论固体潮重力值变化,改正了固体潮对静态观测结果的影响;然后,对单日观测数据以及整体数据进行分析;最后,根据稳定性评估流程,利用固体潮改正后的剩余观测值计算了仪器的零漂率、月漂以及准确度。计算表明,该型重力仪试验月漂值为-1.020 mGal,零漂线性良好且漂移率为-0.034 mGal/day,设备的测量准确度为0.085 mGal,符合重力测量的规范要求,可用于高精度海洋重力测量。

关键词： DGS-AT1M型海洋重力仪; 静态观测; 固体潮; 稳定性; 零点漂移; 测量准确度

Abstract

The performance of marine gravimeters directly determines the quality of measured data, while their stability serves as a critical indicator reflecting their performance. Based on the static test conducted using a DGS-AT1M marine gravimeter, this study analyzed the dominant factors affecting the measured results in the static test. It explored the method and process for stability assessment in the static test, analyzing and assessing the stability of this marine gravimeter.First, this study calculated the changes in the theoretical gravity value of earth tide, correcting the earth tide effect on static measurement results. Then, this study analyzed the single-day data and the overall data. Finally, based on the stability assessment process, this study calculated the zero-drift rate, monthly drift, and accuracy of the marine gravimeter using the residual measured values after earth tide correction. The calculation results show that this marine gravimeter yielded a monthly drift value of -1.020 mGal, and high zero drift linearity at a drift rate of -0.034 mGal/day. This marine gravimeter exhibited a measurement accuracy of 0.085 mGal, aligning with the gravity survey specifications.Therefore, it can be applied to high-precision marine gravity surveys.

Keywords： DGS-AT1M marine gravimeter; static measurement; earth tide; stability; zero drift; measurement accuracy

PDF (2437KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

张彬彬, 万丽丽. DGS-AT1M型海洋重力仪静态观测结果分析与评估[J]. 物探与化探, 2024, 48(4): 1018-1024 doi:10.11720/wtyht.2024.1377

ZHANG Bin-Bin, WAN Li-Li. Analysis and assessment of static measurement results from a DGS-AT1M marine gravimeter[J]. Geophysical and Geochemical Exploration, 2024, 48(4): 1018-1024 doi:10.11720/wtyht.2024.1377

0 引言

重力场是地球最重要的基本物理场之一,海洋重力场作为地球重力场的重要组成部分,在地球科学研究、海洋资源开发、全球空间基准统一、航天工程保障、海战场环境建设与作战运用等多个领域都具有非常重要的应用价值^[1]。目前探测海洋重力场信息的技术手段主要有海面船载重力测量、航空重力测量、卫星重力测量和卫星测高反演重力等,船载海洋重力测量是目前获取高精度、高频海洋重力场信息最有效的方式^[2]。受研究目标的需求,获得精度更高、分辨率更好的重力场数据是未来海洋重力测量的一项重要任务,而海洋重力数据的精度依赖于采集设备的稳定性和测量精度^[3]。目前,国内外海洋重力主流海洋重力测量设备主要是德国的KSS系列海洋重力仪、美国的L&R系列海洋重力仪及其衍生产品、俄罗斯GT系列海洋重力仪等,仪器测量精度均优于1 mGal。随着国内对海洋重力仪的持续研发,也生产了CHZ-Ⅱ型、ZL11型、SGA-WZ型、SAG-2M型海洋重力仪,精度指标也达到国际主流水平。海洋重力仪的静态观测结果是评价仪器稳定性的重要依托,也是计算海洋重力仪零点漂移指标的重要依据。专家学者对此开展了深入的研究和探讨,开展了静态观测数据的基础分析,探讨了静态试验环境与时长要求,提出了仪器零漂率、月漂量、精度等计算方法^{[4⇓⇓⇓-8]}。专家学者在静态观测结果中发现了固体潮等影响因素,但静态观测时间长度、仪器零漂和准确度的计算形式不统一。黄谟涛等^[9]针对分析过程不统一、技术指标欠细化等问题,结合现行规范要求,建立了比较完善的海洋重力仪稳定性评估指标体系。

自然资源部第一海洋研究所于2016年引进了美国DGS公司生产的全反馈磁阻尼AT1M型海洋重力仪,该重力仪采用最先进电子工业技术成果,兼具了直线弹簧重力仪不受交叉耦合影响的动态特性优点,及零长弹簧摆杆重力仪灵敏度高、零点漂移小的静态特性优点^[10]。Zhang等^[11]对AT1M型海洋重力仪做了静、动态试验,讨论了滤波延时计算方法,认定该型重力仪月漂为0.29 mGal,但未展示详细的评估流程,未作准确度计算。本文针对引进AT1M型海洋重力仪,为检验仪器工作性能,确定零点漂移和测量准确度,检验是否符合规范要求,在自然资源部第一海洋研究所实验室进行了静态观测,并对静态观测结果进行了分析与评估。

1 海洋重力仪静态观测结果

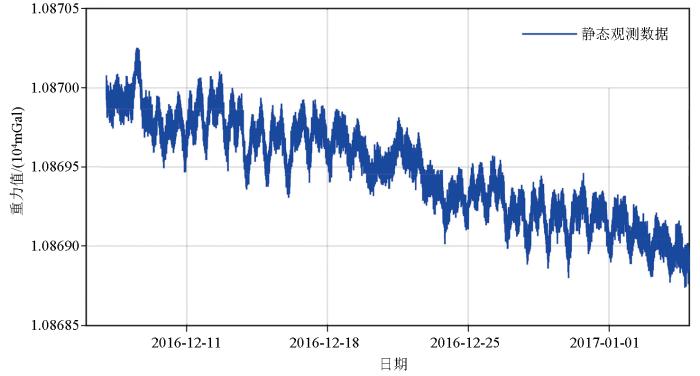
当前,海洋重力测量大多是一种相对观测方法,核心部件中的测量弹簧采用金属材料制成,观测值也随时间缓慢变化,掌握海洋重力仪零点漂移规律是一项十分重要的工作^[12]。静态试验是指将重力仪置于某固定测点而记录重力仪示数变化,观测结果应为测点处的相对重力结果,进而可以计算仪器的零点漂移规律和准确度。本研究中,AT1M型海洋重力仪静态试验在自然资源部第一海洋研究所所区实验室内进行,测试时间为2016年12月7日至2017年1月4日持续时间为29天,是该重力仪进口后第一次长时间静态观测试验。AT1M型海洋重力仪采用双保温及高精度温度电子控制系统,传感器温度持续在49.8°,不易受实验室温度影响。海洋重力仪设置采样间隔为1 s,AT1M型海洋重力仪具有自动滤波功能,滤波长度设置为180 s,观测结果如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 DGS-AT1M型海洋重力仪静态试验结果

Fig.1 Static measurement result of DGS-AT1M marine gravimeter

在静态试验结果中,AT1M型海洋重力仪最大读数为10 870.252 6 mGal,最小读数为10 868.737 4 mGal,最大差值1.515 2 mGal,仪器月漂量小于3 mGal。从图1可以看出,AT1M型海洋重力仪数据输出连续稳定,重力值变化范围较小,月漂值也符合规范要求。同时,在图1中看出重力值曲线有较为规律起伏变化,变化幅度在±0.2 mGal之内。在日月外部引力的影响中,海潮负荷影响在海洋沿岸地区最大也只有微伽级,而重力固体潮效应的最大影响可达±0.35 mGal^[13],因此固体潮对高精度重力仪和相对重力测量影响较大,不容忽视。静态试验是衡量仪器稳定性与计算零点漂移值的重要依据,在静态观测结果分析与评估中,海潮负荷影响几乎可以忽略不记,但是固体潮负荷影响需要去除。

2 重力固体潮理论计算

固体潮是指地球在太阳和月球起潮力的作用下发生周期性形变的现象,使地球表面上任一点至地心距离都随时间变化,其变化幅度为几厘米至几十厘米,所以在地球表面上进行的精密观测都必须考虑固体潮的影响^[14]。AT1M型海洋重力仪分辨率优于0.01 mGal,静态观测记录中包含重力固体潮,在稳定性分析前应作固体潮改正。固体潮理论发展较早,目前已经比较成熟,固体潮计算理论值精度高达微伽级^[15],本文为节约试验成本,应用理论固体潮计算值改正固体潮影响。固体潮理论值的计算公式参见中华人民共和国国土资源部发布重力调查技术规范(1∶50 000)附录B(中华人民共和国国土资源部,2015)^[16]:

(1)

δ g (t) = δ_{t h} G (t) - δ f_{c}

(2)

\begin{array}{l} G (t) = - 165.17 F (φ) {(\frac{c_{m}}{r_{m}})}^{3} (c o s^{2} Z_{m} - \frac{1}{3}) - \\ 1.37 F^{2} (φ) {(\frac{c_{m}}{r_{m}})}^{4} \times c o s Z_{m} (5 c o s^{2} Z_{m} - 3) - \\ 76.08 F (φ) {(\frac{c_{s}}{r_{s}})}^{3} c o s (c o s^{2} Z_{s} - \frac{1}{3}) \end{array}

。

式中: $δ g (t)$ 为固体潮改正值; $δ_{t h}$ 为固体潮因子,取1.16; $φ$ 为测点纬度; $φ'$ 测点地心纬度; $c_{m}$ 地心至月心的平均距离; $r_{m}$ 月心至地心的距离; $c_{s}$ 地心至日心的平均距离; $r_{s}$ 日心至地心的距离; $Z_{m}$ 月亮对测点的地心天顶距; $Z_{s}$ 太阳对测点的地心天顶距。

$δ f_{c}$ 是关于 $φ'$ 的函数,表达式为:

(3)

φ' = φ - 0.193296 s i n 2 φ

(4)

δ f_{c} = - 4.83 + 15.73 s i n^{2} φ' - 1.59 s i n^{4} φ'

。

根据上式,固体潮理论值的计算步骤如下:

1)根据测点的地理纬度,求 $F (φ)$ :

(5)

F (φ) = 0.998327 + 0.00167 c o s 2 φ

。

2)求出计算时刻的儒略世纪数T:

(6)

T = [T_{0} - 2415020.0 + (t - Δ t) / 24] / 36525

。

其中:T₀为计算日的儒略日;t为北京时间; $Δ t$ 为所在地时区。

3)根据所得的儒略世纪数T计算月球的平黄经s、太阳的平黄经h、月球近地点的平黄经p、月球升交点的平黄经N、地球近日点的平黄经p_s、黄赤交角ε等6个天文引数。

4)根据6个天文引数计算月亮的 $c_{m} / r_{m}$ 及 $c o s Z_{m}$ ;太阳的 $c_{s} / r_{s}$ 及 $c o s Z_{s}$ 。

5)将计算所得的 $F (φ)$ 、 $c_{m} / r_{m}$ 、 $c o s Z_{m}$ 、 $c_{s} / r_{s}$ 、 $c o s Z_{s}$ 代入式(2)求取 $G (t)$ ,再将 $G (t)$ 、 $δ f_{c}$ 代入式(1)求得理论固体潮改正值。

6个天文引数、 $c_{m} / r_{m}$ 、 $c o s Z_{m}$ 、 $c_{s} / r_{s}$ 、 $c o s Z_{s}$ 等参数的计算公式详见重力调查技术规范(1∶50 000)附录B重力固体潮改正部分(中华人民共和国国土资源部,2015),理论固体潮计算精度为(10^-8 m/s²)。

根据上述计算流程,结合AT1M型海洋重力仪静态试验结果,计算对应时刻的理论固体潮值,结果如图2所示,蓝色曲线为该型重力仪观测结果,黑色曲线为固体潮计算结果。从理论计算结果发现,重力固体潮理论计算值在±0.2 mGal之间,从图2中可以看出固体潮变化趋势与AT1M型海洋重力仪测量结果相符合,AT1M型海洋重力仪静态观测结果包含固体潮的重力变化。因此,静态试验结果应改正固体潮的影响,有利于仪器的稳定性分析,精确计算仪器的零点漂移与准确度。

图2

新窗口打开| 下载原图ZIP| 生成PPT

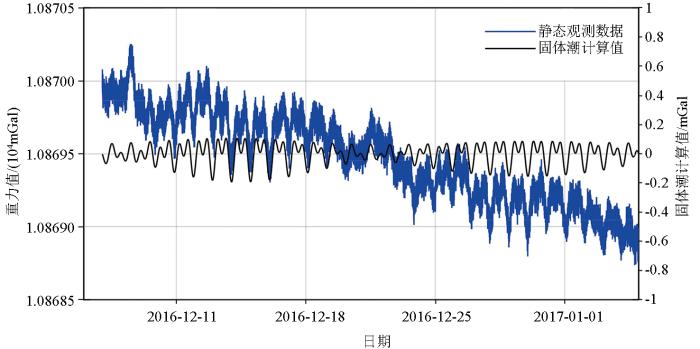
图2 理论固体潮计算值与重力仪静态观测

Fig.2 The value of earth tide and static measurement result

3 稳定性评价依据及计算

海洋重力仪是海洋重力测量的主体,仪器的性能直接决定测量数据的质量^[17],仪器的稳定性则是反映仪器性能的关键性指标,表征仪器自身稳定性的主要因素为零点漂移和测量准确度。零点漂移是指重力仪读数随时间缓慢变化,它是由弹性元件因弹性疲劳而产生的蠕变,若温度恒定则这种影响与时间大致呈线性关系^[18]。由于静态试验时缺乏更高精度的对比基准,测量精度一般采用反映观测值之间离散度的精密度指标即测点中误差表示^[19]。目前,我国现行各类海洋重力测量规范和规程对重力仪性能做出相应要求,但较为一致的要求为:①零点漂移稳定且基本呈线性;②零点月漂小于3 mGal;③测量准确度优于1 mGal^[20]。黄谟涛等^[9]专家对海洋重力仪稳定性与零点漂移问题进行了深入研讨,建立了比较完善的海洋重力仪稳定性指标评价体系,参照其评估测试流程,本文对AT1M型海洋重力的测试流程和评估方法如下:

1)将测试重力仪置于陆地实验室内,按照仪器操作规程连续观测记录重力仪读数,获取时间序列观测量 $g_{0} (t)$ ,根据规范要求连续观测7天以上。

2)根据重力仪静态试验观测的时间序列结果,计算重力固体潮理论值 $δ g (t)$ ,对观测的重力仪读数 $g_{0} (t)$ 进行固体潮改正扣除固体潮的影响,获得剩余观测量 $\tilde{g} (t)$ :

(7)

\tilde{g} (t) = g_{0} (t) - δ g (t)

。

3)利用最小二乘法对剩余观测量做线性拟合处理,即确定 $\tilde{g} (t)$ 中的线性变化部分:

(8)

\bar{g} (t) = a + b t

a和b为线性拟合参数,a为初始时刻相对重力值,b为线性系数(零漂率),t为测量时间,据此求取零点月漂量 $Δ {\bar{g}}^{0}$ ,即 $Δ {\bar{g}}^{0} = b * 30$ 。

4)从剩余观测量 $\tilde{g} (t)$ 分离出线性变化部分,即求偏差:

(9)

Δ \tilde{g} (t) = \tilde{g} (t) - \bar{g} (t)

。

5)求非线性变化中误差M,表征仪器的准确度:

(10)

M = \pm \sqrt{[Δ \tilde{g} (t) \cdot Δ \tilde{g} (t)] / n}

$n$ 代表系列观测量个数。

依据上述流程求得零漂率b、零点月漂量 $Δ {\bar{g}}^{0}$ 、中误差M等参数。零漂率b反映海洋重力仪观测值随时间变化趋势;中误差M反映的是海洋重力仪观测值偏离线性变化的离散化程度;零点月漂量Δ ${\bar{g}}^{0}$ 反映的一个月时间维度上的掉格情况,这3个参数反映了海洋重力仪的稳定性能。

4 静态试验观测结果分析与评估

为评估AT1M型海洋重力仪设备稳定性能,首先对静态观测数据进行固体潮改正,然后对比固体潮改正前后的单日、多日数据,分析仪器的零漂特性与准确度。

4.1 单日数据分析

为评估仪器的单日变化,随机选取两天静态数据进行分析,结果如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

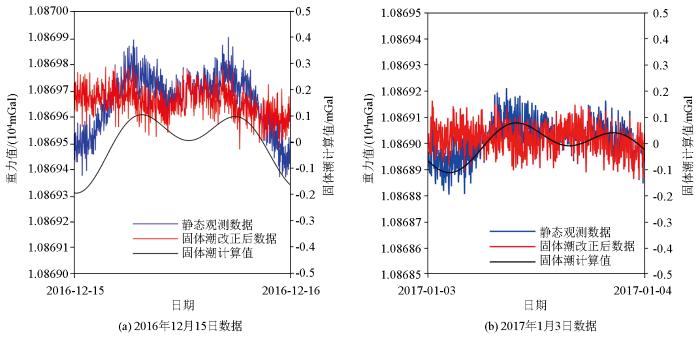
图3 单日静态观测、理论固体潮及改正数据

Fig.3 One day measurement data, earth tide and correction data

图3中,蓝色曲线为重力仪静态试验观测结果,黑色平滑的曲线为计算的固体潮理论值,红色曲线为固体潮改正后的重力值。在选取的单日静态测试中,该设备记录的数据变化明显,曲线变化在幅值和周期上与固体潮重力影响趋势一致。经固体潮改正后,可以看出红色曲线基本呈线性,但仍存在细微抖动,抖动幅度在±0.1 mGal之间,呈非规律性变化,这种变化一直存在,可能与仪器固有特性、观测环境等因素有关。由于单日观测数据不满足规范要求的连续观测天数,不做稳定性分析。

4.2 多日数据分析

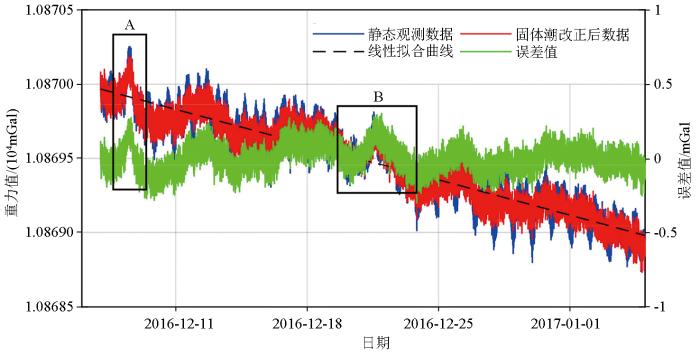
进一步,选取2016年12月7日至2017年1月4日持续时间为29天的静态观测结果,利用第3节所述的稳定性评估方法评估该仪器的性能。首先,根据每个观测值对应的时刻,利用第2节计算公式(1)~(6)计算每一个观测时刻对应的固体潮理论值;然后,根据式(7)从重力观测数据中扣除计算固体潮重力的影响,得到剩余观测量,结果如图4红色曲线所示,从图中可以看出固体潮改正后部分峰值消除、数据线性更加明显,改正掉了固体潮的影响,更加还原仪器自身的测量特性;再次,利用最小二乘法将固体潮改正后的剩余观测量做线性拟合,求得零漂率,拟合曲线如图4中黑色虚线所示;最后,从剩余观测量中减去线性变化部分,如图4中绿色曲线所示,用式(10)计算中误差作为仪器的准确度。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 静态观测数据稳定性评估

Fig.4 Stability assessment of static measurement data

从图4中发现,经固体潮改正后的剩余观测量线性明显,线性拟合后误差更小,在±0.1 mGal内随机变动,计算中误差更加符合仪器特征。经上述方法计算后,求得零漂率为0.034 mGal/day,该设备本次静态试验的月漂为1.020 mGal,静态试验的中误差M结果为0.085 mGal。该型海洋重力仪本次试验月漂为1.020 mGal远小于规范3 mGal的要求,零漂基本呈线性且漂移率为0.034 mGal/day,测量准确度为0.085 mGal,小于规范规定的1 mGal,符合重力测量的行业规范要求。

观察图4中绿色曲线,存在A、B两处误差较大,从仪器静置试验过程分析认为A处是由于仪器初始使用,传感器加热恒定,仪器才开始稳定工作;B处仪器工作已相对稳定,可能由于环境因素或者内部传感器因素导致格值突然变化。在仪器静态试验时,温度、震动及其他随机干扰因素难以定量分析,因此在进行海洋重力仪静态试验时,首先要将仪器放置在地基稳定的专用重力实验室内进行,尽大可能屏蔽掉外界环境因素的影响;其次,要保证静态试验时间要足够长,有足够的观测数据才能反应仪器的本体特性。

Zhang等^[11]完成AT1M型海洋重力仪14天静态试验,计算仪器月漂0.29 mGal,而本次试验计算月漂约为1.020 mGal。表明相同型号的不同台重力传感器零点漂移特性也不尽相同;不同的计算方法得到的结果也不尽相同。因此,应建立比较统一完善的海洋重力仪稳定性评估方法,在做重力调查前应对每一台海洋重力仪做稳定性评估,了解仪器特征,更好得用于后续测量平差,取得高精度海洋重力测量成果。

5 结论

通过对AT1M型海洋重力仪静态观测结果分析,可以得到以下结论:

1)AT1M型海洋重力具有较高的分辨能力,静态试验观测结果能够很好地反映固体潮的变化,在仪器稳定性评估中应扣除固体潮的影响。

2)根据重力仪稳定性评估方法计算,本次试验月漂1.020 mGal,零漂基本呈线性且漂移率为0.034 mGal/day,设备的测量准确度为0.085 mGal,符合重力测量的行业规范要求。

3)应建立比较统一完善的稳定性评估方法,在做重力调查前对每一台海洋重力仪做稳定性评估,更好的应用于后续测量平差,取得高精度海洋重力测量成果。

总之,本次静态试验表明AT1M型海洋重力仪性能稳定,达到了仪器的指标要求,符合有关规范要求。静态观测可以反映仪器的固有特性,用于评估设备的静态稳定程度,但是不符合仪器现场作业工况。为更客观地分析海洋重力仪的性能,建议将仪器安装于系泊状态的船舶上,分析仪器的观测结果,这样更符合实际作业工况,在分析评估时应去除固体潮、高程等变化的影响。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

黄谟涛, 翟国君, 管铮,

等. 海洋重力场测定及其应用[M]. 北京: 测绘出版社, 2005.