激电效应对AMT正演的影响及其在砂岩型铀矿中的数值模拟

doi:10.11720/wtyht.2024.1218

激电效应对AMT正演的影响及其在砂岩型铀矿中的数值模拟

胡英才^,¹^,²^,³, 王瑞廷¹^,², 李貅²

1.西北有色地质矿业集团有限公司,陕西西安 710054

2.长安大学地质工程与测绘学院,陕西西安 710061

3.核工业北京地质研究院中核集团铀资源勘查与评价技术重点实验室,北京 100029

Influence of induced polarization effects on AMT forward modeling and its numerical simulations for sandstone uranium deposits

HU Ying-Cai^,¹^,²^,³, WANG Rui-Ting¹^,², LI Xiu²

1. Northwest Nonferrous Geological and Mining Group Co., Ltd., Xi’an 710054, China

2. School of Geological Engineering and Geomatics, Chang’an University, Xi’an 710061, China

3. Key Laboratory of Uranium Resource Exploration and Evaluation Technology, China National Nuclear Corporation, Beijing Research Institute of Uranium Geology, Beijing 100029, China

第一作者: 胡英才(1985-),男,高级工程师,博士,主要从事地球物理正反演及应用研究工作。Email:hycjlu@163.com

责任编辑: 王萌

收稿日期: 2023-05-22 修回日期: 2023-12-19

基金资助:

西北有色地质矿业集团博士后科研工作站项目(XBDKKJ202111)
国家自然科学基金项目(41604126)

Received: 2023-05-22 Revised: 2023-12-19

摘要

音频大地电磁测深法应用比较广泛,已成为固体矿产深部地球物理探测的主要方法之一,但在处理解释中,往往只考虑电磁效应,忽略了激电效应,这与实际地质情况不相符。本文在实现带激电效应的二维音频大地电磁有限元正演基础上,模拟了激电效应各参数对二维正演响应的影响大小及规律,同时对二连盆地砂岩型铀矿的地电模型进行了数值模拟研究。结果表明:①基于Cole-Cole模型实现的带激电效应二维AMT正演,随着极化率、频率相关系数及时间常数取值的增加,主要降低二维正演视电阻率异常响应值,增大阻抗相位异常响应值,这对探测低阻目标体有利,探测高阻目标体影响较大;②激电效应中的零频电阻率和极化率对二维正演响应影响较大,频率相关系数与时间常数对正演的影响大小主要取决于极化率,当极化率较大时,二者对正演响应同样具有较大的影响;③在砂岩型铀矿中,当砂体中存在浸染状及含硫化物的岩性时,较大的激电效应会对频域电磁测深法探测目标砂体产生较大影响,因此在探测前需进行正演建模,了解激电效应的影响大小。

关键词： 音频大地电磁测深法; 激电效应; 二维正演; 砂岩型铀矿

Abstract

The extensively applied audio magnetotellurics (AMT) has become a primary method for deep geophysical exploration of solid mineral resources. However, its data processing and interpretation often only consider electromagnetic effects but ignore induced polarization (IP) effects, which is inconsistent with actual geological conditions. Based on the two-dimensional AMT finite-element forward modeling with IP effects, this study simulated the magnitude and regularity of the influence of various parameters of IP effects on the two-dimensional forward response. Moreover, this study conducted a numerical simulation on the geoelectric model of sandstone uranium deposits in the Erlian Basin. The results show that: (1) With an increase in the values of polarizability, frequency correlation coefficient, and time constant, the two-dimensional AMT forward modeling with IP effects based on the Cole-Cole model primarily reduced the abnormal response value of two-dimensional forward modeling apparent resistivity and increased the abnormal response value of impedance phase. This is beneficial for detecting low-resistivity targets rather than high-resistivity targets; (2) The zero-frequency resistivity and polarizability in IP effects exhibit a significant influence on the two-dimensional forward response. The influence of both frequency correlation coefficient and time constant on the forward response primarily depends on the polarizability. High polarizability suggests their significant influence on the forward response; (3) In the case of disseminated and sulfide-bearing lithologies in the sand bodies of sandstone uranium deposits, greater IP effects will significantly influence the detection of target sand bodies using frequency-domain AMT. Therefore, forward modeling is necessary before detection to determine the magnitude of IP effects.

Keywords： audio magnetotellurics; induced polarization effect; two-dimensional forward modeling; sandstone uranium deposit

PDF (8319KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

胡英才, 王瑞廷, 李貅. 激电效应对AMT正演的影响及其在砂岩型铀矿中的数值模拟[J]. 物探与化探, 2024, 48(4): 1006-1017 doi:10.11720/wtyht.2024.1218

HU Ying-Cai, WANG Rui-Ting, LI Xiu. Influence of induced polarization effects on AMT forward modeling and its numerical simulations for sandstone uranium deposits[J]. Geophysical and Geochemical Exploration, 2024, 48(4): 1006-1017 doi:10.11720/wtyht.2024.1218

0 引言

音频大地电磁测深法(AMT)是以大地电磁测深理论为基础,主要观测音频段的频域电磁响应信号,与可控源音频大地电磁测深法(CSAMT)基本相同,区别在于前者采集天然场信号,后者采集人工源场信号,其探测深度一般在0~2 km,主要应用在干扰噪声较小的地区^[1-2]。由于AMT探测效率高、成本低,在国内外已广泛应用于多个领域,如固体矿产普查与勘探、地热勘查、地质灾害以及水文工程等^{[3⇓⇓⇓⇓⇓-9]},然而在实际的野外地质条件下,各岩、矿石中不仅存在导电特征,而且也普遍存在激电特征^[10],在进行AMT探测时,特别是在激电效应较高的地区,忽略激电效应可能会对电磁测深法后续的数据处理及解释产生一定的影响。

复电阻率模型的引入,很好地解释了激电效应产生的特征,其模型有多种,其中由Pelton等^[11]提出的Cole-Cole模型各参数物理意义明确,应用相对比较广泛,是常用的描述激电效应的复电阻率模型之一。在带激电效应的频率域电磁法正演模拟中,由Ware^[12]首次开创了频域电磁测深中带激电效应的模拟及提取激电信息的理论研究,随后,国内外众多学者对带激电效应的频率域电磁法正演进行了较多的模拟研究工作。近年来,汤井田等^[13]通过一维带激电效应的CSAMT正演模拟,指出对于低频电流下,应注意激电效应对电磁场处理解释的影响。岳安平等^[14]开展了带激电效应的一维CSAMT正演研究,在考虑激电效应参数后,正演响应会发生明显异常。符超等^[15]基于Cole-Cole模型讨论了中间极化水平层大地电磁的激发极化效应的影响,对极化体厚度和埋深关系进行了讨论。李勇等^[16]在一维CSAMT中研究了含激电效应的电磁测深正演问题,指出了采用电场E_x分量提取IP信息的合理性。朱占升等^[17]开展了考虑激电效应的二维大地电磁正演研究,指出激电效应的存在降低了视电阻率的值,且激电效应各参数对正演响应影响存在差异。王恒等^[18]开展了考虑激电效应的二维大地电磁正演研究,指出激电效应不可忽略,极化率对正演响应影响较大,而频率相关系数和时间常数对视电阻率和相位没有太大影响。徐凯军等^[19]和付振兴^[20]开展了三维大地电磁激电效应特征研究,极化率会使观测的视电阻率降低。黄逸伟^[21]和万伟等^[10]开展了带激电效应的CSAMT三维正演模拟研究,对低阻体模型进行了模拟,指出极化率影响最大,频率相关系数和时间常数影响比较小,且视电阻率和阻抗相位特征更能反应Cole-Cole模型参数的影响,同时很多研究人员也在反演中进行了激电效应参数的提取研究。综上所述,前人在频域电磁法中主要进行了一维、二维及三维的正演模拟研究,指出了激电效应的重要性,但更多的是针对理论模型的对比研究,而对实际的地质模型模拟较少,特别是在砂岩型铀矿的地电模型中研究激电效应的影响还比较少。

由于三维电磁勘探成本巨大,在实际应用中仍然是以二维探测为主,因此本文以带激电效应的二维音频大地电磁为例,分别对极化率、频率相关系数及时间常数对含高、低阻体的AMT二维模型进行正演模拟,同时在砂岩型铀矿中对带激电效应的砂泥互层结构地电模型进行了数值模拟研究,总结激电效应对砂岩型铀矿主要探测目标砂体的正演影响规律,可为频率域电磁法在带激电效应的砂岩型铀矿探测中提供一定的指导作用。

1 带激电效应的音频大地电磁二维正演及验证

1.1 二维正演理论

地下空间整体虽然是三维结构,但在沿构造走向内一定的范围大体呈现二维结构特征,因此研究二维同样具有实际应用价值。二维大地电磁正演模型示意图如图1所示。取构造走向为x轴方向(假设对应的地面为SN方向),剖面方向为y轴方向(地面为EW方向),z轴沿地心竖直向下。假设地下为各向同性介质,从Maxwell方程组中的法拉第定律及安培定律公式出发^[22],取负时谐因子(e^-i^wt),则公式分别变为:

(1)

\nabla \times E = i ω μ H

(2)

\nabla \times H = (σ - i ω ε) E

图1

新窗口打开| 下载原图ZIP| 生成PPT

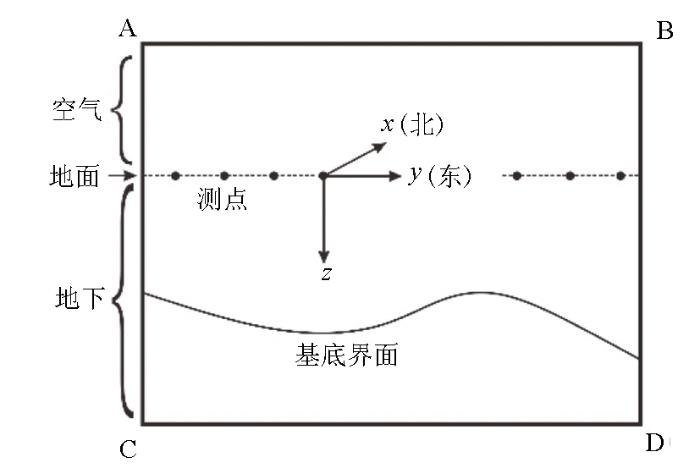
图1 二维音频大地电磁正演模型示意

Fig.1 Schematic diagram of 2D audio magnetotelluric forward modeling

其中:E为电场强度;H为磁场强度;σ为电导率;ω为角频率;μ为介质的磁导率;ε为介电常数。将式(1)和(2)按照旋度公式展开,可推导出TM极化模式和TE极化模式的偏微分方程,如式(3)和(4)^[23]:

(3)

\frac{\partial}{\partial y} (\frac{1}{σ - i ω ε} \frac{\partial H_{x}}{\partial y}) + \frac{\partial}{\partial z} (\frac{1}{σ - i ω ε} \frac{\partial H_{x}}{\partial z}) + i ω μ H_{x} = 0

(4)

\frac{\partial}{\partial y} (\frac{1}{i ω μ} \frac{\partial E_{x}}{\partial y}) + \frac{\partial}{\partial z} (\frac{1}{i ω μ} \frac{\partial E_{x}}{\partial z}) + (σ - i ω ε) E_{x} = 0

式(3)和(4)可统一表示为式(5):

(5)

\nabla \cdot (τ \nabla u) + λ u = 0

其中:Ñ为二维哈密顿算子。

因此,对TM极化模式:

(6)

u = H_{x}, τ = \frac{1}{σ - i ω ε}, λ = i ω μ

对TE极化模式:

(7)

u = E_{x}, τ = \frac{1}{i ω μ}, λ = σ - i ω ε

加入二维研究区域的边界条件,则式(5)的变分问题可写为式(8):

(8)

\{\begin{array}{l} F (u) = \int [\frac{1}{2} τ {(\nabla u)}^{2} - \frac{1}{2} λ u^{2}] d Ω + \int_{C D}^{} \frac{1}{2} τ k u^{2} d Γ, \\ \begin{array}{l} u |_{A B} = 1, \\ δ F (u) = 0 。 \end{array} \end{array}

利用节点有限元法求解变分问题,即可获得每个网格节点的u值,同时计算u沿z方向的偏导数值,即可获得二维音频大地电磁TM极化模式和TE极化模式的正演响应(阻抗Z、视电阻率ρ和阻抗相位Φ)。

TM极化模式下的正演响应为:

(9)

\{\begin{array}{l} Z_{T M} = Z_{y x} = \frac{E_{y}}{H_{x}} = \frac{1}{σ - i ω ε} (\frac{\partial H_{x}}{\partial z}) / H_{x} \\ ρ_{T M} = ρ_{y x} = \frac{1}{ω μ} {|Z_{T M}|}^{2} \\ Φ_{T M} = Φ_{y x} = a r c t a n \frac{I m [Z_{T M}]}{R e [Z_{T M}]} \end{array}

TE极化模式下的正演响应为:

(10)

\{\begin{array}{l} Z_{T E} = Z_{x y} = \frac{E_{x}}{H_{y}} = E_{x} / (\frac{1}{i ω μ} \frac{\partial E_{x}}{\partial z}), \\ ρ_{T E} = ρ_{x y} = \frac{1}{ω μ} {|Z_{T E}|}^{2}, \\ Φ_{T E} = Φ_{x y} = a r c t a n \frac{I m [Z_{T E}]}{R e [Z_{T E}]} 。 \end{array}

1.2 激电模型

地层中的岩、矿石普遍存在激电效应,描述激电效应的复电阻率模型公式有十多种^[24],常用的且被广泛采用的复电阻率模型为Cole-Cole模型^[11],其表达式如式(11),该模型的等效电流如图2所示。

(11)

ρ (i ω) = ρ_{0} \{1 - m [1 - \frac{1}{1 + {(i ω τ)}^{c}}]\}

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 Cole-Cole模型等效电路

Fig.2 Equivalent circuit diagram of Cole-Cole model

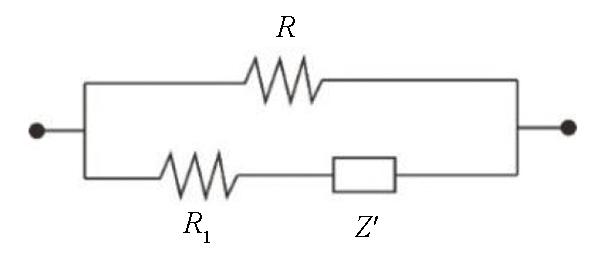
式中:i为复单位;ω为角频率;ρ(iω)为复电阻率;ρ₀为零频电阻率;m为极化率;c为频率相关系数;τ为时间常数。式(11)是使用复电阻率来代替普通的电阻率,并引入3个新的电性参数来准确描述实际岩、矿石的物性特征,从式中可以看出,不同的频率下,地下每一块的岩、矿石的复电阻率是变化的,因此在频域电磁法探测时需特别注意。

1.3 正演结果验证

为验证本文算法及程序的正确性,选取存在解析解的层状模型进行对比验证,以3层介质模型(H型)为例,设置第二层为极化层,模型参数如表1所示,正演计算频率在10 400~0.146 Hz,共计17个频点。一维解析解及二维正演数值解计算结果如表2所示。

表1 层状模型参数

Table 1 Parameters of layered model

层序号	层厚度/m	零频电阻率/(Ω·m)	极化率/%	频率相关系数	时间常数/s
1	200.0	100.0	0	0	0
2	200.0	10.0	0.4	0.5	100.0
3	∞	1000.0	0	0	0

新窗口打开| 下载CSV

表2 层状介质模型一维与二维正演计算结果对比

Table 2 Comparison of one-dimensional and two-dimensional forward calculation results in layered model

频率/Hz	1D视电阻率解析解/(Ω·m)	2D视电阻率数值计算结果/(Ω·m)	视电阻率误差/%	1D阻抗相位解析解/(°)	2D阻抗相位数值计算结果/(°)	阻抗相位误差/%
10400	100.018	100.169	0.151	45.020	45.048	0.062
5200	99.332	99.410	0.079	44.882	44.912	0.067
2600	102.617	102.640	0.022	44.046	44.057	0.025
1300	114.220	114.280	0.053	46.079	46.077	0.004
640	114.751	114.838	0.076	53.415	53.418	0.006
320	91.935	91.989	0.059	61.437	61.446	0.015
159	63.163	63.188	0.040	66.878	66.888	0.015
79	39.078	39.084	0.015	68.978	68.988	0.014
40	23.550	23.550	0	65.185	65.191	0.009
18.8	15.850	15.849	0.006	52.652	52.654	0.004
9.4	15.825	15.825	0	37.224	37.224	0
4.7	22.162	22.163	0.005	24.973	24.972	0.004
2.34	36.640	36.643	0.008	18.387	18.387	0
1.17	62.650	62.654	0.006	16.292	16.293	0.006
0.59	104.479	104.484	0.005	17.018	17.019	0.006
0.293	168.476	168.478	0.001	19.539	19.539	0
0.146	255.138	255.141	0.001	23.081	23.081	0

新窗口打开| 下载CSV

从表2计算结果可以看出,本文算法计算结果与一维解析解计算结果吻合较好,整体误差均小于0.2%,网格剖分精细,计算精度较高。高精度的二维正演也为带激电效应的精细数值模拟提供了保障。

2 不同激电参数对二维AMT正演响应的影响

激电参数中主要有零频电阻率、极化率、频率相关系数和时间常数4个。不同激电参数对二维正演响应的影响采取固定其他参数值不变,并设为较小值,只改变其中一个参数的取值范围来研究二维正演响应(视电阻率及阻抗相位)的变化特征。由于零频电阻率对正演影响较大,当其他激电参数较小时,基本等同于不含激电效应的常规音频大地电磁测深法,其正演响应跟异常体电阻率值大小相关,这里不再单独模拟,在模拟其他激电参数时,在半空间中同时置于高阻体和低阻体两个异常体模型,分别观测各激电参数在同时含高、低阻体模型中对二维正演的影响特征。模型参数为:背景电阻率为500 Ω·m,高、低阻异常体分别为背景半空间电阻率的2.5倍和1/2.5倍,即高阻体为1 250 Ω·m,低阻体为200 Ω·m。为方便且直观显示异常体产生的正演响应特征,将下文中二维正演结果图的横坐标通过 $356 \sqrt{ρ / f}$ 转换为视深度来进行对比研究,图中白色框为异常体的大体位置。

2.1 极化率对二维正演响应的影响

固定频率相关系数和时间常数不变,并设为较小值,选取极化率分别为0、0.2、0.5和0.8进行二维正演计算,通过观测二维AMT视电阻率和阻抗相位的异常特征来了解从低到高的极化率对AMT正演响应的影响规律。模型的参数如表3所示。不同极化率下的二维AMT正演响应计算结果如图3和图4所示。

表3 不同极化率下的二维正演模型参数

Table 3 Parameter of two-dimensional forward modeling with different polarizabilities

名称	埋深/m	电阻率/(Ω·m)	极化率/%	频率相关系数	时间常数/s
背景参数	-	500.0	0	0	0
异常体	100	200.0&1250.0	无极化/0.2/0.5/0.8	0.2	10

新窗口打开| 下载CSV

图3

新窗口打开| 下载原图ZIP| 生成PPT

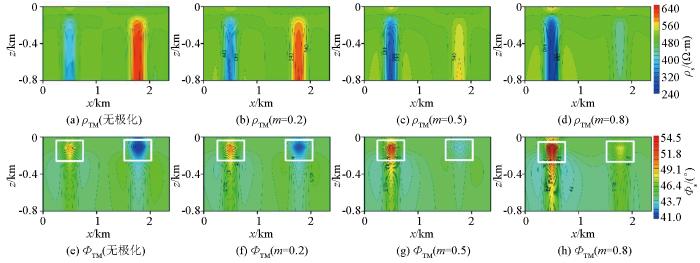
图3 不同极化率的TM模式正演响应结果

Fig.3 Forward response results of different polarizabilities in TM mode

图4

新窗口打开| 下载原图ZIP| 生成PPT

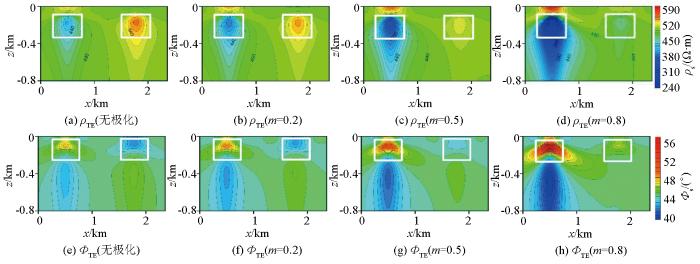
图4 不同极化率的TE模式正演响应结果

Fig.4 Forward response results of different polarizabilities in TE mode

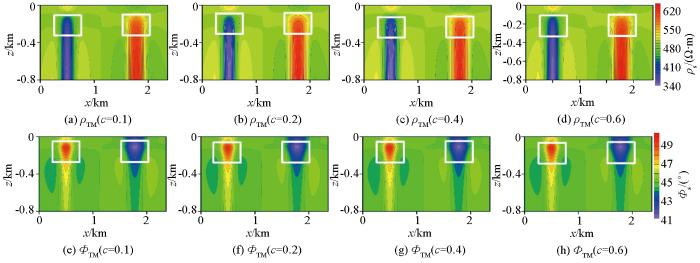
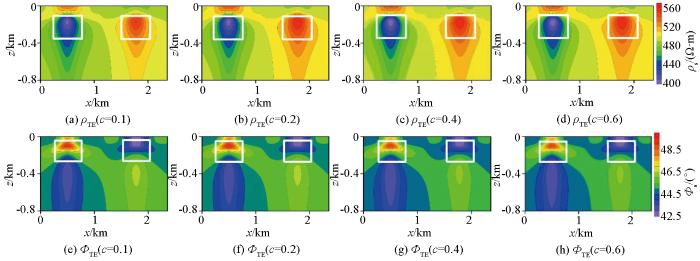
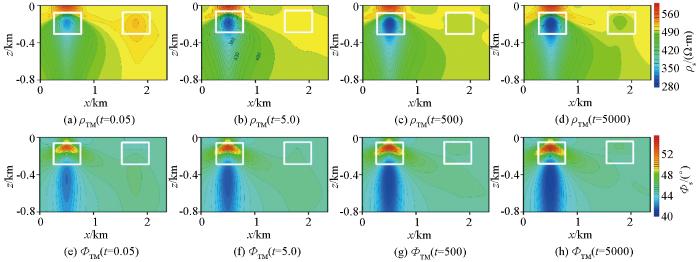
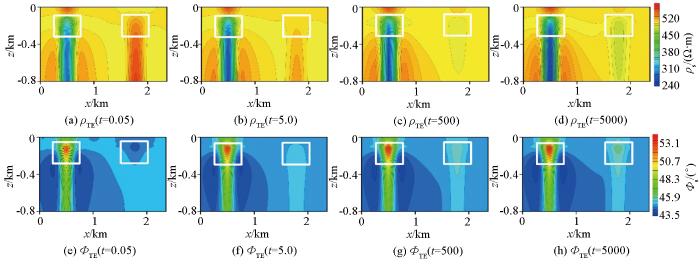
图3为不同极化率TM模式下视电阻率及阻抗相位的正演响应结果,从图3a~d正演中的视电阻率中可以看出,在无极化时,低阻体在对应异常体位置视电阻率表现为低阻特征(图3a蓝色范围),高阻体在对应异常体位置呈现高阻体特征(图3a红色范围),随着极化率从低到高增大,高阻体和低阻体所产生的视电阻率值均逐渐减小(低阻体蓝色逐渐加深,高阻体红色逐渐变淡,最后呈淡蓝色),使得低阻异常特征逐渐明显,而高阻体异常响应特征逐渐降低,最后呈现了低阻体的异常响应特征。同样,从图3e~h阻抗相位中可以看出,在无极化率时,低阻体在对应异常体位置处阻抗相位表现为高值特征(图3a黄色范围),高阻体在对应异常体位置处表现为低值特征(图3a蓝色范围),随着极化率的增大,低阻体的异常响应特征逐渐增强,而高阻体的异常响应特征减弱,直至出现较高阻抗特征。图4为不同极化率TE模式下视电阻率及阻抗相位的正演响应结果。其视电阻率及阻抗相位随着极化率的变换具有与TM模式相同的变化规律,视电阻率响应对于高阻体和低阻体均随极化率的增大而减小,而阻抗相位随极化率增大而增大,只是异常响应的范围和幅值略有一些差别。通过对比不同极化率下二维音频大地电磁正演响应的模拟结果,极化率对二维AMT正演响应影响较大,随着极化率的变大,主要降低异常体产生的视电阻率值,增大其阻抗相位值。

2.2 频率相关系数对二维正演响应的影响

由于Cole-Cole模型公式中,频率相关系数和时间常数前面存在极化率系数,而极化率对正演影响相对较大,因此需考虑极化率对二者的影响。这里设置极化率为一个低值(0.1)和一个高值(0.5)分别进行模拟对比研究,固定时间常数不变,并设为较小值,选取频率相关系数从低到高(0.1、0.2、0.4和0.6)分别进行计算,模型参数如表4所示。

表4 不同频率相关系数下的二维正演模型参数

Table 4 Two dimensional forward modeling parameters with different frequency correlation coefficients

名称	埋深/m	电阻率/(Ω·m)	极化率/%	频率相关系数	时间常数/s
背景参数	-	500.0	0	0	0
异常体	100	200.0&1250.0	0.1/0.5	0.1/0.2/0.4/0.6	10

新窗口打开| 下载CSV

通过带激电效应的二维AMT正演计算,得到了从低到高不同频率相关系数的二维正演响应结果,如图5~图8所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 低极化率条件下不同频率相关系数的二维TM模式正演响应结果

Fig.5 2D TM mode forward response results of different frequency correlation coefficients in low polarizability

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 低极化率条件下不同频率相关系数的二维TE模式正演响应结果

Fig.6 2D TE mode forward response results of different frequency correlation coefficients in low polarizability

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 高极化率条件下不同频率相关系数的二维TM模式正演响应结果

Fig.7 2D TM mode forward response results of different frequency correlation coefficients in high polarizability

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 高极化率条件下不同频率相关系数的二维TE模式正演响应结果

Fig.8 2D TE mode forward response results of different frequency correlation coefficients in high polarizability

图5和图6分别为低极化率条件下不同频率相关系数的二维TM、TE模式视电阻率和阻抗相位计算结果。对比图5a~d视电阻率以及图5e~h阻抗相位计算结果,在极化率较低的情况下,含高阻体、低阻体剖面中所计算的正演响应随着频率相关系数逐渐增大,视电阻率及阻抗相位结果基本不变。同样对比图6a~d视电阻率以及图6e~h阻抗相位结果可以看出,二维TE模式下的视电阻率及阻抗相位计算结果也基本不变。因此在低极化率条件下,无论频率相关系数如何变换,对二维正演响应的影响非常小。

图7为高极化率条件下不同频率相关系数的二维TM模式正演响应结果,从图7a~d正演响应(视电阻率)中可以看出,在极化率较大的情况时,低阻体和高阻体分别表现为低阻特征和高阻特征,随着频率相关系数的增大,低阻体表现的低阻特征逐渐增强,异常范围也逐渐扩大,而高阻体的异常特征逐渐变小,当频率相关系数大于0.4时,其高阻体的异常特征变为低阻特征。对比图7e~h阻抗相位与视电阻率的变化规律基本相同。

图8为高极化率条件下不同频率相关系数的二维TE模式下正演响应结果,对比图8a~d视电阻率计算结果以及图8e~h阻抗相位计算结果,在高极化率情况下,随着频率相关系数的增大,低阻体的异常特征逐渐增强,而高阻体的异常特征逐渐减弱,当频率相关系数较大时,呈现低阻体的异常响应特征。整体TE模式异常响应特征变化相对TM模式较弱。由此可见,当极化率较大时,频率相关系数的改变对二维正演响应的影响较大。

2.3 时间常数对二维正演响应的影响

时间常数与频率相关系数的模型参数设置基本相同,同样设置极化率为一个低值(0.1)和一个高值(0.5)进行比较。选取时间常数从低到高(0.05 s、5 s、500 s和5 000 s)分别进行二维正演模拟,分析时间常数对二维正演响应的影响规律,具体参数如表5所示。

表5 不同时间常数的二维正演模型参数

Table 5 2D forward modeling parameters with different time constants

名称	埋深/m	电阻率/(Ω·m)	极化率/%	频率相关系数	时间常数/s
背景参数	-	500.0	0	0	0
异常体	100	200.0&1250.0	0.1/0.5	0.1	0.05/5/500/5000

新窗口打开| 下载CSV

通过带激电效应的二维音频大地电磁正演计算,得到了从低到高不同时间常数下的二维正演响应结果,如图9~图12所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 低极化率条件下不同时间常数的二维TM模式正演响应结果

Fig.9 2D TM mode forward response results of different time constants in low polarizability

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 低极化率条件下不同时间常数的二维TE模式正演响应结果

Fig.10 2D TE mode forward response results of different time constants in low polarizability

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 高极化率条件下不同时间常数的二维TM模式正演响应结果

Fig.11 2D TM mode forward response results of different time constants in high polarizability

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 高极化率条件下不同时间常数的二维TE模式正演响应结果

Fig.12 2D TE mode forward response results of different time constants in high polarizability

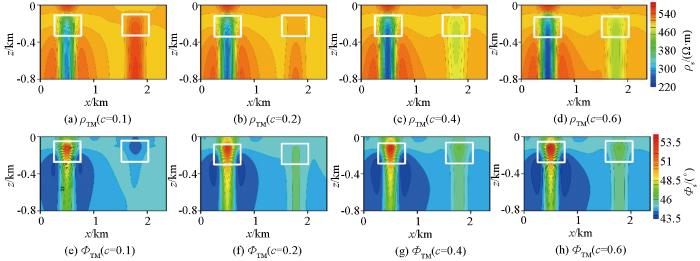
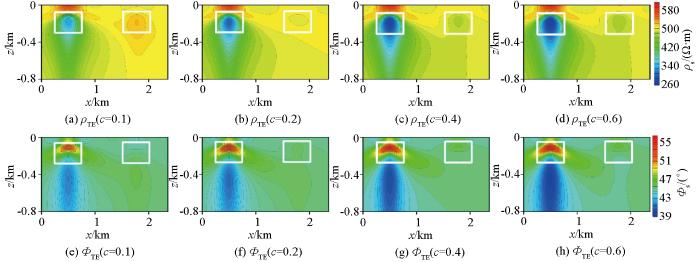
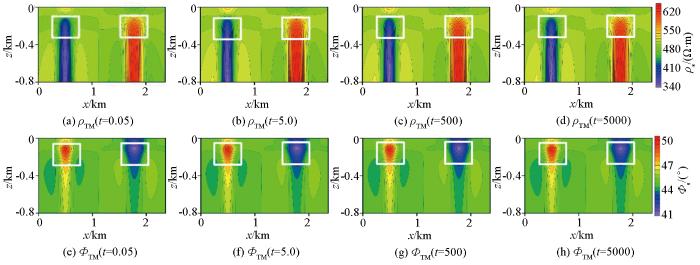
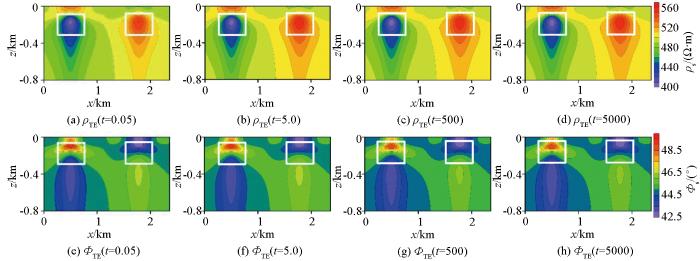
图9为低极化率条件下不同时间常数的二维TM模式正演响应结果,对比图9a~d视电阻率计算结果以及图9e~h阻抗相位计算结果,在极化率较低的情况下,随着时间常数的逐渐增大,剖面中视电阻率及阻抗相位计算结果基本不变。同样从图10a~h二维TE模式下的视电阻率及阻抗相位计算结果可以看出,不同时间常数计算的正演响应也基本不变。因此在低极化率条件下,无论时间常数如何变换,对二维正演响应的影响非常小。

图11为高极化率条件下不同时间常数的二维TM模式下正演响应结果。从图11a~d视电阻率计算结果中可以看出,在极化率较大的情况时,低阻体和高阻体分别表现为低阻特征和高阻特征,随着时间常数的增大,低阻体表现的低阻异常特征逐渐增强,异常范围也逐渐扩大,而高阻体的异常特征逐渐变小,当时间常数较大时,其高阻体的异常特征转变为低阻的响应特征。对比图11e~h阻抗相位的变化规律与视电阻率基本相同。图12为高极化率条件下不同时间常数的二维TE模式下正演响应结果,对比图12a~d视电阻率计算结果以及图12e~h阻抗相位计算结果也可以看出,在高极化率情况下,改变时间常数对二维正演响应同样变化较大,其变化规律与TM模式的基本相同。由此可见,当极化率较大时,时间常数的改变对二维正演响应的影响也比较大。

3 砂岩型铀矿中的数值模拟算例

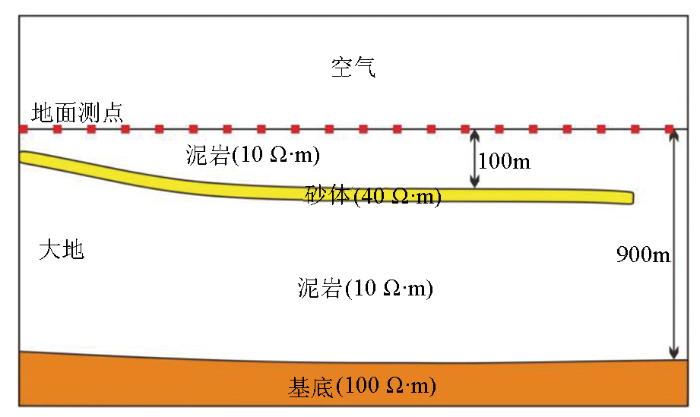
砂岩型铀矿目前已是我国第一大铀矿类型^[25],主要分布于我国的北方各大盆地中。音频大地电磁测深法是砂岩型铀矿地球物理勘探中常用的方法之一,主要探测1 000 m以内的地层结构及砂体分布。胡英才等^[26]基于二连盆地砂岩型铀矿地层结构特点,构建了含砂泥互层的简要地电模型,并进行了相关的数值模拟研究。王恒等^[27]在砂岩型铀矿中进行了带激电效应的可行性研究,调研发现铀矿中若不含电子导电矿物,其极化率通常小于2%,若含有少量的侵染状电子导电矿物,即可引起较高的极化率(通常大于10%),在部分铀多金属矿床中,富集金属硫化物的砂岩,其极化率高达56%以上,而且铀矿往往与其他金属矿伴生。然而激电效应的影响在砂岩型铀矿探测中往往被忽略。从本文激电效应的各参数对二维AMT的正演响应的影响规律及大小可以看出,在极化率较大的地区,激电效应各参数对二维AMT正演影响均比较大。因此,研究激电效应对寻找砂岩型铀矿具有重要的意义。

沉积盆地中的砂岩型铀矿主要探测低阻泥岩中相对高阻特征的砂岩,其铀矿体主要赋存于砂泥互层结构中,本次地电模型以二连盆地砂岩型铀矿为例进行构建,具体参考文献[26],模型示意如图13所示,主要探测的目标砂体埋深100 m,电阻率40 Ω·m,厚度为20 m,分别对砂体中含有侵染状或硫化物岩性所导致的不同极化程度进行正演模拟,固定时间常数和频率相关系数,并设为较小值,以探究极化率对正演响应的影响,二维AMT正演模拟结果如图14~图15所示。当频率相关系数和时间常数假设也较大时,二维AMT视电阻率及阻抗相位模拟结果如图16所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 砂岩型铀矿地电模型示意

Fig.13 Schematic diagram of geoelectric model in sandstone type uranium deposits

图14

新窗口打开| 下载原图ZIP| 生成PPT

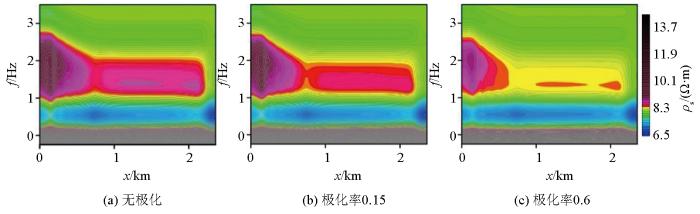
图14 砂岩型铀矿地电模型AMT二维TM模式视电阻率结果

Fig.14 2D TM mode apparent resistivity result map of geoelectric model in sandstone type uranium deposit

图15

新窗口打开| 下载原图ZIP| 生成PPT

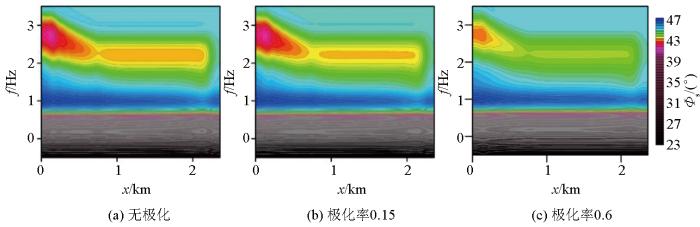
图15 砂岩型铀矿地电模型AMT二维TM模式阻抗相位结果

Fig.15 2D TM mode impedance phase result map of geoelectric model in sandstone type uranium deposit

图16

新窗口打开| 下载原图ZIP| 生成PPT

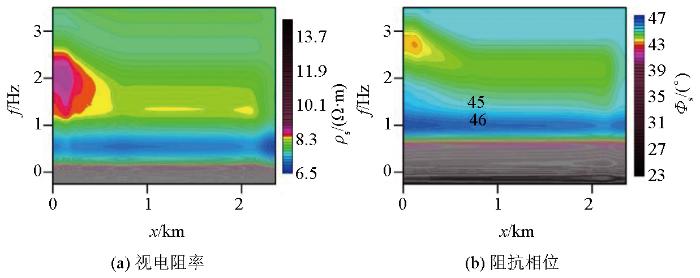
图16 高时间常数和高频率相关系数下AMT二维TM模式正演响应结果

Fig.16 Forward response results of AMT 2D TM mode in high time constant and high frequency correlation coefficient

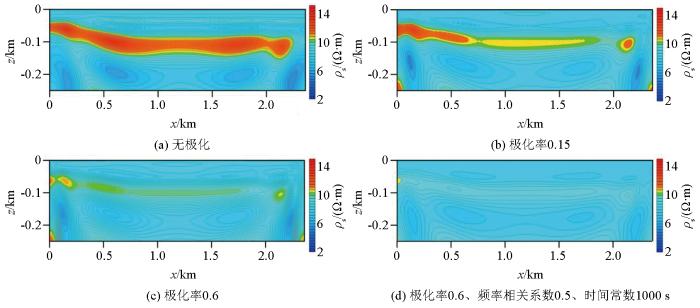
由于砂岩型铀矿的地电模型近似一维模型,这里只以TM模式为例进行对比说明。图14和图15为砂岩型铀矿地电模型AMT二维TM模式视电阻率及阻抗相位结果,通过对比可以看出,当无极化时,砂体在正演拟断面中呈现较明显的高阻特征和低相位特征,当存在侵染状岩性时,其极化率可增大到0.15,其对应的视电阻率异常特征逐渐降低,阻抗相位特征逐渐增大,砂体所引起的正演异常响应特征越不明显,特别是埋藏较深的砂体部分。当极化率较高时(极化率为0.6),其产生的异常特征与围岩已相差较小(图14c和图15c)。

当砂岩型铀矿中也含有较高的频率相关系数(c=0.5)和时间常数(t=1 000 s)时,二维AMT正演计算结果如图16所示,在极化率较高的情况下,砂体的视电阻率和阻抗相位异常响应特征与围岩产生的正演响应几乎相当,特别是埋藏较深的砂体部分,因此,在砂岩型铀矿中,即当极化率较高时,频率相关系数和时间常数对二维AMT正演响应同样产生一定的影响。

将砂岩型铀矿地电模型的正演结果采用商业软件MT Pioneer进行反演计算,反演采用相同的参数设置,拟合差小于0.3后迭代终止,结果如图17所示。当无极化效应时(图17a),反演得到的砂体展布特征与原模型基本相同,当极化率为0.15时(图17b),反演得到的砂体较薄,反演的砂体电阻率较小。当极化较大时(图17c),反演得到的砂体厚度、电阻率及范围均与原模型差别较大,当频率相关系数和时间常数也比较大时(图17d),反演已无法获得砂体的埋深及分布范围等信息。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 不同激电参数下砂岩型铀矿AMT二维反演结果图

Fig.17 2D inversion results of geoelectric models for sandstone type uranium deposits with different IP parameters

因此对砂岩型铀矿来说,激电效应会对砂体的探测产生一定的影响,特别是当极化率较高时,激电效应各参数均会降低砂体产生的异常响应特征,影响探测目标砂体的空间分布特征,甚至会导致探测目标砂体丢失。

4 结论

在实现带激电效应的二维音频大地电磁正演的基础上,分别模拟了Cole-Cole模型中各激电参数对正演响应的影响,同时对砂岩型铀矿的地电模型进行了带激电效应的模拟研究,获得以下3点结论:

1) 基于Cole-Cole模型实现的带激电效应的音频大地电磁正演,随着激电效应各参数(极化率、频率相关系数和时间常数)的增大,主要降低二维正演视电阻率异常响应值,增大阻抗相位异常响应值。因此,当探测目标体为低阻体时,激电效应的影响相对较小,激电效应的存在会增大低阻异常响应特征,更加有利于探测目标体,当探测目标体为高阻体时,需特别关注激电效应的影响,激电效应的存在会降低探测目标高阻异常响应特征,影响探测效果。

2) 在激电效应各参数中,零频电阻率和极化率参数对二维正演响应的影响相对较大,而频率相关系数和时间常数对二维正演响应的影响,主要依赖极化率值的大小。当极化率较小时,频率相关系数和时间常数无论变化多大,对正演响应的影响均较小;当极化率较大时,二者的变化均对正演响应产生一定影响。

3) 在砂岩型铀矿中开展频域电磁法探测时,若目标砂体中存在浸染状或含硫化物的岩性时,需评价极化率的影响大小,可通过电磁正演进行数值模拟研究,防止探测的目标砂体的丢失。对于较强的激电效应,各参数对正演响应均有影响,则必须带激电效应进行反演计算才能获得较准确的砂泥结构。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

汤井田, 何继善.

可控源音频大地电磁法及其应用[M]. 长沙: 中南大学出版社, 2005.