0 引言
探地雷达(ground penetrating radar,GPR)是中浅层目标体探测的有效方法,具有高速采样、高分辨率、高精度、无损等优点,如今已广泛应用于公路检测、桥梁等的无损检测、地下水污染物探测、地质工程探测和考古探测等。通常探地雷达的探测环境比较复杂,环境电磁波干扰等原因造成探测过程中存在频散、衰减、噪声以及其他各种干扰[1],极大地限制了探地雷达对地下隐藏目标体的探测。对于杂波的抑制一直都是国内外探地雷达研究的重要内容,目前探地雷达的去杂波方法很多,按照处理方式不同主要分为时间维和空间维两种。对时间维进行处理主要有常规滤波、小波滤波[2]、S变换[3]等方法,通过改善每一测点的信号质量从而改善整个雷达剖面,为最终地下情况解读提供依据。这些方法都取得了较好的效果,但存在一定缺陷。以目前应用最广泛的小波变换为例,其虽然具备了多分辨的性质,但是存在预选小波基函数复杂等制约因素,限制了其在探地雷达中的推广和应用。经验模态分解(empirical mode decomposition,EMD) [4]将信号按照一定准则分解成若干固有的、内在的本征模态函数(intrinsic mode function,IMF),其根据信号自身特点进行的分解,具有小波变换的多分辨性质,又不需要考虑小波基的选取问题。EMD分解在探地雷达领域已经得到一定的应用。Flandrin等[5]通过对高斯白噪声的分析,发现EMD方法表现为时域的二进制滤波;易洪春等[6]研究EMD去噪方法,将其用于在高压线网下瞬变电磁数据以及探地雷达的回波数据去噪取得了一定效果;冯德山等[7]研究了EMD分解在低信噪比探地雷达数据处理中的应用,表明EMD分解能改进探地雷达的回波剖面。上述研究均是利用了EMD分解的滤波能力,将信号分解到不同IMF上进行观察,并未精确还原信号。空间方面的杂波抑制最简单,常用的是减平均法去杂波[8],它可以去除探地雷达数据中的不变成分,例如地表直达波及其他分层界面回波、天线耦合杂波等,但对于具有起伏特征的界面、非目标体的回波、移动过程中相干干扰杂波等成分无效。另一种常用的去杂波方法是子空间投影法[9-10],将回波数据矩阵进行奇异值分解,收集到的数据映射在由奇异向量组成的子空间上重构信号,该方法能有效去除直达波和部分弱干扰,但对强噪声压制效果不理想。文献[11]提出了一种基于信息熵的杂波去除新方法,通过信息熵对目标区域的信号进行精确地加窗提取,性能优越但对地下多目标情况不适用。KL变换[12⇓-14]具有去相关性的优点,并且是均方误差意义下的最佳变换,能从雷达回波信号中有效去除非相关性杂波,在探地雷达杂波抑制中取得了较好的应用效果。但KL变换在强噪声条件下,去杂波效果不理想并有可能造成目标信号畸变。由于探地雷达杂波强度大,产生原因多样,单一的处理方法很难将其彻底去除,通过分析杂波主要组成及特点,提出从时间、空间两方面对其进行压制,时间维采用EMD阈值处理,空间维采用KL变换。时间维的处理能有效压制强噪声,克服KL变换的缺点,空间维处理能进一步去除时间维残留的噪声,二者优势互补,能呈现清晰的雷达剖面为后续的解释奠定良好的基础。
1 探地雷达杂波的时空抑制方法
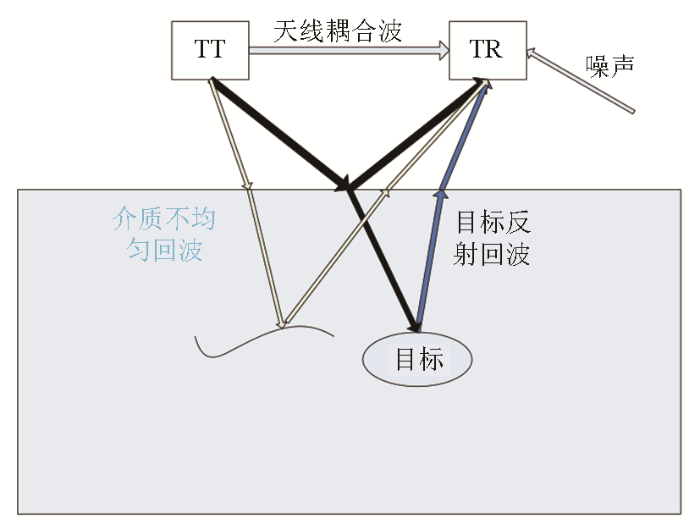
探地雷达接收信号的一般模型如图1所示,发送天线发射电磁波,一部分电磁波经过空气层直接被接收天线接收,形成天线耦合波;一部分回波向下传播,遇到地面后发生反射和透射,反射回波被接收形成地表直达波,透射波继续在地下传播,当遇到地下介质非均匀变化、目标物体、地下其他的埋藏物时产生相应的回波;环境中的电磁波干扰等会以噪声的形式被接收天线接收。对于除目标体外其余的回波统称杂波,天线耦合波和地表直达波回波幅度大,对浅层目标体识别影响较大,但由于其产生机理简单,比较易于去除;地下其他埋藏物产生的回波由于与目标特性相似,需要模式识别的方法进行去除。笔者研究重点是对噪声以及介质非均匀产生的干扰进行抑制。
图1
1.1 时间维处理
探地雷达杂波中对观测影响最大的是噪声,噪声强度过大不仅掩盖隐藏目标体,而且也会降低后续成像的质量。EMD分解具有快速自适应的优点,已经在探地雷达中取得了一定的应用,但由于噪声强度的差异,单纯的EMD分解很难达到理想去噪效果。EMD分解的IMF分量阶数越高,噪声强度越弱,噪声主导的IMF分量并非完全是噪声,可能包含有微弱的有用信号。噪声强度越强,噪声IMF分量越多,则包含的有用信号越多,如果直接去除噪声IMF分量,必定会造成有用信号丢失,如果去除不足,达不到很好的去噪效果。时间维的处理主要针对强随机噪声,利用EMD方法分离探地雷达每道A-scan回波信号中的高频噪声成分,通过能量的方法区分含噪分量和信号分量,对含噪分量引入阈值处理方法克服直接去除的缺点,达到抑制噪声同时保留有用信号细节的目的,最大限度保留信号中的有用成分。
1.1.1 经验模态分解
经验模态分解是Hilbert-Huang变换的重要组成部分,其关键问题是如何把一个非线性非平稳序列分解为有限的IMF分量和一个趋势项。原始信号x(t)经过EMD分解[4]表示为:
式中:ci(t)为n个IMF分量,rn
1.1.2 噪声与信号分界处选择
当阶数i=k能量达到最低点时,即认为此处IMF分量为噪声成分占主导模态与有用信号占主导模态的分界点,从第i=k+1阶IMF分量开始均为有用信号占主导模态部分。
1.1.3 阈值函数确定
对含噪的前K阶IMF分量采用下列软阈值函数进行处理:
根据Donoho[13]提出的噪声阈值选取方法,相应的阈值采用:
式中:N为各IMF分量的长度,σi为IMF分量中所含噪声分量的方差,基于文献[13]的思想,定义σi为
式中:MADi代表第i阶IMF分量的绝对中值偏差,定义为:
Median 。
阈值的选取是去噪效果的关键,对处理效果起决定作用的主要是噪声分量的方差σi。考虑到EMD分解后各个IMF分量的含噪是越来越小的,若对各个IMF分量采用固定的阈值会造成过处理的发生,导致有用信号的丢失。所以将选取阈值的大小与EMD分解的阶数进行关联,由于阶数越大噪声越弱即二者成反比,所以采用新的阈值公式:
新的公式中,对于越高阶的IMF分量,相应的阈值越小,与阶数越高噪声越小的特点相吻合,在保证噪声去除的同时更好地实现了有用信号的保留。将噪声主导前k阶IMF通过阈值去噪后得到的结果与有用信号占主导模态的IMF分量及残余分量进行叠加,去噪后的重构信号为:
1.2 空间维处理
探地雷达数据采集一般采用剖面法,发射天线和接收天线以固定间距沿着侧线同步移动,可以认为相邻的测点间的目标回波信号具有较强的相关性;随机干扰是由各种不可知因素产生的,没有统一的规律,在整个记录上随机出现,因此认为随机干扰之间不具有相关性。空间维处理采用KL变换从数据中提取相关信号,消除时间维处理残留的随机噪声和干扰。探地雷达回波数据的相关性由KL变换后的协方差矩阵的特征值来度量,选取特征值大的成分重建的信号相关性强,选取特征值小的成分重建的信号相关性弱。在噪声强度较大的情况下,KL变换难以取得较好的压制杂波效果,但经过时间轴降噪处理后的残留噪声干扰强度较弱,满足KL变换的条件,选取大的特征值成分重建信号,去除随机的杂波干扰。KL变换原理文献[14]中有详细描述,这里不再赘述。
2 实验与结果
2.1 仿真验证
图2
图2
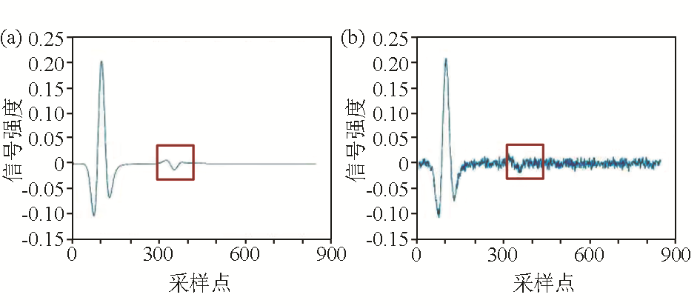
原始探地雷达信号(a)及加噪处理后信号(b)
Fig.2
Original ground penetrating radar signal(a) and signal after noise processing(b)
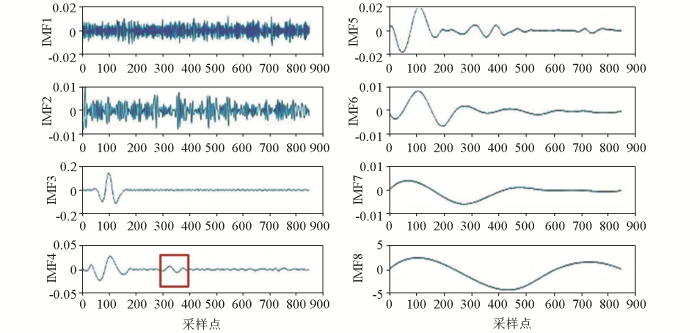
对加噪后的信号进行EMD分解,产生10个IMF分量,残余的2个分量省略如图3。根据图中各个本征模态函数的曲线可以看出:从IMF1到IMF8,噪声强度是依次降低的,其中IMF1和IMF2基本为加入的白噪声,说明EMD分解具有分离高频噪声的功能,去除掉IMF1和IMF2就可达到一定的去噪目的。IMF3主要为直达波分量。由IMF4可见,在350采样点目标体回波处波形明显,说明EMD分解特定的IMF分量具有突出异常信号的能力。由仿真可见EMD非常适合探地雷达数据处理,可以在不同分量上对信号进行解释。
图3
图4
图4
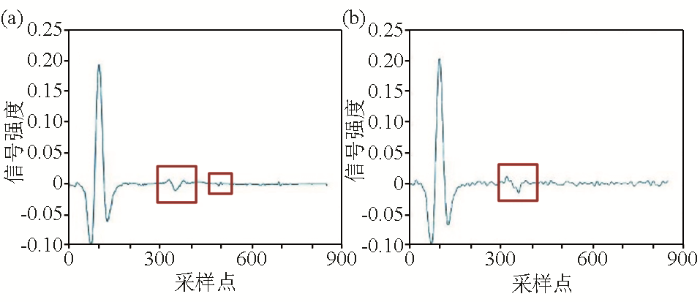
EMD改进阈值去噪(a)与小波去噪(b)对比
Fig.4
Comparison between EMD improved threshold denoising(a) and wavelet denoising(b)
信噪比和均方误差通常是衡量去噪效果的定性指标,其公式如下:
式中:x
表1 信噪比与均方根误差对比
Table 1
| SNR | RMSE | |
|---|---|---|
| 加噪信号 | 10.058 | 0.0099 |
| 小波阈值去噪 | 18.9591 | 0.0036 |
| EMD阈值去噪 | 20.1949 | 0.0031 |
2.2 实测数据验证
对于实际搭建的探地雷达系统采集的数据进行去噪处理。实验主要有2个,实验一选取单道时间轴数据,数据噪声强烈,主要为了验证EMD阈值去噪的效果;实验二选取多道数据,数据时间维噪声相对较弱但空间维杂波干扰较强烈,主要为了验证时空联合杂波抑制效果。
2.2.1 实验一
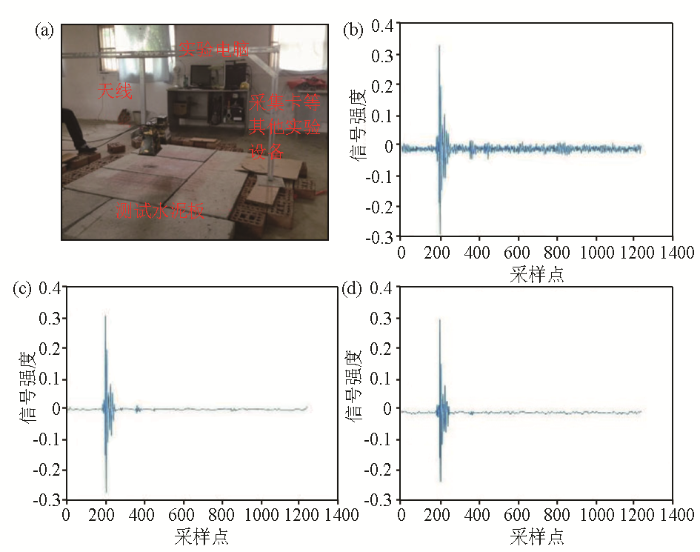
图5
图5
实测场景及数据处理
a—实测场景;b—实测采集回波数据;c—EMD改进阈值去噪;d—小波去噪
Fig.5
Actual measurement scenario and data processing
a—actual measurement scenario;b—measured echo data;c—EMD improved threshold denoising;d—wavelet denoising
2.2.2 实验二
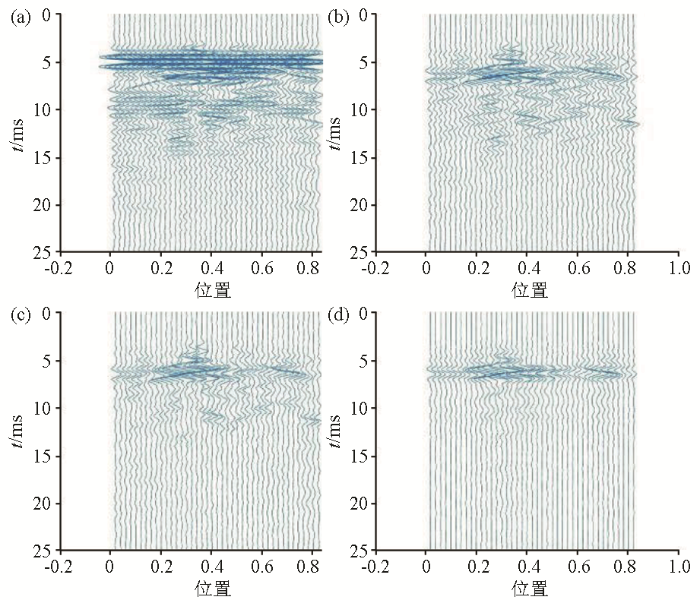
主要实验仪器:脉冲源,低噪放,安捷伦示波器,喇叭天线,数据经过安捷伦示波器进行显示并采集保存。示波器型号ium 80000,采样频率40 GHz,其他设备与试验一相同。实验场景:沙坑中埋有一个拱形的铁片,埋深5 cm,铁片圆面的半径26.5 cm,弦长40 cm,收发分置天线间距35.5 cm,离地10 cm。实验中天线每次移动2 cm,总计采集41次,每一次采集多个周期取平均减少随机误差影响。采集的原始数据组成B-scan如图6a。原始信号随机噪声较弱但干扰厉害,直达波、杂波突出,导致铁皮的回波信号不明显,基本无法识别。使用减平均法去除直达波,结果如图6b。去除直达波后,一部分水平杂波被去除,主要为地表直达波和周围墙体可能产生的水平杂波干扰,圆形铁皮的形状已经基本能分辨出来,铁皮回波主要集中在5~9 ns之间,但是剩余干扰和噪声依旧很强。对每道信号进行EMD阈值去噪重组,结果如图6c,整个剖面部分噪声被去除,剩余的杂波干扰也得到了很大的抑制,例如水平位置0.2~0.4处抑制非常明显,对目标铁皮回波信号基本没有损伤,目标更加突出。对于处理后还存在的干扰主要原因可能是沙坑没有仔细抹平,一些地方突出比较明显,这些干扰不满足噪声去除条件,但是其具有非相关性,在整个雷达剖面中不是连续出现。经过降噪处理后的信号最后进行KL变换处理,选取前2个大的特征值重建信号去除残余的干扰,结果如图6d。由图可见,剩余的杂波干扰基本被压制,整个B-scan剖面中目标体的回波清晰。
图6
图6
原始数据及数据处理结果
a—原始数据;b—去除直达波数据;c—EMD改进阈值去噪;d—时空二维杂波压制
Fig.6
Raw data and data processing results
a—original data;b—remove direct wave data;c—EMD improved threshold denoising;d—time-space two-dimensional clutter suppression
根据文献[1]图像熵标准衡量杂波抑制效果,熵越小,图像越清晰,表示含目标可能性越大。图像熵公式如式(11),m为测点数,n为时间采样点数。
计算去直达波后的回波、EMD阈值处理、KL变换处理后的Q值如表2所示,说明了时间轴和空间轴对杂波的压制都取得了作用,经过时空二维处理后的图像熵值只有原始的一半,说明了时空处理方法的有效性。
3 结论
随着探地雷达应用环境越来越复杂,单一杂波抑制方式难以满足地下解释和后续处理要求。本文提出的时空二维联合去杂波方法互为补充,EMD阈值处理能有效去除强噪声,克服KL变换的缺点;KL变换能够进一步去除EMD阈值处理残余的非相关干扰,获得清晰的回波数据。EMD阈值去噪克服了EMD去噪对强噪声不理想的特点,根据IMF含噪特点引入随阶数变化的阈值函数,其具有自适应特点,不需要像小波变换那样根据情况选择小波基。两组实测实验采集场景和方式不同,得到的数据随机噪声强度和杂波类型不同,验证了EMD阈值去噪以及时空二维联合去杂波是有效的。通过杂波压制,雷达剖面更加清晰,有利于进一步的成像识别等处理。
参考文献
基于图像熵的探地雷达杂波抑制效果评价
[J].
Evaluation method based on image entropy for clutter suppression effect of ground-penetrating radar
[J].
二维物理小波标架去除探地雷达信号随机噪声
[J].
Eliminating random noise interference of ground penetrating radar signal by resorting to 2-D physical wavelet fame
[J].
探地雷达数据的S变换时频分析
[J].
S transform time-frequency analysis of GPR data
[J].
A confidence limit for the empirical mode decomposition and Hilbert spectral analysis
[J].
Empirical mode decomposition as a filter bank
[J].DOI:10.1109/LSP.2003.821662 URL [本文引用: 1]
基于 EMD 去噪方法研究及其在地质勘探中的应用
[J].
Data denoising based on EMD and its ap-plication to geological exploration
[J].
基于经验模态分解的低信噪比探地雷达数据处理
[J].
GPR signal processing under low SNR based on empirical mode decomposition
[J].
Clutter reduction techniques for GPR based buried landmine detection
[C]//
Background removal from GPR data using Eigenvalues
[C]//
基于主成分自动选择准则的探地雷达杂波抑制
[J].
Auto-selected rule on principal component analysis in ground penetrating radar signal denoising
[J].
Ground clutter removal in GPR surveys
[J].DOI:10.1109/JSTARS.4609443 URL [本文引用: 1]
A study of the characteristics of white noise using the empirical mode decomposition method
[J].
De-noising by soft-thresholding
[J].DOI:10.1109/18.382009 URL [本文引用: 3]