0 引言
油气地震勘探的目的是探明地下介质的几何形态、岩性和物性甚至流体分布,进而为钻井井位部署提供依据。目前,石油工业界广泛采用叠前AVO反演获得油气储层弹性参数,在岩石物理分析的基础上,对油气储层进行定量刻画。叠前AVO反演的理论基础是描述平面波在地下介质分界面处发生反射和透射的Zoeppritz方程[1]。20世纪,许多学者提出了大量的AVO线性近似公式[2⇓⇓⇓⇓⇓-8],以此来解决Zoeppritz方程求解的非线性问题,并提高反演的计算效率。然而,这些线性AVO近似基于弱反差介质与小入射角的假设,在强反差介质及大角度入射情形下会产生较大的计算误差[9⇓-11]。随着油气勘探的深入,勘探目标转向非均质性强的复杂油气藏,而长排列地震采集以及角度域成像技术的应用也使得有效地震数据的入射角越来越大,因此迫切需要发展适应强反差介质以及大入射角情形下的AVO反演技术。
近些年,很多学者开始研究基于精确Zoeppritz方程的拟线性及非线性反演方法。刘福平等[12]首次给出了纵波反射系数对纵横波速度一阶偏导数的精确表达式;Zhi等[13]利用精确Zoeppritz方程和PP-PS联合反演得到了界面两侧的密度比和3个速度比;Zong等[14]推导了Zoeppritz方程所描述的纵波反射系数的精确表达式,并结合非线性反演方法估计出了反射界面上下层介质的6个弹性参数;Zhi等[15]提出了基于Zoeppritz方程的迭代正则化Levenberg-Marquardt反演方法;Yin等[16]利用纵波速度反射率、横波速度反射率和密度反射率重新表示Zoeppritz方程,然后基于逆算子估计实现三参数的非线性反演;张凌远等[17]利用快速模拟退火算法实现了基于Zoeppritz方程的横波速度、纵横波速度比反演。尽管基于精确Zoeppritz方程的叠前反演方法获得了较大的发展,但是这类反演方法的计算复杂度高,在实际应用中,特别是针对低信噪比数据,反演结果的准确性以及稳定性等依然存在较大挑战[18⇓-20]。
尽管MCMC算法具有诸多优点,但是在将其应用于叠前弹性参数反演时仍然存在以下两方面的问题:①对于实际复杂地下介质,弹性参数的真实概率分布往往十分复杂,很难寻找一个合适的概率密度函数来描述,常规利用高斯分布刻画弹性参数的统计特征存在较大的局限性;②由于地下模型参数空间巨大以及地震数据中噪声等因素的影响,MCMC对弹性参数后验概率分布的搜索过程极易受到局部极值的影响,这使得MCMC采样过程难以稳定收敛,并且增加了反演结果的不确定性,特别是在低信噪比资料情况下,这种问题更加明显。为了避免这些问题,大多数学者利用Zoeppritz方程的线性近似公式来描述地震正演过程[23⇓⇓⇓-27],并未将MCMC算法应用于求解基于精确Zoeppritz方程的叠前地震反演问题。Pan 等[28]提出了基于精确Zoeppritz方程和MCMC-DRAM(delayed rejection adaptive Metropolis)算法的叠前反演方法,但是DRAM算法无法有效地遍历具有很多局部极值的复杂高维参数空间,而且也难以判断马尔科夫链何时达到收敛[29]。为了降低后验概率分布的复杂度以提高MCMC采样的稳定性与收敛性,Pan等假设弹性参数相互独立且服从高斯分布,然而,该假设条件在实际复杂地下储层中是难以满足的。
本文针对实际复杂储层及低信噪比资料条件下基于精确Zoeppritz方程的叠前地震反演问题,从以下3个方面来提高MCMC叠前AVO反演的稳定性与收敛性:①利用低频模型约束,将待反演参数转换为模型参数的扰动量,从而使得先验概率分布由实际复杂概率分布转换为高斯分布,以降低后验概率分布的复杂度;②通过对似然函数取对数,并利用低频模型来约束地震正演过程;③利用基于随机子空间采样的多链模拟算法对叠前非线性反演问题进行全局寻优,以避免采样过程过早地收敛到局部极值。低信噪比的模拟数据和实际数据测试表明,本文所提方法能够有效提高反演结果的准确性以及稳定性。
1 方法原理
1.1 基于精确Zoeppritz方程的贝叶斯叠前地震反演
贝叶斯理论通过将模型参数视为随机变量,把模型参数的先验分布与似然函数结合起来,从而获得同时反映模型合理性与数据拟合程度的后验概率分布。当给定地震观测数据d时,模型参数x的后验概率分布可以写为[30]:
式中:先验分布P(x)表示独立于实际地震观测数据d的模型参数的已知信息;似然函数P(d|x)描述了实际地震观测数据与由模型参数正演所得模拟地震数据之间的拟合程度。
对于实际地下介质而言,弹性参数的先验概率分布形式通常十分复杂,特别是对于复杂岩性储层[31]。为了充分发挥先验低频模型在叠前随机反演过程中的约束作用,我们将待反演参数由弹性参数本身转换为弹性参数的扰动量。由于弹性参数的扰动量围绕弹性参数的低频趋势m0而变化,因此,不管真实的弹性参数m服从简单单峰分布还是复杂多峰分布,弹性参数扰动量Δm一般表现为单峰分布,其先验概率分布可以用高斯分布来表示:
式中:μΔm和ΣΔm分别为扰动量的先验期望和先验协方差。根据贝叶斯理论,弹性参数扰动量的后验概率分布可以表示为:
假设地震数据中的噪声服从高斯分布,同时考虑到数值计算的稳定性,我们采用对数似然函数:
式中:n为地震数据的样点数;
式中:S为地震子波矩阵;e为服从零均值高斯分布的噪声;c(m)为利用精确Zoeppritz方程(见附录A)计算得到的纵波反射系数,且m=m0+Δm。
1.2 基于随机子空间采样的多链模拟
假设待反演地震道的时间采样点数为T,则待反演的弹性参数扰动量个数d=3×T,d即为模型参数空间的维数。为了避免采样过程过早地收敛到局部极值,本文通过同时运行多条初始状态不同的马尔科夫链来搜索模型空间。此外,在对高维模型参数空间的随机搜索过程中,如果对所有模型参数同时进行更新,通常情况下生成的大量候选点会被拒绝,导致马尔科夫链收敛非常缓慢。为了提高候选点的接受率以加速马尔科夫链的收敛过程,在每次迭代时,随机选择某些模型参数组成子空间,只对子空间内的模型参数进行更新,而对子空间之外的模型参数保留原采样点。
假设用N条马尔科夫链对模型参数空间进行搜索,用xi(i=1,…,N)表示第i条马尔科夫链的取值状态,
1)随机生成弹性参数扰动量的初始样本xi,结合该道的低频模型得到相应的3个弹性参数(纵波速度、横波速度和密度),然后基于精确Zoeppritz方程和褶积模型正演得到该道的模拟地震记录,根据式4计算该样本所对应的似然函数,并将其与弹性参数扰动量的先验分布(式2)相结合得到该样本xi所对应的后验概率密度p(xi);
2)根据原采样点xi计算第i条链的候选点zi:
式中,dxi为模型参数的更新量,可以表示为:
式中:B为由随机选择的d'个模型参数组成的子空间;δ为马尔科夫链的组数;μ和ν均为从{1,…,i-1,i+1,…,N}中随机取出δ个整数所组成的向量,且数值无重复;C为尺度因子;ε为从高斯分布
3)计算候选点所对应的后验概率密度p(zi),然后根据Metropolis准则计算接受概率α(xi,zi)[32]:
4)判断是否接受转移。如果候选点被接受,则xi=zi;否则,xi=xi;
5)对每一个时刻k重复执行步骤2)~4)直至完成N条马尔科夫链的采样,然后进入时刻k+1进行采样直至达到最大迭代次数K。
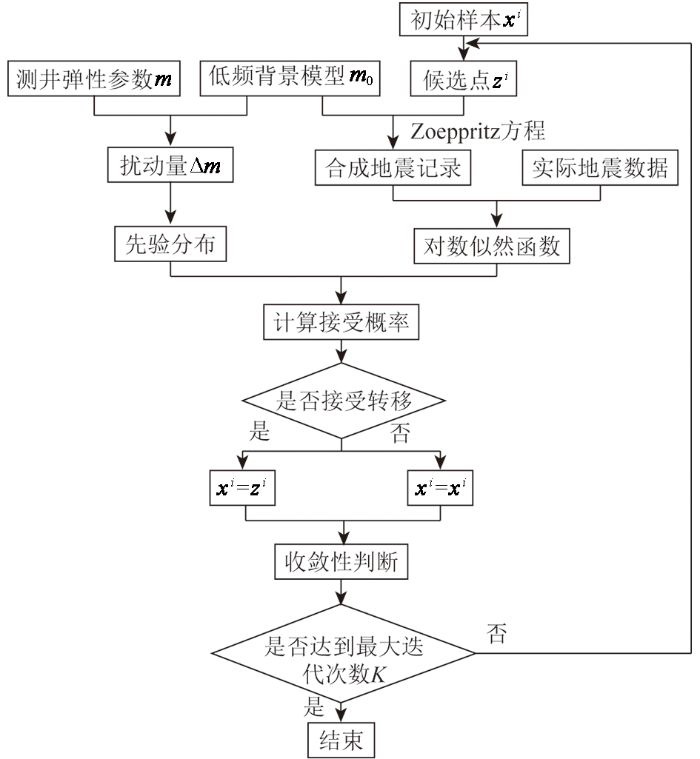
利用多链模拟算法对弹性参数扰动量的随机采样过程如图1所示。Gelman和Rubin[33]指出当马尔科夫链达到收敛后,从不同初始状态出发进行采样的马尔科夫链的统计特征应该是一致的,从而提出了一种非常有效的基于多链方差统计(multi-chain
图1
图1
对弹性参数扰动量的随机采样流程
Fig.1
Flow chart of stochastic sampling for the elastic parameter perturbations
2 模拟数据测试
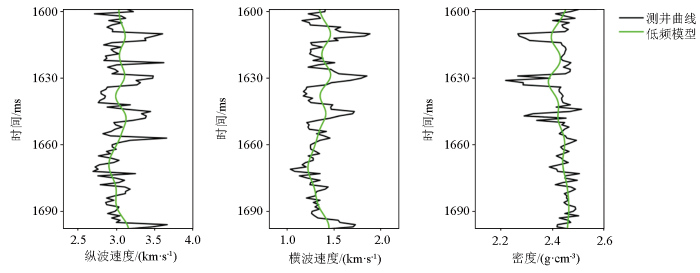
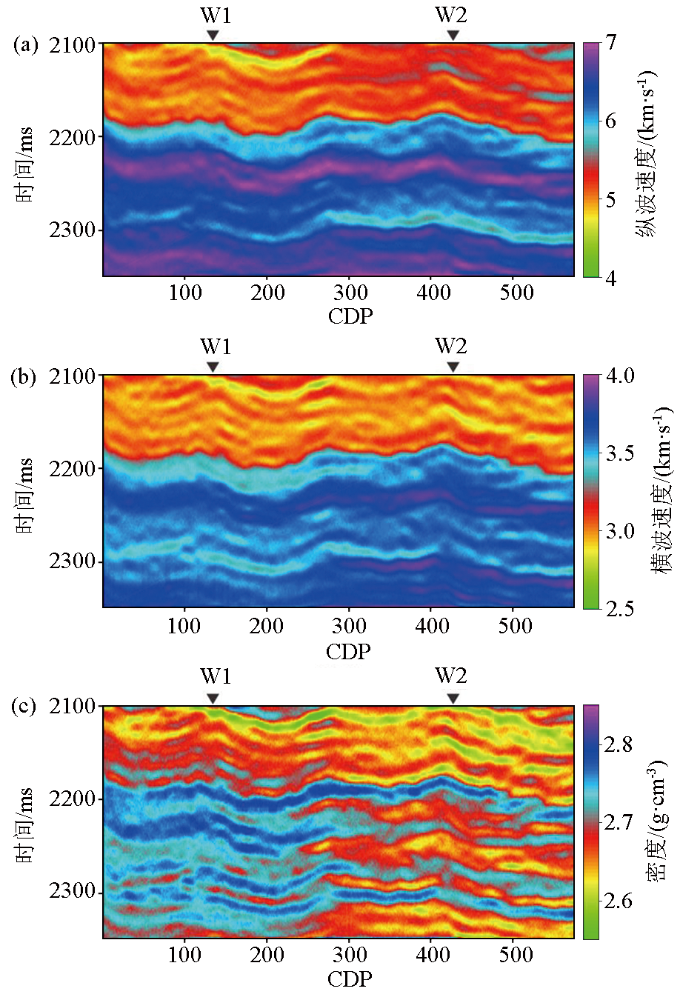
图2
图2
弹性参数的测井曲线及其低频模型
Fig.2
Real well logs of elastic parameters and the corresponding LFMs
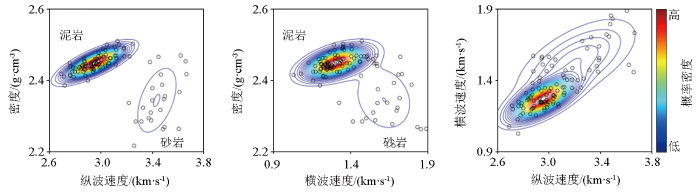
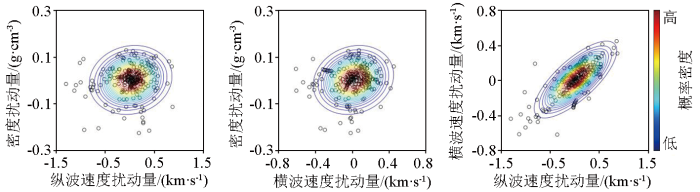
图3
图3
弹性参数的交会及利用高斯混合分布拟合得到的概率密度等值线
Fig.3
Crossplots of the elastic parameters and the corresponding probability density contours obtained by fitting with Gaussian mixture distributions
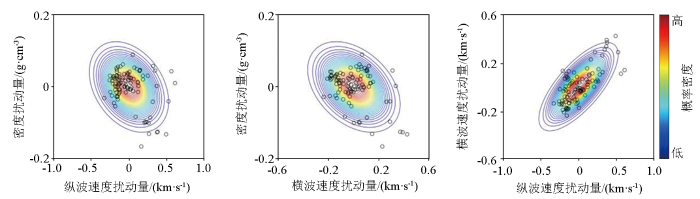
图4
图4
弹性参数扰动量的交会及利用高斯分布拟合得到的概率密度等值线
Fig.4
Crossplots of elastic parameter perturbations and the corresponding probability density contours obtained by fitting with Gaussian distributions
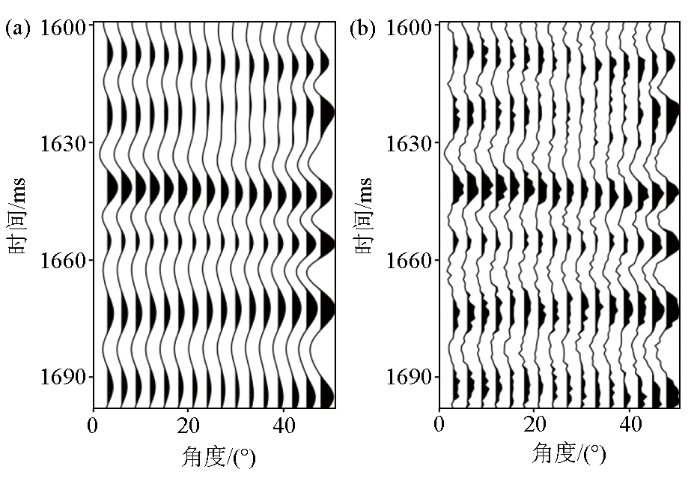
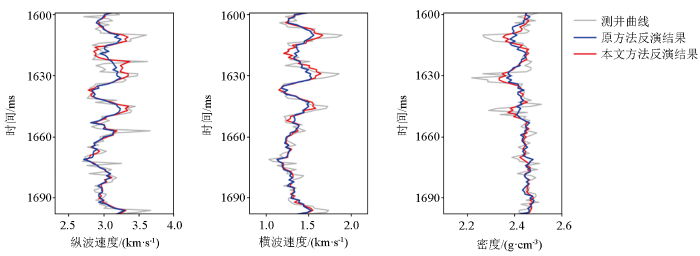
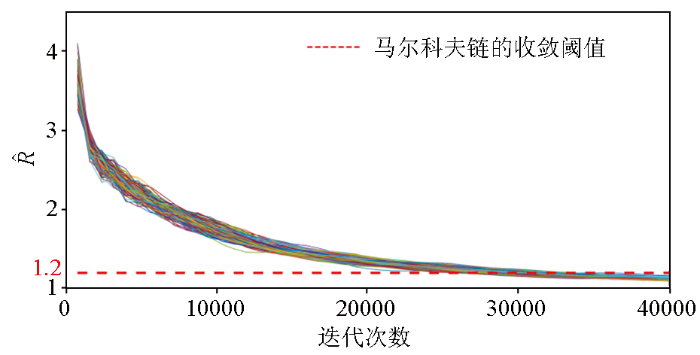
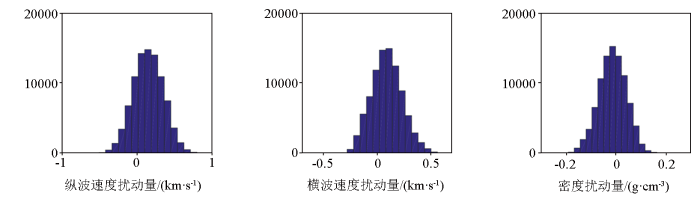
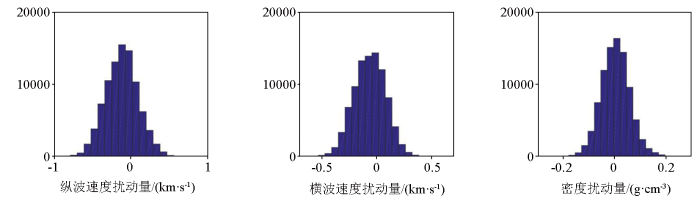
利用精确Zoeppritz方程计算该测井数据的纵波反射系数,并将其与主频为45 Hz的Ricker子波相褶积得到无噪声的地震角道集(图5a),然后加入高斯随机噪声得到最终的模拟地震角道集(图5b),模拟地震数据的信噪比为3,入射角范围为3°~48°,角度采样间隔为3°。图6对比了本文所提改进后的反演方法与改进前的基于Zoeppritz方程反演的效果,可以看出,本文所提方法反演得到的弹性参数与实际测井曲线的拟合度更好。图7为马尔科夫链的收敛性指标随迭代次数的变化,在迭代约32 000次后,马尔科夫链已经达到收敛。图8和图9分别为1 630 ms和1 672 ms处3个弹性参数扰动量的后验统计直方图,不同位置处3个弹性参数扰动量均稳定收敛到后验高斯分布。
图5
图5
模拟地震角道集
a—无噪声;b—信噪比为3
Fig.5
The synthetic seismic angle gathers
a—no noise;b—S/N is 3
图6
图6
含噪声地震数据的弹性参数反演结果
Fig.6
The inversion results of the elastic parameters with noisy seismic data
图7
图7
收敛性指标
Fig.7
The variation of convergence diagnostic
图8
图8
时间为1 630 ms处弹性参数扰动量的后验统计直方图
Fig.8
Statistical histogram of the sampling results for the elastic parameter perturbations at time 1630 ms
图9
图9
时间为1 672 ms处弹性参数扰动量的后验统计直方图
Fig.9
Statistical histogram of the sampling results for the elastic parameter perturbations at time 1672 ms
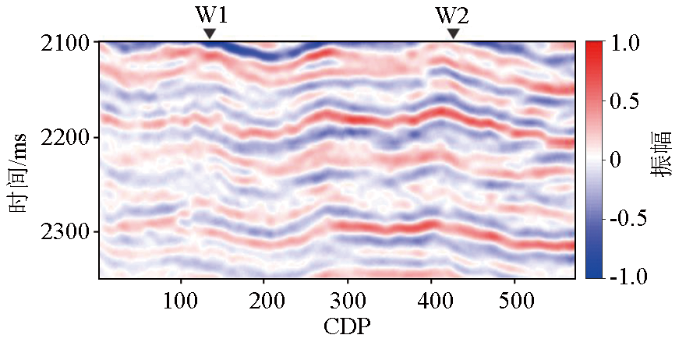
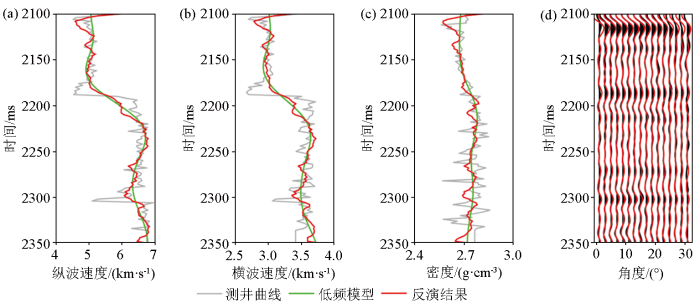
3 实际数据应用
图10
图11
图12
图12
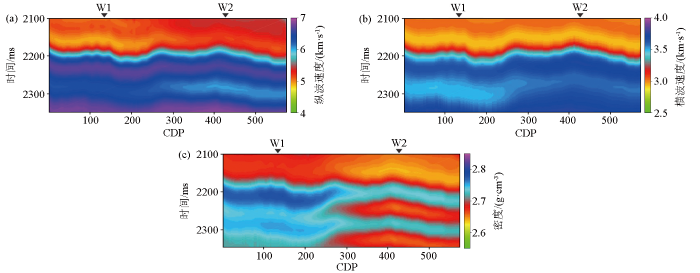
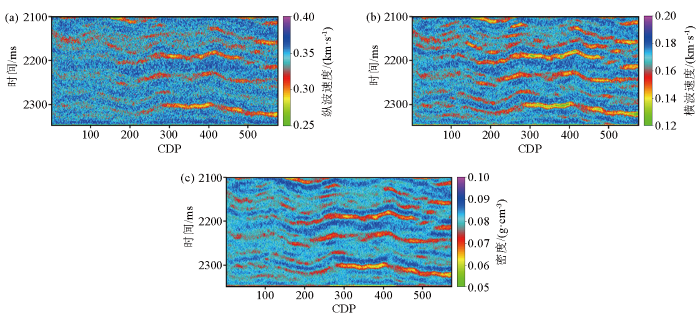
低频模型
a—纵波速度;b—横波速度;c—密度
Fig.12
Low-frequency model
a—P-velocity;b—S-velocity;c—density
图13
图13
测井位置处弹性参数扰动量的交会及其高斯分布拟合结果
Fig.13
Crossplots of elastic parameter perturbations at well locations and the corresponding probability density contours obtained by fitting with Gaussian distributions
图14
图14
弹性参数的反演剖面
a—纵波速度;b—横波速度;c—密度
Fig.14
Inverted results of elastic parameters
a—P-velocity;b—S-velocity;c—density
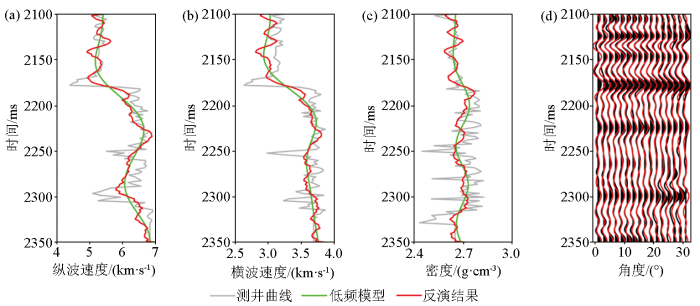
图15
图15
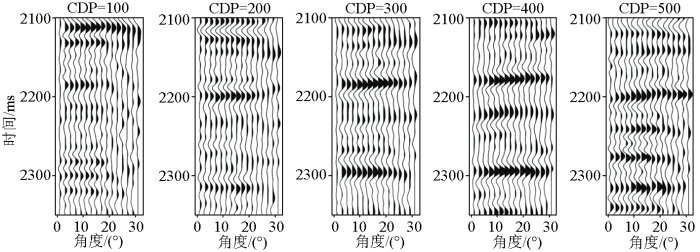
W1井的反演结果
a—纵波速度;b—横波速度;c—密度;d—井旁地震角道集
Fig.15
Inverted results at well W1
a—P-velocity;b—S-velocity;c—density;d—the seismic angle gather at well
图16
图16
W2井的反演结果
a—纵波速度;b—横波速度;c—密度;d—井旁地震角道集
Fig.16
Inverted results at well W2
a—P-velocity;b—S-velocity;c—density;d—the seismic angle gather at well
图17
图17
弹性参数的后验标准差
a—纵波速度; b—横波速度; c—密度
Fig.17
Post standard deviation of elastic parameters
a—P-velocity;b—S-velocity and;c—density
图18
图18
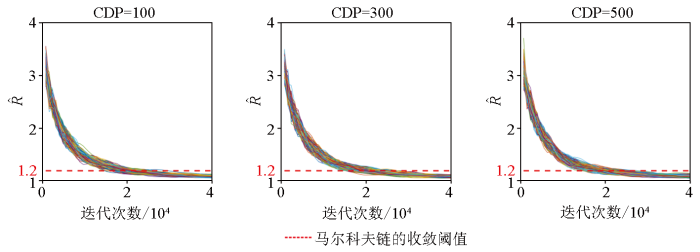
不同CDP位置处收敛性指标
Fig.18
The variation of convergence diagnostic
4 结论
本文针对实际复杂储层及低信噪比资料条件下基于精确Zoeppritz方程的叠前地震反演问题,通过低频模型约束先验概率分布以及地震正演模拟过程,并结合对数似然函数和基于随机子空间采样的多链模拟算法,提出了一种改进的MCMC叠前地震反演方法。低信噪比的模拟数据测试表明,相较于改进前的反演方法,本文所提方法能够获得更加符合实际测井曲线的弹性参数反演结果。二维实际资料的应用效果表明,尽管本文所提方法为逐道反演,但是剖面上相邻两道的反演结果之间具有良好的一致性,这很好地说明了本方法的稳定性;此外,当地震资料的信噪比越低时,弹性参数反演结果的不确定性越大,本文所提方法能够给出可信的、定量的不确定性估计。
附录A Zoeppritz方程
在各向同性的弹性介质中,当平面纵波入射到两层半无限介质的分界面处时,反射系数、透射系数与介质弹性参数和入射角之间的关系可以表示为[1]:
式中:VP,VS和ρ分别表示纵波速度、横波速度和密度,其下标1和2分别表示上层和下层介质;θ1和φ1分别为P波和SV波的反射角;θ2和φ2分别为P波和SV波的透射角;RPP和RPS分别为P波和SV波的反射系数;TPP和TPS分别为P波和SV波的透射系数。
附录B 收敛性检验
对于N条采样长度为T的马尔科夫链,每条链内的方差可以表示为:
Wj=
其中,⌊·」表示取整运算;而所有链之间的方差可以表示为:
Bj/T=
那么,马尔科夫链的收敛性检验指标可以表示为:
其中,
参考文献
On the reflection and propagation of seismic waves
[J].
A simplification of the Zoeppritz equations
[J].
DOI:10.1190/1.1441936
URL
[本文引用: 1]

The compressional wave reflection coefficient R(θ) given by the Zoeppritz equations is simplified to the following: [Formula: see text] The first term gives the amplitude at normal incidence (θ = 0), the second term characterizes R(θ) at intermediate angles, and the third term describes the approach to critical angle. The coefficient of the second term is that combination of elastic properties which can be determined by analyzing the offset dependence of event amplitude in conventional multichannel reflection data. If the event amplitude is normalized to its value for normal incidence, then the quantity determined is [Formula: see text] [Formula: see text] specifies the normal, gradual decrease of amplitude with offset; its value is constrained well enough that the main information conveyed is [Formula: see text] where [Formula: see text] is the contrast in Poisson’s ratio at the reflecting interface and [Formula: see text] is the amplitude at normal incidence. This simplified formula for R(θ) accounts for all of the relations between R(θ) and elastic properties first described by Koefoed in 1955.
Common-depth method for determining and displaying the shear-velocity reflectivities of a geologic formation
[J].
A simple approximation to the P-wave reflection coefficient and its implication in the inversion of amplitude variation with offset data
[J].
DOI:10.1190/1.1443437
URL
[本文引用: 1]

I derive an approximate formula for the plane P‐wave reflection coefficient as a function of ray‐parameter. The approximation shows that the behavior of the P‐wave reflection coefficient at nonnormal angles of incidence is mainly controlled by two parameters: (1) [Formula: see text], the fluid‐fluid reflection coefficient (i.e., the reflection coefficient when the S‐wave velocities in both media are set to zero) and (2) Δμ/ρ, the ratio of the contrast in shear moduli to the average bulk density. I also show that the other formulas for the P‐wave reflection coefficient given by R. Bortfeld and R. Shuey can be approximately derived from my formula. I give numerical examples to demonstrate the accuracy of the formula. Using a least‐squares inversion of theoretical values for the reflection coefficients, I demonstrate that, in a linear inversion of amplitude versus offset data, Δμ/ρ is better estimated than the contrast in Poisson’s ratio, Δσ. Finally, comparing the exact reflection coefficient with Shuey’s approximation for typical shale and Class 1 gas‐sand models, I show that Shuey’s approximation under‐estimates the value of |Δσ| for such reflections.
Detection of gas in sandstone reservoirs using AVO analysis:A 3-D seismic case history using the Geostack technique
[J].
DOI:10.1190/1.1443695
URL
[本文引用: 1]

The Geostack technique is a method of analyzing seismic amplitude variation with offset (AVO) information. One of the outputs of the analysis is a set of direct hydrocarbon indicator traces called “fluid factor” traces. The fluid factor trace is designed to be low amplitude for all reflectors in a clastic sedimentary sequence except for rocks that lie off the (mudrock line.) The mudrock line is the line on a crossplot of P‐wave velocity against S‐wave velocity on which water‐saturated sandstones, shales, and siltstones lie. Some of the rock types that lie off the mudrock line are gas‐saturated sandstones, carbonates, and igneous rocks. In the absence of carbonates and igneous rocks, high amplitude reflections on fluid factor traces would be expected to represent gas‐saturated sandstones. Of course, this relationship does not apply exactly in nature, and the extent to which the mudrock line model applies varies from area to area. However, it is a useful model in many basins of the world, including the one studied here. Geostack processing has been done on a 3-D seismic data set over the Mossel Bay gas field on the southern continental shelf of South Africa. We found that anomalously high amplitude fluid factor reflections occurred at the top and base of the gas‐reservoir sandstone. Maps were made of the amplitude of these fluid factor reflections, and it was found that the high amplitude values were restricted mainly to the gas field area as determined by drilling. The highest amplitudes were found to be located roughly in the areas of best reservoir quality (i.e., highest porosity) in areas where the reservoir is relatively thick.
Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters;“λρ”,“μρ”,&“λ/μ fluid stack”,from P and S inversions
[C]//
Bridging the gap:Using AVO to detect changes in fundamental elastic constants
[C]//
Zoeppritz方程近似解拟合精确解影响因素
[J].
The analysis of influencing factors between Zoeppritz approximate solution and exact solution
[J].
Characterizing the degree of amplitude-variation-with-offset nonlinearity in seismic physical modelling reflection data
[J].DOI:10.1111/gpr.2015.63.issue-1 URL [本文引用: 1]
反演纵横波速度的Jacobian矩阵及精确计算方法
[J].
Jacobian matrix for inversion of P- wave velocity and its accurate calculation method
[J].DOI:10.1360/zd2010-40-11-1608 URL [本文引用: 1]
Joint AVO inversion of PP and PS waves using exact Zoeppritz equation
[C]//
Multi-parameter nonlinear inversion with exact reflection coefficient equation
[J].DOI:10.1016/j.jappgeo.2013.07.012 URL [本文引用: 1]
Amplitude variation with angle inversion using the exact Zoeppritz equations:Theory and methodology
[J].
DOI:10.1190/geo2014-0582.1
URL
[本文引用: 1]

To overcome the weaknesses of conventional prestack amplitude variation with angle inversion based on various linear or quasi-linear approximations, we have conducted a nonlinear inversion method using the exact Zoeppritz matrix (EZAI). However, the inversion using the exact Zoeppritz matrix was highly nonlinear and often unstable, if not properly treated. To tackle these issues, we have used an iteratively regularizing Levenberg-Marquardt scheme (IRLM), which regularizes the inversion problem within an algorithm that minimizes the misfit between the observed and the modeled data at the same time by incorporating the Tikhonov regularization method. As a result, the new EZAI method solved using the IRLM scheme is feasible for seismic data sets with large incidence angles, even up to or beyond the critical angle as well as strong parameter contrasts. Single and multilayered synthetic examples were used to test these features. These tests also showed that EZAI is robust on noisy gathers for parameter extraction and has weak dependence on the initial model. For the influence of inaccurate amplitudes, dominant frequencies, and phase angles, we found that EZAI is less sensitive to the variation in amplitude and phase shifts than to the dominant frequencies. Specifically, the inversion results of EZAI for P- and S-wave velocities and density were reliable if the inaccurate range for the amplitude was within 20% or the angle of the phase shift was no more than 20°. The superiority of EZAI makes it a very promising method for the estimation of subsurface elastic parameters.
Non-linear AVO inversion based on a novel exact PP reflection coefficient
[J].DOI:10.1016/j.jappgeo.2018.09.019 URL [本文引用: 1]
基于Zoeppritz方程的叠前和叠后混合多参数非线性地震反演
[J].
Nonlinear multi-parameter hybrid inversion of prestack and post-stack seismic data based on Zoeppritz equation
[J].
Amplitude-variation-with-offset and prestack-waveform inversion:A direct comparison using a real data example from the Rock Springs Uplift,Wyoming,USA
[J].
DOI:10.1190/geo2014-0233.1
URL
[本文引用: 1]

Recent advances in seismic data acquisition and processing allow routine extraction of offset-/angle-dependent reflection amplitudes from prestack seismic data for quantifying subsurface lithologic and fluid properties. Amplitude-variation-with-offset (AVO) inversion is the most commonly used practice for such quantification. Although quite successful, AVO has a few shortcomings primarily due to the simplicity in its inherent assumptions, and for any quantitative estimation of reservoir properties, they are generally interpreted in combination with other information. In recent years, waveform-based inversions have gained popularity in reservoir characterization and depth imaging. Going beyond the simple assumptions of AVO and using wave equation solutions, these methods have been effective in accurately predicting the subsurface properties. Developments of these waveform inversions have so far been along two lines: (1) the methods that use a locally 1D model of the subsurface for each common midpoint and use an analytical solution to the wave equation for forward modeling and (2) the methods that do not make any 1D assumption but use an approximate numerical solution to the wave equation in 2D or 3D for forward modeling. Routine applications of these inversions are, however, still computationally demanding. We described a multilevel parallelization of elastic-waveform inversion methodology under a 1D assumption that allowed its application in a reasonable time frame. Applying AVO and waveform inversion on a single data set from the Rock Springs Uplift, Wyoming, USA, and comparing them with one another, we also determined that the waveform-based method was capable of obtaining a much superior description of subsurface properties compared with AVO. We concluded that the waveform inversions should be the method of choice for reservoir property estimation as high-performance computers become commonly available.
基于Zoeppritz方程的纵横波模量反演
[J].
Compressional and shear modulus inversion based on Zoeppritz equation
[J].
Constrained nonlinear amplitude variation with offset inversion using Zoeppritz equations
[J].
DOI:10.1190/geo2017-0543.1
URL
[本文引用: 1]

The inversion of prestack seismic data using amplitude variation with offset (AVO) has received increased attention in the past few decades because of its key role in estimating reservoir properties. AVO is mainly governed by the Zoeppritz equations, but traditional inversion techniques are based on various linear or quasilinear approximations to these nonlinear equations. We have developed an efficient algorithm for nonlinear AVO inversion of precritical reflections using the exact Zoeppritz equations in multichannel and multi-interface form for simultaneous estimation of the P-wave velocity, S-wave velocity, and density. The total variation constraint is used to overcome the ill-posedness while solving the forward nonlinear model and to preserve the sharpness of the interfaces in the parameter space. The optimization is based on a combination of Levenberg’s algorithm and the split Bregman iterative scheme, in which we have to refine the data and model parameters at each iteration. We refine the data via the original nonlinear equations, but we use the traditional cost-effective linearized AVO inversion to construct the Jacobian matrix and update the model. Numerical experiments show that this new iterative procedure is convergent and converges to a solution of the nonlinear problem. We determine the performance and optimality of our nonlinear inversion algorithm with various simulated and field seismic data sets.
Uncertainty estimation for amplitude variation with offset(AVO) inversion
[J].
DOI:10.1190/1.1620621
URL
[本文引用: 1]

This paper uses a Bayesian approach for inverting seismic amplitude versus offset (AVO) data to provide estimates and uncertainties of the viscoelastic physical parameters at an interface. The inversion is based on Gibbs' sampling approach to determine properties of the posterior probability distribution (PPD), such as the posterior mean, maximum a posteriori (MAP) estimate, marginal probability distributions, and covariances. The Bayesian formulation represents a fully nonlinear inversion; the results are compared to those of standard linearized inversion. The nonlinear and linearized approaches are applied to synthetic test cases which consider AVO inversion for shallow marine environments with both unconsolidated and consolidated seabeds. The result of neglecting attenuation in the seabed is investigated, and the effects of data factors such as independent and systematic errors and the range of incident angles are considered. The Bayesian approach is also applied to estimate the physical parameters and uncertainties from AVO data collected at two sites along a seismic line in the Baltic Sea with differing sediment types; it clearly identifies the distinct seabed compositions. Data uncertainties (independent and systematic) required for this analysis are estimated using a maximum‐likelihood approach.
基于MCMC的叠前地震反演方法研究
[J].
Study on prestack seismic inversion using Markov chain Monte Carlo
[J].
基于差分进化算法的叠前AVO反演
[J].
Prestack AVO inversion based on the differential evolution algorithm
[J].
Bayesian Gaussian mixture linear inversion for geophysical inverse problems
[J].DOI:10.1007/s11004-016-9671-9 URL [本文引用: 1]
Gaussian mixture Markov chain Monte Carlo method for linear seismic inversion
[J].
DOI:10.1190/GEO2018-0529.1
[本文引用: 1]

We have developed a Markov chainMonte Carlo (MCMC) method for joint inversion of seismic data for the prediction of facies and elastic properties. The solution of the inverse problem is defined by the Bayesian posterior distribution of the properties of interest. The prior distribution is a Gaussian mixture model, and each component is associated to a potential configuration of the facies sequence along the seismic trace. The low frequency is incorporated by using facies-dependent depositional trend models for the prior means of the elastic properties in each facies. The posterior distribution is also a Gaussian mixture, for which the Gaussian component can be analytically computed. However, due to the high number of components of the mixture, i.e., the large number of facies configurations, the computation of the full posterior distribution is impractical. Our Gaussian mixture MCMC method allows for the calculation of the full posterior distribution by sampling the facies configurations according to the acceptance/rejection probability. The novelty of the method is the use of an MCMC framework with multimodal distributions for the description of the model properties and the facies along the entire seismic trace. Our method is tested on synthetic seismic data, applied to real seismic data, and validated using a well test.
Markov chain Monte Carlo algorithms for target-oriented and interval-oriented amplitude versus angle inversions with non-parametric priors and non-linear forward modellings
[J].
DOI:10.1111/1365-2478.12876
[本文引用: 1]

In geophysical inverse problems, the posterior model can be analytically assessed only in case of linear forward operators, Gaussian, Gaussian mixture, or generalized Gaussian prior models, continuous model properties, and Gaussian-distributed noise contaminating the observed data. For this reason, one of the major challenges of seismic inversion is to derive reliable uncertainty appraisals in cases of complex prior models, non-linear forward operators and mixed discrete-continuous model parameters. We present two amplitude versus angle inversion strategies for the joint estimation of elastic properties and litho-fluid facies from pre-stack seismic data in case of non-parametric mixture prior distributions and non-linear forward modellings. The first strategy is a two-dimensional target-oriented inversion that inverts the amplitude versus angle responses of the target reflections by adopting the single-interface full Zoeppritz equations. The second is an interval-oriented approach that inverts the pre-stack seismic responses along a given time interval using a one-dimensional convolutional forward modelling still based on the Zoeppritz equations. In both approaches, the model vector includes the facies sequence and the elastic properties of P-wave velocity, S-wave velocity and density. The distribution of the elastic properties at each common-mid-point location (for the target-oriented approach) or at each time-sample position (for the time-interval approach) is assumed to be multimodal with as many modes as the number of litho-fluid facies considered. In this context, an analytical expression of the posterior model is no more available. For this reason, we adopt a Markov chain Monte Carlo algorithm to numerically evaluate the posterior uncertainties. With the aim of speeding up the convergence of the probabilistic sampling, we adopt a specific recipe that includes multiple chains, a parallel tempering strategy, a delayed rejection updating scheme and hybridizes the standard Metropolis-Hasting algorithm with the more advanced differential evolution Markov chain method. For the lack of available field seismic data, we validate the two implemented algorithms by inverting synthetic seismic data derived on the basis of realistic subsurface models and actual well log data. The two approaches are also benchmarked against two analytical inversion approaches that assume Gaussian-mixture-distributed elastic parameters. The final predictions and the convergence analysis of the two implemented methods proved that our approaches retrieve reliable estimations and accurate uncertainties quantifications with a reasonable computational effort.
Zoeppritz-based AVO inversion using an improved Markov chain Monte Carlo method
[J].DOI:10.1007/s12182-016-0131-4 URL [本文引用: 1]
Markov chain Monte Carlo simulation using the DREAM software package:Theory,concepts,and MATLAB implementation
[J].
Mixture density network applied to reservoir parameter inversion in Bohai Oil field
[C]//
Equation of State Calculations by Fast Computing Machines
[J].
DOI:10.1063/1.1699114
URL
[本文引用: 1]

A general method, suitable for fast computing machines, for investigating such properties as equations of state for substances consisting of interacting individual molecules is described. The method consists of a modified Monte Carlo integration over configuration space. Results for the two-dimensional rigid-sphere system have been obtained on the Los Alamos MANIAC and are presented here. These results are compared to the free volume equation of state and to a four-term virial coefficient expansion.
Inference from iterative simulation using multiple sequences
[J].