0 引言
随着计算机科学与技术的发展,非线性方法在地球物理反演问题中应用越来越广泛。Raiche[7]早在1991年就将神经网络应用于地球物理数据反演中,Calderón-Macías等[8]将神经网络应用于直流电阻率法及地震数据处理,证明了神经网络应用于地球物理数据反演的可行性。国外学者El-Qady等、Stephen等、Mann及Neyamadpour等应用神经网络进行一维、二维电阻率数据反演计算的研究[9⇓⇓-12];Neyamadpour等[13-14]应用神经网络进行三维ERT数据的反演计算,均取得了理想的结果,说明了神经网络进行电法数据的反演计算具备传统线性方法不具备的优越性。国内学者徐海浪等[6]最早应用MATLAB神经网络工具箱进行二维ERT数据的反演计算,指出RPROP算法具备最快的收敛速度。但是由于神经网络学习算法的限制,使神经网络的损失函数在迭代过程中陷入鞍点,使得神经网络进行反演计算的精度受到限制。对于这一问题,国内外学者进行了深入研究,Maiti等[15]使用混合蒙特卡洛算法优化的贝叶斯神经网络进行二维直流电法数据的反演;张凌云[16]对比了多种智能寻优算法优化的BP神经网络进行二维ERT数据的反演计算,指出遗传算法优化后的网络精度最高时间最长;戴前伟等[17-18]使用混沌振荡的PSO算法及差分进化算法优化的BP神经网络实现ERT数据反演成像;高明亮等[19]使用免疫遗传算法优化的BP神经网络进行二维ERT数据反演计算,提出并解决了普通遗传算法的寻优慢、易收敛于局部极小点的问题。
前人成果缺乏训练模型数据集的合理划分、针对实测ERT数据反演成像数据的网络模型数据设计不完全合理。针对这两个问题,本文指出了数据集合理划分的重要性,并提出基于最佳保留策略的自适应遗传算法(OMAGA)优化的BP神经网络ERT反演成像建模方案,通过最小二乘法、BP算法、GA-BP算法及OMAGA-BP算法对仿真模型及防空洞实测数据反演计算精度的对比,证明了本文提出的ERT反演方案可得到高精度的反演结果。
1 OMAGA算法优化BP神经网络原理
1.1 BP神经网络构建原理
1.1.1 BP神经网络算法
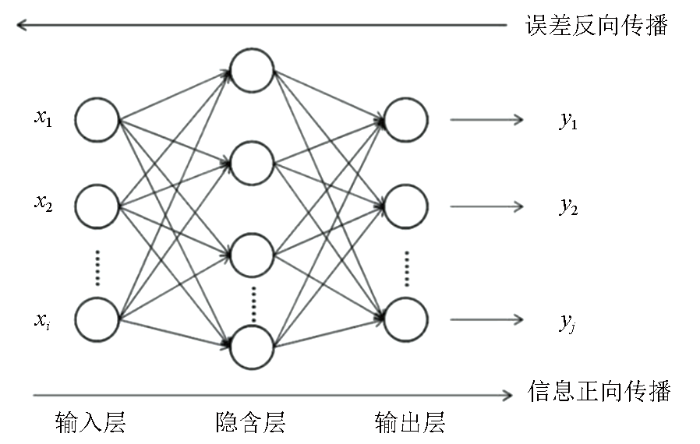
BP神经网络是误差反向传播的多层神经网络,其由输入层、若干隐藏层、输出层及层之间的连接关系构成,图1为三层BP网络示意。i为输入层节点个数, j为输出层节点个数。网络中间结构为隐藏层, BP神经网络的非线性特性正是来自于隐藏层处的非线性激活函数。
图1
图1
三层BP神经网络结构示意
Fig.1
Schematic diagram of three-layer BP neural network structure
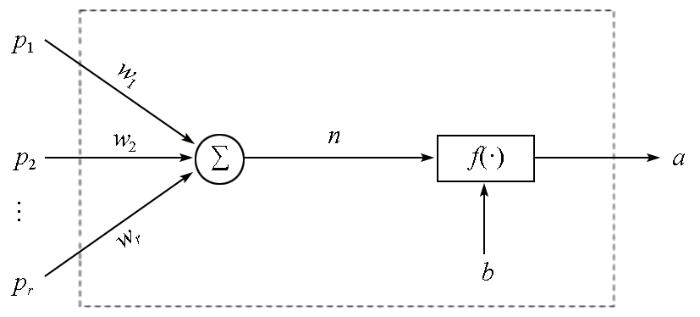
BP神经网络算法分为正向传播拟合及误差反向传播调整网络权值阈值两个部分。正向传播拟合为输入数据通过网络拟合得到预测输出的过程。图2为单神经元算式示意;式(1)为输出值a与输入向量p对应的关系,f为激活函数,w为权值行向量,向量的维度均为r,wj为输入值Pj与神经元之间的权值,b为阈值。
图2
选用均方误差作为网络的损失函数,设第t次迭代时网络对输入数据的拟合结果为
BP神经网络算法通过误差反向传播,使用学习算法调整网络权值阈值直到满足网络训练终止条件,徐海浪等[6]经过对各种学习算法的对比,发现使用RPROP算法表现最优。RPROP算法的运算过程为:
1)赋予每个节点权值阈值初始变化量
2)计算初始化网络后损失函数的数值,并计算其对每个权值阈值的一阶导。
3)根据误差梯度变化调整权值阈值变化步长:
调整权值阈值:
4)重复步骤2)~3)直到满足终止条件。
1.1.2 模型数据集的划分
若想在训练数据数量一定的前提下,训练出具备一定泛化能力的网络,将一小部分训练模型数据划分成测试集和验证集是十分关键的。首先训练集的作用即是训练网络,通过拟合训练集的输入输出数据,达到网络可以精确反演训练集模型类型的数据的基本要求。
验证集不对网络的权值阈值进行调整,通过验证集的数据对调整了几次权值阈值的网络进行精度验证,根据验证集误差结果及时调整网络的权值阈值。Matlab神经网络工具箱具有“validation check”功能,通过函数定义验证集误差最大连续不下降次数,当连续训练网络到此设置次数,验证集数据拟合误差还不下降,网络停止训练,起到“early stopping”的作用[20]:尽管随着网络训练过程,对训练集的输入输出数据非线性关系的拟合程度不断提高,但是由于网络权值阈值的初值很小,而随着迭代次数的增加,权值阈值的数值增大,若验证集误差连续在规定次数内不下降时,停止网络的训练,此时权重阈值很小,网络对于输入、输出数据之间非线性关系的拟合便不能过于依赖网络的某个节点,避免了过拟合现象的发生,保证了网络具备一定的泛化能力。
测试集是数据集中不参与网络训练的数据集合,其有对经过训练及验证的网络精度验证的作用,是对训练好网络的泛化能力的一种近似,如果测试集误差无法达到精度需求,则需重新设定网络的超参数。
从上述3种数据集合划分的作用来看,模型数据集的划分十分关键,要想得到理想性能的网络,不能少划分任何一个数据集。
1.2 OMAGA算法优化BP神经网络
BP算法具备强大的非线性拟合能力,但由于网络的权值阈值总数很大,导致网络损失函数的维度相当高,使得网络损失函数的参数空间含有大量鞍点,使得RPROP算法等传统的学习算法甚至难以调整得到使网络损失函数陷入局部最小点的权值阈值结果[21],这在某种程度上限制了网络的精度。
遗传算法是来源于对生物学中遗传现象模拟的智能寻优算法,通过一代代的遗传进化计算,从而得到目标函数的最优解。而普通遗传算法存在“早熟收敛”问题。恽为民等[22]等说明了采用最佳保留策略的简单遗传算法(OMSGA)及交叉率和变异率自适应变化的自适应遗传算法(AGA)具有一定的全局收敛性。本文采用基于最佳保留策略的自适应遗传算法(OMAGA)对BP神经网络的初始权值阈值进行优化,通过OMAGA算法赋给BP神经网络接近最优的权值阈值初始值,再通过RPROP学习算法训练网络对权值阈值进一步微调,使得网络的损失函数以最大程度上逼近全局最小值,从而达到提升网络预测精度的目的,使用OMAGA算法优化BP算法过程如下:
1)确定网络参数:确定除权值阈值以外的其他参数。
2)选择优化目标:遗传算法通常寻找适应度值大的个体,设网络在第T次迭代后终止训练,本文优化目标函数为:
3)种群大小的选择:种群是遗传算法每次迭代参与计算个体的总数,如果种群规模过小,其降低了个体多样性,导致精度不足,并且得到的解不稳定;若种群规模过大,会严重延长算法寻优时长,导致算法性能下降。本文选择种群规模为100。
4)编码方式选择:本文选择实数编码方式,其避免了基于二进制转换形式的编码方法求解精度受编码长度限制、需要频繁的解码操作影响计算速度等问题,保证了算法的局部搜索能力。
5)初始化种群:其需要满足在解空间内随机采样且均匀分布,初始化结果在可行解范围内。群体中每个个体的基因向量维度大小为网络权值阈值数目总和,选择每个基因的值控制在[-1,1]范围内。初始化生成种群规模数量的个体。
6)以式(7)计算种群中每个个体的适应度值。
7)选择操作:模拟了自然界的“选择”,本文采用轮盘赌算法。
8)交叉操作:其模拟了生物学的基因重组,基于初始化后个体均匀分布于解的编码空间全局,其具有全局寻优性。AGA算法通过自适应调控交叉率,算法迭代前期保证全局寻优能力,而算法迭代后期种群平均适应度
9)变异操作:变异操作是对生物学染色体基因突变的模拟,其较小幅度地改变种群的表现型,体现的是算法局部寻优能力。当平均适应度和最佳适应度接近时,需增大变异率从而加强算法局部寻优能力,使得种群一定概率跳出局部最优解区域。初始变异率选择0.15,变异率自适应选择公式:
10)最佳保留策略:每轮迭代进行完交叉变异等操作后,此策略对比子代与父代最佳适应度大小,如果子代最佳适应度值优于父代,则不对子代进行任何操作,若子代最佳适应度差于父代,则将父代的最佳个体替换给子代的最差个体;即使种群没有进化,也会保证原有最佳个体不受破坏,增强了算法寻优搜索的稳定性。
11)终止条件的选择:选择算法迭代达到一定次数或种群最优适应度值大于所设置值作为算法终止条件。
12)重复6)~10)步直到满足终止条件,将得到最优的权值阈值赋给网络。
2 二维OMAGA-BP高密度电法反演成像
对于OMAGA-BP算法进行二维ERT数据反演成像,其原理是设计训练样本并给定该算法相应参数后,通过该算法学习训练样本中视电阻率和真电阻率的复杂非线性关系; 学习完成之后,向网络中输入有关视电阻率向量即可预测真电阻率值向量,代入相应的坐标绘图即可实现成像。在确定所用算法的参数之前,需确定训练模型设计的方式以及选择反演成像网络建模方式。
模型设计基于RES2DMOD软件,首先要固定装置参数,本文采用电极距为1 m、电极数量为36个的温纳装置,共采集198个视电阻率数据; 其次要基于对装置探测范围内异常体的电性分布范围进行限制,在目标反演区域可先通过线性反演结果、地质资料调查、钻井资料获取等了解目标反演区域地质构造及相应电性特征; 然后大量设计针对目标反演区域电性分布特征的特定模型训练网络,从而在保证反演结果精度的前提下,提高模型设计的效率。
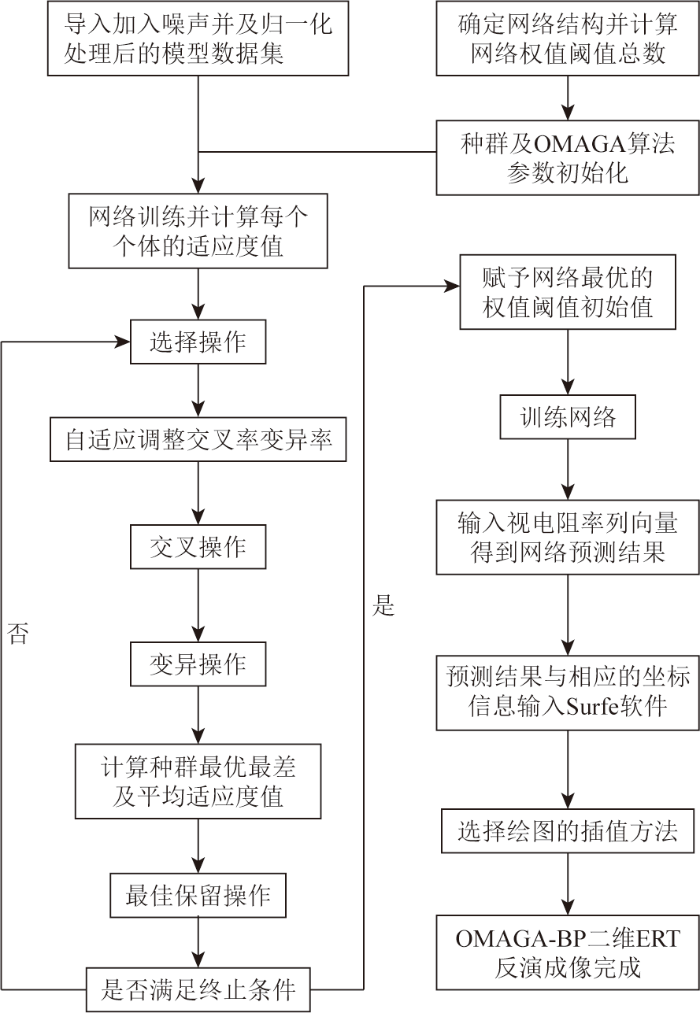
对于BP网络进行ERT二维反演成像,本文选择徐海浪等[6]的网络建模方式,输入向量为198个视电阻率数据,输出向量为1 540个真电阻率数据。而在进行实际野外数据采集时,由于电极位置误差、高密度电法仪器质量不稳定等因素,实测数据的采集不可能不包含误差,主要成分是白噪声。如果将数值模拟得到的数据直接用于训练网络的情况下,相当于这部分白噪声直接被减掉了,而实际情况下干扰一定存在,这会影响网络对实测数据的预测精度。Chen等[23]向输入电阻率向量中加入一定比例的高斯噪声,很好地解决了这一问题;同时在弱噪声的前提下,有学者证明向神经网络的输入加入噪声相当于Tikhonov正则化的作用[24],其提高了神经网络解决回归问题的泛化性能[25]。本文对网络的输入数据矩阵加入2%的高斯噪声,然后对学习样本的输入输出数据进行归一化到[0,1]范围内处理,旨在降低数据之间的大小差距,加快网络的训练速度。图3为二维OMAGA-BP高密度电法反演成像流程。
图3
图3
二维OMAGA-BP高密度电法反演成像流程
Fig.3
2D OMAGA-BP high-density electrical inversion imaging diagram
3 仿真模型反演成像
本节主要对比最小二乘法、BP法、GA-BP法及OMAGA-BP法4种方法进行二维ERT仿真模型反演成像的精细程度,并且通过回归值R(训练集R值、验证集R值、测试集R值和网络整体R值)对比3种非线性反演方法(BP、GA-BP及OMAGA-BP)的精度,回归值R代表网络对输入输出之间非线性关系的拟合程度,其表达式为:
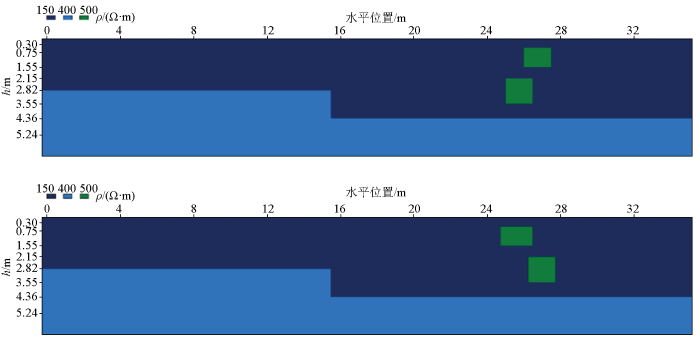
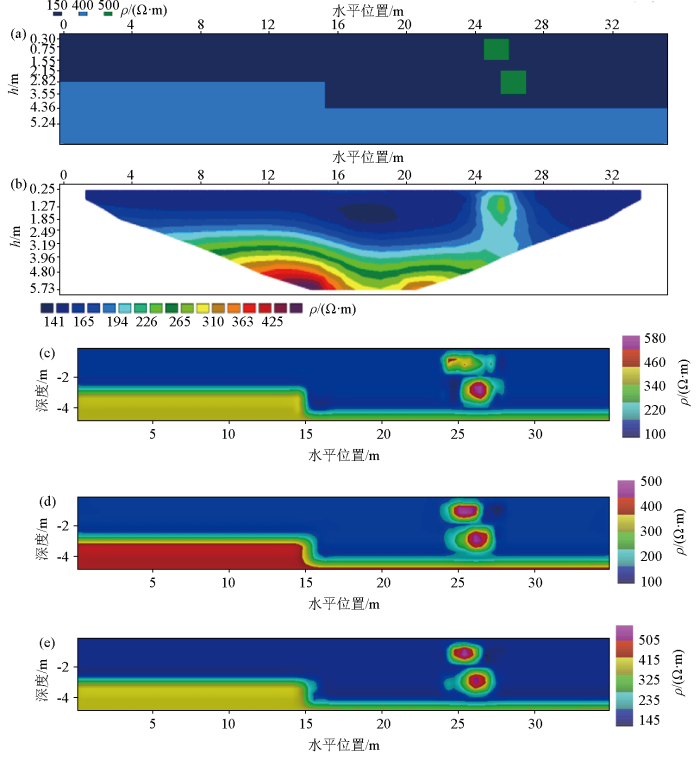
式中:n为网络模型样本总数;R代表网络整体的回归值,若n取训练集、验证集或测试集样本个数,则R分别对应网络对3种数据集拟合的回归值。共制作含双高阻块体的电阻率分界面模型50组,图4为部分模型样本示意,其中训练集∶验证集∶测试集=40∶5∶5,选用四层BP神经网络,第一、二隐藏层节点数分别选择为20和25,激活函数分别选择tansig和logsig,网络终止条件为验证集连续10次误差不下降,关于GA-BP及OMAGA算法参数选择同第1节。
图4
从表1中3种非线性算法回归值R的结果对比可以看出,OMAGA-BP算法得到的各个回归值R结果都优于GA-BP以及BP算法,说明优化后的网络对输入、输出数据间的拟合能力显著提高。从图5显示的结果可以看出,最小二乘法反演结果无法分辨出电阻率分界面的拐点位置,并且两个高阻块体的电性异常叠加在了一起;而BP算法可以准确计算出两个高阻块体的纵向位置,但对两个高阻块体的横向位置反演结果准确性较差,且有较明显的边界失真现象;GA-BP算法可以准确地计算出横纵向位置,但边界失真现象较OMAGA-BP算法得到的结果明显,说明OMAGA-BP算法具备更优的反演计算精度。而3种非线性方法的训练模型样本相同,OMAGA-BP算法的结果更优,在一定程度上可以说明OMAGA-BP算法的泛化能力更优。
表1 模拟数据训练3种网络的性能比较
Table 1
| 反演网络 | 训练集R值 | 验证集R值 | 测试集R值 | 总体R值 |
|---|---|---|---|---|
| BP | 0.96175 | 0.95273 | 0.93846 | 0.95814 |
| GA-BP | 0.97779 | 0.9529 | 0.94298 | 0.97095 |
| OMAGA-BP | 0.99403 | 0.97646 | 0.96735 | 0.98909 |
图5
图5
测试模型示意及不同反演方法成像结果
a—电阻率测试模型示意;b—电阻率模型最小二乘法反演结果;c—BP法反演结果;d—GA-BP法反演结果;e—OMAGA-BP法反演结果
Fig.5
Schematic diagram of the test model and inversion imaging results of different methods
a—schematic diagram of the test resistivity model;b—least-squares inversion result of resistivity model;c—BP inversion result;d—GA-BP inversion result;e—OMAGA-BP inversion result
4 实测数据反演测试
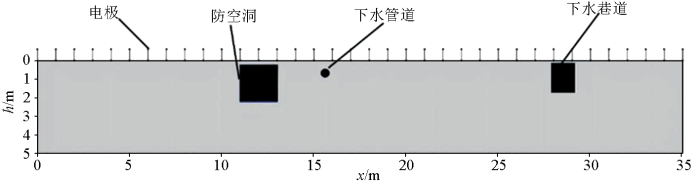
为了进一步说明本文针对高密度电法二维数据反演建模方法的可靠性,笔者进行了实测数据反演测试,实测数据采集地点位于吉林大学朝阳校区篮球馆东侧防空洞,使用EDJD-2数字多功能直流电法仪进行数据采集,选用电极距为1 m、电极个数为36个的温纳装置,共采集11层共198个视电阻率数据。目标为空洞探测,目标一为防空洞,其顶部距离地面将近0.5 m,最深深度约为2.25 m;防空洞北部有一下水巷道,其尺寸为1 m×1.6 m,深度为2 m,而防空洞北侧3.5 m左右有一排水管道,直径不到0.15 m。图6为防空洞及数据采集示意。
图6
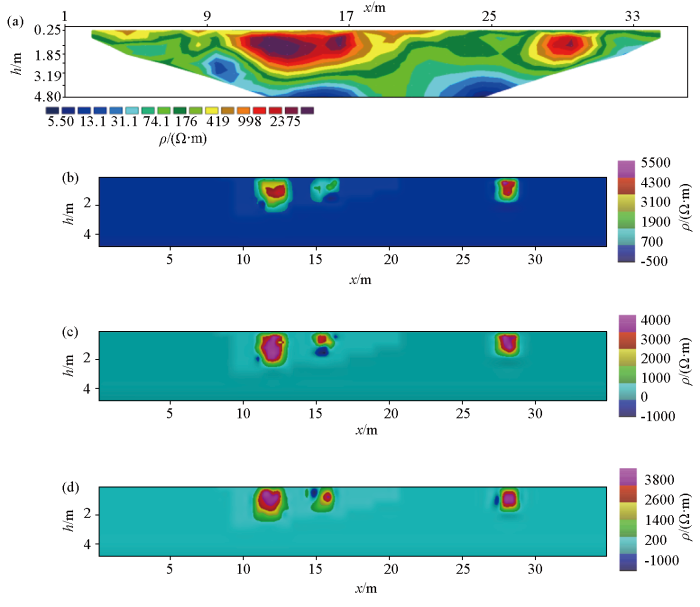
图7为最小二乘法、BP、GA-BP及OMAGA-BP这4种算法对防空洞实测数据得到的反演结果,其中线性反演结果失真很明显,BP法无法准确识别出下水管道的位置。而可以明显地看出GA-BP算法以及OMAGA-BP算法可以更准确地识别异常体的位置及轮廓,且OMAGA-BP算法对下水管的识别更胜一筹,进一步说明OMAGA-BP算法具备更优的反演计算精度及泛化能力;但存在轻微的失真现象,并且有很小的一块计算得到了负的电阻率值,负电阻率值的出现与输入数据归一化到[0,1]范围内有关。同时可以看3种非线性方法反演结果显示下水管道和防空洞附近有浅色阴影异常,这是由于图6所示的防空洞示意是一个三维模型,垂直于测线方向上电性分布明显变化,而网络输入的模型数据是通过2.5 D正演软件设计的,导致计算误差,出现了假异常。
图7
图7
4种反演方法对防空洞数据的反演结果
a—最小二乘法反演结果;b—BP法反演结果;c—GA-BP法反演结果;d—OMAGA-BP法反演结果
Fig.7
Inversion results of air raid shelter data by four inversion methods
a—least-squares inversion result;b—BP inversion result;c—GA-BP inversion result; d—OMAGA-BP inversion result
5 结论及讨论
本文实现了OMAGA-BP算法ERT反演成像方法,改善了BP算法损失函数空间存在大量鞍点,影响网络精度的问题。通过最小二乘法、BP法、GA-BP法、OMAGA-BP法对含双高阻块体的分界面仿真模型及防空洞实测数据的反演成像结果的对比,说明OMAGA-BP算法具备更高的反演计算精度及泛化能力。
本文网络训练模型是通过2.5 D正演软件设计的,而实际反演计算的模型沿垂直测线方向电位分布明显变化,导致产生计算误差及假异常的现象,虽准确识别出异常体的位置及轮廓,但应指出使用2.5 D正演软件设计的模型数据训练的网络应适用于垂直测线方向电性分布不发生明显变化的实测数据。模型设计受限于RES2DMOD软件仅可以设计以规则块体为单元的模型,限制了方法适用目标体的范围,针对此问题将在后续发表的论文中得到解决。
参考文献
电法勘探的发展和展望
[J].
Development and prospect of electrical prospecting method
[J].
高密度电阻率法二维反演在工程勘探中的应用
[J].
The application of high density resistivity 2D inversion to engineering exploration
[J].
高密度电阻率法在地面塌陷调查中的应用
[J].
Application of resistivity tomography survey method in detecting ground subsidence
[J].
Least-squares deconvolution of apparent resistivity pseudosections
[J].
DOI:10.1190/1.1443900
URL
[本文引用: 1]

A fast technique for the inversion of data from resistivity tomography surveys has been developed. This technique is based on the smoothness‐constrained, least‐squares method, and it produces a 2-D subsurface model that is free of distortions in the apparent resistivity pseudosection caused by the electrode array geometry used. A homogeneous earth model is used as the starting model for which the apparent resistivity partial derivative values can be calculated analytically. Tests with a variety of models and data from field surveys show that this technique is insensitive to random noise, provided a sufficiently large damping factor is used, and that it can resolve structures that cause overlapping anomalies in the pseudosection. On a 33 MHz 80486DX microcomputer, it takes about 5 s to process a single data set.
电阻率二维神经网络反演
[J].
2-D resistivity inversion using the neural network method
[J].
A pattern recognition approach to geophysical inversion using neural nets
[J].
DOI:10.1111/j.1365-246X.1991.tb00801.x
URL
[本文引用: 1]

This paper is a philosophical exploration of adaptive pattern recognition paradigms for geophysical data inversion, aimed at overcoming many of the problems faced by current inversion methods. APR (adaptive pattern recognition) methods are based upon encoding exemplar patterns in such a way that their features can be used to classify subsequent test patterns. These paradigms are adaptive in that they learn from experience and are capable of inferring rules to deal with incomplete data. APR paradigms can also be highly effective in dealing with noise and other data distortions through the use of exemplars which characterize such distortions. Rather than merely seeking to reduce the point by point mismatch between data and model curves, effective APR paradigms would match patterns by establishing a feature vocabulary and inferring rules to weight the relative importance of these features in interpreting data. They have the advantage that prototype data sets can include analogue modelling data and field survey data rather than being restricted to models for which a numerical forward model can be calculated. The success of this approach to inversion will depend upon the effectiveness of replacing continuous parameter estimation with microclassification (discretized parameter estimation). Once the viability of APR schemes has been established for inverting data from individual geophysical methods, the task of joint interpretation of data from different geophysical survey methods could be accomplished in an optimum fashion by using hierarchical adaptive schemes.
Artificial neural networks for parameter estimation in geophysics
[J].
DOI:10.1046/j.1365-2478.2000.00171.x
URL
[本文引用: 1]

Artificial neural systems have been used in a variety of problems in the fields of science and engineering. Here we describe a study of the applicability of neural networks to solving some geophysical inverse problems. In particular, we study the problem of obtaining formation resistivities and layer thicknesses from vertical electrical sounding (VES) data and that of obtaining 1D velocity models from seismic waveform data. We use a two‐layer feedforward neural network (FNN) that is trained to predict earth models from measured data. Part of the interest in using FNNs for geophysical inversion is that they are adaptive systems that perform a non‐linear mapping between two sets of data from a given domain. In both of our applications, we train FNNs using synthetic data as input to the networks and a layer parametrization of the models as the network output. The earth models used for network training are drawn from an ensemble of random models within some prespecified parameter limits. For network training we use the back‐propagation algorithm and a hybrid back‐propagation–simulated‐annealing method for the VES and seismic inverse problems, respectively. Other fundamental issues for obtaining accurate model parameter estimates using trained FNNs are the size of the training data, the network configuration, the description of the data and the model parametrization. Our simulations indicate that FNNs, if adequately trained, produce reasonably accurate earth models when observed data are input to the FNNs.
Inversion of DC resistivity data using neural networks
[J].
DOI:10.1046/j.1365-2478.2001.00267.x
URL
[本文引用: 1]

The inversion of geoelectrical resistivity data is a difficult task due to its non‐linear nature. In this work, the neural network (NN) approach is studied to solve both 1D and 2D resistivity inverse problems. The efficiency of a widespread, supervised training network, the back‐propagation technique and its applicability to the resistivity problem, is investigated. Several NN paradigms have been tried on a basis of trial‐and‐error for two types of data set. In the 1D problem, the batch back‐propagation paradigm was efficient while another paradigm, called resilient propagation, was used in the 2D problem. The network was trained with synthetic examples and tested on another set of synthetic data as well as on the field data. The neural network gave a result highly correlated with that of conventional serial algorithms. It proved to be a fast, accurate and objective method for depth and resistivity estimation of both 1D and 2D DC resistivity data. The main advantage of using NN for resistivity inversion is that once the network has been trained it can perform the inversion of any vertical electrical sounding data set very rapidly.
A direct inversion scheme for deep resistivity sounding data using artificial neural networks
[J].DOI:10.1007/BF02701998 URL [本文引用: 1]
Geophysical applications of artificial neural networks and fuzzy logic
[J].
Using artificial neural networks to invert 2D DC resistivity imaging data for high resistivity contrast regions: A MATLAB application
[J].DOI:10.1016/j.cageo.2009.04.004 URL [本文引用: 1]
Inversion of quasi-3D DC resistivity imaging data using artificial neural networks
[J].DOI:10.1007/s12040-009-0061-2 URL [本文引用: 1]
3D inversion of DC data using artificial neural networks
[J].DOI:10.1007/s11200-010-0027-5 URL [本文引用: 1]
Inversion of Schlumberger resistivity sounding data from the critically dynamic Koyna region using the Hybrid Monte Carlo-based neural network approach
[J].
DOI:10.5194/npg-18-179-2011
URL
[本文引用: 1]

. Koyna region is well-known for its triggered seismic activities since the hazardous earthquake of M=6.3 occurred around the Koyna reservoir on 10 December 1967. Understanding the shallow distribution of resistivity pattern in such a seismically critical area is vital for mapping faults, fractures and lineaments. However, deducing true resistivity distribution from the apparent resistivity data lacks precise information due to intrinsic non-linearity in the data structures. Here we present a new technique based on the Bayesian neural network (BNN) theory using the concept of Hybrid Monte Carlo (HMC)/Markov Chain Monte Carlo (MCMC) simulation scheme. The new method is applied to invert one and two-dimensional Direct Current (DC) vertical electrical sounding (VES) data acquired around the Koyna region in India. Prior to apply the method on actual resistivity data, the new method was tested for simulating synthetic signal. In this approach the objective/cost function is optimized following the Hybrid Monte Carlo (HMC)/Markov Chain Monte Carlo (MCMC) sampling based algorithm and each trajectory was updated by approximating the Hamiltonian differential equations through a leapfrog discretization scheme. The stability of the new inversion technique was tested in presence of correlated red noise and uncertainty of the result was estimated using the BNN code. The estimated true resistivity distribution was compared with the results of singular value decomposition (SVD)-based conventional resistivity inversion results. Comparative results based on the HMC-based Bayesian Neural Network are in good agreement with the existing model results, however in some cases, it also provides more detail and precise results, which appears to be justified with local geological and structural details. The new BNN approach based on HMC is faster and proved to be a promising inversion scheme to interpret complex and non-linear resistivity problems. The HMC-based BNN results are quite useful for the interpretation of fractures and lineaments in seismically active region.\n
基于混沌振荡PSO-BP算法的电阻率层析成像非线性反演
[J].
Nonlinear inversion for electrical resistivity tomography based on chaotic oscillation PSO-BP algorithm
[J].
Nonlinear inversion for electrical resistivity tomography based on chaotic DE-BP algorithm
[J].DOI:10.1007/s11771-014-2151-9 URL [本文引用: 1]
基于IGA算法的电阻率神经网络反演成像研究
[J].
DOI:10.6038/cjg20161136
[本文引用: 1]

为满足地球物理资料反演解释的高精度、快速、稳定的要求,本文结合免疫遗传算法寻优速度快和BP神经网络反演不依赖初始模型等优点,设计了一种将BP神经网络和免疫遗传算法进行有机结合的全局优化反演策略,并将该策略成功地应用于二维高密度电法数据反演.利用免疫遗传算法(Immune Genetic Algorithm,简称IGA)对神经网络的反演参数进行同步优化,提高了电阻率反演的精度.仿真和实验结果验证设计的全局优化反演策略取得了较好的效果,通过与线性反演方法和BP法以及遗传神经网络法等反演方法进行比较,得出该方法具有反演精度更高,反演时间更短等显著优势的结论.
Research of resistivity imaging using neural network based on immune genetic algorithm
[J].
A new early stopping algorithm for improving neural network generalization
[C]//
Identifying and attacking the saddle point problem in high-dimensional non-convex optimization
[C]//
遗传算法的全局收敛性和计算效率分析
[J].
The analysis of global convergence and computational efficiency for genetic algorithm
[J].
Probabilistic cracking prediction via deep learned electrical tomography
[J].
DOI:10.1177/14759217211037236
URL
[本文引用: 1]

In recent years, electrical tomography, namely, electrical resistance tomography (ERT), has emerged as a viable approach to detecting, localizing and reconstructing structural cracking patterns in concrete structures. High-fidelity ERT reconstructions, however, often require computationally expensive optimization regimes and complex constraining and regularization schemes, which impedes pragmatic implementation in Structural Health Monitoring frameworks. To address this challenge, this article proposes the use of predictive deep neural networks to directly and rapidly solve an analogous ERT inverse problem. Specifically, the use of cross-entropy loss is used in optimizing networks forming a nonlinear mapping from ERT voltage measurements to binary probabilistic spatial crack distributions (cracked/not cracked). In this effort, artificial neural networks and convolutional neural networks are first trained using simulated electrical data. Following, the feasibility of the predictive networks is tested and affirmed using experimental and simulated data considering flexural and shear cracking patterns observed from reinforced concrete elements.
Training with noise is equivalent to tikhonov regularization
[J].
DOI:10.1162/neco.1995.7.1.108
URL
[本文引用: 1]

It is well known that the addition of noise to the input data of a neural network during training can, in some circumstances, lead to significant improvements in generalization performance. Previous work has shown that such training with noise is equivalent to a form of regularization in which an extra term is added to the error function. However, the regularization term, which involves second derivatives of the error function, is not bounded below, and so can lead to difficulties if used directly in a learning algorithm based on error minimization. In this paper we show that for the purposes of network training, the regularization term can be reduced to a positive semi-definite form that involves only first derivatives of the network mapping. For a sum-of-squares error function, the regularization term belongs to the class of generalized Tikhonov regularizers. Direct minimization of the regularized error function provides a practical alternative to training with noise.
The effects of adding noise during backpropagation training on a generalization performance
[J].
DOI:10.1162/neco.1996.8.3.643
URL
[本文引用: 1]

We study the effects of adding noise to the inputs, outputs, weight connections, and weight changes of multilayer feedforward neural networks during backpropagation training. We rigorously derive and analyze the objective functions that are minimized by the noise-affected training processes. We show that input noise and weight noise encourage the neural-network output to be a smooth function of the input or its weights, respectively. In the weak-noise limit, noise added to the output of the neural networks only changes the objective function by a constant. Hence, it cannot improve generalization. Input noise introduces penalty terms in the objective function that are related to, but distinct from, those found in the regularization approaches. Simulations have been performed on a regression and a classification problem to further substantiate our analysis. Input noise is found to be effective in improving the generalization performance for both problems. However, weight noise is found to be effective in improving the generalization performance only for the classification problem. Other forms of noise have practically no effect on generalization.