E-mail Alert Rss
 

物探与化探, 2023, 47(6): 1467-1478 doi: 10.11720/wtyht.2023.1239

方法研究·信息处理·仪器研制

基于正余弦算法的瑞利波频散曲线反演

付宇,1,2, 艾寒冰1,2,3, 姚振岸,1,2, 梅竹虚1,2, 苏可嘉1,2,4

1.江西省防震减灾与工程地质灾害探测工程研究中心,江西 南昌 330013

2.东华理工大学 地球物理与测控技术学院,江西 南昌 330013

3.中国地质大学(武汉) 地球物理与空间信息学院,湖北 武汉 430074

4.核工业二七0研究所,江西 南昌 330200

Inversion of the Rayleigh wave dispersion curves based on the sine-cosine algorithm

FU Yu,1,2, AI Han-Bing1,2,3, YAO Zhen-An,1,2, MEI Zhu-Xu1,2, SU Ke-Jia1,2,4

1. Engineering Research Center for Seismic Disaster Prevention and Engineering Geological Disaster Detection of Jiangxi Province(East China University of Technology),Nanchang 330013,China

2. School of Geophysics and Measurement-control Technology,East China University of Technology,Nanchang 330013,China

3. School of Geophysics and Geomatics, China University of Geosciences(Wuhan),Wuhan 430074,China

4. Research Institute No.270,CNNC,Nanchang 330200,China

通讯作者: 姚振岸(1990-),男,博士,讲师,硕士研究生导师,主要从事地震勘探方面的科研与教学工作。Email:an6428060@163.com

责任编辑: 叶佩

收稿日期: 2022-08-5   修回日期: 2023-09-26  

基金资助: 江西省教育厅科学技术项目(GJJ200728)
江西省自然科学基金项目(20212BAB211003)
国家自然科学基金项目(42004113)
江西省防震减灾与工程地质灾害探测工程研究中心开放基金项目(SDGD202006)

Received: 2022-08-5   Revised: 2023-09-26  

作者简介 About authors

付宇(1997-),男,在读硕士研究生,主要从事地震面波勘探方面的学习与研究工作。Email:1635504789@qq.com

摘要

瑞利波在工程勘察领域应用广泛,通过反演瑞利波频散曲线可有效地获取地层信息,但频散曲线反演中传统全局优化算法存在收敛速度慢、收敛精度低和易早熟的问题。对此,本文引入一种新的全局优化算法——正余弦算法(SCA)进行瑞利波频散曲线反演研究。SCA基于正余弦函数数学性质,应用多个随机参数和自适应变量调整寻优过程中的探索和开发能力,在获得高精度解的同时还保证了收敛速度以及稳定性。首先利用4个不含噪声模型验证了SCA用于频散曲线反演的可行性;随后往模型中加入15%的随机噪声说明了SCA具有较强的抗干扰能力;接着将SCA与粒子群算法(PSO)进行对比,证明了SCA反演频散曲线能得到高精度和高稳定性的解;最后用冰岛Arnarbælidi和美国怀俄明地区的地震数据检验SCA处理实际数据的能力。理论模型试算与实测资料分析的结果表明,SCA具有快速、高精度、稳定、实用性强的特点,可有效地应用于瑞利波频散曲线的定量解释。

关键词： 瑞利波; 频散曲线反演; 全局优化; 正余弦算法

Abstract

Rayleigh wave is widely used in engineering investigation and surveys.The inversion of its dispersion curves allows for effectively obtaining stratigraphic information.However,conventional global optimization algorithms in the dispersion curve inversion have a slow convergence rate and low convergence precision and are prone to prematurity.Therefore,this study introduced a novel global optimization algorithm—the sine cosine algorithm (SCA)—to solve the problems mentioned above.Based on the mathematical properties of sine and cosine functions,the SCA can adjust the exploration and development capabilities during the optimization using multiple random parameters and adaptive variables.As a result,it can ensure a high convergence rate and great stability while obtaining high-accuracy solutions.First,the feasibility of the SCA for the dispersion curve inversion was verified using four noise-free models.Then,the strong anti-interference ability of the SCA was proved by adding 15% of random noise to the models.Afterward,it was verified that SCA can yield high-precision,high-stability solutions in the dispersion curve inversion by comparison with the particle swarm optimization (PSO) approach.Finally,the practicability of the SCA was confirmed using seismic data from Arnarbælidi in Iceland and Wyoming in the USA.As indicated by the calculation results of theoretical models and the analysis of measured data,the SCA has a high processing speed,precision,stability,and practicability and thus allows for effective quantitative interpretation of the Rayleigh wave dispersion curves.

Keywords： Rayleigh wave; dispersion curve inversion; global optimization; sine-cosine algorithm

PDF (6242KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

付宇, 艾寒冰, 姚振岸, 梅竹虚, 苏可嘉. 基于正余弦算法的瑞利波频散曲线反演[J]. 物探与化探, 2023, 47(6): 1467-1478 doi:10.11720/wtyht.2023.1239

FU Yu, AI Han-Bing, YAO Zhen-An, MEI Zhu-Xu, SU Ke-Jia. Inversion of the Rayleigh wave dispersion curves based on the sine-cosine algorithm[J]. Geophysical and Geochemical Exploration, 2023, 47(6): 1467-1478 doi:10.11720/wtyht.2023.1239

0 引言

随着工程建设场地复杂程度以及施工难度的提高,获得精确的地层信息对于工程的设计和施工变得尤为重要[1]。瑞利波勘探具有浅层分辨率高、抗干扰能力强等优点,在工程勘探中应用广泛[2]。频散曲线反演是瑞利波勘探的关键环节,其反演效果直接决定了获取地层信息的精度。因此,准确地进行频散曲线反演极其重要。

频散曲线反演隶属地球物理反演问题范畴,具有高度非线性、多参数、多极值的特点[3-4]。同时由于地震数据存在噪声、反演多解性等因素的影响,想要精确且高效地反演频散曲线变得非常困难。频散曲线的反演算法可分为局部优化算法和全局优化算法。局部优化算法有最小二乘法[5⇓⇓⇓-9]、L-M算法[10]、Occam算法[11-12]等。早期,局部优化算法因计算速度快而被广泛应用。但此类方法过度依赖于初始模型的建立,初始模型选取和真实情况相近才能获得较好的反演效果。另外,算法易陷入局部极值,并且涉及到的偏导数计算以及反演结果的好坏都受到雅可比矩阵精度的影响[13-14]。这些使局部优化算法在瑞利波反演领域的发展受到限制。另一种全局优化算法因可以很好地避免局部优化算法在反演时遇到的问题,受到学者们的广泛关注。全局优化算法中常用的有遗传算法[15⇓-17]、模拟退火算法[18⇓⇓⇓-22]、粒子群算法等[23-24]。这些算法和局部优化算法相比虽具有不依赖于初始模型、不易陷入局部最优解等优势,但存在运算时间长、容易早熟收敛等缺点。

鉴于此,本文将一种新的正余弦算法(sine cosine algorithm,SCA)用于瑞利波频散曲线的反演研究。为了评价SCA对瑞利波频散曲线反演的可行性、有效性、稳定性和实用性,本文首先利用SCA对4个从简单到复杂的地质模型产生的含噪声与不含噪声的理论频散曲线进行反演,并分析与评价SCA的可行性,有效性和稳定性。接着,通过进一步对比SCA与PSO的反演性能以说明SCA相对于经典的粒子群算法是否具有更稳定、收敛速度更快,反演精度更高的优越性。最后将SCA用于反演来自冰岛Arnarbælidi和美国怀俄明地区的实测数据以检验SCA对瑞利波频散曲线反演的实用性。

1 SCA基本原理

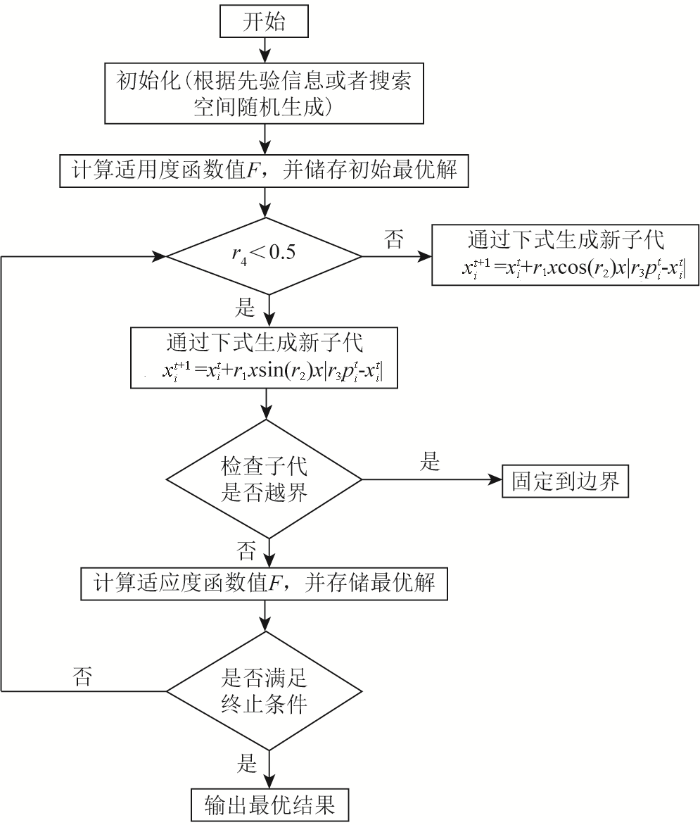
SCA是澳洲学者Seyedali Mirjalili在基于正余弦函数组合,应用多个随机参数和自适应变量调整寻优过程的基础上于2016年提出的一种新型群智能优化算法[25]。SCA与其他群智能优化算法相同,可以根据先验信息给出每个解的初始值。如果先验信息不可用,则可以随机生成初始集合。然后这些解的位置更新方程如下:

xit+1=xit+r1×sin(r2)×r3pit-xit,r4<0.5xit+r1×cos(r2)×r3pit-xit,r4>0.5,

式中:xit表示当前解在第t次迭代时,第i维中的位置,pit是第t次迭代时第i维的最优解。r1、r2、r3和r4都为随机数,其中r2∈[0, 2π]、r3∈[0,2]、r4∈[0,1]。参数r1指示下一个位置的区域(或移动方向),可以是在随机解和最优解之间的空间,也可以是在其之外。参数r2决定了迭代过程中朝着或是远离最优解所移动的距离。参数r3是关于最优解的一个随机权重系数,随机增强(r3> 1)或减弱(r3< 1)最优解对定义距离时所产生的影响。参数r4控制正余弦函数迭代方程的切换。参数r1还能自适应地平衡算法的全局探索和局部开发,其表达式为:

r1=a-taT,

式中:t为当前迭代次数;T为最大迭代次数;a为一常量。图1给出了SCA的算法流程。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   SCA算法流程

Fig.1   Flow chart of SCA


2 理论模型测试

在实际工程应用中,基阶频散曲线能量更强,更易观测,采集数据中大多只含有基阶信息,所以在反演时一般选取基阶频散曲线进行反演[26]。本文考虑到出现高阶频散的情况,对基阶、高阶频散曲线联合反演的情况也进行了测试。在测试中将所有地层信息都设为未知,即同时反演厚度、密度、横波速度以及纵波速度,最后选取对频散曲线有显著影响的层厚和横波速度来进行分析与评价。由于真实的地层情况比较复杂,将模型参数的搜索范围设置为真实模型的50%。对于算法参数设置,SCA中影响算法性能的参数主要为种群数和迭代次数。本文设置SCA的种群数为30,迭代次数为100。为避免算法的随机性,每次理论模型测试都进行独立反演30次,且每次反演初始模型都不相同,最后将30次反演所得数据的均值作为反演结果进而输出,标准差作为衡量算法稳定性的指标进而评价。

瑞利波频散曲线反演的本质是求解适应度函数最小值的优化问题。本文采用的适应度函数是根据反演所得模型能否精确解释观测资料所定[27]:

F=∑i=1MvRobs(i)-vRcal(i)2/M,

式中:vRobs为实测瑞利波相速度;vRcal为理论计算的瑞利波相速度;M为频点数。

为合理评价SCA算法的性能,本文使用4个工程勘察中常见的理论模型对其进行测试。这些模型从简单到复杂逐渐过渡,模型参数见表1。表1中模型A为两层速度递增模型;模型B为4层速度递增模型;模型C为4层含一低速软弱夹层模型;模型D为4层含一高速硬夹层模型。

表1   模型参数及反演搜索范围

Table 1  Model parameter and search space

模型层序号模型参数搜索范围
vs/(m·s-1)vp/(m·s-1)ρ/(g·cm-3)h/mvs/(m·s-1)h/m
模型A12007801.95100~3002.5~7.5
均匀半空间3508501.9∞175~525∞
模型B12006631.92100~3001~3
23009951.94150~4502~6
340013271.96200~6003~9
均匀半空间50016581.9∞250~750∞
模型C12006631.92100~3001~3
21606731.9480~2402~6
330011021.96150~4503~9
均匀半空间40014701.9∞200~600∞
模型D11504981.9275~2251~3
22508291.94125~3752~6
32008411.96100~3003~9
均匀半空间40014701.9∞200~600∞

新窗口打开| 下载CSV


2.1 无噪声数据反演

为合理评测算法,从基础两层模型开始进行测试,随后提升模型复杂度,在四层复杂模型中进行进一步评测。从图2简单两层速度递增模型反演结果可看出,在无任何先验信息的情况下,反演所得频散曲线(图2a中的点线)和理论模拟频散曲线(图2a中的实线)仍具有较高拟合度,并且反演模型和理论模型各参数误差只有0.23%,0.60%和4.76%(表2),30次独立反演所得参数标准差表明30次独立反演整体偏离度较低,验证了SCA用于简单地层结构频散曲线反演的可行性以及稳定性。

图2

新窗口打开| 下载原图ZIP| 生成PPT

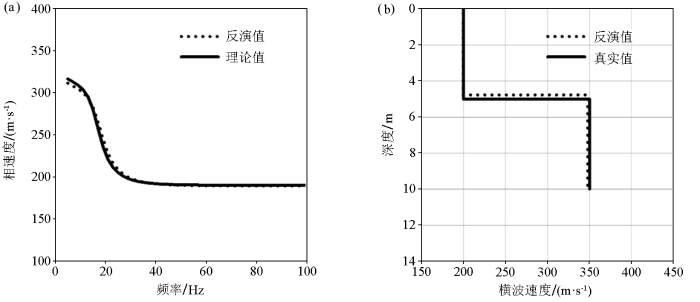
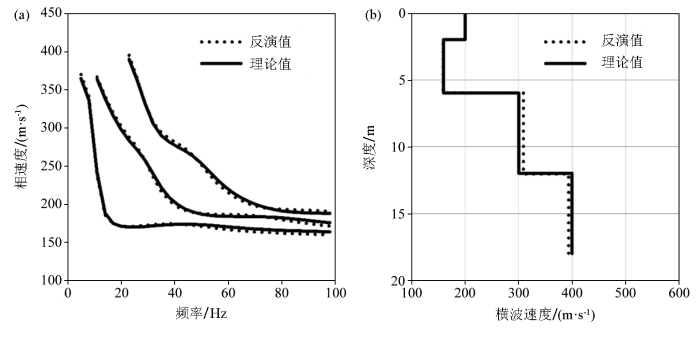
图2   模型A不含噪声理论数据反演结果

a—反演所得频散曲线;b—反演的横波速度剖面

Fig.2   Inversion results of noise-free data of model A

a—inverted response compared with the original one;b—inverted shear-wave velocity profile


表2   模型A、B、C、D含噪声与不含噪声反演结果

Table 2  Inversion results of noise-free and noise-contaminated data with model A,B,C and D

模型参数真实值不含噪声含噪声
反演均值相对误差/%标准差反演均值相对误差/%标准差
模型Avs1/(m·s-1)200199.540.23%1.28199.690.15%2.71
vs2/(m·s-1)350347.900.60%5.98350.790.23%9.07
H1/m54.764.76%0.184.755.00%0.22
模型Bvs1/(m·s-1)200200.940.47%2.52200.950.47%3.82
vs2/(m·s-1)300300.750.25%7.42304.071.36%15.60
vs3/(m·s-1)400399.190.20%9.34391.882.03%25.47
vs4/(m·s-1)500500.190.04%6.03499.620.08%6.80
H1/m22.052.52%0.112.020.83%0.16
H2/m43.990.24%0.283.961.12%0.18
H3/m65.596.76%0.535.616.54%0.97
模型Cvs1/(m·s-1)200197.781.11%9.25199.900.05%14.71
vs2/(m·s-1)160161.150.72%4.52160.550.34%5.35
vs3/(m·s-1)300286.044.65%32.13285.784.74%22.89
vs4/(m·s-1)400397.610.60%13.58397.190.70%18.96
H1/m21.971.57%0.171.914.51%0.23
H2/m43.863.58%0.433.853.71%0.30
H3/m65.626.28%1.095.518.16%0.43
模型Dvs1/(m·s-1)150150.580.39%1.03149.800.13%2.92
vs2/(m·s-1)250252.300.92%4.25251.410.56%7.38
vs3/(m·s-1)200199.810.09%3.94202.011.01%4.41
vs4/(m·s-1)400400.900.23%4.80400.460.12%6.36
H1/m22.031.41%0.072.031.36%0.08
H2/m43.931.78%0.143.980.44%0.24
H3/m66.091.45%0.235.990.14%0.26

新窗口打开| 下载CSV


为进一步测试SCA在复杂地层中的反演表现,将其应用在3种复杂地层:模型B、 C和D中进行反演试算。结果如图3所示,其中a2,b2和c2分别展示了模型B、 C和D的反演结果。从反演结果可以看出,不论是3种模型中的哪一种,利用SCA反演得到的频散曲线(图中a1,b1和c1中的点线)都能与理论频散曲线(图中a1,b1和c1中的实线)吻合良好。3种模型反演所得参数中最大相对误差仅为6.76%,标准差值也相对较小(表2),说明SCA在处理复杂地层模型的频散曲线反演问题时依旧能保持良好的性能。

图3

新窗口打开| 下载原图ZIP| 生成PPT

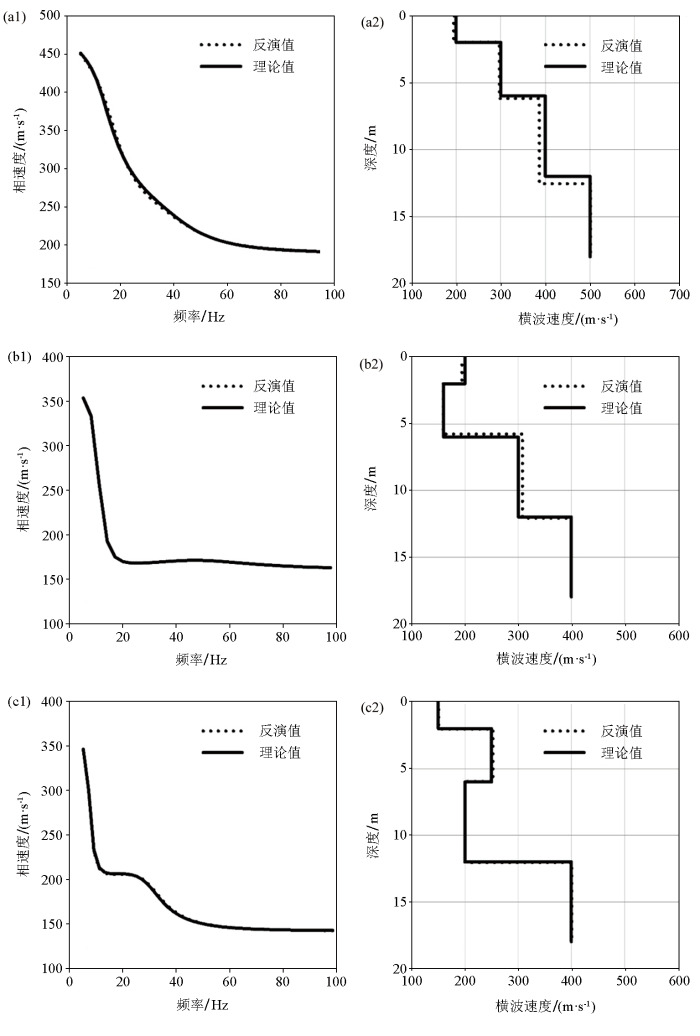
图3   模型B、C和D不含噪声理论数据反演结果

a1,b1,c1—分别为模型B、C和D反演所得频散曲线;a2,b2,c2—分别为模型B、C和D反演的横波速度剖面

Fig.3   Inversion results of noise-free data of model B,C,and D

a1,b1,c1—inverted dispersion curves obtained from model B,C and D respectively;a2,b2,c2—inverted shear-wave velocity profiles obtained from model B,C and D respectively


2.2 含噪声数据反演

在采集地震数据时,噪声是难以避免的。这些噪声会使提取到的频散曲线在小范围内随机扰动,进而影响反演结果。因此,算法用于实际数据处理前需检测其抗噪能力。为测试SCA的抗噪性能,在以上4个理论模型经正演模拟得到的频散曲线中加入15%的随机噪声后进行反演。

SCA用于含噪声模型的反演结果如图4所示,其中a2,b2,c2和d2分别展示了模型A、B、C、D的反演结果。从图a2,b2,c2和d2可以看出,即便加入15%的噪声,反演模型参数和真实模型参数依然相近,并且模型A、B、C、D利用SCA反演所得参数的相对误差仅变为了5.00%,6.54%,8.16%和1.36%(表2)。将其和不加噪声模型反演结果进行对比,可以看出反演所得参数间几乎无偏差(表2),这表明噪声虽然对反演结果具有一定影响,但SCA具有较强的抗噪能力。故SCA适用于包含较强噪声数据的反演。

图4

新窗口打开| 下载原图ZIP| 生成PPT

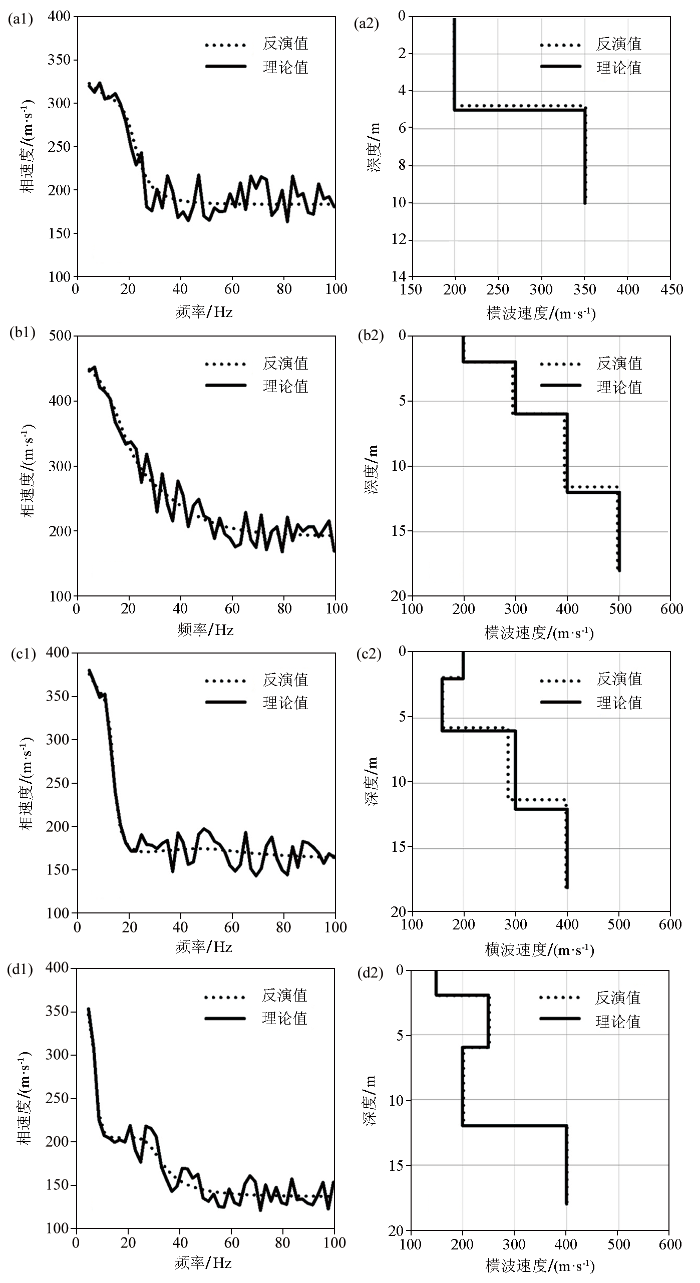
图4   模型A、B、C、D的含噪声理论数据反演结果

a1,b1,c1,d1—分别为模型A、B、C和D反演所得频散曲线;a2,b2,c2,d2—分别为模型A、B、C和D反演的横波速度剖面

Fig.4   Inversion results of noise-contaminated data of model A,B,C,and D

a1,b1,c1,d1—inverted dispersion curves obtained from model A,B,C and D respectively;a2,b2,c2,d2—inverted shear-wave velocity profiles obtained from model A,B,C and D respectively


2.3 多模式频散曲线反演

在一些特殊地层(如软弱夹层),可能会出现高阶波高频部分能量强于基阶波的情况[28],这时若将高阶频散曲线和基阶频散曲线联合起来反演,便可以增加反演的有效信息,进而提升反演所得地层信息的准确度,故检验算法对于多模式频散曲线的反演能力是必要的。此次测试以模型C为例,向模型C的基阶频散曲线数据中加入高阶数据后进行反演试算,反演结果见图5和表3。从图5a1可知,反演得到的频散曲线(点线),无论基阶还是高阶,都与真实模型频散曲线(实线)拟合得很好并且由图5a2可看出,反演所得模型参数(点线)与真实模型参数(实线)相差也较小,说明SCA用于多模式频散曲线反演是可行的。另外,多模式频散曲线反演结果相比单纯基阶频散曲线反演结果的精度总体有所提升,尤其是第三层层厚的相对误差从6.28%降到了1.38%。由此可知,多模式频散曲线反演比只用基阶频散曲线进行反演所得模型参数准确度更高,反演效果更优异。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   模型C多模式数据反演结果

a—反演所得频散曲线;b—反演的横波速度剖面

Fig.5   Inversion results of model C with multi-modal data

a—inverted responses compared with the original ones;b—inverted shear-wave velocity profile


表3   模型C基阶数据和多模式数据反演结果

Table 3  Inversion results of the fundamental-model and multi-model data with model C

参数真实值基阶数据多模数据
反演均值相对误差/%标准差反演均值相对误差/%标准差
vs1/(m·s-1)200197.781.11%9.25200.180.09%9.75
vs2/(m·s-1)160161.150.72%4.52158.980.64%4.60
vs3/(m·s-1)300286.044.65%32.13308.082.93%21.04
vs4/(m·s-1)400397.610.60%13.58393.261.68%15.64
H1/m21.971.57%0.171.990.70%0.23
H2/m43.863.58%0.433.990.28%0.30
H3/m65.626.28%1.096.081.38%0.43

新窗口打开| 下载CSV


3 同粒子群算法的对比

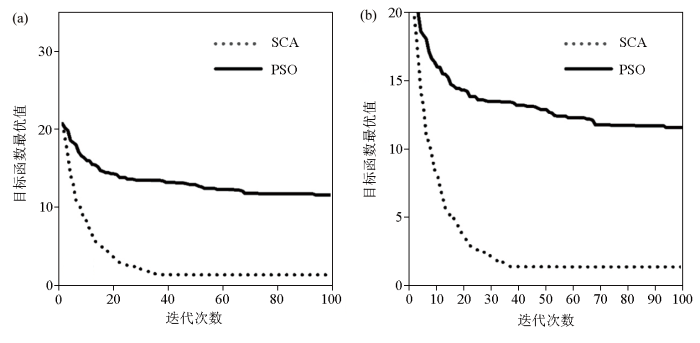
为证实SCA用于频散曲线反演确实能得到较为准确的地层参数,将其和经典的粒子群算法(particle swarm optimization,PSO)一起进行反演测试,对比、分析和评价两者的反演性能。测试在不含噪声的模型D上进行,各单独反演30次。反演时两种算法的种群数目,搜索空间和迭代次数都相同。反演结果如图6所示,具体的反演参数如表4所示。结合图6a2和表4可知,SCA在迭代初期就大致确定了最优解位置,迭代到30次的时候就基本收敛且收敛精度较高为1.35 m/s;PSO的寻优能力较差,在迭代到40次左右才收敛并且在100次左右时还有进一步收敛的趋势,最后收敛的精度也较低为11.57 m/s。除此之外,通过表4中SCA与PSO对于模型各参数反演的标准差可以看到,SCA算法的稳定性远远强于传统的粒子群算法,这得益于SCA独特的更新解的方式。综上可知SCA相较于PSO在瑞雷波频散曲线反演中的表现具有更高的精度,更快的收敛速度以及更强的稳定性。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   SCA与PSO在无噪声模型D中反演收敛过程对比

a—放大前的收敛曲线对比;b—放大后的收敛曲线对比

Fig.6   Comparison of the convergence rate between SCA and PSO on noise-free data from model D

a—comparison of convergence curves before zooming up;b—comparison of convergence curves after zooming up


表4   SCA和PSO反演效果对比

Table 4  Comparison of the inverted results generated by SCA and PSO

参数真实值SCAPSO
反演均值相对误差/%标准差反演均值相对误差/%标准差
vs1/(m·s-1)150150.580.39%1.03148.061.29%9.91
vs2/(m·s-1)250252.300.92%4.25242.063.18%23.34
vs3/(m·s-1)200199.810.09%3.94176.2811.86%37.69
vs4/(m·s-1)400400.900.23%4.80374.896.28%27.63
H1/m22.031.41%0.071.933.5%0.38
H2/m43.931.78%0.143.726.86%0.97
H3/m66.091.45%0.234.0732.14%2.03

新窗口打开| 下载CSV


4 实际资料测试

前面理论模型测试结果表明,SCA用于频散曲线反演是可行且有效的。现用冰岛Arnarbælidi地区数据(数据来源于文献[29])测试SCA反演实际数据的效果。原始地震记录如图7a所示。采集震源为锤击震源,选用的检波器主频为4.5 Hz,共24道,道间距为1 m,偏移距为10 m。图7b为提取的频散能量,从图上可看出高阶波能量弱,基本不发育,反演选用基阶波数据。反演时算法参数同前面理论模型测试时参数设置相同,模型参数按照文献[30]进行设置,所有地层的纵波速度及密度分别设置为1 440 m/s和1 850 kg/m3,其余参数如表5所示。表5中的层厚及S波速度数据来源于文献[29]。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   Arnarbælidi地区地震数据(a)与频散能量图(b)[29]

Fig.7   Field data(a) and its dispersion image(b) in Arnarbælidi [29]


表5   Arnarbælidi地区前人[29]反演模型参数以及搜索范围[30]

Table 5  Reference inversion model [29]parameters and search range[30] in Arnarbælidi region

文献估计层厚文献S波速度S波速度搜索范围厚度搜索范围
/m/(m·s-1)/(m·s-1)/m
0.87860~900.1~1.5
0.58070~1000.1~1.5
0.79280~1100.1~1.5
1.2111100~1500.5~2.0
1.9141120~2000.5~2.0
3.0184150~2502.0~4.0
4.7230200~3003.0~5.5
7.5277250~3506.0~9.0
5.2350300~4004.0~6.0
∞350320~450∞

新窗口打开| 下载CSV


图8a中可看出反演所得频散曲线(黑点)和实测频散曲线(实线)拟合程度非常高;反演模型参数(图8c中黑点)在浅层与文献[29]的参考模型(图8c中实线)参数差别较小,只有第9层横波速度出现较大差别,推测原因是基阶频散曲线低频信息不够充分,故对于深部结果约束性不强所导致。SCA迭代到60次时就基本收敛,其均方根误差仅只有2.90 m/s,这小于文献[29]中所得到的5.18 m/s,故将SCA应用于实际瑞利波频散曲线反演中的效果相较于前人结果具有更为优异的表现。

图8

新窗口打开| 下载原图ZIP| 生成PPT

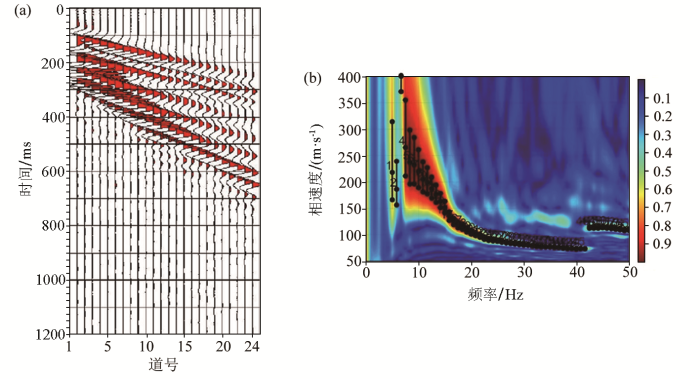
图8   Arnarbælidi地区瑞雷波相速度反演结果

a—反演所得频散曲线;b—最小目标函数值随迭代次数变化情况;c—反演的横波速度剖面

Fig.8   Inversion results in Arnarbælidi region

a—inverted response compared with the original one;b—the minimum value of the objective function changes with the number of iterations;c—inverted shear-wave velocity profile


接着使用美国怀俄明地区数据(数据来源于文献[31])进一步测试SCA反演实际数据的效果。原始地震记录如图9a所示,采集地震数据时,使用了48个检波器,震源为锤击震源,偏移距、道间距都为0.9 m。图9b为提取的频散能量,由于高阶数据出现了模式接吻现象,文中仅选用基阶波数据进行反演。反演时算法参数同前面理论模型测试时参数设置相同,反演的模型参数如表6所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   怀俄明地区地震数据(a)与频散能量(b)[32]

Fig.9   Field data(a) and its dispersion image(b) in Wyoming [32]


表6   怀俄明地区前人[32]反演模型参数及搜索范围

Table 6  Inversion model parameters and search range in Wyoming region[32]

层数vs/(m·s-1)h/m泊松比ρ/(g·cm-3)
1100~3001~50.382.0
2100~4001~50.382.0
3100~6001~50.352.0
4200~6001~50.352.0
5200~800均匀半空间0.302.0

新窗口打开| 下载CSV


反演结果如图10所示,从图10a和10b中可看出,反演得到的频散曲线(图10a中的实线)与实测数据频散曲线(图10a中的点线)拟合得很好、精度较高,反演迭代20多次后就已经收敛,收敛精度为4.40 m/s。在浅部,SCA重建的横波速度模型(图10c中的实线)与测井资料(图10c中带菱形的折线)都吻合得很好,在5 m往深后,重建模型依然能较好地贴近测井数据。可知SCA用于实测数据反演具有较高可信度。

图10

新窗口打开| 下载原图ZIP| 生成PPT

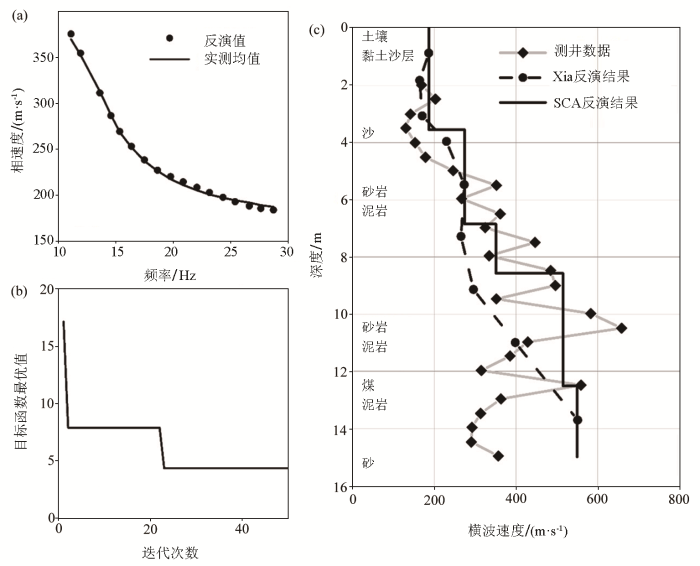
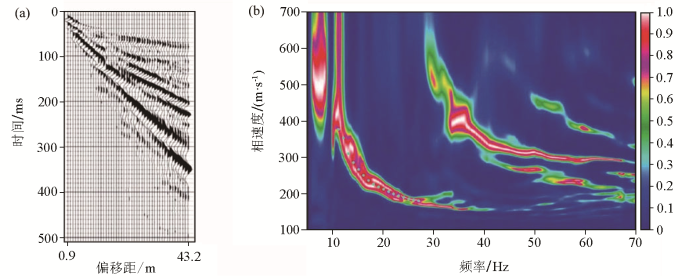
图10   怀俄明地区瑞利波相速度反演结果

a—反演所得频散曲线;b—最小目标函数值随迭代次数变化情况;c—测井数据与反演横波速度剖面对比

Fig.10   Inversion results in Wyoming region

a—inverted response compared with the original one;b—the minimum value of the objective function changes with the number of iterations;c—comparison of the logging data and the inverted shear-wave velocity profile


5 结论

本文将一种新的群智能优化算法——SCA用于瑞利波频散曲线反演的研究当中。在进行具体的反演工作时,通过设置较大的模型参数搜索范围以模拟无先验信息或者仅有少量已知信息的情况,并同时反演厚度、密度、横波速度以及纵波速度以更好适应真实情况(但只选取对频散曲线有显著影响的层厚和横波速度来进行分析与评价)。利用多个理论模型(从简单模型到复杂模型,从无噪声数据到含噪声数据)对SCA性能从理论的角度进行了详尽的测试,最后再采用来自冰岛Arnarbælidi和美国怀俄明地区的实测数据检验了SCA的实用性。测试结果表明:

1)基于正余弦函数组合,应用多个随机参数和自适应变量调整寻优过程的SCA对于频散曲线反演搜索空间具有十分优异的探索和开发能力,在获得高精度地层模型参数的同时还保证了收敛速度以及较强的稳定性,具有良好的发展潜力。

2)SCA相较于传统的粒子群算法在瑞利波频散曲线反演中的表现具有更高的精度、更快的收敛速度以及更强的稳定性。

参考文献

王光文, 王海燕, 李洪强, 等.

面波勘探技术的研究现状及进展

[J]. 地球科学前沿, 2019, 9(9):799-815.

[本文引用: 1]

Wang G W, Wang H Y, Li H Q, et al.

Research status and progress of surface wave exploration technology

[J]. Frontiers of Earth Science, 2019, 9(9):799-815.

[本文引用: 1]

伍敦仕, 孙成禹, 林美言.

基于互相关相移的主动源地震面波频散成像方法

[J]. 地球物理学进展, 2017, 32(4):1693-1700.

[本文引用: 1]

Wu D S, Sun C Y, Lin M Y.

Activeseismic surface wave dispersion imaging method based on cross-correlation and phase-shifting

[J]. Progress in Geophysics, 2017, 32(4):1693-1700.

[本文引用: 1]

Dal Moro G, Pipan M, Gabrielli P.

Rayleigh wave dispersion curve inversion via genetic algorithms and marginal posterior probability density estimation

[J]. Journal of Applied Geophysics, 2007, 61(1):39-55.

DOI:10.1016/j.jappgeo.2006.04.002      URL     [本文引用: 1]

Sun C Y, Wang Y Y, Wu D S, et al.

Nonlinear Rayleigh wave inversion based on the shuffled frog-leaping algorithm

[J]. Applied Geophysics, 2017, 14(4):551-558,622.

DOI:10.1007/s11770-017-0641-x      [本文引用: 1]

Dorman J, Ewing M.

Numerical inversion of seismic surface wave dispersion data and crust-mantle structure in the New York—Pennsylvania area

[J]. Journal of Geophysical Research, 1962, 67(13):5227-5241.

DOI:10.1029/JZ067i013p05227      URL     [本文引用: 1]

Gabriels P, Snieder R, Nolet G.

In situ measurements of shear-wave velocity in sediments with higher-mode Rayleigh waves

[J]. Geophysical Prospecting, 1987, 35(2):187-196.

DOI:10.1111/gpr.1987.35.issue-2      URL     [本文引用: 1]

裴江云, 吴永刚, 刘英杰.

近地表低速带反演

[J]. 长春地质学院学报, 1994, 24(3):317-320,326.

[本文引用: 1]

Pei J Y, Wu Y G, Liu Y J.

Near surface low velocity zone inversion

[J]. Journal of Jilin University:Earth Science Edition, 1994, 24(3):317-320,326.

[本文引用: 1]

Ganji V, Gucunski N, Nazarian S.

Automated inversion procedure for spectral analysis of surface waves

[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(8):757-770.

DOI:10.1061/(ASCE)1090-0241(1998)124:8(757)      URL     [本文引用: 1]

宋先海, 肖柏勋, 黄荣荣, 等.

用等厚薄层权重自适应迭代阻尼最小二乘法反演瑞雷波频散曲线

[J]. 物探与化探, 2003, 27(3):212-216.

[本文引用: 1]

Song X H, Xiao B X, Huang R R, et al.

The inversion of dispersion curves using self-adaptively iterative damping least square method by combining equal thinner layers with weighting matrix

[J]. Geophysical and Geochemical Exploration, 2003, 27(3):212-216.

[本文引用: 1]

Xia J H, Miller R D, Park C B.

Estimation of near-surface shear-wave velocity by inversion of Rayleigh waves

[J]. Geophysics, 1999, 64(3):691-700.

DOI:10.1190/1.1444578      URL     [本文引用: 1]

The shear‐wave (S-wave) velocity of near‐surface materials (soil, rocks, pavement) and its effect on seismic‐wave propagation are of fundamental interest in many groundwater, engineering, and environmental studies. Rayleigh‐wave phase velocity of a layered‐earth model is a function of frequency and four groups of earth properties: P-wave velocity, S-wave velocity, density, and thickness of layers. Analysis of the Jacobian matrix provides a measure of dispersion‐curve sensitivity to earth properties. S-wave velocities are the dominant influence on a dispersion curve in a high‐frequency range (&gt;5 Hz) followed by layer thickness. An iterative solution technique to the weighted equation proved very effective in the high‐frequency range when using the Levenberg‐Marquardt and singular‐value decomposition techniques. Convergence of the weighted solution is guaranteed through selection of the damping factor using the Levenberg‐Marquardt method. Synthetic examples demonstrated calculation efficiency and stability of inverse procedures. We verify our method using borehole S-wave velocity measurements.

艾东海, 程庆群.

低速软弱夹层二维横波速度结构的OCCAM反演

[J]. 工程勘察, 2009, 37(4):87-90.

[本文引用: 1]

Ai D H, Cheng Q Q.

Estimation of 2D s-wave velocity section with low velocity layers by OCCAM algorithm

[J]. Geotechnical Investigation and Surveying, 2009, 37(4):87-90.

[本文引用: 1]

Song X H, Gu H M, Liu J P, et al.

Estimation of shallow subsurface shear-wave velocity by inverting fundamental and higher-mode Rayleigh waves

[J]. Soil Dynamics and Earthquake Engineering, 2007, 27(7):599-607.

DOI:10.1016/j.soildyn.2006.12.003      URL     [本文引用: 1]

Dal Moro G, Pipan M, Gabrielli P.

Rayleigh wave dispersion curve inversion via genetic algorithms and marginal posterior probability density estimation

[J]. Journal of Applied Geophysics, 2007, 61(1):39-55.

DOI:10.1016/j.jappgeo.2006.04.002      URL     [本文引用: 1]

Arai H, Tokimatsu K.

S-wave velocity profiling by joint inversion of microtremor dispersion curve and horizontal-to-vertical (H/V) spectrum

[J]. Bulletin of the Seismological Society of America, 2005, 95(5):1766-1778.

DOI:10.1785/0120040243      URL     [本文引用: 1]

石耀霖, 金文.

面波频散反演地球内部构造的遗传算法

[J]. 地球物理学报, 1995, 38(2):189-198.

[本文引用: 1]

Shi Y L, Jin W.

Genetic algorithms inversion of lithospheric structure from surface wave dispersion

[J]. Chinese Journal of Geophysics, 1995, 38(2):189-198.

[本文引用: 1]

Yamanaka H, Ishida H.

Application of genetic algorithms to an inversion of surface-wave dispersion data

[J]. Bulletin of the Seismological Society of America, 1996, 86(2):436-444.

DOI:10.1785/BSSA0860020436      URL     [本文引用: 1]

A new method for inversion of surface-wave dispersion data is introduced. This method successfully utilizes recently developed genetic algorithms as a global optimization method. Such algorithms usually consist of selection, crossover, and mutation of individuals in a population. To facilitate convergence to an optimal solution, we added elite selection, which ensures that the “best” individual with the smallest misfit value is not excluded from the succeeding generation, and dynamic mutation, which contains a generation-variant mutation probability. Using synthetic and observed earthquake data, we examined the applicability of this genetic surface-wave inversion method in deducing an S-wave profile for sedimentary layers from short- and intermediate-period surface-wave dispersion data. We demonstrated that the method is robust and can be used to interpret surface-wave dispersion data.

张碧星, 肖柏勋, 杨文杰, 等.

瑞利波勘探中“之”形频散曲线的形成机理及反演研究

[J]. 地球物理学报, 2000, 43(4):557-567.

[本文引用: 1]

Zhang B X, Xiao B X, Yang W J, et al.

Mechanism of Zigzag dispersion curves in Rayleigh exploration and its’inversion study

[J]. Chinese Journal of Geophysics, 2000, 43(4):557-567.

[本文引用: 1]

Martínez M D, Lana X, Olarte J, et al.

Inversion of Rayleigh wave phase and group velocities by simulated annealing

[J]. Physics of the Earth and Planetary Interiors, 2000, 122(1-2):3-17.

DOI:10.1016/S0031-9201(00)00183-7      URL     [本文引用: 1]

Beaty K S, Schmitt D R, Sacchi M.

Simulated annealing inversion of multimode Rayleigh wave dispersion curves for geological structure

[J]. Geophysical Journal International, 2002, 151(2):622-631.

DOI:10.1046/j.1365-246X.2002.01809.x      URL     [本文引用: 1]

Calderón-Macías C, Luke B.

Improved parameterization to invert Rayleigh-wave data for shallow profiles containing stiff inclusions

[J]. Geophysics, 2007, 72(1):U1-U10.

[本文引用: 1]

Pei D H, Louie J N, Pullammanappallil S K.

Application of simulated annealing inversion on high-frequency fundamental-mode Rayleigh wave dispersion curves

[J]. Geophysics, 2007, 72(5):R77-R85.

[本文引用: 1]

Lu Y X, Peng S P, Du W F, et al.

Rayleigh wave inversion using heat-bath simulated annealing algorithm

[J]. Journal of Applied Geophysics, 2016, 134:267-280.

DOI:10.1016/j.jappgeo.2016.09.008      URL     [本文引用: 1]

Song X H, Tang L, Lyu X C, et al.

Application of particle swarm optimization to interpret Rayleigh wave dispersion curves

[J]. Journal of Applied Geophysics, 2012, 84:1-13.

DOI:10.1016/j.jappgeo.2012.05.011      URL     [本文引用: 1]

蔡伟, 宋先海, 袁士川, 等.

利用粒子群优化算法快速、稳定反演瑞雷波频散曲线

[J]. 石油地球物理勘探, 2018, 53(1):25-34,4-5.

[本文引用: 1]

Cai W, Song X H, Yuan S C, et al.

Fast and stable Rayleigh-wave dispersion-curve inversion based on particle swarm optimization

[J]. Oil Geophysical Prospecting, 2018, 53(1):25-34,4-5.

[本文引用: 1]

Mirjalili S.

SCA:A sine cosine algorithm for solving optimization problems

[J]. Knowledge-Based Systems, 2016, 96:120-133.

DOI:10.1016/j.knosys.2015.12.022      URL     [本文引用: 1]

杨博, 熊章强, 张大洲, 等.

利用自适应混沌遗传粒子群算法反演瑞雷面波频散曲线

[J]. 石油地球物理勘探, 2019, 54(6):1217-1227,1172.

[本文引用: 1]

Yang B, Xiong Z Q, Zhang D Z, et al.

Rayleigh surface-wave dispersion curve inversion based on adaptive chaos genetic particle swarm optimization algorithm

[J]. Oil Geophysical Prospecting, 2019, 54(6):1217-1227,1172.

[本文引用: 1]

于东凯, 宋先海, 张学强, 等.

蚱蜢算法在瑞雷波频散曲线反演中的应用

[J]. 石油地球物理勘探, 2019, 54(2):288-301,236.

[本文引用: 1]

Yu D K, Song X H, Zhang X Q, et al.

Rayleigh wave dispersion inversion based on grasshopper optimization algorithm

[J]. Oil Geophysical Prospecting, 2019, 54(2):288-301,236.

[本文引用: 1]

高旭, 于静, 李学良, 等.

自适应权重蜻蜓算法及其在瑞雷波频散曲线反演中的应用

[J]. 石油地球物理勘探, 2021, 56(4):745-757,671-672.

[本文引用: 1]

Gao X, Yu J, Li X L, et al.

Rayleigh wave dispersion curve inversion based on adaptive weight dragonfly algorithm

[J]. Oil Geophysical Prospecting, 2021, 56(4):745-757,671-672.

[本文引用: 1]

Ólafsdóttir E Á. Multichannel analysis of surface waves for assessing soil stiffness[D]. University of Iceland, 2016.

[本文引用: 8]

符健. 基于改进非线性算法的瑞利波多模式频散曲线反演研究[D]. 西安: 长安大学, 2019.

[本文引用: 3]

Fu J. Research on multimodal Rayleigh wave dispersion curve inversion based on improved nonlinear algorithms[D]. Xi'an: Chang'an University, 2019.

[本文引用: 3]

Xia J H.

Estimation of near-surface shear-wave velocities and quality factors using multichannel analysis of surface-wave methods

[J]. Journal of Applied Geophysics, 2014, 103:140-151.

DOI:10.1016/j.jappgeo.2014.01.016      URL     [本文引用: 1]

蔡伟, 宋先海, 袁士川, 等.

基于萤火虫和蝙蝠群智能算法的瑞雷波频散曲线反演

[J]. 地球物理学报, 2018, 61(6):2409-2420.

DOI:10.6038/cjg2018L0322      [本文引用: 4]

反演瑞雷波频散曲线能有效获取地层横波速度和厚度.但由于其高度的非线性、多参数、多极值等特点，传统的全局搜索方法易出现收敛速度慢、早熟收敛及搜索精度低的问题.鉴于此，本文提出并测试了基于萤火虫优化算法（FA）和带惯性权重的蝙蝠优化算法（WBA）的新的瑞雷波频散曲线反演策略.在瑞雷波频散曲线反演中，FA全局搜索能力强，但后期搜索精度低，而WBA局部搜索能力强，搜索精度高，但易出现早熟收敛.故本文将二者结合，提出了一种新的优化策略，称其为WFBA，即在反演前期使用FA，后期使用WBA，很好地解决了FA后期搜索精度低及WBA早熟收敛的问题.本文首先反演了三个典型理论模型的无噪声、含噪声的数据，验证了WFBA对瑞雷波数据反演的有效性与稳定性.然后将WFBA与WBA、FA单独反演以及不含惯性权重的FBA和粒子群优化算法（PSO）反演的结果进行了对比，说明了WFBA相对于WBA、FA、FBA和PSO具有更稳定、收敛速度更快、求解精度更高等优点.最后，反演了来自美国怀俄明地区的实测资料，检验了WFBA对瑞雷波数据反演的实用性.理论模型试算和实测资料分析表明，WFBA很适用于瑞雷波频散曲线的定量解释，具有很高的实用性价值.

Cai W, Song X H, Yuan S C, et al.

Inversion of Rayleigh wave dispersion curves based on firefly and bat algorithms

[J]. Chinese Journal of Geophysics, 2018, 61(6):2409-2420.

[本文引用: 4]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com