基于速度移动窗的最小熵法在GPR逆时偏移中的应用

doi:10.11720/wtyht.2023.1556

基于速度移动窗的最小熵法在GPR逆时偏移中的应用

席宇何^,, 王洪华^,, 王欲成, 吴祺铭

桂林理工大学地球科学学院,广西桂林 541004

Application of the minimum entropy method based on a velocity-controlled moving window to the reverse time migration of ground-penetrating radars

XI Yu-He^,, WANG Hong-Hua^,, WANG Yu-Cheng, WU Qi-Ming

College of Earth Sciences,Guilin University of Technology,Guilin 541004,China

通讯作者: 王洪华(1986-),男,博士,副教授,主要从事探地雷达理论方法及应用研究工作。Email:wanghonghua5@163.com

责任编辑: 叶佩

收稿日期: 2022-11-24 修回日期: 2023-08-8

基金资助:

国家自然科学基金项目(42364010)
广西自然科学基金项目(2020GXNSFAA035595)

Received: 2022-11-24 Revised: 2023-08-8

作者简介 About authors

席宇何(1998-),男,硕士研究生,主要从事探地雷达逆时偏移成像方面的研究工作。Email:1076571663@qq.com

摘要

速度是决定探地雷达(GPR)偏移成像分辨率的关键参数,基于图像最小熵与偏移相结合的方法通常将整体偏移剖面作为固定窗计算熵值曲线来估计介质速度,不但难以适用于介质非均匀分布情况,而且试速度过大或过小均会使双曲线绕射波的收敛位置溢出固定窗,降低估计精度。为此,本文利用试速度精确控制偏移剖面中的计算窗,提出了一种基于速度移动窗的最小熵法,并与逆时偏移相结合,估计最佳偏移速度。该方法通过试速度自动调整计算窗位置,可使双曲线绕射波收敛位置始终位于计算窗中心,从而获得稳定、准确的熵值曲线。将一条典型双曲线绕射波的固定窗和速度移动窗最小熵法的计算结果作对比,验证了速度移动窗的最小熵法的正确性和有效性。数值试验和实测数据测试表明:与固定窗最小熵法相比,速度移动窗的最小熵法可将双曲线绕射波收敛位置精确固定于计算窗中心,熵值曲线更稳定,计算量更小,偏移速度估计精度更高,逆时偏移成像效果更好。

关键词： 探地雷达; 速度移动窗; 最小熵法; 逆时偏移

Abstract

Velocity is a key parameter determining the migration imaging resolution of ground penetrating radars (GPR).The method combining minimum image entropy and migration usually estimates the medium velocity by calculating the entropy curves using the overall migration profile as a fixed window.Therefore,such a method is not applicable to non-uniformly distributed media.Moreover,for this method,a too-high or too-low test velocity will make the convergence position of hyperbolic diffracted waves go beyond the fixed window,thus reducing the estimation accuracy.This study proposed a minimum entropy method based on a velocity-controlled moving window,in which the calculation window in the migration profile is accurately controlled by the test velocity.Then,this method was combined with inverse time migration to estimate the optimal migration velocity.By automatically adjusting the position of the calculation window using the trial velocity,this method keeps the convergence position of hyperbolic diffracted waves at the center of the calculation window.In this manner,stable and accurate entropy curves can be obtained.By comparing the calculation results with those of the minimum entropy method based on a fixed window,this study verified the correctness and effectiveness of the minimum entropy method based on a velocity-controlled moving window for a typical hyperbolic diffracted wave.As revealed by numerical experiments and the tests of measured data,compared with the minimum entropy method based on a fixed window,the minimum entropy method based on a velocity-controlled moving window can keep the convergence position of hyperbolic diffracted waves accurately at the center of the calculation window,yielding more stable entropy curves,lower computational complexity,higher estimation accuracy of the migration velocity,and better imaging performance of reverse time migration.

Keywords： ground-penetrating radar (GPR); velocity-controlled moving window; minimum entropy method; reverse time migration

PDF (6342KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

席宇何, 王洪华, 王欲成, 吴祺铭. 基于速度移动窗的最小熵法在GPR逆时偏移中的应用[J]. 物探与化探, 2023, 47(5): 1250-1260 doi:10.11720/wtyht.2023.1556

XI Yu-He, WANG Hong-Hua, WANG Yu-Cheng, WU Qi-Ming. Application of the minimum entropy method based on a velocity-controlled moving window to the reverse time migration of ground-penetrating radars[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1250-1260 doi:10.11720/wtyht.2023.1556

0 引言

偏移速度是决定探地雷达(ground penetrating radar,GPR)逆时偏移分辨率的关键参数。不准确的偏移速度会造成反射波归位不准确、绕射波收敛不完全,降低成像分辨率^[1]。目前,利用GPR数据获取介质电磁波速度方法主要有:刚性边界反射法、共中心点法、层析成像、全波形反演等。其中,刚性边界反射法需对探测区域取岩心,较为费时费力^[2⇓-4];共中心点法通过多次移动收发天线采集多偏移距数据,天线移动误差甚至观测误差会不断积累,降低速度估计精度,且难以应用于剖面法采集的GPR数据中^[5⇓-7]。基于反演理论的全波形反演采用最优化方法进行多次迭代使观测数据与模拟数据的差异最小,从而获得精确的介质速度^[8⇓-10];走时层析成像方法是根据走时和速度的倒数之间的积分关系,利用走时残差来反演介质内部的速度结构^[11];理论上,这两种方法可获取较精确的速度,但都存在计算效率低、噪声影响大、易陷入局部极值、涉及多参数反演等问题,应用于实际工程问题较为困难^[12⇓-14]。

浅层介质中大都存在管线、管道、空洞等异常体,这些异常体在剖面法采集的GPR剖面中大都呈双曲线绕射波,其形态与介质电磁速度密切相关。AL-Nuaimy等^[15]假定双曲线绕射为点反射,构建了相应的数学模型,并根据双曲线方程拟合观测的双曲线绕射波,从而估计介质的电磁波速度;Shihab等^[16]采用最小二乘法法拟合一种含有目标体半径模型的改进双曲线方程,提高介质电磁波速度估计精度;崔凡等^[4]为估计较为准确的偏移速度,使用互相关分析自动提取双曲线坐标点来拟合双曲线方程,并通过模拟和实测数据验证了互相关分析提取坐标点后拟合的偏移速度更贴近真实波速。然而,上述双曲线拟合估计地下介质速度方法受双曲线模型本身缺陷和GPR信号选取误差影响较大,导致介质速度估计精度较低。与此同时,一些国内外学者将图像最小熵法与偏移方法相结合,以量化偏移过程中双曲线绕射波的收敛程度,从而精确估计介质速度,以提高偏移分辨率。De Vries等^[17]在地震波成像领域首次提出可使用最小熵法量化共偏移距数据中双曲线绕射波的收敛程度,从而得到最佳偏移速度的估计;Xu等^[18]和修志杰等^[19]为提高浅层地下目标的定位精度,在频率—波数偏移中采用最小熵法评价GPR剖面中的双曲线绕射波的收敛程度,并用实测数据验证了将最小熵法与频率—波数偏移法相结合可使目标体的成像位置更聚焦。Zhou等^[20]将最小熵法与Stolt偏移法相结合,作用于GPR剖面,实现了背景介质的相对介电常数的精确估计。吴学礼等^[21]为凸显GPR剖面较弱的目标体信号及位置,采用Stolt偏移法进行处理,并通过最小熵法选取偏移速度,提高了偏移剖面分辨率。

上述基于最小熵估计最佳偏移速度方法大都以均匀介质或圆状目标体位于相同速度介质模型为基础,将滤除直达波后的GPR整体偏移剖面作为计算窗(固定窗)计算熵值曲线,以估计最佳偏移速度。然而,当基于固定窗的最小熵法应用于包含多个圆状目标体的非均匀介质结构的GPR探测剖面时,不但难以有效估计不同目标体附近的介质速度,且选取的试速度较大或较小时,收敛位置极易溢出固定窗。若将固定窗扩大,试速度较小易使其他位置的双曲线绕射波的收敛位置也出现在计算窗中,影响熵值曲线的稳定性,甚至无法确定最小熵值。

为此,本文提出一种基于速度移动窗的最小熵法,并将其与GPR逆时偏移方法相结合用来估计最佳偏移速度。该方法利用试速度控制计算窗位置,使双曲线绕射波的收敛位置始终位于计算窗中心,从而获得稳定、准确的熵值曲线,并用模拟和实测数据测试了基于速度移动窗的最小熵法在提高熵值曲线稳定性、计算精度方面的可行性和有效性。

1 方法原理

目前,GPR偏移方法有很多,各有优势,其中逆时偏移以其理论简单、成像分辨率高、可适应复杂模型的优点,在成像领域得到广泛关注^[22⇓-24],相关理论和实现过程可参考文献[25 ⇓⇓-28]。本文采用逆时偏移方法对GPR数据进行处理,并与最小熵法相结合,以估计介质的最佳偏移速度。

1.1 常规固定窗的最小熵法

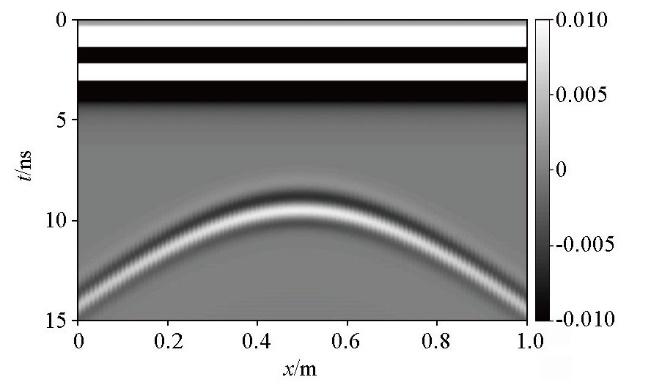
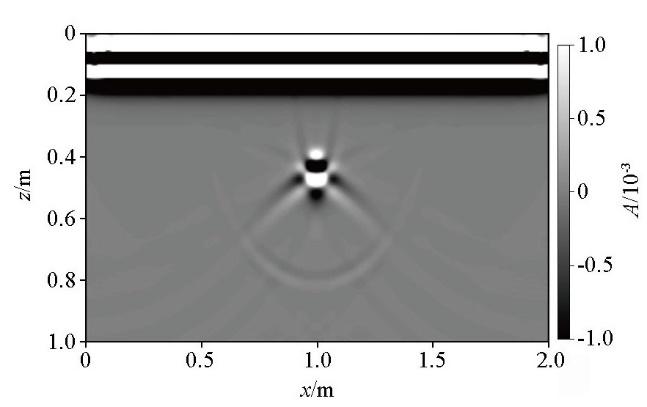
图1为包含一条双曲线绕射波的GPR二维剖面,从数学上看,该剖面可表示为^[19]:

(1)$\boldsymbol{D}=\left[\begin{array}{cccccc}d_{1,1} & d_{1,2} & \cdots & d_{1, j} & \cdots & d_{1, m} \\d_{2,1} & d_{2,2} & \cdots & d_{2, j} & \cdots & d_{2, m} \\\vdots & \vdots & \ddots & \vdots & & \vdots \\d_{i, 1} & d_{i, 2} & \cdots & d_{i, j} & \cdots & d_{i, m} \\\vdots & \vdots & & \vdots & \ddots & \vdots \\d_{n, 1} & d_{n, 2} & \cdots & d_{n, j} & \cdots & d_{n, m}\end{array}\right],$

式中: $d_{i, j}$ 表示第j道信号中的第i个采样点的GPR信号;n为采样点总数;m为道数。根据图像最小熵理论,图像矩阵D的熵可计算为^[29⇓-31]:

(2)

E = {(\overset{n}{\sum_{i = 1}} \overset{m}{\sum_{j = 1}} d_{i j}^{2})}^{2} / \overset{n}{\sum_{i = 1}} \overset{m}{\sum_{j = 1}} d_{i j}^{4}

。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 含有一条双曲线的GPR二维剖面

Fig.1 GPR 2D section with a hyperbola

由式(2)可知,若单道信号只存在一个单位幅度的脉冲时,熵值为最大值1,单位幅度的脉冲越多,熵值越大。由此可见,熵值的大小决定图像聚焦程度,图像越聚焦,熵值越低;图像越杂乱,熵值越高^[19]。因此,熵值可用于定量评价GPR偏移剖面中双曲线绕射波的收敛聚焦程度,收敛最好即熵值最小处对应的速度为最佳偏移速度。

固定计算窗的最小熵法与逆时偏移结合估计最佳偏移速度的步骤如下:

1)确定试速度最大值 $v_{m a x}$ 、最小值 $v_{m i n}$ 和步长 $Δ v$ ;

2)先从最大试速度 $v_{m a x}$ 开始,对GPR数据进行逆时偏移处理;

3)根据该偏移剖面双曲线绕射波收敛位置确定去除直达波的局部剖面作为当前以及后续的固定计算窗,并利用式(2)计算相应熵值;

4)随后利用 $v_{m a x} - Δ v$ , $v_{m a x} - 2 Δ v$ , $\dots$ ,直到速度到 $v_{m i n}$ 为止对相应试速度的剖面进行逆时偏移处理,并使用与步骤(3)相同位置的固定窗计算熵值;

5)假设共有p个试速度,计算出的相应熵值记为 $E_{1} 、 E_{2} 、 \dots 、 E_{p}$ ,获得熵值随速度变化曲线;

6)根据熵值曲线,确定熵值最小点,最小点对应的试速度即为最佳偏移速度。

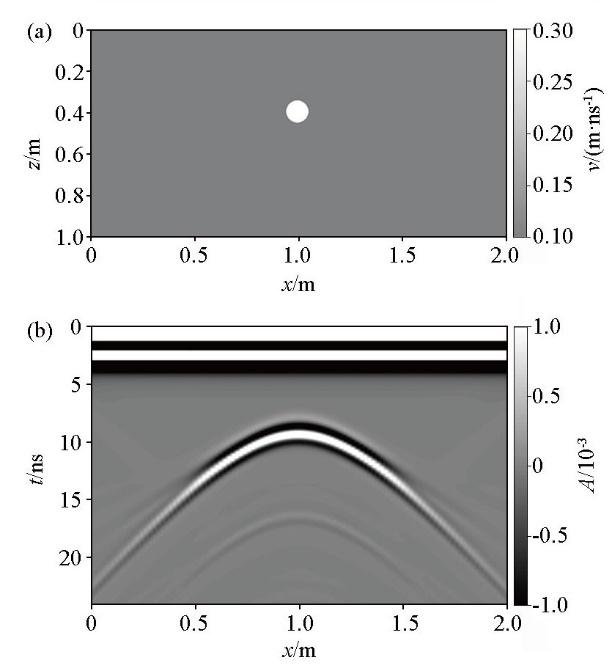
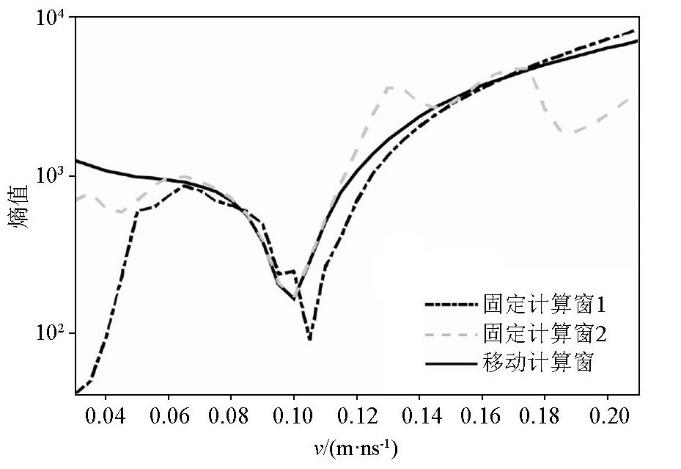
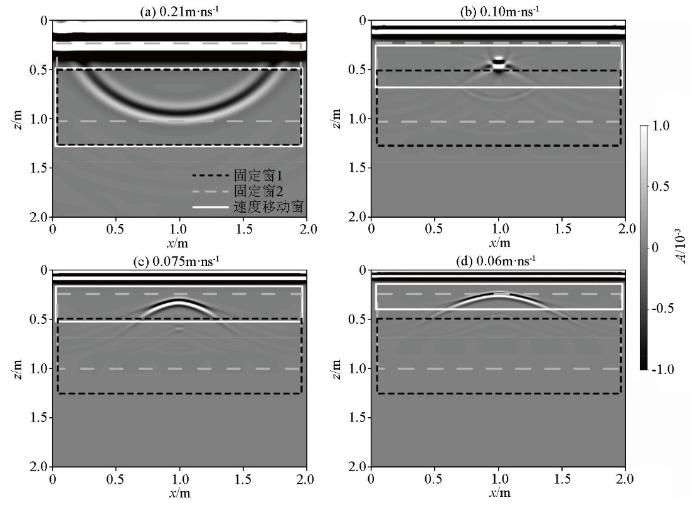
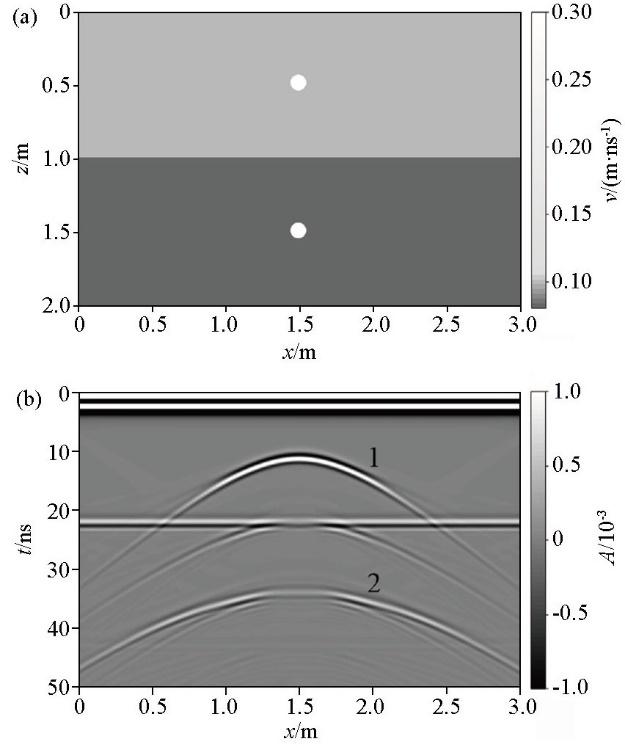
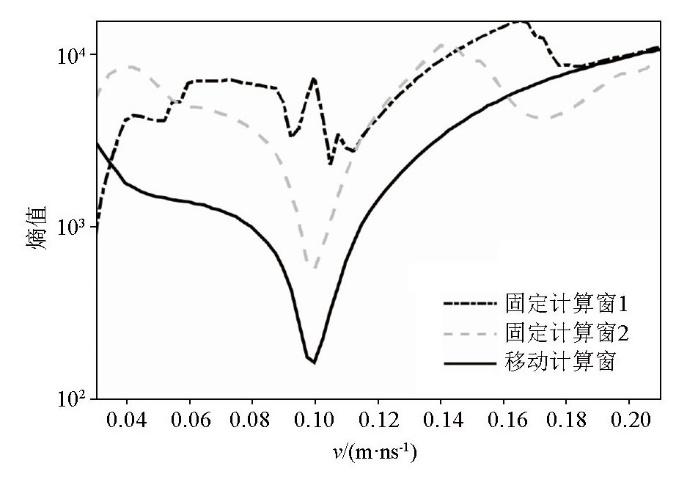
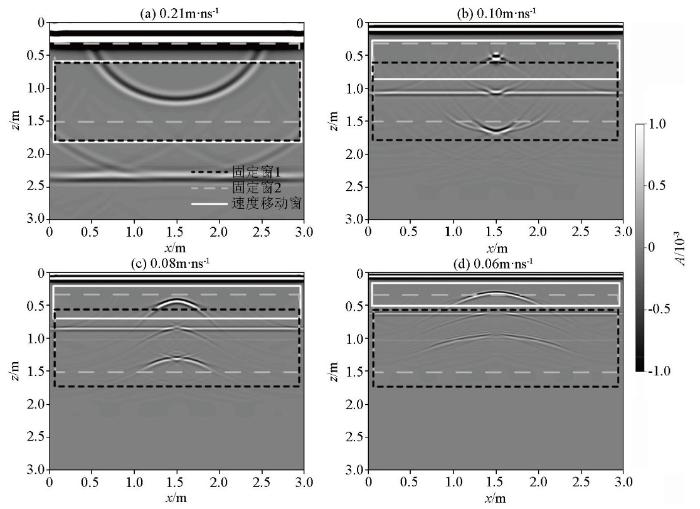
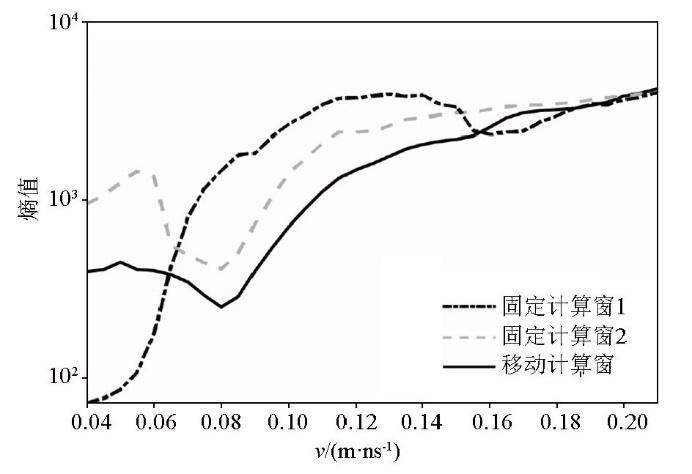
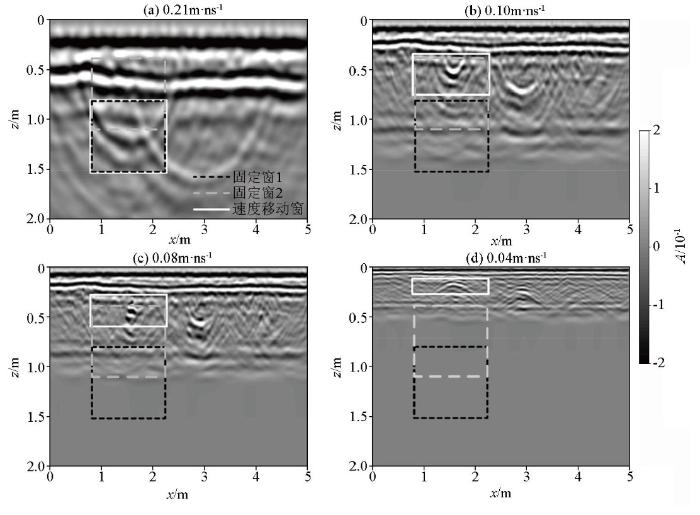
图2a、b所示的圆形空洞模型为GPR剖面法模拟剖面,圆形空洞产生的双曲线绕射波清晰可见。利用基于固定窗的最小熵法和逆时偏移法对其进行计算:试速度最大值 $v_{m a x}$ = 0.21 m/ns,最小值 $v_{m i n}$ = 0.03 m/ns,试速度步长 $Δ v$ = 0.005 m/ns,共计算37次,获得的熵值曲线如图3所示,其中黑虚线和灰虚线分别表示利用固定窗1和固定窗2的计算结果, 平均计算时间为365 s,所用内存为32.17 Mb。固定窗1和固定窗2分别如图4所示的逆时偏移剖面中的黑虚线和灰虚线框所示。由图可见,利用固定窗1计算熵值曲线时,当试速度为0.105 m/ns时,熵值最小,与真实速度0.1 m/ns相比,误差为5%,这是因为试速度较小时固定窗未包含绕射波的收敛位置,如图4b、c、d黑虚线框所示。固定窗2是在固定窗1基础上进行上移的计算窗,分析其熵值曲线可知,虽然熵值最小处的速度为真实的介质速度,但由于计算窗的上移,试速度较大时将直达波能量包含在固定窗中,如图4a灰虚线框所示;导致熵值曲线在速度大于0.12 m/ns时上下波动,熵值曲线不稳定。因此,由于双曲线绕射波收敛位置随试速度变化在偏移剖面中上下移动,且收敛程度变化较大, 因而固定窗位置的选取会严重影响熵值计算的准确性和稳定性。其次,如果GPR剖面存在多条双曲线绕射波时,固定窗的熵值曲线可能更加不稳定。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 均匀介质的速度模型(a)及其正演剖面(b)

Fig.2 Velocity model of homogeneous medium(a) and its forward simulation profile(b)

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 采用不同窗口计算的熵值曲线

Fig.3 Entropy curve calculated with different windows

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 计算过程中不同试速度的逆时偏移剖面

Fig.4 Reverse time migration profile of the uniform cavity model with different test velocities

1.2 速度移动窗的最小熵法

针对固定窗最小熵法的上述问题,本文提出了一种基于速度移动窗的最小熵法,将其与逆时偏移相结合,以获得最佳偏移速度。基于速度移动窗的最小熵法的计算步骤如下:

1)确定试速度最大值 $v_{m a x}$ 、最小值 $v_{m i n}$ 和步长 $Δ v$ ,并通过实测或正演GPR剖面确定绕射波顶点到时 $t_{0}$ 。

2)选取时间改变量 $Δ t$ ,一般为正演GPR剖面总时窗记录长度的0.1~0.2倍,利用式(3)加(减)绕射波顶点到时作为计算窗的上下边界时刻 $T_{m i n}$ 和 $T_{m a x}$ :

(3)$\begin{array}{l}\mathrm{T}_{\text {min }}=t_{0}-\Delta t, \\\mathrm{~T}_{\text {max }}=t_{0}+\Delta t。\end{array}$

3)利用相应试速度 $v_{i}$ 对GPR数据进行逆时偏移处理。

4)利用试速度 $v_{i}$ 和偏移模型垂直方向的网格步长 $d y$ ,确定计算窗的上下边界位置 $Y_{m i n}$ 和 $Y_{m a x}$ ,其计算公式可表示为:

(4)$\begin{array}{l}Y_{\text {min }}=\left[\left(T_{\min } \times v_{i}\right) / 2\right] / d y, \\Y_{\text {max }}=\left[\left(T_{\max } \times v_{i}\right) / 2\right] / d y。\end{array}$

由此可见,速度移动窗上下边界位置会随试速度变化而自动地上下移动。其左右边界位置可根据绕射波收敛位置的水平范围或整个剖面的水平长度确定。

5)利用式(2)计算试速度 $v_{i}$ 的逆时偏移剖面中计算窗的熵值。

6)从最大试速度 $v_{m a x}$ 开始,利用 $v_{m a x}$ 、 $v_{m a x} - Δ v$ 、 $v_{m a x} - 2 Δ v$ 、 $\dots$ 、 $v_{i}$ 、 $\dots$ 、 $v_{m i n}$ ,重复步骤3)、4)、5),计算每个试速度对应的熵值,假设共有p个试速度,计算出的相应熵值记为 $E_{1} 、 E_{2} 、 \dots 、 E_{p}$ ,获得熵值随试速度变化曲线。

7)根据熵值曲线,确定熵值最小点;最小点对应的试速度即为最佳偏移速度。

为说明速度移动窗的最小熵法的有效性,对图2模型采用相同试速度计算局部熵值曲线。根据正演剖面可知,双曲线绕射波顶点到时 $t_{0} = 9 n s$ ;选取总时窗的0.125倍即 $Δ t = 3 n s$ ,确定计算窗的上下边界时刻 $T_{m i n} = 6 n s$ 和 $T_{m a x} = 12 n s$ ;最后在逆时偏移的同时由相应偏移速度可得到计算窗的具体位置,如图4白实线框所示。对比如虚线所示的固定窗位置可知:速度移动窗随绕射波收敛位置变化而变化,使收敛位置始终位于计算窗中心;且计算窗大小随试速度减小而减小,使计算窗只包含目标绕射波收敛点,不受其他干扰波和非目标绕射波收敛位置的影响。采用速度移动窗计算的熵值曲线如图3黑实线所示,计算时间为358 s,所用内存为32.08 Mb。熵值最小点时的速度为0.1 m/ns,符合真实介质速度,熵值曲线更平滑,无强烈突变点,更加稳定,且计算时间相比固定窗更少,计算所耗内存更低。

因此采用速度移动窗的最小熵法计算出的最佳偏移速度0.1 m/ns进行逆时偏移成像,得到如图5所示的逆时偏移剖面。由图可知,此速度计算出的偏移剖面中的绕射波收敛完全,成像效果较好。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 采用最佳偏移速度0.1 m/ns计算出的逆时偏移剖面

Fig.5 The reverse time migration profile calculated with the best migration velocity of 0.1 m/ns

2 数值算例

图6a是大小为3.0 m×2.0 m的层状空洞模型,模型被埋深为1.0 m的水平界面分成上、下两层,上层介质的电磁波速度为0.1 m/ns,下层介质的电磁波速度为0.08 m/ns;其上下两层分别埋有一个半径0.05 m的圆形空洞,圆心位置分别为(1.5 m,0.5 m)、(1.5 m,1.5 m)。图6b为该模型正演计算获得的GPR模拟剖面,剖面总时窗为50 ns。由图可见,两条空洞产生的绕射波1、绕射波2以及水平反射波清晰可见易识别。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 层状介质的速度模型(a)及其正演剖面(b)

Fig.6 Velocity model of layered media(a) and its forward simulation profile(b)

首先采用常规固定窗的最小熵法计算图6b中双曲线绕射波1偏移后的熵值曲线,获取第一层介质的电磁波速度。试速度最小值为0.03 m/ns,最大值为0.21 m/ns,试速度步长取0.0025 m/ns,共计算73次,获得的熵值曲线如图7所示,计算所用时间为3 365 s,使用内存为69.11 Mb。黑虚线和灰虚线分别表示固定窗1和固定窗2的熵值曲线,其固定窗1和固定窗2的位置分别是如图8所示的逆时偏移剖面中的黑虚线和灰虚线框。由熵值曲线可知,利用固定窗1计算熵值曲线时熵值曲线最小值对应的速度为0.105 m/ns,与真实速度0.1 m/ns,误差约为5 %;且在最小熵值附近,出现局部多个局部极大和极小值,严重降低了熵值曲线的稳定性。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 采用不同窗口计算绕射波1的熵值曲线

Fig.7 Calculate entropy of diffraction 1 in different windows

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 计算绕射波1过程中不同试速度的逆时偏移剖面

Fig.8 Reverse time migration profiles of different test velocities in the calculation of diffraction 1

这是由于图8b、c、d中黑虚线框所示的固定窗1没有完全包含该绕射波收敛位置,同时将下层绕射波2的收敛位置包含在计算窗内。利用固定窗2计算熵值曲线时,虽可估计出真实速度,但由于窗口上移,当试速度较大时直达波也计算在了固定窗中,如图8a所示,导致熵值曲线在速度为0.17 m/ns附近时波动严重,降低了熵值曲线的稳定性和熵值计算精度。

利用基于速度移动窗的最小熵法计算双曲线绕射波1的熵值曲线如图7黑实线所示,计算时间为3 359 s,使用内存为68.46 Mb。根据速度移动窗构建原理,其确定流程如下:首先,根据绕射波顶点到时,确定计算窗中心时刻为12 ns;然后将正演剖面总时窗的0.1倍即5 ns,上下拓展计算窗,获得计算窗上下边界的时刻7 ns和17 ns;最后通过偏移速度可自动确定移动窗在各个试速度剖面的位置,如图8白实线框所示。对比固定窗位置,速度移动窗随双曲线绕射波收敛位置而上、下移动,且收敛位置完全位于计算窗中心,未包含水平反射波和下层的收敛位置。其次,随电磁波速度减小,计算窗口更加精准、更小,可有效减少计算量。由该速度移动窗计算的熵值曲线可知,熵值最小点时的速度为0.1 m/ns,符合真实介质速度,且此速度对应的逆时偏移剖面中绕射波1完全收敛,如图8b所示。对比固定窗计算的熵值曲线可知,速度移动窗计算的熵值曲线更平滑、更稳定,不存局部极大值或极小值;且由于绕射点收敛位置更精确,使得所有速度的熵值更小,计算精度更高。

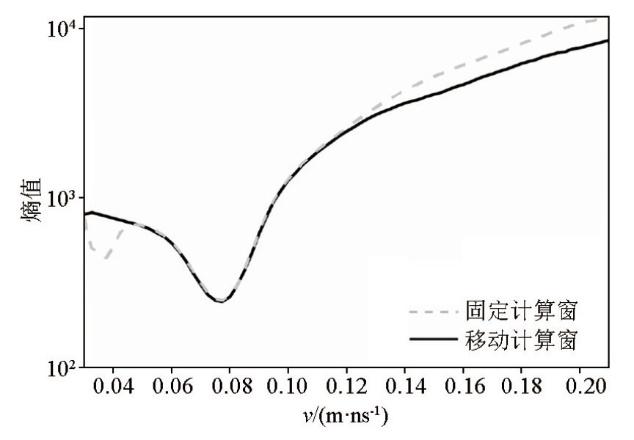
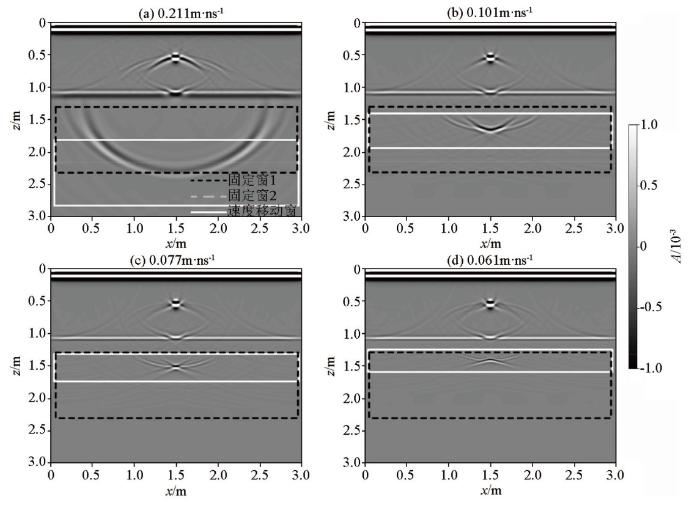
分别利用固定窗和速度移动窗计算双曲线绕射波2的熵值曲线,试速度最小值为0.031 m/ns,最大值为0.211 m/ns,试速度步长取0.002 m/ns,共计算91次,计算结果如图9所示。固定窗和移动窗的位置分别为图10的黑虚线框和白实线框。由熵值曲线可知,两种窗口计算出了相同速度的最小熵点,得到的速度为0.077 m/ns,与真实速度0.08 m/ns相比误差仅3.75%,在此试速度时两种计算窗都圈定了收敛完全的绕射波位置,如图10c所示。但固定窗计算的熵值曲线在速度大于0.1 m/ns时相比移动窗有所增大,这是由于绕射波收敛位置在固定窗中不断变化,未精确将收敛位置确定在窗口中心, 如10a、b黑虚线框所示,导致计算的熵值较大。其次,当试速度小于0.06 m/ns时,固定窗的熵值曲线在出现较为强烈的波动,且有局部极小值。这是因为如图10d黑虚线框所示的固定窗范围过大,绕射波收敛位置仅在计算窗顶部,包含的其他干扰波较多,降低了熵值曲线的稳定性;而移动窗的熵值曲线整体平滑,无强烈波动,更有利于最小熵值点的判断。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 采用不同窗口计算绕射波2的熵值曲线

Fig.9 Calculate entropy of diffraction 2 in different windows

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 计算绕射波2过程中不同试速度的逆时偏移剖面

Fig.10 Reverse time migration profiles of different test velocities in the calculation of diffraction 2

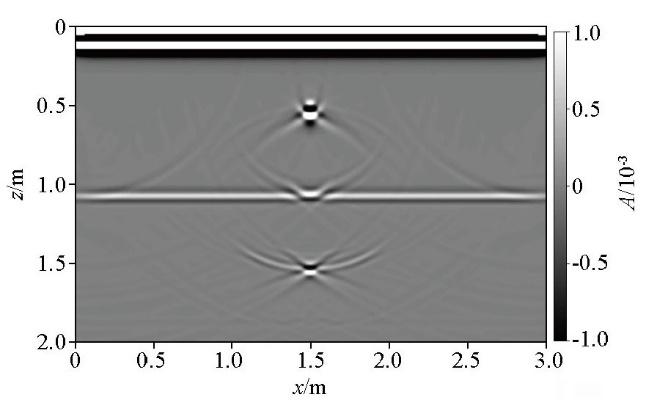
采用速度移动窗的最小熵法计算出的最佳偏移速度进行逆时偏移成像,绕射波1的偏移速度为0.1 m/ns,绕射波2为0.077 m/ns,得到如图11所示的逆时偏移剖面。由图可知,逆时偏移剖面中上层和下层的绕射波都收敛完全,说明了速度移动窗在计算层状模型的绕射波最佳偏移速度时,可得到较为准确的偏移速度,成像效果较好。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 采用最佳偏移速度计算出的逆时偏移剖面

Fig.11 The reverse time migration profile calculated with the best migration velocity

3 实测数据测试

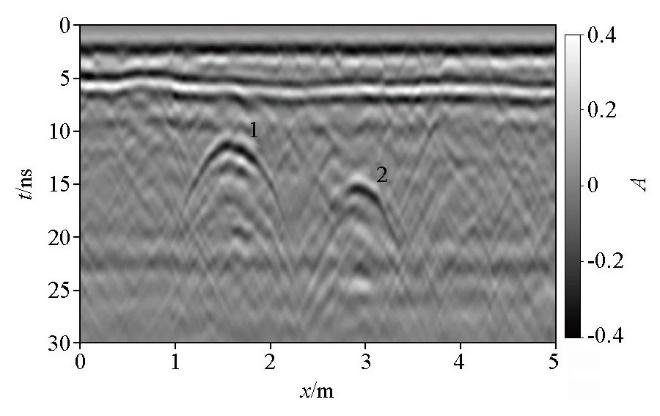
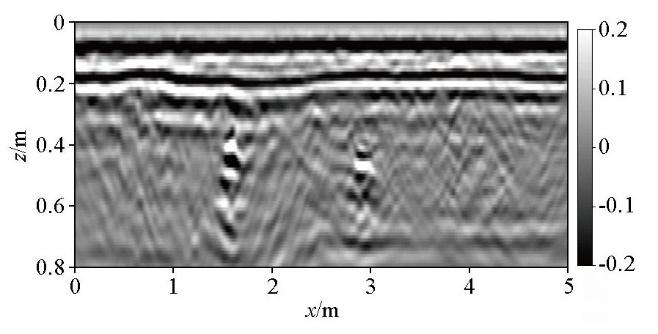
为测试速度移动窗的最小熵法与逆时偏移结合方法的实用性,在某道路进行GPR探测,获得的GPR剖面如图12所示。采集参数如下:收发天线的中心频率为400 MHz,采样点数为500,时间长度为30 ns。由图可见,5 ns时刻出现一条强烈的水平反射波;水平位置1.0~2.0 m处和2.5~3.5 m处分别出现两条能量较强的双曲线绕射波。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 实测GPR二维剖面

Fig.12 Measured GPR 2D profile

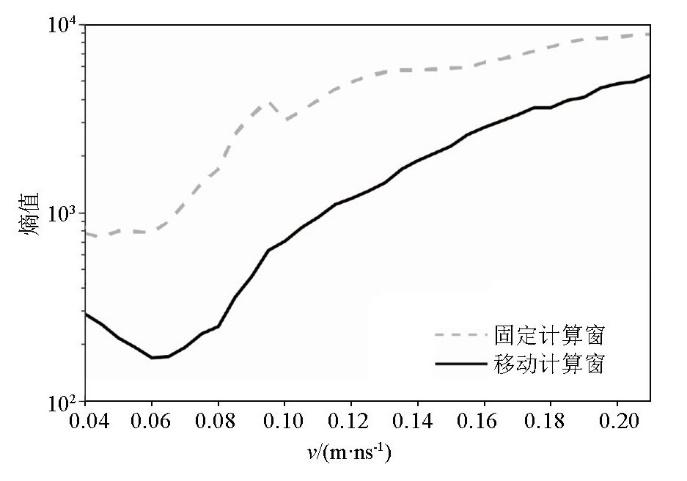
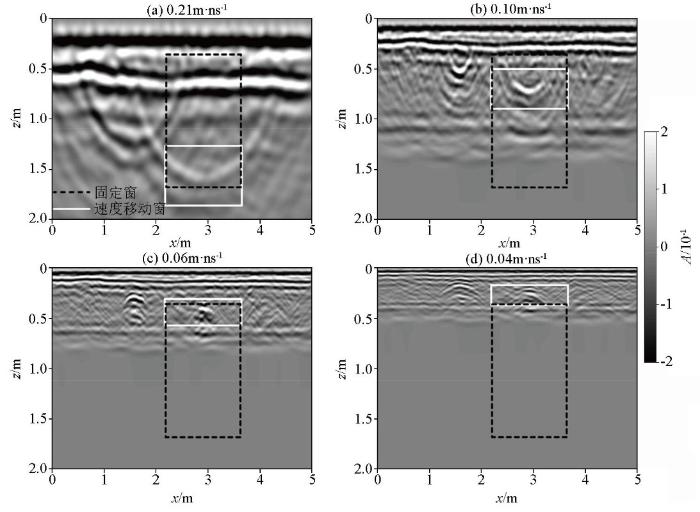
利用最小熵法与逆时偏移结合方法对两条双曲线绕射波进行速度估计(图13)。试速度最小值为0.04 m/ns,最大值为0.21 m/ns,试速度步长为0.005 m/ns,共计算35次。先计算左侧绕射波1的熵值曲线。为避开水平反射波,先采用图14a中黑虚线框的固定窗1计算熵值,得到的熵值曲线如图13黑虚线所示。由曲线可知,使用该计算窗未找到合适的最小熵值点。这是由于试速度较小时的固定窗没有包含双曲线绕射波的收敛位置,如图14b、c、d的黑虚线框所示,因而难以获得最小熵值点。随后将计算区域向上移动,采用图14中灰虚线框所示的固定窗2计算熵值曲线,以尽可能地将所有试速度偏移后的绕射波收敛位置都包含在计算窗内,得到的熵值曲线如图13灰虚线所示,最小熵值点对应的速度为0.08 m/ns,但速度在0.04~0.08 m/ns的熵值波动严重,曲线稳定性差;因为固定窗2在此速度的偏移剖面中同样没有包含绕射波收敛位置,如图14d灰虚线所示。因此,应用固定窗计算熵值曲线时,若要在所有试速度剖面将目标绕射波收敛位置完全包含在计算窗内较为困难,需要进行多次调整,利用影响最小熵值法来估计介质速度的实用性。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 不同窗口计算绕射波1的熵值曲线

Fig.13 Calculate entropy of diffraction 1 in different windows

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 计算绕射波1过程中不同试速度的逆时偏移剖面

Fig.14 Reverse time migration profiles of different test velocities in the calculation of diffraction 1

利用速度移动窗的最小熵法与逆时偏移相结合方法对上述绕射波1进行计算,获得的熵值曲线如图13黑实线所示。通过实测剖面确定了左侧绕射波的顶点时刻为11 ns;再将剖面总时窗的0.1倍即3 ns来拓展窗口的上下边界时刻;结合相应试速度得到计算窗位置随试速度变化而上下移动,如图14白实线框所示。由熵值曲线可知,在速度为0.08 m/ns时得到了最小熵值。对比虚线固定窗的熵值曲线,整体曲线相比较为平滑,没有强烈的突变点,熵值更小。因其可随速度变化而上下移动,绕射波收敛位置始终位于计算窗中心;且在此速度逆时偏移剖面中的绕射波1完全收敛,如图14c所示,而其他试速度逆时偏移剖面中,绕射波收敛不完全。由此可见,速度移动窗可有效计算介质的最佳偏移速度;其计算区域更小,计算得到的熵值更小、精度更高。

利用固定窗和速度移动窗的最小熵值法对双曲线绕射波2进行计算,获得的熵值曲线如图15中灰虚线和黑实线所示。固定窗和速度移动窗分别如图16中黑虚线和白实线框所示。由图可知,从固定窗的熵值曲线中无法确定最小熵值点,这是由于试速度较小时,绕射波收敛位置只位于固定窗的顶部,而固定窗大部分区域含有较多无效能量,如图16c、d的黑虚线框所示,从而导致熵值随试速度变小而变小。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 不同窗口计算绕射波2的熵值曲线

Fig.15 Calculate entropy of diffraction 2 in different windows

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 计算绕射波2过程中不同试速度的逆时偏移剖面

Fig.16 Reverse time migration profiles of different test velocities in the calculation of diffraction 2

从速度移动窗熵值曲线可精确确定最小熵值对应的速度为0.06 m/ns,曲线相对平滑,且此速度的逆时偏移剖面的绕射波2对比其他速度收敛更完全,如图16c所示。因为速度移动窗可根据试速度变化而上下移动,将任何绕射波收敛位置固定在计算窗中心,如图16白实线框所示。其次,计算两条绕射波最小熵时采用固定窗的计算时间平均为96.6 s,占用内存为22.83 Mb;采用速度移动窗的计算时间平均为96.2 s,占用内存为22.75 Mb。测试结果充分验证了速度移动窗在保证计算效率和占用内存相当,甚至更优的情况下,所计算的熵值曲线更稳定、速度计算精度更高,且对GPR剖面含有多条绕射波时具有更好的适应能力;利用估计的最佳偏移速度进行逆时偏移成像的效果更好。

为此,使用左侧绕射波1和右侧绕射波2的最佳偏移速度0.08 m/ns和0.06m/ns进行逆时偏移成像,得到的剖面如图17所示,由图可知,两条绕射波经偏移成像后基本得到了收敛,说明了速度移动窗针对实测剖面中含有多条较为明显的绕射波时,其可计算出每条绕射波的最佳偏移速度。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 采用最佳偏移速度计算出的逆时偏移剖面

Fig.17 The reverse time migration profile calculated with the best migration velocity

4 结论

1)本文利用试速度自动调整计算窗位置和大小,使得绕射波收敛位置始终位于窗口中心,提出了一种基于速度移动窗的最小熵与逆时偏移相结合估计最佳偏移速度的方法。

2)数值试验表明,相比于基于固定窗最小熵法,速度移动窗的最小熵法在保证计算效率和占用内存相当,甚至更优的情况下,可获取更稳定、更平滑的熵值曲线,且更易确定最佳偏移速度;最佳偏移速度估计精度更高,误差小于4%;采用估计的最佳偏移速度的逆时偏移成像效果更好。为GPR共偏移距数据构建偏移速度找到了一种计算效率高、结果准确的方法。

3)实际雷达剖面中双曲线绕射波较多,如何利用本文提出的方法分别估计所有双曲线绕射波的最佳偏移速度,并通过合理插值方式构建较为精确的二维偏移速度模型,以提高复杂地质结构的逆时偏移成像分辨率,还有待进一步研究。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

甄志中, 王晋国, 石显新.

2D有限差分偏移技术在探地雷达信号成像中的应用

[J]. 煤田地质与勘探, 2007, 35(6):57-60.