E-mail Alert Rss
 

物探与化探, 2023, 47(5): 1226-1235 doi: 10.11720/wtyht.2023.0086

方法研究·信息处理·仪器研制

不同骨料混凝土模型中瑞利波传播特性研究

项诸宝,1,2, 张大洲,1,3, 朱德兵1,3, 李明智4, 熊章强3

1.高速铁路建造技术国家工程研究中心,湖南 长沙 410075

2.中国中铁股份有限公司,北京 100039

3.中南大学 地球科学与信息物理学院,湖南 长沙 410083

4.广西交通设计集团有限公司,广西 南宁 530029

Exploring the Rayleigh wave propagation characteristics in different aggregate concrete models

XIANG Zhu-Bao,1,2, ZHANG Da-Zhou,1,3, ZHU De-Bing1,3, LI Ming-Zhi4, XIONG Zhang-Qiang3

1. National Engineering Research Center of High-speed Railway Construction Technology, Changsha 410075, China

2. China Railway Group Limited, Beijing 100039, China

3. Central South University, School of Geosciences and Info-physics, Changsha 410083, China

4. Guangxi Communications Design Group Co., Ltd. Nanning 530029, China

通讯作者: 张大洲(1979-),男,博士,副教授,主要从事面波正反演及背景噪声成像方面的研究工作。Email:dazhou2010@csu.edu.cn

责任编辑: 叶佩

收稿日期: 2023-03-6   修回日期: 2023-04-25  

基金资助: 中国中铁股份有限公司科技研究开发计划项目(2020-专项-02)
湖南省自然科学基金项目(S2023JJMSXM2207)

Received: 2023-03-6   Revised: 2023-04-25  

作者简介 About authors

项诸宝(1993-),男,硕士,工程师,主要从事工程物探技术及装备相关的研究工作。Email:zhubaoxiang2022@163.com

摘要

为避免用瑞利波检测混凝土时骨料对探测目标体的干扰,保证混凝土质量检测的可靠性,需要区分骨料异常信号和目标体异常信号,为此,对含骨料混凝土中的瑞利波传播特性展开了研究。通过建立细观结构的骨料随机模型,采用高阶交错网格有限差分法,研究骨料的随机性、形状、粒径和含量对瑞利波波场及频散曲线的影响,得到不同骨料参数下的瑞利波散射情况、能量衰减、畸变特性以及频散曲线特征。通过不同骨料混凝土模型正演数据,定量地了解到骨料引起的瑞利波波场与频散曲线的异常大小与影响范围。研究结果表明:骨料的随机性与含量会对直达瑞利波的衰减产生影响,骨料形状的差异对瑞利波波场的影响很小,骨料粒径的变化对波场影响较大,当粒径超过1/2主频波长时瑞利波会产生较强的散射,波形会产生畸变;对频散曲线而言,骨料的随机性、形状、粒径和含量的变化均不会引起频散曲线异常,因此,使用瑞利波法进行混凝土检测时,采用频散曲线对数据进行分析,可避免骨料对目标体的干扰。

关键词： 高频瑞利波; 混凝土; 质量检测; 骨料性质; 频散曲线

Abstract

To avoid aggregate interference on the detection target in concrete quality detection by Rayleigh waves, the abnormal signals from the aggregate and the target should be distinguished for high detection reliability. Hence, this study explored the propagation characteristics of Rayleigh waves in aggregate concrete. By building the mesostructural random aggregate models and employing the high-order staggered-grid finite difference scheme, this study examined the effects of the randomness, shape, size, and content of aggregate on the Rayleigh wave field and dispersion curves, thus obtaining the Rayleigh wave scattering, energy attenuation, distortion, and dispersion curve characteristics under different aggregate parameters. Based on the forward modeling data of different aggregate concrete models, this study quantitatively analyzed the sizes and influence ranges of aggregate-induced anomalies of the Rayleigh wave field and dispersion curves. The results are as follows. The randomness and content of aggregate could affect the energy attenuation of direct Rayleigh waves. The Rayleigh wave field was slightly influenced by the aggregate shape but significantly impacted by the aggregate size. When the aggregate size exceeded half of the dominant wavelength, Rayleigh waves would produce strong scattering, distorting its waveforms. In contrast, these aggregate parameters caused no anomalies in the dispersion curves. Therefore, data analysis using dispersion curves can avoid aggregate interference on the target in concrete quality detection by Rayleigh waves.

Keywords： high-frequency Rayleigh wave; concrete; quality detection; aggregate property; dispersion curve

PDF (1444KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

项诸宝, 张大洲, 朱德兵, 李明智, 熊章强. 不同骨料混凝土模型中瑞利波传播特性研究[J]. 物探与化探, 2023, 47(5): 1226-1235 doi:10.11720/wtyht.2023.0086

XIANG Zhu-Bao, ZHANG Da-Zhou, ZHU De-Bing, LI Ming-Zhi, XIONG Zhang-Qiang. Exploring the Rayleigh wave propagation characteristics in different aggregate concrete models[J]. Geophysical and Geochemical Exploration, 2023, 47(5): 1226-1235 doi:10.11720/wtyht.2023.0086

0 引言

我国高速铁路、桥梁、房屋等工民建筑皆以混凝土结构为主,混凝土质量的好坏直接影响工民建筑及人民群众生命财产的安全。针对混凝土质量检测的方法目前主要有弹性波法(如冲击共振波法、冲击回波法、面波法)[1⇓⇓-4]、探地雷达法[1,5]、超声波法[6⇓-8]和红外成像法[1,9],其中瑞利波法[11⇓-13]是近些年来发展速度较快的一种无损检测方法。利用瑞利波进行混凝土无损检测一般基于两个方面:一是瑞利波传播速度与材料的干密度、抗压强度等具有良好的相关性;二是瑞利波具有频散特性,即不同频率的瑞利波穿透深度不同,这一特性使得激发一次瑞利波可获得混凝土内不同深度的信息[13]。瑞利波的这两个特性使其在混凝土无损检测方面具有独特的优势。

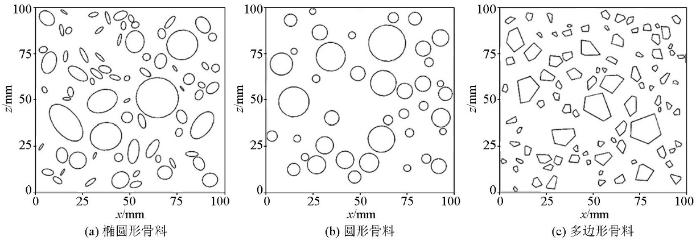
在常规的瑞利波法勘探中,由于非均匀体的尺寸远小于瑞利波波长,介质的非均匀性对瑞利波传播的影响非常小,因此可近似地将岩土体视为均匀介质。但在混凝土质量检测中,瑞利波的频率一般都比较高,最高可达n×104 Hz,这种情况下,骨料将会使瑞利波产生较为明显的反射、散射以及衰减等效应,引起波场异常。此外,与常见的非均匀体不同,由于骨料在混凝土中的位置、几何尺寸和倾角等参数在微观上不可控制,具有很强的随机性,同时,骨料的形状、粒径大小以及骨料的含量均会对瑞利波传播产生不同程度的影响,因此,了解骨料对瑞利波传播的影响是进行瑞利波混凝土检测的基础。

有关利用瑞利波法对混凝土质量进行检测,目前已有学者做了相关研究工作。袁士川等[14]通过有限差分模拟表明瑞利波振幅发生衰减时高频成分比低频成分衰减更加剧烈,衰减程度随着偏移距增大而增强,瑞利波相速度发生的频散现象随频率增大而增强;Wu等[15] 使用交错网格有限差分法研究了混凝土中钢筋对瑞利波散射和瑞利波速度的影响,并设计了不同排列的钢筋混凝土模型,但在研究过程中将混凝土介质按照均匀介质来处理,研究较为简单;Zerwer等[16]使用数值模型与物理模型探讨了瑞利波探测裂隙尺寸的可行性,得出在频率—波速域无法得到裂隙深度的结论;Aggelis等[17]用瑞利波波场估算混凝土中裂隙参数以及修复效果,该研究虽通过对实际混凝土构件中瑞利波传播进行了分析,但却未对混凝土结构作详细描述,也忽略了骨料对瑞利波传播的影响;Kim等[18]利用非线性瑞利波产生的二次谐波进行微小的裂隙探测,通过对比加入减缩剂和不加减缩剂时的非线性系数,得出了利用非线性系数可以探测到混凝土内部的微小变化;练小聪[19]在对混凝土介质中瑞利波传播特性的研究中引入随机骨料模型,分析了骨料的形状以及钢筋对瑞利波的影响,但未对骨料的随机性等是否会对瑞利波频散曲线产生影响做相关的分析。

本文基于混凝土骨料的随机特性,建立混凝土骨料随机模型,从骨料的随机性、粒径、形状及含量等4个方面进行研究,得到不同骨料参数下的瑞利波散射情况、能量衰减、畸变特性以及频散曲线特征。通过研究,定量地了解到骨料引起的瑞利波波场与频散曲线的异常大小和影响范围,便于在数据处理时区分骨料异常与目标体异常,可为采用瑞利波法对混凝土介质进行质量检测时的异常分析和解释提供参考。

1 数值模拟与混凝土模型建立

1.1 地震波场数值模拟

混凝土介质中瑞利波数值模拟采用高阶交错网格有限差分法,均匀各向同性介质中交错网格的一阶速度—应力弹性波动方程式为[20]

$\left\{\begin{array}{c}v_{x}^{\prime}=\rho_{x}^{-1}\left(D_{x} \sigma_{x x}+D_{z} \sigma_{x z}\right), \\v_{z}^{\prime}=\rho_{z}^{-1}\left(D_{z} \sigma_{z z}+D_{x} \sigma_{x z}\right), \\\sigma_{x x}^{\prime}=(\lambda+2 \mu) D_{x} v_{x}+\lambda D_{z} v_{z}, \\\sigma_{z z}^{\prime}=(\lambda+2 \mu) D_{z} v_{z}+\lambda D_{x} v_{x}, \\\sigma_{x z}^{\prime}=\mu_{x z}\left(D_{x} v_{z}+D_{z} v_{x}\right)。\end{array}\right.$

式中:Dx、Dz分别表示x、z方向上的差分;λ与μ为拉梅常数;ρx、ρz分别为x、z方向上的密度;vx、vz为x、y个方向上的速度;σxx、σzz为x、y方向上的正应力;σxz为剪应力;“'”表示该变量对时间t的一阶导数。

混凝土属于高度非均匀介质,在处理这种非均匀介质时,密度和剪切模量需要采用附近网格点的平均值[21-22],自由界面与吸收边界条件采用文献[23]的处理方法。

1.2 数值混凝土模型的建立

数值混凝土模型是通过数值方法建立混凝土模型,使其在物质组成、材料参数、骨料形态与位置分布上符合真实的混凝土在统计学上的意义[24]。混凝土是由水泥浆、砾石、沙等组成的一种复杂多相复合凝聚体,本文采用随机骨料模型,将其简化为由骨料与水泥砂浆组成的二相体。

准确建立数值混凝土模型的关键是骨料级配问题,骨料级配即各粒径骨料数量的相对多少。在工程实践中,骨料级配如果接近或符合一个良好的连续级配曲线,则所配制成的混凝土将具有较好的强度和良好的力学性能,常用的理想级配曲线是富勒提出的最大密实度曲线。瓦拉文根据三维富勒级配推导出二维截面内任意粒径的骨料出现的概率[25],其表达式为:

$\begin{array}{l}P_{c}\left(D<D_{0}\right)=P_{k}\left[1.065\left(\frac{D_{0}}{D_{\max }}\right)^{0.5}-0.053\left(\frac{D_{0}}{D_{\max }}\right)^{4}-\right. \\\left.0.012\left(\frac{D_{0}}{D_{\max }}\right)^{6}-0.0045\left(\frac{D_{0}}{D_{\max }}\right)^{8}+0.0025\left(\frac{D_{0}}{D_{\max }}\right)^{10}\right],\end{array}$

式中:D0表示筛孔的直径;Dmax表示骨料的最大直径;Pk为骨料体积占混凝土总体积的百分比; Pc(D<D0)是二维截面上某骨料直径D的累计概率。

假设混凝土骨料中粒径最大为Dmax,最小为Dmin,并将其分为3个级配,则每个级配的粒径范围为{[Dmin,D1],[D1,D2)],[D2,Dmax]},每个粒径范围内的骨料个数计算公式为

$N_{i}=\left[P_{c}\left(D<D_{i}\right)-P_{c}\left(D<D_{i-1}\right)\right] \frac{S}{S_{i}},$

式中:Ni为第i个级配的骨料个数;S为模型总面积;Si为第i个粒径范围内的骨料平均面积。

混凝土模型详细建立的过程见文献[26]。图1为3种不同骨料形状生成的混凝土骨料模型。骨料和水泥砂浆物理参数设置见表1[27]。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   三种形状的骨料混凝土数值模型

Fig.1   Aggregate numerical model of three shapes


表1   混凝土模型中的物质材料参数

Table 1  Material parameters of concrete

项目vp/(m·s-1)vs/(m·s-1)ρ/(kg·m-3)
水泥砂浆395022502050
骨料440025002610

新窗口打开| 下载CSV


2 骨料对瑞利波传播的影响分析

针对骨料的特性,本文从骨料的随机性、形状、粒径与含量4个方面来研究骨料对瑞利波波场与频散曲线的影响。

2.1 骨料随机性的影响

混凝土生成中,可以宏观控制骨料的整体几何尺寸与含量,但每个骨料的具体尺寸大小、在混凝土中的位置与倾角等参数是不可控的,不同的混凝土模型其内部每个骨料的具体情况都不相同。研究中对相同的模型参数骨料级配参数采用圆形骨料进行多次建模,由于骨料的具体尺寸大小及在混凝土中的位置是随机生成的,因此多次建立的模型在每个网格点处的弹性波参数是不同的。通过对多次建模后的模型进行正演模拟,对比模拟结果,可分析其具体尺寸大小及位置的随机特性对于面波传播的影响。

设计二维模型横向长400 mm,垂向长 200 mm,骨料为三级级配,各粒级参数为{[3,10],[11,17],[18,24]} mm,不同粒级骨料比例按计算公式(3)设置;使用椭圆形骨料,骨料占混凝土体积比Pk=0.4。正演模拟参数设置如下:震源位置(100,0) mm;网格间距1 mm;时间采样步长1×10-7 s;主频20 000 Hz;采样点数3 000个;检波器位于地表垂向z=0处,道间距为10 mm。

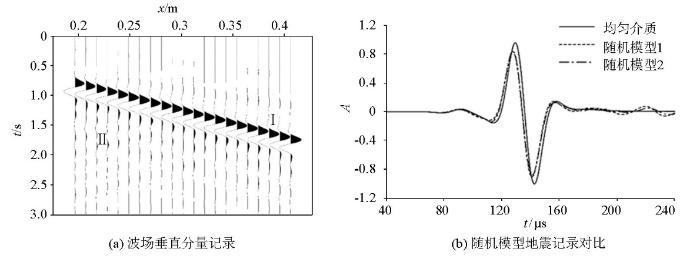
利用高阶交错网格有限差分法对所建混凝土模型进行正演模拟,得到的椭圆形骨料位置分布随机模型的弹性波场垂直分量记录如图2a所示。在波场记录中可明显看到直达瑞利波Ⅰ(下文简称为直达波)和由骨料引起的散射瑞利波Ⅱ(下文简称为散射波,散射波中包含散射瑞利波与散射体波,但由于体波能量远小于瑞利波,文中所讨论的散射波特指散射瑞利波)。取坐标(300,0) mm处2个随机模型和均匀介质的单道记录进行对比(图2b),可以看出:①骨料会引起瑞利波散射,在波尾部可明显观察到散射波振动;②骨料同时会引起面波能量的衰减,加入骨料后模型的直达波振幅小于均匀介质中直达波的振幅;③骨料使直达波的波峰到达时间变早,提高了直达波波速。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   随机模型的地震记录

Fig.2   Seismic records of random model


表2为取坐标(300,0) mm处的地震数据,从散射波最大振幅、总振幅以及直达波的衰减量和形变量4个方面进行分析。散射波最大振幅为能量最强的散射波振幅与直达波振幅的比值;散射波总振幅为较明显的散射波(本文取散射波振幅/直达波振幅>3%)振幅值之和;直达波衰减量为均匀介质和混凝土介质直达波振幅之差与均匀介质直达波振幅的比值,引起波场的衰减因素主要为介质内摩擦产生的热能耗散以及非均匀介质引起的散射、反射等现象造成的能量衰减,本文使用完全弹性介质模型,仅研究由骨料界面产生散射、反射以及转换波等引起的衰减;直达波形变量用于衡量骨料引起的直达波波形的畸变效应的大小,对均匀介质模型获得的直达波与骨料模型获得的直达波的最大振幅与位置进行归一化,使用公式为

$e=\frac{\sum\left|A_{1 t}-A_{t}\right|}{\sum\left|A_{t}\right|} ,$

表2   骨料随机性对波场的影响

Table 2  Influence for wave field of aggregate randomness

随机
模型		散射瑞利波直达瑞利波
最大振幅/%总振幅/%衰减量/%形变量/%
模型18.013.29.94.4
模型25.510.912.23.5
模型38.414.410.72.4
模型48.614.95.66.4
误差/%3.14.06.64.0

新窗口打开| 下载CSV


式中:A1t为质点在骨料模型中t时刻的直达波幅值;At为质点在均匀介质中t时刻的直达波幅值。

表2显示:①对散射波最大能量而言,模型1、3、4的散射波振幅均为直达波振幅的8%左右,但模型2的散射波振幅为直达波振幅的5.5%,由随机性引起的散射波能量差异为3.1%;②散射波总能量方面,模型4的总能量最强,为14.9%,模型2的最小,为10.9%,两者相差4.0%;③4个随机模型直达波衰减量均值为9.6%,最大值与最小值相差6.6%,差异较大;④对于直达波的波形变量,模型4引起的波形误差最大,为6.4%,模型3获得的直达波波形与标准波形最接近,为2.4%,两者相差4.0%。通过以上分析可知:骨料的随机性对散射波影响较小,而对直达波的衰减影响较大。在数值模拟中,为避免骨料的随机性引起的误差,可采用同参数生成多个随机模型并对正演结果取均值的做法;在实际工作中,对同一目标进行多个排列的测量也可减小骨料随机性引起的误差。

为了研究骨料的频散特性,使用相移法[28]对4个随机模型与均匀介质模型正演得到的数据提取频散曲线(图3),4个随机模型的频散曲线形态一致。通过计算可得4个模型的瑞利波波速均值分别为2 069.6、2 061.9、2 060.9、2 060.7 m/s,最大与最小均速之差为8.9 m/s,以4条曲线的总体均速度2 063.3 m/s为标准值,均速度最大误差为0.43%。对单个频率进行分析,4条曲线的最大差异位于15.3 kHz处的模型1与模型2之间,两者相差29.0 m/s,误差为1.41%。由此可见,骨料的随机性对频散曲线的影响非常小。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   不同随机模型的频散曲线

Fig.3   Dispersion comparison chart of random model


2.2 骨料形状的影响

在实际混凝土介质中,碎石骨料与卵石骨料较为常见。数值建模时,碎石骨料在二维截面可近似为凸多边形,卵石骨料可近似为椭圆形,而圆形骨料在实际中存在非常少,但其在数值模型中具有生成简单、计算效率高、占用内存少等优点。为了研究混凝土骨料形状对瑞利波传播的影响,特设计圆、椭圆、凸多边形3种模型进行对比分析,模型大小400 mm×200 mm,骨料占混凝土体积比Pk=0.4,各粒级参数为{[3,10],[11,17],[18,24]}mm,正演模拟参数设置与2.1节相同。

图4为坐标(300,0) mm处接收的3种形状骨料模型获得的波形对比。由图4可见:3种骨料模型得到的波形差异较小,直达波基本重合,波形尾部均存在散射波,散射波能量无明显差异。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   不同骨料形状的波形对比

Fig.4   Waveform comparison chart of different shape aggregate


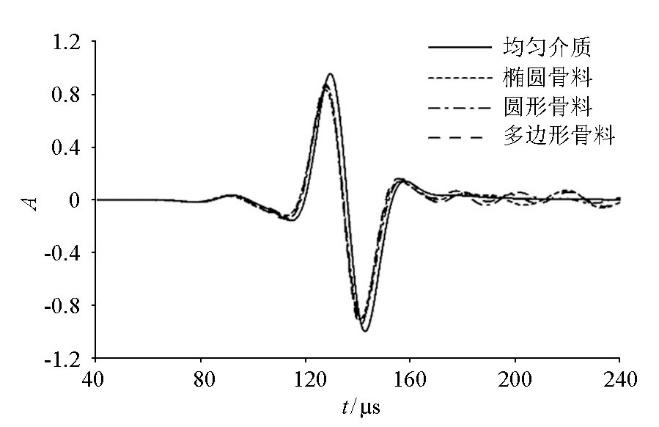
表3为坐标(300,0) mm处的3种形状骨料引起的波场差异分析。为减小由骨料随机性引起的误差,每种形状骨料均生成3个随机模型,表中的数据为3个随机模型数值的均值。可以看出:骨料形状引起的瑞利波场差异非常小,其中,散射波最大振幅差异为1.3%,总振幅差异为1.4%;直达波能量衰减差异为1.4%,形变量差异为2.2%。

表3   骨料形状对波场的影响

Table 3  Influence for wave field of aggregate shape

骨料
形状		散射瑞利波直达瑞利波
最大振幅/%总振幅/%衰减量/%形变量/%
椭圆形7.312.810.64.3
圆形8.314.29.26.0
多边形7.013.89.83.8
误差/%1.31.41.42.2

新窗口打开| 下载CSV


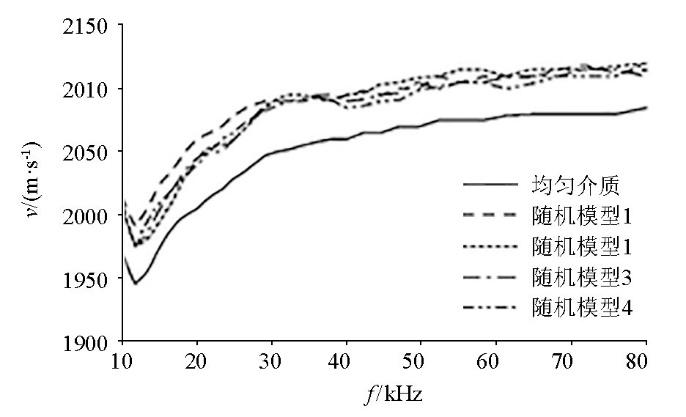
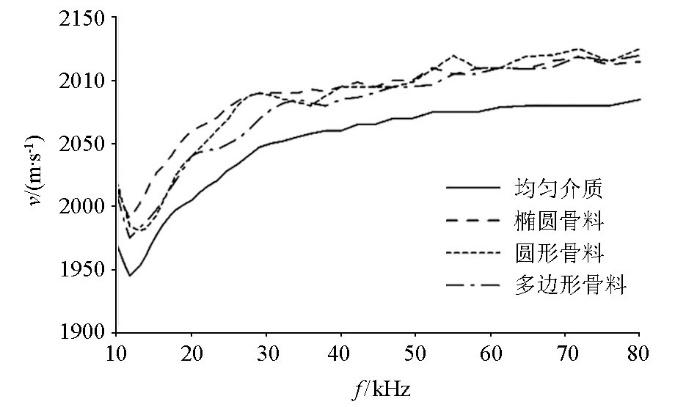
使用相移法对3种形状骨料模型与均匀介质模型正演得到的数据提取频散曲线(图5),3种骨料模型的频散曲线形态一致。经计算可得平均速度:椭圆形骨料为2 069.6 m/s;圆形骨料为2 062.4 m/s;多边形骨料为2 055.9 m/s;平均速度最大差异为13.7 m/s,以总体平均速度作为标准值,误差为0.66%。对单个频率分析,4条曲线的最大差异位于15.3 kHz处的椭圆形骨料与圆形骨料之间,两者相差33.1 m/s,误差为1.60%。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   不同骨料形状的频散曲线

Fig.5   Dispersion comparison chart of different shape aggregate


以上研究表明,针对不同的骨料形状,瑞利波在混凝土介质中的传播其能量和形变特征几乎是相同的,频散曲线受到的影响也非常小,说明骨料形状对瑞利波在混凝土中的传播基本没有影响。下文混凝土模型均采用椭圆形骨料。

2.3 骨料粒径的影响

骨料的粒径大小是影响波传播的一个重要方面,不同的粒径引起的散射效应不同。当障碍物粒径较小时,波会绕过障碍物继续前进,产生绕射,反射波能量较小;当障碍物粒径较大时,波会在障碍物表面产生反射,在其边缘有少量绕射发生。为了了解骨料粒径对波场的影响,设计4个级配模型,骨料占混凝土体积比Pk=0.4,模型骨料级配为:{[2,5],[6,9],[10,12]}mm,{[3,10],[11,17],[18,24]}mm,{[6,20],[21,35],[36,50]}mm,{[9,30],[31,50],[51,75]}mm。正演模拟参数与2.1节中的参数相同。根据上文可得瑞利波波速约为2 060.0 m/s,则主频为20 kHz的瑞利波对应波长为100 mm,4个级配模型最大粒径分别为主频波长的1/8、1/4、1/2、3/4倍。

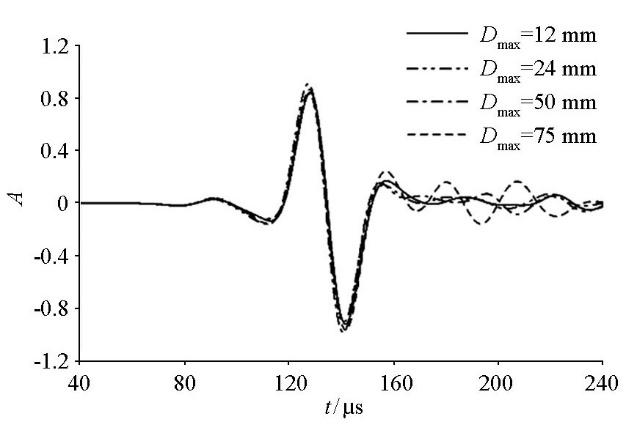
图6为4个级配模型位于(300, 0) mm处接收的波场记录。由图可见,骨料粒径的增大会引起散射波的变化,Dmax=75 mm的骨料模型散射波能量最强,其次为Dmax=50 mm模型,而Dmax=24 mm与Dmax=12 mm模型散射波能量无明显差异。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   不同骨料粒径的波场记录

Fig.6   Waveform comparison chart of different diameter aggregate


表4为坐标(300, 0) mm处波场数据分析结果。为减小由于骨料随机性引起的误差,每个粒径设计3个模型,表中的数据为3个模型的均值。从表4中可以看出:对于散射波,Dmax=75 mm散射波最大增幅达到直达波的14.2%,总振幅达到直达波的29.4%,大于Dmax=50 mm粒径骨料引起的散射波,而Dmax=24 mm、Dmax=12 mm两个模型散射波差异较小;对于直达波,4个粒径模型引起的直达波衰减差异较小,但形变差异较大,其中Dmax=75 mm的骨料引起的直达波形变达14.7%,明显大于其他3个模型。

表4   骨料粒径对波场的影响

Table 4  Influence for wave field of aggregate diameter

骨料粒
径/mm		散射瑞利波直达瑞利波
最大振幅/%总振幅/%衰减量/%形变量/%
126.010.59.24.1
247.312.210.93.4
509.416.87.96.2
7514.229.49.214.7
误差/%8.218.93.011.3

新窗口打开| 下载CSV


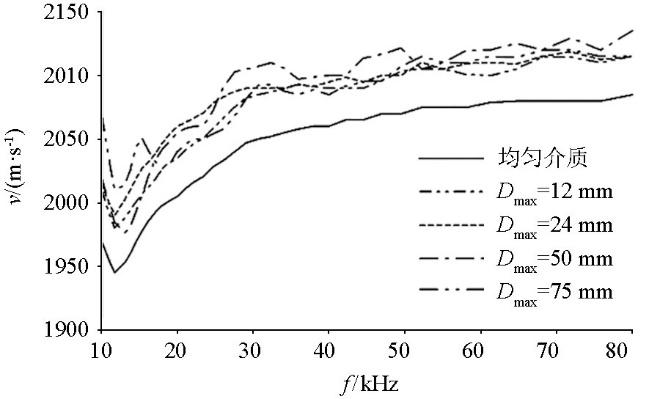
图7为4种不同粒径的骨料模型提取的频散曲线,Dmax=75 mm模型的频散曲线在20 kHz以内起伏较大,Dmax=50 mm模型在10 kHz~20 kHz、30 kHz附近与45 kHz附近呈现一定的起伏,而Dmax=12 mm与Dmax=24 mm模型的频散曲线形态较为稳定,但总体而言,频散曲线的误差较小。经计算得到4个模型的均速分别为2 059.6、 2 069.9、2 071.3和2 071.0 m/s,均速度最大误差为11.7 m/s;最大误差为10 kHz处的Dmax=75 mm与Dmax=12 mm两个模型,均速度为60.0 m/s。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   不同骨料粒径的频散曲线

Fig.7   Dispersion comparison chart of different diameter aggregate


通过以上分析可知,当骨料粒径小于波长的1/2时,骨料引起的波场异常差别较小,当大于波长的1/2时会引起较为明显的波场异常。实际工作中,在满足精度要求下使用低频率的震源可减小骨料引起的波场异常,使用频散曲线进行数据分析也可减小骨料粒径引起的波场异常对结果的影响。

2.4 骨料含量的影响

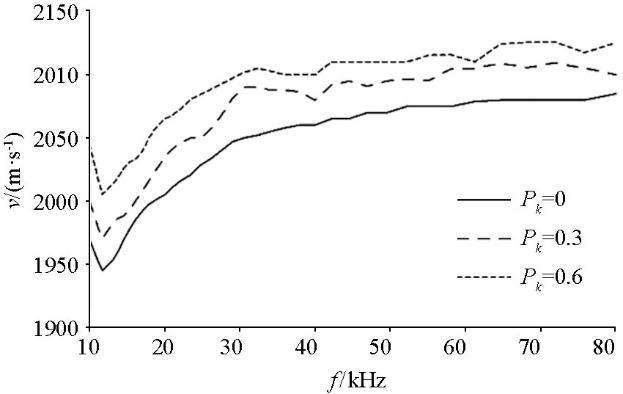
为研究混凝土骨料含量对混凝土传播的影响,对Pk分别为0.3、0.6与0(即均匀介质)的3个模型进行对比分析,模型大小为400 mm×200 mm,骨料为三级级配,各粒级参数为{[3,10],[11,17],[18,24]}mm,正演模拟参数设置与2.1节中的参数相同。

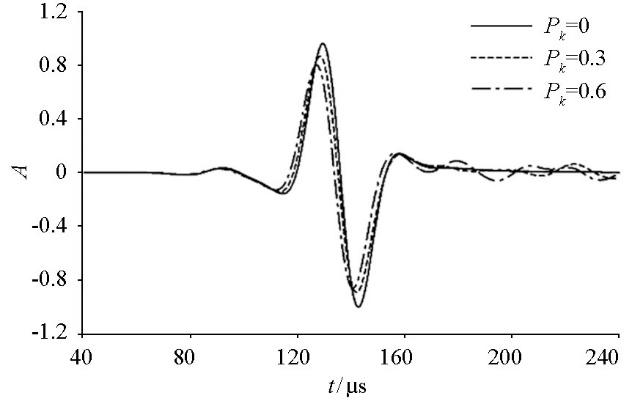
图8为坐标(300, 0) mm处接收的3个模型波场记录,可以看出:①Pk=0.6时的骨料模型直达波波峰到达时间早于Pk=0.3时的骨料模型,表明骨料含量的增加提高了波速;②Pk=0.3的骨料模型直达波振幅大于Pk=0.6的骨料模型;③Pk=0.3与Pk=0.6的骨料模型波尾均可观察到明显的散射震动,但散射波振幅差异不明显。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   骨料含量不同的模型波场记录

Fig.8   Waveform comparison chart of different aggregate content


表5为2种级配模型的坐标为(300, 0) mm处的波场记录分析。为减小由于骨料随机性引起的误差,每个级配设计4个模型,表中的数据为4个模型均值。从表中可以看出:骨料含量的增加对散射波最大振幅、总振幅与直达波波形影响都很小,误差均在3%以内,但对直达波能量的衰减有所影响;骨料颗粒的增加会使直达波衰减加强,Pk=0.6的直达波较Pk=0.3的直达波衰减更为明显。

表5   骨料含量对波场的影响

Table 5  Influence for wave field of aggregate content

Pk散射瑞利波直达瑞利波
最大振幅/%总振幅/%衰减量/%形变量/%
0.39.416.210.15.9
0.68.519.014.54.7
误差/%0.92.84.41.2

新窗口打开| 下载CSV


图9为3种不同骨料含量模型提取的频散曲线,3条频散曲线基本处于平行状态。由于骨料的波速大于水泥浆的波速,骨料的含量越高,瑞利波波速也越高,Pk=0.3时其平均波速为2 054.3 m/s,Pk=0.6时为2 078.7 m/s。因此,骨料含量的变化仅会引起频散曲线在图中坐标位置的变化,但不会影响频散曲线的形态。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   不同骨料含量的频散曲线

Fig.9   Dispersion comparison chart of different aggregate content


2.5 内部缺陷的影响

混凝土可能受材料质量差、生产养护不规范、荷载过量、高温雨水环境、地基沉降等因素影响而出现内部缺陷,通常表现形式为裂缝和空洞(脱空)。以内部空洞缺陷模型为例,设计模型大小600 mm×200 mm,空洞4个顶点坐标为(400,-20)、(460,-20)、(400,-60)、(460,-60) mm。骨料为三级级配,各粒级参数为{[3,10],[10,17],[17,24]} mm,骨料占混凝土体积比Pk=0.4。正演数值模拟参数设置如下:震源位置(50,0)mm;网格间距为0.001 m;采样步长为0.000 000 1 s;主频为20 kHz;采样点数2 500。

考虑实际情况中震源波形多为不规则且采集数据存在噪音干扰,因此通过空洞缺陷引起的波形畸变与反射波很难准确判断空洞的存在,所以本文直接通过频率域特征来分析内部空洞缺陷对瑞利波传播特性的影响。

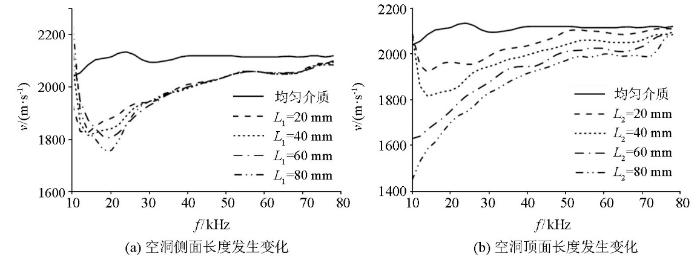
图10为不同规模空洞引起的频散曲线异常对比,空洞顶面埋深30 mm。其中,图10a为空洞顶面长度40mm保持不变,侧面长度L1不断变化,空洞的4个顶点坐标分别为(280,-30)、(320,-30)、(280,-30- L1)、(320,-30- L1) mm;图10b为空洞侧面长度保持不变,空洞顶面长度L2不断变化,空洞4个顶点坐标为(300- L2/2,-30)、(300+ L2/2,-30)、(300- L2/2,-70)、(300+ L2/2,-70)] mm。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   空洞规模变化引起的频散曲线异常对比

Fig.10   Comparison of anomalous dispersion curves caused by changes in cavity size


由图10可以看出:1)正常情况下的混凝土频散曲线为一条曲线,低频部分有一定的波动,高频部分较为平直,总体误差较小,最大值与最小值差异仅为94 m/s,相较于2 100 m/s的平均速度,误差仅为4.5%。但当混凝土中存在空洞时,频散曲线速度明显降低,速度降低的数值与空洞的参数有关。

2)图10a中,空洞侧面长度的改变并没有引起频散曲线产生明显的差异,不同的侧面长度模型频散曲线高频部分基本重合,低频部分略有差异,频散曲线与纵坐标的交点值随着侧面长度的增加而增加,4个交点值依次为1 930、2 085、2 135、2 240 m/s,两者呈正相关关系。总体而言,空洞侧面长度变化对频散曲线影响较小。

3)图10b中,空洞的顶面长度不同时频散曲线产生了明显的差别,且空洞顶面长度越长,频散曲线速度越低。通过对比图10a与图10b可知,空洞顶面长度对频散曲线影响较大,空洞侧面长度变化对频散曲线影响较小。

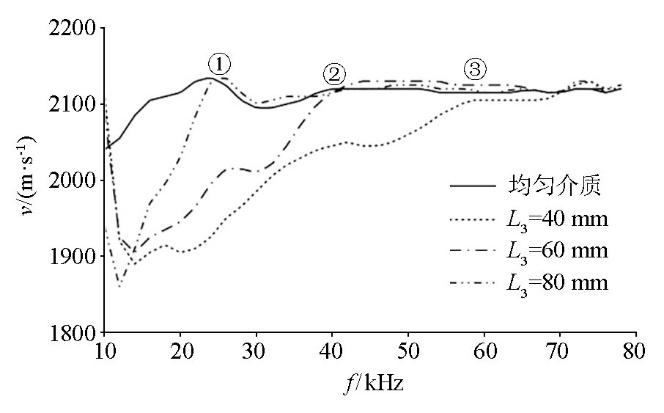
图11为不同深度的空洞引起的频散曲线异常,空洞规模不变,深度L3变化,空洞坐标可表示为(280,- L3)、(320,- L3)、(280,- L3-40)、(320,- L3-40) mm。通过图11可知:

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   空洞深度变化引起的频散曲线

Fig.11   Comparison of anomalous dispersion curves caused by changes in cavity depth


1)空洞的深度变化对频散曲线有明显的影响,空洞深度越浅,频散曲线速度越低。

2)不同深度的空洞对频散曲线的影响不同。由于瑞利波的穿透范围在一个波长以内,空洞越深,则影响的频带越少。图中序号①、②、③分别对应L3=80、60、40 mm时与无空洞模型频散曲线交点,其值为2.55×104、3.86×104和5.86×104。使用该频率对应的速度除以频率,得到3个频率对应的波长分别为:82、54、36 mm,与空洞深度的误差分别为2、6、4 mm,三者误差均在10%以内。由此可知,通过计算空洞模型频散曲线与正常混凝土模型频散曲线的交点,可大致估算空洞的深度。

通过以上分析可知:1)通过波场记录中的反射波同相轴与散射波,可圈定空洞的横坐标。

2)空洞会引起频散曲线速度降低;空洞的顶面长度越长,频散曲线速度越低;空洞的侧面长度变化对频散曲线影响较小。

3)通过异常频散曲线与正常频散曲线的交点,可大致估计空洞的深度。

3 结语

通过上述研究及模型分析可得到如下结论:1)混凝土骨料的随机性对散射波能量影响较小,但对直达波能量的衰减与波形有一定影响。为了避免由于骨料的随机性引起误差,在波场正演模拟时宜对生成多个随机模型正演后将结果取均值。

2)骨料的形状几乎不对瑞利波波场产生影响。

3)骨料粒径的变化是引起波场变化的一个重要因素。当粒径小于1/2波长时,骨料粒径的变化对波场影响较小;当粒径大于1/2波长时,骨料会引起明显的散射波且会导致直达波波形畸变。在精度允许范围内,降低震源主频,提高瑞利波波长是减小骨料影响的有效途径。

4)骨料的含量仅会影响直达波的衰减,含量越高,直达波衰减越强。

5)骨料的随机性、形状、粒径与含量的改变均不会引起瑞利波频散曲线发生明显的变化,骨料不会引起频散曲线的形态出现异常。

6)当混凝土内部存在空洞缺陷时,从频率域分析,空洞会引起频散曲线速度降低,空洞的上表面是引起频散曲线发生异常的原因,空洞上表面长度越长,频散曲线速度越低,空洞的侧面变化对频散曲线无明显影响;通过异常频散曲线与正常频散曲线的交点可大致估计空洞的深度。

因此,在利用瑞利波法进行混凝土构件缺陷检测时,使用频散曲线进行数据分析和对异常进行解释,可避免混凝土骨料对检测结果的影响。

参考文献

尚新想, 谢友均, 马昆林, 等.

基于应力波的混凝土抗压强度无损检测试验研究

[J]. 铁道科学与工程学报, 2022, 19(8):2305-2312.

[本文引用: 3]

Shang X X, Xie Y J, Ma K L, et al.

Experimental study on nondestructive testing of concrete compressive strength based on stress wave

[J]. Journal of Railway Science and Engineering, 2022, 19(8):2305-2312.

[本文引用: 3]

姜勇, 吴佳晔, 马永强, 等.

基于冲击弹性波的隧道衬砌混凝土强度检测技术研究和应用

[J]. 铁道建筑, 2020, 60(6):1-5,11.

[本文引用: 1]

Jiang Y, Wu J H, Ma Y Q, et al.

Research and application of tunnel lining concrete strength detection technology based on shock elastic wave

[J]. Railway Engineering, 2020, 60(6):1-5,11.

[本文引用: 1]

姚菲, 陆幸奇, 陈光宇.

基于冲击回波法的混凝土—围岩缺陷检测与信号处理研究

[J]. 铁道科学与工程学报, 2021, 18(9):2316-2323.

[本文引用: 1]

Yao F, Lu X Q, Chen G Y.

Experimental and signal processing research on concrete-rock structural defects by impact-echo method

[J]. Journal of Railway Science and Engineering, 2021, 18(9):2316-2323.

[本文引用: 1]

王庆彦, 王浩丞, 郁明理.

无损检测技术在混凝土性能检测中的应用

[J]. 中国建材科技, 2022, 31(3):134-136.

[本文引用: 1]

Wang Q Y, Wang H C, Yu M L.

Application of nondestructive testing technology in concrete performance inspection

[J]. China Building Materials Science & Technology, 2022, 31(3):134-136.

[本文引用: 1]

Potapov A I, Shikhov A I, Dunaeva E N.

Nondestructive quality testing of concrete and asphalt concrete pavements

[J]. Journal of Physics:Conference Series, 2021, 1753(1):012053.

DOI:10.1088/1742-6596/1753/1/012053      [本文引用: 1]

The technical level of the applied methods and controls has an impact on the result of construction and installation works. One of the main tasks of contractors in the process of paving is to quickly determine the parameters of asphalt pavement. The quality of the asphalt pavement device allows you to increase the service life and reduce the cost of repairing road surfaces. A number of methods and means of nondestructive quality testing of concrete and asphalt concrete pavements are considered. Some characteristics of defects of concrete and asphalt concrete pavements are given. The main attention is paid to ground-penetrating radar methods, eddy-current, radiation and acoustic, also the devices implementing these methods are considered.

杨道煌, 刘江平, 程飞, 等.

超声面波法在混凝土强度检测中的应用研究

[J]. 物探与化探, 2020, 44(3):626-634.

[本文引用: 1]

Yang D H, Liu J P, Cheng F, et al.

The application of ultrasonic surface wave method to concrete strength testing

[J]. Geophysical and Geochemical Exploration, 2020, 44(3) :626-634.

[本文引用: 1]

刘杨, 邵志伟, 张慧杰, 等.

钢管混凝土密实度超声波层析成像无损检测研究

[J]. 工业建筑, 2021, 51(10):189-200.

[本文引用: 1]

Liu Y, Shao Z W, Zhang H J, et al.

Research on nondestructive testing of CFST by ultrasonic tomography

[J]. Industrial Construction, 2021, 51(10):189-200.

[本文引用: 1]

李军伟, 徐飞, 王兵, 等.

混凝土不同骨料粒径对声发射检测的影响

[J]. 山东大学学报:工学版, 2021, 51(5):84-90.

[本文引用: 1]

Li J W, Xu F, Wang B, et al.

Influence of concrete aggregate particle size on acoustic emission detection

[J]. Journal of Shandong University: Engineering Science, 2021, 51(5):84-90.

[本文引用: 1]

刘豪, 侯德鑫, 郑刚兵, 等.

基于热成像的钢管混凝土脱空检测技术研究

[J]. 红外技术, 2021, 43(11):1119-1126.

[本文引用: 1]

Liu H, Hou D X, Zheng G B, et al.

Infrared thermography-based void detection technology for concrete-filled steel tubes

[J]. Infrared Technology, 2021, 43(11):1119-1126.

[本文引用: 1]

杨相如.

瑞雷波在台涵背填筑质量控制中的应用

[J]. 地下空间与工程学报, 2019, 15(2):505-512.

Yang X R.

Application of Rayleigh wave in the back filling of abutment in Quality Control

[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(2):505-512.

罗广衡, 潘坚文, 王进廷.

瑞利波法检测混凝土表面裂缝深度的影响因素研究

[J]. 水利水电技术, 2021, 52(9):165-171.

[本文引用: 1]

Luo G H, Pan J W, Wang J T.

Study on influencing factors of detecting surface crack depth with Rayleigh wave detection method

[J]. Water Resources and Hydropower Engineering, 2021, 52(9):165-171.

[本文引用: 1]

童凯, 周建庭, 张森华, 等.

基于激光激发瑞利波的混凝土表面裂缝检测

[J]. 中国科技论文, 2022, 17(6):667-672.

[本文引用: 1]

Tong K, Zhou J T, Zhang S H, et al.

Crack detection of concrete surface based on laser excited Rayleigh wave

[J]. China Science Paper, 2022, 17(6):667-672.

[本文引用: 1]

贺会团, 张献民, 赵维炳.

瞬态瑞雷面波检测碎石桩复合地基承载力研究

[J]. 岩土工程学报, 2006, 28(8):1039-1043.

[本文引用: 2]

He H T, Zhang X M, Zhao W B.

Studies on capacity of gravel-piled compound detected by transient Rayleigh surface wave

[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(8):1039-1043.

[本文引用: 2]

袁士川, 宋先海, 张学强, 等.

黏弹性介质瑞雷波有限差分模拟与特性分析

[J]. 地球物理学报, 2018, 61(4):1496-1507.

[本文引用: 1]

Yuan S C, Song X H, Zhang X Q, et al.

Finite-difference modeling and characteristics analysis of Rayleigh waves inviscoelastic media

[J]. Chinese J Geophys, 2018, 61(4):1496-1507.

[本文引用: 1]

Wu T T, Sun J H, Tong J H.

On the study of elastic wave scattering and Rayleigh wave velocity measurement of concrete with steel bar

[J]. NDT&E International, 2000, 33(6):401-407.

DOI:10.1016/S0963-8695(00)00012-8      URL     [本文引用: 1]

Zerwer A, Polak M A, Santamarina J C.

Detection of surface breaking cracks in concrete members using Rayleigh waves

[J]. Journal of Environmental & Engineering Geophysics, 2012, 10(3):295-306.

[本文引用: 1]

Aggelis D G, Shiotani T.

Repair evaluation of concrete cracks using surface and through-transmission wave measurements

[J]. Cement & Concrete Composites, 2007, 29(9):700-711.

[本文引用: 1]

Kim G, In C W, Kim J Y, et al.

Air-coupled detection of nonlinear Rayleigh surface waves in concrete:Application to microcracking detection

[J]. NDT&E International, 2014, 67(8):64-70.

DOI:10.1016/j.ndteint.2014.07.004      URL     [本文引用: 1]

练小聪. 混凝土介质中瑞雷面波传播特性的研究[D]. 长沙: 中南大学, 2014:43-46.

[本文引用: 1]

Lian X C. The study of Rayleigh wave propagation characteristics of the concrete medium[D]. Changsha: Central South University, 2014:43-46.

[本文引用: 1]

董良国, 马在田, 曹景忠, 等.

一阶弹性波方程交错网格高阶差分解法

[J]. 地球物理学报, 2000, 43(3):411-419.

[本文引用: 1]

Dong L G, Ma Z T, Cao J Z, et al.

A staggered-grid high order difference method of one-order elastic wave equation

[J]. Chinese Journal of Geophysics, 2000, 43(3):411-419.

[本文引用: 1]

Xu Y X, Xia J H, Miller R D.

Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach

[J]. Geophysics, 2007, 72(5):147-153.

[本文引用: 1]

孙卫涛. 弹性波动方程的有限差分数值方法[M]. 北京: 清华大学出版社, 2009:56-59.

[本文引用: 1]

Sun W T. Finite difference method for elastic wave equation[M]. Beijing: Tsinghua University Press, 2009:56-59.

[本文引用: 1]

熊章强, 张大洲, 秦臻, 等.

瑞雷波数值模拟中的边界条件及模拟实例分析

[J]. 中南大学学报:自然科学版, 2008, 39(4):824-830.

[本文引用: 1]

Xiong Z Q, Zhang D Z, Qin Z, et al.

Boundary conditions and case analysis of numerical modeling of Rayleigh wave

[J]. Journal of Central South University:Science and Technology, 2008, 39(4):824-830.

[本文引用: 1]

高政国, 刘光廷.

二维混凝土随机骨料模型研究

[J]. 清华大学学报:自然科学版, 2004, 43(5):710-714.

[本文引用: 1]

Gao Z G, Liu G T.

Two-dimensional random aggregate structure for concrete

[J]. Journal of Tsinghua University:Science and Tech-nology, 2004, 43(5):710-714.

[本文引用: 1]

Walraven, Reinhardt.

Theory and experiments on the mechanical behavior of cracks in plain and reinforced concrete subject to shear loading

[J]. Heron, 1991, 26(1A):26-35.

[本文引用: 1]

张剑, 金南国, 金贤玉, 等.

混凝土多边形骨料分布的数值模拟方法

[J]. 浙江大学学报:工学版, 2004, 38(5):581-585.

[本文引用: 1]

Zhang J, Jin N G, Jin X Y, et al.

Numerical simulation method for polygonal aggregate distribution in concrete

[J]. Journal of Zhejiang University:Engineering Science, 2004, 38(5):581-585.

[本文引用: 1]

Schubert F, Schechinger B.

Numerical modeling of acoustic emission sources and wave propagation in concrete

[J]. Journal of Nondestructive Testing:Germany, 2002, 7(9):1-8.

[本文引用: 1]

Park C B, Miller R D, Xia J.

Imaging dispersion curves of surface waves on multi-channel record

[C]// SEG Expanded Abstracts, 1998, 17(1):1377-1380.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com