E-mail Alert Rss
 

物探与化探, 2023, 47(4): 1040-1047 doi: 10.11720/wtyht.2023.1303

方法研究信息处理仪器研制

微动信号模拟及其在微动勘探中的应用

李传金,1,2,3, 王强1, 渐翔1, 郑涛1, 詹素华1,2, 陈绍伟1

1.福建理工大学 土木工程学院,福建 福州 350118

2.福建理工大学 岩土工程研究所,福建 福州 350118

3.福建理工大学 地下工程福建省高校重点实验室,福建 福州 350118

Microtremor signal simulation and its application in microtremor exploration

LI Chuan-Jin,1,2,3, WANG Qiang1, JIAN Xiang1, ZHENG Tao1, ZHAN Su-Hua1,2, CHEN Shao-Wei1

1. School of Civil Engineering,Fujian University of Technology,Fuzhou 350118,China

2. Institute of Geotechnical Engineering,Fujian University of Technology,Fuzhou 350118,China

3. Key Laboratory of Underground Engineering in Universities of Fujian Province,Fujian University of Technology,Fuzhou 350118,China

第一作者: 李传金(1982-),男,博士,副教授,主要从事微动勘探研究工作。Email:licj04@126.com

责任编辑: 叶佩

收稿日期: 2022-06-16   修回日期: 2023-02-1  

基金资助: 中国科学院重点部署项目(ZDRW-ZS-2021-3-1)
福建理工大学科研发展基金(GY-Z17157)

Received: 2022-06-16   Revised: 2023-02-1  

摘要

对于简正振型叠加法合成的微动信号,使用空间自相关法计算的频散曲线与理论频散曲线对比,发现两者具有较好的一致性。模拟微动信号时涉及许多参数,这些参数对微动勘探开展具有重要意义。对这些参数进行了数值试验,试验结果表明:震源距离和台阵尺寸对结果有明显影响,在复杂地层情况下应考虑高阶面波,在安静的观测场地应用小尺寸台阵往往能获得更高频率的频散信息从而提高浅层分辨率。因此,在实际开展微动勘探时,应考虑震源分布、台阵尺寸和高阶面波等因素对勘探结果的影响。

关键词： 微动信号; 简正振型叠加; 微动勘探; 频散曲线; 空间自相关法

Abstract

This study synthesized microtremor signals using the normal mode superposition.The dispersion curves of the synthesized microtremor signals were calculated using the spatial autocorrelation method,and the calculated results agreed well with theoretical dispersion curves.The simulation of microtremor signals involves many parameters,which are of great significance for microtremor exploration.As shown by results from numerical experiments of these parameters,the hypocentral distance and array size had a significant influence on the results.Moreover,high-order surface waves should be considered for complex strata,while small-size arrays tended to yield high-frequency dispersion information at quiet observation sites,thus improving the resolution of shallow strata.Therefore,it is necessary to consider the influences of hypocenter distribution,array size,and high-order surface waves on exploration results in microtremor exploration.

Keywords： microtremor signal; normal mode superposition; microtremor exploration; dispersion curve; spatial autocorrelation method

PDF (3904KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

李传金, 王强, 渐翔, 郑涛, 詹素华, 陈绍伟. 微动信号模拟及其在微动勘探中的应用[J]. 物探与化探, 2023, 47(4): 1040-1047 doi:10.11720/wtyht.2023.1303

LI Chuan-Jin, WANG Qiang, JIAN Xiang, ZHENG Tao, ZHAN Su-Hua, CHEN Shao-Wei. Microtremor signal simulation and its application in microtremor exploration[J]. Geophysical and Geochemical Exploration, 2023, 47(4): 1040-1047 doi:10.11720/wtyht.2023.1303

0 引言

微动(microtremor)是指地球表面的微弱震动,来源于天气、海浪和潮汐变化等自然现象和车辆行驶、机械以及生产活动等人类活动,由体波和面波组成的一种复杂振动。微动勘探通过阵列观测,从微动信号中提取面波频散曲线,再反演频散曲线,最终获得地下介质的横波速度结构。近些年,微动勘探在工程物探中的应用越来越广泛[1⇓⇓⇓-5]。在微动勘探理论方面,学者们对阵列形式[6]、高阶频散曲线提取[7⇓⇓-10]等方面进行了深入研究。

在微动勘探研究中,微动信号模拟在算法验证、阵列适用性评价、高阶频散曲线提取等方面起重要作用[7,11-12]。微动信号模拟方法有广义射线法[8]、简正振型叠加法[11]、有限差分法[12]等。每种方法有各自特点。由于在微动信号模拟过程中,需要计算大量的理论地震图,所需时间一般比较长,而简正振型叠加法具有计算速度快、时间短的优点[13]。因此,本文应用简正振型叠加法合成微动信号,并研究其在微动勘探中的应用。

1 理论

1.1 简正振型叠加法

简正振型叠加法是一种理论地震图计算的常用方法。该方法通过地球自由振荡的各个振型叠加的方式表示位移场。Gilbert[14]首先提出用振型叠加的形式表示位移,给出了激发函数表达式。Woodhouse[15]提出了径向本征函数的计算方法,使得通过简正振型叠加计算理论地震图成为可能。 Dahlen 等[16]在前人工作基础上,系统总结了简正振型理论、简正振型叠加法等内容。Yang等[17]推导了更简洁实用的位移表达式。

对于给定点源激发的位移场,可以通过简正振型线性叠加计算得出。假设在x'处有一点源激发,按简正振型叠加法,在x处的位移表示为[16-17]

gx,t;x'=∑kAkx',tskx,

式中:sk为第k个振型的本征函数;Ak为点源在x'处的第k个振型的激发函数;下标k封装了4个指标q,n,l,m,其中q只有两个取值(球状振型或环状振型),n为径向阶,l为角阶,m为方位角阶。本征函数sk由球谐函数和径向本征函数构成,具体表达式参考Gilbert等[14]和Yang等[17]的文章。振型激发函数Ak的表达式为[16-17]

Akx',t=M:εk*rs1-expiσktcosωktωk2,

式中:M为震源矩张量;εk为模态应变;ωk和σk分别为简正振型本征频率的实部和虚部。

1.2 瑞利波频散曲线

在层状介质中瑞利波具有频散特性,不同频率的瑞利波具有不同的相速度。瑞利波频散曲线的计算方法有Haskell法[18]、Knopoff 法[19]、δ 矩阵法[20]、Abo-Zena法[21]、广义反射透射系数法[22]和快速矢量传递算法[23]等。这些方法都通过求解瑞利波频散方程获得相速度,从而得到理论瑞利波频散曲线。

求解瑞利波频散方程时,同一个频率可能有多个解,即同一频率的瑞利波可以以不同相速度传播。因此,理论频散曲线不只有1条相速度曲线,而是有多条相速度曲线,称这些相速度曲线为多阶瑞利波频散曲线。在多阶瑞利波频散曲线中,具有最低相速度值的频散曲线称为基阶瑞利波频散曲线,具有较高相速度值的频散曲线称为高阶瑞利波频散曲线[11]。根据相速度的大小,高阶瑞利波频散曲线进一步细分为一阶波、二阶波等。

不同阶的频散曲线可以按能量占比复合而成的一条曲线,称为视频散曲线。在实际观测中,采用空间自相关法从实测微动数据中提取的频散曲线不是多阶瑞利波频散曲线,而是视频散曲线[7,11]。通过介质响应函数可以计算理论上的视频散曲线,其关键是计算各阶瑞利波能量在总能量中的占比。各阶瑞利波能量在总能量中的占比可表示为[24]

pifpf=cifAi2f∑icifAi2f,

式中:f为频率;i为第i阶瑞利波;ci(f)为相速度;pi(f)为各瑞利波的能量;pi(f)/p(f)为各瑞利波能量在总能量中的占比;Ai(f)为介质响应函数。介质响应函数Ai(f)是地层介质对瑞利波传播的响应函数,可表示为

Ai(f)=NR∂FR/∂ki,

式中:i表示瑞利波的阶数,k是波数,NR是与瑞利波的传递矩阵相关的表达式,FR是瑞利波的频散函数[25]。

2 微动信号模拟

本文采用的微动信号模拟方法是先通过简正振型叠加法计算理论地震图,再由多个理论地震图合成微动信号。微动信号模拟涉及地层模型、阵列布置、震源分布、面波阶数等多个参数。

2.1 地层模型

选取3层结构的速度递增型地层模型,参数如表1所示。

表1   地层模型参数

Table 1  Parameters of geological model

序号层厚
度/m		纵波速度/
(m·s-1)		横波速度/
(m·s-1)		密度/
(g·cm-3)
1101 3002001.9
2501 8005002.2
3∞2 5001 0002.5

新窗口打开| 下载CSV


2.2 台阵布置

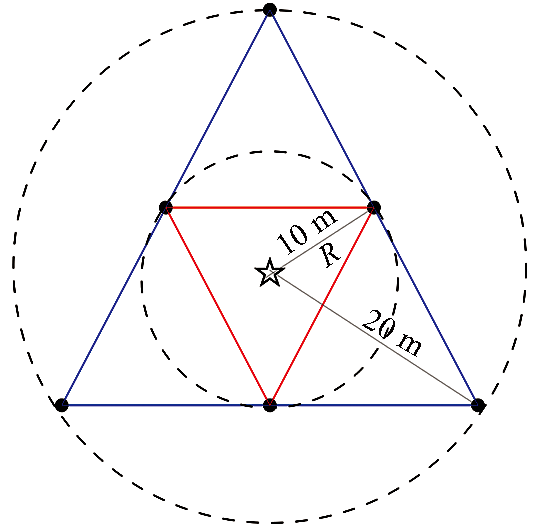
按图1所示布置观测台阵,采用微动勘探中常用的双重圆形阵列,共布置7个台站,观测半径分别为10 m和20 m。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   台阵布置

Fig.1   Array configuration


2.3 震源分布

在距离台阵中心500~1 000 m的圆环范围内随机布置1 000个震源(如图2所示)。震源位于地表,方位和强度随机选取,在观测时长内随机出现。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   震源分布

Fig.2   Sources distribution


2.4 合成微动信号

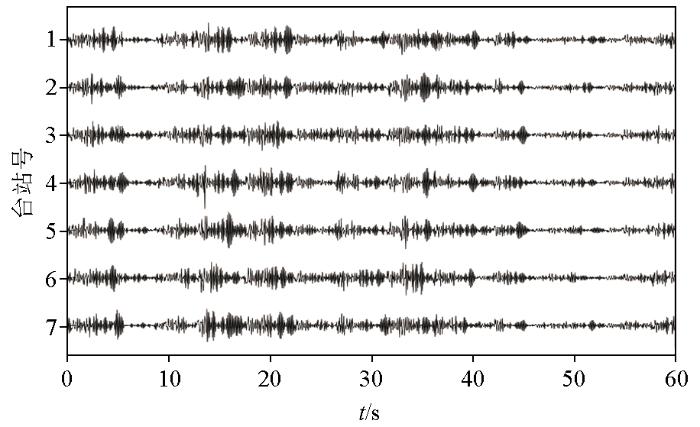
每个震源生成1个地震记录,所有的地震记录按时间先后顺序合并成1个微动信号。合成时,根据需要选择不同的面波阶数。当地质模型存在高低速夹层时,高阶模式起重要作用,必须考虑高阶模式。与基阶瑞利波频散曲线对比时,只选择基阶模式,不考虑高阶模式。合成微动信号的时长为30 min,采样率为100 Hz。合成微动信号有3个分量,其中2个为水平分量,1个为垂直分量。空间自相关法主要使用垂直分量。图3为合成微动信号垂直分量的波形。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   合成微动信号垂直分量的波形

Fig.3   The vertical component wave of the synthetic microtremor signal


3 合成微动信号在微动勘探中的应用

微动勘探方法的关键技术是从微动信号中提取频散曲线。从微动信号中提取频散曲线方法有频率波数法(FK法)和空间自相关法(SPAC法)。本文采用空间自相关法计算频散曲线。

3.1 空间自相关系数

将时长 30 min的合成微动信号按40.96 s分段。对于每段数据,计算两个台站间的空间自相关函数,叠加平均所有台站距离相等的空间自相关函数得到空间自相关系数。计算完所有数据段后,计算空间自相关系数的均值和标准差。按图1所示的台站布置,计算两个台站之间的距离并进行分组排序,获得5个不同的台站距离,每1个距离对应1个空间自相关系数。图4显示了这5个不同台站距离的空间自相关系数。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   空间自相关系数

Fig.4   Spatial autocorrelation coefficients


3.2 频散曲线

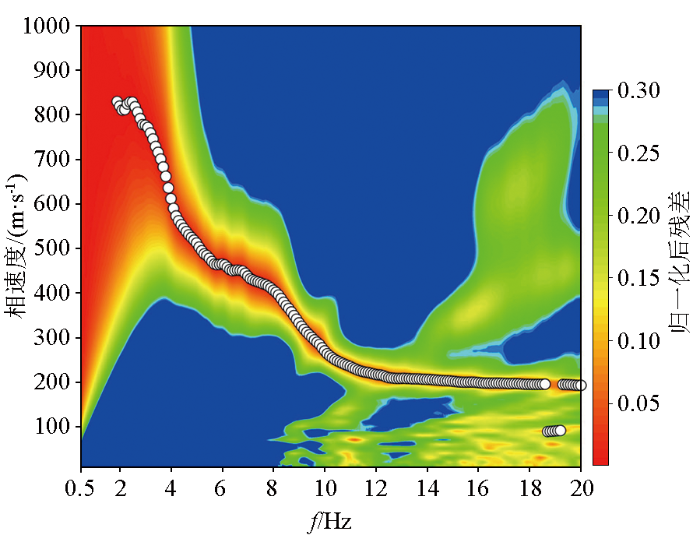
采用扩展空间自相关法(ESPAC)[26]计算频散曲线。相速度选取范围为10~1 000 m/s,间隔为10 m/s。频率选取范围为0.5~20 Hz,间隔为0.1 Hz。

对于某一频率f,由不同距离d和对应空间自相关系数组成一序列。用不同相速度生成零阶贝塞尔函数,并计算零阶贝塞尔函数和该序列之间残差。在选取的频谱范围内计算残差,对残差进行归一化。如图5所示,以横坐标为频率,纵坐标为相速度,按残差大小生成频谱(图5)。在频谱图中用不同颜色表示残差的大小,用红色表示最小的残差。为突显残差较小值区域的特征,将频谱图中残差大于0.3的部分统一用蓝色表示。拾取残差最小值处的相速度并连成线,获得频散曲线。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   合成微动信号的频谱

Fig.5   Frequency spectrogram of synthetic microtremor signal


图5中不同频率范围的频谱特征有明显差异。频率在4~12 Hz时,频谱能量集中,容易拾取频散曲线。频率小于2 Hz时,频谱颜色几乎都为红色,结果有明显偏差,没有拾取频散曲线。频率在2~4 Hz范围,在较大相速度范围内,归一化后残差都小于0.05,频谱颜色都接近红色。对于这一范围的频谱,虽然颜色差异较小,但依然可以通过残差的大小提取频散曲线。频率大于12 Hz时,频谱能量分散,对频散曲线的拾取造成一定的干扰。

3.3 和理论频散曲线对比

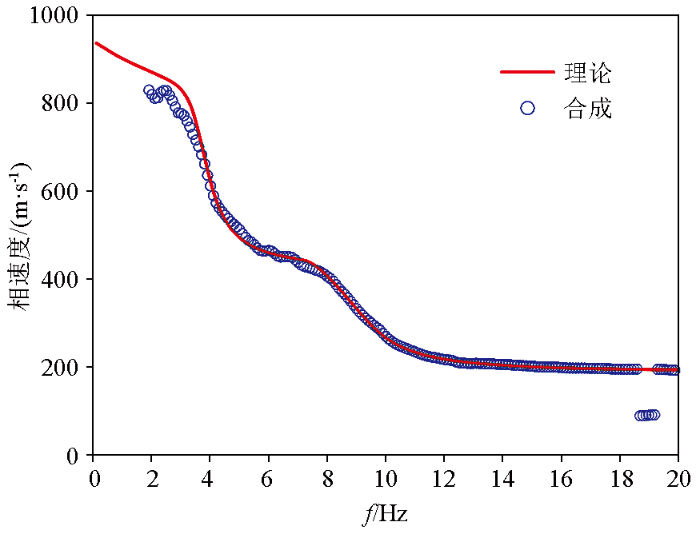
使用表1所示的地层模型,采用Haskell传递矩阵法[18]计算理论频散曲线。在图6中,对比合成微动信号计算的频散曲线与理论频散曲线,发现两者在整体上具有较好的一致性。合成频散曲线和理论频散曲线具有相似特征,都可以划分出3个近似水平段,频率范围分别为2.5~3 Hz、5~7.5 Hz和大于10 Hz,对应的相速度范围分别为800~850 m/s、450~500 m/s和190~200 m/s。频散曲线的这种特征与地层模型的3层结构有关,和横波速度由深到浅分别为1 000 m/s、500 m/s和200 m/s有一一对应关系。通过对比还发现,在不同频率段合成频散曲线和理论频散曲线略有差异。在3.5~18 Hz部分几乎完全重合;小于3.5 Hz的低频部分略有差异;大于18 Hz的高频部分合成频散曲线不连续,出现跳变,和理论频散曲线有较大差异。导致这种差异的原因是台阵尺寸有限,无法准确计算高低频部分的合成频散曲线。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   理论频散曲线与合成频散曲线对比

Fig.6   Comparison of theoretical and synthetic dispersion curves


4 参数分析与讨论

微动信号模拟涉及许多参数,这些参数对微动勘探开展具有重要意义。本文对这些参数进行了数值试验,不同的参数设置得到不同的结果。试验结果分析如下。

4.1 震源距离

对不同距离的震源进行数值试验。图2中所示的震源距离为500~1 000 m。图7中补充了震源距离为1~50 m和50~200 m的试验结果。由图7可知,在不同震源距离情况下,频散曲线可以拾取的最低频率有明显差别。当震源距离为1~50 m时,拾取的最低频率为6.2 Hz;当震源距离为50~200 m时,拾取的最低频率为3.3 Hz;当震源距离为500~1 000 m时,拾取的最低频率为2.3 Hz。这说明,模拟微动信号时,如果震源距离设置太小,缺乏远距离震源,将无法准确获得低频部分的频散曲线。因此,模拟微动信号时应合理设置震源距离。

图7

新窗口打开| 下载原图ZIP| 生成PPT

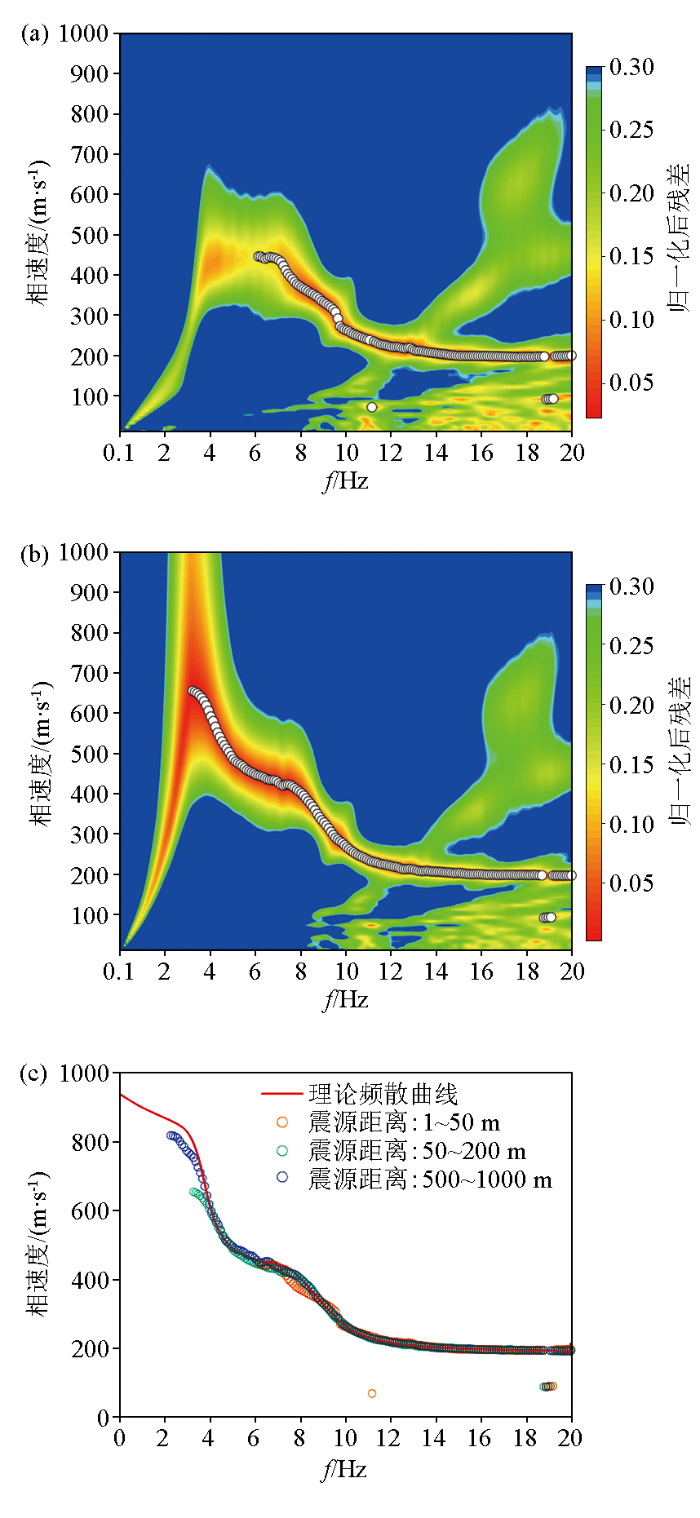
图7   使用不同震源距离计算的频散曲线

a—震源距离1~50 m;b—震源距离50~200 m;c—频散曲线对比

Fig.7   Dispersion curves with different sources distances

a—source distance in the range of 1 to 50 m;b—source distance in the range of 50 to 200 m;c—comparison of dispersion curves


4.2 台阵尺寸

图6对比了合成频散曲线与理论频散曲线,发现两者总体上具有较好的一致性,但在小于3 Hz的低频部分和大于18 Hz的高频部分略有差异。这种差异可能与台阵尺寸有关。对不同尺寸的阵列进行数值试验。台阵的类型还是图1所示双重圆形阵列,台阵尺寸发生变化,半径R(指内圆的半径)由10 m变成1 m和100 m。

图8为不同台阵尺寸得到的频散曲线。由图8可知,表明不同尺寸的台阵得到的频散曲线是有所差别的。在图8a中,频率小于10 Hz时,在较大相速度范围频谱颜色几乎都为红色,说明较小尺寸(半径R=1 m)的台阵难以获得低频的频散曲线。在图8b中,较大尺寸(半径R=100 m)的台阵可以准确估算低频的频散曲线,但在大于8 Hz的高频部分频散曲线有明显偏差。在图8c中,合成频散曲线和理论频散曲线对比结果表明:较大尺寸的台阵得到的频散曲线在低频部分较准确,在高频部分误差较大;较小尺寸的台阵得到的频散曲线在高频部分较准确,低频部分误差较大。因此,实际观测时应根据勘探深度的要求,合理选择台阵尺寸。

图8

新窗口打开| 下载原图ZIP| 生成PPT

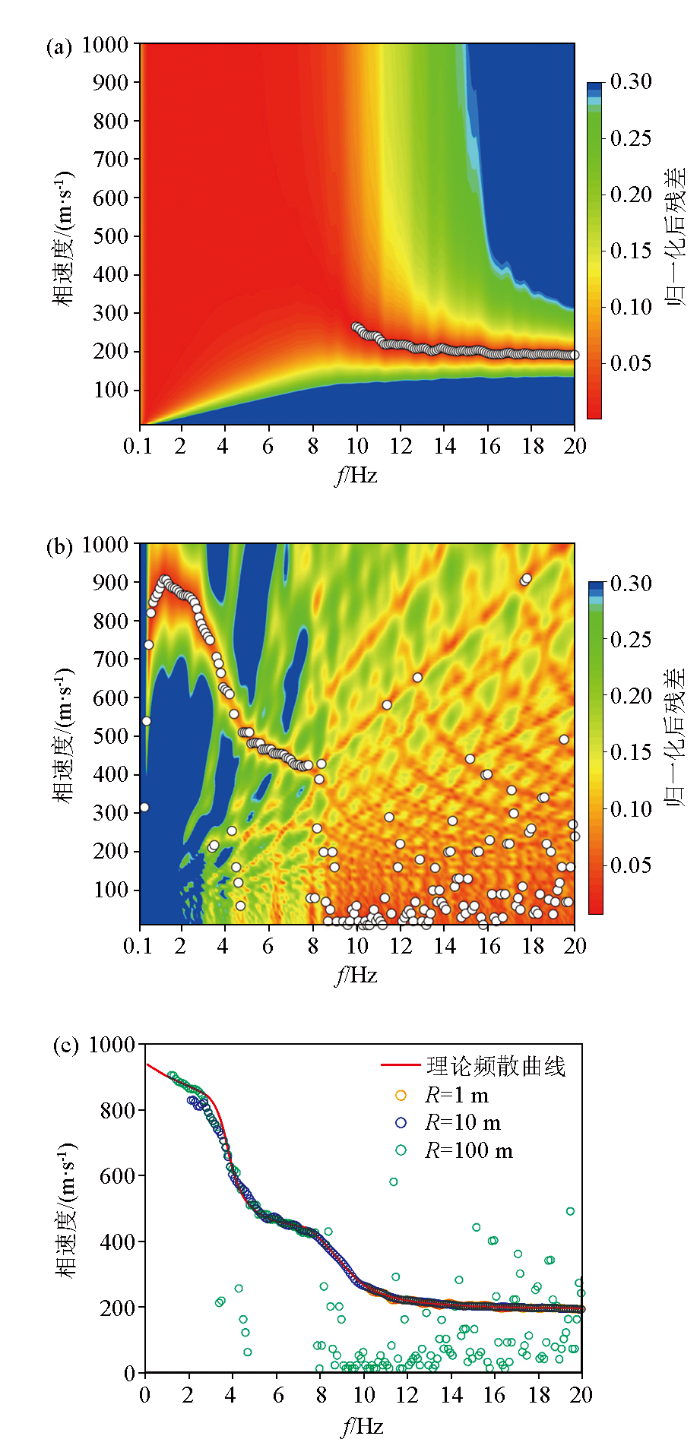
图8   使用不同台阵尺寸计算的频散曲线

a—台阵半径R=1 m;b—台阵半径R=100 m;c—频散曲线对比

Fig.8   Dispersion curves with different array sizes

a—R=1 m;b—R=100 m;c—comparison of dispersion curves


4.3 基阶和高阶

图6中所示的合成频散曲线,采用表1所示的速度递增型地层模型,数值试验时只用面波的基阶模式,没用考虑高阶模式。除了速度递增型地层模型外,常见的地层模型还有含低速软夹层型和含高速硬夹层型[7,11-12]。表2显示了含高速硬夹层的地层模型,其中第2层的横波速度为500 m/s,比相邻上下两层的速度都高。

表2   含高速硬夹层的地层模型参数

Table 2  Parameters of geological model with high velocity interlayer

序号层厚
度/m		纵波速度/
(m·s-1)		横波速度/
(m·s-1)		密度/
(g·cm-3)
11013002001.9
23018005002.2
32020003002.0
4∞250010002.5

新窗口打开| 下载CSV


图9为用表2的地质模型参数进行数值试验得到的结果。图9a为频谱,从中可以提取频散曲线。图9b为不同阶瑞利波的能量占比。从图9b中可知,在特定频率范围高阶瑞利波能量占主导地位。如在2 Hz附近和5~8 Hz范围,一阶瑞利波占主导地位,在14~20 Hz部分,二阶瑞利波的能量占比随频率的增大而增大。

图9

新窗口打开| 下载原图ZIP| 生成PPT

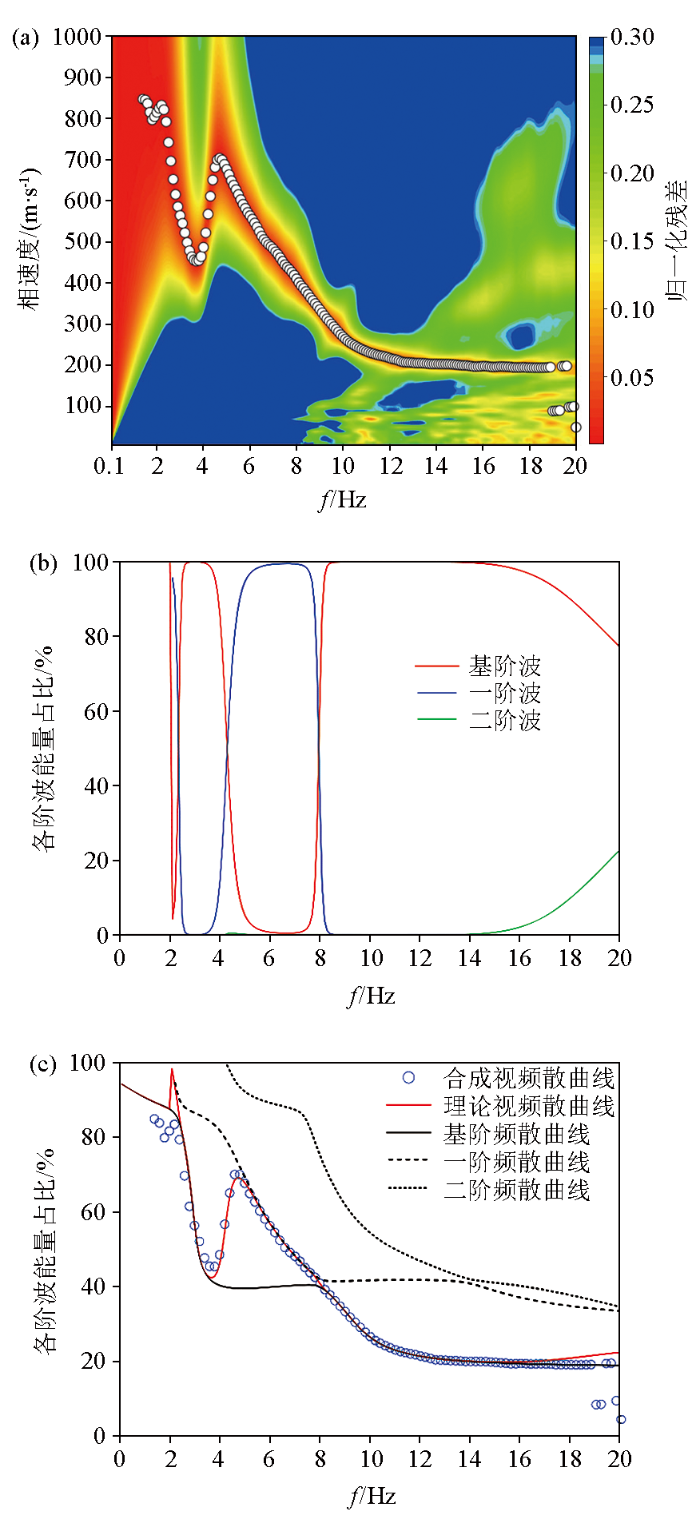
图9   含高速硬夹层的地层模型计算的频散曲线

a—合成微动信号的频散曲线;b—各阶瑞利波能量占比;c—频散曲线对比

Fig.9   Dispersion curves with high velocity interlayer

a—dispersion curve calculated by synthetic microtremor signal;b—power fractions to different modes of Rayleigh waves;c—comparison of dispersion curves


图9c为多阶瑞利波频散曲线、理论视频散曲线和合成频散曲线对比图。由图9c可知,频散曲线呈现“之”字形。在5~8 Hz范围,合成频散曲线和一阶频散曲线具有较好的一致性。在2 Hz附近和4~5 Hz范围,合成频散曲线主要由基阶和一阶的频散曲线按能量占比复合而成。在其他频率范围,合成频散曲线和基阶频散曲线有较好的一致性。在图9c中,理论视频散曲线和合成频散曲线整体上具有较好的一致性,在高频部分略有差别。频率大于16 Hz时,理论视频散曲线呈现上升趋势,这与二阶瑞利波的能量占比不断提高有关。而合成频散曲线不存在明显的上升趋势,并且出现不连续现象。

理论视频散曲线和合成频散曲线在高频处的差异可能与台阵尺寸有关,试验所用的台阵难以准确估算大于18 Hz部分的合成频散曲线,只有更小尺寸的台阵才能准确地估算高频部分的频散曲线。

徐佩芬、杜亚楠等[7,11]指出用空间自相关法计算的频散曲线是由不同阶的频散曲线按能量占比复合而成。当地下介质存在低速软弱夹层或高速硬夹层时,在特定频率范围内高阶波的能量会占主导地位,频散曲线呈现“之”字形[27]。在复杂地层介质情况下,如果忽略高阶波仅对基阶频散曲线反演,会对反演精度产生不利影响。对于复杂地层介质,采用小台站微动勘探技术,可以取得较好的效果[1]。

4.4 频散曲线的有效最高频率

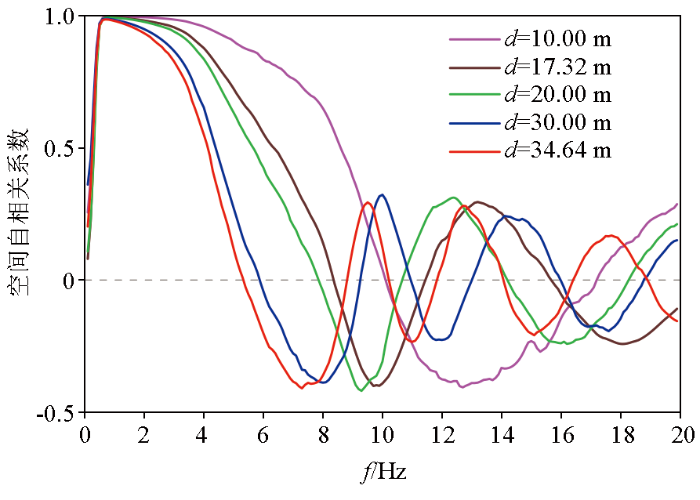
联合分析图5、6可知,虽然合成频散曲线在大于13 Hz部分频谱能量较分散(图5),但合成频散曲线与理论频散曲线在13~18 Hz范围仍较具有较好的一致性(图6)。这一结果表明频散曲线的有效最高频率至少为18 Hz。由图4可知,13 Hz是台站距离为10 m的空间自相关系数曲线的第一个极小值对应的频率,而台站距离10 m是台站距离组合中最小的一个。为了表述方便,将台站距离最小的空间自相关系数的第一个极小值点对应的频率,简称为“第一极小值频率”。对于本文合成的微动数据,因震源分布均匀,没有其他类型噪声,提取的频散曲线的有效最高频率突破了第一极小值频率的限制,达到了更高的18 Hz。对于实际采集的微动数据,由于台站数量有限、震源分布不均匀和存在非相关噪声等因素,提取的频散曲线有一定偏差,频散曲线的有效最高频率一般略小于第一极小值频率。采用小尺寸台阵,可以获得较高的第一极小值频率,从而提高频散曲线的有效最高频率。因此,对于微动波场较为均匀的安静场地,应用小尺寸台站往往能获得更高频的频散信息,有利于提高浅层分辨率。

5 结论

本文采用简正振型叠加法合成微动信号,应用空间自相关法计算合成频散曲线,并与理论频散曲线进行对比,发现两者具有较好的一致性。对微动信号模拟涉及的参数进行了数值试验,得到以下结论:

1)震源距离和台阵尺寸对结果有明显影响。模拟微动信号时应合理设置震源距离,实际观测时应根据勘探深度合理选择台阵尺寸。

2)在地层介质较复杂的情况下,特定频率范围的高阶瑞利波能量占主导地位,频散曲线呈现“之”字形,在这种情况下开展微动勘探应考虑高阶面波的影响。

3)在安静的观测场地,应用小尺寸台阵往往可以获得更高频的频散信息,有利于提高浅层分辨率。

参考文献

Xu P, Ling S, Long G, et al.

ESPAC-based 2D mini-array microtremor method and its application in urban rail transit construction planning

[J]. Tunnelling and Underground Space Technology, 2021, 115(3):104070.

DOI:10.1016/j.tust.2021.104070      URL     [本文引用: 2]

徐佩芬, 侍文, 凌苏群, 等.

二维微动剖面探测“孤石”:以深圳地铁7号线为例

[J]. 地球物理学报, 2012, 55(6):2120-2128.

[本文引用: 1]

Xu P F, Shi W, Ling S Q, et al.

Mapping spherically weathered "Boulders" using 2D microtremor profiling method:A case study along subway line 7 in Shenzhen

[J]. Chinese Journal of Geophysics, 2012, 55(6):2120-2128.

[本文引用: 1]

杜亚楠, 徐佩芬, 凌甦群.

土石混合滑坡体微动探测:以衡阳拜殿乡滑坡体为例

[J]. 地球物理学报, 2018, 61(4):1596-1604.

[本文引用: 1]

Du Y N, Xu P F, Ling S Q.

Microtremor survey of soil-rock mixture landslides:An example of Baidian township,Heng yang City

[J]. Chinese Journal of Geophysics, 2018, 61(4):1596-1604.

[本文引用: 1]

徐浩, 吴小平, 盛勇, 等.

微动勘探技术在城市地面沉降检测中的应用研究

[J]. 物探与化探, 2021, 45(6):1512-1519.

[本文引用: 1]

Xu H, Wu X P, Sheng Y, et al.

Application of microtremor survey method in detection of urban land subsidence

[J]. Geophysical and Geochemical Exploration, 2021, 45(6):1512-1519.

[本文引用: 1]

李巧灵, 张辉, 雷晓东, 等.

综合利用多道瞬态面波和微动探测分析斜坡内部结构

[J]. 物探与化探, 2022, 46(1):258-267.

[本文引用: 1]

Li Q L, Zhang H, Lei X D, et al.

Analysis of internal structure of slope by using multi-channel transient surface wave exploration and microtremor survey

[J]. Geophysical and Geochemical Exploration, 2022, 46(1):258-267.

[本文引用: 1]

李井冈, 谢朋, 王秋良, 等.

不同台阵形式对微动探测结果的影响

[J]. 大地测量与地球动力学, 2020, 40(1):98-103.

[本文引用: 1]

Li J G, Xie P, Wang Q L, et al.

Influence of different array type on the results of microtremor survey

[J]. Journal of Geodesy and Geodynamics, 2020, 40(1):98-103.

[本文引用: 1]

徐佩芬, 杜亚楠, 凌甦群, 等.

微动多阶瑞雷波SPAC系数反演方法及应用研究

[J]. 地球物理学报, 2020, 63(10):3857-3867.

[本文引用: 5]

Xu P F, Du Y N, Ling S Q, et al.

Microtremor survey method based on inversion of the SPAC coefficient of multi-mode Rayleigh waves and its application

[J]. Chinese Journal of Geophysics, 2020, 63(10):3857-3867.

[本文引用: 5]

Wang J, Wu G, Chen X.

Frequency-Bessel transform method for effective imaging of higher-mode Rayleigh dispersion curves from ambient seismic noise data

[J]. Journal of Geophysical Research:Solid Earth, 2019, 124(4):3708-3723.

DOI:10.1029/2018JB016595      URL     [本文引用: 2]

It has been widely recognized that the cross‐correlation function of ambient seismic noise data recorded at two stations approximates to the part of Greens function between two stations. Therefore, the cross‐correlation function should include higher modes, aside from the fundamental mode. However, the problem of measuring or extracting overtones from ambient seismic noise data remains. In this paper, we propose the frequency‐Bessel transform method (F‐J method) for extracting the dispersion curves of higher modes from ambient seismic noise data. We then assess the validity, accuracy, and applicability of the F‐J method by conducting extensive numerical simulations and processing the observed ambient seismic noise data of the USArray. As demonstrated in this study, the F‐J method is a convenient, practical, and accurate method for extracting the dispersion curves of multimodes from ambient seismic noise data and therefore has significant potentiality in the field of ambient seismic noise tomography.

李雪燕, 陈晓非, 杨振涛, 等.

城市微动高阶面波在浅层勘探中的应用:以苏州河地区为例

[J]. 地球物理学报, 2020, 63(1):247-255.

[本文引用: 1]

Li X Y, Chen X F, Yang Z T, et al.

Application of high-order surface waves in shallow exploration:An example of the Suzhou river,Shanghai

[J]. Chinese Journal of Geophysics, 2020, 63(1):247-255.

[本文引用: 1]

周晓华, 陈祖斌, 曾晓献, 等.

交错网格有限差分法模拟微动信号

[J]. 吉林大学学报:地球科学版, 2012, 42(3):852-857.

[本文引用: 1]

Zhou X H, Chen Z B, Zeng X X, et al.

Simulation of microtremor using staggered-grid finite difference method

[J]. Journal of Jilin University:Earth Science Edition, 2012, 42(3):852-857.

[本文引用: 1]

杜亚楠. 基于多阶瑞雷波视频散曲线和椭圆率曲线联合反演的微动探测方法研究[D]. 北京: 中国科学院大学, 2019.

[本文引用: 6]

Du Y N. The study on the microtremor survey method based on joint inversion of apparent dispersion curves with consideration of both fundamental and higher modes of Rayleigh waves,and ellipticity curve[D]. Beijing: University of Chinese Academy of Sciences, 2019.

[本文引用: 6]

周晓华, 林君, 张怀柱, 等.

微动中多模式面波频散曲线的映射式提取方法

[J]. 地球物理学报, 2014, 57(8):2631-2643.

[本文引用: 3]

Zhou X H, Lin J, Zhang H Z, et al.

Mapping extraction dispersion curves of multi-mode Rayleigh waves in microtremor

[J]. Chinese Journal of Geophysics, 2014, 57(8):2631-2643.

[本文引用: 3]

Herrmann R B.

Computer programs in seismology:An evolving tool for instruction and research

[J]. Seismological Research Letters, 2013, 84(6):1081-1088.

DOI:10.1785/0220110096      URL     [本文引用: 1]

Gilbert F.

Excitation of the normal modes of the earth by earthquake sources

[J]. Geophysical Journal of the Royal Astronomical Society, 1971, 22(2):223-226.

[本文引用: 2]

Woodhouse J H.

The calculation of the eigenfrequencies and eigenfunctions of the free oscillations of the Earth and the Sun

[J]. Seismological Algorithms, 1988, 230:321-370.

[本文引用: 1]

Dahlen F A, Tromp J. Theoretical global seismology[M]. Princeton: Princeton University Press, 1998.

[本文引用: 3]

Yang H Y, Zhao L, Hung S H.

Synthetic seismograms by normal-mode summation:A new derivation and numerical examples

[J]. Geophysical Journal International, 2010, 183(3):1613-1632.

DOI:10.1111/j.1365-246X.2010.04820.x      URL     [本文引用: 4]

Haskell N A.

The dispersion of surface waves on multilayered

[J]. Bulletin of the Seismological Society America, 1953, 43(1):17-34.

DOI:10.1785/BSSA0430010017      URL     [本文引用: 2]

A matrix formalism developed by W. T. Thomson is used to obtain the phase velocity dispersion equations for elastic surface waves of Rayleigh and Love type on multilayered solid media. The method is used to compute phase and group velocities of Rayleigh waves for two assumed three-layer models and one two-layer model of the earth's crust in the continents. The computed group velocity curves are compared with published values of the group velocities at various frequencies of Rayleigh waves over continental paths. The scatter of the observed values is larger than the difference between the three computed curves. It is believed that not all of this scatter is due to observational errors, but probably represents a real horizontal heterogeneity of the continental crusts.

Knopoff L.

A matrix method for elastic wave problems

[J]. Bulletin of the Seismological Society of America, 1964, 54(1):431-438.

DOI:10.1785/BSSA0540010431      URL     [本文引用: 1]

The solution to problems of elastic wave propagation in multilayered media, in which each layer is homogeneous and where the ensemble of layers has physical properties that vary only with one coordinate, may be given as the quotient of products of matrices. In the case of SH waves, the matrices are of order two; in the case of P-SV waves the matrices are of order four. The individual matrix elements are themselves determinants of order two or four in the two cases. The solution is obtained by means of Laplace's development by minors.

Buchen P W, Ben Hador R.

Free-mode surface-wave computations

[J]. Geophysical Journal International, 1996, 124(3):869-887.

DOI:10.1111/gji.1996.124.issue-3      URL     [本文引用: 1]

Abo Z A.

Dispersion function computations for unlimited frequency values

[J]. Geophysical Journal International, 1979, 58(1):91-105.

DOI:10.1111/j.1365-246X.1979.tb01011.x      URL     [本文引用: 1]

Chen X F.

A systematic and efficient method of computing normal modes for multilayered half-space

[J]. Geophysical Journal International, 1993, 115(2):391-409.

DOI:10.1111/gji.1993.115.issue-2      URL     [本文引用: 1]

凡友华, 刘家琦, 肖柏勋.

计算瑞利波频散曲线的快速矢量传递算法

[J]. 湖南大学学报, 2002, 29(5):25-30.

[本文引用: 1]

Fan Y H, Liu J Q, Xiao B X.

Fast vector-transfer algorithm for computation of Rayleigh wave dispersion curves

[J]. Journal of Hunan University:Natural Sciences Edition, 2002, 29(5):25-30.

[本文引用: 1]

Tokimatsu K, Tamura S, Kojima H.

Effects of multiple modes on Rayleigh wave dispersion characteristics

[J]. Journal of Geotechnical Engineering, 1992, 118(10):1529-1543.

DOI:10.1061/(ASCE)0733-9410(1992)118:10(1529)      URL     [本文引用: 1]

Harkrider D G.

Surface waves in multilayered elastic media. I. Rayleigh and Love waves from buried sources in a multilayered elastic half-space

[J]. Bulletin of the Seismological Society of America, 1964, 54(2):627-679.

DOI:10.1785/BSSA0540020627      URL     [本文引用: 1]

A matrix formulation is used to derive integral expressions for the time transformed displacement fields produced by simple sources at any depth in a multilayered elastic isotropic solid half-space. The integrals are evaluated for their residue contribution to obtain surface wave displacements in the frequency domain. The solutions are then generalized to include the effect of a surface liquid layer. The theory includes the effect of layering and source depth for the following: (1) Rayleigh waves from an explosive source, (2) Rayleigh waves from a vertical point force, (3) Rayleigh and Love waves from a vertical strike slip fault model. The latter source also includes the effect of fault dimensions and rupture velocity. From these results we are able to show certain reciprocity relations for surface waves which had been previously proved for the total displacement field. The theory presented here lays the ground work for later papers in which theoretical seismograms are compared with observations in both the time and frequency domain.

Ling S Q. Research on the estimation of phase velocities of surface waves in microtremors[D]. Sapporo: Hokkaidou University, 1994.

[本文引用: 1]

张碧星, 鲁来玉, 鲍光淑.

瑞利波勘探中“之”字形频散曲线研究

[J]. 地球物理学报, 2002, 45(2):263-274.

[本文引用: 1]

Zhang B X, Lu L Y, Bao G S.

A study on zigzag dispersion curves in Rayleigh wave exploration

[J]. Chinese Journal of Geophysics, 2002, 45(2):263-274.

[本文引用: 1]

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com