E-mail Alert Rss
 

物探与化探, 2023, 47(3): 810-815 doi: 10.11720/wtyht.2023.1086

方法研究·信息处理·仪器研制

测井方位遮挡下的反距离加权建模方法

王振涛,

胜利油田分公司 物探研究院,山东 东营 257022

Inverse-distance weighted modeling method under logging azimuth occlusion

WANG Zhen-Tao,

Geophysical Research Institute of SINOPEC Shengli Oilfield Branch Company,Dongying 257022,China

第一作者: 王振涛(1980-),男,高级工程师,2003年7月毕业于合肥工业大学资源与环境工程学院勘查技术与工程专业,主要从事地震反演和储层预测方法研究以及生产应用等工作。Email:wangzhentao998.slyt@sinopec.com

责任编辑: 叶佩

收稿日期: 2022-03-21   修回日期: 2022-11-28  

基金资助: 中国石化科技攻关项目“基于粘弹介质地震流体识别新技术研究”(P21046)

Received: 2022-03-21   Revised: 2022-11-28  

摘要

现有测井建模方法未考虑地质沉积方向性,建模精度低,为了解决这一问题,通过对测井反距离加权建模方法优缺点分析,提出了一种测井方位遮挡下的反距离加权建模方法。该方法采用方位遮挡反距离加权插值公式,在考虑已知信息点与插值点的距离影响因素的同时,还考虑了已知信息点间的方位遮挡因素,通过综合非方位遮挡权系数来定量描述已知样本间方位遮挡影响。数值试验和实际资料对该方法和传统方法的对比结果表明,该方法建模结果空间变化更加平缓和自然,符合地质沉积变化规律。测井方位遮挡下的反距离加权建模方法,体现了地质沉积空间连续性和方位性的特点,在提高测井地质建模精度方面优势明显,具有很好的实际应用价值。

关键词： 测井建模; 方位遮挡; 反距离权系数; 非方位遮挡权系数

Abstract

Existing log modeling methods fail to consider the directionality of geological deposition, yielding low modeling precision.To overcome this obstacle,this study proposed an inverse-distance weighted (IDW) modeling method under logging azimuth occlusion by analyzing the advantages and disadvantages of the IDW log modeling method.The new method proposed in this study adopted the IDW interpolation formula under azimuth occlusion.In addition to the influencing factors of the distance between known information points and interpolation points,the new method also considered the azimuth occlusion between known information points.Moreover,this study quantitatively described the influence of azimuth occlusion between known samples by integrating the weighting coefficients of non-azimuth occlusion.As indicated by the comparison between the new method and conventional methods based on numerical experiments and actual data,the modeling results of the new method showed gentler and more natural spatial variation,which conformed to the variation patterns of geological deposition.In sum,the method proposed in this study reflects the spatial continuity and directionality of geological deposition,has distinct advantages in improving the precision of geological log modeling,and thus can be widely applied to practical applications.

Keywords： log modeling; azimuth occlusion; inverse-distance weighting coefficient; non-azimuth occlusion weighting coefficient

PDF (2876KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

王振涛. 测井方位遮挡下的反距离加权建模方法[J]. 物探与化探, 2023, 47(3): 810-815 doi:10.11720/wtyht.2023.1086

WANG Zhen-Tao. Inverse-distance weighted modeling method under logging azimuth occlusion[J]. Geophysical and Geochemical Exploration, 2023, 47(3): 810-815 doi:10.11720/wtyht.2023.1086

0 引言

地震和测井数据是油气勘探开发中最为常用的两类地球物理观测数据。地震数据对地质构造空间描述性强,但其信息频带有限,往往不能满足薄储层研究要求。测井数据具有频带宽、精度高及靶向性强等特点,可较好揭示井点处储层厚度、岩性、物性及流体等油藏特征,但测井数据是一维数据,难以表征地质储层三维空间连续变化。地震构造约束下构建测井模型能够直观表征地质储层空间变化,可直接用于油气勘探开发储层油藏描述[1⇓⇓⇓-5],还可用于地震反演约束,提高地震弹性参数反演精度,再进行储层油藏描述[6⇓⇓-9]。利用已知点数值估计未知点数值是测井插值建模的关键,常用的方法有反距离加权法、克里金插值、最近邻点插值等方法,建模方法众多,最终结果也不尽相同。因此,针对不同的数据需要根据其类型、分布特征及相关性等影响因素进行优选[9⇓⇓⇓⇓⇓⇓⇓-17]。

测井数据具有空间相关性,符合地理学第一定律:地理空间上的所有值均互相联系,且距离近的值联系更强[18]。因此,反距离加权作为描述数据距离相关性的方法在数据建模中得到广泛应用,其具有以下假设:2个物体相似性随距离增大而减小,以插值点与样本点的距离的倒数作为加权系数进行样本点数值加权平均,从而得到插值点数值。该方法中每个样本点均会对插值点有贡献,只是贡献大小会随距离远近而变化,离插值点越近的样本点贡献越大,越远的样本点贡献越小,如2个样本点与插值点相同,其贡献就完全相同。

最近邻点插值方法和克里金插值法中,只有靠近插值点的已知点有贡献,反距离加权方法所有未知点都会有贡献,贡献大小与距离相关[19-20]。克里金插值方法也是常用的一种数据建模方法,是由法国地理学家Matheron和南非矿山工程师Krige提出,用于矿山勘探。与反距离加权方法最大的不同在于加权系数的求取,克里金法加权系数是满足插值点估计值与期望值差最小目标条件的一套优化权系数,需要计算半方差函数(也称为变差函数或变异函数),利用观测数据两两计算距离和半方差数据对,然后利用球状、指数及高斯等理论模型拟合距离和半方差关系函数,一般距离近方差小,距离远方差大,方差随着距离变化到一定程度会相对稳定不再变化,称为基台值,此时对应的距离称为变程。利用变差函数可估算插值点到任意距离样本点的半方差,然后利用方差函数并优化目标函数得到权系数,其加权系数仍为与距离有关的函数,距离插值点越近的样本点贡献越大。克里金插值方法与反距离插值方法的不同在于,样本点对插值点贡献大小并非由距离倒数决定,而是取决于变差函数,同时当样本点与插值点距离超过统计变程就不会产生贡献。克里金方法用变程距离描述了空间数据不相关性,更匹配实际数据变化情况。

最近邻点插值、反距离加权和克里金插值等方法均只考虑了数据点空间相关性与距离关系。由于地质沉积具有连续性和方向特点,因此测井数值大小与地质构造和沉积物源方向密切相关,测井数据不仅具有强空间相关性,而且具有连续性和方向性。测井建模中除了要考虑距离因素,还应该考虑方位因素,距离预测点近的测井会对较远测井产生方位遮挡,常用测井插值建模方法只考虑距离而没考虑这种方位遮挡关系,影响测井建模精度。

针对常用插值方法存在的问题,笔者提出了一种测井方位遮挡反距离加权插值方法,在常规插值建模分析对比的基础上,构建了方位遮挡反距离加权插值公式,研究距离和方位双影响因素的权系数计算方法,并利用模型数据进行了数值对比试验,并且在实际资料中开展了应用。

1 方法原理

1.1 测井反距离加权建模

测井反距离加权插值是常用的测井建模方法,其插值建模公式通常表示为:

z=∑i=1nzi1dip∑i=1n1dip

式中:z为待插数值;zi为测井点号i处对应的测井数值,i=1,2,…,n;di为插值点到已知测井点的距离;1di为反距离加权系数;p称为加权幂指数,是大于0的常数,该值越大插值结果会越平滑。

从式(1)中可以看出,测井样本点对插值点的影响除了样本点自身的属性大小外,只与2点间的距离远近有关系,距离越远的样本点对插值点贡献会越小,任一测井样本点会对任何位置和方向的点产生影响,但该方法只考虑了空间数据相关性,没有考虑地质沉积由于物源和构造控制造成的空间数据方向性。

1.2 测井方位遮挡反距离加权建模

针对地质沉积和测井数据具有空间相关性和方向性的特点,研究发展并形成测井方位遮挡反距离加权插值方法,其插值建模公式为:

z=∑i=1nziβiq1dip∑i=1nβiq1dip

相比式(1),式(2)中增加了综合非方位遮挡权系数βi,描述了测井点被其他测井遮挡情况,q同样为加权幂指数,是大于0的常数,该值越大插值结果会越平滑。在相同方位上,距离插值点近的测井样本点会对远距离的测井产生遮挡,测井点对插值点的贡献不仅与距离有关,而且与其他测井点的分布方位有关。

图1为测井方位遮挡反距离加权建模方法示意,测井点zk(x1,y1)对插值点z(x,y)的贡献不仅与两者距离d1有关,而且也与距离插值点更近的测井点对其遮挡有关,图1中,测井点zk(x2,y2)会对测井点zk(x1,y1)产生遮挡效应,用综合非方位遮挡权系数βij定量表示,计算过程为:以插值点z(x,y)为顶点,以测井点zk(x1,y1)和zk(x2,y2)到插值点z(x,y)连线为边组成夹角∂12,该角度越小,zk(x1,y1)被zk(x2,y2)遮挡越严重,当夹角为0时,可认为zk(x1,y1)被完全遮挡,其对插值点无贡献;随着该夹角增大,zk(x1,y1)受zk(x2,y2)遮挡影响小,可设定最大遮挡夹角角度ω,当夹角∂12大于ω时,认为zk(x1,y1)不受zk(x2,y2)遮挡,其对插值点贡献由其到插值点的距离决定。两个测井间的这种遮挡关系,可以用非方位遮挡权系数β表示,样本点zk(xi,yi)被样本点zk(xj,yj)的两两非方位遮挡权系数计算公式为:

βij=sin∂ij 0≤∂ij<ω,dj<di1 其他  

式中:∂ij为遮挡角度,0°≤∂ij≤180°;ω为根据实际数据分析确定的最大遮挡角度,一般取值0°≤ω≤90°。

图1

新窗口打开| 下载原图ZIP| 生成PPT

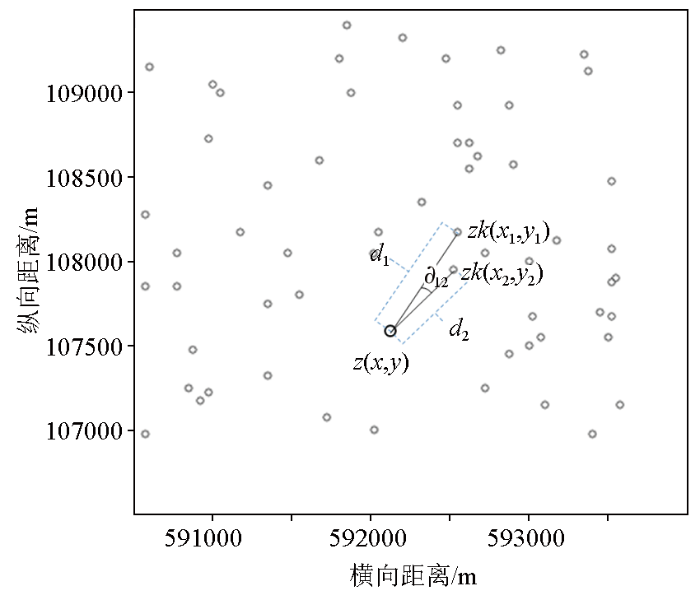
图1   测井方位遮挡反距离插值原理示意

Fig.1   Schematic diagram of logging azimuth occlusion inverse distance interpolation


通过测井已知点两两组合可以得到测井点相互间的非方位遮挡权系数,然后将每个测井点与其他测井点计算得到非方位遮挡权系数相乘,就可以得到每个测井点对插值点的综合非方位遮挡权系数,计算公式为:

βi=∏j=1nβij 。

与距离倒数作用一样,综合非方位遮挡权系数的大小也会影响样本点对插值点的贡献,该值越大,测井点受其他测井点方向遮挡越小,与距离插值点相同测井点相比,对插值点的贡献越大,最后插值大小是由所有测井数值进行反距离加权系数和综合非方位遮挡权系数进行加权平均得到。通过理论方法对比可以看出,该方法考虑到地质数据空间的相关性和方向性,相比反距离加权建模方法更适合测井数据建模。

2 数值试验

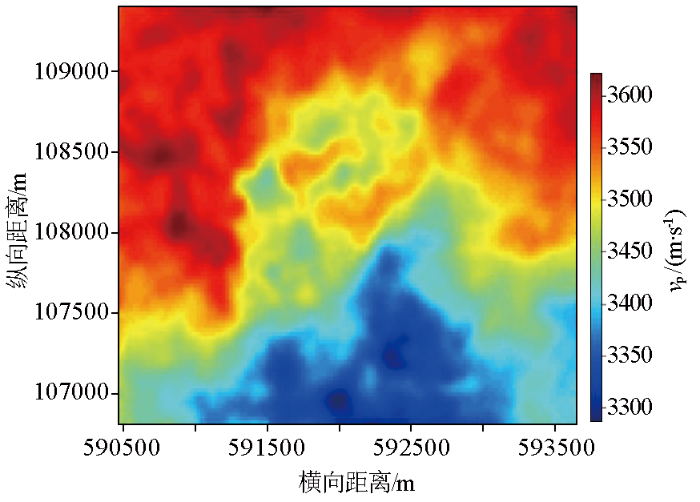
图2为从三维速度体提取的一平面切片。作为数值试验平面比对速度模型,模型纵、横向长均为3 000 m,是面积为9 km2的正方形,根据实际地震采集处理参数,设置网格为25 m×25 m。可以看出,提取模型属性中,速度宏观表现为北高南低,局部速度存在变化。从该平面比对速度模型中分别随机提取60个点和120个点速度值并记录坐标,用来模拟测井点某沉积时期的平均速度,然后分别利用测井方位遮挡反距离加权建模方法和测井反距离加权建模方法进行建模试验,并与平面比对速度模型进行对比分析。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   实际速度模型平面切片

Fig.2   Actual velocity model flat slice


图3为采用60个模拟测井点进行建模试验结果,模拟测井点分布密度为6.6个/km2,与平面比对速度模型对比(图2)可以看出:两种建模方法结果均能宏观表现速度北高南低变化特征;测井反距离加权建模速度存在井点局部异常“牛眼效应”(图3a);而测井方位遮挡反距离加权建模速度变化自然,在试验工区南部低速度区域,控制井位少,因为考虑了井间方位遮挡,不会受高速度区域内大数量测井点的影响,建模结果体现了区域速度特点,与平面比对速度模型吻合情况更好(图3b)。

图3

新窗口打开| 下载原图ZIP| 生成PPT

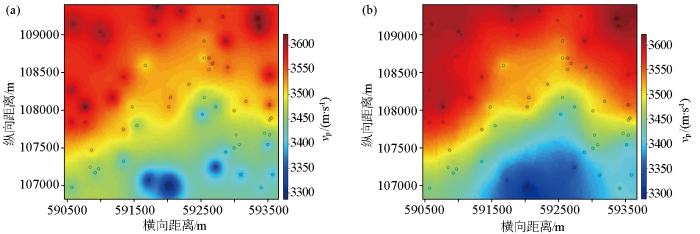
图3   采用60个模拟测井点速度建模切片

a—测井反距离加权建模;b—测井方位遮挡反距离加权建模

Fig.3   Velocity modeling slice with 60 simulated logging points

a—inverse distance weighted modeling of logging;b—inverse distance weighting modeling under logging azimuth occlusion


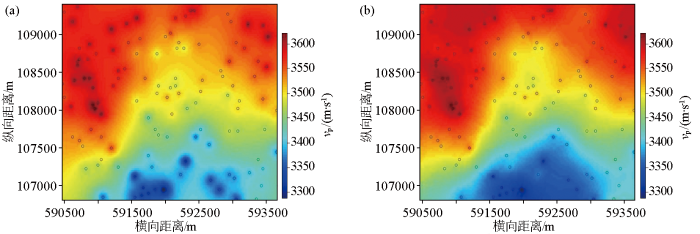
图4为采用120个模拟测井点进行插值建模的试验结果,模拟测井分布密度为13.3个/km2,相比图3所示试验,样本点增加一倍。试验结果表明,2种建模方法精度均随着测井控制点数量增多而提高。测井反距离加权建模方法在测井局部分布密度低、速度横向变化快的区域,依然存在局部异常“牛眼效应”,只是异常范围变小(图4a)。测井方位遮挡反距离加权建模结果速度变化自然(图4b),相比采用60个模拟测井点进行平面速度建模试验结果(图3b),由于增加了测井控制点,模型速度横向细节变化表现能力增强,同时较好地保持宏观速度变化特征,与比对模型速度吻合程度进一步提高了。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   采用120个模拟测井点速度建模切片

a—测井反距离加权建模;b—测井方位遮挡反距离加权建模

Fig.4   Velocity modeling slice with 120 simulated logging points

a—inverse distance weighted modeling of logging;b—inverse distance weighting modeling under logging azimuth occlusion


3 实际数据应用

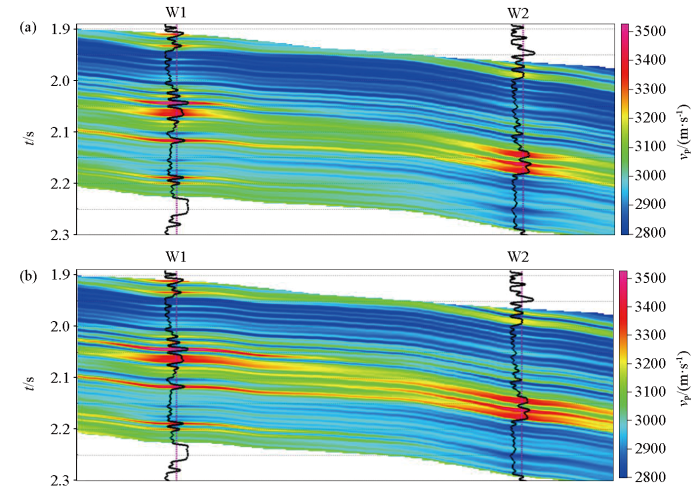
在SL油田开展了实际资料测井速度建模应用,工区网格为25 m×25 m,面积约为55 km2,采用7口测井数据,井口分布密度相对较低,仅为0.13口/ km2,为匹配实际地震频带,将测井速度曲线进行了高截频滤波处理,高截频率120 Hz,然后开展了测井速度模型构建。

图5为采用不同建模方法获得的速度模型剖面对比,2种速度建模结果中,井点处模型速度与测井速度都吻合较好。图5a采用测井反距离加权建模方法得到速度剖面,可以看出,井点周围受井影响明显,测井横向连续性差。图5b采用测井方位遮挡反距离加权建模方法得到速度剖面,井间速度过渡变化更加自然。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   SL油田测井速度建模剖面

a—测井反距离加权建模;b—测井方位遮挡反距离加权建模

Fig.5   Velocity modeling profile of SL oil field

a—inverse distance weighted modeling of logging;b—inverse distance weighting modeling under logging


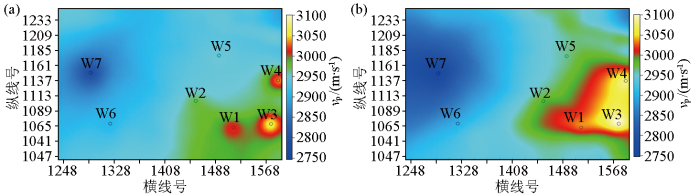
对速度建模提取的整个模型时窗平均速度平面属性进行分析(图6)可以看出,2种方法均能够反映区域速度宏观变化特征,整个建模工区为深湖相沉积,物源来自东南方向,西北部为沉积洼陷中心,主要为低速度泥岩沉积地层,东南部靠近物源,地层为深湖相泥岩夹浊积砂岩组合,砂泥比相对较高,因此地层速度整体偏高。2种方法对比显示,图6a为采用测井反距离加权建模方法得到速度平面属性,井点周围受井影响明显,有明显的“牛眼现象”,当井与其他钻井速度差异大时,这种现象会更明显;图6b为采用测井方位遮挡反距离加权方法速度建模剖面,速度变化更加自然,体现地质沉积空间方向性和连续性的特征,该速度模型提高了地质研究人员区域地质沉积认识,可为地震反演提供更可靠的初始速度模型。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   SL油田速度建模切片

a—测井反距离加权建模;b—测井方位遮挡反距离加权建模

Fig.6   Velocity modeling slice of SL oil field

a—inverse distance weighted modeling of logging;b—inverse distance weighting modeling under logging


4 结论与认识

本文研究了测井方位遮挡反距离加权建模方法,利用反距离权系数和综合非方位遮挡权系数联合加权建模,并提供了非方位遮挡权系数的计算方法,该方法能够顾及测井距离和方位双重因素影响,更能够体现地质沉积岩性空间相关性和方向性特点。测井方位遮挡反距离加权建模方法能够提高建模精度,建模结果变化过渡自然,符合地质沉积变化,测井控制点越多,建模精度越高;在测井及其他非均匀离散数据建模中具有广阔的推广应用前景。

参考文献

Vail P R, Michum R M, Thompson S.

Global cycles of relative changes of sea level

[J]. AAPG Memoir, 1977, 26:83-97.

[本文引用: 1]

Vail P R.

Sequence stratigraphy workbook,fundamentals of sequence stratigraphy

[J]. AAPG Annual Converntion Short Course:Sequence Stratigraphy Interpretation of Seismic Stratigraphy Interpretation Procedure,1988.

[本文引用: 1]

凌云, 郭向宇, 夏竹, 等.

基于储层构造和沉积等时格架的储层静态建模实例而研究

[J]. 石油地球物理勘探, 2014, 49(1):795-806.

[本文引用: 1]

Ling Y. Guo X Y, Xia Z, et al.

A case study of reservoir static modeling based on reservoir structure and sedimentary isochronous framework

[J]. Oil Geophysical Prospecting, 2014, 49(1):795-806.

[本文引用: 1]

孙伟, 刘远洋, 高蕾, 等.

储层速度建模分析及域转换

[J]. 成都理工大学学报:自然科学版, 2017, 44(6):744-755.

[本文引用: 1]

Sun W, Liu Y Y, Gao L, et al.

Analysis of reservoir velocity modeling and domain conversion

[J]. Journal of Chengdu University of Technology:Science & Technology Edition, 2017, 44(6):744-755.

[本文引用: 1]

黄继新, 彭仕宓, 黄健全.

储集层参数随机建模方法在扇三角洲储集层非均质性研究中的应用

[J]. 石油勘探与开发, 2005, 32(6):52-55.

[本文引用: 1]

Huang J X, Peng S M, Huang J Q.

Application of stochastic simulation of reservoir parameters on heterogeneity in fan delta reservoir

[J]. Petroleum Exploration & Development, 2005, 32(6):52-55.

[本文引用: 1]

伍宁南, 陈玉明, 刘漪.

测井约束反演技术在建南地区南部储层预测中的应用

[J]. 长江大学学报:自然科学版, 2011, 8(2):44-45.

[本文引用: 1]

Wu N N, Chen Y M, Liu Q.

Application of logging constrained inversion technology in reservoir prediction in the south of Jiannan District

[J]. Journal of Yangtze University:Natural and Science Edition, 2011, 8(2):44-45.

[本文引用: 1]

姜雄鹰, 傅志飞.

高分辨率地震反演技术及应用

[J]. 成都理工大学学报:自然科学版, 2011, 38(3):271-276.

[本文引用: 1]

Jiang X Y, Fu Z F.

High-resolution seismic inversion technology and its application

[J]. Journal of Chengdu University of Technology:Science & Technology Edition, 2011, 38(3):271-276.

[本文引用: 1]

余为维, 冯磊, 杜艳艳, 等.

测井约束与神经网络联合反演储层预测技术

[J]. 地球物理学进展, 2016, 31(5):2232-2238.

[本文引用: 1]

Yu W W, Feng L, Du Y Y, et al.

Reservoir prediction technology based on joint inversion of logging-constrained and neural network

[J]. Progress in Geophsics, 2016, 31(5):2232-2238.

[本文引用: 1]

尹力, 方伍宝, 李振春, 等.

测井模型约束全波形反演的应用

[J]. 大庆石油地质与开发, 2015, 34(3):156-160.

[本文引用: 2]

Yin L, Fang W B, Li Z C, et al.

Application of the well logging model constraining the full waveform inversion

[J]. Petroleum Geology & Oilfield Development in Daqing, 2015, 34(3):156-160.

[本文引用: 2]

郭良辉, 孟小红, 郭志宏, 等.

地球物理不规则分布数据的空间网格化法

[J]. 物探与化探, 2005, 29(5):438-442.

[本文引用: 1]

Guo L H, Meng X H, Guo Z H, et al.

Gridding methods of geophysical irregular data in space domain

[J]. Geophysical and Geochemical Exploration, 2005, 29(5):438-442.

[本文引用: 1]

李小东, 金胜, 王阳玲, 等.

散乱离散点数据的三角形网格化快速成图

[J]. 物探与化探, 2015, 39(1):156-160.

[本文引用: 1]

Li X D, Jin S, Wang Y L, et al.

Triangular grid-based rapid mapping of scattered data

[J]. Geophysical and Geochemical Exploration, 2015, 39(1):156-160.

[本文引用: 1]

刘兆平, 杨进, 武炜.

地球物理数据网格化方法的选取

[J]. 物探与化探, 2010, 34(1):93-97.

[本文引用: 1]

Liu Z P, Yang J, Wu W.

The choice of gridding methods for geophysical data

[J]. Geophysical and Geochemical Exploration, 2010, 34(1):93-97.

[本文引用: 1]

王长海, 陈碧宇.

基于离散光滑插值的三维地质体构造网格模型

[J]. 深圳大学学报:理工版, 2014, 31(6):600-607.

[本文引用: 1]

Wang C H, Chen B Y.

3D geological grid model based on discrete smooth interpolation

[J]. Journal of Shenzhen University Science and Engineering, 2014, 31(6):600-607.

DOI:10.3724/SP.J.1249.2014.06600      URL     [本文引用: 1]

余继峰, 于泳, 付文钊, 等.

测井数据Matlab插值与地质旋会性分析应用

[J]. 煤炭学报, 2011, 36(10):1679-1682.

[本文引用: 1]

Yu J F, Yu Y, Fu W Z, et al.

Application of interpolation of well logs based on Matlab to analysis of geological cyclicity

[J]. Journal of China Coal Society, 2011, 36(10):1679-1682.

[本文引用: 1]

刘志怀.

沿层微测井插值方法反演复杂地区近地表模型

[J]. 郑州大学报:工学版, 2013, 34(1):121-124.

[本文引用: 1]

Liu Z H.

Near-surface model inversion in complex terrain area by along-horizon interpolation method

[J]. Journal of Zhengzhou University:Engineering Science, 2013, 34(1):121-124.

[本文引用: 1]

张学宏, 李颜, 郝培章, 等.

水文资料插值计算方法探讨

[J]. 海洋预报, 2008, 25(1):5-13.

[本文引用: 1]

Zhang X H, Li Y, Hao P Z, et al.

Discussion on the interpolation calculation methods of hydrological data

[J]. Marin Forecasts, 2008, 25(1):5-13.

[本文引用: 1]

胡刚, 赵刚, 宋慧.

不同插值方法对降水量空间不确定性的影响

[J]. 济南大学学报:自然科学版, 2012, 26(4):428-432.

[本文引用: 1]

Hu G, Zhao G, Song H.

Influence of different interpllation methods on spatial univertainty of rainfall

[J].

Journal of University of Jinan:Sci.and Tech.

2012, 26(4):428-432.

[本文引用: 1]

Tobler W R.

A computer movie simulating urban growth in the Detroit region

[J]. Economic Geography, 1970, 46(s1):234-240.

DOI:10.2307/143141      URL     [本文引用: 1]

刘国峰, 孟小红, 岳延波, 等.

克里金法在GPS数据内插中的应用

[J]. 物探与化探, 2006, 30(2):175-178.

[本文引用: 1]

Liu G F, Meng X H, Yue Y B, et al.

The application of keiging to GPS data interpolation

[J]. Geophysical and Geochemical Exploration, 2006, 30(2):175-178.

[本文引用: 1]

段平, 盛业华, 李佳, 等.

自适应的IDW插值方法及其在气温场中的应用

[J]. 地理研究, 2014, 33(8):1417-1426.

DOI:10.11821/dlyj201408003      [本文引用: 1]

反距离权重(Inverse Distance Weighting,IDW)插值通常采用距离搜索策略选择插值参考点,当采样点集分布不均匀时,距离搜索策略使得参考点聚集一侧影响插值精度。自然邻近关系具有良好的自适应分布特性,可有效地解决参考点分布不均匀问题。结合自然邻近关系,提出自适应的反距离权重(Adaptive-IDW,AIDW)插值方法。首先对采样数据构建初始Delaunay三角网,然后采用逐点插入法,将待插值点插入初始Delaunay三角网中,局部调整得到新的Delaunay三角网,以待插值点的一阶邻近点作为IDW插值的参考点,使参考点自适应均匀地分布在待插值点周围,再进行IDW插值计算。利用AIDW插值方法对Franke函数、全国气温观测数据进行插值实验,结果表明此方法具有较高的精度,且减少了“牛眼”现象。

Duan P, Sheng Y H, Li J, et al.

Adaptive IDW interpolation method and its application in the temperature field

[J]. Geographical Research, 2014, 33(8):1417-1426.

DOI:10.11821/dlyj201408003      [本文引用: 1]

The Inverse Distance Weighting (IDW) interpolation has the advantage of simpleness, convenience for calculation, and high compatibility with Tobler's first law. It is widely used in construction of DEM, weather analysis, hydrological analysis, and so on. Distance search strategy is usually adopted by the IDW interpolation to select referent points. However, referent points gathering in one side may cause the loss of interpolation accuracy when sampling points are unevenly distributed. The natural adjacency spatial relationship with good adaptive characteristics about choosing referent points can effectively solve the problem of reference points’ uneven distribution. Based on this, the adaptive inverse distance weighting (AIDW) interpolation method was proposed in this paper. Firstly, the initial Delaunay triangulation was built with the sampling data points. Secondly, interpolative points were inserted one by one, the purpose of which was making the referent points evenly distributed around the interpolative points by taking the first-order neighboring of interpolative points as referent points. At last, IDW was interpolated. In step two, when each point was inserted, the Delaunay triangulation should be reconstructed, which elapseded time a lot. To solve this problem, the patial grid index was built in order to raise the speed of Delaunay triangulation's reconstruction. Compared with ordinary IDW, there was no need to assign the number of referent points or search radius in the AIDW, because the referent points could be adaptively selected with the natural adjacency spatial relationship of interpolative points. Especially when referent points were too intensive, the problem of superfluous points being inserted could be avoided. Two experiments were conducted in this paper, which were the theoretical surface reconstruction of the Franke and the national surface air temperature field reconstruction respectively. The results were compared with IDW interpolation methods with different search strategies in ArcGIS 10.1, which verify that the proposed method have higher accuracy. Meanwhile, the results of the proposed method show that the 'buphthalmos' phenomenon is reduced. All the outcomes indicate that the proposed method can be applied in the interpolation of geographical phenomenon as a new method.

/

〈 〉

京ICP备05055290号-3
版权所有 © 2021《物探与化探》编辑部
通讯地址：北京市学院路29号航遥中心 邮编：100083
电话：010-62060192；62060193 E-mail：whtbjb@sina.com , whtbjb@163.com