0 引言
随着时代的发展和技术进步,地质目标逐渐趋向于复杂的地质构造,因此对于地震成像的精度和准确性有了更高的要求。速度是地震勘探领域最重要的参数之一,对高精度地震成像以及储层岩性的刻画起着非常重要的作用。确定地层的速度是地震勘探的核心内容之一。
1 全波形反演方法的发展历程
全波形反演算法的理论基础是基于1983年Lailly[11]推导的基于波动方程的模型参数梯度公式,由散射波理论将模型参数与波长分解为背景值与扰动量,利用共轭状态思想得到模型修正量与扰动波场的关系,形成了基于误差反传的梯度求取方法。Tarantola[12]在20世纪80年代,提出了基于广义最小二乘的时间域全波形反演,奠定时间域全波形反演的理论基础,该方法适用于多种观测系统,反演时利用多种波形信息,摆脱了仅用反射波的局限性,与常规偏移成像的方法截然不同[12⇓⇓⇓-16]。自此全波形反演被大力发展,其后也有大量的学者为全波形反演体系的发展添砖加瓦,Tarantola借鉴共轭状态求梯度的思想,由炮点正传波场与检波点残差逆转波场互相关估计出梯度方向,避开了Frecher导数的直接计算[17⇓-19]。Pratt等[20]在 20世纪90年代提出了频率域全波形反演,将FWI技术带领到一条新的道路上,使得全波形反演更易于实用。2008年,Shin等和Lee等[21⇓⇓-24]提出了Laplace域全波形反演方法,由衰减波形记录的直流分量进行反演。以此来产生宏观模型,这个宏观模型对初始模型不敏感,以这个宏观模型为初始模型进行全波形反演。Sheng等[25]在2012年提出了反射波波形反演的方法,这个方法在实际的陆上资料应用中取得了不错的效果,被大众所接受,这也代表了一种独特的特征波全波形反演。
目前,主流的3种全波形反演方法各有特点:时间域全波形反演的优势在于能够灵活的对地震数据进行必要的预处理和选择需要的特征波,对内存的需求较小,但是由于时间域资料的连续性,在反演过程中会增加全波形反演解的非唯一性,使得迭代过程逐渐收敛于局部极小值;频率域全波形反演能够直接在频率域求解,仅需要几个离散的频率数据就可以完成高精度的速度建模,更加高效、准确,但是受到内存需求以及庞大的计算量限制;Laplace域全波行反演可以得到更可靠的低频数据与长波长信息,但是反演的精度明显低于时间域全波形反演与频率域全波形反演。这三类全波形反演方法各有优缺点,都在不停的发展与改善当中。
2 全波形反演的原理与方法
全波形反演方法是利用叠前地震波场的运动学和动力学信息,重建地下速度结构,具有揭示复杂地质背景下构造与岩性细节信息的潜力。原则上全波形反演适用所有类型的地震波,如直达波、绕射波、回折波、折射波、透射波、反射波、多次波等。
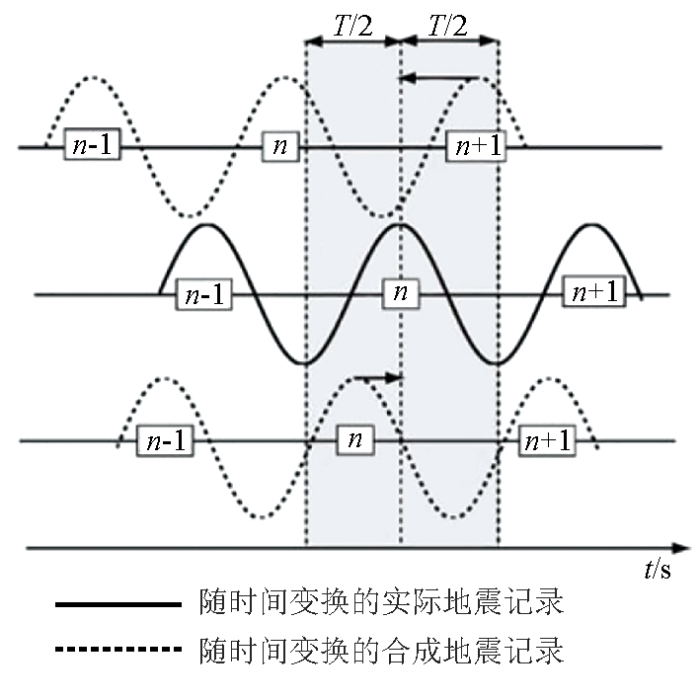
全波形反演(FWI)是通过选择一组震源和一个初始模型来展开的,两者是通过正演模拟计算得到合成地震记录所必需的,将得到的合成地震记录与观测地震记录进行比较,利用对比得到的误差共同定义目标函数,对目标函数进行伴随模拟后再进行反复的梯度计算,通过反复迭代来更新初始模型,直到反演达到目标函数的最小值为止。全波形反演数据处理流程见图1。
图1
2.1 初始模型
对于常规的全波形反演算法来说,反演过程中需要一个接近真实的准确的初始速度模型,要求根据初始模型得到的模拟地震记录与观测地震记录的波形走时差异小于半个波长,即走时差异应小于
图2
走时层析成像作为常用的速度建模方法[30⇓⇓-33],利用了地震波的走时信息来进行速度建模,通过拾取到时信息对数据进行预处理后,选择合适的偏移距构建速度模型,将该模型与走时数据联合迭代反演获得层析成像速度结构,对层析成像速度结构进行平滑处理得到我们需要的最终初始速度模型。崔永福等[34]采用多尺度时间域分层全波形反演方法,将层析成像的结果作为全波形反演的初始模型,利用回转波层析成像技术建立浅层的速度模型,再使用反射波层析成像建立中层与深层的各向同性速度模型来进行分层全波形反演,通过曲波变换联合去噪技术在保护地震资料低频信息和波的动力学特征前提下,满足了全波形反演对数据的需求,得到了合理且高精度的反演结果。
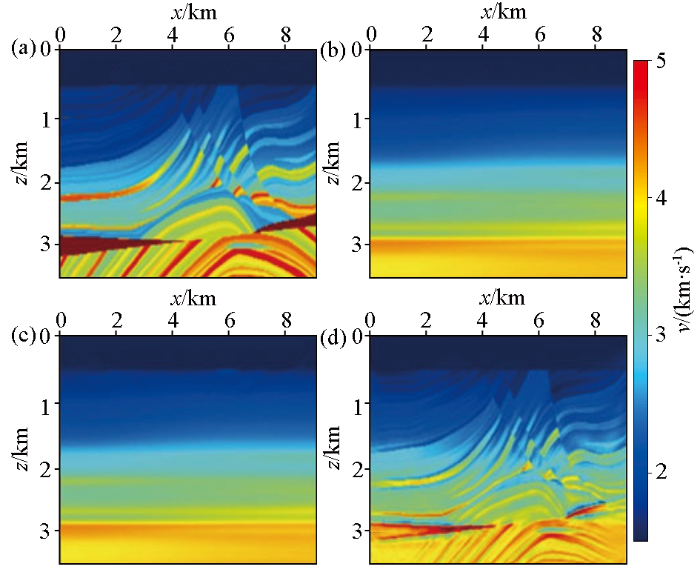
和走时层析成像不同,偏移后的成像数据由于具有更高的信噪比、相干性更好的同相轴以及更简单的波形等优点在反演数据空间的提取方面具有更大的优势,对一个给定的初始模型进行叠前深度偏移,估算速度误差并且更新初始速度模型,反复迭代更新直至误差小于某一条件,得到最终的初始速度模型。Biondi和Almomin[35]联合了偏移速度分析与全波形反演提出了TFWI(tomographic full waveform inversion),对Marmousi模型进行了测试,结果如图3,测试结果表明TFWI对初始模型的精度要求不是很高,却能很好地全局收敛,并展示出了很好精确性。但偏移速度分析方法需要对反射界面进行拾取其计算成本过高以及存在局部极小值等问题,国内外学者也多把该方法用于偏移成像领域而不是全波形反演的初始模型。
图3
更准确的初始模型可以避免在反演过程中陷入局部极值的困境,而正演模拟是反演的基础,反演的精度和效率很大程度上取决正演模拟的精度与效率[37]。
2.2 正演模拟
通过给定的初始模型和震源参数来模拟地震波的传播过程即为正演模拟。
有限元可模拟任意复杂的介质模型,处理自由界面时相较于其他方法也更加方便与准确[46],但是由于算法复杂、计算代价高且受限于计算机等因素,使得高阶有限元模拟十分困难。所以波场正演模拟多选用更易于实现、计算更加高效的有限差分法。Mora[47]利用有限差分法来进行波动方程的数值模拟计算,实现了时间域的全波形反演,Bunks等[48]也提出了基于有限差分法的时间域的多尺度的反演方法,将问题分成了多空间尺度求解来保证反演的收敛,节省计算成本,可以处理复杂的地质模型,大大提高了反演的速度。吴国忱、梁锴、殷文等[18,49 -50]将25权平均差分算子用于弹性介质与各向异性介质中波场的高精度有限差分模拟中。
通过初始模型与正演模拟获得一个满意的合成地震记录后,选取一个合适的目标函数对于后续的反演也至关重要。
2.3 目标函数
构造一个合适的目标函数可以极大地提高反演结果的分辨率,可以通过目标函数来衡量最优化的过程是否收敛。定义全波形反演的目标函数种类众多。
最传统也是最早被使用的目标函数为合成地震记录与观测地震记录之间差值的最小二乘形式即:
式中:
最小二乘法范数即L2范数为频率域全波形反演提供了最常见的框架[55],但是其数据与模型表现为高度非线性,抗噪性较差,反演容易陷入局部极小值,因此可以考虑其他范数。
定义好所需的目标函数后,接下来需要对目标函数的优化更新。
2.4 优化方法
目标函数的优化过程即速度模型迭代更新的过程。多采用局部优化反演方法使目标函数达到最小。现有的优化方法多是基于梯度的局部优化算法与基于牛顿的局部优化算法。
最速下降法[63]、共轭梯度法[64-65]等基于梯度的局部优化算法通过求解梯度来获得误差函数的最快上升方向,通过估算步长和负梯度方向求取反演模型的更新量来进行迭代运算,相较于牛顿类算法收敛速度较慢;牛顿类算法(牛顿法、高斯—牛顿法等)利用目标函数的一阶偏导的梯度算子和二阶偏导的Hessian矩阵进行约束,反演更稳定,理论收敛速度更快。但是需要对Hessian矩阵求逆,计算量巨大,显式计算和存储Hessian及其逆算子十分困难。拟牛顿法[19,53]利用目标函数梯度和模型参数构造近似Hessian矩阵,利用近似Hessian矩阵来代替Hessian矩阵,稳健性和收敛速度都优于常规的梯度类方法,被认为是最为实用的牛顿类算法。
上述局部优化方法都面临着局部最小值的问题:即受初始模型差、缺乏低频数据、数据质量差等问题影响时,可能无法收敛到局部极小值,计算方法的改进与计算硬件的更新使模拟退火算法[71-72]和遗传算法[73-74]等全局优化算法也被应用到全波形反演中。全局优化方法对于初始模型的依赖程度较低,有限避免了周期跳跃现象的产生,但全局优化算法的收敛速度慢且计算量庞大。所以地球物理学者们结合了全局优化算法和局部优化算法,采用先全局优化全波形反演建立可靠的初始模型,再展开基于局部优化算法的全波形反演,有效压制了周期跳跃问题[75]。有学者进一步提出基于迭代反演策略的混合优化全波形反演方法,提高了部分计算量,但是反演精度得到了明显提升[76-77]。
通过以上的迭代,如果目标函数的数值不断减小,而且迭代模型趋于稳定,则在一定迭代次数之后,我们可以得到一个最终优化的模型。
3 全波形反演方法的研究与应用
3.1 海上地震资料的应用
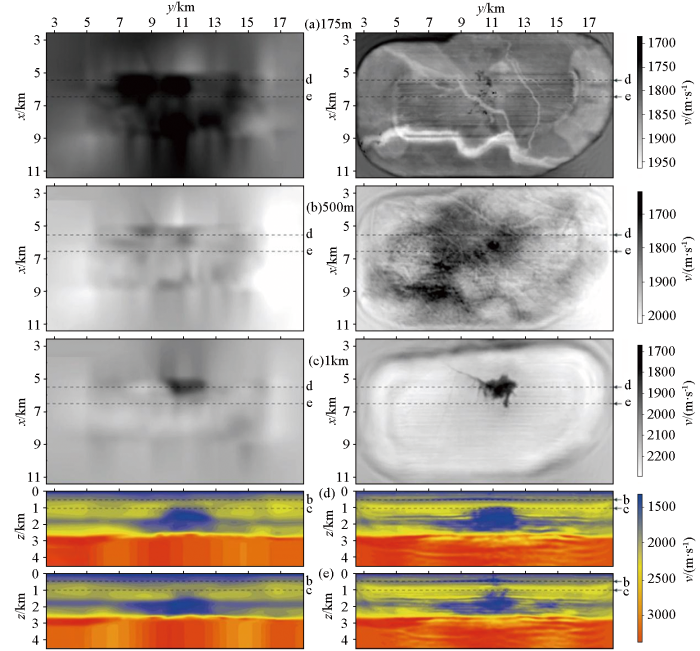
由于海上地震数据在均匀的海水中激发和接收获取的,震源的子波特征易于记录,目前,全波形反演已在海洋地震资料处理中获得了成功应用。例如,Sirgue等[79]在Valhall油田成功进行了3D频率域的全波形反演应用,该油田位于北海70 m的深水区,受浅部气层影响导致常规射线方法难以对气层以下区域成像,通过基于射线的反射层析得到了合适的初始模型,成功实现了对浅层气藏、古河道沉积以及古海底冰川移动划痕的准确成像(图4),左侧为初始垂向纵波速度模型(由反射走时层析成像获得),右侧为相应的全波形反演模型。经过全波形反演后,在图4a中175 m处可见古河道沉积,图4b中500 m深处切片可见冰川移动划痕,图4c中1 km深处可见清晰的气藏结构与裂缝构造。
图4
图4
Valhall油田的多参数粘滞声波全波形反演实例[79]
a、b、c—不同深度垂向纵波速度反演结果(左)和相应的全波形反演结果(右);d、e—a、b、c虚线标示位置纵向速度切片
Fig.4
Multi-parameter visco-acoustic FWI of the Valhall oil field[79]
a、b、c—the inversion results of vertical longitudinal wave velocity(left) and the corresponding full waveform inversion results(right) at different depths;d、e—the inline vertical slices pass at marked position in figure a,b,c
3.2 陆上地震资料的应用
3.3 深地震反射资料的应用
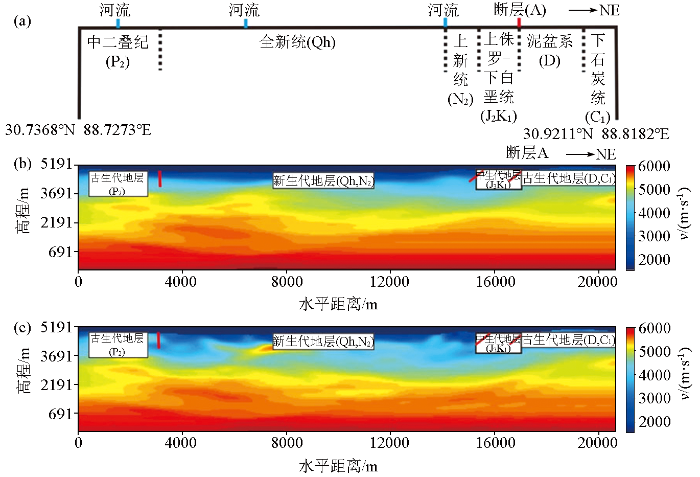
深反射地震技术激发能量更强、记录长度更长、偏移距更大,所以更容易构建高精度的初始模型。部分地球物理学者采用深反射地震数据进行全波形反演也获得了更加精细的浅层速度结构。Davy等[83]利用全波形反演方法对西班牙加利西亚地区深部大陆构造边缘进行精细速度结构成像,相对于传统的层析成像,剖面的质量有明显的提高,特别是对于断层位置的刻画,成像效果得到明显改善。Zhang等[84]通过全波形反演方法对深反射地震剖面中的初至波场(主要是主折射波场和多折射波场)进行了处理,获得了浅部地壳约5 km的精细速度结构(图5)。明显看出最南端的古沉积层间有非常清晰的边界,横向差异明显。全波形反演的结果相较于层析成像结果还可以观察到在水平位置8 000 m,高程约3 800 m,有一个形状清晰的高速体,横向延伸,横向尺度约2 000 m。
图5
4 全波形反演方法存在的问题和发展方向
4.1 全波形反演方法存在的问题
在过去的40余年里,全波形反演技术迅速发展并且已经在科学界与工业界产生了巨大的影响。但该方法在实际地震资料中的应用存在一定的困难与挑战:
1) 多参数全波形反演从理论到实际应用存在瓶颈。地震波的传播过程中受到速度、密度、各向异性及吸收衰减等因素的影响。早期的全波形反演多是对于单一的纵波速度参数进行反演,通过经验公式求取横波速度、密度等其他参数。随着全波形反演技术的发展以及硬件计算能力的提高,利用实测数据开展多参数联合反演必然成为未来的发展趋势,成为未来全波形反演广泛应用的突破方向。但多参数全波形反演一方面需求更加强大的计算机计算能力及存储能力,另一方面存在严重的参数耦合问题,提升计算能力与解决参数耦合性问题是推动多参数全波形反演走向实用化的关键。
2)全波形反演数据预处理方法亟需优化。预处理主要包括静校正、多域保幅去噪、归一化数据等。海上地震数据得益于海水介质的均匀性,接收到的子波特征相对比较一致,容易被记录下来,去除相关噪声更加简单,但是对于陆上地震数据来说,复杂的地表条件导致观测地震记录难以反映真实的介质参数,且全波形反演要求全方位角、大偏移距的观测系统,传统的观测系统服务于反射波勘探,偏移距较小。震源子波相位变化会引起波形变化,会影响全波形反演的梯度计算,同时子波主频也是影响全波形反演的重要因素[86]。所以在预处理过程中如何既去除噪声的影响又不破坏地震波的动力学特征是个难题。鉴于上述情况,在施工布设过程中应该酌情增加长排列、大偏移距的采集方式,在数据处理中采用组合静校正、多域组合去噪技术等反射地震处理方法进行预处理有利于全波形反演。
3)深地(>5 km)全波形反演成像面临挑战。由于透射波的穿透深度有限,全波形反演多用于反演5 km以内的速度结构,多是结合反射地震剖面叠加结果来进行联合解释。深地探测要求向地壳深部进军,而实现对深层目标的反演成像,反射波是唯一的信息来源,相较于传统全波形反演,反射波全波形反演的梯度剖面中具有更加丰富的低波数信息,可以有效改善全波形反演的深层反演效果。但反射波全波形反演比常规传播学反演对于初始模型精度要求更高,且在计算过程中需要偏移获得扰动速度,导致反射波全波形反演的计算量巨大,所以实现大规模的应用仍具有一定的困难。
4.2 全波形反演方法发展方向
综上所述,在过去的40余年里,全波形反演技术迅速发展且已经在科学界与工业界产生了巨大的影响。尽管该方法在实际地震资料中的应用存在一定的困难与挑战,但作为地球模型提高成像精度的先进方法技术,它依旧值得被持续的研究与发展。对于油气勘探领域和地质构造结构研究领域,全波形反演方法都产生了深远影响。在深地震反射资料的处理当中,它也可以起到提高成像精度的作用。可以预期,随着数据处理方法的不断进步、计算方法的飞速发展、认识的不断深入,全波形反演方法也将进一步帮助人类探测地下空间、发现新的油藏和认识深部地壳结构。
参考文献
粒子群-梯度算法在频率域地震波形反演中的应用
[J].
PSO-gradient algorithm and its application to seismic waveform inversion for velocity structure in frequency domain
[J].
Two-grid full-waveform Rayleigh-wave inversion via a genetic algorithm—Part 1:Method and synthetic examplesGA-FWI of Rayleigh waves—Method
[J].
DOI:10.1190/geo2018-0799.1
URL
[本文引用: 1]

When reliable a priori information is not available, it is difficult to correctly predict near-surface S-wave velocity models from Rayleigh waves through existing techniques, especially in the case of complex geology. To tackle this issue, we have developed a new method: two-grid genetic-algorithm Rayleigh-wave full-waveform inversion (FWI). Adopting a two-grid parameterization of the model, the genetic algorithm inverts for unknown velocities and densities at the nodes of a coarse grid, whereas the forward modeling is performed on a fine grid to avoid numerical dispersion. A bilinear interpolation brings the coarse-grid results into the fine-grid models. The coarse inversion grid allows for a significant reduction in the computing time required by the genetic algorithm to converge. With a coarser grid, there are fewer unknowns and less required computing time, at the expense of the model resolution. To further increase efficiency, our inversion code can perform the optimization using an offset-marching strategy and/or a frequency-marching strategy that can make use of different kinds of objective functions and allows for parallel computing. We illustrate the effect of our inversion method using three synthetic examples with rather complex near-surface models. Although no a priori information was used in all three tests, the long-wavelength structures of the reference models were fairly predicted, and satisfactory matches between “observed” and predicted data were achieved. The fair predictions of the reference models suggest that the final models estimated by our genetic-algorithm FWI, which we call macromodels, would be suitable inputs to gradient-based Rayleigh-wave FWI for further refinement. We also explored other issues related to the practical use of the method in different work and explored applications of the method to field data.
基于混合自适应遗传算法的稳健全波形反演
[J].
Robust full waveform inversion based on hybrid adaptive genetic algorithm
[J].
Nonlinear two-dimensional elastic inversion of multioffset seismic data
[J].
DOI:10.1190/1.1442384
URL
[本文引用: 1]

The treatment of multioffset seismic data as an acoustic wave field is becoming increasingly disturbing to many geophysicists who see a multitude of wave phenomena, such as amplitude‐offset variations and shearwave events, which can only be explained by using the more correct elastic wave equation. Not only are such phenomena ignored by acoustic theory, but they are also treated as undesirable noise when they should be used to provide extra information, such as S‐wave velocity, about the subsurface. The problems of using the conventional acoustic wave equation approach can be eliminated via an elastic approach. In this paper, equations have been derived to perform an inversion for P‐wave velocity, S‐wave velocity, and density as well as the P‐wave impedance, S‐wave impedance, and density. These are better resolved than the Lamé parameters. The inversion is based on nonlinear least squares and proceeds by iteratively updating the earth parameters until a good fit is achieved between the observed data and the modeled data corresponding to these earth parameters. The iterations are based on the preconditioned conjugate gradient algorithm. The fundamental requirement of such a least‐squares algorithm is the gradient direction which tells how to update the model parameters. The gradient direction can be derived directly from the wave equation and it may be computed by several wave propagations. Although in principle any scheme could be chosen to perform the wave propagations, the elastic finite‐ difference method is used because it directly simulates the elastic wave equation and can handle complex, and thus realistic, distributions of elastic parameters. This method of inversion is costly since it is similar to an iterative prestack shot‐profile migration. However, it has greater power than any migration since it solves for the P‐wave velocity, S‐wave velocity, and density and can handle very general situations including transmission problems. Three main weaknesses of this technique are that it requires fairly accurate a priori knowledge of the low‐ wavenumber velocity model, it assumes Gaussian model statistics, and it is very computer‐intensive. All these problems seem surmountable. The low‐wavenumber information can be obtained either by a prior tomographic step, by the conventional normal‐moveout method, by a priori knowledge and empirical relationships, or by adding an additional inversion step for low wavenumbers to each iteration. The Gaussian statistics can be altered by preconditioning the gradient direction, perhaps to make the solution blocky in appearance like well logs, or by using large model variances in the inversion to reduce the effect of the Gaussian model constraints. Moreover, with some improvements to the algorithm and more parallel computers, it is hoped the technique will soon become routinely feasible.
Thematic set:Full waveform inversion:The next leap forward in imaging at Valhall
[J].
全波形反演研究现状及发展趋势
[J].
DOI:10.3969/j.issn.1000-1441.2014.01.011
[本文引用: 1]

全波形反演技术是当前勘探地球物理领域的研究热点之一。新一轮的全波形反演研究触及了波场模拟、梯度估计、数据预处理、目标泛函的选择等诸多深层次的内容,逐渐将全波形反演对实际观测系统、地震数据等要求的局限性以及其具备的潜力揭示出来。通过对全波形反演理论和技术研究进展及应用现状的全面调研,介绍了全波形反演算法研究从时间域到频率域、再到混合域和拉普拉斯域的发展进程;阐明了全波形反演技术已实现海上地震资料应用但对陆上地震资料还没有真正成功实例的应用现状;着重分析了陆上资料全波形反演应用的瓶颈主要在于观测系统的限制、低频数据的缺失、数据预处理面临的挑战以及近地表条件和激发-接收的影响等;指出了发展分步骤、分尺度的反演方法和反演策略以及多种手段的有效联合是实现陆上资料全波形反演的有效途径。
Research status and development trend of full waveform inversion
[J].
DOI:10.3969/j.issn.1000-1441.2014.01.011
[本文引用: 1]

<p> Full waveform inversion(FWI)is one of the hot issue in the geophysics exploration. The new round study involvees in many deeper issues,such as wavefield simulation,gradient estimation,data pre-processing,objective function and so on. Those further studies reveal the limtations of geometry and seismic data, as well as the potiential of FWI,through an overall investigation on the FWI theory,technology and application status,we introduce FWI development,from time domain to frequency domain and Laplace domain,especially to the hybrid domain. It is shown that FWI has been already successfully used in the marine data,however it is still a challenge in land data application;bottlenecks of the land data application are analyzed,such as limitation of geometry,lack of low-frequency component of data,the challenge of data pre-processing,the near surface conditions and source-receiver limitation of land acquisition;Finally it is concluded that step-by-step hierarchical multi-scale strategies and combination of different methods would be available to realize the land data FWI application.</p>
Multiscale imaging of complex structures from multifold wide-aperture seismic data by frequency-domain full-waveform tomography:Application to a thrust belt
[J].DOI:10.1111/gji.2004.159.issue-3 URL [本文引用: 1]
Application of acoustic full waveform inversion to a low-frequency large-offset land data set
[C]//
Resolving the fine-scale velocity structure of continental hyperextension at the Deep Galicia Margin using full-waveform inversion
[J].DOI:10.1093/gji/ggx415 URL [本文引用: 1]
Refraction waves full waveform inversion of deep reflection seismic profiles in the central part of Lhasa Terrane
[J].DOI:10.1016/j.tecto.2021.228761 URL [本文引用: 3]
Preliminary division of tectonic units of the Qinghai-Tibet Plateau and its adjacent regions
[J].
Angle-domain common-image gathers for migration velocity analysis by wavefield-continuation imaging
[J].
DOI:10.1190/1.1801945
URL
[本文引用: 1]

We analyze the kinematic properties of offset‐domain common image gathers (CIGs) and angle‐domain CIGs (ADCIGs) computed by wavefield‐continuation migration. Our results are valid regardless of whether the CIGs were obtained by using the correct migration velocity. They thus can be used as a theoretical basis for developing migration velocity analysis (MVA) methods that exploit the velocity information contained in ADCIGs.
Estimation of a two-dimensional seismic compressional-wave velocity distribution by iterative tomographic imaging
[J].DOI:10.1002/(ISSN)1098-1098 URL [本文引用: 1]
波形反演在天然气水合物中的应用研究进展
[J].
Application of full waveform inversion to gas hydrate research
[J].
Wavepath eikonal traveltime inversion:Theory
[J].
DOI:10.1190/1.1443514
URL
[本文引用: 1]

We present a general formula for the back projection of traveltime residuals in traveltime tomography. For special choices of an arbitrary weighting factor this formula reduces to the asymptotic back‐projection term in ray‐tracing tomography (RT), the Woodward‐Rocca method, wavepath eikonal traveltime inversion (WET), and wave‐equation traveltime inversion (WT). This unification provides for an understanding of the differences and similarities among these traveltime tomography methods. The special case of the WET formula leads to a computationally efficient inversion scheme in the space‐time domain that is, in principle, almost as effective as WT inversion yet is an order of magnitude faster. It also leads to an analytic formula for the fast computation of wavepaths. Unlike ray‐tracing tomography, WET partially accounts for band‐limited source and shadow effects in the data. Several numerical tests of the WET method are used to illustrate its properties.
时间域地震全波形反演方法进展
[J].
Progress in the time do omain full waveform inversion
[J].
地震全波形反演及其探测壳—幔结构的研究进展
[J].
Progress of seismic full-waveform inversion and its applications in investigating the crust-mantle structure
[J].
地震勘探全波形反演的应用与发展分析
[J].
DOI:10.3724/SP.J.1047.2014.00396
[本文引用: 1]

本文首先对20世纪80年代发展起来的全波形反演应用及其在勘探地球物理领域的发展进行了分析;其次,面对定量化、精细化的地震勘探要求,提出了将地震勘探全波形反演与其他数据处理环节或处理技术相结合的研究设想,并展望了全波形反演的发展趋势;最后,论述了全波形反演研究中地震波场数值模拟、反演初始速度模型获取、目标函数形式选择、寻优算法启用及各向异性介质中的应用等关键问题,并总结了通过Laplace域的全波形反演获取反演初始速度模型、结合射线追踪并充分发挥并行计算之于波动方程方法来模拟地震波场的巨大优势,及灵活选用反演目标函数形式和寻优算法更新速度模型参数来加快全波形反演方法的实用化进程。
Application and development of full waveform inversion research in the seismic exploration
[J].
反射波全波形反演
[J].
Reflection full waveform inve rsion
[J].
陆上地震资料全波形反演策略研究
[J].
DOI:10.3969/j.issn.1000-1441.2017.01.010
[本文引用: 1]

全波形反演已成功应用于海上地震资料,而陆上地震资料全波形反演应用还面临诸多难点。研究给出了一种针对陆上地震资料的全波形反演策略:首先采用相位拟合互相关目标泛函增强全波形反演的适用性;其次构建动态波数域滤波梯度预处理方法压制梯度噪声;最后采用构造倾角信息约束的自适应高斯平滑算子改善反演结果质量。二维陆上地震资料的反演结果表明,该策略可有效实现陆上地震资料高波数全波形反演速度建模。
Strategy study on full waveform inversion for the land seismic data
[J].
DOI:10.3969/j.issn.1000-1441.2017.01.010
[本文引用: 1]

Full waveform inversion of marine seismic data has been successfully applied,however,the application of this technology for onshore seismic data faces many difficulties.In this study,a robust strategy of full waveform inversion for onshore seismic data is presented.Firstly,the phase-matched cross-correlation cost function is adopted to improve the applicability of full waveform inversion.Secondly,dynamic wavenumber domain gradient preprocessing method is used to suppress gradient noise.Finally,an adaptive Gaussian smoothing operator is applied to improve the quality of inversion results.The inversion case of two-dimensional onshore seismic data shows that this strategy presented in this study can effectively realize high wavenumber onshore seismic data velocity modeling.
Inverse theory applied to multi-source cross-hole tomography.Part 1:Acoustic wave-equation method 1
[J].DOI:10.1111/gpr.1990.38.issue-3 URL [本文引用: 1]
Frequency-domain elastic wave modeling by finite differences:A tool for crosshole seismic imaging
[J].
DOI:10.1190/1.1442874
URL
[本文引用: 1]

The migration, imaging, or inversion of wide‐aperture cross‐hole data depends on the ability to model wave propagation in complex media for multiple source positions. Computational costs can be considerably reduced in frequency‐domain imaging by modeling the frequency‐domain steady‐state equations, rather than the time‐domain equations of motion. I develop a frequency‐domain approach in this note that is competitive with time‐domain modeling when solutions for multiple sources are required or when only a limited number of frequency components of the solution are required.
The seismic inverse problem as a sequence of before stack migrations
[C]//
Inversion of seismic reflection data in the acoustic approximation
[J].
DOI:10.1190/1.1441754
URL
[本文引用: 2]

The nonlinear inverse problem for seismic reflection data is solved in the acoustic approximation. The method is based on the generalized least‐squares criterion, and it can handle errors in the data set and a priori information on the model. Multiply reflected energy is naturally taken into account, as well as refracted energy or surface waves. The inverse problem can be solved using an iterative algorithm which gives, at each iteration, updated values of bulk modulus, density, and time source function. Each step of the iterative algorithm essentially consists of a forward propagation of the actual sources in the current model and a forward propagation (backward in time) of the data residuals. The correlation at each point of the space of the two fields thus obtained yields the corrections of the bulk modulus and density models. This shows, in particular, that the general solution of the inverse problem can be attained by methods strongly related to the methods of migration of unstacked data, and commercially competitive with them.
An overview of full-waveform inversion in exploration geophysics
[J].
DOI:10.1190/1.3238367
URL
[本文引用: 3]

Full-waveform inversion (FWI) is a challenging data-fitting procedure based on full-wavefield modeling to extract quantitative information from seismograms. High-resolution imaging at half the propagated wavelength is expected. Recent advances in high-performance computing and multifold/multicomponent wide-aperture and wide-azimuth acquisitions make 3D acoustic FWI feasible today. Key ingredients of FWI are an efficient forward-modeling engine and a local differential approach, in which the gradient and the Hessian operators are efficiently estimated. Local optimization does not, however, prevent convergence of the misfit function toward local minima because of the limited accuracy of the starting model, the lack of low frequencies, the presence of noise, and the approximate modeling of thewave-physics complexity. Different hierarchical multiscale strategies are designed to mitigate the nonlinearity and ill-posedness of FWI by incorporating progressively shorter wavelengths in the parameter space. Synthetic and real-data case studies address reconstructing various parameters, from [Formula: see text] and [Formula: see text] velocities to density, anisotropy, and attenuation. This review attempts to illuminate the state of the art of FWI. Crucial jumps, however, remain necessary to make it as popular as migration techniques. The challenges can be categorized as (1) building accurate starting models with automatic procedures and/or recording low frequencies, (2) defining new minimization criteria to mitigate the sensitivity of FWI to amplitude errors and increasing the robustness of FWI when multiple parameter classes are estimated, and (3) improving computational efficiency by data-compression techniques to make 3D elastic FWI feasible.
A strategy for nonlinear elastic inversion of seismic reflection data
[J].
DOI:10.1190/1.1442046
URL
[本文引用: 1]

The problem of interpretation of seismic reflection data can be posed with sufficient generality using the concepts of inverse theory. In its roughest formulation, the inverse problem consists of obtaining the Earth model for which the predicted data best fit the observed data. If an adequate forward model is used, this best model will give the best images of the Earth’s interior. Three parameters are needed for describing a perfectly elastic, isotropic, Earth: the density ρ(x) and the Lamé parameters λ(x) and μ(x), or the density ρ(x) and the P-wave and S-wave velocities α(x) and β(x). The choice of parameters is not neutral, in the sense that although theoretically equivalent, if they are not adequately chosen the numerical algorithms in the inversion can be inefficient. In the long (spatial) wavelengths of the model, adequate parameters are the P-wave and S-wave velocities, while in the short (spatial) wavelengths, P-wave impedance, S-wave impedance, and density are adequate. The problem of inversion of waveforms is highly nonlinear for the long wavelengths of the velocities, while it is reasonably linear for the short wavelengths of the impedances and density. Furthermore, this parameterization defines a highly hierarchical problem: the long wavelengths of the P-wave velocity and short wavelengths of the P-wave impedance are much more important parameters than their counterparts for S-waves (in terms of interpreting observed amplitudes), and the latter are much more important than the density. This suggests solving the general inverse problem (which must involve all the parameters) by first optimizing for the P-wave velocity and impedance, then optimizing for the S-wave velocity and impedance, and finally optimizing for density. The first part of the problem of obtaining the long wavelengths of the P-wave velocity and the short wavelengths of the P-wave impedance is similar to the problem solved by present industrial practice (for accurate data interpretation through velocity analysis and “prestack migration”). In fact, the method proposed here produces (as a byproduct) a generalization to the elastic case of the equations of “prestack acoustic migration.” Once an adequate model of the long wavelengths of the P-wave velocity and of the short wavelengths of the P-wave impedance has been obtained, the data residuals should essentially contain information on S-waves (essentially P-S and S-P converted waves). Once the corresponding model of S-wave velocity (long wavelengths) and S-wave impedance (short wavelengths) has been obtained, and if the remaining residuals still contain information, an optimization for density should be performed (the short wavelengths of impedances do not give independent information on density and velocity independently). Because the problem is nonlinear, the whole process should be iterated to convergence; however, the information from each parameter should be independent enough for an interesting first solution.
频率域全波形反演方法研究进展
[J].
Progress in the frequency-domain full waveform inversion method
[J].
三维声波全波形反演的实现与验证
[J].
DOI:10.3969/j.issn.1000-1441.2013.04.012
[本文引用: 1]

全波形反演利用叠前地震波场的运动学和动力学信息重建地下地球物理参数,具有揭示复杂地质背景下构造细节及岩性的潜在能力。介绍了频率域反演联合时间域正演的优化算法的三维声波全波形反演方法及算法实现。该算法的正演实现使用了伪保守形式的一阶速度-压力场声波方程。应用三维SEG/EAGE模型反演实例验证了三维声波全波形反演方法的有效性。
Implementation and validation of 3D acoustic full waveform inversion
[J].
DOI:10.3969/j.issn.1000-1441.2013.04.012
[本文引用: 1]

The full waveform inversion (FWI) method makes use of the kinematic and dynamic information of pre-stack seismic data to rebuild underground geophysical parameters.Due to its high resolution,it has the potential of revealing structure details and lithology characteristic under complex geological background.We present some methodological and algorithmic developments of 3D acoustic full waveform inversion by frequency-domain inversion combined with time-domain forward.The FWI algorithm relies on a pseudo-conservative form of the velocity-stress acoustic wave equation.The numerical simulation data of 3D SEG/EAGE target model verified 3D acoustic full waveform inversion algorithm.
A mixed-grid finite element method with PML absorbing boundary conditions for seismic wave modelling
[J].DOI:10.1088/1742-2132/11/5/055009 URL [本文引用: 2]
高精度频率域弹性波方程有限差分方法及波场模拟
[J].
The method of finite difference of high precision elastic wave equations in the frequency domain and wave_field simulation
[J].
Site characterization using Gauss-Newton inversion of 2-D full seismic waveform in the time domain
[J].DOI:10.1016/j.soildyn.2012.07.004 URL [本文引用: 3]
Seismic waveform inversion in the frequency domain,Part 2:Fault delineation in sediments using crosshole data
[J].
DOI:10.1190/1.1444598
URL
[本文引用: 1]

A crosshole experiment was carried out in a layered sedimentary environment in which a normal fault is known to cut through the section. Initial traveltime inversions produced stable but low‐resolution images from which the fault could be only vaguely inferred. To image the fault, wavefield inversion was used to produce a velocity model consistent with the detailed phase and amplitude of the data at a number of frequencies. Our wavefield inversion scheme uses a classical, descent‐type algorithm for decreasing the data misfit by iteratively computing the gradient of this misfit by repeated forward and backward propagations. Our propagator is a full‐wave equation, frequency‐domain, acoustic, finite‐difference method. The use of the frequency‐space domain yields computational advantages for multisource data and allows an easy incorporation of viscous effects. By running wavefield inversion on the field data, a quantitative velocity image was produced that yielded a significantly improved image of the fault (when compared with the original traveltime inversions). Because the original field data were noisy and contained a high degree of multiple scattering (from the layering of the sediments), the transmitted arrivals were selectively windowed to enhance the image. The sediments at the site were strongly attenuating; we therefore used a viscoacoustic model during the modeling and the inversion that correctly simulated the observed decrease in amplitude with increasing frequency and source‐receiver offset. Furthermore, since the traveltime inversion indicated a high degree of anisotropy at the site, a fixed, homogeneous level of anisotropy was used during the inversion. Tests at varying levels of anisotropy confirmed the improvement in image quality and in data fit when anisotropy was incorporated. The final image was verified by examining the distribution of the residuals in the frequency domain, by comparing time‐domain modeled wavefields with the observed data, and by direct comparison with borehole logs.
Waveform inversion in the Laplace—Fourier domain
[J].DOI:10.1111/gji.2009.177.issue-3 URL [本文引用: 2]
A comparison between the behavior of objective functions for waveform inversion in the frequency and Laplace domains
[J].
Waveform inversion in the Laplace domain
[J].DOI:10.1111/gji.2008.173.issue-3 URL [本文引用: 1]
The direct-removal method of waveform inversion in the Laplace inversion for deep-sea environments
[C]//
Inversion on reflected seismic wave
[C]//
Seismic wavefield imaging of Earth's interior across scales
[J].
Preliminary reference Earth model
[J].DOI:10.1016/0031-9201(81)90046-7 URL [本文引用: 1]
Three-dimensional seismic models of the Earth's mantle
[J].
Assessment of global phase velocity models
[J].DOI:10.1046/j.1365-246x.2001.00307.x URL [本文引用: 1]
中国大陆及其邻近地区的地震层析成象
[J].
Seismic tomography of the Chinese Continent and adjacent region
[J].
全波形反演初始模型建立策略研究综述
[J].
Review of full waveform inversion initial model building strategy
[J].
Tomographic determination of velocity and depth in laterally varying media
[J].
DOI:10.1190/1.1441970
URL
[本文引用: 1]

Estimation of reflector depth and seismic velocity from seismic reflection data can be formulated as a general inverse problem. The method used to solve this problem is similar to tomographic techniques in medical diagnosis and we refer to it as seismic reflection tomography. Seismic tomography is formulated as an iterative Gauss‐Newton algorithm that produces a velocity‐depth model which minimizes the difference between traveltimes generated by tracing rays through the model and traveltimes measured from the data. The input to the process consists of traveltimes measured from selected events on unstacked seismic data and a first‐guess velocity‐depth model. Usually this first‐guess model has velocities which are laterally constant and is usually based on nearby well information and/or an analysis of the stacked section. The final model generated by the tomographic method yields traveltimes from ray tracing which differ from the measured values in recorded data by approximately 5 ms root‐mean‐square. The indeterminancy of the inversion and the associated nonuniqueness of the output model are both analyzed theoretically and tested numerically. It is found that certain aspects of the velocity field are poorly determined or undetermined. This technique is applied to an example using real data where the presence of permafrost causes a near‐surface lateral change in velocity. The permafrost is successfully imaged in the model output from tomography. In addition, depth estimates at the intersection of two lines differ by a significantly smaller amount than the corresponding estimates derived from conventional processing.
A decade of tomography
[J].
DOI:10.1190/1.2969907
URL
[本文引用: 1]

Over the past 10 years, ray-based postmigration grid tomography has become the standard model-building tool for seismic depth imaging. While the basics of the method have remained unchanged since the late 1990s, the problems it solves have changed dramatically. This evolution has been driven by exploration demands and enabled by computer power. There are three main areas of change. First, standard model resolution has increased from a few thousand meters to a few hundred meters. This order of magnitude improvement may be attributed to both high-quality, complex residual-moveout data picked as densely as [Formula: see text] to [Formula: see text] vertically and horizontally, and to a strategy of working down from long-wavelength to short-wavelength solutions. Second, more and more seismic data sets are being acquired along multiple azimuths, for improved illumination and multiple suppression. High-resolution velocity tomography must solve for all azimuths simultaneously, to prevent short-wavelength velocity heterogeneity from being mistaken for azimuthal anisotropy. Third, there has been a shift from predominantly isotropic to predominantly anisotropic models, both VTI and TTI. With four-component data, anisotropic grid tomography can be used to build models that tie PZ and PS images in depth.
全波形反演在缝洞型储层速度建模中的应用
[J].
Application of full waveform inversion velocity model-building technology for the fractured-vuggy reservoir
[J].
Tomographic full waveform inversion (TFWI) by combining full waveform inversion with wave-equation migration velocity anaylisis
[C]//
An efficient multiscale method for time-domain waveform tomography
[J].
DOI:10.1190/1.3151869
URL
[本文引用: 1]

This efficient multiscale method for time-domain waveform tomography incorporates filters that are more efficient than Hamming-window filters. A strategy for choosing optimal frequency bands is proposed to achieve computational efficiency in the time domain. A staggered-grid, explicit finite-difference method with fourth-order accuracy in space and second-order accuracy in time is used for forward modeling and the adjoint calculation. The adjoint method is utilized in inverting for an efficient computation of the gradient directions. In the multiscale approach, multifrequency data and multiple grid sizes are used to overcome somewhat the severe local minima problem of waveform tomography. The method is applied successfully to 1D and 2D heterogeneous models; it can accurately recover low- and high-wavenumber components of the velocity models. The inversion result for the 2D model demonstrates that the multiscale method is computationally efficient and converges faster than a conventional, single-scale method.
Two-dimensional nonlinear inversion of seismic waveforms:Numerical results
[J].
DOI:10.1190/1.1442188
URL
[本文引用: 2]

The nonlinear problem of inversion of seismic waveforms can be set up using least‐squares methods. The inverse problem is then reduced to the problem of minimizing a lp;nonquadratic) function in a space of many [Formula: see text] variables. Using gradient methods leads to iterative algorithms, each iteration implying a forward propagation generated by the actual sources, a backward propagation generated by the data residuals (acting as if they were sources), and a correlation at each point of the space of the two fields thus obtained, which gives the updated model. The quality of the results of any inverse method depends heavily on the realism of the forward modeling. Finite‐difference schemes are a good choice relative to realism because, although they are time‐consuming, they give excellent results. Numerical tests performed with multioffset synthetic data from a two‐dimensional model prove the feasibility of the approach. If only surface‐recorded reflections are used, the high spatial frequency content of the model (but not the low spatial frequencies) is recovered in few (≃5) iterations. By using transmitted data also (e.g., between two boreholes), all the spatial frequencies are recovered. Since the problem is nonlinear, if the initial guess is far enough from the true solution, the iterative algorithm may converge into a secondary solution. A nonlinear inversion with 8 shots, each shot recorded at 400 receiver locations, with 700 samples in each seismogram, corresponding to a 2-D model described by 40 000 grid points, takes approximately 1 hour in a CRAY 1S supercomputer.
稀疏存储的显式有限元三角网格地震波数值模拟及其 PML 吸收边界条件
[J].
Explicit finite element method with triangle meshes stored by sparse format and its perfectly matched layers absorbing boundary condition
[J].
A simple method to calculate Green's functions for elastic layered media
[J].
DOI:10.1785/BSSA0710040959
URL
[本文引用: 1]

Green's functions for an elastic layered medium can be expressed as a double integral over frequency and horizontal wavenumber. We show that, for any time window, the wavenumber integral can be exactly represented by a discrete summation. This discretization is achieved by adding to the particular point source an infinite set of specified circular sources centered around the point source and distributed at equal radial interval. Choice of this interval is dependent on the length of time desired for the point source response and determines the discretized set of horizontal wavenumbers which contribute to the solution. Comparisons of the results obtained with those derived using the two-dimensional discretization method (Bouchon, 1979) are presented. They show the great accuracy of the two methods.
复杂地表边界元—体积元波动方程数值模拟
[J].
Boundary-volume integral equation numerical modeling for complex near surface
[J].
The pseudospectral method:Accurate representation of interfaces in elastic wave calculations
[J].
DOI:10.1190/1.1442497
URL
[本文引用: 1]

When finite‐difference methods are used to solve the elastic wave equation in a discontinuous medium, the error has two dominant components. Dispersive errors lead to artificial wave trains. Errors from interfaces lead to circular wavefronts emanating from each location where the interface appears “jagged” to the rectangular grid. The pseudospectral method can be viewed as the limit of finite differences with infinite order of accuracy. With this method, dispersive errors are essentially eliminated. The mappings introduced in this paper also eliminate the other dominant error source. Test calculations confirm that these mappings significantly enhance the already highly competitive pseudospectral method with only a very small additional cost. Although the mapping method is described here in connection with the pseudospectral method, it can also be used with high‐order finite‐difference approximations.
伪谱法地震波正演模拟的多线程并行计算
[J].
Parallel algorithm based on the multithread technique for pseudospectal modeling of seismic wave
[J].
地震波有限差分模拟综述
[J].
The review of the finite-difference elastic wave motion modeling
[J].
Propagation of elastic waves in layered media by finite difference methods
[J].
Synthetic seismograms:A finite-difference approach
[J].
DOI:10.1190/1.1440605
URL
[本文引用: 1]

Recent interest in the extraction of fine detail from field seismograms has stimulated the search for numerical modeling procedures which can produce synthetic seismograms for complex subsurface geometries and for arbitrary source‐receiver separations. Among the various techniques available for this purpose, the replacement of the two‐dimensional wave equation by a suitable finite‐difference representation offers distinct advantages. This approach is simple and may be readily implemented. It automatically accounts for the proper relative amplitudes of the various arrivals and includes the contributions of converted waves, Rayleigh waves, diffractions from faulted zones, and head waves. Two computational schemes have been examined. For the so‐called “homogeneous formulation,” the standard boundary conditions between media of different elastic properties must be satisfied explicitly. In the case of the alternate “heterogeneous formulation”, these elastic properties may be specified at each grid point of a finite‐difference mesh, and the boundary conditions are satisfied implicitly. The proper simulation of the source requires special treatment for both cases. Synthetic seismograms computed for several models of exploration interest serve to illustrate how the technique may help the interpreter. The examples also illustrate various implementational aspects of the finite‐difference approach, which involve such phenomena as grid dispersion, artificial reflections from the edge of the model, and choice of spatial and temporal sampling increments.
横向各向同性介质中地震波场谱元法数值模拟
[J].
Numerical spectral-element modeling for seismic wave propagation in transversely isotropic medium
[J].
Nonlinear two-dimensional elastic inversion of multioffset seismic data
[J].
DOI:10.1190/1.1442384
URL
[本文引用: 1]

The treatment of multioffset seismic data as an acoustic wave field is becoming increasingly disturbing to many geophysicists who see a multitude of wave phenomena, such as amplitude‐offset variations and shearwave events, which can only be explained by using the more correct elastic wave equation. Not only are such phenomena ignored by acoustic theory, but they are also treated as undesirable noise when they should be used to provide extra information, such as S‐wave velocity, about the subsurface. The problems of using the conventional acoustic wave equation approach can be eliminated via an elastic approach. In this paper, equations have been derived to perform an inversion for P‐wave velocity, S‐wave velocity, and density as well as the P‐wave impedance, S‐wave impedance, and density. These are better resolved than the Lamé parameters. The inversion is based on nonlinear least squares and proceeds by iteratively updating the earth parameters until a good fit is achieved between the observed data and the modeled data corresponding to these earth parameters. The iterations are based on the preconditioned conjugate gradient algorithm. The fundamental requirement of such a least‐squares algorithm is the gradient direction which tells how to update the model parameters. The gradient direction can be derived directly from the wave equation and it may be computed by several wave propagations. Although in principle any scheme could be chosen to perform the wave propagations, the elastic finite‐ difference method is used because it directly simulates the elastic wave equation and can handle complex, and thus realistic, distributions of elastic parameters. This method of inversion is costly since it is similar to an iterative prestack shot‐profile migration. However, it has greater power than any migration since it solves for the P‐wave velocity, S‐wave velocity, and density and can handle very general situations including transmission problems. Three main weaknesses of this technique are that it requires fairly accurate a priori knowledge of the low‐ wavenumber velocity model, it assumes Gaussian model statistics, and it is very computer‐intensive. All these problems seem surmountable. The low‐wavenumber information can be obtained either by a prior tomographic step, by the conventional normal‐moveout method, by a priori knowledge and empirical relationships, or by adding an additional inversion step for low wavenumbers to each iteration. The Gaussian statistics can be altered by preconditioning the gradient direction, perhaps to make the solution blocky in appearance like well logs, or by using large model variances in the inversion to reduce the effect of the Gaussian model constraints. Moreover, with some improvements to the algorithm and more parallel computers, it is hoped the technique will soon become routinely feasible.
Multiscale seismic waveform inversion
[J].
DOI:10.1190/1.1443880
URL
[本文引用: 1]

Iterative inversion methods have been unsuccessful at inverting seismic data obtained from complicated earth models (e.g. the Marmousi model), the primary difficulty being the presence of numerous local minima in the objective function. The presence of local minima at all scales in the seismic inversion problem prevent iterative methods of inversion from attaining a reasonable degree of convergence to the neighborhood of the global minimum. The multigrid method is a technique that improves the performance of iterative inversion by decomposing the problem by scale. At long scales there are fewer local minima and those that remain are further apart from each other. Thus, at long scales iterative methods can get closer to the neighborhood of the global minimum. We apply the multigrid method to a subsampled, low‐frequency version of the Marmousi data set. Although issues of source estimation, source bandwidth, and noise are not treated, results show that iterative inversion methods perform much better when employed with a decomposition by scale. Furthermore, the method greatly reduces the computational burden of the inversion that will be of importance for 3-D extensions to the method.
VTI 介质频率—空间域准 P 波正演模拟
[J].
Quasi P-wave forward modeling in frequency-space domain in VTI media
[J].
TTI 介质 qP 波方程频率—空间域加权平均有限差分算子
[J].
Weighted mean finite-difference operator of qP wave equation in frequency-space domain for TTI medium
[J].
Fourth-order finite-difference P-SV seismograms
[J].
DOI:10.1190/1.1442422
URL
[本文引用: 1]

I describe the properties of a fourth‐order accurate space, second‐order accurate time, two‐dimensional P-SV finite‐difference scheme based on the Madariaga‐Virieux staggered‐grid formulation. The numerical scheme is developed from the first‐order system of hyperbolic elastic equations of motion and constitutive laws expressed in particle velocities and stresses. The Madariaga‐Virieux staggered‐grid scheme has the desirable quality that it can correctly model any variation in material properties, including both large and small Poisson’s ratio materials, with minimal numerical dispersion and numerical anisotropy. Dispersion analysis indicates that the shortest wavelengths in the model need to be sampled at 5 gridpoints/wavelength. The scheme can be used to accurately simulate wave propagation in mixed acoustic‐elastic media, making it ideal for modeling marine problems. Explicitly calculating both velocities and stresses makes it relatively simple to initiate a source at the free‐surface or within a layer and to satisfy free‐surface boundary conditions. Benchmark comparisons of finite‐difference and analytical solutions to Lamb’s problem are almost identical, as are comparisons of finite‐difference and reflectivity solutions for elastic‐elastic and acoustic‐elastic layered models.
一阶弹性波方程交错网格高阶差分解法
[J].
A study on stability of the staggered grid high order difference method of first order elastic wave equation
[J].
Time domain Gauss—Newton seismic waveform inversion in elastic media
[J].DOI:10.1111/gji.2006.167.issue-3 URL [本文引用: 2]
Full waveform tomography for lithospheric imaging:Results from a blind test in a realistic crustal model
[J].DOI:10.1111/gji.2007.168.issue-1 URL [本文引用: 1]
Inversion of seismic reflection data in the acoustic approximation
[J].
DOI:10.1190/1.1441754
URL
[本文引用: 1]

The nonlinear inverse problem for seismic reflection data is solved in the acoustic approximation. The method is based on the generalized least‐squares criterion, and it can handle errors in the data set and a priori information on the model. Multiply reflected energy is naturally taken into account, as well as refracted energy or surface waves. The inverse problem can be solved using an iterative algorithm which gives, at each iteration, updated values of bulk modulus, density, and time source function. Each step of the iterative algorithm essentially consists of a forward propagation of the actual sources in the current model and a forward propagation (backward in time) of the data residuals. The correlation at each point of the space of the two fields thus obtained yields the corrections of the bulk modulus and density models. This shows, in particular, that the general solution of the inverse problem can be attained by methods strongly related to the methods of migration of unstacked data, and commercially competitive with them.
Parsimonious staggered grid finite-differencing of the wave equation
[J].DOI:10.1029/GL017i002p00155 URL [本文引用: 1]
A new take on FWI-wavefield reconstruction inversion
[C]//
互相关与最小二乘加权目标函数全波形反演
[J].
Full waveform inversion based on weighted cross-correlaton and least squares objective function
[J].
Seismic envelope inversion and modulation signal model
[J].
DOI:10.1190/geo2013-0294.1
URL
[本文引用: 1]

We recognized that the envelope fluctuation and decay of seismic records carries ultra low-frequency (ULF, i.e., the frequency below the lowest frequency in the source spectrum) signals that can be used to estimate the long-wavelength velocity structure. We then developed envelope inversion for the recovery of low-wavenumber components of media (smooth background), so that the initial model dependence of waveform inversion can be reduced. We derived the misfit function and the corresponding gradient operator for envelope inversion. To understand the long-wavelength recovery by the envelope inversion, we developed a nonlinear seismic signal model, the modulation signal model, as the basis for retrieving the ULF data and studied the nonlinear scale separation by the envelope operator. To separate the envelope data from the wavefield data (envelope extraction), a demodulation operator (envelope operator) was applied to the waveform data. Numerical tests using synthetic data for the Marmousi model proved the validity and feasibility of the proposed approach. The final results of combined [Formula: see text] (envelope-inversion for smooth background plus waveform-inversion for high-resolution velocity structure) indicated that it can deliver much improved results compared with regular full-waveform inversion (FWI) alone. Furthermore, to test the independence of the envelope to the source frequency band, we used a low-cut source wavelet (cut from 5 Hz below) to generate the synthetic data. The envelope inversion and the combined [Formula: see text] showed no appreciable difference from the full-band source results. The proposed envelope inversion is also an efficient method with very little extra work compared with conventional FWI.
基于反射地震数据的时频域包络反演
[J].
Reflection seismic data based envelope inversion in the time-frequency domain
[J].
Application of optimal transport and the quadratic Wasserstein metric to full-waveform inversion
[J].
DOI:10.1190/geo2016-0663.1
URL
[本文引用: 1]

Conventional full-waveform inversion (FWI) using the least-squares norm as a misfit function is known to suffer from cycle-skipping issues that increase the risk of computing a local rather than the global minimum of the misfit. The quadratic Wasserstein metric has proven to have many ideal properties with regard to convexity and insensitivity to noise. When the observed and predicted seismic data are considered to be two density functions, the quadratic Wasserstein metric corresponds to the optimal cost of rearranging one density into the other, in which the transportation cost is quadratic in distance. Unlike the least-squares norm, the quadratic Wasserstein metric measures not only amplitude differences but also global phase shifts, which helps to avoid cycle-skipping issues. We have developed a new way of using the quadratic Wasserstein metric trace by trace in FWI and compare it with the global quadratic Wasserstein metric via the solution of the Monge-Ampère equation. We incorporate the quadratic Wasserstein metric technique into the framework of the adjoint-state method and apply it to several 2D examples. With the corresponding adjoint source, the velocity model can be updated using a quasi-Newton method. Numerical results indicate the effectiveness of the quadratic Wasserstein metric in alleviating cycle-skipping issues and sensitivity to noise. The mathematical theory and numerical examples demonstrate that the quadratic Wasserstein metric is a good candidate for a misfit function in seismic inversion.
基于最优输运原理的陆上单分量资料弹性波全波形反演
[J].
Elastic full-waveform inversion of land single-component seismic data based on optimal transport theory
[J].
Full waveform inversion and the truncated Newton method:quantitative imaging of complex subsurface structures
[J].DOI:10.1111/gpr.2014.62.issue-6 URL [本文引用: 1]
Function minimization by conjugate gradients
[J].DOI:10.1093/comjnl/7.2.149 URL [本文引用: 1]
Conjugate gradient method
[J].DOI:10.1002/wics.v1:3 URL [本文引用: 1]
Seismic imaging of complex onshore structures by 2D elastic frequency-domain full-waveform inversion
[J].
DOI:10.1190/1.3215771
URL
[本文引用: 1]

Quantitative imaging of the elastic properties of the subsurface at depth is essential for civil engineering applications and oil- and gas-reservoir characterization. A realistic synthetic example provides for an assessment of the potential and limits of 2D elastic full-waveform inversion (FWI) of wide-aperture seismic data for recovering high-resolution P- and S-wave velocity models of complex onshore structures. FWI of land data is challenging because of the increased nonlinearity introduced by free-surface effects such as the propagation of surface waves in the heterogeneous near-surface. Moreover, the short wavelengths of the shear wavefield require an accurate S-wave velocity starting model if low frequencies are unavailable in the data. We evaluated different multiscale strategies with the aim of mitigating the nonlinearities. Massively parallel full-waveform inversion was implemented in the frequency domain. The numerical optimization relies on a limited-memory quasi-Newton algorithm thatoutperforms the more classic preconditioned conjugate-gradient algorithm. The forward problem is based upon a discontinuous Galerkin (DG) method on triangular mesh, which allows accurate modeling of free-surface effects. Sequential inversions of increasing frequencies define the most natural level of hierarchy in multiscale imaging. In the case of land data involving surface waves, the regularization introduced by hierarchical frequency inversions is not enough for adequate convergence of the inversion. A second level of hierarchy implemented with complex-valued frequencies is necessary and provides convergence of the inversion toward acceptable P- and S-wave velocity models. Among the possible strategies for sampling frequencies in the inversion, successive inversions of slightly overlapping frequency groups is the most reliable when compared to the more standard sequential inversion of single frequencies. This suggests that simultaneous inversion of multiple frequencies is critical when considering complex wave phenomena.
Scale and parameter adaptive model based gradient pre-conditioner for elastic full-waveform inversion
[J].DOI:10.1093/gji/ggu175 URL [本文引用: 1]
基于 L-BFGS 算法的时间域全波形反演
[J].
Full waveform inversion in time domain based on limited-memory BFGS algorithm
[J].
基于 L-BFGS 算法和同时激发震源的频率多尺度全波形反演
[J].
Frequency multi-scale full waveform inversion based on L-BFGS algorithm and simultaneous sources approach
[J].
基于修正拟牛顿公式的全波形反演
[J].
Full waveform inversion based on modified quasi-Newton equation
[J].
Nonlinear multiparameter optimization using genetic algorithms:Inversion of plane-wave seismograms
[J].
DOI:10.1190/1.1442992
URL
[本文引用: 1]

Seismic waveform inversion is one of many geophysical problems which can be identified as a nonlinear multiparameter optimization problem. Methods based on local linearization fail if the starting model is too far from the true model. We have investigated the applicability of “Genetic Algorithms” (GA) to the inversion of plane‐wave seismograms. Like simulated annealing, genetic algorithms use a random walk in model space and a transition probability rule to help guide their search. However, unlike a single simulated annealing run, the genetic algorithms search from a randomly chosen population of models (strings) and work with a binary coding of the model parameter set. Unlike a pure random search, such as in a “Monte Carlo” method, the search used in genetic algorithms is not directionless. Genetic algorithms essentially consist of three operations, selection, crossover, and mutation, which involve random number generation, string copies, and some partial string exchanges. The choice of the initial population, the probabilities of crossover and mutation are crucial for the practical implementation of the algorithm. We investigated the effects of these parameters in the inversion of plane‐wave seismograms in which a normalized crosscorrelation function was used as the objective or fitness function (E). We also introduce the concept of “update” probability to control the influence of past generations. The combination of a low value of mutation probability (∼0.01), a moderate value of the crossover probability (∼0.6) and a high value of update probability (∼0.9) are found to be optimal for the convergence of the algorithm. Further, we show that concepts from simulated annealing can be used effectively for the stretching of the fitness function which helps in the convergence of the algorithm. Thus, we propose to use exp (E/T) rather than E as the fitness function, where T (analogous to temperature in simulated annealing) is a properly chosen parameter which can change slowly with each generation. Also, by repeating the GA optimization procedure several times with different randomly chosen initial model populations, we derive “a very good subset” of models from the entire model space and calculate the a posteriori probability density σ(m) ∝ exp (E(m)/T). The σ(m) ’s are then used to calculate a “mean” model, which is found to be close to the true model.
Optimization by simulated annealing
[J].
DOI:10.1126/science.220.4598.671
PMID:17813860
[本文引用: 1]

There is a deep and useful connection between statistical mechanics (the behavior of systems with many degrees of freedom in thermal equilibrium at a finite temperature) and multivariate or combinatorial optimization (finding the minimum of a given function depending on many parameters). A detailed analogy with annealing in solids provides a framework for optimization of the properties of very large and complex systems. This connection to statistical mechanics exposes new information and provides an unfamiliar perspective on traditional optimization problems and methods.
基于分段快速模拟退火的零偏 VSP 全波形反演
[J].
DOI:10.3969/j.issn.1000-1441.2019.01.012
[本文引用: 1]

基于常规模拟退火算法的零偏VSP全波形反演面临着计算量大和耗时长的问题。为此提出了一种不同阶段对应不同扰动模型和退火方式的分段快速模拟退火(segmented fast simulated annealing,SFSA)反演策略,以提高零偏VSP资料全波形反演的效率。在反演前期采用大模型扰动空间和较慢温度衰减速度,充分发挥全局搜索能力,而在后期引入限制因子产生扰动模型,在迭代不断增加的时候逐渐减小模型的扰动空间,同时采用较快的温度衰减速度,有效提高反演的速度,使反演快速收敛到最优解。基于相同的初始温度和马尔可夫链长度,分别利用基于SFSA和非常快速模拟退火(very fast simulated annealing,VFSA)方法进行零偏VSP纵波速度全波形反演测试。结果表明,基于SFSA的反演方法的反演效率提高约50%,在迭代次数更少的条件下能获得更好的反演效果。基于SFSA的零偏VSP全波形反演具有高效和高精度的特点,其反演结果为地震地质层位标定、成果解释及油气预测奠定了基础。
Zero-offset VSP velocity inversion with FWI using segmented fast simulated annealing
[J].
DOI:10.3969/j.issn.1000-1441.2019.01.012
[本文引用: 1]

<p> The application of the full-waveform inversion technique based on the conventional simulated annealing algorithm to zero-offset VSP data is time consuming and complex.This paper therefore proposes an efficient segmented fast simulated annealing (SFSA) strategy,which uses different disturbance models and annealing methods at different stages to improve the waveform inversion efficiency of zero-offset VSP data.In the early stage of inversion,large model perturbation space and slow decay rate of temperature were adopted to fully perform global search;in late stage,the perturbation model with restriction factor was adopted;the model perturbation space was gradually reduced as the iteration increased,with a faster decay rate of temperature,to improve the efficiency of the inversion and help the algorithm converge to the optimal solution quickly.Finally,SFSA and conventional very fast simulated annealing (VFSA) algorithms were compared for P-wave velocity inversion of zero-offset VSP.The test results showed that the SFSA algorithm can improve the inversion efficiency by 50%,while a better inversion effect could be obtained using less iteration.The proposed method could lay the foundation for the calibration of seismic geological horizons,seismic interpretation,and reservoir prediction.</p>