0 引言
叠后地震数据纵波阻抗反演是地震储层预测的基础,可将地震剖面转化为反映岩性信息的数据体,继而完成岩性识别、含油气预测等工作。按反演方法划分,阻抗反演可以分为随机反演和确定性反演两类[1]。随机反演以马尔科夫链—蒙特卡罗(MCMC)[2-3]、模拟退火[4]等方法生成一系列阻抗,然后从中选择最合适的阻抗作为最终反演结果,该类方法通常会获得概率解。随机反演同样包括地质统计学反演[5]、基于傅里叶谱模拟(FFT-MA)的随机反演[6-7]等,这些方法的优势在于反演分辨率高,缺点为计算时间长,反演数据体随机性高。确定性反演通常利用线性化的反演公式,可直接求解,如包含TV约束和低频约束的稀疏脉冲反褶积[8],可直接得到绝对纵波阻抗;该类方法仍包括基于初始模型的广义线性反演[9]、有色反演[10]等算法。同样,也可以通过某种算法得到反射系数,然后通过递推的方式获得纵波阻抗,如稀疏脉冲反褶积[11]、谱反演等[12]。除这些算法之外,深度学习近几年也被应用到阻抗反演中,取得了较好的应用效果[13-14]。
谱反演的基础是奇偶分解和频谱白化,奇偶分解可以减弱薄层之间的调谐效应[15],频谱白化的优势在于可以灵活选择参与计算的频带[16],这两种算法的结合,使得谱反演的分辨率高于稀疏脉冲反褶积[17]。谱反演的研究仍处于探索阶段,和所有反演方法一样,谱反演也是由部分频带的地震记录反演全频带的反射系数,需要加入先验信息,以减少反演误差,目前主要集中于改进其对反射系数约束项,包括平滑约束(L2-norm)[18]、以压缩感知理论[19]为基础的L1-norm[12]等,考虑到地层存在吸收衰减,叠后地震数据通常具有非稳态特征[20],进而提出了非稳态地震数据的谱反演[21]。而由于递推反演可以基于反射系数获得阻抗[22],已有学者将谱反演和递推反演相结合获得阻抗数据体[23]。
综上所述,本文提出基于谱反演的叠后纵波阻抗反演方法,通过施加TV约束,直接反演相对阻抗,然后基于频率域的能量匹配的方法进行高低频的融合,得到绝对阻抗数据。由于谱反演的分辨率高于稀疏脉冲反褶积,直接反演相对阻抗可避免递推反演导致的横向不连续性,因此,本文方法的横纵向分辨率均高于传统的递推反演。模型和实际数据表明,本文提出的方法在叠后地震阻抗反演中具有一定的应用价值。
1 理论
1.1 基于L1范数的地震数据谱反演
地震记录s可写为是反射系数r和子波w的褶积,并添加高斯分布的随机噪声n,即:
公式两边进行傅里叶变换,即
式中:W、R、S分别代表着子波w,反射系数r和地震数据s的傅里叶变换。公式两侧同时除以子波的振幅谱,即:
频率域反射系数R可以通过时间域反射系数的傅里叶变换得到,同时考虑到除法的不稳定性,引入预白化因子ε>0改善不稳定性,即:
式中:r是反射系数r的向量形式;F表示傅里叶变换矩阵;i=
由于实偶函数的傅里叶变换是实偶函数,实奇函数的傅里叶变换是虚偶函数。式(5)可写为:
Im[F]ro+Im
式中:Re[·]和Im[·]表示实部和虚部,令Fcos=Re[F],Fsin=Im[F],合并式(6)并化简为:
式中:ae是偶分量权重,ao是奇分量权重,re+ro=r。由于地震频带有限,取有效频带内mc个点(假设地震记录采样点数为m)用于全频带反演,截断后的傅里叶矩阵为Fsin∈
式中:λ为正则化参数,λ越大,反射系数越稀疏。式(8)可以通过交替方向乘子法(ADMM)[24]等有效求解。
1.2 基于谱反演方法的叠后纵波阻抗反演
常规纵波阻抗可由反射系数进行递推得到,但是这种方式易造成误差累积,且横向连续性差,因此,本研究中,将阻抗的求解直接写入式(8)中,获得直接优化相对阻抗的目标方程,然后将所求解的相对阻抗和预先建立的低频模型进行频率域的融合,得到绝对阻抗。
在反射系数‖r‖∞<0.3时,反射系数r可以被表示为地震相对纵波阻抗z的对数差分形式,即
式中:r∈ℝm×1;z∈ℝ(m+1)×1;
事实上,由于差分矩阵(10)的行数小于列数,又因为谱反演自主选择频带,故而在不包含零频率和极低频率的情况下,已知反射系数通过式(9)可求得的对数纵波阻抗
其中,
根据式(8),所求解的相对阻抗可写为
式中,‖
式中:ztrue为绝对纵波阻抗;zmodel由所建立的低频模型提供;c表示常数,可由测井数据的中高频
2 数值试验
2.1 参数测试
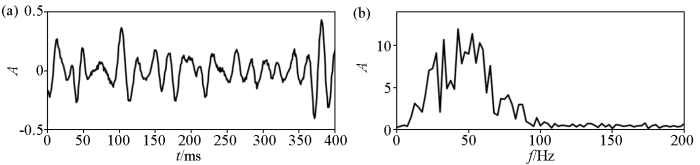
图1
图1
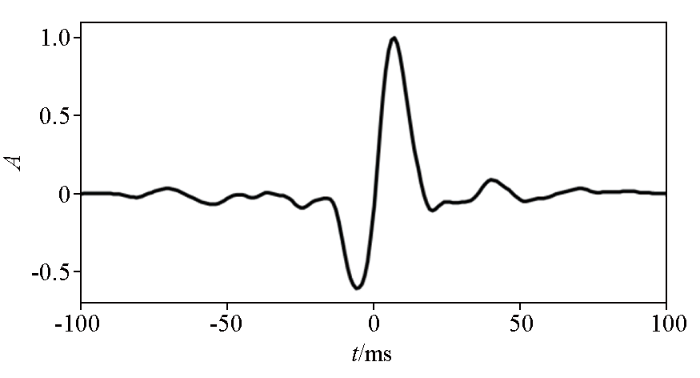
合成的时间域信号及其振幅谱
a—时间域信号;b—振幅谱
Fig.1
Synthetic signal in time domain and its amplitude spectrum
a—signal in time domain;b—amplitude spectrum
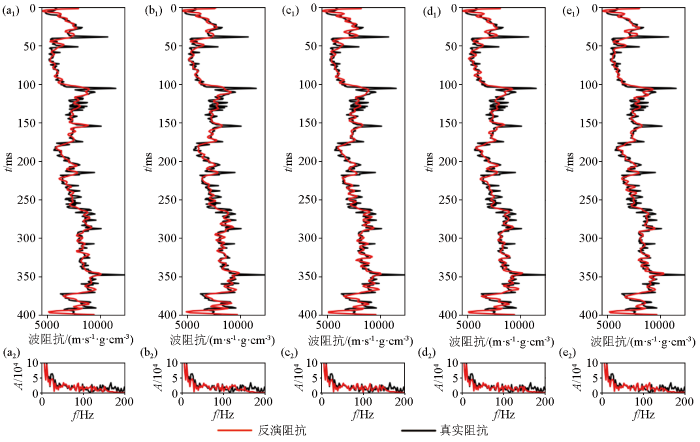
图2
图2
正则化参数测试
a—正则化参数:5e-5;b—正则化参数:1e-4;c—正则化参数:5e-4;d—正则化参数:1e-3;e—正则化参数:5e-3
Fig.2
Regularization parameter tests
a—regularization parameter:5e-5;b—regularization parameter:1e-4;c—regularization parameter:5e-4;d—regularization parameter:1e-3;e—regularization parameter:5e-3
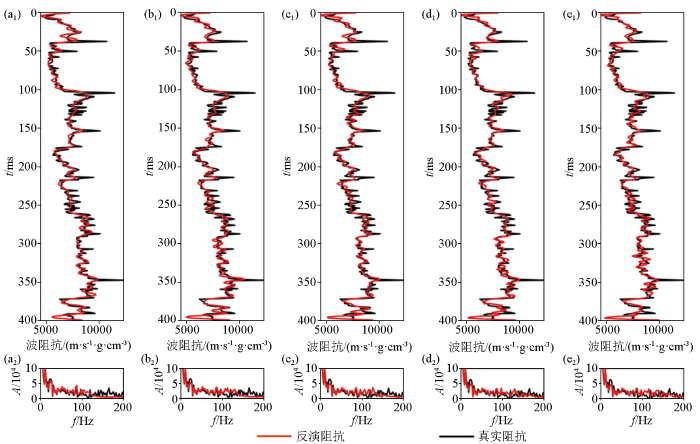
图3
图3
上限频率测试
a—上限频率:120 Hz;b—上限频率:135 Hz;c—上限频率:150 Hz;d—上限频率:165 Hz;e—上限频率:180 Hz
Fig.3
Upper limit frequency tests
a—upper limit frequency:120 Hz;b—upper limit frequency:135 Hz;c—upper limit frequency:150 Hz;d—upper limit frequency:165 Hz;e—upper limit frequency:180 Hz
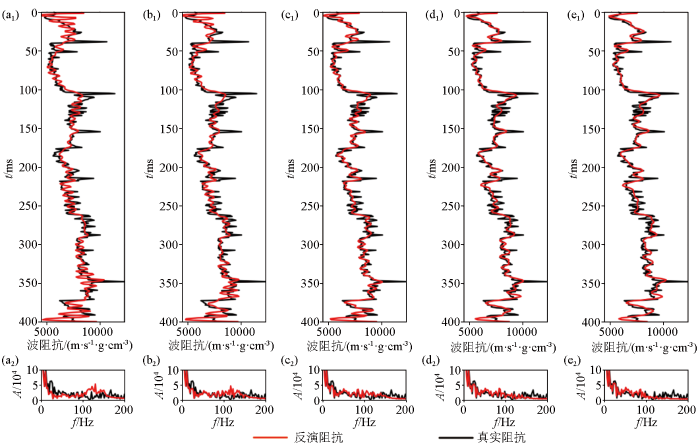
图4
图4
预白化因子参数测试
a—预白化因子:0.005;b—预白化因子:0.01;c—预白化因子:0.02;d—预白化因子:0.04;e—预白化因子:0.08
Fig.4
Pre-whiten factor parameter tests
a—pre-whiten factor:0.005;b—pre-whiten factor:0.01;c—pre-whiten factor:0.02;d—pre-whiten factor:0.04;e—pre-whiten factor:0.08
虽然上述3个参数的效果类似,但存在差异:正则化参数主要表征TV约束的强弱,其值范围同地震数据和地震子波的最大振幅比有关,在这个范围内参数越大,反演阻抗方波化越明显,当信噪比足够高时,一般取0.1倍的最大振幅比;上限频带只通过调整频带范围控制反演精度,可通过地震分频剖面确定,即选取最后一个信噪比高的频段所对应的主频;而预白化因子用于提高反演稳定性,除作用于能量较弱的高频部分外,也作用于子波振幅谱能量较弱的其他部分,视选取的上限频带范围和振幅谱确定。
2.2 二维模型测试
图5
图5
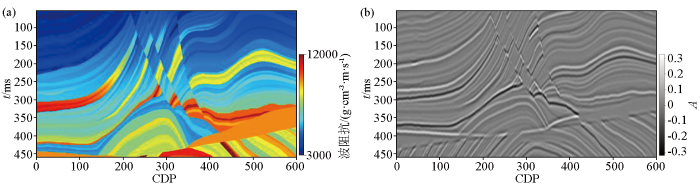
部分Marmousi2模型及合成地震记录
a—部分Marmousi2模型;b—合成地震记录
Fig.5
Partial Marmousi2 model and corresponding synthetic record
a—partial Marmousi2 model;b—synthetic record
图6
图6
低频模型及纵波阻抗反演数据
a—低频模型;b—本文方法;c—稀疏脉冲反褶积后的递推反演
Fig.6
Low-frequency model and acoustic impedance inversion results
a—low-frequency model;b—the proposed method;c—recursive inversion of sparse spike deconvolution
3 实例应用
图7
图7
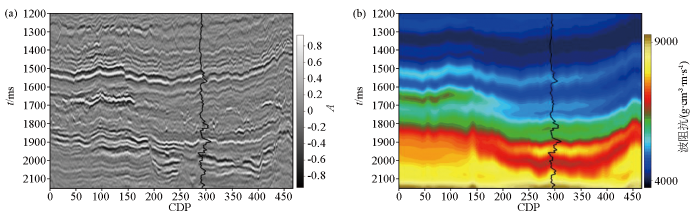
实际地震数据及纵波阻抗低频模型
a—实际地震数据;b—纵波阻抗低频模型
Fig.7
Field data and low-frequency model
a—field data;b—low-frequency model
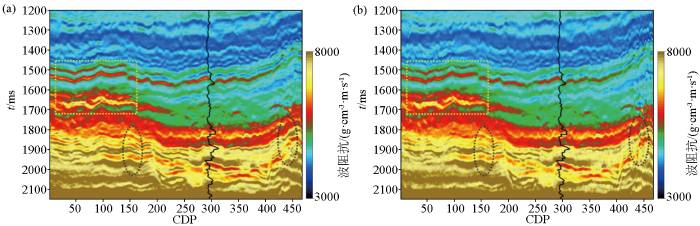
图8
图9
图9
fx-Decon前纵波阻抗反演结果
a—本文方法;b—稀疏脉冲反褶积后的递推反演
Fig.9
Acoustic impedance inversion results before fx-Decon
a—the proposed method;b—recursive inversion of sparse spike deconvolution
图10
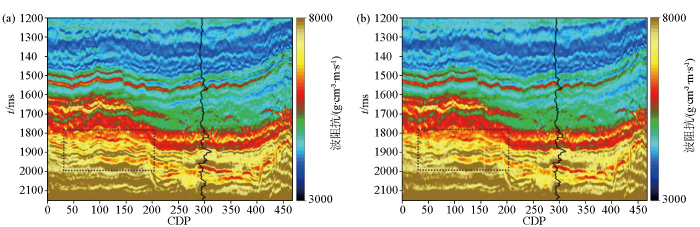
图10
fx-Decon后纵波阻抗反演结果
a—本文方法;b—稀疏脉冲反褶积后的递推反演
Fig.10
Acoustic impedance inversion results after fx-Decon
a—the proposed method;b—recursive inversion of sparse spike deconvolution
4 结论及讨论
本文提出一种基于谱反演的叠后纵波阻抗反演方法,其结合了谱反演的高分辨率和直接得到相对阻抗的优点,且算法参数意义明确,易于测试和应用,相比于稀疏脉冲反褶积后的递推反演,本文方法分辨率高,反演的剖面横向连续性好,具有一定应用价值。可基于本文算法开展如下研究:
1)叠前反演可以通过反演弹性阻抗得到弹性参数,基于Zoeppritz近似方程,本文方法可以很容易地推至叠前反演,进而提高叠前反演的精度。
2)本算法中,可以通过给定非稳态子波以完成非稳态地震数据的反演。
同时,基于谱反演的叠后纵波阻抗反演方法也存在如下问题:
1)该方法的绝对阻抗是由相对阻抗和低频模型频率融合获得,对拼接部分具有相位一致性要求,在后续研究中将考虑解决该问题。
2)算法所使用的TV约束是阻抗差分的L1范数,会压制弱反射系数地层,后续研究将基于柯西约束等构造全新的“TV约束”以获得更精细的反演结果。
附录A: 交替方向乘子法(ADMM)
基于交替方向乘子法求解式(13),即求解:
将上式简化为:
其中,A=
分裂变量[
其中,与
其中,u表示对偶变量,方程(A-3)只涉及L2-norm可直接求解:
[we,wo]T更新为:
因为L呈病态,基于投影次梯度法,设置子循环迭代次数变量i,式(A-5)可解为:
其中,sign(·)表示符号函数,α为迭代步长;当(A-5)相邻两次迭代的[we,wo]T(i+1)和[we,wo]T(i)基本一致时,子循环达到收敛,此时[we,wo]T(k+1):[we,wo]T(i+1)。
最后,对偶变量u使用对偶上升法进行更新,相应的更新迭代方程为:
重复上述迭代,当满足相邻两次迭代的阻抗基本一致时视为算法收敛,可输出反演的阻抗
参考文献
几种地震波阻抗反演方法的比较分析与综合应用
[J].
Comparison of seismic impedance inversion methods and an application case
[J].
基于MCMC的叠前地震反演方法研究
[J].
Study on prestack seismic inversion using Markov Chain Monte Carlo
[J].
Inversion of post-stack seismic data using simulated annealing
[J].DOI:10.1111/gpr.1991.39.issue-5 URL [本文引用: 1]
Geostatistical inversion:a sequential method of stochastic reservoir modeling constrained by seismic data
[J].
The FFT moving average(FFT-MA) generator:An efficient numerical method for generating and conditioning Gaussian simulations
[J].DOI:10.1023/A:1007542406333 URL [本文引用: 1]
基于FFT-MA谱模拟的快速随机反演方法研究
Study of fast stochastic inversion based on FFT-MA spectrum simulation
[J].
基于TV约束和Toeplitz矩阵分解的波阻抗反演
[J].
Wave impedance inversion based on TV regularization and Toeplitz-sparse matrix factorization
[J].
Generalized linear inversion of reflection seismic data
[J].
DOI:10.1190/1.1441497
URL
[本文引用: 1]

Generalized linear inversion, sometimes known as model perturbation, nonlinear regression, or inverse modeling, is applied to synthetic and real seismic data sets with the objective of obtaining an impedance profile as a function of time. The impedances solved for are parameterized in a manner that describes the unknown earth using fewer variables than previous seismic generalized linear inversion techniques. In this application only single traces of common‐midpoint (CMP) processed data will be inverted. The method of generalized linear inversion (GLI) presented here is designed to improve on the shortcomings of recursive inversion with respect to relative and absolute scale of the impedance results, resolution of impedance boundaries, and distortion from residual wavelet effects. In obtaining these goals other advantageous aspects of GLI were discovered. For example, it is insensitive to noise in many cases, and it will allow an interpreter to fix the impedance of any number of known lithologies in an interval being inverted. This last property is extremely useful when evaluating a prospect on an otherwise well‐understood seismic line. The GLI method is illustrated on a number of synthetic examples and one field data set from the Powder River basin of Wyoming.
Fast-track “colored” inversion
[C]//
Deconvolution with the L1-norm
[J].
DOI:10.1190/1.1440921
URL
[本文引用: 1]

Given a wavelet w and a noisy trace t + s * w + n, an approximation ŝ of the spike train s can be obtained using the [Formula: see text] norm. This extraction has the advantage of preserving isolated spikes in s. On some types of data the spike train ŝ can represent s as a sparse series of spikes, which may be sampled at a rate higher than the sample rate of the data trace t. The extracted spike train ŝ may be qualitatively much different than those commonly extracted using the [Formula: see text] norm. The [Formula: see text] norm can also be used to extract a wavelet ŵ from a trace t when a spike train s is known. This wavelet extraction can be constrained to give a smooth wavelet which integrates to zero and goes to zero at the ends. Given a trace t and an initial approximation for either s or w, it is possible to alternately extract spike trains and wavelets to improve the representation of trace t. Although special algorithms have been developed to solve [Formula: see text] problems, all of the calculations can be performed using a general linear programming system. Proper weighting procedures allow these methods to be used on ungained data.
地震数据谱反演压缩感知算法实现及应用
[J].
Implementation and application of compressed sensing algorithm for seismic spectrum inversion
[J].
基于先验约束的深度学习地震波阻抗反演方法
[J].
Deep learning seismic impedance inversion based on prior constraints
[J].
时域卷积神经网络地震波阻抗反演因素影响的研究
[J].
Study on the influence of preprocessing and hyperparameters on Temporal convolutional network seismic impedance inversion
[J].
模型约束基追踪反演方法
[J].
DOI:10.3969/j.issn.1000-1441.2016.01.015
[本文引用: 1]

基于反射系数奇偶分解的基追踪反演方法,补充了地震资料中所缺失的低频与高频信息,较好地提高了反演结果对地层的分辨能力。但仅仅使用稀疏约束加入的低频信息缺乏合理性,可能与工区的实际地质情况不符,需要进一步改善反演结果的横向连续性。因此,提出在基追踪反演目标函数中加入模型约束,得到模型约束的基追踪反演目标函数,并使用梯度投影稀疏重构(Gradient Projection for Sparse Reconstruction,GPSR) 算法进行求解。模型约束的加入增强了反演的稳定性,使得反演结果中的低频信息更加符合工区实际地质背景信息,并且能够改善反演结果的横向连续性。楔形模型和实际数据测试结果表明,模型约束基追踪反演方法不仅保持了基追踪反演的稀疏性,地层阻抗呈现块化,反射界面刻画清晰,而且反演方法更为稳定,反演结果的横向连续性得到了改善,从而验证了该方法的可行性。
Basis pursuit inversion method under model constraint
[J].
DOI:10.3969/j.issn.1000-1441.2016.01.015
[本文引用: 1]

The basis pursuit inversion (BPI) method based on the dipole decomposition of reflection coefficients compensates the low-frequency and high-frequency information lacked in the seismic data,which can well improve the identification capability of inversion results on formations.However,it might not be reasonable to add the low frequency information just by the sparse constraint,and the information might not coincide with the true geological background.Therefore,we derived the model constrained BPI objective function by putting the model constraint to the origin objective function of BPI,and utilized the gradient projection for sparse reconstruction (GPSR) algorithm to solve the problem.It would not only enhance the inversion stability and make the low frequency information contained in inversion results more consistent with the actual work area,but also improve the lateral continuity of the inversion results.The results of the wedge model and real field data testing demonstrate that the model constrained BPI method not only keep the sparsity of the inversion results and shows the impedance in blocky,which characterizes the interface more clearly and improves the reliability of the inversion and the lateral continuity of the inversion results.
地震数据的谱白化处理
[J].谱白化处理是提高地震勘探分辨能力的行之有效的方法。本文简述了谱白化处理的原理、实现过程及其参数的选择和使用。从实际处理中我们认识到该方法具有适应性广、可控性强、效果稳定的特点。文中给出的实例说明该方法既能提高分辨能力又不致将噪音放大得太厉害。最后还讨论了该方法的其它一些优点。
Spectral whitening of seismic data
[J].In seismic exploration, the spectral whitening is an effective measure for increasing the resolution. In this paper, the principle, the implementation procedure as well as the parameter selection and application of the spectral whitening were briefed to the point.We recognized by practice that this technique has the characteristics of wide adaptability, strong controllability as well as the stability in effects. Examples show that it could not only increase the resolution but it could also control the noise to some extent.
地震薄层反射系数谱反演算法研究及应用
[J].
Thin-bed reflectivity inversion and seismic application
[J].
谱反演方法在致密薄层砂体预测中的应用研究
[J].
DOI:10.3969/j.issn.1000-1441.2015.03.013
[本文引用: 1]

在以致密砂岩为储层的非常规致密油勘探开发中,由于靶区选择和水平井部署的需要,落实致密砂体的横向展布至关重要。松辽盆地北部白垩系扶余油层致密砂体整体薄层发育,特别是T<sub>2</sub>强反射界面屏蔽问题的存在,一直制约着致密薄层砂体的识别精度。为此,开展了针对大庆长垣扶余油层致密薄砂体预测的谱反演方法应用研究。在简介谱反演方法原理的基础上,为了保证反演算法的计算精度,利用复数域快速匹配追踪算法提高时频转换的精度;通过提取时变子波提高反射系数时频谱的准确性。应用研究结果表明,将谱反演得到的地震反射系数体与宽频零相位子波进行褶积运算,获得的研究区宽频保幅地震数据有效削弱了T<sub>2</sub>的屏蔽效应,改善了复合波的叠置问题,清晰地反映出了薄层砂体顶、底界面,并很好地保持了振幅与砂体的对应关系。
Application of spectral inversion for tight thin-bed sand body prediction
[J].
DOI:10.3969/j.issn.1000-1441.2015.03.013
[本文引用: 1]

Due to the need of selecting target areas and deploying horizontal wells,it is very important to understand the lateral distribution of tight sand bodies in unconventional tight sandstone reservoir exploration and development.The tight sandstone is characterized by the development of Cretaceous thin-beds for Fuyu reservoir in the north of Songliao Basin.And the identification accuracy of the thin-bed sand bodies is restricted by the shielding effect from the strong reflection interface T2.Therefore,we study spectral inversion technique for the prediction of the tight thin-bed sand bodies in Fuyu formation,Daqing Placanticline.In order to ensure the accuracy of spectral inversion,fast matching pursuit algorithm in complex domain is used to improve the precision of the time-frequency conversion and the accuracy of time-frequency spectrum of reflection coefficient is increased by the time-varying wavelet extraction.The results of spectral inversion show that:the seismic reflection coefficient volumes from spectral inversion are convoluted with the broadband zero-phase wavelet,thus obtained broadband preserved amplitude seismic data effectively suppress the shielding effect from T2 in target area.The results also indicate the improvements of composite reflections overlay,the top and the bottom interface of the thin-bed sandstone detected clearly,and the favorable correspondence between amplitude attributes and sand bodies.
Compressed sensing
[J].DOI:10.1109/TIT.2006.871582 URL [本文引用: 1]
Inverse Q-filter for seismic resolution enhancement
[J].
DOI:10.1190/1.2192912
URL
[本文引用: 1]

A principal limitation on seismic resolution is the earth attenuation, or [Formula: see text]-effect, including the energy dissipation of high-frequency wave components and the velocity dispersion that distorts seismic wavelets. An inverse [Formula: see text]-filtering procedure attempts to remove the [Formula: see text]-effect to produce high-resolution seismic data, but some existing methods either reduce the S/N ratio, which limits spatial resolution, or generate an illusory high-resolution wavelet that contains no more subsurface information than the original low-resolution data. In this paper, seismic inverse [Formula: see text]-filtering is implemented in a stabilized manner to produce high-quality data in terms of resolution and S/N ratio. Stabilization is applied to only the amplitude compensation operator of a full inverse [Formula: see text]-filter because its phase operator is unconditionally stable, but the scheme neither amplifies nor suppresses high frequencies at late times where the data contain mostly ambient noise. The latter property makes the process invertible, differentiating from some conventional stabilized inverse schemes that tend to suppress high frequencies at late times. The stabilized inverse [Formula: see text]-filter works for a general earth [Formula: see text]-model, variable with depth or traveltime, and is more accurate than a layered approach, which involves an approximation to the amplitude operator. Because the earth [Formula: see text]-model can now be defined accurately, instead of a constant-[Formula: see text] layered structure, the accuracy of the inverse [Formula: see text]-filter is much higher than for a layered approach, even when implemented in the Gabor transform domain. For the stabilization factor, an empirical relation is proposed to link it to a user-specified gain limit, as in an explicit gain-controlling scheme. Synthetic and real data exam-ples demonstrate that the stabilized inverse [Formula: see text]-filter corrects the wavelet distortion in terms of shape and timing, compensates for energy loss without boosting ambient noise, and produces desirable seismic images with high resolution and high S/N ratio.
Nonstationary spectral inversion of seismic data
[C] //
Three-parameter prestack seismic inversion based on L1-2 minimization
[J].
DOI:10.1190/GEO2018-0730.1
[本文引用: 1]

Prestack inversion has become a common approach in reservoir prediction. At present, the critical issue in the application of seismic inversion is the estimation of elastic parameters in the thin layers and weak reflectors. To improve the resolution and the accuracy of the inversion results, we introduced the difference of L-1 and L-2 norms as a nearly unbiased approximation of the sparsity of a vector, denoted as the L1-2 norm, to the prestack inversion. The nonconvex penalty function of the L1-2 norm can be decomposed into two convex subproblems via the difference of convex algorithm, and each subproblem can be solved efficiently by the alternating direction method of multipliers. Compared with the L-1 norm regularization, the L1-2 minimization can reconstruct reflectivities more accurately. In addition, the f-x predictive filtering was introduced to guarantee the lateral continuity of the location and the amplitude of the reflectivity series. The generalized linear inversion and f-x predictive filtering are combined for stable elastic impedance inversion results, and three parameters of P-wave velocity, S-wave velocity, and density can be inverted with the Bayesian linearized amplitude variation with offset inversion. The inversion results of synthetic and real seismic data demonstrate that the proposed method can effectively improve the resolution and accuracy of the inversion results.
Accurate estimation of acoustic impedance based on spectral inversion
[J].DOI:10.1111/1365-2478.12538 URL [本文引用: 1]
Distributed optimization and statistical learning via the alternating direction method of multipliers
[J].DOI:10.1561/2200000016 URL [本文引用: 1]
Marmousi2:An elastic upgrade for Marmousi
[J].DOI:10.1190/1.2172306 URL [本文引用: 1]