地震分频迭代反演在薄层河道砂体预测中的应用

doi:10.11720/wtyht.2023.1175

地震分频迭代反演在薄层河道砂体预测中的应用

任宪军^,¹, 李钟^,², 马应龙³, 董萍⁴, 田行达⁵

1.中国石化东北油气分公司勘探开发研究院,吉林长春 130062

2.中海油田服务公司物探事业部研究院特普数据中心,广东湛江 524057

3.中石油塔里木油田勘探开发研究院,新疆库尔勒 841000

4.华北油田公司第三采油厂工程技术研究所,河北沧州 062450

5.长江地球物理探测(武汉)有限公司,湖北武汉 430010

Application of seismic frequency-divided iterative inversion in the prediction of thinly laminated channel sand bodies

REN Xian-Jun^,¹, LI Zhong^,², MA Ying-Long³, DONG Ping⁴, TIAN Xing-Da⁵

1. Exploration and Development Research Institute,Sinopec Northeast Oil and Gas Company,Changchun 130062,China

2. Data Processing Center(Zhanjiang),Research Institute,Geophysical Branch,China Oilfield Services Limited,CNOOC,Zhanjiang 524057,China

3. Research Institute of Exploration Development,PetroChina Tarim Oilfield Company,Kuerle 841000,China

4. Engineering Technology Research Institute,No. 3 Oil Production Plant of Huabei Oilfileld Company,Cangzhou 062450,China

5. Changjiang Geophysical Exploration & Testing Co.,Ltd.,Wuhan 430010,China

通讯作者: 李钟(1996-),男,汉族,中国石油大学(北京)硕士研究生毕业,主要进行地震解释和储层预测研究工作。Email:2643539019@qq.com

第一作者: 任宪军(1982-),男,汉族,副研究员,主要从事油气勘探开发工作。Email:516479506@qq.com

责任编辑: 叶佩

收稿日期: 2022-04-19 修回日期: 2023-02-1

基金资助:

国家自然科学基金项目“裂缝性储层地震定量预测及流体识别方法研究”(41974124)

Received: 2022-04-19 Revised: 2023-02-1

摘要

龙凤山地区河道砂储层符合典型岩性油气藏特征,其砂体厚度薄、河道窄、岩性纵横向非均质性强,对5 m以下储层预测难度大。分频迭代反演充分利用全频段地震资料,对不同频段、尺度的地震信息逐级传递,优化反演结果。文中具体利用匹配追踪算法实现地震信号频段划分得到不同尺度地震数据体,在测井约束下,以低频大尺度的反演结果作为下一级频段反演的初始模型,调整反演结果;在反演过程中,通过相关算法自适应选取子波,增强反演准确性,基于贝叶斯理论自适应选取正则化参数,调节分辨率和稳定性关系达到最佳平衡,避免反演出现混沌现象。2019年该区新钻四口井钻遇营城组1-2-6和1-2-8小层的气层,同反演预测结果吻合。证明本文方法相较于常规分频反演而言,具有反演精度高、忠实于地震信息、频段应用充分的优点,可以有效提高薄层河道砂的识别能力,指导相关岩性油气藏的勘探开发。

关键词： 薄层河道砂; 匹配追踪; 分频迭代反演

Abstract

The channel sand reservoirs in the Longfengshan area have the characteristics of typical lithologic reservoirs.This area has thin sand bodies,narrow channels,and strong vertical and horizontal lithologic heterogeneity.It is difficult to predict the reservoirs at a depth of 5 m or greater.The frequency-divided iterative inversion can fully utilize the full-frequency band seismic data and transmit the seismic information of different frequency bands and scales step by step,thus optimizing the inversion results.In this study,the seismic signal frequency bands were divided using the matching pursuit algorithm to obtain seismic data volumes of different scales.Under the constraints of log data,the low-frequency,large-scale inversion results were used as the initial model for the next-order frequency band inversion,and the inversion results.During the inversion,wavelets were adaptively selected using the correlation algorithm to enhance the inversion accuracy.Regularization parameters were adaptively selected based on the Bayesian theory to adjust the relationship between resolution and stability to achieve the optimal balance and avoid chaos in inversion.In 2019,gas reservoirs in subzones 1-2-6 and 1-2-8 of the Yingcheng Formation were encountered in the drilling of four wells in the Longfengshan area.This result is consistent with the inversion prediction results.Therefore,compared with conventional frequency division inversion,the method proposed in this study has the advantages of high inversion accuracy,coincidence with seismic information,and full application of frequency bands.This method can effectively improve the identification performance of thinly laminated channel sand bodies and guide the exploration and development of related lithologic reservoirs.

Keywords： thinly laminated channel sand; matching pursuit; frequency-divided iterative inversion

PDF (6781KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

任宪军, 李钟, 马应龙, 董萍, 田行达. 地震分频迭代反演在薄层河道砂体预测中的应用[J]. 物探与化探, 2023, 47(2): 420-428 doi:10.11720/wtyht.2023.1175

REN Xian-Jun, LI Zhong, MA Ying-Long, DONG Ping, TIAN Xing-Da. Application of seismic frequency-divided iterative inversion in the prediction of thinly laminated channel sand bodies[J]. Geophysical and Geochemical Exploration, 2023, 47(2): 420-428 doi:10.11720/wtyht.2023.1175

0 引言

为了解决常规地震反演难以预测厚度薄、横向变化大、隐蔽性强的河道砂储层的问题,地震分频反演应运而生。由于地震分频反演充分利用频率和地质尺度之间的关系,对小尺度地质体有很高的识别精度,近年来,分频反演的方法被不断研究完善:2006年,于建国等^[1]充分发掘测井和地震资料之间的关系,将AVF作为独立信息引入SVM方法中进行反演,提高分辨率的同时减小了薄层反演的不确定性;2007年,吴媚等^[2]利用小波变换基于测井曲线分频分析对于不同频率尺度下的岩石物理参数进行非线性联合反演,得到了高分辨率的结果;2008年,龚洪林等^[3]利用地震分频属性成功识别了碳酸盐岩中的薄储层;2014年,王振卿等^[4]优选广义S变化分频方法进行频谱分解,通过带通滤波得到优势频段的纯波数据后再反演,取得了良好的应用效果;2018年,朱超等^[5]采用分频非线性反演方法,用低频模型约束,实现对复杂储层的预测;2019年,倪祥龙等^[6]将AVF反演技术应用于柴达木盆地中,降低了反演多解性;2021年,代玲等^[7]发掘不同频带的尺度信息,将不同频带的地震数据体加权平均求和,完成了分频建模;同年,肖曦等^[8]将分频反演和迭代约束稀疏脉冲反演相结合,把分频数据体应用测井插值获取低频模型,进行迭代反演。

龙凤山区块沉积的河道砂受到相带控制,整体呈扇状分布,厚度中心呈条带状,砂体沉积扇及多期沉积的薄层受到退积作用的影响成为良好的气层,但该区气层纵向分散、跨度大、单层厚度小,适合水平钻探开发,经过扇体后要尽可能多钻遇气层且需准确钻入优势单砂层,达到生产标准,这对反演的分辨率要求极高,此前靶区为了提高反演分辨率采取的主要措施是引入高频信息,通过测井信息拓宽频带,提高分辨率^[9],但在无井和少井的情况下反演分辨率受到了极大的限制。总结之前的研究发现:常规分频反演主要是分为两种,一是直接将频率和振幅的变化关系作为媒介,频率作为单独信息参与反演,但是计算过程复杂,稳定性较差;二是先分频,后分频段反演,缺点是存在频率信息间断,不同频段范围数据之间关系分裂,不同频段的优势信息不能传递保存。本文中地震分频迭代反演应用匹配追踪算法对地震数据进行多尺度分频处理,更加区分储层和围岩的细小差别,联合测井信息构建初始低频模型,低频大尺度的反演结果作为下一级频段尺度的初始模型,分尺度逐级迭代反演,增加了地震反演对小层刻画的能力,同时,结合贝叶斯理论,自适应设置适用于不同尺度反演的正则化参数,减小了反演问题的不适定性,在纵向分辨率极高的测井信息的控制下,可以实现对靶区河道砂岩形态特征精细刻画的目的。

在2021~2022年之间,靶区应用本文方法共进行了2-1、2-2、……、2-7等7口水平井的钻探工作,利用地震分频迭代反演的对薄层表征清晰的优势,刻画出单砂体的分布,取得了良好的生产效益,证明了该方法可以克服常规分频反演的缺陷,保证计算过程稳定的同时,对整个地震频段的数据信息进行发掘,解决纵横向差异大、厚度薄的问题。

1 方法原理

地震信号波场特征分析是分频反演的前提,一般地震信号中的高频信息对应着地层中相对薄的地层,高频地震信号比低频部分在地下传播过程中被吸收衰减的更严重,所以提高纵向分辨率的方法就是补偿高频部分、压缩子波等。对于地震信号多尺度的划分主要分为3种:①低频信息反映大尺度信号,高频信息反映小尺度信号;②单一尺度层序频率固定且稳定在某一确定范围内;③大尺度层序里包含着小尺度层序^[10]。

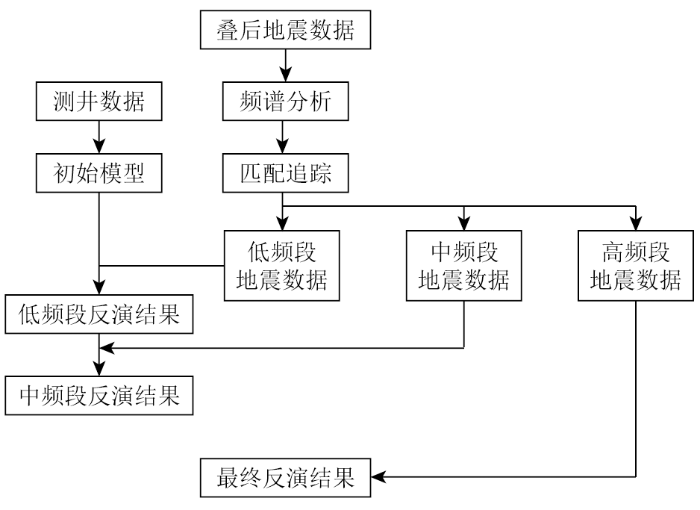
地震分频反演的基础是地震数据的内部拓频处理,首先,利用匹配追踪算法进行频谱分解将地震数据体按照频率和尺度分解成低频段、中频段和高频段3个数据体,进而减弱不同频率信号间的调谐作用,增强地震资料中被压制的高、低频信息。之后,在测井信息的约束下构建初始模型,并根据频率与尺度的对应关系开展逐级迭代反演,将低频率大尺度数据体反演结果作为中频率中尺度反演的初始模型,中频率中尺度的反演结果作为高频率小尺度反演的初始模型,反演结果对初始模型的依赖性因此而降低,同时可将不同尺度的信息进行传递,最终的反演结果可以精细刻画地下岩性变化特征,识别小尺度薄层信息;在反演过程中,在子波库中自适应地选取不同尺度数据体的反演子波,使得真实数据与模型响应匹配良好,反演结果更加准确可靠,图1为总体技术流程。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 分频反演技术流程

Fig.1 Technical process of frequency division inversion

1.1 测井、地震信息的多尺度分析

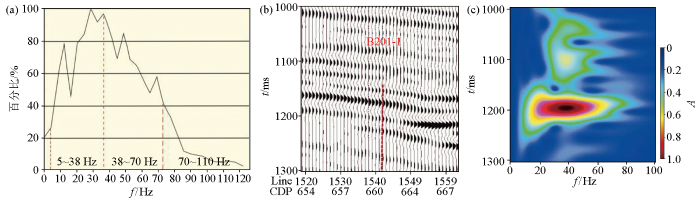
地震信号存在多尺度性特征,在地震信号中大尺度信号与地下厚层对应,相对而言,小尺度信号对应的就是地下薄层响应,小尺度和大尺度之间的关系就是一种嵌套关系(图2)。小波变换相对于傅里叶变换具有优良的时频分析特性,弥补了傅里叶变换的缺点,是人们用来考察信号特征的有力工具^[11],但是相比于小波变换和S变换等方法,匹配追踪算法具有薄层识别能力,同时也具备更快的计算效率,故而本文选择匹配追踪算法对地震信号进行相应处理。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 地震信号的多尺度性

a—地震道频谱分析;b—地震剖面;c—井旁道时频谱分析

Fig.2 Multiscale properties of seismic signals

a—seismic channel spectrum analysis;b—seismic profile;c—time spectrum analysis of well bypass

地震数据体的多尺度分解是在匹配追踪构建的过完备时频原子库中展开,利用匹配追踪可以分离频段的特性,实现地震数据体的自适应分解,为分频反演提供数据基础^[10]。对地震数据和井数据进行多尺度分解是多尺度混合反演的关键,分解之后可以将需要的局部频段的信号独立出来,充分发掘高频和低频信号,减少其他频段的影响,提高反演结果的精度和可靠性^[12]。

1.2 匹配追踪

匹配追踪算法(MP)实际就是不断迭代寻找最优时频原子的算法^[13]。匹配追踪的基本原理就是在已建立的超完备时频原子库中寻找与地震信号最匹配的原子与组合。该方法理解和应用上都很简单,而且能够自由地选择子波基函数,改变参数来调整子波库以满足实际情况,因此在应用上具有很高的研究价值^[14]。

首先,构建完备的时频原子库是匹配追踪实现的基础,这里选取随频率具有衰减性的Morlet小波函数为例,3个可调参数分别是相位 $φ$ 、主频 $f$ 和能量衰减因子 $β$ ,当衰减因子 $β = 4 l n 2$ 时,式(1)是标准的Morlet小波函数,式(1)表示完备时频原子库中的小波函数:

(1)

m (t) = e x p [- β f^{2} {(t - τ)}^{2} \times e^{i [2 π f (t - τ) + φ]}]

式中: $τ$ 为中心时间; $f$ 为主频; $φ$ 为相位; $β$ 为能量衰减因子,通过改变能量衰减因子 $β$ 可以改变小波属性和频率之间的关系,进而改变小波的变化特征,通过调节三参数,使小波呈现多种振幅特征,从而保证原子库的完备性。用简化的式(2)表示完备的时频原子库:

(2)

D = {m_{γ k}, γ k \in C}

式中: $m_{γ k}$ 表示每一次提取的最匹配小波原子, $γ k = (τ_{k}, f_{k}, φ_{k}, β_{k})$ , $τ_{k} 、 f_{k} 、 φ_{k} 、 β_{k}$ 分别表示第 $k$ 次迭代时的中心时间、主频、相位和衰减因子; $C$ 是各个参数的定义域。

经过 $N$ 次迭代后,地震信号 $S (t)$ 表示为:

(3)

S (t) = \overset{N - 1}{\sum_{n = 0}} a_{n} m_{γ n} + R^{(N)} f

式中: $a_{n}$ 为 $m_{γ k}$ 的振幅; $R^{(N)} f$ 为残差, $R^{(0)} f = s (t)$ 。之后利用复地震道技术先确定原子的先验信息,再局部动态扫描最优原子^[15-16],根据式(3)有:

(4)

R^{(N)} f = a_{n} m_{γ n} + R^{(N + 1)} f

由式(4)可知,在求取振幅和最匹配原子时,需要 $‖R^{(n + 1)} f‖$ 最小,在局部范围内动态扫描 $m_{γ n}$ 的参数,即有:

(5)

m_{γ n} = a r g m a x \frac{| < R^{(N)} f, m_{γ n} > |}{‖m_{γ n}‖}

。

在得到最匹配原子的主频、相位和能量哀减因子信息后,可由式(6)计算振幅:

(6)

a_{n} = \frac{| < R^{(N)} f, m_{γ n} > |}{m_{γ n}^{2}}

。

匹配追踪是一个反复迭代的过程^[17],判断迭代终止的条件可以是确定的迭代次数或者残差信号符合规定的约束值。

1.3 地震分频迭代反演

常规分频方法就是利用上面得到的分频段数据体开始分别进行反演,本文中分频迭代反演则将大尺度低频数据体反演的结果作为下一个频段的数据体的初始模型,对接下来的反演进行约束,也将低频反演的结果信息传递保留下来。

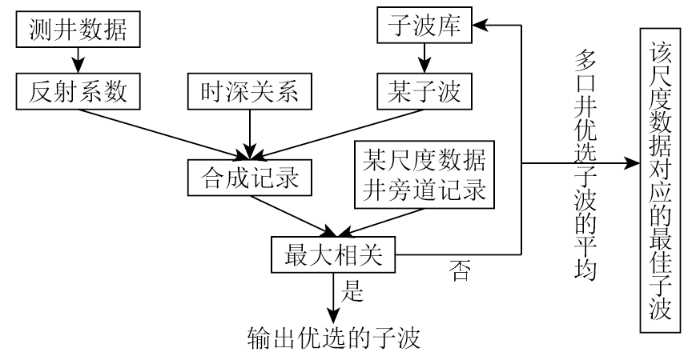
在反演过程中,子波的自适应选择也尤为重要,不同尺度反演需要选取不同的子波。通过已知测井数据求得的反射系数R,与主频不同的子波W褶积形成的合成记录,同井旁道最大相关时的主频即为优选主频。使用均方根校正的原理,将子波振幅与地震道匹配,得到该尺度的优选子波(图3)。式(7)为均方根校正公式:

(7)

ρ_{x y} = \frac{\sum_{n} x (n) y (n)}{[\sum_{n} x^{2} (n) \sum_{n} y^{2} {(n)]}^{\frac{1}{2}}}

。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 子波优选流程

Fig.3 Wavelet optimization flow chart

基于地震道非线性最优化反演思想,同时克服反演的不适定问题,引入正则化参数,将地震道与波阻抗关系的初始目标函数定义为式(8),即求目标函数在最小二乘意义下的极小值:

(8)

m i n {{‖G^{j} Δ z^{j} - Δ s^{j}‖}_{2}^{2} + λ^{j} ‖Δ z^{j}‖

式中,雅克比矩阵G为合成地震道对阻抗的偏导数。s是地震道数据,Δs为地震道数据改变量。z代表阻抗。Δz为阻抗改变量 $λ$ 表示迭代过程中的正则化参数。为了体现分频迭代过程,引入 $j$ 参量作为上标,代表选取初始模型和地震数据的状态。

通过对非线性混沌反演的分析,正则化参数越趋近于1,反演稳定性越高,分辨率越低;正则化参数越小,分辨率越高,稳定性越低。所以为了减小人为设置正则化参数引入的不确定性,确保计算过程的稳定性,使用贝叶斯原理设置正则化参数,从而对目标函数进行修改,使得正则化参数可以在分频迭代过程中自适应修改,似然函数和先验分布可以表示为:

(9)

P (Δ s| Δ z) = \frac{1}{{(\sqrt{2 π})}^{m + L - 2} C_{n}} \times e x p [- \frac{1}{2} {(G Δ z - Δ s)}^{T} C_{n}^{- 1} (G Δ z - Δ s)]

(10)

P (Δ z) = \frac{1}{{(\sqrt{2 π})}^{L} C_{z}} e x p (- \frac{1}{2} Δ z^{T} C_{z}^{- 1} Δ z)

式中: $m$ 是地震子波长度; $L$ 代表采样点; $C_{n} = σ_{n}^{2} I$ , $C_{z} = σ_{z}^{2} I$ ; $C_{n}$ 和 $C_{z}$ 分别表示噪声和模型的协方差矩阵。

忽略常数项,根据贝叶斯公式,后验概率分布可写为:

(11)

P (Δ z| Δ s) \propto e x p [- \frac{1}{2} (\frac{1}{σ_{z}^{2}} {‖Δ z‖}_{2}^{2} + \frac{1}{σ_{n}^{2}} {‖G Δ z - Δ s‖}_{2}^{2})]

。

对上式取对数,并求取后验概率的极大值,得到目标函数如下:

(12)

\underset{z}{m i n} J = \underset{z}{m i n} \frac{1}{2} (\frac{1}{σ_{z}^{2}} {‖Δ z‖}_{2}^{2} + \frac{1}{σ_{n}^{2}} {‖G Δ z - Δ s‖}_{2}^{2})

对式(12)求导并令其等0,得到正则化因子 $λ$ 的表达式:

(13)

λ = σ_{n}^{2} / σ_{z}^{2}

$σ_{n}^{2}$ 和 $σ_{z}^{2}$ 表示噪声和模型的方差。将式(13)代入到式(8)中,得到最终目标函数:

(14)

m i n {{‖G^{j} Δ z^{j} - Δ s^{j}‖}_{2}^{2} + {(\frac{σ_{n}^{2}}{σ_{z}^{2}})}^{j} ‖Δ z^{j}‖

} 。

对式(14)目标函数求导,得到阻抗变量表达式:

(15)

\begin{array}{l} Δ z_{k}^{j} = [G^{j} T_{k - 1} G_{k - 1}^{j} + λ_{k - 1}^{j} {I]}^{- 1} [G^{j} T_{k - 1} (s^{j} - s_{k - 1}^{j})], \\ (k = 1,2, 3, \dots; j = 1,2, 3,4) \end{array}

(16)

z_{k}^{j} = z_{k - 1}^{j} + Δ z_{k}^{j}

(17)

z_{1}^{j} = z_{k}^{j - 1}

。

当 $j$ =1时,初始模型由测井构建,地震数据选择低频段数据体,式(15)~(17)表示为:

(18)

\begin{array}{l} Δ z_{k}^{1} = {[G^{1} T_{k - 1} G_{k - 1}^{1} + {(\frac{σ_{n}^{2}}{σ_{z}^{2}})}_{k - 1}^{1} I]}^{- 1} [G^{1} T_{k - 1} (s^{1} - s_{k - 1}^{1})], \\ (k = 1,2, 3, \dots; j = 1) \end{array}

(19)

z_{k}^{1} = z_{k - 1}^{1} + Δ z_{k}^{1}

(20)

z_{1}^{2} = z_{k}^{1}

。

当j=2,初始模型由低频地震数据反演结果构建,使用的地震数据选用中频段,当j=3时,初始模型是中频段地震数据反演的结果,地震数据选用高频段,迭代过程重复式(18)~(20):

(21)

z_{1}^{4} = z_{k}^{3}

。

当j=4时, $z_{1}^{4}$ 是最终反演的结果,如式(21)。

在保证密度为常数的情况下,波阻抗反演可以转化为速度反演,最终得到了纵波速度数据体,可以通过速度来求取选定的层位之间的厚度,如式(22):

(22)

h = \int_{t_{1}}^{t_{2}} v t

dt,

式中,v表示速度,t₁、t₂分别是所求厚度的层的底顶时间,h表示厚度。

2 模型验证

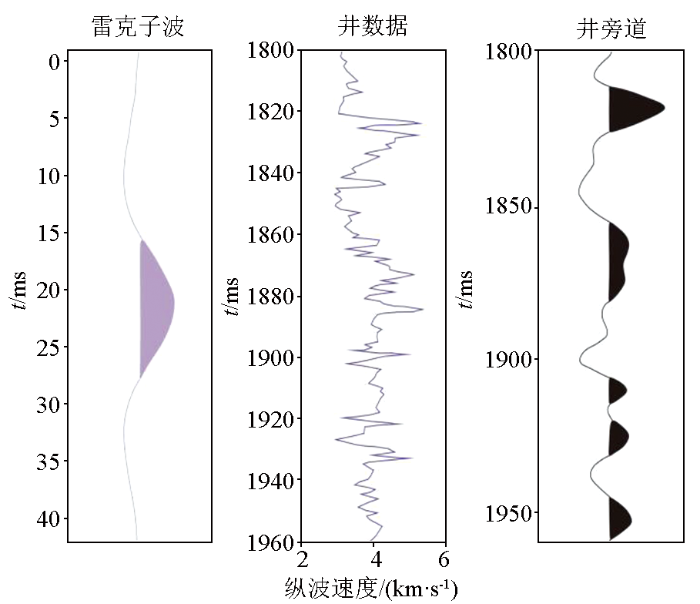
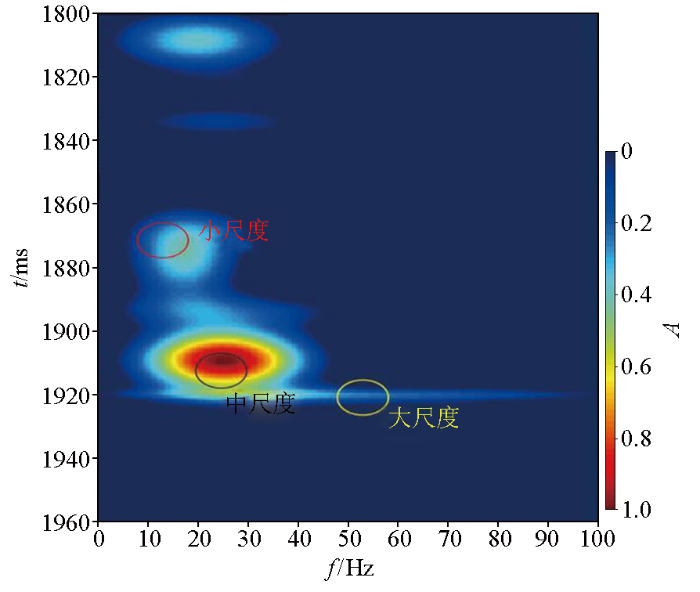
对某区块实际井资料进行重采样,构建一维理论模型,并利用主频35 Hz的雷克子波正演得到模型地震记录(图4),图5为井旁道时频谱,可以对大、中、小尺度地震信息的优势频段进行筛选。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 井曲线和地震记录

Fig.4 Well curves and seismic records

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 井旁道时频谱

Fig.5 Well bypass time spectrum

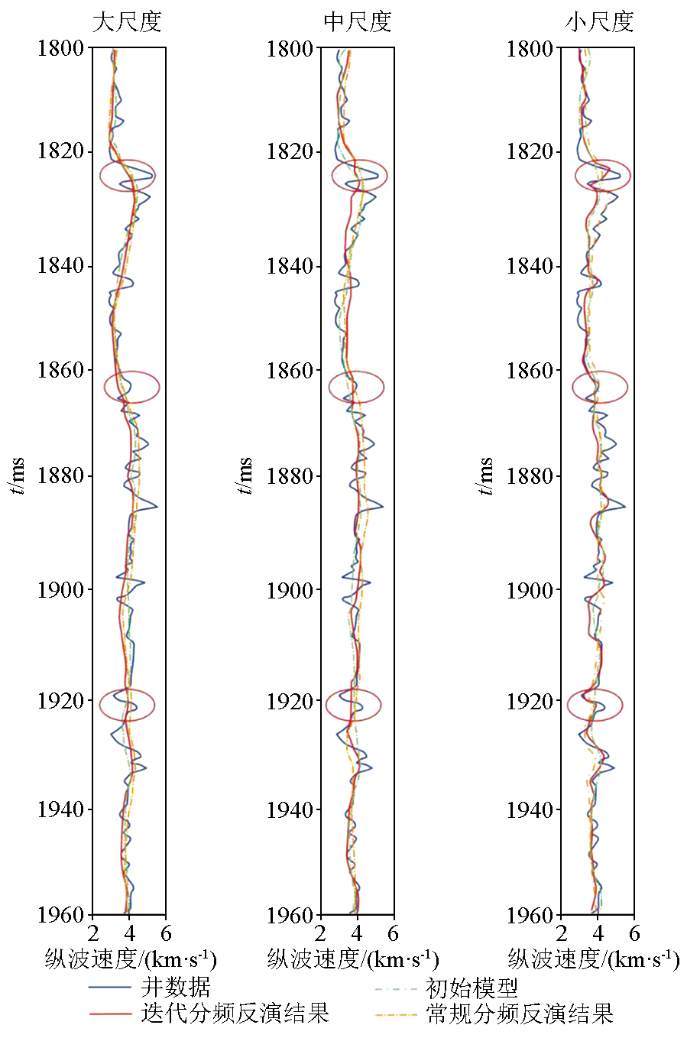
各尺度优选主频分别为13、34、45 Hz的雷克子波。反演结果如图6和7所示。图6中地震分频记录与对应尺度反演的初始模型合成记录相关系数分别为81%、50%、40%,反演结束后,其结果同分频记录相关系数均达到98%以上;图7中,随着尺度从大到小,反演结果分辨率逐级精细化,并向实际测井数据收敛,证明分频迭代反演可以有效利用地震记录中的各个频段信息,提高分辨率和稳定性。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 反演前后分频记录对比

Fig.6 Composite records before and after inversion

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 各尺度反演结果

Fig.7 All scale inversion results

3 河道砂储层反演工区应用

3.1 工区特征

龙凤山气田靶区位于松辽盆地长岭凹陷南部鼻状构造带,北正镇断阶带和长岭次凹陷。区内主要发育4套含油气层系,分别是登楼库组、营城组、沙河子组和火石岭组,其中沙河子组是主力烃源岩,营城组的泥岩和火山岩是主力盖层,为形成油气藏提供了良好的封闭条件,形成了断层和岩性匹配的构造岩性油气藏,营城组的碎屑岩则是主力气层。

营城组岩性主要以砂砾岩、含砾细砂岩、细砂岩和泥岩为主,层理形态主要是水平层理和斜层理,营城组整体呈三角洲进积的反旋回特征,主要亚相为扇三角洲前缘和前三角洲,发育微相类型为水下分流河道、席状砂、河口坝、河间道类型。由于该区沉积期次转换较快,导致该区砂体厚度薄、扇体面积小、多期河道叠加,气藏类型复杂。

3.2 频谱分解与分析

利用工区实际井约束进行反演,根据井旁道频谱分析,采用大尺度5~38 Hz、中尺度38~70 Hz、小尺度70~110 Hz这3个尺度进行反演,反演子波主频分别为28 Hz、34 Hz和40 Hz。

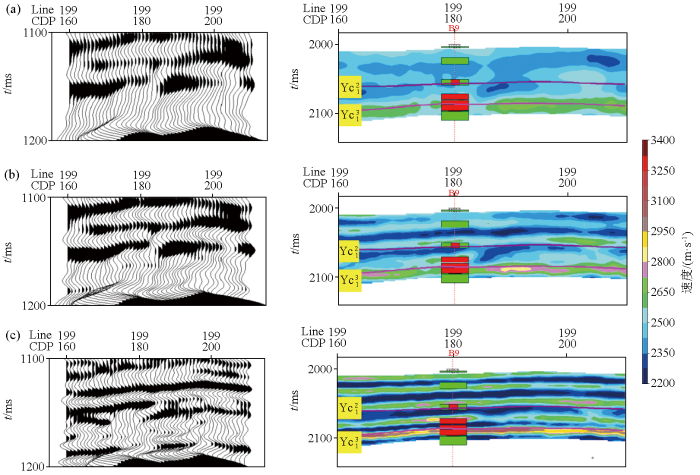
地震剖面分频处理后,随着频率增高、尺度减小,同相轴增多,降低了低频对高频的压制作用,提高了分辨率(图8)。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 地震数据多尺度分解(左)与反演剖面(右)对比

a—大尺度(5~38 Hz);b—中尺度(38~70 Hz);c—小尺度(70~110 Hz)

Fig.8 Multi scale decomposition of seismic data(left) and comparison of inversion profiles(right)

a—big scale(5~38 Hz);b—middle scale(38~70 Hz);c—small scale(70~110 Hz)

为了分析反演分辨率和储层刻画能力在尺度间的变化,保存反演过程中每个尺度的反演结果(图8),从中可以看到由宏观到细节的变化。尺度由大(图8a)到中(图8b)再到小(图8c),储层识别精度逐渐提高,薄层形态逐步清晰,细节更加明显,与测井结果吻合。

3.3 反演结果

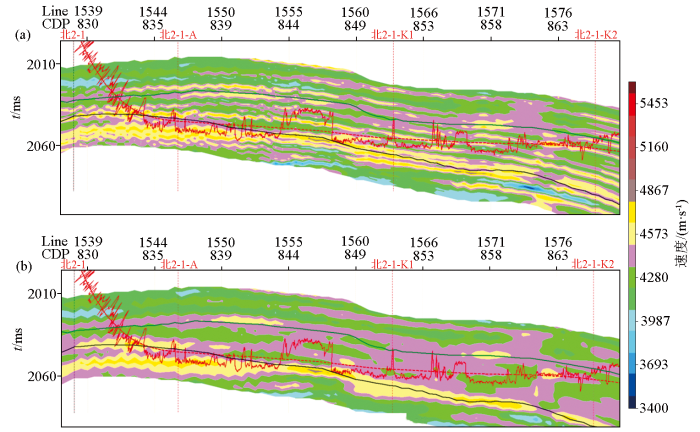
为了验证地震分频反演方法的优势,选择龙凤山气田相关靶区地震数据进行反演,如图9所示,选取相应的约束层位进行反演,对比分频迭代反演和常规分频反演的效果,发现分频迭代反演分辨明显更高,对小尺度信息反映清晰。自然伽马测井曲线可以反演岩性的变化,在地震分频迭代反演的剖面中,低伽马值对应砂岩、高伽马值对应泥岩,由于分频迭代反演的初始模型是上一级频段反演的结果,地震频段信息充分叠加利用,反演结果比分频后直接反演的准确性更高。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 靶区分频迭代反演(a)和常规分频反演(b)的对比(图中曲线为自然伽马曲线)

Fig.9 Comparison of frequency division iterative inversion(a) and conventional frequency division inversion(b) in target area(The curve in the figure is GR curve)

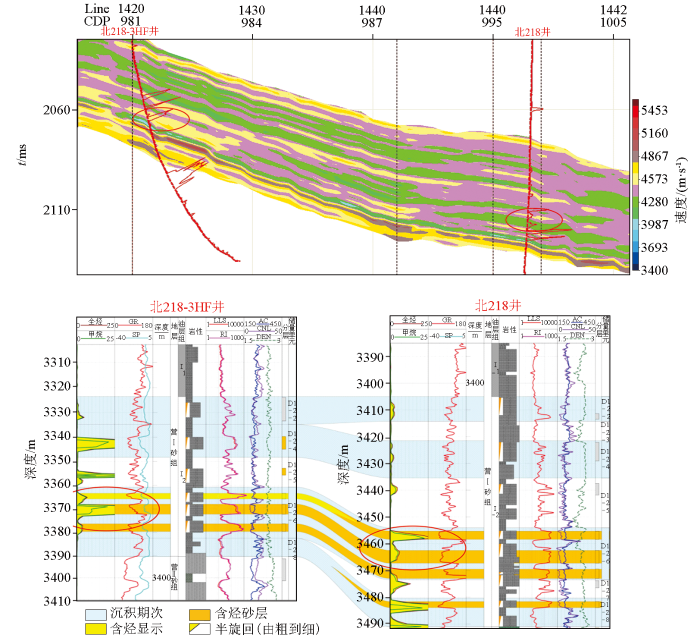
图10是在地震分频迭代反演的结果上拉取218-3和218井的联井剖面,全烃测井曲线同反演剖面中砂体对应准确,营城组1-2-6小层中砂泥互层刻画清晰,联合测井划分的砂体连通关系,精准刻画了该套含气储层的分布,证明了分频迭代反演不仅可以在纵向上保持较高的分辨率和精度,对于储层横向变化特征也可以细致刻画,与高精度的测井结果相吻合,可靠性强,在井位部署和指导油气田开发中具有重要意义。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 靶区分频迭代反演过井剖面与测井对比(图中曲线为全烃曲线)

Fig.10 Comparison between cross well profile of frequency division iterative inversion and logging profile in target area (The curve in the figure is the total hydrocarbon curve)

3.4 储层预测

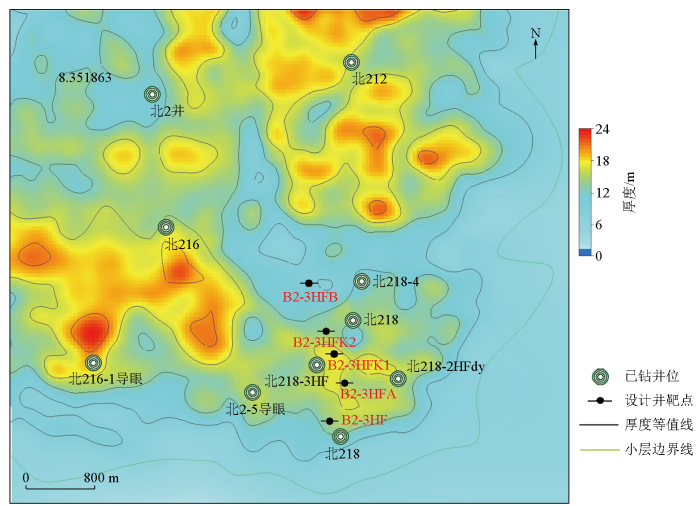
基于岩石物理储层速度范围分析的结果,根据砂泥岩的纵波速度差别,在对应层位的约束下,提取对应的叠后反演速度体对应的储层厚度,其中深度域的储层厚度由层位所限定的时间厚度,与各点的反演速度相乘所得,图11是对龙凤山靶区1-2-6小层厚度的平面预测,对储层的特征刻画清晰,预测结果和已开发钻井吻合率高,2021年新钻井2-3井依赖图中位置部署,开采1-2-6单砂层,取得了良好的含气显示,与反演预测结果吻合。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 靶区营城组1-2-6砂体厚度

Fig.11 1-2-6 sand body thickness of Yingcheng formation in target area

4 结论

应用匹配追踪算法分频处理后的地震数据体,在测井资料的约束下,开展分频迭代逐级反演,低频的反演结果作为高频的初始模型,反演结果不断优化,信息逐级传递,有效提高了反演的分辨率,并成功应用于龙凤山气田靶区薄层河道砂储层预测中,得到如下认识:

1)地震分频迭代反演对于全频带地震信息应用充分,将低一级频段的反演结果作为高一级频段的反演初始模型,纵向分辨率不断提高的同时,反演结果也在不断调整优化,相较于传统分频后分开反演选优的结果更加具有科学性,在薄层的预测中具有明显优势。

2)反演的主体算法相对于传统方法,引入了均方根校正原理自适应选取不同频段反演所用的子波,基于贝叶斯概率表示正则化参数,避免混沌现象发生,保证反演的分辨率和稳定性达到平衡,反演得到的结果稳定可靠。

3)针对龙凤山工区的实际情况,需要进行水平井勘探,地震分频迭代反演既能减弱反演结果对初始模型的依赖,又能在充分发掘利用低、高频信息,避免引入假象,提供高纵向分辨率、高精确性、横向关系明显、构造和局部特征清晰的反演结果,指导和调整水平井钻探钻入目的薄层,保证生产开发。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

于建国, 韩文功, 刘力辉.

分频反演方法及应用

[J]. 石油地球物理勘探, 2006, 41(2):193-197.