半航空瞬变电磁一维聚焦反演研究

doi:10.11720/wtyht.2023.1337

半航空瞬变电磁一维聚焦反演研究

王仕兴^,¹, 何可^,²^,³, 尹小康¹, 魏栋华¹, 赵思为¹, 郭明³

1.中国中铁二院工程集团有限责任公司,四川成都 610031

2.西华师范大学教育信息技术中心,四川南充 637002

3.成都理工大学地球物理学院,四川成都 610059

One-dimensional focusing inversion of the semi-airborne transient electromagnetic method and its application

WANG Shi-Xing^,¹, HE Ke^,²^,³, YIN Xiao-Kang¹, WEI Dong-Hua¹, ZHAO Si-Wei¹, GUO Ming³

1. China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, China

2. Education Information Technology Center, West China Normal University, Nanchong 637002, China

3. College of Geophysics, Chengdu University of Technology, Chengdu 610059, China

通讯作者: 何可(1988-),男,在读博士,主要从事半航空瞬变电磁法正反演研究工作。Email:hk812760098@163.com

第一作者: 王仕兴(1997-),男,硕士,2022年毕业于成都理工大学地球探测与信息技术专业,主要从事电磁法勘探原理及应用研究工作。Email: wangshix97@163.com

责任编辑: 王萌

收稿日期: 2022-07-13 修回日期: 2022-09-24

基金资助:

中国中铁股份有限公司科技研究开发计划(CZ01-重点-05)

Received: 2022-07-13 Revised: 2022-09-24

摘要

半航空瞬变电磁法(SATEM)是一种采用地面发射—空中接收的新兴地球物理勘探方法,具有灵活、高效的特点。目前应用于SATEM的反演方法往往基于最大平滑准则,使反演结果较平滑,无法较好地识别具体的层界面信息。本文将聚焦反演理论引入到半航空瞬变电磁一维反演中,通过选择合适的聚焦因子和正则化因子来确定聚焦反演稳定器,然后对包含聚焦反演稳定器反演目标函数进行求解,使得反演结果更能清晰识别层状地层突变的界面。设置多个层状地电模型验证聚焦反演的可靠性,同时与Occam反演结果进行对比,突出了聚焦反演识别界面的优势。对某地区地下水探测的实际数据进行聚焦反演计算,与水文地质资料、测井信息进行综合分析,查明了该区域地下含水层的位置及其空间展布情况,同时验证了半航空瞬变电磁对地下水探测的可行性。

关键词： 半航空瞬变电磁法; 聚焦反演; 地下水探测

Abstract

The semi-airborne transient electromagnetic method (SATEM) is an emerging flexible and efficient geophysical exploration method using ground launch and air reception. The present inversion methods applied to the SATEM produce very smooth inversion results since they apply the maximum smoothing criterion, thus failing to effectively identify the information of specific layer interfaces. This study introduced the focusing inversion theory to the one-dimensional inversion of the SATEM. First, a focusing inversion stabilizer was determined by selecting appropriate focusing and regularization factors. Then, the inversion objective function including the focusing inversion stabilizer was solved to allow the inversion results to effectively identify the abrupt interfaces of layered strata. Furthermore, multiple layered geoelectric models were built to verify the reliability of the focusing inversion. Moreover, the focusing inversion results were compared with the Occam inversion results to highlight the advantages of the focusing inversion in interface identification. This study conducted the focusing inversion calculation of actual data on groundwater detection of a certain area. The calculation results were then combined with the hydrogeological and logging data for comprehensive analysis. Finally, this study determined the locations and spatial distribution of underground aquifers in the area, verifying the feasibility of the SATEM for groundwater detection.

Keywords： semi-airborne transient electromagnetic method; focusing inversion; groundwater detection

PDF (3837KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王仕兴, 何可, 尹小康, 魏栋华, 赵思为, 郭明. 半航空瞬变电磁一维聚焦反演研究[J]. 物探与化探, 2023, 47(2): 410-419 doi:10.11720/wtyht.2023.1337

WANG Shi-Xing, HE Ke, YIN Xiao-Kang, WEI Dong-Hua, ZHAO Si-Wei, GUO Ming. One-dimensional focusing inversion of the semi-airborne transient electromagnetic method and its application[J]. Geophysical and Geochemical Exploration, 2023, 47(2): 410-419 doi:10.11720/wtyht.2023.1337

0 引言

半航空瞬变电磁法(semi-airborne transient electromagnetic method, SATEM)是一种结合了地面瞬变电磁法(transient electromagnetic method, TEM)和航空瞬变电磁法(airborne transient electromagnetic method, ATEM)优势的新兴地球物理勘探方法^[1⇓-3]。其工作方式是采用接地长导线源在地面进行发射,空中通过无人机搭载的接收系统进行信号采集,具有灵活、高效的特点,可适应在多种复杂环境下进行勘探任务。半航空瞬变电磁法的数据量较庞大,加之瞬变电磁法二维、三维正反演计算量过大^[4],故针对实际资料的处理,一维正反演技术还是首要选择。半航空瞬变电磁法中常用的反演方法可分为阻尼最小二乘法以及基于Occam方法的正则化反演,主要有许洋^[5]、张澎等^[6]提出的自适应正则化反演;赵涵等^[7]提出的基于Occam反演方法的地空瞬变电磁反演;杨聪等^[8]提出的半航空瞬变电磁自适应正则化—阻尼最小二乘算法;张振雄等^[4]提出的基于最小构造模型的地空瞬变电磁一维正反演方法;马振军等^[9]提出的考虑高度及感应电流差异的电阻率—深度成像方法;何可等^[10-11]提出的半航空瞬变电磁L1范数自适应正则化反演算法以及基于混合范数的半航空瞬变电磁数据空间约束反演方法等。这些反演方法大多是基于L2范数的正则化反演,虽然其具有反演连续性强的特点,但也会平滑掉地质结构突变的特征,弱化地质体层位面信息。

聚焦反演方法是一种突出不同地质体层位面的反演算法,最早Oleg Portniaguine等^[12]提出用于处理重力数据。该算法通过引入聚焦正则化因子来提高反演解的稳定性,通过改变稳定器的类型来识别物性差异较大的地层界面,广泛应用于大地电磁测深反演^[13⇓-15]、重力反演^[16-17]等方面。针对上述特征,本文将聚焦反演理论引入半航空瞬变电磁反演计算中用于地下水层界面识别,通过选择合适的聚焦因子和正则化因子确定聚焦反演稳定器,然后对包含聚焦反演稳定器反演目标函数进行求解,实现分辨模型参数的突变,使反演结果能更清晰识别层界面。

本文推导了半航空瞬变电磁一维聚焦反演算法,针对多种层状地电模型设计了正演模拟验证了聚焦反演算法的正确性。同时,将聚焦反演结果与Occam反演结果对比,验证了聚焦反演算法的有效性。最后对某地区的半航空瞬变电磁实测数据进行反演计算,与水文地质资料、测井信息进行综合解释分析,验证了半航空瞬变电磁一维聚焦反演方法的有效性和可靠性。

1 半航空瞬变电磁一维正演理论

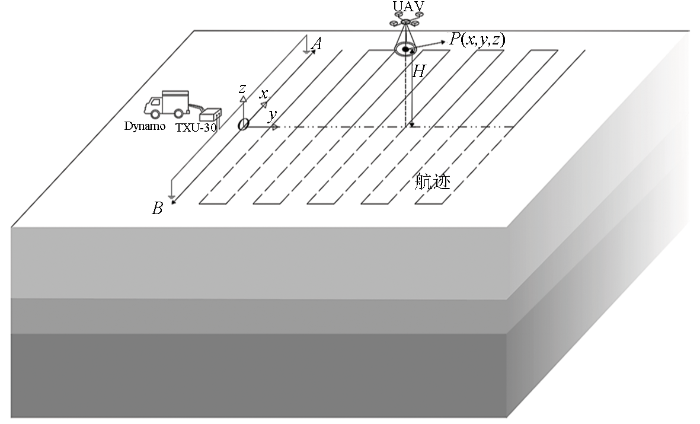
半航空瞬变电磁法工作示意如图1所示。在长导线瞬变电磁法勘探中,其接收线圈主要接收的是垂直分量的频率域磁场响应 $H_{z}$ ,本文一维正演基于分析水平层状垂直分量 $H_{z}$ :

(1)

H_{z} = [\frac{I}{4 π} \int_{- L}^{L} \frac{y}{R} \int_{0}^{\infty} (1 + γ_{T E}) e^{u_{o} z} \frac{λ^{2}}{u_{0}} J_{1} (λ R) d λ d x^{'}]

(2)

R = \sqrt{(x - x^{'})^{2} + y^{2}}

。

其中: $H_{z}$ 表示垂直分量的频率域磁场响应,A/m;I为发射电流强度大小,A;L表示线源长度的一半;R表示测点位置的偏移距; $(x, y, z)$ 表示测点相对坐标位置; $x^{'}$ 表示长导线上任一点的坐标; $γ_{T E}$ 表示TE模式下的反射系数; $λ$ 表示积分变量; $u_{0} = \sqrt{λ^{2} - {k_{0}}^{2}}$ , $k_{0}$ 为空气介质波数; $z$ 表示接收线圈离地高度,m; $J_{1}$ 表示一阶贝塞尔函数。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 半航空瞬变电磁法工作方式示意

Fig.1 Schematic diagram of the working mode of semi-airborne transient electromagnetic method

为求得时间域的感应电动势响应,对 $H_{z}$ 分量的求解主要分为3步:第一步是通过汉克尔积分^[18]求解一阶贝塞尔函数;第二步是通过高斯数值积分对长导线进行积分,本文利用20点高斯数值积分进行求解;第三步进行频时变换,采用余弦变换—折线逼近法^[19]将频率域响应转换为时间域响应。

2 聚焦反演理论

地球物理反演常将非线性问题线性化,吉洪诺夫的正则化思想指出:

(3)

P {(m)}^{α} = φ_{d} (m) + α s (m)

式中: $φ_{d} (m)$ 为数据拟合项,表示为正演响应数据与实测数据之差的平方和; $s (m)$ 为稳定器,即为模型稳定函数; $α$ 为正则化因子; $m$ 为模型向量。

(4)

φ_{d} (m) = ‖ W_{d} [F (m) - d^{o b s}] ‖_{}^{2}

其中: $W_{d}$ 为数据加权系数矩阵; $F (m)$ 为正演响应函数; $d^{o b s}$ 为实测数据向量。

常规的稳定器大多是基于最大平滑准则,所以在反演时得到的结果是光滑的。当在二维或三维反演中,地下异常体与围岩的分界面不易区分,同样在一维反演中,层状介质的分界面也难以分辨。一种新的稳定器由Last等^[20]提出,这种稳定器的主要特点是能将模型参数里面的目标体剖面的面积收缩到最小,这便是聚焦一词的核心之处。

引入模型参数的积分方程:

(5)

J_{β} (m) = \int_{v}^{} \frac{m^{2}}{m^{2} + β^{2}} d v

式中: $β$ (聚焦因子)为不为0的极小值,就解决的模型参数为0时的奇异点。将式(5)改写为:

(6)

\begin{array}{l} J_{β} (m) = \int_{s p t m}^{} (1 - \frac{m^{2}}{m^{2} + β^{2}}) d v = s p t m - \\ β^{2} \int_{s p t m}^{} (\frac{1}{m^{2} + β^{2}}) d v \end{array}

式中: $s p t m$ 为引入的模型参数支撑^[12],显而易见,当 $β$ 趋于0时,有 $J_{β} (m)$ 趋于 $s p t m$ ,所以可得 $J_{β} (m)$ 与模型参数支撑成正比关系,因此可将式(5)作为最小支撑泛函:

(7)

\begin{array}{l} s_{β M S} (m) = J_{β} (m - m_{r e f}) = \int_{v}^{} \frac{(m - m_{r e f})^{2}}{(m - m_{r e f})^{2} + β^{2}} d v \\ = [\frac{m - m_{r e f}}{{[(m - m_{r e f})^{2} + β^{2}]}^{\frac{1}{2}}}, \frac{m - m_{r e f}}{{[(m - m_{r e f})^{2} + β^{2}]}^{\frac{1}{2}}}], \end{array}

式(7)的一个重要特点是将模型参数与先验模型信息之间的非零偏差减小到最小区域,当模型参数与先验信息差别较大时会受到较大的惩罚,反之则反,因此在一维反演中,该最小支撑泛函可提高层状地下介质界面的分辨率。同理,可以轻而易举的得到最小梯度支撑泛函:

(8)

s_{β M G S} (m) = J_{β} (\nabla m) = \int_{v}^{} \frac{\nabla m \cdot \nabla m}{\nabla m \cdot \nabla m + β^{2}} d v

将反演问题求解简单化,式(7)可写为最小二范数的形式,可令变权泛函:

(9)

ω_{β} (m) = \frac{1}{{[(m - m_{r e f})^{2} + β^{2}]}^{\frac{1}{2}}}

式(7)可改写为:

(10)

\begin{array}{l} {s_{β}}_{M}_{S} (m) = (ω_{β} (m) (m - m_{r e f}), ω_{β} (m) \\ (m - m_{r e f})) = ‖ ω_{β} (m) (m - m_{r e f}) ‖^{2} \end{array}

将式(9)带入式(3)可得反演目标函数:

(11)

\begin{array}{l} P {(m)}^{α} = φ_{d} (m) + α s (m) = ‖ W_{d} [F (m) - d^{o b s}] ‖_{}^{2} \\ + α ‖ ω_{β} (m) W_{m} (m - m_{r e f}) ‖_{}^{2} \end{array}

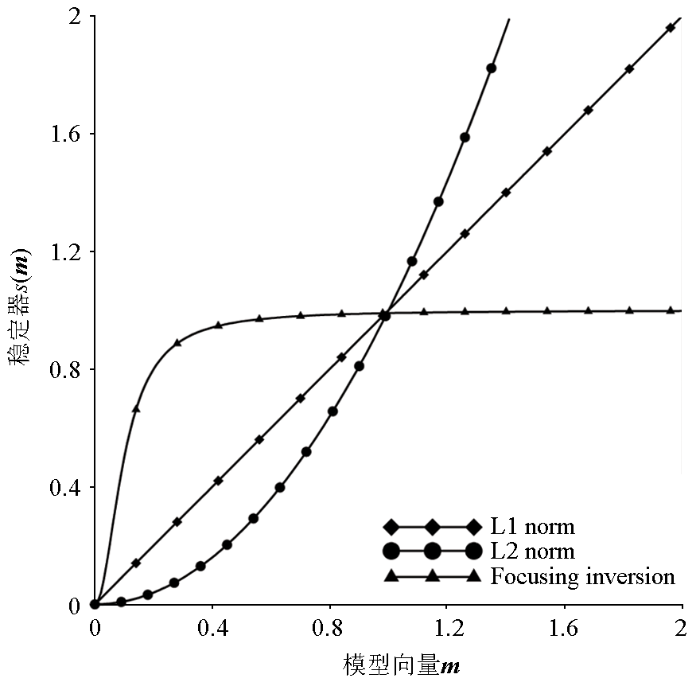
图2为不同的稳定器 $s (m)$ 的变化曲线,分别表示聚焦反演稳定器、L1范数稳定器、L2范数稳定器。L1、L2范数稳定器在零附近的曲线斜率小于聚焦反演稳定器,故聚焦反演稳定器趋于零的速度更快,这就代表在进行最小化模型约束的时候,将会使模型参数的梯度快速趋近于0,从而使模型变得更加连续;当 $m$ 值增大时,模型参数的梯度也随之增大,这样便能更好地分辨模型参数的突变;聚焦反演稳定器 $s (m)$ 的值只存在两种情况,即趋于0或趋于1,则在背景区域时,聚焦反演方法结果比L1范数和L2范数反演结果更连续,在异常区域时,聚焦反演结果比L1范数和L2范数反演结果更突变。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 不同稳定器随模型参数梯度的变化

Fig.2 Variation of different stabilizers with the gradient of model parameters

式(11)中 $W_{m}$ 为模型加权(模型协方差)矩阵,令 $W_{e} = ω_{β} (m) W_{m}$ ,当迭代计算到第k次,模型参数为 $m_{k}$ ,所以可得 $W_{e} = W_{e} (m_{k})$ ,随着迭代次数而变化。式(11)可写为:

(12)

\begin{array}{l} P {(m)}^{α} = ‖ W_{d} [F (m) - d^{o b s}] ‖_{}^{2} + \\ α ‖ W_{e} (m - m_{r e f}) ‖_{}^{2} \end{array}

对式(12)中正演响应函数 $F (m)$ 进行一阶泰勒展开,即:

(13)

F (m) = F (m_{k}) + J Δ m_{k}

其中: $Δ m_{k}$ 为模型修正量, $J$ 为雅克比矩阵(灵敏度矩阵),可采用中心差分方式求取:

(14)

J = \frac{F (m_{k} + Δ m) - F (m_{k} - Δ m)}{2 Δ m}

由于反演计算过程中,需要不断的进行迭代计算,这是一个非常耗时的过程,在计算雅克比矩阵时,采用并行计算,可大大提高计算效率,节省反演计算的时间。在求解式(12)时,将其对模型修正量求一阶偏导并置为0:

(15)

\frac{\partial P^{α}}{\partial Δ m} = 0

得到反演方程:

(16)

\begin{array}{l} [{J^{T}}_{k} {W^{T}}_{d} W_{d} J_{k} + α {W^{T}}_{e} W_{e}] Δ m_{k} = {J^{T}}_{k} {W^{T}}_{d} W_{d} \\ [F (m) - d^{o b s}] + α {W^{T}}_{e} W_{e} [m_{k} - m_{r e f}] \end{array}

将 $W_{d}$ 置为单位矩阵,通过解式(16)可求得第k次迭代的模型修正量 $Δ m_{k}$ ,则第k+1次迭代的模型参数向量为:

(17)

m_{k + 1} = m_{k} + Δ m_{k}

由于半航空瞬变电磁法响应值呈数量级关系变化,为保证求解过程的稳定性,在进行反演计算时,对数据空间和模型空间均求取对数,这是由于模型修正时模型增量有数量级差距,反演可能存在不稳定情况,改到对数域反演则模型增量差距较小,反演相对稳定。求得模型修正量后,进行反对数计算可得实际模型修正量。

聚焦反演结果的聚焦质量由聚焦因子决定,当聚焦因子选取较大时,聚焦效果不明显,当聚焦因子选择较小时,会使得反演结果不稳定;本文经过多次实验计算,聚焦因子的选取参考白宁波等^[14]文中自适应衰减因子的方法,令聚焦因子为:

(18)

β = e^{- λ k}

其中: $λ$ 表示控制系数,本文取1;k表示为迭代次数。

正则化因子的选取对反演结果至关重要,它是模型函数与数据目标函数之间的权重参数,其变化值决定了反演计算时拟合是否向数据或者模型方向靠拢,当正则化因子趋于无穷大时,则反演计算时将先验模型作为主要目标,当正则化因子趋于0时,则反演计算时将数据拟合作为主要目标;因此如何保证在反演时,充分拟合实际采集数据的同时还能使反演结果满足先验模型信息,这是一个非常复杂的问题,前人在这个方面进行了大量的研究,本文采用陈小斌等^[21]提出的CMD方案。正则化因子主要用于调节目标函数数据拟合项和模型约束项的反演权重,采用自适应的方式能满足大多数情况下反演收敛和稳定性的要求,且能够防止正则化因子迭代时逐渐减小而引起的反演不稳定情况。

(19)

α^{k} = \frac{{φ_{d}}^{k - 1}}{{φ_{d}}^{k - 1} + {s_{m}}^{k - 1}}

其中: ${φ_{d}}^{k - 1}$ 为数据拟合项; ${s_{m}}^{k - 1}$ 为模型拟合项。

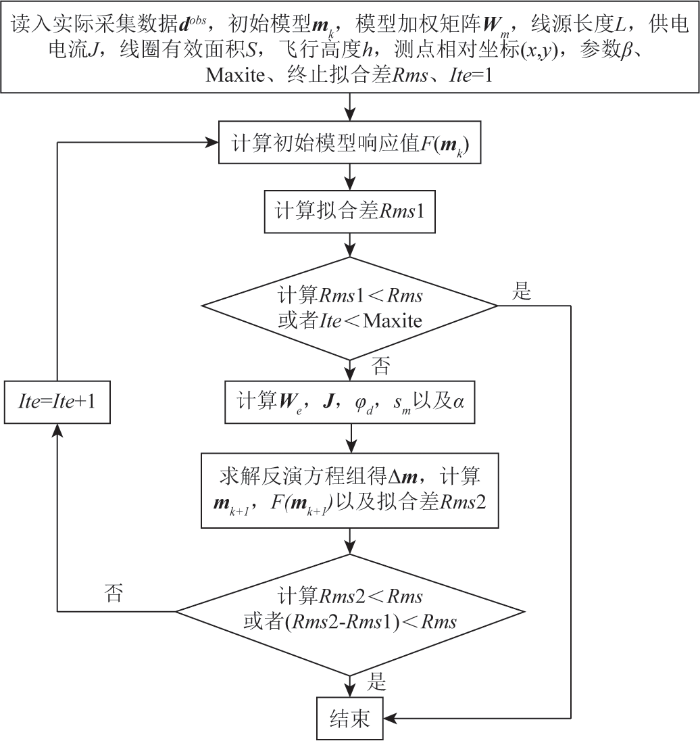
反演终止条件:①迭代次数达到设置的最大迭代次数;②Rms_k小于给定的值;③相邻拟合差之差小于给定的值,即: $Δ R m s_{} = R m s_{k} - R m s_{k - 1}$ ,这意味着拟合差减小的幅度相当小,故可结束反演计算;拟合差计算公式为:

(20)

R m s_{} = \sqrt{\frac{\overset{N}{\sum_{i = 1}} {[\frac{l n (F_{i} (m)) - l n (d_{i}^{o b s})}{l n (d_{i}^{o b s})}]}^{2}}{N}}

其中:N为采样时间个数; $d_{i}^{o b s}$ 为实际采集的数据向量; $F_{i} (m)$ 为反演模型的理论正演响应值,聚焦反演流程如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 聚焦反演流程

Fig.3 Focused inversion flowchart

3 反演试算

为验证一维聚焦反演对界面分辨能力的可靠性及其准确性,设置理论层状地电模型,正演对应模型的感应电动势响应,利用一维聚焦反演与Occam反演进行试算,就计算结果进行对比分析。模型参数为:供电线源长度2 000 m,供电大小20 A,接收线圈的有效面积进行归一化,线圈离地高度30 m,偏移距250 m,测点坐标(0,250,30);采样延时在0.01~10 ms范围内,按自然对数取32个采样时间点。

3.1 三层模型反演算例

设置三层H、K型地电模型,模型参数见表1,以中间层(第二层)为研究对象,反演初始模型地层数设置为50层,第一层厚度为1.02 m,其他层厚度按等比系数1.05增加,考虑场的扩散规律,以及模型异常体的埋深和厚度,故而设计层厚按照指数倍增长,每层电阻率值均设置为150 Ω·m;反演终止条件为当最大迭代次数达到40次或前后两次迭代拟合差之差小于10^-6。

表1 三层地电模型参数

Table 1 Three-layer geoelectric model parameters

地电模型	电阻率/(Ω·m)	层厚/m
H型 K型	ρ₁=300、ρ₂=50、ρ₃=100 ρ₁=50、ρ₂=200、ρ₃=100	h₁=100、h₂=40、h₃=∞ h₁=100、h₂=40、h₃=∞

新窗口打开| 下载CSV

H、K型地电模型反演结果如图4a、图5a所示,针对三层地电模型,聚焦反演和Occam反演都能较好地反演出理论地电模型。其主要差异是在模型覆盖层(第一层)深度范围内,聚焦反演结果与真实模型较吻合,Occam反演结果会出现波动变化。在中间层深度范围内,两种反演方法均能较好地反演出模型电阻率值,但是在层界面位置时,聚焦反演结果较Occam反演结果更为尖锐,能产生突变的现象。而Occam反演在分界面处呈现光滑的特点,电阻率

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 H型地电模型反演结果

Fig.4 Inversion results of H-type geoelectric model

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 K型地电模型反演结果

Fig.5 Inversion results of K-type geoelectric model

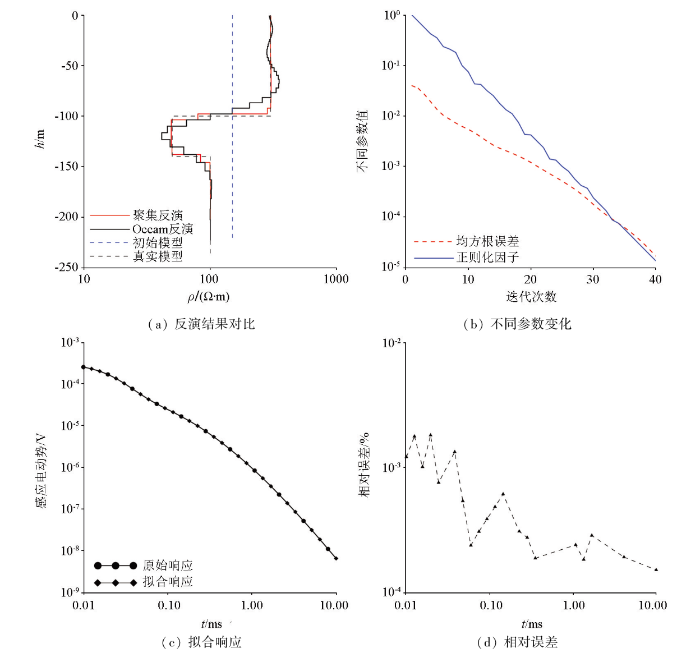
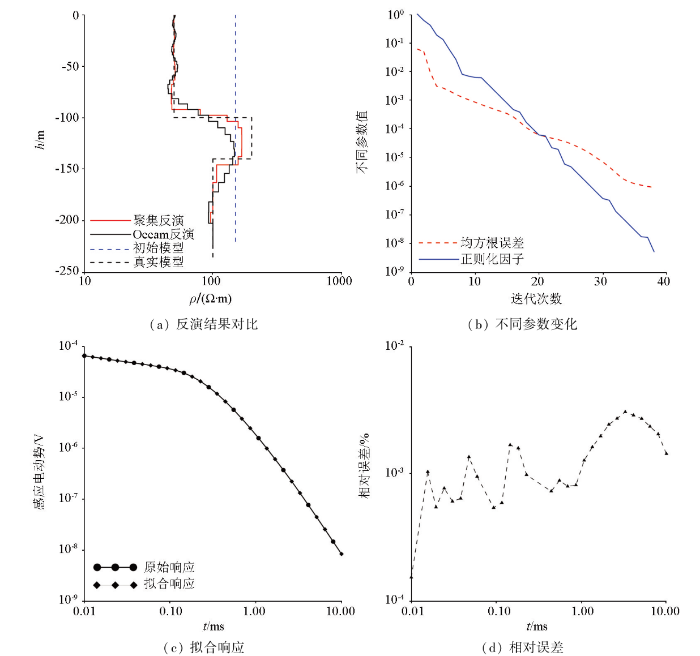
值缓慢过渡变化。从反演拟合差与正则化因子变化趋势图中可以看到随着迭代计算次数的增加,正则化因子缓慢减小,反演便以拟合数据为目标;同时,反演拟合差也同样出现缓慢减小形态。从真实模型正演的响应值与聚焦反演结果响应值对比中可以看到真实模型与反演结果正演响应值近乎相同;由相对误差示意图中可见最大相对误差小于0.003%,表明拟合程度较高。

3.2 四层模型反演算例

设置高阻覆盖层四层HK型、KH型地电模型,其模型参数见表2,以第二层和第三层为目标层,反演初始模型地层数设置为50层,第一层厚度为1.02 m,其他层厚度按等比系数1.063增加,考虑场的扩散规律,以及模型异常体的埋深和厚度,故而设计层厚按照指数倍增长,每层电阻率值均设置为150 Ω·m;反演终止条件是当最大迭代次数到达40次或前后两次迭代拟合差之差小于10^-6。

表2 四层地电模型参数

Table 2 Four-layer geoelectric model parameters

地电模型	电阻率/(Ω·m)	层厚/m
HK型	ρ₁=300、ρ₂=100、 ρ₃=200、ρ₄=50	h₁=100、h₂=80、 h₃=100、h₄=∞
KH型	ρ₁=50、ρ₂=200、 ρ₃=100、ρ₄=200	h₁=100、h₂=80、 h₃=100、h₄=∞

新窗口打开| 下载CSV

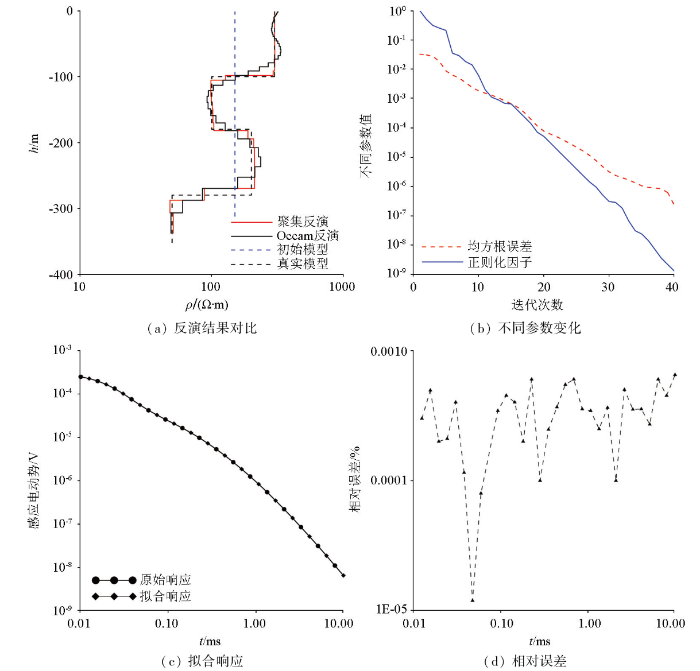
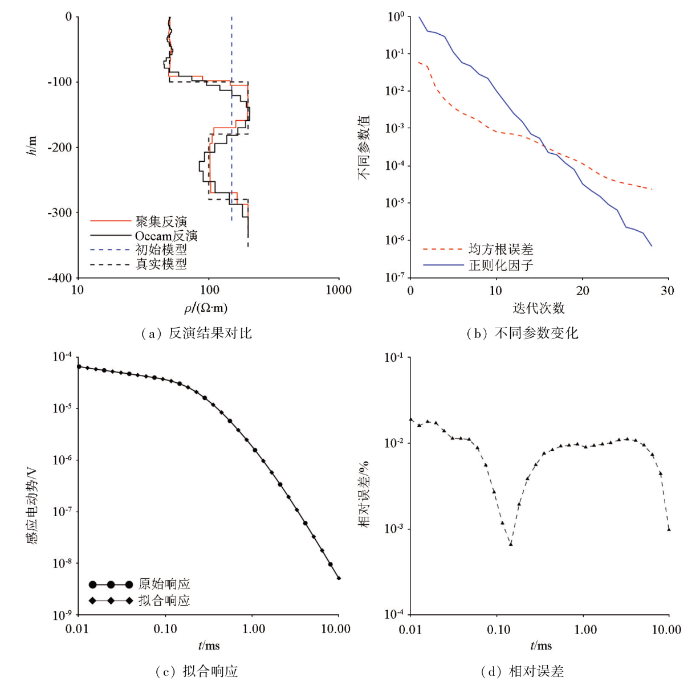
HK型、KH型地电模型反演结果如图6a、7a所示,从整体上看,聚焦反演结果和Occam反演结果均能较好地反映出理论地电模型,每一层的深度和电阻率值均对应较好,在第一层地层介质深度范围内,聚焦反演结果几乎与真实模型电阻率值相同,而Occam反演结果以真实模型电阻率值为中心左右波动。在分界面处聚焦反演结果电阻率值呈跳跃变化,突出了其较强的突变特点;由于Occam反演的光滑思想使其电阻率值在分界面处呈连续变化。从反演拟合差与正则化因子变化趋势图中可见随着迭代次数的增大,拟合差和正则化因子逐渐减小,符合反演过程。从地电模型正演响应值与聚焦反演结果响应值对比可以看出二者曲线拟合程度较高,根据相对误差可进一步看出每一时间采样点对应的相对误差值,最大相对误差值仅为0.02%,表明聚焦反演效果较好。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 HK型地电模型反演结果

Fig.6 Inversion results of HK-type geoelectric model

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 KH型地电模型反演结果

Fig.7 Inversion results of KH-type geoelectric model

综上所述,无论对于高、低阻覆盖层三层地电模型还是高、低阻覆盖层四层地电模型,两种反演方法都能较准确地反演出真实地电模型,聚焦反演结果相较于Occam反演结果,可以更好地反映出地层分界面信息且聚焦反演在覆盖层深度范围内不会出现电阻率波动异常现象。

3.3 实例应用

为进一步验证聚焦反演在半航空瞬变电磁法中应用的有效性和可靠性,对白城市乾安县某区域地下水探测的半航空瞬变电磁实测数据进行了反演。选取其中标志性的一条测线进行反演解释,结合地质资料与测井曲线进行综合解释,查明了工区地下含水层的位置及空间展布情况。

该地区浅部地下水类型主要可分为:潜水、潜水—微承压水、承压水和砂岩、砂砾岩孔隙裂隙承压水4大类。这4种类型的地下水均在深度300 m以浅,符合半航空瞬变电磁法的探测深度范围。图8所示为钻孔的深度侧向电阻率测井曲线示意,可见在300 m范围内深、浅侧向电阻率曲线整体较为平缓且呈低值,在75~215 m深度范围内电阻率值较高。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 深度侧向电阻率测井曲线

Fig.8 Depth lateral resistivity logging curve

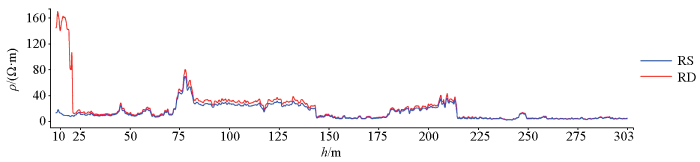
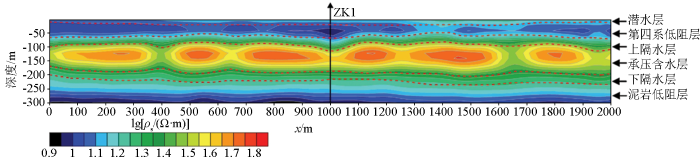
通过半航空瞬变电磁聚焦反演计算,由图9实测数据电阻率反演结果可知,在300 m深度范围内,电性结构层状特征分布明显,根据电性特征,可将其大致分为6层,其电阻率变化形态与测井曲线吻合较好。根据水文地质资料以及钻孔资料综合解释如下:0~20 m深度范围内,推测为第四系潜水层,主要为黏土层;20~70 m深度范围内,推测为第四系低阻层,其反演电阻率值较上一层低,解释为砂砾岩层;70~100 m深度范围内,反演电阻率有所上升,推测为新近系上隔水层,泥质岩性;100~190 m深度范围内,反演电阻率值显著增大,结合水文地质资料,推测为承压含水层,包含新近系泰康组和大安组,岩性主要为砂砾岩,由多层含水层组成,鉴于瞬变电磁法的特点无法有效分辨;190~210 m深度范围内,反演电阻率值呈下降趋势,推测为下隔水层,岩性为泥岩;210~300 m深度范围内,反演电阻率值较上一层低,推测为泥岩低阻层。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 实测数据电阻率反演结果

Fig.9 Measured data resistivity inversion results

4 总结

基于最大平滑度准则的半航空瞬变电磁反演方法无法有效识别出具体的层界面信息,由此引入了聚焦反演方法,将其运用到半航空瞬变电磁法中,设置多个层状地电模型验证其准确性,并与Occam反演结果进行对比分析;后对地下水探测实际数据进行处理并与地质资料相结合解释,得到以下结论:

1)在反演目标函数中,不同的反演稳定器有不同的特点,在背景区域,聚焦反演稳定器趋于0的速度更快,所以所得结果更为连续;在异常区域,聚焦反演稳定器趋于1,所得结果更为突变。

2)根据设置的层状地电模型进行反演试算,聚焦反演和Occam反演均能较为准确地拟合出真实模型,但在地层分界面处,聚焦反演能较好地分辨出突变信息;在异常和背景区域内部,聚焦反演结果电阻率值变化幅度远小于Occam反演结果。

3)针对某工区进行地下水探测,结合水文地质资料、电阻率测井资料以及半航空瞬变电磁法反演结果进行综合解释,探明了含水层的大致位置;表明聚焦反演方法在此工区具有较好的效果,对地下介质电阻率变化较为敏感,为该区域的地下水评估及开采利用提供一定的参考依据。

致谢

感谢中国地质科学院地球物理地球化学勘查研究所为本文提供的地质资料,感谢审稿专家提出的修改意见和编辑部的大力支持!

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

林君, 薛国强, 李貅.

半航空电磁探测方法技术创新思考

[J]. 地球物理学报, 2021, 64(9):2995-3004.