基于U-Net网络的FWI地震低频恢复方法

doi:10.11720/wtyht.2023.1125

基于U-Net网络的FWI地震低频恢复方法

王莉利^,¹^,², 杜功鑫¹, 高新成³, 王宁⁴, 王维红⁴

1.东北石油大学计算机与信息技术学院,黑龙江大庆 163318

2.黑龙江省油气地球物理勘探重点实验室,黑龙江大庆 163318

3.东北石油大学现代教育技术中心,黑龙江大庆 163318

4.东北石油大学地球科学学院,黑龙江大庆 163318

FWI seismic low frequency recovery method based on the U-Net

WANG Li-Li^,¹^,², DU Gong-Xin¹, GAO Xin-Cheng³, WANG Ning⁴, WANG Wei-Hong⁴

1. School of Computer & Information Technology,Northeast Petroleum University,Daqing 163318,China

2. Heilongjiang Provincial Key Laboratory of Oil and Gas Geophysical Exploration,Daqing 163318,China

3. Modern Education Technology Center, Northeast Petroleum University,Daqing 163318,China

4. School of Earth Science,Northeast Petroleum University,Daqing 163318,China

第一作者: 王莉利(1979-),女,博士,副教授,主要从事基于人工智能技术的地震数据处理等领域的科研工作。Email:lily@nepu.edu.cn

收稿日期: 2022-03-22 修回日期: 2023-02-1

基金资助:

国家重点自然科学基金项目“粘声介质最小二乘逆时偏移及全波形反演研究”(41930431)
国家自然科学基金项目“基于数据驱动的逆散射级数层间多次波压制方法”(41974116)
黑龙江省自然科学基金联合引导项目“深部储层衰减补偿逆时偏移成像研究”(LH2021D009)
东北石油大学引导性创新基金项目“基于自适应卷积神经网络的地震速度建模方法研究”(2020YDL-03)

Received: 2022-03-22 Revised: 2023-02-1

摘要

由于实际地震资料中缺乏低频数据,使得全波形反演易陷入局部极小值,导致反演质量差,结果不可靠。为解决这一问题,本文利用数据驱动低频恢复映射思想,分别利用高通和低通滤波器从原始数据中分离出高频数据和低频数据,对其进行一系列数据预处理操作,将处理后的数据作为模型的训练集;利用U-Net网络为基础构建模型,建立高低频之间的映射关系。为了有效防止模型过拟合,本文在U-Net模型基础上添加了Dropout层和批处理层。利用训练后的模型从高频数据中预测对应低频数据并进行逆数据预处理,对比分析逆数据预处理后的预测低频数据和真实低频数据之间误差,并利用多尺度全波形反演在洼陷模型和Marmousi模型进行有效性验证。实验结果表明:训练与测试数据的预测低频与真实低频数据的平均相对误差为5.02%和13.32%,误差较小,数据吻合良好;洼陷模型、Marmousi模型以及实际数据的反演结果表明加入预测低频后反演质量得到显著提高,并且对处理含较大噪声的数据也有很好的效果。

关键词： 全波形反演; 低频恢复; 局部极小值; 能量均衡; U-Net

Abstract

The lack of low-frequency data in actual seismic data makes the full waveform inversion (FWI) tend to fall into the local minimum,resulting in poor inversion quality and unreliable results.In view of this,data-driven low-frequency recovery mapping was adopted in this study.First,high-pass and low-pass filters were employed to separate high-frequency and low-frequency data from raw data,respectively,and then data preprocessing was carried out.The processed data were used as the training set of the model.Then,the model was built based on the U-Net to establish the mapping relationship between high and low frequencies.To effectively prevent the model from overfitting,the dropout layer and batch processing layer were added based on the U-Net model.Finally,the trained model was used to predict the corresponding low-frequency data from the high-frequency data and conduct inverse data preprocessing.The errors between the predicted low-frequency data after inverse data preprocessing and the real low-frequency data were compared and analyzed,The effectiveness of multi-scale FWI was verified using the depression and Marmousi models.The experimental results show that the average relative errors between the predicted low-frequency data and the real low-frequency data were 5.02% and 13.32%,respectively for training and test data,indicating small errors and high data coincidence.The inversion results of the depression model,the Marmousi model,and actual data show that the prediction of low-frequency data significantly improved the inversion quality and delivered a great performance in the processing of data with much noise.

Keywords： full waveform inversion; low frequency recovery; local minimum; energy equalization; U-Net

PDF (5479KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王莉利, 杜功鑫, 高新成, 王宁, 王维红. 基于U-Net网络的FWI地震低频恢复方法[J]. 物探与化探, 2023, 47(2): 391-400 doi:10.11720/wtyht.2023.1125

WANG Li-Li, DU Gong-Xin, GAO Xin-Cheng, WANG Ning, WANG Wei-Hong. FWI seismic low frequency recovery method based on the U-Net[J]. Geophysical and Geochemical Exploration, 2023, 47(2): 391-400 doi:10.11720/wtyht.2023.1125

0 引言

全波形反演(full waveform inversion,FWI)可以通过数据拟合建立高分辨率地下速度模型,是一种建立在非线性优化算法基础上的地震处理技术。然而,许多现有FWI算法都存在一个主要缺点:易陷入局部极值^[1]。反演过程中产生的周波跳跃现象是使FWI陷入局部极值的直接原因,导致周波跳跃的原因主要包括地震信号缺失低频成分和初始速度模型与地下真实速度模型相差过大。由于传统地震采集技术的限制以及地震资料处理过程中面波压制等原因,对于反演精度至关重要的低频信息往往是缺失的。有效缓解FWI周波跳跃问题的方法是从地震数据中“挖掘”出低频信息,再结合多尺度反演策略,实现高精度的速度建模。

常见的地震数据低频信息恢复方法主要分为两类。第一类是基于数学原理,包括包络计算^[2-3]、零频率阻尼波场^[4]、基于相位跟踪方法的低频恢复^[5]、数据拍音反演^[6]、拉普拉斯域反演^[7]等。第二类是基于神经网络学习类算法。2108年,Jin等^[8]第一次提出利用数据驱动方法解决低频缺失问题,通过基于深度初始建立的卷积神经网络来学习FWI中的低频信息。Sun等^[9]通过将低频预测作为回归问题来研究卷积神经网络的低频带宽扩展方法。2019年,Ovcharenko等^[10]训练卷积神经网络获得多偏移地震数据恢复低频信息,此外,其还通过迁移学习方法来预测低频信息^[11]。2020年,Sun等^[12]提出采用一维卷积神经网络模型从频带受限的数据中恢复丢失的低频。Fang等^[13]提出通过训练二维卷积神经网络模型,学习建立高低频之间的隐性映射关系,提出了一种基于高频信号深度学习的低频恢复方法。2021年,Hu等^[14]提出基于深度神经网络,利用地下地质和地球物理特性,将低频数据和高频数据隐式联系起来,用以预测缺少的低频分量,有效地抑制FWI中周波跳跃现象。

通过学习高频分量和低频分量之间潜在的非线性关系来预测缺失的低频数据,是近年来活跃的一个信号处理领域^[15]。由于震源激发时难以产生低频信号以及检波器很难检测出地震信号中的低频分量信息,导致低频分量在实际地震数据中严重缺失或能量微弱。因此,本文利用数据驱动思想,提出一种基于U-Net网络的FWI地震数据低频预测方法。通过对改进的U-Net网络模型进行训练,建立高低频之间的映射关系,有效缓解低频缺失带来的问题。通过对比预测低频分量和真实低频分量的误差,利用多尺度全波形反演应用在洼陷模型和相对复杂的Marmousi模型来验证预测低频信号的有效性。

1 方法原理

1.1 改进U-Net网络架构

U-Net模型于2015年由Ronneberger等^[16]提出,其继承了FCN的语义分割思想,并在FCN的基础之上进行延伸。其基于编码器与解码器,采用对称U型结构,使网络在结构设计上更加贴合实际分割需求。随着U-Net层数的加深,维数也在不断扩大,有利于模型学习到更多和更深层次的特征,其反复卷积及融合低层次与高层次特征图的跳跃连接结构,可以得到精度更高的结果。U-Net模型根据具体样本与预测环境,还有可更改及提升的空间,如增加或减少网络层数、增加卷积的数量及修改卷积、池化方式等方法。

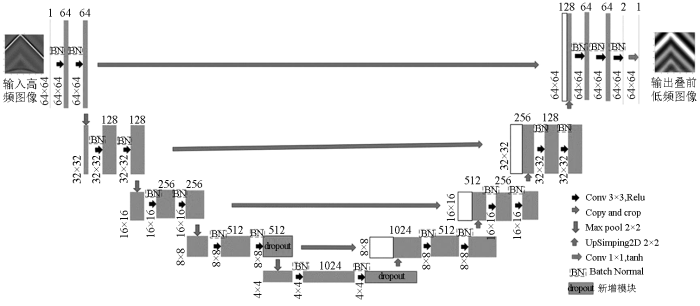
本文是在继承 U-Net网络模型优点的同时,还对传统U-Net网络模型进行了优化。针对其收敛速度慢和易发生梯度消失的问题,本文在每个卷积层中加入批处理层(batch normal,BN),使每层神经元的输入规范化,对每个卷积层的输出结果进行归一化,整体提升梯度,改善梯度弥散问题,加快模型训练速度。此外,加入批处理层还可以在一定程度上防止模型的过拟合。本文还在编码器下采样的第四层和第五层卷积池化加入Dropout层,Dropout层可以在每次迭代时随机“杀死”设定比例的神经元,减少模型体量的同时,还可以有效地预防模型过拟合,提高模型泛化能力。本文 Dropout 设置为0.5,每次训练都会随机舍弃50%的神经元。具体结构如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 改进后的U-Net模型网络结构

Fig.1 Network structure of improved U-Net model

1.2 相关公式

假设高频和低频数据的函数关系如下:

(1)

L (x, t) = G (H (x, t))

式中:H表示高频数据;L表示低频数据;G表示两者的隐式映射关系。通过引入深度神经网络U-Net来逼近映射关系,表达式如下:

(2)

\tilde{L} (θ, x, t) = N e t (θ, H (x, t))

式中: $\tilde{L}$ 表示预测的低频数据;Net表示U-Net网络结构; $θ$ 表示网络参数。从而使得:

(3)

L (x, t) \approx \tilde{L} (θ, x, t)

。

此外,还需要提供一系列经过预处理的训练集切片对 ${H_{n}, L_{n}}_{n}^{N} = 1$ 。 $L_{n}$ 表示切片对中高频数据 $H_{n}$ 对应的低频数据,N表示切片对的数量。在U-Net模型训练过程中,目标函数是通过解决以下最小二乘优化问题来建立高低频数据之间的隐性关系,表达式如下所示:

(4)

J = a r g \underset{θ}{m i n} \frac{1}{q N} \sum_{i = 1}^{N} [L_{i} (x, t) - {\tilde{L}}_{i} {(θ, x, t)}^{2}

式中: $J$ 表示模型的目标函数,用来衡量模型预测数据 $\tilde{L}$ 和真实低频数据L之间的误差;q表示每个数据集的像素总数。

为更新模型参数,求取目标函数对网络参数的导数:

(5)

\frac{\partial J}{\partial θ} = \frac{1}{N} \sum_{i - 1}^{N} {L_{i} (x, t) - {\tilde{L}}_{i} (θ, x, t)} \frac{\partial {\tilde{L}}_{i} (θ, x, t)}{\partial θ}

网格参数具体化为 $θ = (W, b)$ 。

经过BN层批标准化后,第k个卷积核的输出特征图中的第 $i$ 个像素点:

(6)

P_{i}^{' k} = \frac{P_{i}^{k} - μ_{b a t c h}^{k}}{σ_{b a t c h}^{k}}

式中: $P_{i}^{k}$ 表示批标准化前,第k个卷积核输出特征图中第 $i$ 个像素点; $μ_{b a t c h}^{k}$ 表示批标准化前,第k个卷积核batch张输出特征图中所有像素点平均值; $σ_{b a t c h}^{k}$ 表示批标准化前,第k个卷积核batch张输出特征图中所有像素点标准差。计算公式如下:

(7)

σ_{b a t c h}^{k} = \sqrt{δ + \frac{1}{m} \overset{m}{\sum_{i = 1}} (P_{i}^{k} - μ_{b a t c h}^{k})}

(8)

μ_{b a t c h}^{k} = \frac{1}{m} \overset{m}{\sum_{i = 1}} P_{i}^{k}

(9)

P_{i}^{k} = γ_{k} P_{i}^{' k} + β_{k}

式中: $γ_{k}$ 为缩放因子; $β_{k}$ 为偏移因子。为每个卷积核引入可训练参数 $γ$ 和 $β$ ,调整批归一化的力度。

为了加速收敛,本文采用Adadelta梯度下降法^[17]来优化算法模型,其具有较短的收敛时间和较低的错误率,并且在训练时,学习率可以自动调整,无需人为设置。

2 实验与分析

2.1 实验环境

实验环境主要由软件和硬件两部分构成。

硬件方面:主要体现在显卡性能方面,随着NVIDIA系列的Cuda和Cudnn等图形加速计算工具的发展,使用GPU加速训练神经网络,极大地提高了深度学习的效率,节省了训练的时间。

软件方面:选择使用语言为Python和Matlab,深度学习框架为TensorFlow2.0及Keras,地震处理软件为Madagascar,编译软件为Pycharm和Matlab R2016a,操作系统为Ubuntu 18.04,具体实验环境数据如表1所示。

表1 实验环境

Table 1 Experimental environment

名称	版本或参数
CPU	Intel Xeon Sliver 4210 @2.20GHz 500GB
GPU	GeForce RTX 2080(16GB)
CUDA	CUDA 9.0.176
CUDNN	CUDNN 7.6.5
操作系统	Ubuntu 18.04
编译软件	Pycharm 2019、Matlab R2016a
地震处理软件	Madagascar
Pyhton解释器	Python 3.8
深度学习框架	TensorFlow2.1.0、Keras2.3.1

新窗口打开| 下载CSV

2.2 数据准备与处理

2.2.1 数据集构建

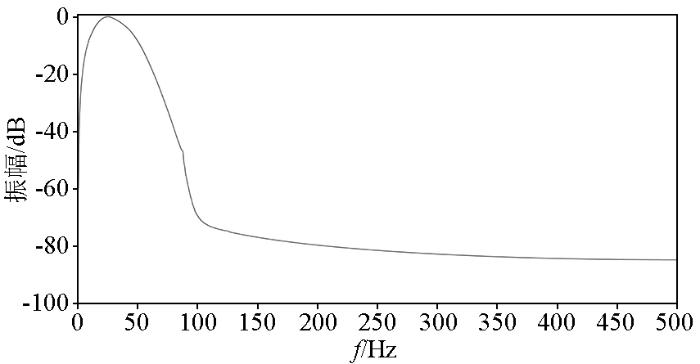
本文采用有限差分求解波动方程,差分阶数为时间方向二阶、空间方向十阶,利用正演模拟方法生成观测数据。地表均匀放置40个震源,120个检波器。正演建模详细参数如表2所示,频谱见图2。准备训练和测试切片对数据集,根据实际资料中常常缺失6 Hz以下的低频数据,首先使用6 Hz高低通截止滤波器过滤原始观测数据,将缺失6 Hz以下的数据看作高频数据,低于6 Hz的数据作为低频数据。将数据集中过滤后的高低频数据切分成46 224个大小为64×64的高低频切片数据对(如图3部分显示),随机取其中75%(34 668个)的数据作为训练集,利用构建的神经网络进行40次迭代训练。再利用剩余的25%(11 556个)的高低频数据中的高频数据作为测试集,将其放入经过训练集训练好的模型中进行测试,确保训练数据集与测试数据集互不相交。

表2 有限差分正演参数

Table 2 Finite difference forward modeling parameters

参数名称	参数值
震源数量	40
检波点数量	120
空间间隔/m	10
采样间隔/ms	1
雷克子波/Hz	15
最大旅行时/ms	2560

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 观测数据频谱(部分)

Fig.2 Spectrum of observation data(part)

2.2.2 数据预处理及逆数据预处理

数据预处理是影响网络训练和泛化能力的关键步骤。而在实际的原始数据采集中因为大地吸收作用,使得单炮记录远道能量比近道弱,深层反射能量比浅层弱,因此,需要对原始数据进行自动增益控制(AGC)处理,达到振幅保真的效果。为了提高网络的训练效率以及泛化能力,还对分离后的高低频数据进行归一化处理、切块处理以及数据增强处理。其中逆数据预处理为数据预处理的反向操作。

1) AGC能量平衡

地震资料的振幅在时域上是平衡的。但是,地震资料的震级变化很大,反射波的能量远小于直达波,如果直接将归一化地震数据输入到网络中,反射波对网络训练的贡献太小,会影响网络性能。自动增益控制方法是地震资料处理中的一个常用振幅处理模块,由于其具有振幅恢复功能和完全可逆的特征,本文通过自动增益控制方法来均衡幅度,增强弱信号,抑制强信号。能量平衡后的数据计算公式:

(10)

\frac{s_{i, j}}{\frac{1}{(2 K + 1) (2 M + 1)} \sum_{k = - K}^{K} \sum_{m = - M}^{M} | s_{i + k, j + m} |}

逆AGC能量均衡是AGC能量均衡的逆处理操作,计算公式如下:

(11)

\frac{1}{(2 K + 1) (2 M + 1)} \overset{K}{\sum_{k = - K}} \overset{M}{\sum_{m = - M}} | s_{i + k, j + m} | * s_{i, j}^{'}

式中: $s_{i, j}$ 表示第j个样本的第i个地震道; $s_{i, j}^{'}$ 表示预测第j样本的第i个地震道;2K+1和2M+1表示窗口两侧的长度。

2) 数据归一化处理

由于各个像素点位置及其身处环境的不同,会导致各个像素点的数量级及量纲产生巨大的差异。因此需要对原始数据进行归一化处理,统一数量级和量纲,加快模型迭代及收敛速度。

Min-max归一化方法很适合处理像素值,其具体公式如下:

(12)

x_{i}^{'} = \frac{x_{i} - x_{m i n}}{x_{m a x} - x_{m i n}}

其逆归一化公式如下:

(13)

x_{i} = x_{i}^{'} (x_{m a x} - x_{m i n}) + x_{m i n}

式中: $x_{i}$ 表示第i个待处理数据; $x_{i}^{'} 表示第 i$ 个归一化处理完数据; $x_{m a x}$ 和 $x_{m i n}$ 分别表示待处理数据中的最大值和最小值。

本文使用Min-max方法来对样本数据进行归一化处理,将像素在[0,255]区间的影像压缩到[0,1]区间内,以便模型训练。

3) 数据切片处理

由于分离后的高低频信号分量样本图像尺寸过大,无法将整张图像全放入模型进行训练,否则会有内存溢出的风险。因此需要对图像进行块状的裁剪,分成尺寸大小一样的小块再进入模型训练,可有效避免内存溢出。本文采用的样本及标签宽度和高度为64×64(图3)。数据的切片处理和其逆处理(缝合拼接)可通过计算机程序直接完成。

4) 数据增强

数据增强是一项对于训练样本进行各种变换从而间接扩充样本数量的技术。主要是对原始数据的拉伸、反转、旋转等操作,增加样本的丰富程度,可以有效地预防因数据量不足而导致的模型精度低的情况。使用数据增强进行训练与没有使用数据增强相比,在训练数据时成倍增加了数据量,可以有效地预防模型的过拟合。因此,无需进行处理操作。

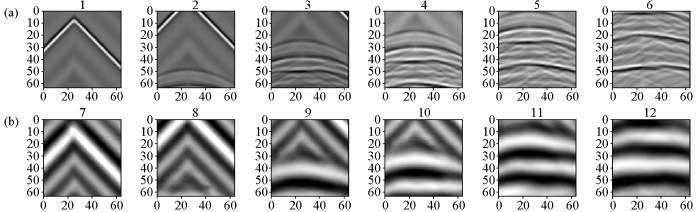
图3

新窗口打开| 下载原图ZIP| 生成PPT

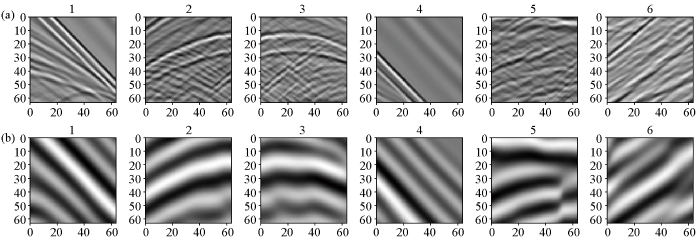
图3 训练集高频数据与对应低频标签可视化展示

a—6张大小64×64的训练集输入高频数据;b—图a中高频数据对应低频标签数据

Fig.3 Visual display of training set high-frequency data and corresponding low-frequency tags

a—6 high frequency datas input from 64×64 training sets;b—fig.a low frequency label datas corresponding to high frequency data

2.3 网络模型训练

2.3.1 激活函数

本文实验是基于Tensorflow2.0和Keras框架搭建网络模型,模型中除了最后一层使用tanh作为激活函数外,其他各层均使用ReLU作为激活函数,二者表达式为:

(14)

t a n h (x) = \frac{s i n h (x)}{c o s h (x)} = \frac{e^{2 x} - 1}{e^{2 x} + 1}

(15)

R e L U (x) = \{\begin{array}{l} x, x > 0 \\ 0, 其 他 \end{array}

因为没有复杂的指数运算,ReLU在随机梯度下降中的收敛速度要比sigmoid和tanh快很多,计算速度非常快,并且在一定程度上有效地缓解了训练过程中梯度爆炸和梯度消失问题。最后一层选用tanh,可以比sigmoid延迟进入饱和期。

2.3.2 参数设置

本文实验使用自适应学习率的Adadelta优化算法进行网络优化,使用均方误差作为计算低频标签与预测低频之间的误差损失函数。U-Net模型中编码器区域和解码器区域的卷积核尺寸均为3×3,填充方式为全零填充,编码器区域池化(下采样)方式选择的是最大池化,池化核尺寸大小均为2×2,解码器区域反卷积(上采样)的卷积核均为2×2,最后一层卷积的卷积大小为1×1。此外,卷积层初始化权重的方法为glorot_uniform,参数从[-limit, limit]的均匀分布产生,其中limit为 $s q r t [6 / (f a n_{i n} + f a n_{o u t})]$ 。 $f a n_{i n}$ 为权值张量的输入单元数, $f a n_{o u t}$ 是权值张量的输出单元数。

2.3.3 训练结果

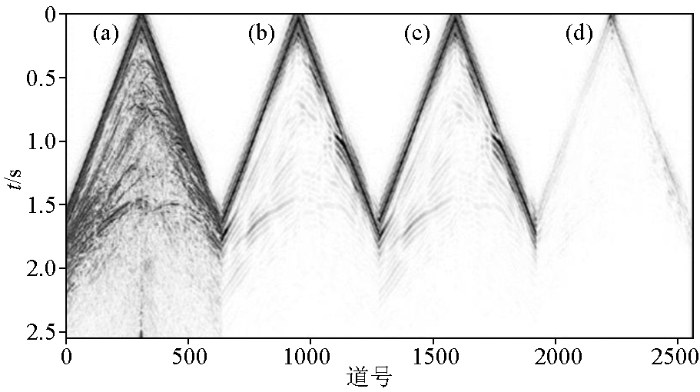
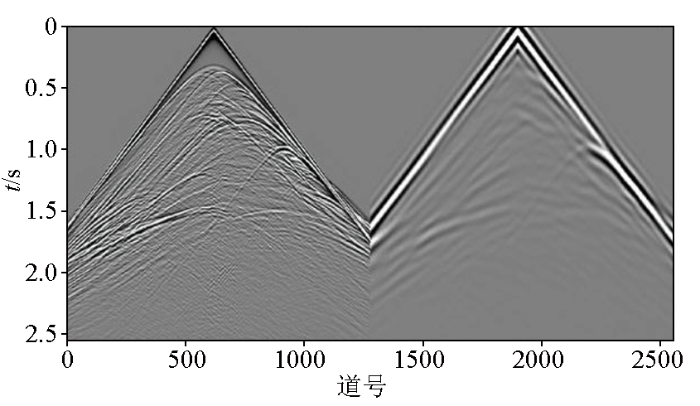
通过比较图4所示的道集及计算误差表达式:

(16)

\frac{1}{q N} \overset{N}{\sum_{n = 1}} \frac{|L (x, t) - N e t [θ, H (x, t)] |}{| m a x [L (x, t)] |}

。

得出切片对训练数据和测试数据的平均相对误差分别为5.02%和13.32%,结果表明:经过能量校正的预测炮道集类似于真实的低频炮道集,它们之间的误差很小,为可接受范围之内的。为了进一步验证,图5显示了原始数据、缺失低频数据、真实低频数据以及预测低频数据之间的振幅频谱对比,图中预测频率道集的曲线与其真实低频道集的曲线十分接近。图6、图7分别为原始数据、缺失低频数据以及补充预测低频数据后的道集对比图和对应的频谱对比。图中显示补充预测低频的数据与原始数据十分接近,效果良好。图8展示了第250道的原始数据、缺失低频数据、真实低频以及预测低频之间的波形对比。

图4

新窗口打开| 下载原图ZIP| 生成PPT

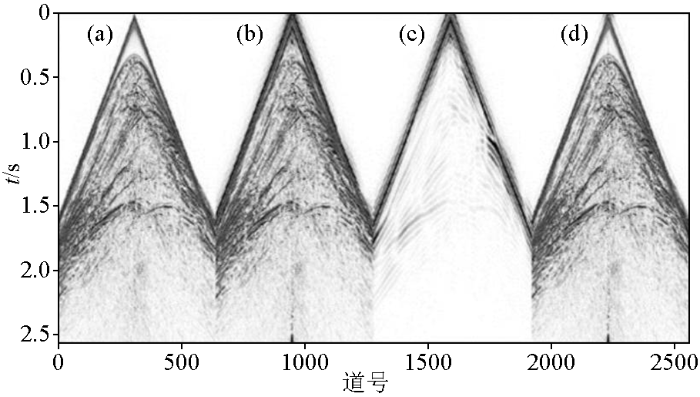
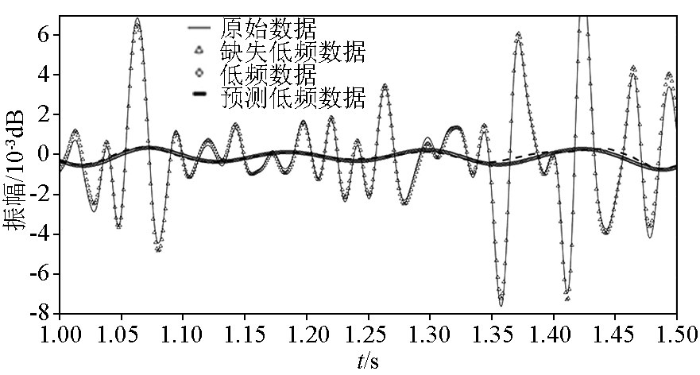
图4 真实低频与预测低频道集图像对比

a—缺失低频数据;b—预测低频数据;c—真实低频数据;d—预测和真实低频数据之间的误差

Fig.4 Comparison of real low frequency and predicted low frequency channel set images

a—missing low frequency data;b—predicted low frequency data;c—true low frequency data;d—error between prediction and real low-frequency data

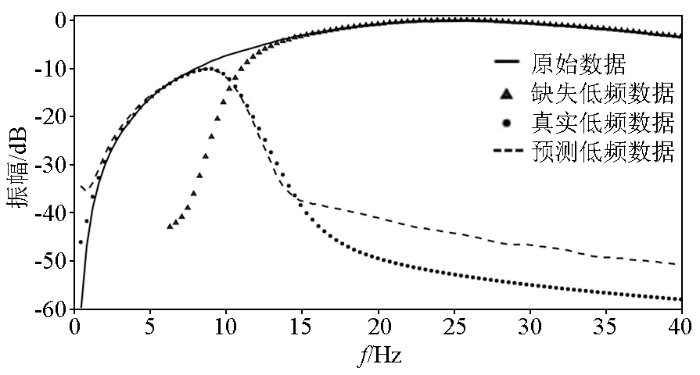
图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 真实低频与预测低频频谱对比

Fig.5 Spectrum comparison between real low frequency and predicted data

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 原始与补充低频数据道集图像对比

a—原始数据;b—缺失低频数据;c—预测低频数据;d—补充预测低频后的数据

Fig.6 Comparison of original and supplementary low frequency data gather images

a—original data;b—missing low frequency data;c—predicted low frequency data;d—supplementary data after low frequency prediction

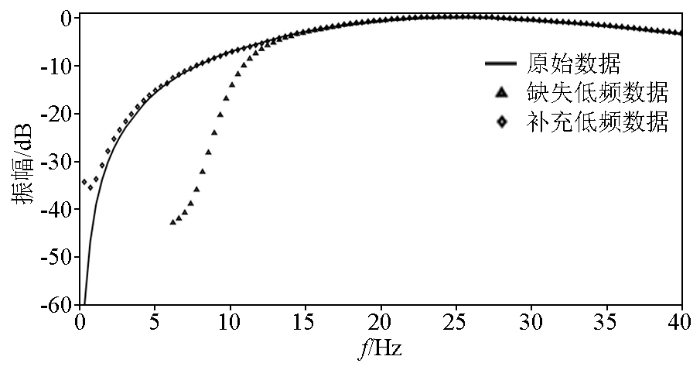
图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 观测数据与补充低频数据的频谱对比

Fig.7 Spectrum comparison between observed data and supplementary low frequency data

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 第250道的波形对比

Fig.8 Waveform comparison of trace 250

2.4 中间层可视化分析

为了形象直观地展示数据在网络模型中的变化过程,分析网络模型各个模块的中间运行状态,可视化展示6组测试数据(图9a)、对应预测低频结果(图9b)以及在U-Net模型各模块的部分特征图(图10)。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 测试集高频数据与对应预测低频结果可视化展示

a—6张大小为64×64的测试高频数据;b—图a中数据对应预测低频数据

Fig.9 Visual display of test high frequency set and prediction results

a—6 pieces of test high frequency data with the size of 64×64;b—fig. a prediction of low frequency data from test data

图10

新窗口打开| 下载原图ZIP| 生成PPT

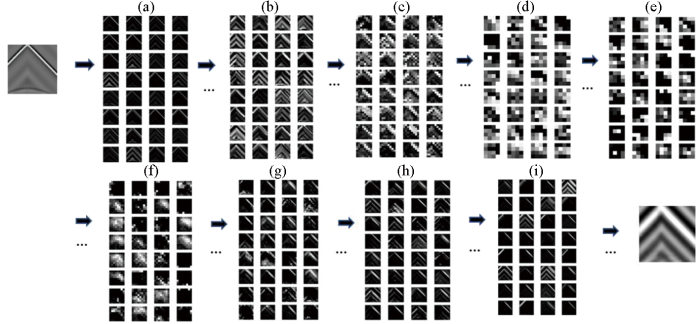
图10 网络模型提取特征过程可视化展示

a~e—编码过程下采样提取特征;f~i—解码过程上采样恢复特征

Fig.10 Visual display of feature extraction process of network model

a~e—sampling and feature extraction in the coding process;f~i—upper sampling recovery feature during decoding

图10中模块1、2、3、4、5是U-Net编码过程,属于下采样提取特征的模块,模块6、7、8、9是解码过程,属于上采样恢复特征的模块。从图10a~e中可以直观地看出:模块1~5可以有效地提取出高频数据特征,随着网络深度的不断加深,提取到的特征也越来越抽象,经过多层卷积、池化后,特征图就含有较为丰富的语义信息。从图10f~i可以看出:模块6~9开始逐步将特征信息恢复出来,最终得到本文所需低频数据。其中的跳跃连接结构也有效地帮助上采样恢复图像信息,把编码器所生成的整张特征图与解码器连接。

3 低频预测数据有效性验证

为了验证本文低频预测方法的有效性,分别采用洼陷模型、Marmousi模型和现场实际数据进行验证。同时为了考虑噪声的影响,对洼陷模型进行了噪声实验,并在本节最后对结果统一分析。

3.1 洼陷模型

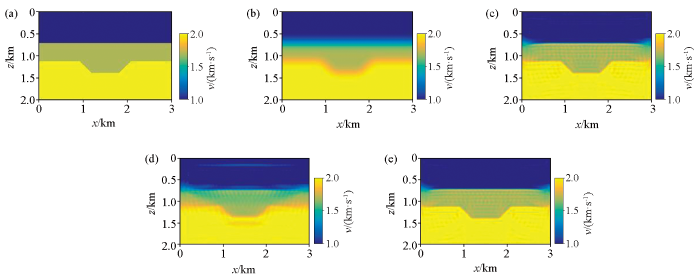
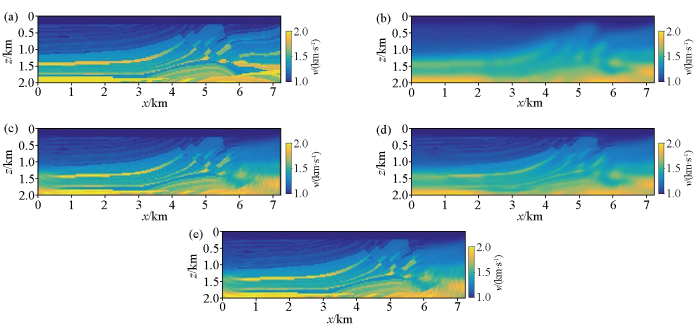
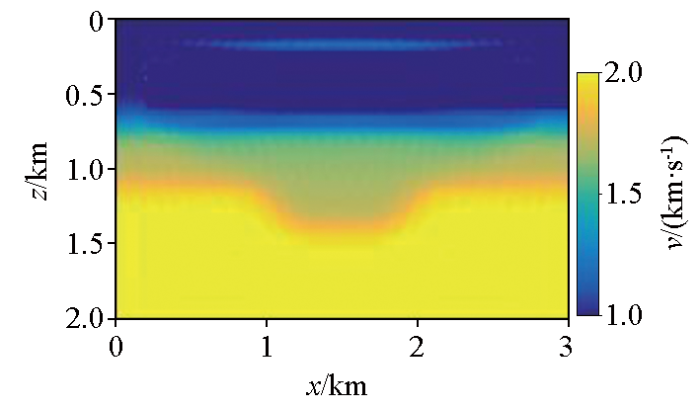
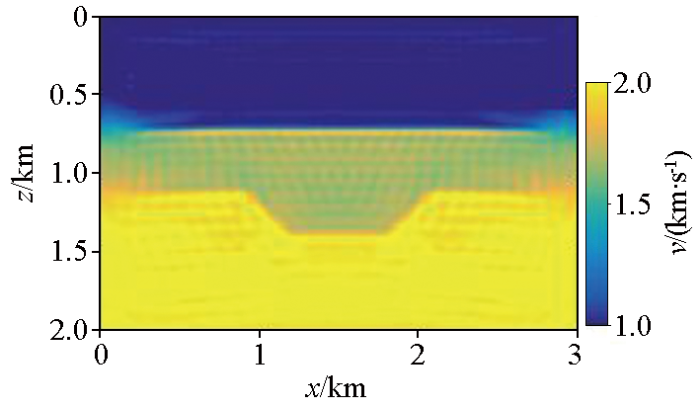
为了验证低频预测数据的有效性,本文首先选取相对简单的洼陷模型进行反演模拟。图11a为洼陷速度模型,图11b为初始速度模型,网格大小为x方向上300个网格点,z方向上200个网格点,空间采用间隔为10 m,共设置29炮震源激发,均匀分布于水下10 m,水平方向0.4~2.6 km范围内。每炮87道接收,检波点均匀分布于地表水平方向0.4~2.6 km范围内,不随炮点移动。选取主频为10 Hz的雷克子波作为震源,采用完全匹配层(PML)吸收边界条件。选取12个频率数据进行全波形反演,频率范围在0~20 Hz,对这12个频段的多尺度FWI^[18]进行了40次迭代,且目标函数收敛阈值设定为0.01。图11c为原始数据的反演结果,图11d为缺失低频数据的反演结果,图11e为补充低频数据的的反演结果。图12为洼陷模型某1炮原始数据及其预测低频道集。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 洼陷模型试验反演结果

a—洼陷速度模型;b—初始速度模型;c—原始数据的反演结果;d—缺失低频的反演结果;e—补充预测低频

Fig.11 Inversion results of depression model experiment

a—velocity model of depression;b—initial velocity model;c—inversion result of original data;d—inversion result of missing low frequency;e—supplementary prediction low frequency

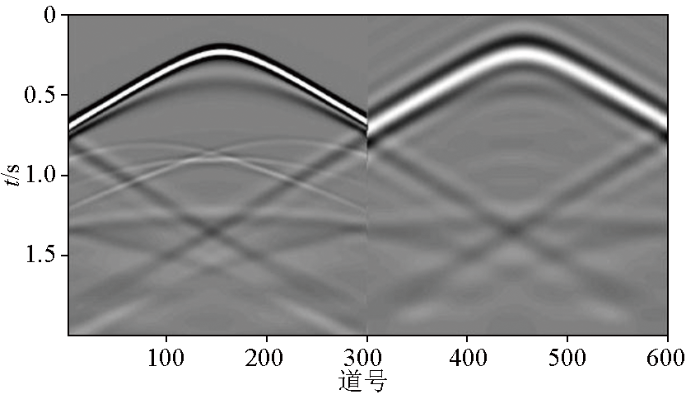
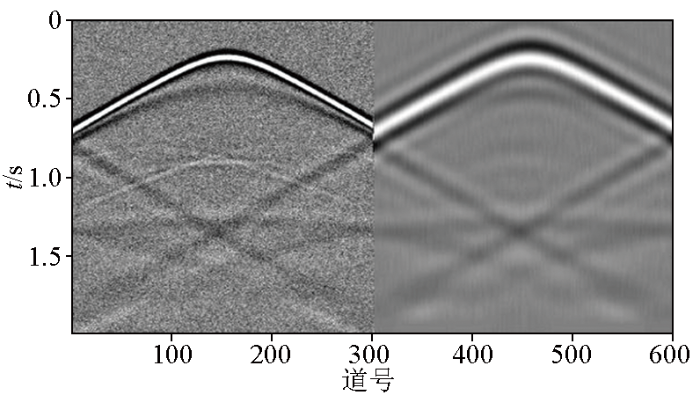
图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 洼陷模型某一炮原始数据及其预测低频数据道集

Fig.12 Original data of a certain shot of depression model and its predicted low-frequency data gathers

3.2 Marmousi模型

本文还在复杂的Marmousi模型上进行反演模拟,图13a为Marmousi速度模型,图13b为初始速度模型,网格大小为x方向上722个网格点,z方向上200个网格点,空间采用间隔为10 m,共设置29炮震源激发,均匀分布于地表水平方向0.4~7 km范围内。每炮87道接收,检波点均匀分布于地表水平方向0.4~7 km范围内,不随炮点移动。选取主频为25 Hz的雷克子波作为震源子波,采用完全匹配层(PML)吸收边界条件,减少左右底边的非物理反射。采用多尺度FWI技术,选取0~20 Hz中12个频率进行反演,最大迭代次数为40次,目标函数收敛阈值设定为0.01,保证数据可以在给定的最大迭代次数范围内充分迭代。图13c为原始数据的反演结果,图13d为缺失低频数据的反演结果,图13e为补充低频数据的的反演结果。图14为Marmousi模型某1炮原始数据及其预测低频道集。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 Marmousi模型试验反演结果

a—Marmousi速度模型;b—初始速度模型;c—原始数据的反演结果;d—缺失低频的反演结果;e—补充预测低频的反演结果

Fig.13 Inversion results of Marmousi model test

a—velocity model of depression;b—initial velocity model;c—inversion result of original data;d—inversion result of missing low frequency;e—supplementary prediction low frequency

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 Marmousi某1炮原始数据及其预测低频数据道集

Fig.14 Original data and predicted low-frequency data athers of a certain shot in Marmousi

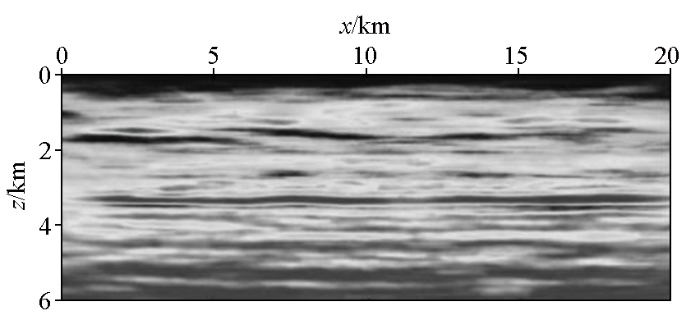
3.3 实际数据

本文还在现场实际数据中进行反演模拟。所选网格大小为x方向上800个网格点,z方向上240个网格点,空间采用间隔为25 m,对实际数据和补充预测低频的实际数据进行多尺度FWI,选取0~25 Hz中12个频率进行反演,最大迭代次数为40次,目标函数收敛阈值设定为0.01,保证数据可以在给定的最大迭代次数范围内充分迭代。反演结果如图15、16所示。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 实际数据的反演结果

Fig.15 Inversion results of actual data

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 加入预测低频的实际数据的反演结果

Fig.16 Inversion results of actual data with redicted low frequency

3.4 加入噪声的洼陷模型

考虑到噪声可能对低频预测方法的影响,因此向洼陷模型的模拟出的原始数据道集中添加了信噪比为20的高斯噪声(如图17所示),将其放入本文方法模型中训练,训练的预测低频结果如图18所示。同时还将预测出的低频数据补入原始数据中,并进行多尺度FWI,参数设置与3.1小节中相同,反演结果如图19、20所示。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 洼陷原始数据及加入噪声后的数据道集

Fig.17 Original data of depression and data trace set after adding noise

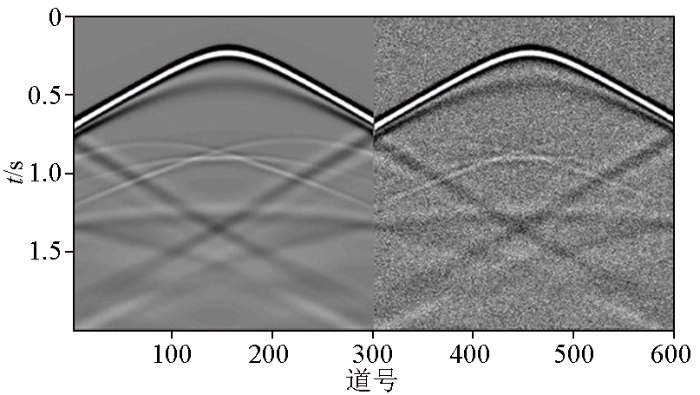
图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 加入噪声的洼陷原始数据及其预测低频数据的道集

Fig.18 Trace plot of original data of depression with noise and its predicted low-frequency data

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 加入噪声的洼陷原始数据反演结果

Fig.19 Inversion results of sag original data with noise

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20 补充低频的噪声洼陷原始数据反演结果

Fig.20 Inversion results of original data of low frequency noise sag supplemented

3.5 结果分析

原始数据、缺失低频的高频数据以及加入预测低频的高频数据在洼陷模型和Marmousi模型上最终的反演结果如图11c~e以及13c~e所示:图11c与图13c说明,即使初始速度是粗糙的,仍然可以使用多尺度FWI和原始观测数据建立高精度的速度模型。图11d和图13d说明,当观测数据缺失低频分量数据时,传统的FWI目标函数容易陷入局部极小值,导致反演结果的反演精度较低,速度模型图像模糊。图11e和图13e说明,当加入预测的低频数据后,利用补充低频的数据进行反演,可以得到与原始数据反演结果相差无几的高精度反演速度模型,由此可见预测低频分量可以显著提高反演质量,有效解决FWI周波跳跃问题。此外,通过计算式(16)可得出:洼陷模型数据平均相对误差为12.41%,Marmousi模型数据平均相对误差为13.26%,结果表明模型预测低频与实际低频数据之间十分接近,可以用预测低频代替实际低频数据,并且将预测低频加入缺失低频的数据之中进行全波形反演的结果质量也相当不错。通过对比图15和图16的实际数据反演结果,不难看出本文方法也可以很好地应用在实际地震数据的处理中,可以得到较好的层间连续性和丰富的背景信息。噪声对本文方法的影响,通过对比图12和图18,可以看出加入噪声后对预测低频的结果影响较小;通过对比图11d、图19以及图20可知:加入噪声,对于原始数据反演结果的影响较大,但是补充低频后的反演结果质量有明显提高,说明本文方法可以处理存在一定范围内的含噪声数据。

4 结论与讨论

为了解决因实际地震资料缺乏低频信号导致全波形反演易陷入局部极值问题,本文提出了一种基于深度学习U-Net网络的FWI地震低频数据预测恢复方法。

1)利用高通和低通滤波器对原始数据分离出高低频分量,对其进行一系列数据预处理得到模型训练集,其中通过AGC能量均衡,达到振幅保真效果,并利用AGC完全可逆的特征,在最后对预测的低频分量进行逆能量均衡校正可以进一步对地震低频资料进行保幅预测。数据预处理和逆数据预处理操作可以更有效地提取样本特征,提高模型训练精度。

2)基于U-Net网络进行合理优化有利于提高模型的训练效率。为了防止模型过拟合,本文在所有卷积层中都加入批处理层,使每层神经元的输入规范化,加快模型训练速度。此外,还在其第四和第五层后添加dropout层,随机“杀死”设定比例的神经元,提高模型泛化能力。

3)使用多尺度FWI在洼陷模型、Marmousi模型、实际数据上验证预测低频数据的有效性,实验表明添加预测低频分量的高频数据可以有效缓解因缺失低频信号而导致反演陷入局部极小问题,显著提高全波形反演的反演效果。此外,本方法对于含有加入较大噪声的原始数据也有很好的处理结果,具有一定的抗噪能力。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Tarantola

Linearized inversion of seismic reflection data

[J]. Geophysical Prospecting, 1984, 32(6):998-1015.

DOI:10.1111/gpr.1984.32.issue-6 URL [本文引用: 1]

[2]

R S

, Luo

, Wu

Seismic envelope inversion and modulation signal model

[J]. Geophysics, 2014, 79(3):WA13-WA24.

DOI:10.1190/geo2013-0294.1 URL [本文引用: 1]

We recognized that the envelope fluctuation and decay of seismic records carries ultra low-frequency (ULF, i.e., the frequency below the lowest frequency in the source spectrum) signals that can be used to estimate the long-wavelength velocity structure. We then developed envelope inversion for the recovery of low-wavenumber components of media (smooth background), so that the initial model dependence of waveform inversion can be reduced. We derived the misfit function and the corresponding gradient operator for envelope inversion. To understand the long-wavelength recovery by the envelope inversion, we developed a nonlinear seismic signal model, the modulation signal model, as the basis for retrieving the ULF data and studied the nonlinear scale separation by the envelope operator. To separate the envelope data from the wavefield data (envelope extraction), a demodulation operator (envelope operator) was applied to the waveform data. Numerical tests using synthetic data for the Marmousi model proved the validity and feasibility of the proposed approach. The final results of combined [Formula: see text] (envelope-inversion for smooth background plus waveform-inversion for high-resolution velocity structure) indicated that it can deliver much improved results compared with regular full-waveform inversion (FWI) alone. Furthermore, to test the independence of the envelope to the source frequency band, we used a low-cut source wavelet (cut from 5 Hz below) to generate the synthetic data. The envelope inversion and the combined [Formula: see text] showed no appreciable difference from the full-band source results. The proposed envelope inversion is also an efficient method with very little extra work compared with conventional FWI.

[3]

Boßmann

, Ma

Asymmetric chirplet transform for sparse representation of seismic data

[J]. Geophysics, 2015, 80(6):WD89-WD100.

DOI:10.1190/geo2015-0063.1 URL [本文引用: 1]

For a fast and accurate extraction of important information in seismic signals, a sparse representation based on the physical parameters of the given data is crucial. We have used the asymmetric Gaussian chirplet model (AGCM) and established a dictionary-free variant of the orthogonal matching pursuit, a greedy algorithm for sparse approximation. The atoms of AGCM, so-called chirplets, display asymmetric oscillation attenuation properties, which make the AGCM very suitable for sparse representation of absorption decay seismic signals. Unlike the Fourier transform, which assumes that the seismic signals consist of plane waves, the AGCM assumes that the seismic signal consists of nonstationary compressed plane waves, i.e., symmetric or asymmetric chirplets. Thus, AGCM is a general model for seismic wave simulation, and its model parameters include an envelope part and a phase part. We have mainly concentrated on the parameters of the envelope part, such as the envelope amplitude and arrival time. We provide numerical examples using the algorithm for seismic signal approximation and arrival-time detection. The results indicated promising performance but also may be improved considering the spatial correlations of seismic data.

[4]

Shin

, Cha

Y H

Waveform inversion in the Laplace domain

[J]. Geophysical Journal International, 2008, 173(3):922-931.

DOI:10.1111/gji.2008.173.issue-3 URL [本文引用: 1]

[5]

Y E

, Demanet

Full-waveform inversion with extrapolated low-frequency data

[J]. Geophysics, 2016, 81(6):R339-R348.

DOI:10.1190/geo2016-0038.1 URL [本文引用: 1]

The availability of low-frequency data is an important factor in the success of full-waveform inversion (FWI) in the acoustic regime. The low frequencies help determine the kinematically relevant, low-wavenumber components of the velocity model, which are in turn needed to avoid convergence of FWI to spurious local minima. However, acquiring data less than 2 or 3 Hz from the field is a challenging and expensive task. We have explored the possibility of synthesizing the low frequencies computationally from high-frequency data and used the resulting prediction of the missing data to seed the frequency sweep of FWI. As a signal-processing problem, bandwidth extension is a very nonlinear and delicate operation. In all but the simplest of scenarios, it can only be expected to lead to plausible recovery of the low frequencies, rather than their accurate reconstruction. Even so, it still requires a high-level interpretation of band-limited seismic records into individual events, each of which can be extrapolated to a lower (or higher) frequency band from the nondispersive nature of the wave-propagation model. We have used the phase-tracking method for the event separation task. The fidelity of the resulting extrapolation method is typically higher in phase than in amplitude. To demonstrate the reliability of bandwidth extension in the context of FWI, we first used the low frequencies in the extrapolated band as data substitute, to create the low-wavenumber background velocity model, and then we switched to recorded data in the available band for the rest of the iterations. The resulting method, extrapolated FWI, demonstrated surprising robustness to the inaccuracies in the extrapolated low-frequency data. With two synthetic examples calibrated so that regular FWI needs to be initialized at 1 Hz to avoid local minima, we have determined that FWI based on an extrapolated [1, 5] Hz band, itself generated from data available in the [5, 15] Hz band, can produce reasonable estimations of the low-wavenumber velocity models.

[6]

FWI without low frequency data-beat tone inversion

[C]// SEG Technical Program Expanded Abstracts 2014,Society of Exploration Geophysicists, 2014:1116-1120.

[本文引用: 1]

[7]

刘张聚, 童思友, 方云峰, 等.

基于时域加权的拉普拉斯—频率域弹性波全波形反演

[J]. 石油地球物理勘探, 2021, 56(2):302-312.

[本文引用: 1]

Liu

Z J

, Tong

S Y

, Fang

Y F

, el

Full waveform inversion of elastic wave in Laplace frequency domain based on time domain weighting

[J] Oil Geophysical Prospecting, 2021, 56(2):302-312.

[本文引用: 1]

[8]

Jin

, Hu

, Wu

, et al.

Learn low wavenumber information in FWI via deep inception based convolutional networks

[C]// 2018 SEG International Exposition and Annual Meeting,OnePetro, 2018.

[本文引用: 1]

[9]

Sun

, Demanet

Low frequency extrapolation with deep learning

[C]// SEG Technical Program Expanded Abstracts 2018,Society of Exploration Geophysicists, 2018:2011-2015.

[本文引用: 1]

[10]

Ovcharenko

, Kazei

, Kalita

, et al.

Deep learning for low-frequency extrapolation from multioffset seismic data

[J]. Geophysics, 2019, 84(6):R989-R1001.

DOI:10.1190/GEO2018-0884.1 [本文引用: 1]

Low-frequency seismic data are crucial for convergence of full-waveform inversion (FWI) to reliable subsurface properties. However, it is challenging to acquire field data with an appropriate signal-to-noise ratio in the low-frequency part of the spectrum. We have extrapolated low-frequency data from the respective higher frequency components of the seismic wavefield by using deep learning. Through wavenumber analysis, we find that extrapolation per shot gather has broader applicability than per-trace extrapolation. We numerically simulate marine seismic surveys for random subsurface models and train a deep convolutional neural network to derive a mapping between high and low frequencies. The trained network is then tested on sections from the BP and SEAM Phase I benchmark models. Our results indicate that we are able to recover 0.25 Hz data from the 2 to 4.5 Hz frequencies. We also determine that the extrapolated data are accurate enough for FWI application.

[11]

Ovcharenko

, Kazei

, Peter

, et al.

Transfer learning for low frequency extrapolation from shot gathers for FWI applications

[C]// 81^st EAGE Conference and Exhibition 2019,European Association of Geoscientists & Engineers, 2019(1):1-5.

[本文引用: 1]

[12]

Sun

, Demanet

Deep learning for low frequency extrapolation of multicomponent data in elastic full waveform inversion

[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60:1-11.

[本文引用: 1]

[13]

Fang

, Zhou

, Elita

Li Y

, et al.

Data-driven low-frequency signal recovery using deep-learning predictions in full-waveform inversion

[J]. Geophysics, 2020, 85(6):A37-A43.

DOI:10.1190/geo2020-0159.1 URL [本文引用: 1]

The lack of low-frequency signals in seismic data makes the full-waveform inversion (FWI) procedure easily fall into local minima leading to unreliable results. To reconstruct the missing low-frequency signals more accurately and effectively, we have developed a data-driven low-frequency recovery method based on deep learning from high-frequency signals. In our method, we develop the idea of using a basic data patch of seismic data to build a local data-driven mapping in low-frequency recovery. Energy balancing and data patches are used to prepare high- and low-frequency data for training a convolutional neural network (CNN) to establish the relationship between the high- and low-frequency data pairs. The trained CNN then can be used to predict low-frequency data from high-frequency data. Our CNN was trained on the Marmousi model and tested on the overthrust model, as well as field data. The synthetic experimental results reveal that the predicted low-frequency data match the true low-frequency data very well in the time and frequency domains, and the field results show the successfully extended low-frequency spectra. Furthermore, two FWI tests using the predicted data demonstrate that our approach can reliably recover the low-frequency data.

[14]

, Jin

, Wu

, et al.

Progressive transfer learning for low-frequency data prediction in full waveform inversion

[J]. Geophysics, 2021, 86(4):1-82.

[本文引用: 1]

[15]

Mousavi

, Baraniuk

R G

Learning to invert:Signal recovery via deep convolutional networks

[C]// 2017 IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP),IEEE, 2017:2272-2276.

[本文引用: 1]

[16]

Ronneberger

, Fischer

, Brox

U-net:Convolutional networks for biomedical image segmentation

[C]// International Conference on Medical Image Computing and Computer-Assisted Intervention,Springer,Cham, 2015:234-241.

[本文引用: 1]

[17]

Zeiler

M D

Adadelta:an adaptive learning rate method

[J]. Computer Science, 2012:1-6.

[本文引用: 1]

[18]

Bunks

, Saleck

F M

, Zaleski

, et al.

Multiscale seismic waveform inversion

[J]. Geophysics, 1995, 60(5):1457-1473.

DOI:10.1190/1.1443880 URL [本文引用: 1]

Iterative inversion methods have been unsuccessful at inverting seismic data obtained from complicated earth models (e.g. the Marmousi model), the primary difficulty being the presence of numerous local minima in the objective function. The presence of local minima at all scales in the seismic inversion problem prevent iterative methods of inversion from attaining a reasonable degree of convergence to the neighborhood of the global minimum. The multigrid method is a technique that improves the performance of iterative inversion by decomposing the problem by scale. At long scales there are fewer local minima and those that remain are further apart from each other. Thus, at long scales iterative methods can get closer to the neighborhood of the global minimum. We apply the multigrid method to a subsampled, low‐frequency version of the Marmousi data set. Although issues of source estimation, source bandwidth, and noise are not treated, results show that iterative inversion methods perform much better when employed with a decomposition by scale. Furthermore, the method greatly reduces the computational burden of the inversion that will be of importance for 3-D extensions to the method.

Linearized inversion of seismic reflection data

1984

... 全波形反演(full waveform inversion,FWI)可以通过数据拟合建立高分辨率地下速度模型,是一种建立在非线性优化算法基础上的地震处理技术.然而,许多现有FWI算法都存在一个主要缺点:易陷入局部极值^[1].反演过程中产生的周波跳跃现象是使FWI陷入局部极值的直接原因,导致周波跳跃的原因主要包括地震信号缺失低频成分和初始速度模型与地下真实速度模型相差过大.由于传统地震采集技术的限制以及地震资料处理过程中面波压制等原因,对于反演精度至关重要的低频信息往往是缺失的.有效缓解FWI周波跳跃问题的方法是从地震数据中“挖掘”出低频信息,再结合多尺度反演策略,实现高精度的速度建模. ...

Seismic envelope inversion and modulation signal model

2014

... 常见的地震数据低频信息恢复方法主要分为两类.第一类是基于数学原理,包括包络计算^[2-3]、零频率阻尼波场^[4]、基于相位跟踪方法的低频恢复^[5]、数据拍音反演^[6]、拉普拉斯域反演^[7]等.第二类是基于神经网络学习类算法.2108年,Jin等^[8]第一次提出利用数据驱动方法解决低频缺失问题,通过基于深度初始建立的卷积神经网络来学习FWI中的低频信息.Sun等^[9]通过将低频预测作为回归问题来研究卷积神经网络的低频带宽扩展方法.2019年,Ovcharenko等^[10]训练卷积神经网络获得多偏移地震数据恢复低频信息,此外,其还通过迁移学习方法来预测低频信息^[11].2020年,Sun等^[12]提出采用一维卷积神经网络模型从频带受限的数据中恢复丢失的低频.Fang等^[13]提出通过训练二维卷积神经网络模型,学习建立高低频之间的隐性映射关系,提出了一种基于高频信号深度学习的低频恢复方法.2021年,Hu等^[14]提出基于深度神经网络,利用地下地质和地球物理特性,将低频数据和高频数据隐式联系起来,用以预测缺少的低频分量,有效地抑制FWI中周波跳跃现象. ...

Asymmetric chirplet transform for sparse representation of seismic data

2015

Waveform inversion in the Laplace domain

2008

Full-waveform inversion with extrapolated low-frequency data

2016

FWI without low frequency data-beat tone inversion

2014

基于时域加权的拉普拉斯—频率域弹性波全波形反演

2021

基于时域加权的拉普拉斯—频率域弹性波全波形反演

2021

Learn low wavenumber information in FWI via deep inception based convolutional networks

2018

Low frequency extrapolation with deep learning

2018

Deep learning for low-frequency extrapolation from multioffset seismic data

2019

Transfer learning for low frequency extrapolation from shot gathers for FWI applications

2019

Deep learning for low frequency extrapolation of multicomponent data in elastic full waveform inversion

2022

Data-driven low-frequency signal recovery using deep-learning predictions in full-waveform inversion

2020

Progressive transfer learning for low-frequency data prediction in full waveform inversion

2021

Learning to invert:Signal recovery via deep convolutional networks

2017

... 通过学习高频分量和低频分量之间潜在的非线性关系来预测缺失的低频数据,是近年来活跃的一个信号处理领域^[15].由于震源激发时难以产生低频信号以及检波器很难检测出地震信号中的低频分量信息,导致低频分量在实际地震数据中严重缺失或能量微弱.因此,本文利用数据驱动思想,提出一种基于U-Net网络的FWI地震数据低频预测方法.通过对改进的U-Net网络模型进行训练,建立高低频之间的映射关系,有效缓解低频缺失带来的问题.通过对比预测低频分量和真实低频分量的误差,利用多尺度全波形反演应用在洼陷模型和相对复杂的Marmousi模型来验证预测低频信号的有效性. ...

U-net:Convolutional networks for biomedical image segmentation

2015

... U-Net模型于2015年由Ronneberger等^[16]提出,其继承了FCN的语义分割思想,并在FCN的基础之上进行延伸.其基于编码器与解码器,采用对称U型结构,使网络在结构设计上更加贴合实际分割需求.随着U-Net层数的加深,维数也在不断扩大,有利于模型学习到更多和更深层次的特征,其反复卷积及融合低层次与高层次特征图的跳跃连接结构,可以得到精度更高的结果.U-Net模型根据具体样本与预测环境,还有可更改及提升的空间,如增加或减少网络层数、增加卷积的数量及修改卷积、池化方式等方法. ...

Adadelta:an adaptive learning rate method

2012

... 为了加速收敛,本文采用Adadelta梯度下降法^[17]来优化算法模型,其具有较短的收敛时间和较低的错误率,并且在训练时,学习率可以自动调整,无需人为设置. ...

Multiscale seismic waveform inversion

1995

... 为了验证低频预测数据的有效性,本文首先选取相对简单的洼陷模型进行反演模拟.图11a为洼陷速度模型,图11b为初始速度模型,网格大小为x方向上300个网格点,z方向上200个网格点,空间采用间隔为10 m,共设置29炮震源激发,均匀分布于水下10 m,水平方向0.4~2.6 km范围内.每炮87道接收,检波点均匀分布于地表水平方向0.4~2.6 km范围内,不随炮点移动.选取主频为10 Hz的雷克子波作为震源,采用完全匹配层(PML)吸收边界条件.选取12个频率数据进行全波形反演,频率范围在0~20 Hz,对这12个频段的多尺度FWI^[18]进行了40次迭代,且目标函数收敛阈值设定为0.01.图11c为原始数据的反演结果,图11d为缺失低频数据的反演结果,图11e为补充低频数据的的反演结果.图12为洼陷模型某1炮原始数据及其预测低频道集. ...

〈

〉