一种重力异常向上延拓高度最优化确定方法

doi:10.11720/wtyht.2023.2356

一种重力异常向上延拓高度最优化确定方法

孙争^,, 王俊^,, 丁鹏, 谭鑫

中国地质大学(北京) 地球物理与信息技术学院,北京 100083

Amethod for determining the optimal height for upward continuation of gravity anomalies

SUN Zheng^,, WANG Jun^,, DING Peng, TAN Xin

School of Geophysics and Information Technology, China University of Geosciences (Beijing), Beijing 100083, China

通讯作者: 王俊(1989-),男,副教授,主要从事位场方法技术与应用研究工作。Email:wangj@cugb.edu.cn

责任编辑: 王萌

收稿日期: 2021-06-24 修回日期: 2021-09-4

基金资助:

中国地质大学(北京)大学生创新创业训练计划项目(202011415297)

Received: 2021-06-24 Revised: 2021-09-4

作者简介 About authors

孙争(1999-),男,在读本科生,研究方向为重磁数据处理。Email:1010181224@cugb.edu.cn

摘要

向上延拓方法是重力异常分离中的重要方法之一,但在应用时如何定量地选取合适的延拓高度是一直以来存在的问题。本文针对该问题展开研究,提出一种基于二乘误差的曲率分析方法来定量地给出相对合理的延拓高度。该方法对观测数据进行相邻不同高度的向上延拓,并用二乘法估算相邻高度延拓值的二乘误差,在各相邻高度延拓值二乘曲线中存在一个曲率最大值,在这个点最大程度地使局部异常衰减并尽可能地保留区域异常,可近似视为最佳延拓高度。利用理论模型数据对所提出的方法进行了测试,表明该方法能够定性给出较合适的延拓高度,从而为实际应用中延拓高度的选取提供参考。

关键词： 重力异常; 解析延拓; 向上延拓高度

Abstract

Upward continuation is one of the important methods used to separate gravity anomalies. However, how to quantitatively select an appropriate upward-continuation height has always been a problem in the application of this method. Given this, this paper proposes a curvature analysis method based on the least square method to quantitatively determine a reasonable upward-continuation height. The steps of this method are as follows. Perform upward continuation to different adjacent heights for observation data, and then use the least square method to estimate the least square error of the upward continued value of adjacent heights.There is a maximum curvature in the least square curve of upward-continued values of all adjacent heights.At the point of the maximum curvature, the local anomalies are attenuated to the greatest extent, while the regional anomalies are preserved as far as possible. Therefore, this point can be approximately regarded as the optimal upward-continuation height. As indicated by tests using the data of a theoretical model, the method proposed in this paper can be used to qualitatively determine a suitable upward-continuation height, thus providing an important reference for the selection of upward-continuation height in practical applications.

Keywords： gravity anomaly; analytic continuation; upward-continuation height

PDF (5587KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

孙争, 王俊, 丁鹏, 谭鑫. 一种重力异常向上延拓高度最优化确定方法[J]. 物探与化探, 2023, 47(1): 162-170 doi:10.11720/wtyht.2023.2356

SUN Zheng, WANG Jun, DING Peng, TAN Xin. Amethod for determining the optimal height for upward continuation of gravity anomalies[J]. Geophysical and Geochemical Exploration, 2023, 47(1): 162-170 doi:10.11720/wtyht.2023.2356

0 引言

重力异常是由地下物质密度分布不均匀引起的空间上重力变化,其包含了从地表到深部所有密度不均匀体所引起的重力效应。在实际的重力勘探中,为了研究地球内部特定的地质体,如矿床、地壳内大型构造等,通常需要对重力异常进行深、浅部异常的分离,从而获得由目标地质体引起的重力异常^[1]。

目前,解析延拓法、高次导数法、多项式拟合法、平滑法、匹配滤波法、小波分析法等都是比较成熟的重力异常分离方法^{[2⇓⇓⇓⇓-7]}。其中,解析延拓法是比较常用的方法,该方法具体包括向上延拓和向下延拓,即根据观测平面或剖面上的重力异常值计算高于(或低于)它的某个平面或剖面上异常值,从而突出深部异常或者浅部异常^[8-9]。进行上延计算时,随高度增加,由浅部场源体引起的局部异常衰减速度相较于由深部场源体引起的区域异常衰减速度明显更快^[10-11]。因此,向上延拓更有利于突出深部异常特征^[12-13]。但与此同时,随着上延高度的增加,浅部场源体引起的“高频”异常快速衰减的同时,所研究深部场源体引起的“低频”异常也随之缓慢衰减,即所需要的长波长信息发生了衰减,这将对下一步的处理反演解释造成影响^[14⇓-16]。因此,如何选择一个合适的高度,使延拓后区域重力异常得到分离的同时,局部异常信息也较好保存下来是目前研究所关注的热点^[16]。

针对上述问题,Pawlowski^[17]提出优选延拓法,通过数学推导设计的一种在延拓过程中保留区域重力异常的滤波器,可以有效保留长波信息而减小短波信息。Jacobson^[18]提出以深部场源顶部深度的二倍可以作为最佳向上延拓高度。曾华霖等^[19]提出对相邻高度向上延拓数据进行相关系数分析可以估计最佳向上延拓高度。以上的方法都能够在一定的条件下给出良好的分离效果,但是在深部异常体与浅部异常体埋藏深度较近时分离效果欠佳。本文针对该问题进行研究,提出了一种基于二乘法的曲率分析方法,首先对相邻高度的延拓数据进行二乘计算处理,再对所得结果曲线进行曲率分析得到延拓高度的最佳选取点,并通过模型试验展示了该方法的适用性。

1 方法原理

1.1 理论最佳延拓高度分析

关于重力异常,已知重力异常的向上延拓值随着延拓高度的增加而逐渐衰减,且局部重力异常的衰减速率要快于区域重力异常,那么存在一个延拓高度使区域异常尽可能保留的同时,局部异常衰减的最大,这个高度称为理论最佳延拓高度。而对于如何定义此理论最佳延拓高度,曾华霖等^[19]提出一种基于相关系数的分析方法,对各延拓高度得到的延拓场与理论区域场作相关系数分析,相关系数最大的高度即为理论最佳延拓高度。

相关系数是用以反映变量之间相关关系密切程度的统计指标,是按积差方法计算,同样以两变量与各自平均值的离差为基础,通过两个离差相乘来反映两变量之间相关程度。假设两组数据函数图像形状相似,而数值差别很大,运用相关系数后仍能得到较高的相关度,这是因为相关系数着重于线性的单相关系数,而不能体现两组数据间的误差^[20]。由以上分析可以得知,当深部异常和浅部异常埋藏深度较近时,用相关系数法确定的理论最佳延拓高度未必是理论区域异常与延拓后异常值最相近的值,从而可能得到的分离效果不佳。

本文提出运用二乘误差分析:现有两组二维数据 $A_{m \times n}$ 和 $B_{m \times n}$ ,其维数相同,将两组数据中对应的元素做差再平方求和,如式(1),其结果 $ε$ 越小,说明两组数据之间的误差越小,从而有着更高的相似度。

(1)

ε = \overset{m}{\sum_{i = 0}} \overset{n}{\sum_{j = 0}} (A_{i j} - B_{i j})^{2}

。

对理论区域场与延拓后位场运用二乘法计算出其误差,误差越小代表着延拓后的位场与理论区域场越相近。用此种方法表示出的误差值可以真实地反映数据的相近程度,而不受深部与浅部异常体距离的影响。因此用此方法替代相关系数法,对各高度的延拓场与理论区域场作二乘误差,误差值最小的高度即为理论最佳延拓高度。

1.2 相邻高度延拓值分析

通过理论分析得知,存在一个理论上的最佳延拓高度使得延拓后的位场与理论区域场的误差最小。但在实际应用中,理论区域重力异常是不可知的,我们无法直接通过延拓值与理论值的相关系数得到一个存在极值的曲线,而只能从观测值出发进行分析。

本文通过计算相邻高度的两个重力异常向上延拓值的二乘值来分析:当向上延拓高度小于理论最佳高度时,观测面上区域重力异常的向上延拓值,包含了区域重力异常与局部重力异常上延值之和,由于局部重力异常的向上延拓值会随向上延拓高度的增大而迅速衰减,使得向上延拓异常值会随延拓高度的变化而迅速变化,因而两个相邻高度处重力异常向上延拓值的二乘值与高度的关系曲线在此时具有较大的斜率。

反之,当向上延拓高度大于理论最佳高度时,观测面上区域重力异常的向上延拓值主要只存在区域重力异常。由于区域重力异常的向上延拓值随向上延拓高度增大,有较慢的衰减速度,使得向上延拓异常值随高度的增加而变化较慢,因而该关系曲线在此处具有较小的斜率。因此如何定义这个转折点成为了确定最佳延拓高度的关键。

1.3 离散曲率分析

上述讨论引出如何确定一个转折点来估计最佳延拓高度的问题。这里引入离散点曲率^[21],公式推导如下:

在二维解析情况下曲率公式的标量形式为

(2)

k = \frac{|x ″ y' - x' y ″|}{{[{(x')}^{2} + {(y')}^{2}]}^{3 / 2}}

对于离散的点,使用3个相邻点(x₁,y₁)、(x₂,y₂)、(x₃,y₃)确定的二次曲线的曲率作为(x₂,y₂)处的曲率,设二次曲线的参数方程表达式为:

(3)

\{\begin{array}{l} x = a_{1} + a_{2} t + a_{3} t^{2} \\ y = b_{1} + b_{2} t + b_{3} t^{2} \end{array}

要确定该函数表达式,需要列出6个方程,解出(a₁,a₂,a₃)与(b₁,b₂,b₃)即可。在这里使用2段矢量的长度作为取值范围:

(4)

t_{a} = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}

(5)

t_{b} = \sqrt{(x_{3} - x_{2})^{2} + (y_{3} - y_{2})^{2}}

那么参数方程中的t满足以下条件:

(6)

{(x, y)|}_{t = - t_{a}} = (x_{1}, y_{1})

(7)

{(x, y)|}_{t = 0} = (x_{2}, y_{2})

(8)

{(x, y)|}_{t = t_{b}} = (x_{3}, y_{3})

则有:

(9)

(\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}) = (\begin{array}{l} 1 & - t_{a} & t_{a}^{2} \\ 1 & 0 & 0 \\ 1 & t_{b} & t_{b}^{2} \end{array}) (\begin{array}{l} a_{1} \\ a_{2} \\ a_{3} \end{array})

(10)

(\begin{array}{l} y_{1} \\ y_{2} \\ y_{3} \end{array}) = (\begin{array}{l} 1 & - t_{a} & t_{a}^{2} \\ 1 & 0 & 0 \\ 1 & t_{b} & t_{b}^{2} \end{array}) (\begin{array}{l} b_{1} \\ b_{2} \\ b_{3} \end{array})

由以上矩阵解得(a₁,a₂,a₃)与(b₁,b₂,b₃),就得到了曲线的解析方程,再利用解析方程求曲率,计算变量的导数:

(11)

x' = {\frac{d x}{d t}|}_{t = 0} = a_{2}

(12)

x ″ = {\frac{d^{2} x}{d t^{2}}|}_{t = 0} = 2 a_{3}

(13)

y' = {\frac{d y}{d t}|}_{t = 0} = b_{2}

(14)

y ″ = {\frac{d^{2} y}{d t^{2}}|}_{t = 0} = 2 b_{3}

求得最终离散点的曲率为

(15)

k = \frac{| x ″ y' - x' y ″ |}{{[{(x')}^{2} + {(y')}^{2}]}^{3 / 2}} = \frac{2 (a_{3} b_{2} - a_{2} b_{3})}{(a_{2}^{2} + b_{2}^{2})^{3 / 2}}

对相邻延拓高度得到的曲线进行离散曲率分析,理论上能得到一个曲率的极大值,可将此极大值近似看作最佳延拓高度。

2 模型测试

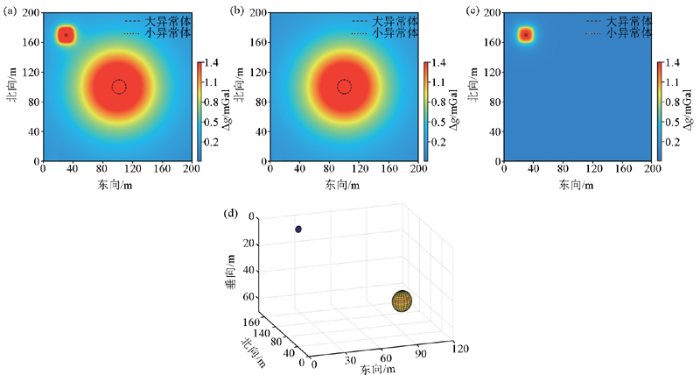
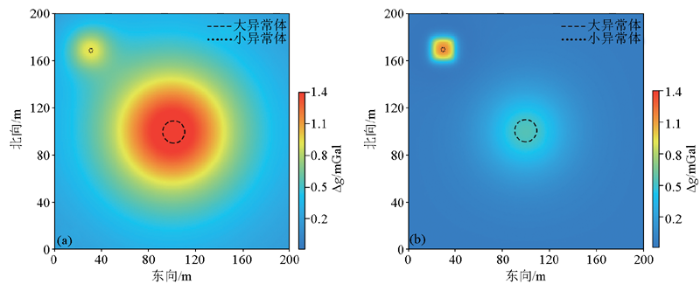
设计密度模型由深浅不同的两球体构成,球体几何及物性参数见表1。区域重力异常及局部重力异常分别由不同埋藏深度的球体引起。球体剩余密度均匀且半径远小于自身埋藏深度,因此可视为点源,但是球体半径没有远小于埋藏深度差,相差尺度不超过一个数量级,因此将模型看作近源模型。观测面位于球体的垂直正上方,观测数据网度为1 m×1 m,共计201个数据点,图1a为由该组合密度模型在观测面所引起的重力异常,图1b和1c分别为由深部及浅部场源体所引起的重力异常,用来模拟叠加异常中的区域异常和局部异常,图1d展示了异常体的空间位置,其中,图1a~c中的虚线展示了2个异常体的水平位置及规模大小,图1d为异常体的空间位置示意图。

表1 球形重力异常体的几何和物性参数

Table 1 Geometric and physical parameters of spherical gravity anomaly

球体	中心坐标	埋藏深度/m	球体半径/m	剩余密度/(g·cm^-3)
A	(101,101)	57	8	0.5
B	(31,171)	9	2.5	0.25

新窗口打开| 下载CSV

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 理论重力异常

a—总场;b—区域场;c—局部场;d—异常体空间位置

Fig.1 Theoretical gravity anomaly

a—total anomaly;b—regional anomaly;c—residual anomaly;d—patial location of the anomaly bodies

2.1 理论最佳延拓高度分析

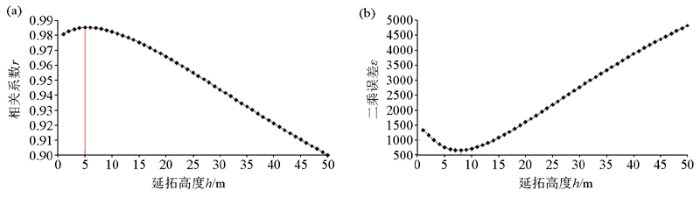
首先对理论重力异常进行以1 m为间隔的从1~50 m高度的向上延拓,并将延拓值与理论区域场进行相关系数的分析,得到相关系数曲线如图2a,从图中可明显看出此曲线先上升后下降并存在一个明显的极大值点,该极大值位置处所对应的高度即为理论最佳延拓高度(5 m)。用相关系数法求得的理论最佳延拓高度点,其意义是延拓后数据形状与延拓前最相似的点,但实际上在形状变化的同时,重力异常值的大小在逐渐减少,因此形状最相似的点未必是数据值大小最接近的点,尤其在这种深部异常体和浅部异常体距离较近的情况下,区域场和局部场衰减的速度趋于一致,局部场难以观察到明显的衰减,此时延拓后形状与理论区域场最相似的高度未必有明确的意义,即在这种情况下理论最佳延拓高度得到的延拓效果并不理想。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 理论最佳延拓高度分析曲线

a—由相关系数法确定的理论最佳延拓高度;b—由二乘法确定的理论最佳延拓高度

Fig.2 Analysis of the theoretical continuation height curves

a—best continuation height determined by the correlation coefficient method;b—best continuation height determined by the proposed method

接着对理论区域场与延拓后位场运用二乘法计算出其误差,误差越小代表着延拓后的位场与理论区域场越相近。用此种方法表示出的误差值可以真实的反映数据的相近程度,而不受深部与浅部异常体距离的影响。

根据上述模型,对观测场进行以1 m为间隔的从1~50 m高度的向上延拓,并将延拓值与理论区域场进行二乘法的计算,得到曲线如图2b。从该曲线可以看出曲线在8 m处存在一个明显的极小值点。

从图2中可以看出,对于两种方法,当向上延拓高度小于最佳高度时,观测面上重力异常的向上延拓值是区域重力异常向上延拓值和局部重力异常向上延拓值之和,由于浅部异常的延拓值随高度增加衰减速度十分快,所以叠加的异常延拓值和区域重力异常越来越接近,从而相关系数越来越大,二乘误差越来越小;而当向上延拓高度到达最佳高度之后,局部重力异常已经经过快速衰减,观测面重力异常的向上延拓值主要是区域重力异常的向上延拓值,随着高度增加,区域重力异常延拓值进一步衰减,观测重力异常延拓值与区域重力异常的相关系数越来越小,二乘误差越来越大。

但由于两种方法的算法不同,导致其极值点即理论最佳延拓高度不同,相关系数法与二乘法得到的理论最佳延拓高度分别为5 m、8 m。现对理论重力异常进行5 m的向上延拓得到图3a,对观测场进行8 m的向上延拓得到延拓后的场如图3b。

图3

新窗口打开| 下载原图ZIP| 生成PPT

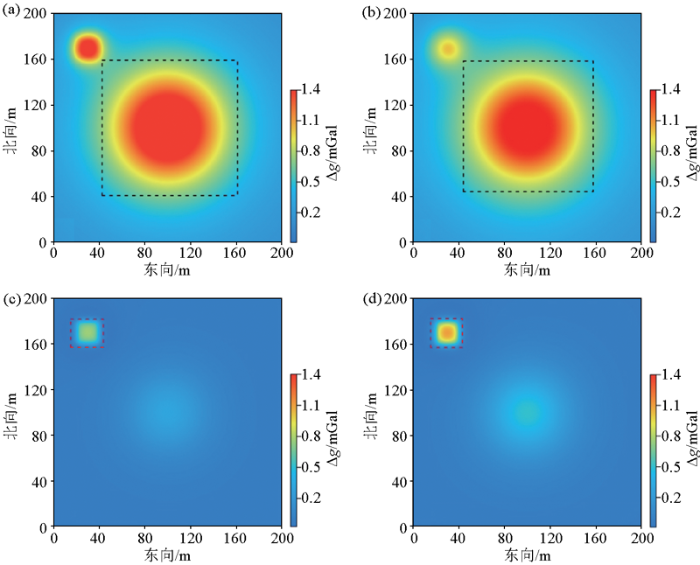
图3 理论最佳延拓高度的延拓场

a—5 m的向上延拓场;b—8 m的向上延拓场;c—5 m的向上延拓剩余场;d—8 m的向上延拓剩余场

Fig.3 The continued anomaly at the best continuation height

a—continued anomaly at 5 m;b—continued anomaly at 8 m;c—residual anomaly at 5 m;d—residual anomaly at 8 m

将图3与图1对比可以看出,由相关系数法得到的延拓场在区域异常部分较为接近理论区域场,但剩余场与理论局部场差异较大。取延拓场的部分(41~161,41~161)即图3黑色虚线框部分,与理论区域场的相应区域计算相对误差,5 m与8 m的延拓分别得到11%和14%的误差;取剩余场的部分(16~46,156~186)即图3红色虚线框部分,与理论局部场的相应区域计算相对误差分别得到47%和18%。对比相对误差可以看出,5 m的延拓虽然在区域异常部分有着略微优势,但在局部异常部分与理论值相差过大,而8 m的延拓使区域和局部异常都得到了与理论值比较接近的值。

从原理角度分析,在这种近源情况下,局部异常与区域异常延拓过程中衰减速度相近,其数据形状在延拓前后是相近的,用相关系数法计算的理论最佳延拓高度没有明确意义,而二乘法得到的理论最佳延拓高度是延拓后与理论区域场在数值上最接近的场,即在尽可能保留区域异常的同时,最大程度减弱了局部异常。因此,二乘法在深部与浅部场源距离较近的情况下分离效果更好。

2.2 相邻高度延拓值二乘曲线分析

由于在实际应用中,理论区域重力异常是不可知的,我们无法直接通过延拓值与理论值的相关系数得到一个存在极值的曲线,而只能从观测值出发进行分析。

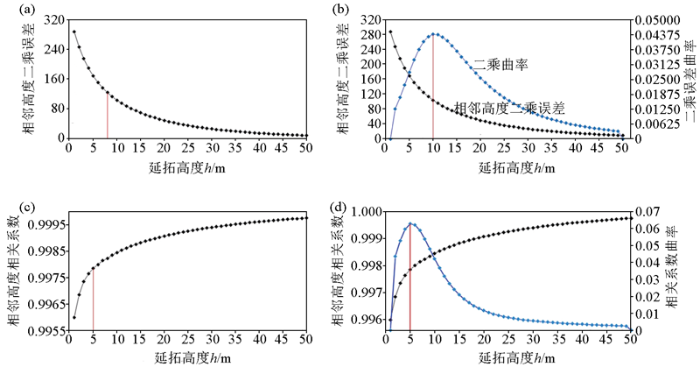
下面通过计算相邻高度的两个重力异常向上延拓值的二乘值来分析。以Δh=1 m为间隔,作从1~50 m向上延拓,并与其高度间隔为Δh的延拓值作二乘计算,得到关系曲线如图4a,红线为模型试验中得到的理论最佳延拓高度。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 相邻高度延拓分析

a—相邻高度延拓值的二乘分析;b—二乘误差离散曲率分析;c—相邻高度延拓值的相关系数分析;d—相关系数离散曲率分析

Fig.4 Adjacent height continuation analysis

a—the square curve of adjacent height;b—discrete curvature of the square curve;c—the correlation coefficient of adjacent height;d—discrete curvature of the correlation coefficient

从图中可以看出曲线形状符合理论分析,当向上延拓高度小于理论最佳高度时,两个相邻高度处重力异常向上延拓值的相关系数与高度的关系曲线在此时具有较大的斜率;当向上延拓高度大于理论最佳高度时,该关系曲线在此处具有较小的斜率。

为了寻找用以估计最佳延拓高度的转折高度,首先将用二乘法得到的相邻高度延拓值曲线做坐标轴等比例变换,使其图像的形状在两轴等比例尺情况下保持相同。再应用此曲率算法处理相邻高度延拓值二乘曲线后得到一个存在极值的曲线见图4b。此极值点即可视为相邻高度二乘误差的转折点,称其为最佳延拓高度。而对比相关系数法图4c得到的相邻高度曲线,应用曲率算法后得到图4d,此方法得到的最佳选取高度为5 m,而在2.1节中已说明以5 m为延拓高度效果不佳,因此在这个模型下,用二乘法的相邻高度求解比相关系数法更具有优势。

以此算法得到的最佳选取高度10 m为延拓高度,对观测场进行延拓,得到图5,其中5a为延拓后的场即求得的区域场,5b为剩余场,可以看出区域异常和局部异常得到了较好的分离,说明此算法是有一定意义的。但此最佳选取高度与理论最佳高度有偏差,这是因为相邻高度延拓值二乘计算得到的曲线,其转折点取决于分离异常在频率上的差异,差异越大,转折点越清晰,但并不是一个绝对准确的转折点,而只是一个由曲率算法确定的模糊转折点,因此最佳选取点与理论最佳高度可能不会完全重合,但会比较接近。因此在实际的延拓过程中,还需要结合具体情况来进一步确定最佳高度^[22]。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 最佳选取高度的延拓场(a)与剩余场(b)

Fig.5 The continued anomaly (a) and the residual field (b) at the optimal continuation height

3 实际资料处理

根据上述模型的分析,二乘曲率法确定最佳延拓高度理论上可行,为进一步验证该方法在实际重力勘探中的效果,应用该方法处理一组实测数据,观察重力异常分析效果。重力异常观测场数据来自吉林省某矿区布格重力异常,数据矢量化来源于文献[1](图6)。

图6

新窗口打开| 下载原图ZIP| 生成PPT

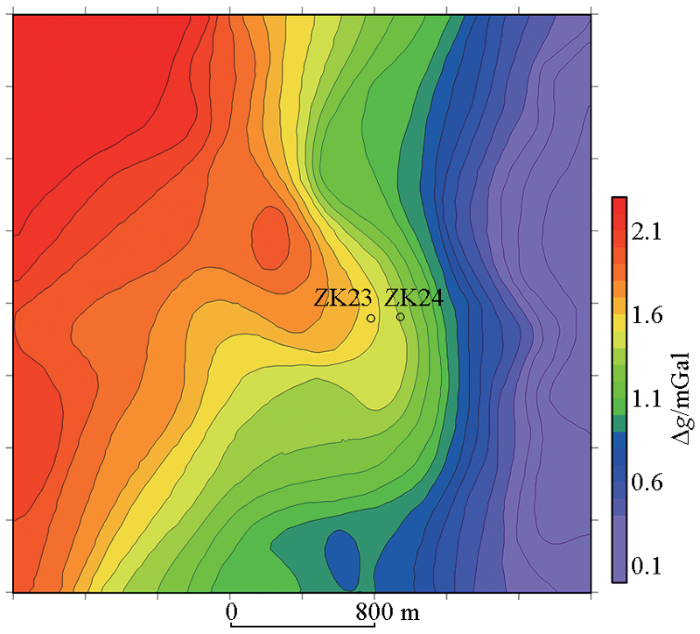
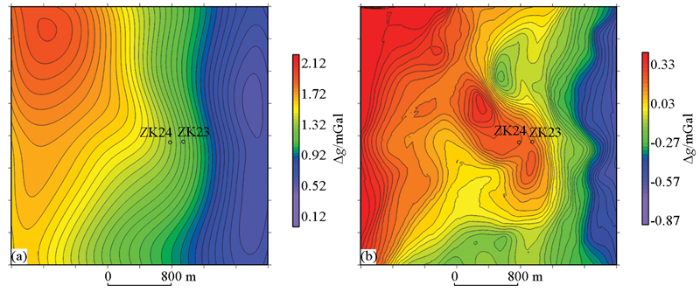
图6 吉林省某矿区布格重力异常

Fig.6 Bouguer gravity anomaly of a mining area of Jilin Province

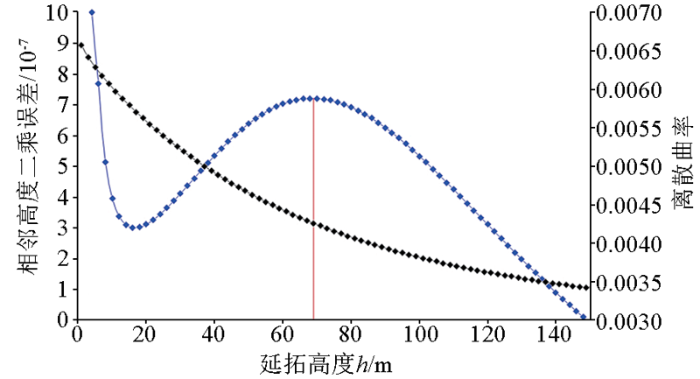
首先结合该地区的地质资料,估算异常体的深度范围,对观测场进行从1~150 m的向上延拓,间隔高度为1 m。将每个延拓高度与其相邻高度的延拓值作二乘误差计算,得到关系曲线如图7,可以看出随着延拓高度的增加,相邻高度延拓值的二乘误差越来越小,符合理论模型。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 延拓高度分析曲线

Fig.7 Continuation height analysis curve

对上述计算得到的关系曲线进行离散曲率计算,得到关系曲线如图7,观察到曲线在68 m附近存在一个极大值,也符合理论模型试验的结果,即在68 m左右的延拓高度可以使区域场尽可能的保留而最大程度地减小局部场的影响。

根据曲率关系曲线最大点确定选取点的范围,对28、48、68、88 m的高度进行延拓如图8。为消除浅部干扰,突出图中的区域异常,向上做了 28 m延拓之后,重力异常等值线存在少量的浅层干扰,包括一些可能由浅部异常引起的极小型圈闭,当延拓距离增大到68 m时,极小圈闭消失,浅部干扰已经得到了很好的压制^[22],故选择68 m为最佳延拓高度选取点。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 以h为延拓高度的延拓场

Fig.8 Continued anomaly at the height of h

以68 m为延拓高度后的向上延拓场和局部场如图9,可以看出区域场和局部场得到了很好的分离效果。图9b虚线内为已知矿点,位于应用该算法得到的剩余场的高异常处,满足理论要求。因此该延拓高度得到的剩余场可看作局部异常场,从而进一步用于找矿或构造等。

图9

新窗口打开| 下载原图ZIP| 生成PPT

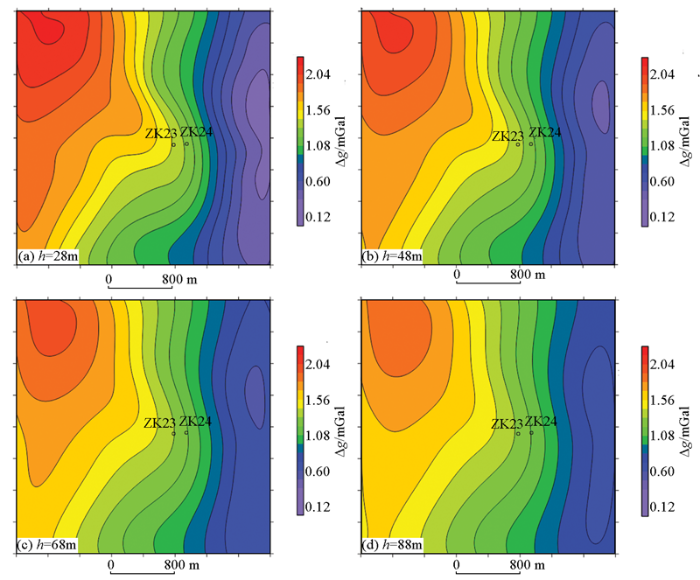
图9 最佳选取高度得到的延拓场(a)和剩余场(b)

Fig.9 The continued anomaly (a) and the residual anomaly (b) at the optimal continuation height

4 结论与建议

本研究提出一种用以确定最佳延拓高度使得向上延拓分离深部重力异常效果最佳的方法,通过对理论模型的试验,验证了所提出的分析方法可以在深部异常体与浅部异常体埋藏深度较近时也可得到较好的分离效果。

通过模型试验可以看出,此方法给出的最佳延拓高度与理论最佳延拓高度并不完全重合,在实际的问题中,此算法只能给出一个最佳选取点的模糊范围。在最佳选取高度附近进行延拓,得到延拓后重力异常等值线图,观察等值线的分布,当等值线较为平滑、无非正常陡变,由于浅部干扰引起的极小圈闭基本消失时,浅部干扰得到很好的压制,此时对应的延拓高度可以作为分离效果最好的高度。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

曾华霖.

重力场与重力勘探[M]. 北京: 地质出版社, 2005.

[本文引用: 2]

Zeng

H L

Gravity field and gravity exploration[M]. Beijing: Geological Publishing House, 2005.

[本文引用: 2]

[2]

曾华霖.

重力梯度测量的现状及复兴

[J]. 物探与化探, 1999, 23(1):1-6.