航磁测量系统的外符合精度评估

doi:10.11720/wtyht.2023.2682

航磁测量系统的外符合精度评估

王云鹏^,¹^,², 刘晓刚^,¹^,², 邱雪峰³, 宋颖¹^,²

1.地理信息工程国家重点实验室,陕西西安 710054

2.西安测绘研究所,陕西西安 710054

3.61365部队,天津 300140

Evaluation of the external coincidence precision of the aeromagnetic survey system

WANG Yun-Peng^,¹^,², LIU Xiao-Gang^,¹^,², QIU Xue-Feng³, SONG Ying¹^,²

1. State Key Laboratory of Geo-Information Engineering, Xi'an 710054, China

2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China

3. Unit 61365, Tianjin 300140, China

通讯作者: 刘晓刚(1983-),男,博士,副研究员,主要从事地球重磁场探测技术及数据处理工作。Email:liuxiaogang_1949@163.com

责任编辑: 王萌

收稿日期: 2021-12-20 修回日期: 2022-04-3

基金资助:

国家自然科学基金(42174001)
国家自然科学基金(41774018)
国防科技基础加强计划技术领域基金项目(2022-JCJQJJ-0519)
地理信息工程国家重点实验室开放研究基金(SKLGIE2021-ZZ-4)

Received: 2021-12-20 Revised: 2022-04-3

作者简介 About authors

王云鹏(1986-),男,硕士,助理研究员,主要从事地球重磁场探测技术及数据处理工作。Email:wangyp1813@163.com

摘要

航磁测量系统的精度评估是磁测工作的一个重要内容。在内蒙古某测区开展了飞行实验,获得了航空和地面磁力测量数据,利用插值—迭代法和等效源法,将地面高精度磁力测量数据延拓到空中,通过与航空磁测数据进行比较,完成了航磁测量系统的外符合精度评估。两种延拓方法的精度评估结果均优于5 nT,真实反映了航磁测量系统的实际精度水平。本文研究方法不仅可以为航磁测量系统的外符合精度评估提供参考,也可以应用于新研航空磁力仪的尺度因子、偏差等参数的在线标定。

关键词： 航磁测量系统; 地面磁测; 精度评估; 插值—迭代法; 等效源法; 向上延拓

Abstract

The precision evaluation of an aeromagnetic survey system is an important part of a magnetic survey. This study obtained airborne and ground magnetic data through flight experiments in a certain survey area of Inner Mongolia. Then, the high-precision ground magnetic survey data was upward-continued to the height of the flight course using the interpolation-iteration and equivalent source methods. Finally, the external coincidence precision of the aeromagnetic survey system was evaluated by comparison with the aeromagnetic survey data. The precision evaluation results of the two continuation methods are better than 5 nT, reflecting the actual precision level of the aeromagnetic survey system. Therefore, the research methods in this study can provide references for the evaluation of the external coincidence precision of an aeromagnetic survey system and can also be used for online calibration of the scale factor, deviation, and other parameters of newly developed aerial magnetometers.

Keywords： aeromagnetic survey system; ground magnetic survey; precision evaluation; interpolation-iteration method; equivalent source method; upward continuation

PDF (3728KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王云鹏, 刘晓刚, 邱雪峰, 宋颖. 航磁测量系统的外符合精度评估[J]. 物探与化探, 2023, 47(1): 129-134 doi:10.11720/wtyht.2023.2682

WANG Yun-Peng, LIU Xiao-Gang, QIU Xue-Feng, SONG Ying. Evaluation of the external coincidence precision of the aeromagnetic survey system[J]. Geophysical and Geochemical Exploration, 2023, 47(1): 129-134 doi:10.11720/wtyht.2023.2682

0 引言

航磁测量系统能够快速获取区域地磁场信息,具有工作效率高、受地形限制少等优点,目前已广泛应用于矿产勘探、地磁导航等诸多领域。航磁测量系统在投入生产作业前需要评估其性能指标是否满足要求,通常采用重复测线或交叉点不符值进行内符合精度评估^[1],采用位场延拓方法进行外符合精度评估^[2]。

插值—迭代法和等效源法适用于曲面位场延拓,能够消除观测面起伏对延拓结果的影响,进而得到更加可靠的评估结果,因此,本文采用这2种方法进行航磁测量系统的外符合精度评估。徐世浙院士^[3]提出的积分—迭代法能够实现位场大距离延拓,延拓精度较好,但该方法一般只能用来处理小面积数据,实用性受到限制。空间域迭代法是在积分—迭代法的基础上提出来的,延拓效果显著优于快速傅里叶变换法(FFT)^[4]。插值—迭代法将空间域迭代法应用于曲面位场数据处理,向下延拓深度可达资料点距的10~20倍^[5]。插值—迭代法的理论基础是Poisson积分方程,而等效源法则是通过构建一组简单的场源体,简化了位场数据处理过程,是一种简洁、有效的重磁数据处理方法^[6]。等效源法应用过程中,许多学者基于Dampney的思想将等效源设计成单层模型^[7⇓⇓-10],相对于单层模型,多层模型更能保证位场延拓的精度^[11⇓-13]。从前人的研究成果可以看出,插值—迭代法和等效源法均得到了深入研究,理论完善,应用效果好。

本文利用插值—迭代法和等效源法,将内蒙古某测区地面磁力测量数据延拓到空中,通过与航空磁测数据进行比较,完成了航磁测量系统的外符合精度评估。

1 数据采集和处理方法

1.1 数据采集

本文使用的实测数据来自内蒙古某测区,实验区范围为14.3 km×11.0 km,地面高程(大地高)范围为0.97~1.07 km,实际飞行高度约190~260 m,SW向测线间隔约500 m,SN向测线间隔约250 m。航磁测量系统采用CS-3型铯光泵磁力仪,绝对精度优于2.5 nT,数据采样率设置为10 Hz;地面磁力测量采用GSM-19T型质子磁力仪,绝对精度优于0.1 nT,数据采样间隔设置为3 s。日变站位于实验区中心,地磁日变基值为56 867.95 nT。

1.2 处理方法

1.2.1 插值—迭代法

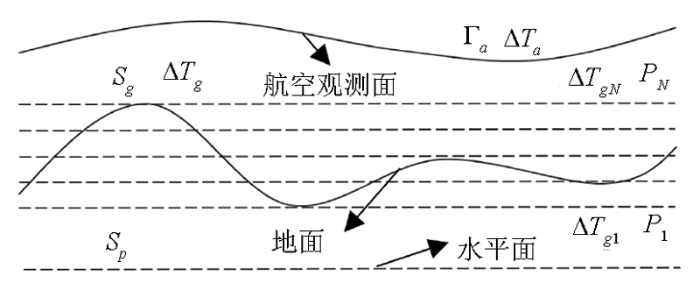
直角坐标系3个轴x、y、z的正向分别指向地理北、地理东和垂直向下, $(x, y, z)$ 为平面直角坐标。用 $Δ T (x, y, 0)$ 表示平面 $z = 0$ 的磁异常, $Δ T (x, y, h)$ 表示平面 $z = - h$ ( $h$ 为向上延拓的高度)的磁异常。两平面之间磁异常的FFT向上延拓公式为

(1)

Δ T (x, y, h) = F^{- 1} [e^{- h \sqrt{k_{x}^{2} + k_{y}^{2}}} S_{Δ T} (k_{x}, k_{y}, 0)]

式中: $F^{- 1}$ 为傅里叶反变换; $S_{Δ T} (k_{x}, k_{y}, 0)$ 为 $Δ T (x, y, 0)$ 的傅里叶变换; $k_{x}$ 、 $k_{y}$ 为 $x$ 、 $y$ 方向的波数。

图1中, $Δ T_{g}$ 是地面 $S_{g}$ 上的实测磁异常, $Δ T_{a}$ 是飞行测线 $Γ_{a}$ 上的待求磁异常, $S_{p}$ 是位于地面下方的水平面。利用插值—迭代法^[5,14]将磁异常从地面延拓到飞行测线的步骤如下:

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 插值—迭代法向上延拓示意

Fig.1 Diagram of upward continuation by interpolation-iteration method

第1步:将 $S_{g}$ 上的磁异常 $Δ T_{g}$ 垂直放置到 $S_{p}$ 上,作为 $S_{p}$ 上的初值;

第2步:用若干个水平面 $P_{1}, P_{2}, \dots, P_{N}$ 切割 $S_{g}$ (通常取4~6个);

第3步:用FFT法将 $S_{p}$ 上的磁异常分别延拓到这些水平面上,得到 $Δ T_{g 1}, Δ T_{g 2}, \dots, Δ T_{g N}$ ;

第4步:沿高程方向,用样条函数法插值得到 $S_{g}$ 上的磁异常计算值,与实测值做差,利用差值对 $S_{p}$ 上的磁异常进行加权改正^[3⇓-5];

第5步:重复第3步和第4步,直到 $S_{g}$ 上磁异常差值小到可以忽略为止;

第6步:利用第2步和第3步的方法,将 $S_{p}$ 上的磁异常向上延拓到 $Γ_{a}$ 的切割面(通常取4~8个)上,用三元Lagrange插值法^[15]逐点计算飞行测线上的磁异常 $Δ T_{a}$ 。

1.2.2 等效源法

在场源真实磁化方向未知的情况下,等效源磁化方向通常选择与现今地磁场磁化方向一致^[16]。此时,基于磁异常的磁偶极子模型为

(2)

\overset{n}{\sum_{i = 1}} a_{i j} m_{i} = Δ T_{j} (j = 1, \dots, n)

a_{i j} = \frac{μ_{0}}{4 π r_{i j}^{3}} [3 (L_{0} L_{1} + M_{0} M_{1} + N_{0} N_{1})^{2} - 1]

L_{1} = \frac{x_{j} - ξ_{i}}{r_{i j}}

M_{1} = \frac{y_{j} - η_{i}}{r_{i j}}

N_{1} = \frac{z_{j} - ζ_{i}}{r_{i j}}

r_{i j} = \sqrt{(x_{j} - ξ_{i})^{2} + (y_{j} - η_{i})^{2} + (z_{j} - ζ_{i})^{2}}

式中: $μ_{0}$ 为导磁系数; $L_{0}$ 、 $M_{0}$ 、 $N_{0}$ 为正常场 $T_{0}$ 的方向余弦; $(ξ_{i}, η_{i}, ζ_{i})$ 为磁偶极子的坐标, $(x_{j}, y_{j}, z_{j})$ 为观测点的坐标; $r_{i j}$ 为磁偶极子与观测点之间的距离; $m_{i}$ 为第 $i$ 个磁偶极子的磁化强度; $Δ T_{j}$ 为第 $j$ 个观测点的磁异常; $n$ 为磁偶极子数(与观测点个数相同)。

本文采用三层等效源模型,由深至浅逐层解算磁偶极子的磁化强度^[13]。利用等效源法将磁异常从地面延拓到飞行测线的步骤如下:

第1步:设置磁偶极子的水平位置和埋深;

第2步:利用地面磁异常,通过逐层反演得到磁偶极子的磁化强度;

第3步:用反演得到的磁偶极子模型,采用式(2)计算飞行测线上的磁异常。

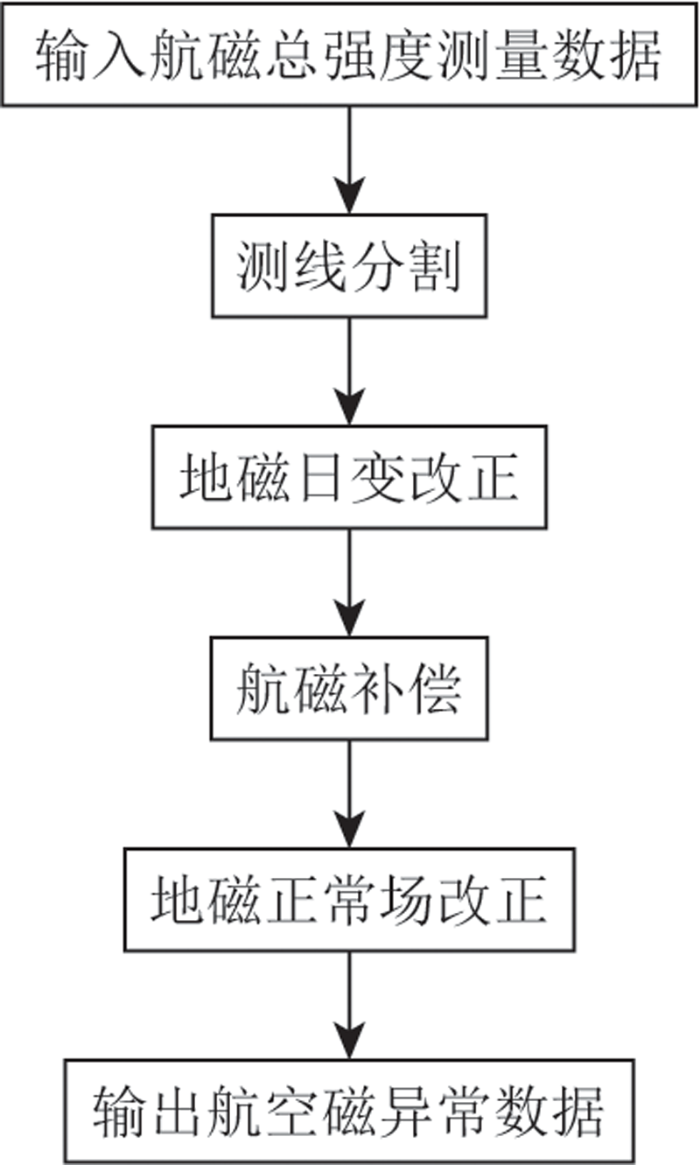
2 资料处理流程

数据处理对于航磁资料的应用至关重要,处理方法和计算流程直接影响航磁数据成果的质量。本文航磁测量数据的处理内容包括测线分割、地磁日变改正、航磁补偿、地磁正常场改正等,处理流程如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 航磁测量数据处理流程

Fig.2 Flow diagram of aeromagnetic survey data processing

2.1 测线分割

测线分割能够去除多余观测数据,提取与设计测线相对应的实际测线,便于飞行质量评价和后续数据处理。计算步骤为:首先,去除实验区外部多余观测数据;然后,根据设计测线坐标提取实际测线(以实际测线与设计测线的平均距离小于某一给定值D作为提取标准,本次飞行试验中D取50 m),同时对提取的测线进行编号。

以实际测线与设计测线的水平和垂直偏差为评价标准,利用测线分割后的数据对交叉测线飞行质量进行评价,评价结果见表1。

表1 交叉测线飞行质量评价

Table 1 Flight quality evaluation of cross-line

	最小值/ m	最大值/ m	平均值/ m	标准差/ m	均方根误差/m
水平偏差	-59.29	73.31	1.06	13.28	15.49
垂直偏差	-17.76	13.73	0.06	2.03	3.80

新窗口打开| 下载CSV

由表1可以看出,本次试验的飞行质量较好,实际测线与设计测线水平偏差(均方根误差)为15.49 m,垂直偏差为3.8 m,达到了此次航磁测量的要求。

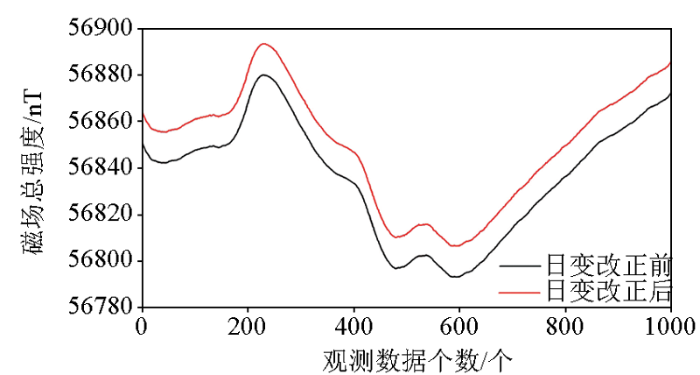
2.2 地磁日变改正

地磁日变改正的主要目的是消除周日变化和短周期扰动等变化磁场的影响,从而得到稳定磁场^{[17⇓⇓-20]}。本文采用的计算步骤为:首先,利用日变站观测数据和地磁日变基值计算得到日变站地磁日变改正值;然后,通过时差(地方时)改正得到测量点的日变改正值。以一条SN向测线为例,日变改正效果如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 日变改正前后对比

Fig.3 Comparison before and after diurnal variation correction

由图3可以看出,地磁日变改正的最大值可达十几nT。因此,为了得到高质量的航磁测量数据,必须进行地磁日变改正。

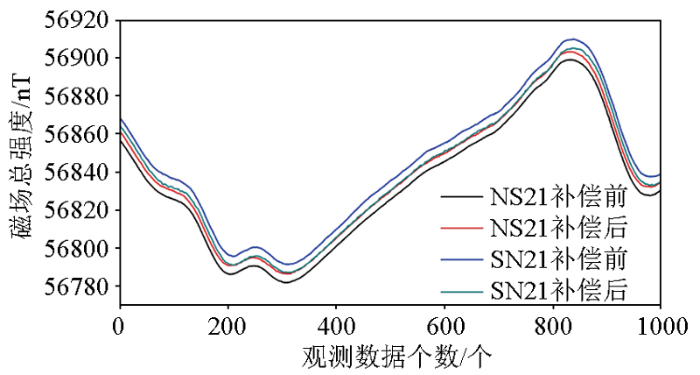
2.3 航磁补偿

对于航空磁力测量来说,飞机本身就是一个复杂的干扰体,飞机上的磁性物体、电子元件产生的干扰磁场会对磁力仪产生很大的磁干扰,因而必须补偿这部分干扰磁场的影响。本文采用Tolles-Lawson方程(简称T-L方程)进行航磁补偿^[21-22],以2条重复测线NS21和SN21为例(飞行方向分别为从N到S和从S到N),航磁补偿效果如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 航磁补偿前后对比

Fig.4 Comparison before and after aeromagnetic compensation

由图4可以看出,补偿前NS21和SN21的磁场数据存在明显的系统差,补偿后系统差基本被消除。可见,航磁补偿能够消除飞机干扰磁场的影响,显著改善观测数据的质量。

2.4 地磁正常场改正

为了在精度评估过程中消除背景场的影响,提高向上延拓精度,需要进行地磁正常场改正。国际地磁参考场模型IGRF能够较好地表示地磁场的分布特点。因此,本文采用IGRF对航磁测量数据进行地磁正常场改正。计算步骤为:首先,利用IGRF-13计算观测点正常场T₀;然后,从总强度数据中减去T₀,得到航空磁异常^[23]。

3 处理结果分析

采用插值—迭代法和等效源法对地面磁异常进行向上延拓,构建航线上的磁力参考值,从而实现航磁测量系统的外符合精度评估。插值—迭代法的计算步骤为:①根据飞行测线的切割面构建空间三维格网(切割面个数为8,相邻面高差为10 m);②将地面磁异常向上延拓到航空切割面(位于地面下方的水平面高度取0.9 km);③利用三元Lagrange插值法逐点计算飞行测线上的磁异常(插值多项式阶数取3)。利用等效源法向上延拓时,采用的磁倾角为50°、磁偏角为5°(利用IGRF-13计算得到)。三层等效源模型均水平分布,第一层等效源与地面观测点在垂直方向上一一对应,共2 610(58×45)个格网点,格网分辨率为250 m×250 m,埋深750 m(相对于地形平均高度面,下同);第二层等效源分布区域中心与实验区中心重合,共208(16×13)个格网点,格网分辨率为1 km×1 km,埋深为2.25 km;第三层等效源分布区域中心位置同样为实验区中心,共30(6×5)个格网点,格网分辨率为4 km×4 km,埋深为9 km。

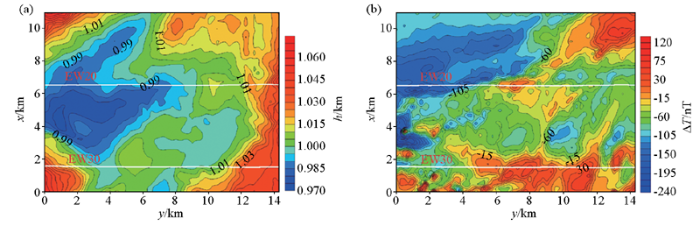
同样,采用IGRF-13对地面磁力测量数据进行地磁正常场改正,然后,利用克里金方法进行网格化处理,形成2 610(58×45)个格网点,格网分辨率为250 m×250 m。地面高程及磁异常如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 地面高程(a)及磁异常(b)

Fig.5 Ground elevation (a) and magnetic anomaly (b)

由图5可以看出,实验区磁场信息非常丰富,既有区域异常,又有局部异常,既有高磁异常,又有低磁异常,磁异常低值区位于实验区西北角,高值区位于东北角及南部边界。在飞行数据中选取2条测线EW20和EW30(平面位置如图5所示),分别进行外符合精度评估,原始观测剖面(已经过各项改正)及向上延拓结果如图6和图7所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

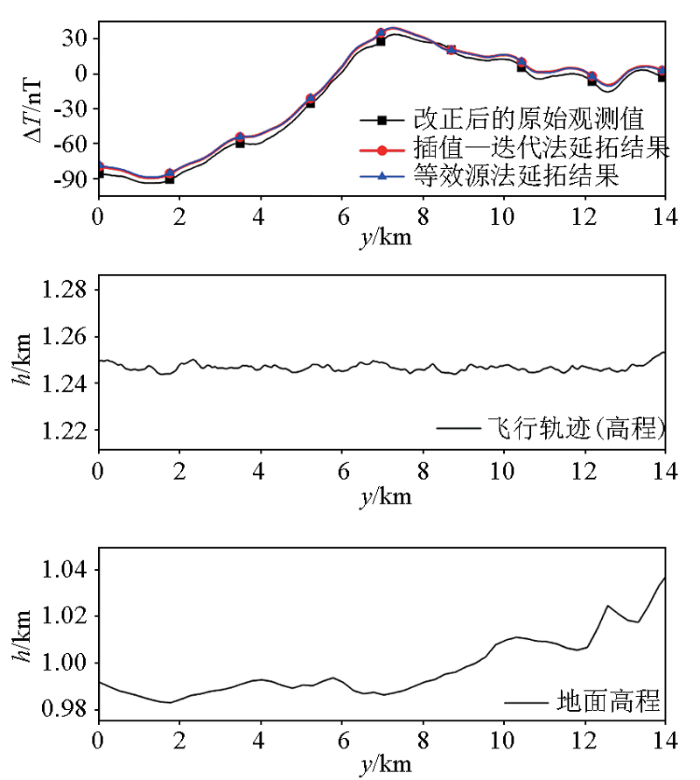
图6 EW20原始观测剖面及向上延拓结果

Fig.6 Original observation profile of EW20 and upward continuation results

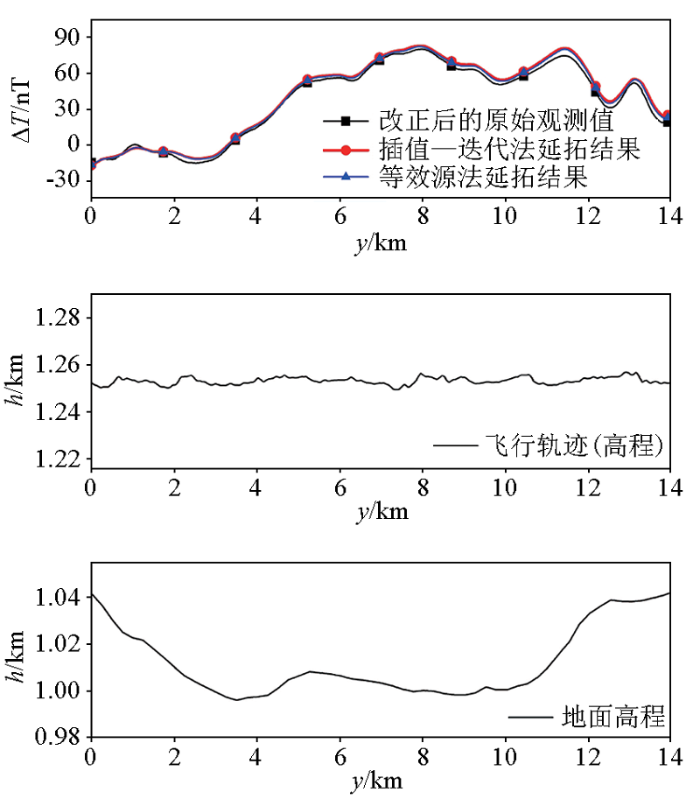
图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 EW30原始观测剖面及向上延拓结果

Fig.7 Original observation profile of EW30 and upward continuation results

由图6和图7可以看出,2种评估方法的延拓曲线几乎重合,且与原始观测剖面的差异较小。利用插值—迭代法对EW20测线的评估结果为:均方根误差4.81 nT,平均相对误差13.32%;对EW30测线的评估结果为:均方根误差3.92 nT,平均相对误差14.54%。利用等效源法对EW20测线的评估结果为:均方根误差4.85 nT,平均相对误差13.43%;对EW30测线的评估结果为:均方根误差2.91 nT,平均相对误差10.79%。实验区所有飞行测线的外符合精度评估结果(航磁数据与向上延拓结果做差)如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

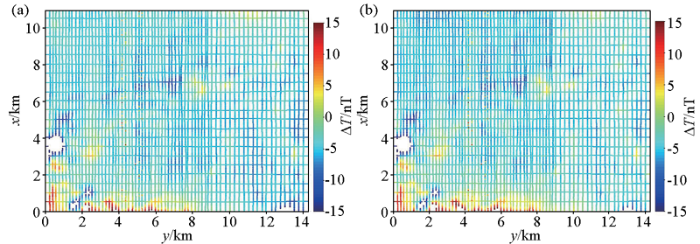
图8 外符合精度插值—迭代法(a)和等效源法(b)的评估结果

Fig.8 The evaluation results of interpolation-iteration method (a) and eauivalent source method (b) of external coincidence precision evaluation

由于实验区边界位置存在高磁局部异常(图5b),边界效应对向上延拓的影响较大。因此,精度评估前,首先需要剔除粗差(3倍均方根准则)。表2给出了剔除粗差后的外符合精度评估结果。

表2 外符合精度评估结果

Table 2 The results external coincidence precision evaluation

评估方法	统计值
评估方法	最大值/nT	最小值/nT	平均值/nT	标准差/nT	均方根误差/nT	平均相对误差/%
插值—迭代法	14.91	-14.87	4.21	2.65	4.98	13.88
等效源法	14.79	-14.74	4.07	2.78	4.93	13.76

新窗口打开| 下载CSV

由表2可以看出:①插值—迭代法和等效源法对航磁测量系统的外符合精度评估结果很接近,说明两种方法应用的有效性,且均能反映测量数据的实际情况;②剔除粗差后,两种方法确定的航磁测量系统外符合精度优于5 nT。

4 结论

本文利用插值—迭代法和等效源法,对内蒙古某测区的航磁测量数据进行了精度评估,得到以下研究结论:

1)插值—迭代法和等效源法均能用于航磁测量系统的外符合精度评估,评估结果真实、可靠。

2)本文对插值—迭代法进行了改进,能够将地面格网数据延拓到飞行测线,实现航磁测量系统的外符合精度评估。

3)文中给出的磁偶极子等效源模型,算法简单,计算量小,具有一定的应用价值,值得推广使用。

4)在航磁补偿时,本文仅对飞机产生的干扰磁场进行了补偿,未全面考虑其他干扰源的影响,后续工作中将进一步深入开展这方面的研究工作。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

刘晓刚, 姬剑锋, 管斌, 等.

基于重复测线不符值的航空磁力矢量仪飞行试验数据精度评估

[J]. 地球物理学进展, 2020, 35(2):433-437.