0 引言
随机噪声压制是地震信号处理的常规环节之一,虽然业内已经提出了众多的去噪算法,但同时实现最大程度压制随机噪声和最小程度损害有效信号依然是地球物理学界的一个开放问题[4]。已有的随机噪声压制算法可以归纳为5类:①预测滤波算法,利用了信号空间方向具有可预测性,主要包括f-x域反褶积[6]、f-x EMD预测滤波[7]、t-x域预测滤波[8]等方法。这类算法的优点是同时处理多道信号,能够有效利用信号的道间相干性,有效压制随机噪声,缺点是容易损害有效信号,尤其是陡倾同相轴。②基于信号分解的去噪算法,将含噪声信号分解为不同分量,舍弃噪声能量占主导的分量实现噪声压制;常用的分解算法主要有经验模态分解(empirical mode decomposition, EMD)[7,9-10]和变分模态分解(variational mode decomposition,VMD)[11]2类。③基于稀疏变换的去噪算法,基于地震信号可以在变换域中被压缩表示,有效信号表现为高幅度系数,而随机噪声为低幅度系数,采用阈值函数就能实现噪声衰减;常用的变换算法包括Fourier和短时Fourier变换[12]、S和广义S变换[13]、wavelet变换[14]、curvelet变换[15]和稀疏表示[16]等。④基于低秩方法的去噪算法,这类方法对地震信号作时频分析或Hankel变换后,假设纯净完整的地震数据具有低秩特征,而混叠噪声和缺失地震道会使数据的秩增加;主要包括矩阵低秩方法[4,12,17]和高维张量低秩去噪[18-19]2类,其缺点是矩阵低秩方法本质是单道去噪不能有效利用信号的道间相干性,而高维去噪算法计算复杂度过高。⑤基于深度学习的去噪方法,利用卷积神经网络(convolutional neural network, CNN)[20⇓⇓-23]、自编程机(Autoencoders)[24]或生成对抗网络(generative adversarial networks, GAN)[25]等网络结构实现随机噪声压制,但深度神经网络依赖大量带标签的训练样本,限制了深度学习去噪算法的广泛应用。
结合多类方法构造合成去噪算法是近年来随机噪声压制领域的热点研究方向,尤其是稀疏变换与f-x域算法和低秩、降秩算法的结合,其目的是结合2类算法的优势,克服各自算法缺陷或假设条件。合成去噪算法主要包括:①结合f-x域算法与信号稀疏变换,如混合时频分析技术[13]能够同时压制随机噪声和陡倾相干噪声;②结合f-x域算法与信号分解算法,如f-x EMD[9]、f-x VMD[11]和f-x EMD预测滤波[7]克服了f-x域算法的平稳信号假设条件;③结合f-x域算法与低秩算法,如Hankel低秩近似[26]能够有效利用地震信号的f-x域特征,提高算法去噪能力;④结合信号分解和低秩算法,如经验低秩近似算法[27]通过EMD将地震信号分解为若干低秩分量,避免了低秩近似算法的小分析窗要求;⑤结合稀疏分解和低秩算法,如地震信号的时频谱具有低秩特征,时频域低秩矩阵近似[4,12,17]能够结合时频分析和低秩矩阵近似2种算法优势,提高去噪能力。
低秩矩阵算法主要包括低秩稀疏分解(low-rank and sparse decomposition)和低秩近似(low-rank matrix approximation)。其中,低秩矩阵近似一般采用核范数正则化项,利用奇异值阈值(singular value thresholding, SVT)实现快速求解[28]。但SVT不能准确估算矩阵的非零奇异值,而采用非凸正则项能够提高奇异值估算的准确性[29⇓-31]。常用的非凸惩罚函数包括加权核范数[32]、Transformed Schatten-1[33]和p范数[31]3种。引入非凸正则化的缺点是低秩矩阵近似问题的目标函数变为非凸函数,难以优化,且受局部最小值干扰。Ankit和Selesnick[29]提出合理构造非凸正则项,同时保证目标函数为严格的凸函数。
共偏移距道集具有平缓(甚至近似水平)的同相轴结构,满足f-x域去噪线性同相轴假设前提。结合f-x域去噪、时频分析和非凸正则化低秩矩阵近似这3种算法的优势,提出基于f-x域时频低秩矩阵近似的共偏移距道集去噪方法。该方法能够同时克服f-x域去噪的平稳信号假设和时频域稀疏低秩去噪算法难以利用信号的道间相干性这2种缺陷,同时利用多元回归理论对噪声标准差进行估计,估算出最佳的奇异值阈值。通过数值模拟和实际地震资料试算验证,所提方法能够有效压制地震随机噪声,同时保持有效信号不受损害。
1 方法原理
1.1 共偏移距道集f-x域去噪
假设地震数据中混叠随机噪声,将有效信号和随机噪声分别记为
式中:t和x分别表示时间坐标和偏移距。进一步假设地震信号由单个线性同相轴构成:
式中:
式中:f和ω分别为频率和角频率,
由式(1)~(3)可知,t-x域线性同相轴映射为f-x域中的复谐波,且t-x域中地震信号为有效信号s和随机噪声n的叠加,这种加性关系在f-x域仍然成立。因此,对于t-x域中单一线性同相轴模型,f-x域中有效信号表现为规则谐波震荡,而随机噪声则被映射为高波数随机震荡。通过将信号变换到f-x域,能够增加信号和噪声的分布差异。类似地,当地震信号由p个线性同相轴组成时,由Fourier变换的线性性质可知,f-x域中地震信号表现为p个谐波的叠加,因此,对每一单频分量做滤波处理就能够分离地震噪声。
传统的f-x域去噪处理共炮点道集或共中心点(common mid-point, CMP)道集,而这2种道集中反射波为双曲线同相轴,直达波、折射波和面波为倾斜同相轴,倾角各不相同,且面波存在频散特征。因此,共炮点道集和CMP道集均不满足f-x域去噪假设前提,直接采用f-x域去噪会损害倾斜(尤其是陡倾)同相轴。而共偏移距道集具有平缓甚至接近水平的同相轴结构,基本满足f-x域去噪的线性同相轴假设前提。因此,在共偏移距道集中执行f-x域去噪,其去噪能力和有效信号保持能力必然会提高。
1.2 f-x域时频低秩矩阵近似去噪方法
上述推导过程建立在固定子波和线性同相轴基础上,假设地震信号为稳定信号。但实际介质为非均匀各向异性粘弹性介质,地震子波随能量传播而变化,因而,地震信号不能被视为平稳信号,要求引入非平稳信号分析方法处理每一单频分量。
时频分析能够从时间和频率2个维度对非平稳信号的变化特征进行度量。常用的时频分析方法主要有短时Fourier变换、广义S变换、wavelet变换和Wigner-Ville分布等。其中,Wigner-Ville分布为chen类分布,虽具有高时频分辨率的优点,但受交叉项干扰,在地震信号分析处理领域应用较少。短时Fourier变换、广义S变换和wavelet变换为线性时频分析方法,受测不准原理制约,不能同时实现最佳的时间分辨率和频率分辨率,但这类方法不受交叉项干扰,并且具有较高的计算效率,在地球物理学领域广泛应用。其中尤以广义S变换同时兼具较好的时频分辨率,且可以借助快速Fourier变换高效实现,本研究中将其用于分解f-x域中的每一单频分量。
由于f-x域中地震信号为谐波的叠加,因此,记f-x域中某一单频分量为
f-x域时频低秩矩阵近似去噪方法的计算流程为:①由共炮点道集或CMP道集抽取共偏移距道集;②逐道作Fourier变换,将共偏移距道集变换到f-x域;③对f-x域中每一单频分量
1.3 非凸正则化低秩矩阵近似
低秩矩阵近似的目的是从含噪声矩阵Y中估计纯净的低秩矩阵X:
式中:N为噪声矩阵,R为实数集,m和n分别为矩阵的行、列数。低秩矩阵近似是一个欠定的逆问题,需要引入正则化项φ(·)对解空间进行约束:
式中:k=min(m,n);σi(X)为矩阵X的第i个奇异值;λ为正则项参数,用于平衡目标函数中拟合项和正则化项;a≥0为非负参数,控制正则化项的非凸程度;矩阵Y的Frobenius范数定义为
当φ(x)=
φ(·)的临近算子(proximal operator)定义为
当按照式(6)、式(7)取值时,最优化问题(式(5))存在唯一的全局最优解:
式中:Y=UΣVT为Y的奇异值分解(singular value decomposition, SVD);a取0≤a<1/λ。
1.4 噪声估计和最佳奇异值阈值
噪声标准差σ可以通过多元回归理论(multiple regression theory)进行估计。定义
式中:
估算噪声为
计算
2 数值模拟
2.1 核范数正则化与非凸正则化对比
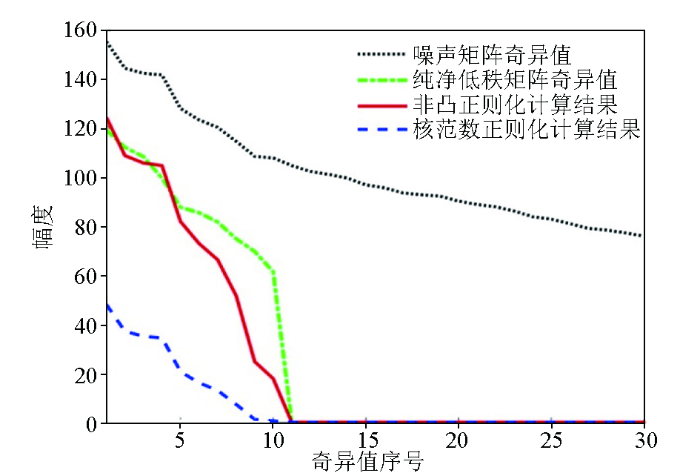
通过数值模拟对比核范数正则化与非凸正则化。实验首先生成2个零均值单位方差的Gaussian独立同分布(i.i.d.Gaussian distribution)随机矩阵L100×10和R10×100,然后生成低秩矩阵Y0=LRT。向Y0中混入σ=6的随机噪声,对比传统低秩矩阵近似(采用核范数正则化)和非凸正则化低秩矩阵近似(采用非凸正则化函数)计算奇异值(图1)。图1中绿色点划线和黑色虚线分别表示纯净低秩矩阵和噪声矩阵的奇异值,可见当矩阵混叠随机噪声后其秩必然增加;图中蓝色虚线和红色实线分别为核范数正则化和非凸正则化低秩矩阵近似2种算法估算的奇异值,对比可见非凸正则化算法估算的奇异值与真实奇异值更为接近,估计出矩阵的秩与真实值相同。
图1
图1
核范数正则化与非凸正则化对比分析
Fig.1
Comparison of standard nuclear norm and nonconvex regularizations
2.2 地质模型与地震正演
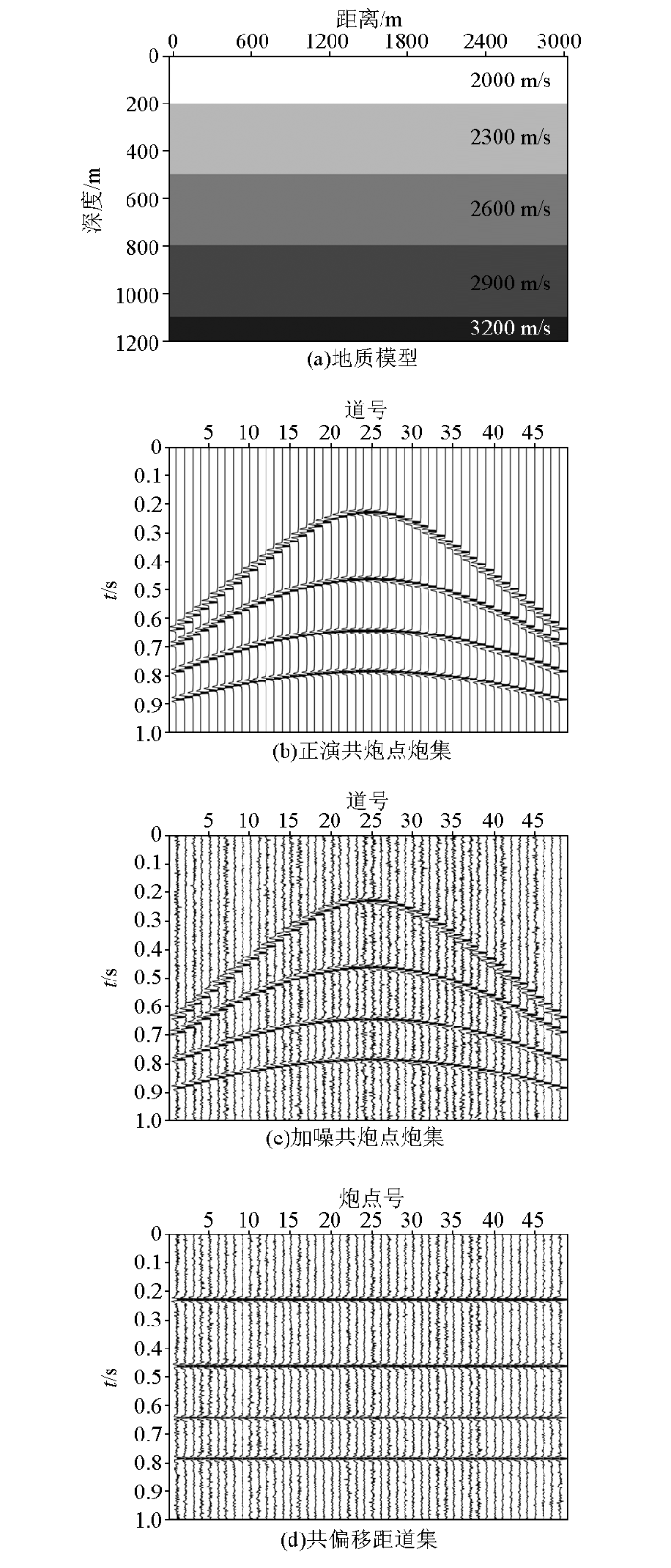
为了验证所提基于f-x域时频非凸正则化低秩矩阵近似的共偏移距道集去噪方法的有效性,建立如图2a所示的5层地质模型,地层速度分别为2 000、2 300、2 600、2 900和3 200 m/s,地层埋深分别为200、500、800和1 100 m。实验采用中间放炮、双边接收观测系统模拟地震采集,道间距和炮间距均为50 m,每炮48道接收,共激发48炮。图2b、c分别为第1炮正演共炮点道集和加噪炮集。为了增加实验难度,逐道加入不同幅度的随机噪声,含噪声地震道信噪比在1~10 dB范围随机变化。共炮点道集中反射波均为双曲线型同相轴,不同深度反射波倾角各不相同,因此,共炮点道集不能视为由线性同相轴叠加而成,不满足f-x域去噪假设前提。图2d为偏移距为50 m的共偏移距道集,道集中各地层反射波均为水平同相轴,满足f-x域去噪假设前提。因此,在共偏移距道集中执行f-x域去噪,其结果的精度必然提高。
图2
2.3 共偏移距道集去噪算法对比
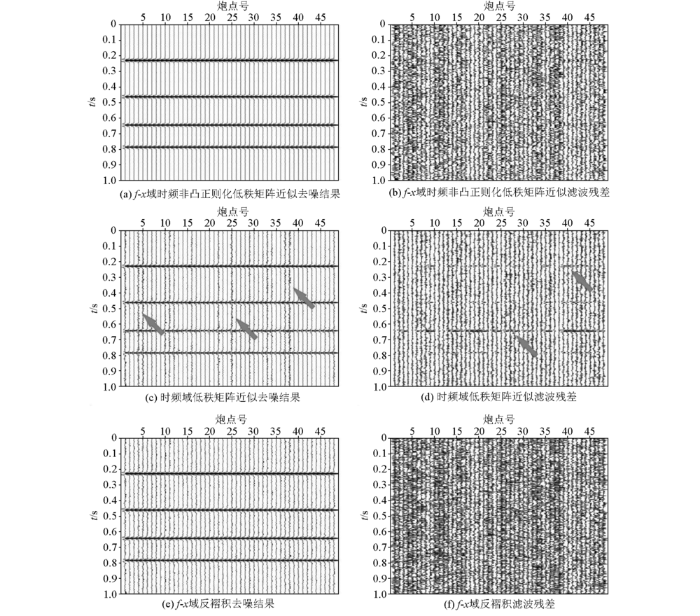
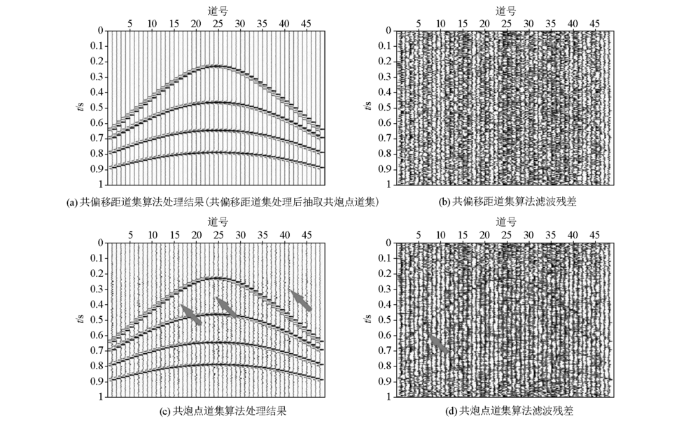
图3所示为地震道集抽取共偏移距道集,在共偏移距道集中试算f-x域时频非凸正则化低秩矩阵近似、时频域低秩矩阵近似和f-x域反褶积3种算法。f-x域时频非凸正则化低秩矩阵近似采用1.2节所述算法流程,去噪结果和滤波残差分别如图3a、b所示。与图2d所示的含噪共偏移距道集对比可以发现,处理后随机噪声得到压制,剖面信噪比提高,无明显残留随机噪声(图3a),残差剖面符合随机噪声分布规律,无连续同相轴泄露(图3b),说明f-x域时频非凸正则化低秩矩阵近似算法兼具良好的去噪能力和有效信号保持能力。图3c、d分别为时频域低秩矩阵近似算法去噪结果和滤波残差,该算法逐道处理各道地震数据,对单一地震道作广义S换后,再对时频谱做低秩矩阵近似计算。可以看出,处理后部分地震道残留随机噪声(如图3c中箭头所示),残差剖面存在连续同相轴(如图3d中箭头所示),说明单道算法不能有效利用信号的道间相干性,去噪能力和有效信号保持能力有限。图3e、f分别为f-x域反褶积去噪结果和滤波残差,共偏移距道集满足f-x域去噪的线性同相轴假设条件,该域中计算f-x域反褶积能够同时实现压制随机噪声和保持有效信号不被损害,残差剖面上无残留连续同相轴(图3f),但该算法去噪不彻底,处理结果中仍残留小幅度随机噪声(图3e)。通过对比可知,所提出的f-x域时频非凸正则化低秩矩阵近似具有明显优势。
图3
图3
共偏移距道集去噪算法对比
Fig.3
Denoised results and noise sections in the common offset gathers
图4
图4
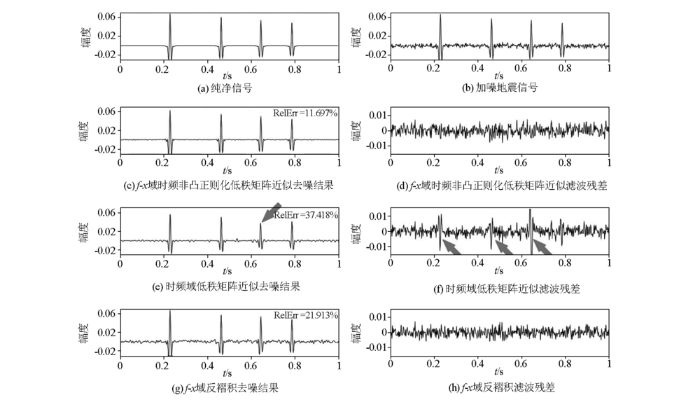
单道对比3种共偏移距道集去噪算法
Fig.4
Comparison of the three denoising algorithms in the common offset gathers with a single trace
2.4 共偏移距道集和共炮点道集处理结果对比
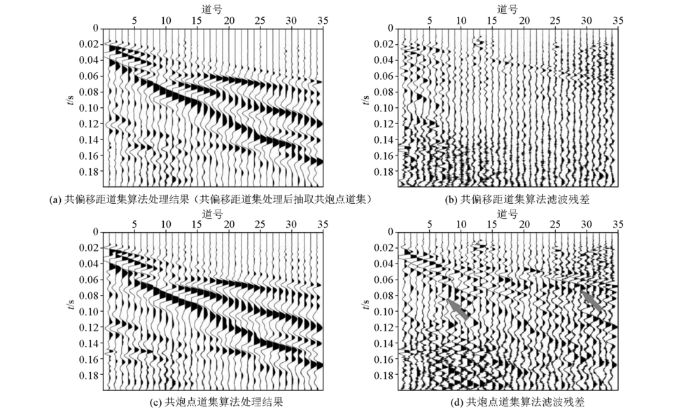
将图3a所示共偏移距道集f-x域时频非凸正则化低秩矩阵近似算法处理结果反变换回共炮点道集。在共炮点道集对比共偏移距道集算法处理结果和滤波残差如图5a、b所示,同样可以说明共偏移距道集近似满足f-x域去噪算法的线性同相轴假设,处理后随机噪声得到压制,且有效信号保持良好。为了进一步说明共偏移距道集算法的优势,在共炮点道集中对f-x域时频非凸正则化低秩矩阵近似算法进行试算。去噪结果和滤波残差分别如图5c、d所示,可以发现,时频稀疏低秩近似算法虽然具有较好的去噪能力,但因共炮点道集不满足f-x域去噪算法假设前提,两者结合不能发挥各自算法优势,处理后剖面仍残留随机噪声(图5c),有效信号保持能力不足,残差剖面泄露连续同相轴。对比结果说明,共偏移距道集近似满足f-x域去噪算法的线性同相轴假设,在该域中进行去噪处理能够提高算法的处理效果。
图5
图5
共偏移距道集和共炮点道集处理结果对比
Fig.5
Comparison of denoising results of two domains in common shot gathers
3 应用实例
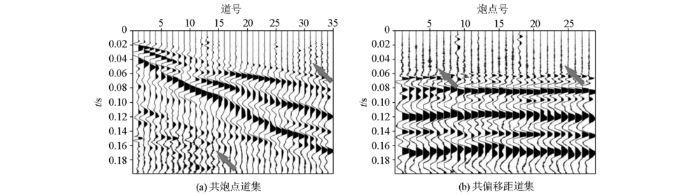
利用某区实际地震数据,验证所提f-x域时频非凸正则化低秩矩阵近似算法的有效性。该数据震源为30.06来复枪,井深25 cm;测量仪器采用L40A 100 Hz检波器和BISON 24096型96道工程地震仪。图6a为第1001炮共炮点道集,可以看出剖面受随机噪声干扰严重(图中箭头所示),同时,该数据还受面波和低频干扰污染,共炮点道集中,直达波和面波具有倾斜同相轴特征,反射波为双曲线同相轴,不满足f-x域去噪的线性同相轴假设前提。图6b为偏移距为15 m的共偏移距道集,剖面表现为平缓的同相轴结构特征,各波型均为近似水平的同相轴。因此,共偏移距道集基本满足f-x域去噪的线性同相轴假设前提,在该域中进行去噪处理,能够发挥去噪算法的优势。
图6
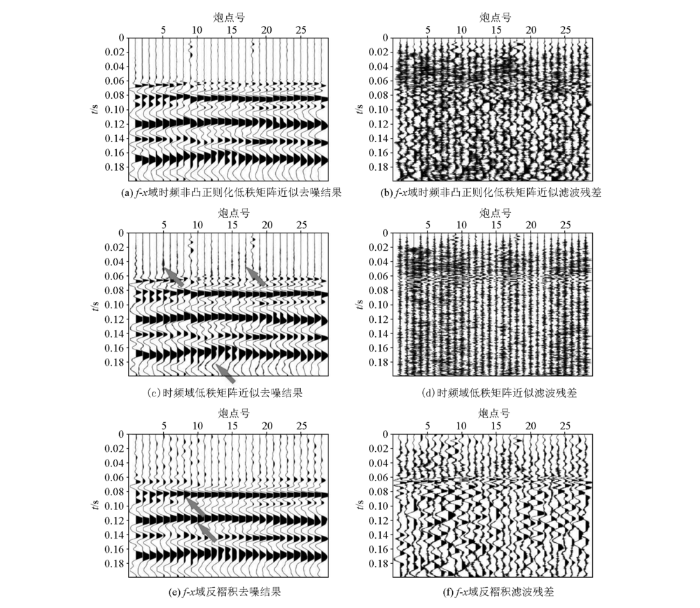
抽取共偏移距道集试算3种算法(图7)。图7a、b分别为f-x域时频非凸正则化低秩矩阵近似算法去噪结果和滤波残差,与原始共偏移距道集(图6b)对比可以发现,该算法能够有效压制随机噪声和低频干扰,去噪后剖面信噪比提高,无残留随机噪声(图7a);且该算法在去噪同时未损害有效信号,残差剖面无连续同相轴泄露(图7b),说明该算法能够结合f-x域去噪与时频域低秩矩阵近似2种算法的优势,提高去噪和有效信号保持能力。图7c、d为时频域低秩矩阵近似算法去噪结果和滤波残差,结果显示随机噪声得到一定压制,但剖面仍残留小幅度随机噪声(如图7c中箭头所示),残差剖面符合随机噪声分布规律(图7d),其原因是传统时频域低秩矩阵近似算法处理单道地震信号,没有利用信号道间相干性。图7e、f分别为f-x域反褶积去噪结果和滤波残差,该算法能够有效压制随机噪声,但有效信号保持能力不足,处理后同相轴结构发生改变(如图7e中箭头所示),其原因是f-x域反褶积要求待处理信号为平稳信号,而实际地震信号为非平稳信号。通过实际数据试算对比,进一步验证了所提算法能够有效压制随机噪声,同时保持有效信号不被破坏。
图7
图7
实际数据共偏移距道集去噪算法对比
Fig.7
Comparison of denoising algovithms for common offset gathers of the field data
图8
图8
实际数据共偏移距道集和共炮点道集处理结果对比
Fig.8
Comparison of the field data’s denoising results of the two domains in common shot gathers
4 结论
1)f-x域去噪算法假设地震剖面由线性同相轴叠加而成,共炮点道集和CMP道集中直达波、折射波和面波为倾斜同相轴,反射波为双曲线同相轴,且不同地层各波型同相轴倾角不同,甚至互相干涉叠加。地震道集不能视为由线性同相轴叠加而成。当处理共炮点道集和CMP道集时,f-x域去噪算法会损害倾斜(尤其是陡倾)同相轴。而共偏移距道集具有平缓甚至接近水平的同相轴结构,基本满足线性同相轴假设条件,在共偏移距道集道集中执行f-x域去噪能够提高算法性能。
2)f-x反褶积等f-x域去噪算法假设地震信号为平稳信号,而实际地震信号为非平稳信号,不满足算法假设条件,需要将非平稳信号去噪算法引入f-x域。时频分析是一种有效的非平稳信号分析方法,且时频域数据具有稀疏低秩特征。将时频稀疏低秩近似去噪引入f-x域,能够克服传统f-x域去噪算法的平稳信号假设条件。多道地震信号同时处理,能够利用信号道间相干性提高去噪能力。
3)正则项参数λ的选择会影响低秩矩阵近似算法的计算结果,λ的选择取决于信号的噪声情况,建议取
参考文献
改进的小波阈值法及其在地震数据降噪处理中的应用
[J].
The application of the improved wavelet threshold method to seismic data de-noising
[J].
三维边缘保持滤波方法在海上地震数据噪声压制中的应用研究——以东海某凹陷为例
[J].
The application of 3D edge-preserving de-noising methods based on structure oriented in a complex faults block:A case study of C oilfield in East China Sea
[J].
Random noise attenuation of 2D seismic data based on sparse low-rank estimation of the seismic signal
[J].DOI:10.1016/j.cageo.2019.104376 URL [本文引用: 4]
Random noise reduction
[C]//
Random noise attenuation by f-x empirical-mode decomposition predictive filtering
[J].
Lateral prediction for noise attenuation by t-x and f-x techniques
[J].DOI:10.1190/1.1443920 URL [本文引用: 1]
Random and coherent noise attenuation by empirical mode decomposition
[J].
一种集成经验模态分解的样本熵阈值微地震信号降噪方法
[J].
A denoising method for microseismic signal based on the ensemble empirical mode decomposition of sample entropy threshold
[J].
Seismic signal denoising using f-x variational mode decomposition
[J].DOI:10.1109/LGRS.2019.2948631 URL [本文引用: 2]
Seismic random noise attenuation using sparse low-rank estimation of the signal in the time-frequency domain
[J].
DOI:10.1109/JSTARS.2019.2906360
[本文引用: 3]

Suppression of random noise in seismic data is a challenging preprocessing task. We propose a new denoising method, which includes the following steps. First, the short-time Fourier transform of the noisy seismic signal is computed. Then, a sparse low-rank matrix is estimated based on solving a nonconvex penalty function. A threshold function associated with the penalty function based on the optimal shrinkage of the singular values is employed to solve the penalty function. The nonconvex penalty function induces sparsity to the time-frequency (TF) matrix, and the optimal shrinkage optimizes the thresholding function to extract the singular values. Finally, the seismic signal is synthesized based on the estimated sparse low-rank TF matrix. We evaluate the proposed method by using a synthetic seismic section contaminated by random noise and a prestack real seismic dataset from an oil field in the southwest of Iran. The synchrosqueezed wavelet transform-OptShrink, synchrosqueezed wavelet transform-Go Decomposition, and classical f - x singular spectrum analysismethods are selected to compare the performance of the proposed method. The results indicate the superiority of the proposed method compared to the other state-of-the-art noise suppression methods.
Seismic data denoising based on mixed time-frequency methods
[J].DOI:10.1007/s11770-011-0300-6 URL [本文引用: 2]
Sparse time-frequency representation for seismic noise reduction using low-rank and sparse decomposition
[J].
Seismic denoising using curvelet analysis
[J].DOI:10.1016/j.physa.2011.04.009 URL [本文引用: 1]
Sparse bayesian learning-based seismic denoise by using physical wavelet as basis functions
[J].DOI:10.1109/LGRS.2017.2745564 URL [本文引用: 1]
A robust random noise suppression method for seismic data using sparse low-rank estimation in the time-frequency domain
[J].DOI:10.1109/ACCESS.2020.3028145 URL [本文引用: 2]
Parallel matrix factorization algorithm and its application to 5D seismic reconstruction and denoising
[J].
A tensor higher-order singular value decomposition for prestack seismic data noise reduction and interpolation
[J].
Seismic interference noise attenuation by convolutional neural network based on training data generation
[J].DOI:10.1109/LGRS.2020.2982323 URL [本文引用: 1]
Deep learning for denoising
[J].
Unsupervised seismic random noise attenuation based on deep convolutional neural network
[J].
DOI:10.1109/ACCESS.2019.2959238
[本文引用: 1]

Random noise attenuation is one of the most essential steps in seismic signal processing. We propose a novel approach to attenuate seismic random noise based on deep convolutional neural network (CNN) in an unsupervised learning manner. First, normalization and patch sampling are required to build training dataset and test dataset from raw noisy data. Instead of using synthetic noise-free data or denoised results via conventional methods as training labels, we adopt only the training set constructed from the raw noisy data as the input and design a robust deep CNN that just relies on the noisy input to learn the hidden features. The cross-entropy is chosen as the error criterion for establishing the cost function, which is minimized by the back-propagation algorithm to obtain the optimized parameters of the network. Then, we can reconstruct all patches of the test dataset via the optimized CNN. After patching processing and inverse normalization, the final denoised result can be obtained from reconstructed patches. Experimental tests on synthetic and real data demonstrate the effectiveness and superiority of the proposed method compared with state-of-the-art denoising methods.
超参数对GRU-CNN混合深度学习弹性阻抗反演影响研究
[J].
A study of the effect of hyperparameters GRU-CNN hybrid deep learning EI inversion
[J].
Self-supervised learning for seismic data reconstruction and denoising
[J].
Generative adversarial networks in seismic data processing
[M]//
Simultaneous seismic data denoising and reconstruction via multichannel singular spectrum analysis
[J].
Empirical low-rank approximation for seismic noise attenuation
[J].DOI:10.1109/TGRS.2017.2698342 URL [本文引用: 1]
A singular value thresholding algorithm for matrix completion
[J].DOI:10.1137/080738970 URL [本文引用: 1]
Enhanced low-rank matrix approximation
[J].DOI:10.1109/LSP.2016.2535227 URL [本文引用: 3]
Generalized singular value thresholding
[J].
Nonconvex splitting for regularized low-rank+sparse decomposition
[J].DOI:10.1109/TSP.2012.2208955 URL [本文引用: 2]
Weighted nuclear norm minimization with application to image denoising
[C]//
Transformed schatten-1 iterative thresholding algorithms for low rank matrix completion
[J].
De-noising by soft-thresholding
[J].DOI:10.1109/18.382009 URL [本文引用: 1]
Probing the pareto frontier for basis pursuit solutions
[J].DOI:10.1137/080714488 URL [本文引用: 1]