黏声波高阶傅里叶有限差分法参数优化成像

doi:10.11720/wtyht.2022.1419

黏声波高阶傅里叶有限差分法参数优化成像

肖世鹏^,, 熊高君, 袁梦雨, 毛明秋, 王胜艺, 韦增涛

成都理工大学地球物理学院,四川成都 610000

Parameter optimization and imaging of visco-acoustic media using high-order Fourier finite-difference method

XIAO Shi-Peng^,, XIONG Gao-Jun, YUAN Meng-Yu, MAO Ming-Qiu, WANG Sheng-Yi, WEI Zeng-Tao

College of Geophysics, Chengdu University of Technology, Chengdu 610000,China

责任编辑: 叶佩

收稿日期: 2021-08-11 修回日期: 2022-05-18

基金资助:

四川省教育厅地震正演模拟项目(KZB029)

Received: 2021-08-11 Revised: 2022-05-18

作者简介 About authors

肖世鹏(1997-),男,在读硕士研究生,从事地震勘探方面的研究工作。Email:Xiao_Shipeng@163.com

摘要

黏声波高阶傅里叶有限差分法数值模拟可以更精准地反映具有大地吸收效应的高倾角地层地震响应,它能适应任意横向速度变化并压制大倾角处有限差分法出现的频散现象及背景噪声。高倾角地层偏移精度取决于差分算子常系数确定及阶数的求取。本文使用梯度下降法对傅里叶有限差分算子中的高阶有限差分校正项进行了优化,根据相对误差和约束系数优化结果,在不提高方程阶次的情况下达到更高阶方程的逼近效果,并将其扩展到黏声介质。通过设计的模型算例可以得出,文中方法适应具有吸收衰减效应的强空间变速介质的正演模拟,且具有较高的计算精度和计算效率,能对复杂地质构造进行准确的地震数值模拟。

关键词： 傅里叶有限差分法; 黏声波介质; 地震数值模拟; 偏移; 衰减

Abstract

The numerical simulation of visco-acoustic media using the high-order Fourier finite-difference method can reflect the seismic response of high-dip strata with geo-absorption effects more accurately.It can adapt to any lateral speed changes and suppress the dispersion and background noise at large dip angles caused by the finite-difference method.The migration precision of the high-dip strata depends on the determination of the constant coefficient of the difference operator and the calculation of the order.In this study,the gradient descent method was used to optimize the high-order finite-difference correction item in the Fourier finite-difference operator.According to the optimization results of the relative errors and constraint coefficients,the approximation effects of higher-order equations were achieved without increasing the order of the equation and then were expanded to viscoelastic media.Using the designed model,it can be concluded that the proposed method is applicable to the forward simulation of the strong spatial variable speed media with absorption and attenuation effects and has high calculation accuracy and efficiency.Accurate seismic numerical simulation of complex geological structures further confirmed the effectiveness of this method.

Keywords： Fourier finite difference method; visco-acoustic media; seismic numerical simulation; migration; attenuation

PDF (3287KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

肖世鹏, 熊高君, 袁梦雨, 毛明秋, 王胜艺, 韦增涛. 黏声波高阶傅里叶有限差分法参数优化成像[J]. 物探与化探, 2022, 46(5): 1207-1213 doi:10.11720/wtyht.2022.1419

XIAO Shi-Peng, XIONG Gao-Jun, YUAN Meng-Yu, MAO Ming-Qiu, WANG Sheng-Yi, WEI Zeng-Tao. Parameter optimization and imaging of visco-acoustic media using high-order Fourier finite-difference method[J]. Geophysical and Geochemical Exploration, 2022, 46(5): 1207-1213 doi:10.11720/wtyht.2022.1419

0 引言

目前的理论研究和实际观测表明地球介质普遍存在非完全弹性特征,介质的黏滞效应会显著影响地震波的动力学特征,包括波性改造、振幅衰减、频率降低等。这种大地吸收效应主要与岩石岩性、含流体性质、饱和度以及渗透率等有关,也是造成高频成分衰减的主要原因之一^[1-2],针对不同衰减理论也有着不同的补偿方法^[3⇓-5]。黏弹性地层对地震波的吸收效应直接导致了地震记录中深层信息的模糊不清,地震资料分辨率的降低,并间接影响到深层地震数据的处理效果^[6]。因此通过引入品质因子和复值速度来考虑实际地层的衰减特性进行黏声波数值模拟,研究地震波传播规律过程并分析衰减特征,具有一定的实际意义^[7]。

自Stocks首次研究黏弹性介质及其地震波传播以来^[8],出现了许多描述黏弹性介质的数学模型,主要包含Kelvin-Voigt模型、Maxwell模型、标准线性模型等^[9]。Auld在1990年指出无论是一维空间还是三维空间的弹性介质和黏弹性介质,二者之间的本构方程和弹性模量都遵循对应规则。而Kelvin-Voigt模型对地下介质的描述既简单又较为符合地下的实际情况。

黏声波介质相较完全弹性介质引入了波的衰减和频散,导致地震子波发生畸变^[10-11],因此在数值模拟方法中受到了较多的限制^[12],射线追踪法只能保持波的运动学特征,不适于模拟衰减和频散效应;波动方程法能全面反映地震波的运动学和动力学特征,模拟精度高^[13]。波动方程法又分为有限差分法、有限元法、伪谱法和相移法。其中相移法具有简单、快速、对地层倾角无限制好等优点^[14],且在频率—波数域进行更易于引入吸收衰减,但当速度有横向变化时,就只能得到近似的正演结果^[15]。Stoffa等在相移法的基础上引入背景速度概念,在频率—空间域增加误差校正项,提出分步傅里叶法(SSF)能适应更强的速度横向变化^[16];Ristow等提出了傅里叶有限差分法(FFD),该方法在SSF的基础上增加了有限差分补偿项^[17];张金海等将FFD法推广到了黏声波介质的正演领域^[15]。

高阶傅里叶有限差分法有着结合相移法的精准和有限差分法能适应速度横向变化的优点。本文用Kelvin-Voigt模型构建黏声波方程,使用梯度下降法对傅里叶有限差分算子中的有限差分项进行了全局参数优化,在不提高方程阶次的情况下达到更高阶方程的逼近效果,并用该方法所求近似解对复杂模型的零炮检距地震记录进行了数值模拟。

1 方法原理

1.1 傅里叶有限差分

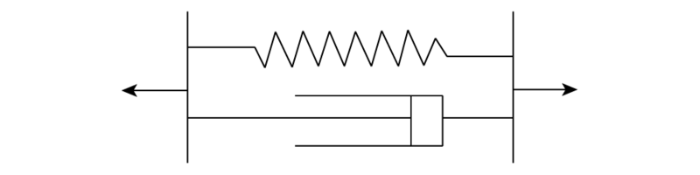
Kelvin(开尔文)黏弹性介质单元体是由一个弹性单元与一个黏性单元体并联组成^[18]。三维空间时,介质中的每个体积元就是一个Kelvin单元体,并且在立体空间与其他单元空间相互联结在一起。如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 开尔文模型

Fig.1 Kelvin model

频率空间域的二维单程波延拓方程为^[19]:

(1)

P (x, z_{n + 1}, ω) = P (x, z_{n}, ω) e x p (i k_{z} Δ_{z}),

式中:P(x,z,ω)为频率空间域二维地震波场;ω为频率;(x,z)为二维剖面的坐标;k_z为波场延拓算子;Δ_z为深度上的步长。在已知黏弹性介质中相速度V(ω)和品质因子Q的情况下,可以完成黏弹性介质的波场延拓和偏移成像^[8]。

(2)

k (ω) = \frac{ω}{V (ω)} \approx k_{e l a s} (1 - i \frac{1}{2 Q}) = \frac{ω}{V} (1 + i \frac{1}{2 Q}),

式中:k_elas=ω/V,其中V近似为均匀弹性各向同性介质中波的相速度;Q为品质因子。将复波数k(ω)代入式(1),进行单程波分解,并利用分裂算法把高阶近似方程分解为N-1个(N为高阶方程的阶数)二阶串联方程,可极大程度地减少计算量^[20]。将其中的根式进行泰勒展开得黏弹性介质中向下延拓算子k_z。

(3)

\begin{array}{l} k_{z} = k_{z}^{0} + ω Δ s + \frac{ω}{V} (1 - i \frac{1}{2 Q}) (1 - p) \times \\ \overset{N}{\sum_{n = 1}} \frac{a_{n} \frac{V^{2}}{ω^{2}} \frac{\partial^{2}}{\partial x^{2}}}{1 + b_{n} (1 + p + p^{2}) \frac{V^{2}}{ω^{2}} {(1 - i \frac{1}{2 Q})}^{- 2} \frac{\partial^{2}}{\partial x^{2}}}, \end{array}

式中: $k_{z}^{0}$ = $\sqrt{\frac{ω^{2}}{c^{2}} {(1 - i \frac{1}{2 Q})}^{2} + \frac{\partial^{2}}{\partial x^{2}}}$ ;c为背景速度,满足c≤V(x,z),本文选取c=min(V_z);p=v/Va_n,是背景速度与当前速度的速度比;a_n、b_n为高阶有限差分算子;与Muir展开法对比,即N=2,a₁=2,b₁=0时,获得黏弹性介质的15°方程;N=2,a₁=2,b₁=0.5时获得45°方程^[7]。

考虑式(3),将k_z按照多参量全局优化的方法拓展为:

(4)

\begin{array}{l} k_{z} = k_{z}^{0} + ω Δ s + \frac{ω}{V} (1 - i \frac{1}{2 Q}) (1 - p) \times \\ \overset{N}{\sum_{n = 1}} \frac{a_{n} \frac{V^{2}}{ω^{2}} \frac{\partial^{2}}{\partial x^{2}}}{1 + (b_{n} + c_{n} p + d_{n} p^{2}) \frac{V^{2}}{ω^{2}} {(1 - i \frac{1}{2 Q})}^{- 2} \frac{\partial^{2}}{\partial x^{2}}} 。 \end{array}

式(4)为本文的高阶多参量优化傅里叶有限差分算子,其中(a_n,b_n,c_n,d_n)为待定系数。本文采用梯度优化法确定。

1.2 系数优化方法

为确定式(4)中待定系数的值,常规优化方法仅考虑速度的对比度^[21]。本文增加多阶次速度对比度系数并考虑当前频率及延拓步长等参量的影响,选取单平方根算子k_z与真实值的误差为目标函数^[22],用多元非线性梯度下降法对待定系数做全局优化求解。

在Kelvin-Voigt模型中用传播角θ表示水平波数和垂直波数^[17],即 $k_{x}^{2}$ = $\frac{ω^{2}}{V^{2}} {(1 - i \frac{1}{2 Q})}^{2}$ sin²θ, $k_{z}^{2}$ = $\frac{ω^{2}}{V^{2}} {(1 - i \frac{1}{2 Q})}^{2}$ cos²θ,则式(4)的损失函数为

(5)

\begin{array}{l} E_{2 N} = c o s^{2} θ - \sqrt{\frac{1}{p^{2}} - s i n^{2} θ} - (1 - \frac{1}{p}) + \\ (1 - p) \overset{N}{\sum_{n = 1}} \frac{a_{n} s i n^{2} θ}{1 - (b_{n} + c_{n} p + d_{n} p^{2}) s i n^{2} θ} 。 \end{array}

对a_n、b_n、c_n及d_n估计的优化过程是使积分最小化的过程,所求残差应为最小值,即

(6)

J = \int_{0}^{Φ} E_{2 N}^{2} (θ) d θ,

上式中J为近似解与精确解的误差总和;Φ为波传播的最大角度,J与精确解的比称为相对误差^[23]。优化系数如表1所列;优化结果如图2。

表1 系数优化

Table 1 Coefficient optimization

N	a_n	b_n	c_n	d_n
N=1	0.4078	0.4877	0.2539	0.1519
N=2	0.3522	-0.6803	-0.0696	0.0942
	0.2400	0.7290	-0.0605	0.2647

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

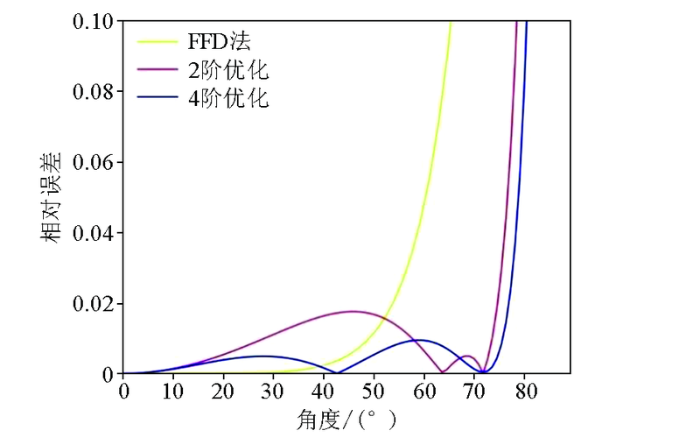
图2 相对误差随传播角变化曲线

(p=c/v=0.5)

Fig.2 Relative error changes with propagation angle

(p=c/v=0.5)

由图2可以看出,2阶优化相比FFD法有着低角度的误差,但在70°多出一个过零点;4阶优化平衡了低角度的误差。

1.3 偏移算法

频率空间域的单程波波场延拓公式为:

(7)

\frac{\partial P (x, z, ω)}{\partial z} = i k_{z} P (x, z, ω),

其中k_z如式(3)所示。利用绝对稳定的Crank-Nicolson差分格式^[24],式(7)可化简为:

(8)

[\begin{array}{l} * & a & 0 & 0 & 0 \\ a & 1 - 2 a & a & 0 & 0 \\ 0 & a & 1 - 2 a & a & 0 \\ 0 & 0 & a & 1 - 2 a & a \\ 0 & 0 & 0 & a & * \end{array}] [\begin{array}{l} p_{z}^{1} \\ p_{z}^{2} \\ p_{z}^{3} \\ p_{z}^{4} \\ p_{z}^{5} \end{array}] = [\begin{array}{l} p_{z + 1}^{1} \\ p_{z + 1}^{2} \\ p_{z + 1}^{3} \\ p_{z + 1}^{4} \\ p_{z + 1}^{5} \end{array}]

上式中a为将所有常数缩减为的系数;“*”号表示的值是可调节的,并按旁侧边界条件来调节。矩阵(8)是一个三对角复数矩阵^[25]。

延拓完成后,对频率空间域计算结果进行傅里叶反变换:

(9)

p (x, z, t) = \int_{- \infty}^{\infty} p (x, z, ω) e^{i ω t} d ω,

根据t=0成像得:

(10)

\begin{array}{r} p (x, z, t = 0) & = \int_{- \infty}^{\infty} p (x, z, ω) d ω \\ = \overset{n / 2}{\sum_{- n / 2}} p (x, z, n Δ ω) Δ ω \\ = \overset{n / 2}{\sum_{- n / 2}} p (x, z, n Δ ω) \\ = \sum_{ω} p (x, z, ω), \end{array}

(11)

p (x, z + Δ z, t = 0) = \sum_{ω} p (x, z + Δ z, ω) 。

上述延拓过程是对每一个ω进行的。每步延拓之后对每一个ω求和,即得偏移结果。

2 模型试算

为验证黏弹性介质高角度傅里叶有限差分正演模拟的正确性和模拟效果,本文分别进行了点绕射模型和Marmousi模型的数值模拟实验。

2.1 点绕射模型

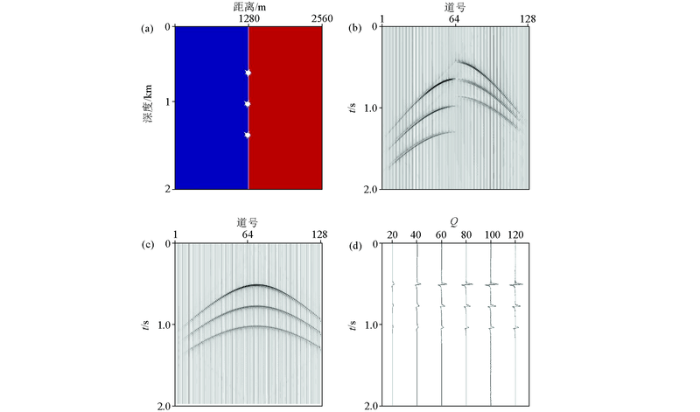
图3是分别用相移法和傅里叶有限差分法正演的零炮检距地震记录。点绕射模型由强烈横向变速的简单均匀介质组成,速度从左至右分别为4 000 m/s、6 000 m/s;纵横向采样点数为100×128;纵横向采样间隔均为20 m;3个模拟点震源分别位于(33,64)、(50,64)和(66,64)处,记录网格长256,采样间隔4 ms。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 点绕射模型

a—均匀介质中的点绕射模型;b—四阶有限差分算子优化正演;c—相移法正演;d—不同Q值波场变化对比

Fig.3 Point diffraction model

a—point diffraction model;b—forward results of fourth-order optimized;c—phase shift method forward;d—comparison of different Q values

从图中可以明显看出:①黏滞性对振幅、频带和波性都有着明显的改造作用,随着传播时间的增加,子波的主峰振幅和高频成分都出现明显的衰减趋势,且Q值越小,地下黏滞性特征越明显,如图3d。②由于常规的频率—波数域相移法外推算子只计算水平界面的平均速度,考虑放射点在垂向上的移动,故对于横向速度有变化的地层不敏感,水平速度界面在零炮检距模拟记录上形态将保持不变,如图3c,而傅里叶有限差分法兼顾相移法成像精度高、稳定性好和计算速度快之外还能适应速度的纵横向任意变化,并在时间剖面上正确成像。

2.2 层状模型

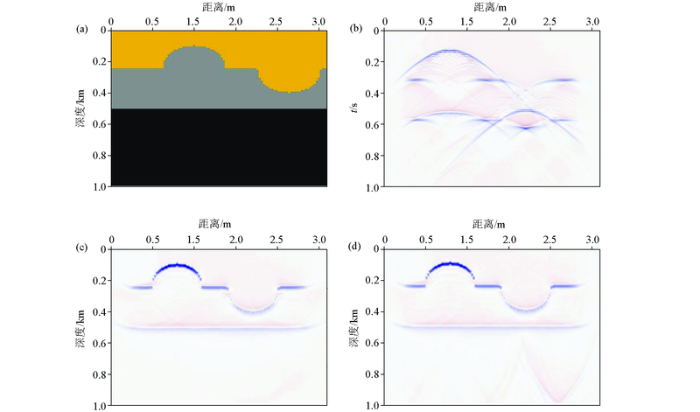
图4为简单层状模型零炮检距合成地震记录。其模型是由背斜构造、向斜构造及一个水平界面组成,3层介质速度由上至下分别为3 000 m/s、4 000 m/s、5 000 m/s;纵、横向采样点数为100×128;纵横向采样间隔皆为20 m;时间采样间隔为4 ms;记录长度为1 024 ms。在记录图4b上均可以清晰地看到背斜和向斜构造产生的“蝴蝶结”形地震反射特征。由于背斜顶部凸界面的反射存在发散现象,如图4b,分配到单位面积上的波的能量会减弱。凸度越大,埋藏越深,射线发散越严重,地震波的振幅也越小^[26]。如图4a所示的速度模型中,凹界面的向斜模型曲率中心刚好在地层下,这时射线发生交叉,同相轴出现回转,最凹点处波的旅行路径比两边短,因此在时间剖面上将出现凸起,如图4b,向斜两翼的反射特征会左右颠倒,形成回转波,在实际为向斜的部位深处又出现一个“背斜”。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 层状模型

a—黏弹性介质速度模型;b—系数优化后傅里叶有限差分正演结果;c—傅里叶有限差分偏移结果;d—优化系数后4阶傅里叶有限差分偏移结果

Fig.4 Layered model

a—velocity model of viscoclastic media;b—parameter optimization forward results;c—migration results;d—migration results of fourthorder optimized

图4c为常规傅里叶有限差分法的偏移结果,图中因回转波所造成的“背斜”消失,背斜构造及向斜构造都得到完全归位,这表明常规FFD法能很好地解决横向速度变化不大及频散现象的问题。图4d是优化系数后的傅里叶有限差分法偏移结果,与图4c相比,背斜构造及向斜构造完全归位证明了该方法的正确性,成像结果更干净,佐证了该方法的优越性。两种偏移方法所得结果基本相同,这和模型的复杂程度有关,简单的层状模型横向倾角变化低,属于常规FFD法的倾角包含范围,故复杂模型的成像结果能更好地体现两种方法的差异性。

2.3 Marmousi模型

SEG的Marmousi模型存在背斜、尖灭和断层等复杂地质构造和较强的横向速度变化,是数值模拟中广泛使用的标准模型之一。本文将使用该模型验证黏弹性介质高阶傅里叶有限差分法对较强横向速度变化和Q值变化的适应能力。

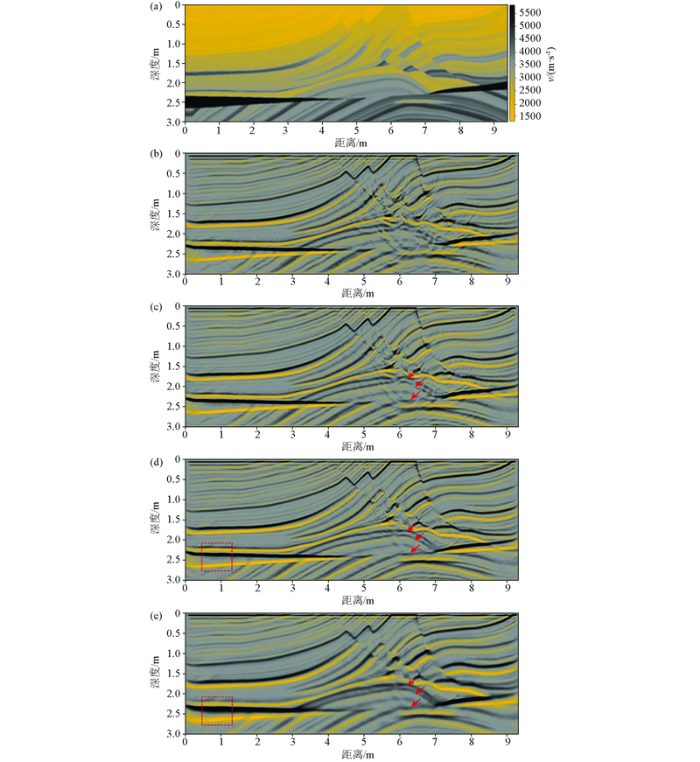
图5是用不同方法对Marmousi模型进行实验和对比。速度模型网格点数为300×941;网格间距10 m;模型最小相速度1 000 m/s,最大相速度2 600 m/s,其背景参考为每层最小相速度;所用零炮检距记录共941道,每道1 022个时间采样点,采样间隔为4 ms。由图5b可以看出,常规二阶傅里叶有限差分法可以较为准确地对地下界面进行简单成像,如地层分界面及隆起进行成像,但对模型复杂构造及陡倾角断层存在较大误差,图5c为本文二阶优化法(N=1),其计算效率与常规二阶傅里叶有限差分法相当,在不提高方程阶次的情况下兼顾陡倾角误差,明显提高了成像信噪比。图5d为本文四阶优化法(N=2),偏移结果具有较高的信噪比,各复杂构造边界清晰,反射界面清晰,陡倾角断层及下伏隆起界面同相轴连续且几乎不存在归位误差(如图5c和图5d箭头所示),成像精度进一步提高。图5e为本文四阶优化法在纵向变Q值介质中的应用效果,Q值由浅至深取20~100,对比完全弹性介质可知,其振幅和相位特征只有在传播时间短且距地面距离较近处的部位才较吻合,表明黏滞吸收作用会对地震波波性、相位及振幅等产生很大影响,随着传播距离的增加,波场高频成分明显衰减,波性逐渐变宽、能量逐渐变弱(如图5d和图5e红框所示),这些规律直接反映了黏滞性吸收的基本特征及本文方法在黏声介质中的应用效果。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 不同方法的Marmousi模型成像结果对比

a—Maimousi速度模型;b—2阶FFD正演(Q=∞);c—2阶优化FFD正演(Q=∞);d—4阶优化FFD正演(Q=∞);e—4阶优化FFD正演(变Q介质)

Fig.5 Marmousi model imaging by different mothods

a—Marmousi velocity model;b—second-order FFD forward(Q=∞);c—second-order optimized FFD forward(Q=∞);d—fourth-order optimized FFD forward(Q=∞);e—fourth-order optimized FFD forward(changing Q value)

3 结论

本文使用的黏声波高阶傅里叶有限差分法是一种混合域的计算方法,其波场外推算子由相移项、折射项(时移项)和有限差分项组成。用梯度法近似确定的差分项外推算子,可在阶数不变的情况下求解高阶非线性方程组,适应强空间变速介质。数值实验的对比分析表明,优化后的黏声波高阶傅里叶有限差分法相比常规FFD法及低阶优化的FFD法有着频散低、模拟结果反射特征清楚、复杂地质结构更精确成像等优点。并通过黏声模型模拟结果对比,充分说明了优化后黏声波高阶傅里叶有限差分法成像的优越性。本文方法可以处理二维复杂地质构造中波传播问题,一般情况下二阶优化差分项已达到成像精度要求,四阶有限差分项反而会影响计算效率,且在三维模型中差分项存在的双向分裂会引起方位各向异性误差,直接影响成像精度。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

俞寿朋

. 高分辨率地震勘探[M]. 北京: 石油工业出版社,1993.